Spatio-temporal modeling of chronic PM10 exposure for the Nurses’ Health Study

Abstract

Chronic epidemiological studies of airborne particulate matter (PM) have typically characterized the chronic PM exposures of their study populations using city- or countywide ambient concentrations, which limit the studies to areas where nearby monitoring data are available and which ignore within-city spatial gradients in ambient PM concentrations. To provide more spatially refined and precise chronic exposure measures, we used a Geographic Information System (GIS)-based spatial smoothing model to predict monthly outdoor PM₁₀ concentrations in the northeastern and midwestern United States. This model included monthly smooth spatial terms and smooth regression terms of GIS-derived and meteorological predictors. Using cross-validation and other pre-specified selection criteria, terms for distance to road by road class, urban land use, block group and county population density, point- and area-source PM₁₀ emissions, elevation, wind speed, and precipitation were found to be important determinants of PM₁₀ concentrations and were included in the final model. Final model performance was strong (cross-validation R²=0.62), with little bias (−0.4 μg m⁻³) and high precision (6.4 μg m⁻³). The final model (with monthly spatial terms) performed better than a model with seasonal spatial terms (cross-validation R²=0.54). The addition of GIS-derived and meteorological predictors improved predictive performance over spatial smoothing (cross-validation R²=0.51) or inverse distance weighted interpolation (cross-validation R²=0.29) methods alone and increased the spatial resolution of predictions. The model performed well in both rural and urban areas, across seasons, and across the entire time period. The strong model performance demonstrates its suitability as a means to estimate individual-specific chronic PM₁₀ exposures for large populations.

1. Introduction

Previous epidemiological studies have shown that chronic exposure to airborne particulate matter (PM) is related to increased mortality as well as lung cancer, ischemic heart disease, dysrhythmias, heart failure, and cardiac arrest (Dockery et al. 1993; Pope et al. 1995; Abbey et al. 1999; Pope et al. 2002; Finkelstein et al. 2003; Pope et al. 2004). These health studies have typically characterized the chronic PM exposures of their study populations using city- or county-wide ambient concentration measurements, which generally do not account for within-city spatial gradients in ambient PM concentrations or changes in spatial gradients over time. This failure to account for within-city spatial gradients results in decreased statistical power and, depending on the nature of the resulting measurement error (Zeger et al. 2000), may cause the chronic health effects of particles to be underestimated. Recent studies suggest that within-community mortality effects may be as large as those found in between-community studies (Jerrett et al. 2005; Miller et al. 2007), though both of these studies derive exposure estimates from a single year, 2000, after or at the end of their follow-up periods and assume that spatial relationships in PM levels are constant back in time. Further, given their reliance on nearby monitors, health studies using city- or county-wide ambient concentration measurements are limited to areas where nearby monitoring data are available.

Within-city spatial gradients have been estimated using simple spatial interpolation of ambient PM concentrations. Wong et al. (2004) discussed and compared several of these methods, including inverse distance weighting (Schwartz 2001), nearest neighbor techniques (Schwartz and Zeger 1990; Stern et al. 1994; Vedal et al. 1998; Pope et al. 2004), moving window or “spatial averaging” techniques (Chestnut et al. 1991), and kriging. These methods, however, are limited by methodological restrictions that require assumptions regarding the form of the distance-weighting function and by the often sparse spatial distribution of air monitoring sites, which allows interpolation to capture only large-scale spatial gradients over most of the domain.

Other studies have used land use regression models (Briggs et al. 2000; Hoek et al. 2001; Brauer et al. 2003; Jerrett et al. 2007) to predict spatial variation based on land use variables. These models are often limited, as they generally include land use variables as categorical variables or as simple linear forms, and have generally not modeled residual spatial variability or allowed these residual spatial surfaces to vary over time.

To circumvent the limitations of the nearby community monitor and the simple spatial interpolation approaches, we used generalized additive models (GAMs) to predict monthly outdoor mass concentrations of airborne inhalable particles (aerodynamic diameter<10 μm; PM₁₀) across 13 states in the northeastern and midwestern United States (US). GAMs use semi-parametric methods to model non-linear, uni-dimensional and multi-dimensional functional forms using penalized splines (Hastie and Tibshirani 1990; Nychka 2000; Wood 2000, 2003, 2004), are computationally efficient, and avoid arbitrary assumptions regarding the distance-weighting function used to model spatial trends. In addition to spatial trends, we included site-specific land use information, obtained from a Geographic Information System (GIS), in our model to address issues related to data sparseness and to help explain fine-scale spatial variation in outdoor PM₁₀. By combining spatial smoothing with land use predictors, our model is able to account for within-city spatial gradients, larger-scale regional gradients, and temporal trends in PM₁₀ concentrations across a large area. The model was developed for use in a larger study of the chronic health impact of PM, as part of the Nurses’ Health Study, a large prospective cohort study of US women.

2. Methods

A model to predict outdoor PM₁₀ concentrations across the northeastern and midwestern United States was developed by combining spatial smoothing with GIS-derived and meteorological predictors. This model uses ambient PM₁₀ data measured as part of air quality and research monitoring networks together with meteorological variables from weather data bases and site characteristics from a GIS. An important feature of our model was the incorporation of space-time interactions at the monthly level. The model was developed in several stages, with preliminary models built to identify important covariates and explore temporal structure, a final model constructed to estimate PM₁₀ spatial surfaces, and “sensitivity” models constructed to examine the impact of model choices, assumptions, and GIS-derived covariates. Model performance was evaluated using cross-validation techniques.

2.1 Statistical Models

2.1.1 Modeling Approach

We modeled spatial and temporal trends in the PM₁₀ monitoring data using a generalized additive mixed model (GAMM) with bivariate penalized spline terms for space, and one-dimensional penalized spline terms for GIS-derived and meteorological predictors. Simpler, preliminary models were also constructed for preliminary covariate selection and to determine the appropriate spatio-temporal structure of the model, but for brevity only the final modeling approach is described below. The form of the model was:

$$\begin{array}{l}{y}_{i,t}=a+d_1(X_{i,1})+\dots +d_Q(X_{i,Q})+g(s_i)+f_1(Z_{i,t,1})+\dots +f_P(Z_{i,t,P})+(a_t+g_t(s_i))+b_i+e_{i,t};\\ b_i\sim N(0,{{\sigma }_b}^2);e_{i,t}\sim N(0,{{\sigma }_e}^2)\end{array}$$ 1)

where y_i,t is the natural-log transformed PM₁₀ monthly site average (for i=1,…, I, I = 922 monitoring sites in the study region and t=1, …, T, T = 180 monthly time periods from 1988 to 2002), and g_t(s_i) accounts for time-period-specific residual spatial variability whereas g(s_i) accounts for time-invariant spatial variability. Also, s_i is the projected spatial coordinate pair for the ith location, Z_i,t,1 through Z_i,t,P are time-varying covariates, and X_i,1 through X_i,Q are time-invariant GIS-derived covariates. We also note that b_i is essentially a site-specific random effect in this model, hence our characterization of the model as a GAMM.

However, for computational reasons, the model in Equation 1 was fit in two stages: the first to estimate site-specific terms adjusting for time-varying covariates and time-varying residual spatial variability and the second to model the site-specific terms using site-specific time-invariant GIS-derived predictors and by modeling residual time-invariant spatial variability. The form of the two-stage model was:

$$y_{i,t}=u_i+f_1(Z_{i,t,1})+\dots +f_P(Z_{i,t,P})+(a_t+g_t(s_i))+e_{i,t};e_{i,t}\sim N(0,{{\sigma }_{e,t}}^2)$$ 2)

$${\widehat{u}}_i=a+d_1(X_{i,1})+\dots +d_Q(X_{i,Q})+g(s_i)+b_i;b_i\sim N(0,{{\sigma }_b}^2)$$ 3)

where û_i is an estimated site-specific intercept that represents the adjusted long term mean at each location. Both stages of the model were fit using the gam() function in the mgcv library in R (2006). Because of the time-period-specific spatial terms, the first stage (Equation 2) was fit iteratively in a back-fitting arrangement (Hastie and Tibshirani 1990) with u_i + f₁()…f_p() first estimated jointly and a_t+g_t (s_i ) then estimated separately for each month, such that variability in the concentrations is parsed between the covariates and the residual spatial terms in the first stage. 15 iterations were used to allow all models to converge, and to provide consistency in comparing across models, though typically only eight to 12 iterations were necessary to achieve model convergence. We note that the error variance in the first stage (Equation 2), σ_e,t ², is indexed by t because we fit monthly smooth spatial terms (a_t+g_{t (}s_i ) in separate models. The second stage (Equation 3) was then fit to the estimated site-specific û_i terms using a separate call to the gam() function. Note that by separating the model (Equation 1) into two stages (Equations 2 and 3), the site-specific random effect, b_i, becomes a spatial residual. Also note that while observations in the first stage are specific to location and time, there are only I observations (i.e., one per site) available in the second stage. Predictions, exp(ŷ_i,t), were generated from the model by assigning the GIS-derived and meteorological predictors to prediction locations for each month following procedures described in the Geographic Data and Meteorological Data sections, and exponentiating back to the original scale.

The uncertainty in the model predictions (on the log-scale) was calculated by summing across the three sources of uncertainty: 1) time-varying spatial and regression functions, 2) time-invariant spatial and regression functions, and 3) residual site and time-varying variance components:

$$SE({\widehat{y}}_{i,t})=\sqrt{\sum _p\widehat{\mathit{Var}}({\widehat{f}}_p(Z_{i,t,p}))+\widehat{\mathit{Var}}[{\widehat{a}}_t+{\widehat{g}}_t(s_i)]+\widehat{\mathit{Var}}\left[(\widehat{a}+\widehat{g}(s_i))+\sum _q\widehat{d}(X_{i,q})\right]+{{\widehat{\sigma }}_b}^2+{{\widehat{\sigma }}_{e,t}}^2}$$

where the residual variances σ̂_e,t ² and σ̂_e,t ² account for prediction uncertainty in addition to contributions from functional uncertainty. Note that we assume σ̂ _e,t ² represents local heterogeneity and not instrument error. On the original scale, we estimate the prediction uncertainty using a Taylor series approximation, the delta method (Casella and Berger 2002):

$$\widehat{S}E(exp({\widehat{y}}_{i,t}))=\widehat{S}E({\widehat{y}}_{i,t})·exp({\widehat{y}}_{i,t})$$

For simplicity, this approach ignores the correlation of the uncertainties of the smooth terms. However, the prediction interval coverage suggests that the approach provides an adequate representation of uncertainty (results not shown). We also assessed the relative contribution of each of these sources of uncertainty to the total. Spatial variability of the estimated standard errors was assessed by plotting these values across the domain for selected time periods.

2.1.2 Covariate Selection

Covariates that we expected a priori to have a physical influence on PM₁₀ were considered for inclusion in the model. The potential covariates (as described below) were air temperature, sea-level adjusted barometric pressure (SLBP), wind speed, air stagnation, distance to nearest roadway by road class, population density at the block group, tract, and county level, point-source PM₁₀ emissions within 1 and 10 kilometer (km) buffers, point-source PM₁₀ emissions estimated using a kernel density function with neighborhoods of varying size, county-level area-source PM₁₀ emissions, urban land use, and elevation. Model covariates were chosen from this list based primarily on comparisons of model performance with alternative covariate sets (as assessed using the cross-validation R²), examination of the smooth functions of each term, and on statistical significance in the second stage of the model. In a limited number of cases, some covariates were also included in the model based on a priori scientific considerations.

Only those covariates that had a relationship with PM₁₀ concentrations consistent with known pollutant behavior and that improved predictive performance were kept in the model, with the aim of achieving a parsimonious model specification. Non-linearity in the covariate effects was accounted for using spline terms, with seven to eight degrees of freedom considered sufficient to describe the general shape of each function. In the event that a smooth term used more than approximately eight degrees of freedom, the smoothing parameter in the gam() function was used to reduce the degrees of freedom and force a smoother function across the range of the covariate to reduce the potential for overfitting to the data.

2.1.3 Model Comparisons

To evaluate simpler spatio-temporal structures, the performance of the final model with monthly spatial terms was compared to a model with the same covariates but with seasonal spatial terms:

$$y_{i,t}=u{}_i+f_1(Z_{i,t,1})+\dots +f_P(Z_{i,t,P})+(a_{\mathit{Season}}+g_{\mathit{Season}}(s_i))+h(t)+e_{i,t}$$ 4)

$${\widehat{u}}_i=a+d_1(X_{i,1})+\dots +d_Q(X_{i,Q})+g(s_i)+b_i$$ 5)

where Season has four levels (winter, spring, summer, and fall). Also, a smoothly-varying intercept, h(t), where t=1,…, T, T=180, was added to allow for monthly control for the mean across all sites.

To evaluate the contribution of GIS-derived and meteorological covariates to model performance, the final model was compared to a set of monthly GAMs with only spatial terms ( y_it = a_t + g_t (s_i) + e_it ). The final model was also compared to a conventional method of spatial interpolation, inverse distance weighting (IDW), with the inverse of the squared distance (1/d²) used as the weighting function. Finally, the final model was compared to a simplistic but commonly used approach of using the measured value from the nearest monitor within a radius of 50 km (31.1 miles).

2.1.4 Cross-validation

Cross-validation techniques were used both to inform decisions about covariate selection, as well as to compare among alternative model specifications. Cross-validation procedures followed those outlined in Efron and Gong (1983), where monitoring sites in the study region were selected at random and were assigned exclusively to one of 10 sets. Data from Sets One through Nine were held out in turn, with predictions generated at the locations of the held-out observations. The predictive ability of the model was determined using the squared correlation between the held-out values and the observations (referred to as the cross-validation R²), with both on the original scale rather than the log scale. Prediction errors were calculated by subtracting held-out observations from the model predictions. The potential for bias in model predictions was determined using the mean prediction error and the slopes from linear regression of the held-out values against the observations. The precision of model predictions was estimated by taking the square root of the mean of the squared prediction errors (RMSPE).

Since the covariate selection process involved fitting multiple candidate models to the same data, data from Set Ten was used to examine generalizability of the model to unmeasured locations, assessing whether the covariate selection process itself contributed to overfitting. To do this, data from Set Ten were used only to evaluate predictions from the final model.

2.2 Data

2.2.1 PM₁₀ Data

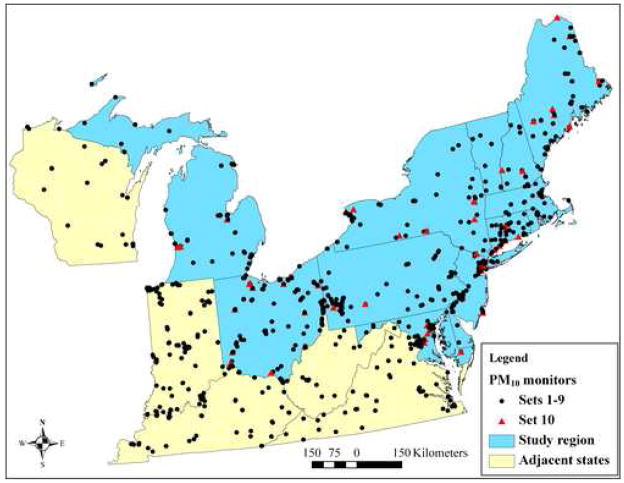
Outdoor PM₁₀ concentration data from 13 states in the northeast US, referred to as the study region, were included in this analysis (Figure 1). Data collected in states adjacent to this study region were also included in the spatio-temporal models to avoid boundary effects to the extent possible (Figure 1). PM₁₀ concentration data were obtained from the US Environmental Protection Agency (USEPA) on a DVD compiled for four USEPA-funded epidemiological studies from the USEPA’s Air Quality System (AQS), from the Visibility Information Exchange Web System (VIEWS) for the Interagency Monitoring of Protected Visual Environments (IMPROVE) network, and from Harvard research studies including the 24 Cities Study and 5 Cities Study (Spengler et al. 1996; Suh et al. 1997). Data from all sites that report to the AQS were included regardless of the stated primary monitoring objective, because excluding sites near point sources, for example, would have prevented the model from capturing these sources of spatial variability, and because monitoring objective information is not available for many AQS sites or for monitoring sites of other monitoring networks.

Figure 1.

Map of the northeast states showing the study region, states adjacent to the study region, and PM₁₀ monitoring sites (sites in Set 10 were not used during covariate selection).

Both hourly and daily PM₁₀ data were reported to the various monitoring networks. For monitors that reported hourly PM₁₀, these data were averaged from midnight to midnight to generate daily means. However, daily means were not calculated when 18 or more valid hourly values were not available. Daily PM₁₀ data reported using standardized volumes were converted to local conditions using estimates of daily temperature, SLBP, and site elevation. Daily PM₁₀ data were then averaged across co-located monitors into daily means for each monitoring site, and these daily site means were then averaged over the month to generate monthly site means. As was done for the hourly data, monthly site means were considered valid only if greater than approximately 70% of the nominal days had valid daily PM₁₀ values.

2.2.2 Geographic Data

Several characteristics of the PM monitoring sites were described using a GIS. Site-specific geographic data on distance to roadways by road class, urban land use, population density at the block group, tract, and county level, point-and area-source PM₁₀ emissions, and elevation were compiled using ArcGIS 9 (ESRI, Redlands, CA). These variables are derived at the monitoring locations as well as at model prediction locations (collectively referred to as point locations), which can be computationally intensive when making predictions at many locations.

The distance from each point location to the nearest roadway by road class was calculated in the GIS using ESRI StreetMap road data. Road segments were first classified by US Census Feature Class Code (CFCC) as A1 (primary roads, typically interstates, with limited access), A2 (primary major, non-interstate roads), A3 (smaller, secondary roads, usually with more than two lanes), or A4 (two lane, typically surface roads used for local traffic). Distances less than four meters were set to four meters since values less than four meters were likely due either to spatial error in the georeferencing of the road data or to inaccurate geographic coordinates. Distance to road data were log-transformed, since data were highly right-skewed, which could introduce instability into the estimated smooth functions due to sparse covariate values in the right tails of the distributions.

Land use data were compiled from the US Geological Survey (USGS) 1992 National Land Cover Dataset (NLCD), which provides data on 19 categories of land use in raster image files with one arc-second (about 30 m) spatial resolution. Low-intensity residential, high-intensity residential, and industrial/commercial/transportation land uses were summarized using a moving window technique (“Neighborhood statistics” in ESRI Spatial Analyst) to estimate the proportion of urban land use within 1 km of each point location. Because we intended to capture neighborhood-scale variability in urban land use patterns, a 1 km radius was considered appropriate.

Population density values were assigned to each point location using the GIS with data from the 1990 US Census at three aggregation levels: block group, tract, and county. In the event that a location was outside the Census boundaries (resulting from slight spatial inaccuracies in either the boundary files or the geographic coordinates of the location), the population density from the nearest area was used.

PM₁₀ emissions from nearby point sources were estimated at each point location using the 1999 USEPA National Emissions Inventory (NEI) facility emissions report. One and ten km radius circular buffers were created around each point location, and the reported point source emissions within these buffers summed. Because the distributions of point-source emissions were highly right-skewed, natural log transforms of these data were performed. To facilitate natural log transformation, locations reporting zero point-source PM₁₀ emissions within the appropriate buffer were assigned a value of one-half the minimum value among all monitoring locations. We also explored using a kernel density function to interpolate the point-source emissions data, using neighborhoods of 5, 7.5, and 10 km.

Area-source PM₁₀ emissions for each point location were estimated using USEPA NEI tiered emissions reports, which provide estimates of total area-source emissions of PM₁₀ by county and year. Thus, these data were treated as a time-varying covariate. The reports include information on residential combustion, including wood smoke emissions, and highway and off-highway vehicular emissions. In the event that area-source emissions data were unavailable for a given county and year, these data were replaced with data from a previous or later year, if available. If data for a county were not reported in any year from 1988 to 2002, then the minimum value among the monitoring locations was assigned. Data were log-transformed since their distribution was highly right-skewed.

Elevation data were compiled from the USGS National Elevation Dataset (NED). Elevation data are provided as raster image files with one arc-second spatial resolution, and an elevation was assigned to each point location using the GIS.

2.2.3 Meteorological Data

Monthly average temperature, wind speed, SLBP, and total precipitation were obtained from the National Climatic Data Center (NCDC) from the TD3280 and TD3220 data products by averaging or summing daily data over each month for each meteorological monitoring site. Again, as for PM₁₀ concentration data, monthly values of the meteorological predictors were calculated only for months with more than 70% valid daily values. Monthly values for each of the meteorological predictors were estimated at each point location by spatially smoothing monthly data from the meteorological monitoring sites using a GAM with a bivariate penalized spline smooth term of the projected spatial coordinates for each month. Similarly, daily temperature and SLBP used to correct standardized volumes were estimated at each PM₁₀ monitoring site by spatially smoothing daily means of temperature and SLBP on a daily basis.

Data on air stagnation were compiled by NCDC (Air Stagnation Index) on a 0.25 by 0.25 degree grid covering the continental US based on the work of Wang et al. (1999). Stagnant days were defined by a sea-level geostrophic wind speed less than eight meters per second, 500 millibar pressure-level wind speed less than 13 meters per second, and no precipitation. When there was a temperature inversion below the 850 millibar pressure level, the eight meter per second wind speed threshold was relaxed by 10% (to 8.8 meters per second) (Air Stagnation Index). The percentage of days per month that met the stagnant air criteria were assigned to each point location for each month.

3. Results

3.1 PM₁₀ Data Summary

A summary of monthly-average PM₁₀ concentration measurements and monitoring locations is presented in Table 1. The USEPA AQS network provided 98% of the PM₁₀ concentration values and 93% of the monitoring locations in the study region. Monthly- average PM₁₀ concentrations were approximately log-normally distributed, with geometric mean and standard deviation of 23.5 μg m⁻³ and 1.5 μg m⁻³, respectively, across the study region. The distribution of the measured monthly-average PM₁₀ values in the study region is presented by state or state group and by season in Table 2.

Table 1.

Number of monthly average PM₁₀ concentration values and number of sites by monitoring network and region for 1988–2002

Region	Monitoring network
	USEPA Air Quality System		IMPROVE		Harvard 5 Cities		Harvard 24 Cities		All networks
	na	n sitesa	n	n sites	n	n sites	n	n sites	n	n sites
Study region	47 970	597	836	21	172	17	66	6	49 044	641
Study region and adjacent states	68 755	861	1 498	29	208	22	111	10	70 572	922

^a“n” is number of monthly average concentrations, “n sites” is number unique sites reporting valid monthly average concentrations.

Table 2.

Summary of the distribution of measured monthly-average PM₁₀ concentrations by state or state group and season in the study region

Grouping		Measured monthly-average PM10 concentration (μg m−3)
		5%	25%	50%	75%	95%	n	GM	GSD
By state or state group (1988–2002)	Northern New England (ME, NH, VT)	7.7	13.0	17.6	23.2	35.2	7 376	17.1	1.6
	Southern New England (CT, MA, RI)	11.1	17.1	22.1	28.3	40.1	7 277	21.8	1.5
	NY	9.7	16.3	21.4	27.4	40.2	6 265	20.8	1.5
	Western Mid-Atlantic (MD, NJ, PA)	15.8	21.8	27.6	34.7	47.2	12 937	27.5	1.4
	Midwestern (OH, MI)	13.6	20.1	26.5	33.6	46.7	14 710	26.0	1.5
	DE	19.0	24.4	29.3	35.5	48.7	469	29.4	1.3
By season (across study region)	Winter	9.9	17.6	23.0	29.8	43.3	11 875	22.3	1.6
	Spring	10.6	17.4	22.6	29.0	42.0	12 347	22.1	1.5
	Summer	14.8	22.8	29.1	36.3	48.8	12 387	28.3	1.4
	Fall	10.2	17.1	22.4	28.6	41.0	12 435	21.7	1.5
Across study region and seasons		11.1	18.3	24.2	31.3	44.6	49 044	23.5	1.5

3.2 Model Development

A summary of the distributions of the GIS-derived and meteorological covariates included in the final model, their units, and the number of estimated degrees of freedom in their smooth terms is presented in Table 3.

Table 3.

Summary of GIS-derived and meteorological covariates included in the final model

Category	Description	Unitsb	Time-varying?	Summary of covariate distribution					Edf of smooth termc
				5%	25%	50%	75%	95%
Distance to road	Distance to nearest A1 roada	ln(m)	No	4.7	6.7	7.8	9.2	10.9	2.5
	Distance to nearest A2 roada	ln(m)	No	3.9	5.9	7.2	8.2	9.3	1.0
	Distance to nearest A3 roada	ln(m)	No	3.5	5.7	6.7	7.6	8.7	1.0
Urban land use	Percentage of urban land use within 1 km	%	No	0.1	21.0	59.7	81.7	95.4	2.4
Population density	Block group population density	persons mile−2	No	26	174	1 441	4 640	15 650	4.5
	County population density	persons mile−2	No	24	140	375	1 428	11 038	4.9
Point source emissions	PM10 emissions within 1 km	ln(tons year−1)	No	−6.9	−6.9	−6.9	0.7	5.1	1.0
	PM10 emissions within 10 km	ln(tons year−1)	No	−6.5	4.2	5.8	7.0	8.5	2.3
Elevation	Elevation above sea-level	m	No	3.4	48.2	176.4	233.3	359.0	1.4
Area-source emissions	PM10 emissions by county and year	ln(tons year−1)	Yes	7.4	8.7	9.3	10.0	10.7	7.2
Precipitation	Total monthly precipitation	inches (cm)	Yes	1.2 (3.0)	2.2 (5.6)	3.2 (8.1)	4.5 (11.4)	6.9 (17.5)	7.6
Wind speed	Monthly-average surface wind speed	m s−1	Yes	2.6	3.3	3.8	4.3	4.8	6.4

^aDesignated by Census Feature Class Codes, from ESRI StreetMap road data.

^bln’ is natural log.

^cEdf is estimated degrees of freedom of smooth term in the final model.

3.2.1 Time-varying predictors

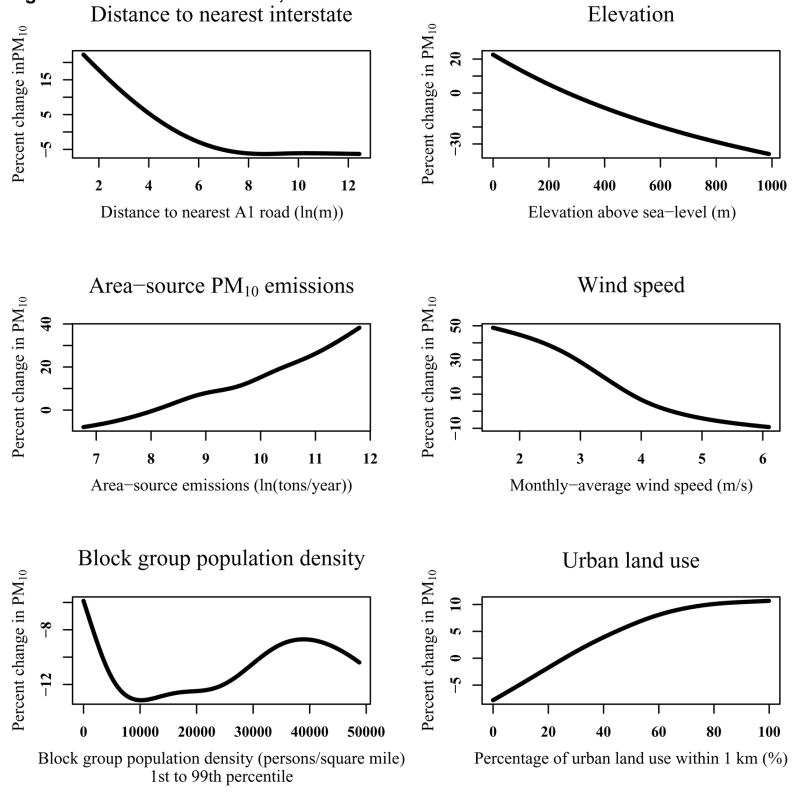
Estimates of yearly area-source PM₁₀ emissions, wind speed, and precipitation were selected for model inclusion based on the increased predictive ability of the model (as assessed using the cross-validation R²) when these terms were included. As expected, monthly PM₁₀ concentrations increased with area-source emissions (Figure 2) and with decreasing wind speed (Figure 2) and precipitation. Although significant, air stagnation was not included as a model predictor because of its strong negative correlation with wind speed (Pearson r=−0.59), its greater and more locally heterogeneous variation in space, and its poorer predictive performance. The degrees of freedom used in estimating the smooth functions of the yearly area-source PM₁₀ emissions and monthly precipitation terms were reduced slightly from the default approach to attenuate small, local variations in the shape of the functions, which may have been caused by the numerous observations at each location. However, these reductions did not change the fundamental relationship between the predictors and the PM₁₀ concentrations. Preliminary model results showed that the relationship between monthly-average SLBP and PM₁₀ concentrations was contrary to known particle behavior, and the addition of SLBP offered no improvement in predictive performance. The same was true for air temperature, so both SLBP and air temperature were removed from further consideration as predictors.

Figure 2.

Smooth plots from the final model showing non-linear effects of selected predictors and the associated percent change in predicted PM₁₀ concentrations.

3.2.2 Time-invariant predictors

Nine location-specific GIS-derived covariates, including distance to nearest roadway for road classes A1, A2, and A3, urban land use, population density at the block group and county level, point-source PM₁₀ emissions within 1 and 10 km buffers, and elevation, were found to be important predictors in the model using the selection criteria. Each was statistically significant (p<0.05) (Wood 2006), except for the point-source PM₁₀ emissions within 1 km, which was only marginally significant (p=0.09), but was kept in the model because it increased predictive performance.

The three smooth terms for the distance to nearest A1, A2, and A3 roadway showed increased concentrations near roadways, with larger effects for the larger road classes. The smooth function for distance to the nearest A1 road shows strong non-linearity (Figure 2); terms for the other road classes are essentially linear (Table 3). The distance to nearest class A4 roadway was not included in the model because this term did not improve predictive ability, and had essentially no effect when other predictors were included in preliminary models.

The smooth term for the proportion of urban land use within 1 km showed greater urbanization to be associated with higher PM₁₀ concentrations (Figure 2), while block group (Figure 2) and county population density were generally negatively associated with PM₁₀ at low population densities and positively associated at higher densities. Although these three predictors were correlated, they were included in the model because each was significant and improved predictive performance. The tract level population density term, in contrast, was insignificant and offered no improvement in predictive performance, and therefore was not included in the final model.

The smooth functions for the point-source emissions terms showed increased PM₁₀ concentrations with increasing emissions, with a small linear effect for the 1 km radius and a larger, non-linear effect for the larger 10 km radius. Terms representing the point-source PM₁₀ emissions using a kernel density function were not included in the model because of their computational intensity and their weaker predictive performance relative to the simpler circular buffer approach.

PM₁₀ concentrations decreased nearly linearly with increasing elevation (Figure 2).

3.3 Model comparisons

The final model with monthly spatial terms and the above GIS-derived and meteorological covariates explained 62% of the variability in measured PM₁₀ levels at held-out locations, with this value being substantially higher than that explained by a GAM spatial smoothing only model with no covariates (cross-validation R²=0.51) (Table 4), demonstrating the importance of including GIS-derived and meteorological predictors with respect to model performance. Plots of the predicted concentration surfaces also revealed much more local spatial variability in predictions from the final model compared to those from the GAM spatial smoothing only model.

Table 4.

Predictive performance of the final model and alternative models

Model description				Cross-validation results
	Number of spatial termsa	Covariates included	Model fit R2,b	Interceptc	Slopec	Cross-validation R2,d
Final model	180 monthlye	All	0.74	2.4 +/− 0.9	0.92 +/− 0.003	0.62
Seasonal spatial terms	4 seasonale	All	0.59	2.1 +/− 0.1	0.94 +/− 0.004	0.54
GAM spatial smoothing only	180 monthly	None	0.76	3.7 +/− 0.1	0.87 +/− 0.004	0.51
Inverse distance weighted interpolation	NA	None	NA	8.3 +/− 0.1	0.65 +/− 0.005	0.29
Nearest neighbor interpolation	NA	None	NA	15.5 +/− 0.2	0.42 +/− 0.006	0.22f

^aCorresponds to the extent of control for space-time interaction in the model.

^bDerived from fitting the model to all data from sets 1 through 9, including data from states adjacent to the study region.

^cPresented as (parameter estimate +/− standard error) from linear regression of observations on predictions.

^dDerived from cross-validation on sets 1 through 9, with each set held out in turn (one site in Pennsylvania was removed as an outlier); 43 345 observations total.

^eRefers to number of time-varying spatial terms fit in the first stage of the model in addition to one spatial term fit in the second stage.

^fBecause the nearest monitor was not always within the 50 km neighborhood, only 20 189 pairs of observations are available rather than the full set of 43 345 observations.

Predictive performance also increased with increasing temporal resolution, as the final model with 180 monthly spatial terms (cross-validation R²=0.62) performed better than an alternative model with four seasonal spatial terms and identical covariates (cross-validation R²=0.54) (Table 4). These results indicate that the monthly spatial terms are better able to capture residual spatio-temporal variability in ambient PM₁₀ concentrations than are seasonal terms, even given the relatively sparse spatial data distribution.

The final model also performed better than the other approaches using IDW (cross-validation R²=0.29) or nearest neighbor spatial interpolators (cross-validation R²=0.22) (Table 4). As shown by the regression of predicted on measured values at the cross-validation locations, the final model also exhibited less multiplicative bias than the interpolation methods (slope of 0.92 for the final model vs. that of 0.65 and 0.42 for the IDW and nearest neighbor methods, respectively).

3.4 Final Model Predictions

3.4.1 Trends in model predictions

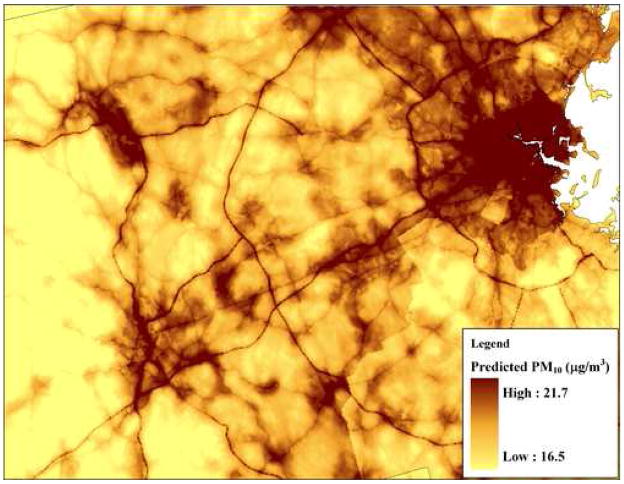
Generally, PM₁₀ concentrations during the winter season were found to be more spatially variable than for other seasons, with the spatial terms in winter using the most degrees of freedom and spring the fewest. Figure 3 shows the spatial surface of the predicted PM₁₀ concentrations in the study region averaged across all months from 1988–2002. As shown in Figure 3, PM₁₀ concentrations are higher in and around many major urban areas, with areas of lower PM₁₀ concentration found in more rural areas in northern Michigan, New Hampshire, and Maine, as well as much of northern New York. The total amount of variability in model predictions at the gridded locations shown in Figure 3, using conventional sums of squares decomposition, was 46% spatial, 30% temporal, and 24% due to spatio-temporal interaction. PM₁₀ predictions from the final model for a typical month are shown with greater spatial resolution in eastern Massachusetts in Figure 4. The micro-scale and neighborhood-scale impacts of large roadways and urban land use are evident.

Figure 3.

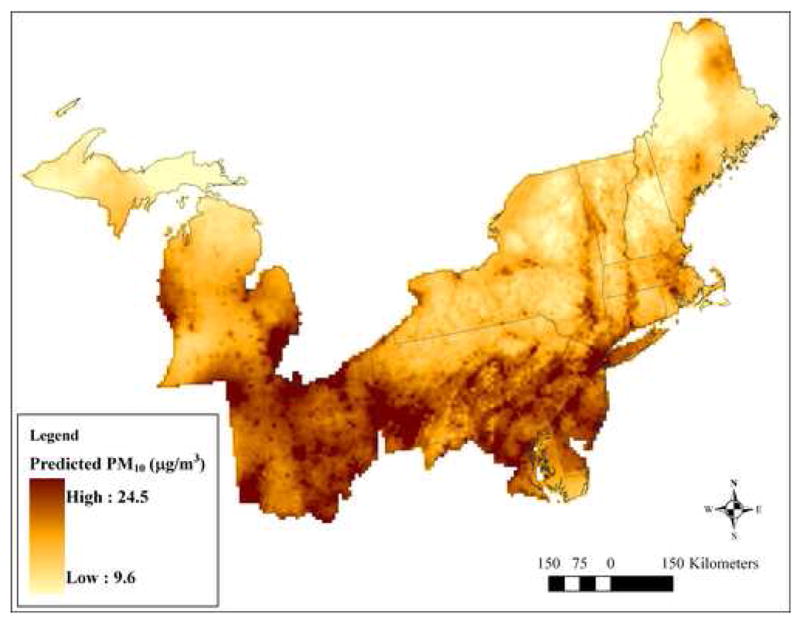
Map of the predicted PM₁₀ concentration surface over the entire study region averaged across all months from 1988–2002. For display purposes, the map shows the 5^th to the 95^th percentile of predicted PM₁₀ concentrations.

Figure 4.

Map of the predicted PM₁₀ concentration surface in eastern Massachusetts for March 2000 from the final model. For display purposes, the map shows the 5^th to the 95^th percentile of predicted PM₁₀ concentrations.

3.4.2 Accuracy and Precision

The accuracy and precision of the final model predictions, as described by the bias and RMSPE values, respectively, are presented in Table 5. The results indicate strong model performance, irrespective of season, location, urbanness, and to a lesser extent monitoring network and monitoring objective. The model performed slightly better in the summer as compared to winter with respect to both accuracy and precision. The model also performed consistently well across the time period of interest, with bias nearly constant and approximately equal to −0.4 μg m⁻³ across years, though slightly higher for 1988 at −1.0 μg m⁻³. Model precision across years was also nearly constant and equal to 6.4 μg m⁻³, though slightly better after the year 2000 at 5.4 μg m⁻³ on average.

Table 5.

Accuracy and precision of model predictions by state or state group, season, quartiles of urban land use and block group population density, monitoring network, and monitoring objective determined using cross-validation

Grouping		Na	Biasb (μg m−3)	RMSPEc (μg m−3)
By state or state groupd (1988–2002)	Northern New England (ME, NH, VT)	6 362	−1.1	6.6
	Southern New England (CT, MA, RI)	6 658	−0.6	5.0
	NY	5 307	0.1	5.8
	Western Mid-Atlantic (MD, NJ, PA)	11 630	−0.7	7.2
	Midwestern (OH, MI)	12 919	0.2	6.4
	DE	469	−2.7	6.3
By season (across study region)	Winter	10 478	−0.7	7.1
	Spring	10 896	−0.5	6.5
	Summer	10 967	−0.04	6.0
	Fall	11 004	−0.4	5.9
By quartiles of urban land use	1	10 842	−0.3	6.0
	2	10 899	0.1	7.4
	3	10 805	−0.8	6.1
	4	10 799	−0.6	6.0
By quartiles of block group population density	1	10 827	−0.3	6.2
	2	10 819	−0.9	7.3
	3	10 885	0.2	6.1
	4	10 814	−0.6	5.9
By monitoring network	AQSe	42 271	−0.5	6.4
	IMPROVEf	836	1.8	4.6
	Harvard 5 Cities	172	4.7	7.7
	Harvard 24 Cities	66	−1.8	6.8
By monitoring objectiveg	Unknown (Other networks)	1 074	2.0	5.4
	Unknown (AQS sites)	5 286	−1.8	8.0
	Population Exposure	18 794	0.4	5.7
	Highest Concentration	15 127	−1.3	6.9
	General/Background	1 173	0.8	5.0
	Other	1 139	−1.0	5.2
	Upwind Background	287	2.1	5.2
	Source Oriented	209	1.3	3.7
	Maximum Ozone	145	1.8	4.3
	Concentration
	Maximum Precursor	111	4.8	5.4
	Emissions Impact
Across all observationsa		43 345	−0.4	6.4

^a“N” is number of pairs of measurements and cross-validation predictions; data from one site in Pennsylvania were removed.

^bMean prediction error (cross-validation predictions minus measurements).

^cRMSPE is root mean squared prediction error, describing precision of the model predictions.

^dWhere results were similar, nearby states were grouped.

^eFrom the USEPA’s Air Quality System monitoring network.

^fFrom the Interagency Monitoring of Protected Visual Environments (IMPROVE) monitoring network.

^gDefined for sites in the USEPA Air Quality System (AQS) network only.

Mapping the bias and RMSPE values by monitoring site indicated no apparent spatial patterns in the data across the study region (results not shown). The model performed equally well for areas of varying urbanness, with no prominent trend across quartiles of urban land use or block group population density. However, the model predictions were generally lower than the measured values at sites in the AQS and Harvard 24 Cities networks, higher on average at sites in the IMPROVE network (IMPROVE sites are typically in very rural locations), and substantially higher at sites in the Harvard 5 Cities network. Precision of the model predictions was comparable across networks, except that IMPROVE sites showed slightly improved precision. The model performance varied slightly with the stated monitoring objective for the AQS sites, with bias less than 2 μg m⁻³ for all but the “upwind background” and “maximum precursor emissions impact” sites, which represent less than one percent of the data. Model precision also varied across monitoring objectives, with sites from the AQS network where the monitoring objective was not reported (listed as “unknown”) having the poorest precision (8.0 μg m⁻³) followed by “highest concentration” sites (6.9 μg m⁻³) (Table 5).

3.4.3 Predictive Uncertainty

The spatial pattern of uncertainty in the model predictions, as reflected by the standard errors, is similar to that of the predicted concentrations. This similarity is partially due to the exponentiation of the standard errors to the original scale, causing higher predicted concentrations to have higher estimated standard errors. When the standard errors were averaged across all months from 1988–2002, the 5^th and 95^th percentiles of the mean standard error values across location were 2.6 and 5.8 μg m⁻³, respectively, with an overall mean of 4.2 μg m⁻³. Uncertainties were elevated in several areas with high concentrations, especially those with few nearby monitors such as in northeastern Maine, as well as in several urban areas such as Detroit, MI, Cleveland, OH, Pittsburgh, PA, and New York City, NY. The impact of monitor sparseness on model performance is illustrated by model predictions for Maine, which are inflated in the northeastern part of the state and deflated in the northwestern part of the state. Since few people live in this area, the impact of poor predictive ability for this region on chronic exposure estimation is likely to be small.

We also examined the relative contribution of each source of uncertainty (on the log scale for convenience) to the standard errors and found that that the residual spatial and spatio-temporal variance components, σ²b and σ²_e,t, contributed the most, at 41% and 39%, respectively, of the prediction variance. Also, estimation of the time-invariant spatial and regression functions accounted for 11% of the uncertainty, time-varying spatial functions for 9%, and time-varying regression functions less than one percent. These results indicate that the largest contributor to model uncertainty is unexplained local spatial variability, both time-varying and time-invariant. For simplicity this analysis ignores other sources of error, such as instrument error in measured PM₁₀ concentrations and error induced by averaging daily measures to the monthly level. Though a very dense network of monitors could potentially reduce the error associated with the unexplained local spatial variability, such a network is likely infeasible on a large spatial scale. Additionally, while averaging PM₁₀ data over longer time periods than monthly, say seasonally or annually for example, may reduce the uncertainty induced by the spatio-temporal variance component of the model, such a model would not provide monthly estimates of PM₁₀, which were needed for our corresponding health study to relate monthly changes in exposure to health outcomes and to allow straightforward aggregation of monthly values into longer-term moving averages, such as the average exposure for the 3, 6, or 12 months previous to an event. Thus, our choice to use the monthly time-scale represents as balance between reducing temporal uncertainty and describing local spatio-temporal variability.

3.4.4 Overfitting

The final model R² of 0.74 was higher than the cross-validation R² of 0.62, which suggests that the model is overfitting, as the model fits the data better at measured as compared to unmeasured locations. In contrast, the cross-validation R² for Set Ten (i.e., data from locations not used to select the covariates in the model) of 0.63 was comparable to 0.62, the cross-validation R² across Sets One through Nine, suggesting that model overfitting did not result from the covariate selection process. If it had, the cross-validation R² for Set Ten would be substantially lower than that across Sets One to Nine.

4. Discussion

Our results demonstrate the ability of our GIS-based spatial smoothing model to predict monthly outdoor PM₁₀ concentrations across the entire northeastern US. Model performance was strong and substantially better than smoothing or interpolation methods alone, predicting monthly PM₁₀ concentrations with a high degree of accuracy and precision over a large geographic region. Further, the model performed well in both rural and urban areas, across seasons, and across the entire time period. Its strong performance combined with its several key features make the model a new, powerful, and efficient tool for chronic epidemiologic studies of particulate matter and represents a significant advance over previously available methods. The model’s key features are its inclusion of monthly-varying smooth spatial terms as well as smooth terms of GIS-derived and meteorological predictors, which provides highly spatially resolved (down to the level of the residential address) and temporally resolved estimates of chronic PM exposures, even for individuals living in areas with no nearby monitors (albeit with greater uncertainty for locations with distant monitors). Finally, the model is able to make predictions at large numbers of locations in a computationally efficient manner, a necessity for assigning exposures over a long time period to large numbers of subjects and/or locations.

Results from our analyses showing the importance of GIS-derived predictors were consistent with those of Brauer et al. (2003) and Briggs et al. (2000), who used GIS-derived predictors (but not spatial smoothing techniques) in multiple linear regression models to explain spatial variability in annual PM_2.5 and NO₂ concentrations, respectively. Although Briggs et al. compared their ‘regression-mapping’ approach with spatial interpolation methods, neither paper compared their approach with one that combines spatial modeling and GIS-derived predictors in one model. Recent work by Gryparis et al. (2007) showed that including GIS-derived covariates was important and improved predictive performance in modeling traffic-related air pollutant levels in eastern Massachusetts.

Smith et al. (2003) used a spatial smoother combined with the effect of an additional covariate. Our approach extends this methodology by 1) allowing for linear, categorical, and non-linear time-invariant or time-varying effects (or any combination of the above) of additional covariates using GAMs, and 2) allowing for complex space-time interaction by modeling separate spatial surfaces at different time periods using bivariate penalized splines to perform spatial smoothing rather than kriging, which can be computationally burdensome when making predictions at large numbers of locations. Sahu et al. (2006) described a spatio-temporal model that allows for nonstationarity depending on urbanness, though we suspect that the implementation of such a model using Gaussian random fields and Bayesian fitting methods may be computationally infeasible for our application. Also, Liao et al. (2006) applied ordinary kriging models to daily PM₁₀ data from the year 2000 across the US, and reported a mean prediction error of 0.06μg m⁻³, smaller than but comparable to that in the current study of −0.4 μg m⁻³. By contrast, though, the mean of the standard errors in our study was considerable smaller that that reported in Liao et al. (4.2 μg m⁻³ across the northeastern and midwestern US across 1988 to 2002 vs. 16.3 μg m⁻³ for the entire continental US for the year 2000 from a lognormal kriging model). This larger uncertainty may in part be because their kriging model relied on spatial modeling alone and did not incorporate GIS-derived predictors, but also may be due to their modeling of daily PM₁₀ levels versus monthly average PM₁₀ in the present study and the larger domain of their study.

Bivariate penalized splines were considered an appropriate means of modeling residual spatial variation in both the first and second stages of the model because these surfaces were expected to vary smoothly in space after accounting for local variations using the other covariates and because spline functions are sufficiently flexible to describe complex spatial trends in the data. However, results from the final model provided some evidence of overfitting, likely associated primarily with the monthly spatial surfaces, which were fit using relatively sparse and noisy data. A denser monitoring network, with monitors located more uniformly across the domain may reduce the potential for overfitting.

Our modeling approach assumes isotropy and stationarity of the spatial surfaces, normality and homoscedasticity of residuals, independence of the monthly spatial terms, uniform effects of GIS-derived and meteorological covariates across space, and no interactions of these covariates with one another. The model presented in this paper represents a balance between model complexity and computational efficiency with respect to the amount of time required to fit the various candidate models and the final model, and to predict concentrations at large numbers of locations. However, results in Paciorek et al. (unpublished data), which examines different spatial smoothing methods and variations on other aspects of the model, demonstrate that little, if any, improvement in predictive performance is gained from the use of more complex spatial modeling methods or from other changes to the final model. In conclusion, the strong performance of our modeling approach demonstrates its suitability as a means to estimate individual-specific chronic PM₁₀ exposures for large populations, and that the approach has the potential to reduce measurement error in epidemiologic studies by improving the accuracy of chronic exposure estimates. We are currently using this model to examine the chronic health impacts of particles in the Nurses Health Study cohort.

Abbreviations

AQS

Air Quality System

CFCC

Census Feature Class Code

ESRI

Environmental Systems Research Institute

GAM

generalized additive model

GIS

Geographic Information System

IDW

inverse distance weighting

IMPROVE

Interagency Monitoring of Protected Visual Environments

km

kilometer

NCDC

National Climatic Data Center

NLCD

National Land Cover Dataset

NEI

National Emissions Inventory

NED

National Elevation Dataset

PM

particulate matter

PM₁₀

mass concentration of airborne inhalable particles (aerodynamic diameter<10 μm)

RMSPE

square root of the mean of the squared prediction errors

SLBP

sea-level adjusted barometric pressure

US

United States

USEPA

US Environmental Protection Agency

USGS

US Geological Survey

VIEWS

Visibility Information Exchange Web System