Children’s understanding of the relationship between addition and subtraction

Abstract

In learning mathematics, children must master fundamental logical relationships, including the inverse relationship between addition and subtraction. At the start of elementary school, children lack generalized understanding of this relationship in the context of exact arithmetic problems: they fail to judge, for example, that 12 + 9 − 9 yields 12. Here, we investigate whether preschool children’s approximate number knowledge nevertheless supports understanding of this relationship. Five-year-old children were more accurate on approximate large-number arithmetic problems that involved an inverse transformation than those that did not, when problems were presented in either non-symbolic or symbolic form. In contrast they showed no advantage for problems involving an inverse transformation when exact arithmetic was involved. Prior to formal schooling, children therefore show generalized understanding of at least one logical principle of arithmetic. The teaching of mathematics may be enhanced by building on this understanding.

To a large degree, mathematics is the discovery and use of general, abstract principles that make hard problems easy. The inverse relationship between addition and subtraction is a case in point. Problems of the form x + y − z = ? are intractable for those who lack knowledge of specific arithmetic facts (e.g., what is x + y?), and they require two successive calculations for those who possess the relevant knowledge. In contrast, problems of the form x + y − y = ? can immediately be solved, without arithmetic fact knowledge or calculation, by anyone who understands the logical relationship between addition and subtraction. The present research explores the origins of this understanding in children on the threshold of formal instruction in arithmetic.

Previous research suggests that children’s understanding of this relationship develops over many years of instruction in elementary mathematics. Children who have received arithmetic instruction perform more accurately on inverse problems of the form x + y − y than on matched problems of the form x + y − z (e.g. Bisanz & LeFevre, 1990; Bryant, Christie & Rendu, 1999; Gilmore & Bryant, 2006, Gilmore 2006; Rasmussen, Ho & Bisanz, 2003; Siegler & Stern, 1998; Stern 1992), but they appear to learn about this principle in a piecemeal fashion. For example, children may recognize that subtracting 4 cancels the operation of adding 4, but they fail to recognize inversion as a general principle that can be applied to all numbers (Bisanz & LeFevre, 1990). Furthermore, these studies all involved children who were already receiving formal instruction in arithmetic, and thus the roots of this understanding are unclear.

Studies involving preschool children have not demonstrated generalized understanding of inversion. While some 4 year-old children correctly solved inverse problems involving addition and subtraction of one or two objects (Klein and Bisanz, 2000; Villette, 2002), this ability was restricted to children who were able to perform addition and subtraction computations. Thus, it is not clear on what basis children solved these problems. Some 4-year-old children were found to solve inverse problems more accurately than control problems, when problems were presented with concrete items (Rasmussen et al., 2003). However, mean performance was less than 50%, the inverse effect size was small, and no child solved all the inverse problems correctly. Moreover, each of these studies employed problems involving very small numerosities (e,g, addends and subtrahends less than 5). Thus, there is no evidence that children understand the logic of inversion applied to numbers of any size, prior to the onset of formal schooling.

To our knowledge, all previous studies of children’s understanding of inversion have used problems involving exact numbers, typically presented in verbal or written symbolic form. It is possible, therefore, that preschool children have a conceptual understanding of the relationship between addition and subtraction, but fail to apply their understanding to exact symbolic arithmetic problems. This understanding may be revealed through the use of problems of approximate arithmetic on numbers presented in nonsymbolic form.

Two lines of research provide reasons to consider this possibility. One set of studies tested young children’s understanding of the inverse relationship between adding and subtracting one (Lipton & Spelke, 2006). Children who were unable to count beyond 60, and who could not judge whether “86” denoted a larger or smaller number than “67,” were shown a jar of marbles and were told that there were (e.g.) “86 marbles” in the jar. Children judged that the jar no longer contained 86 marbles after a single object was added or removed, whereas it still contained 86 marbles after the marbles were stirred with no addition or subtraction: findings that indicate that “86” denoted a specific, exact numerosity. When one marble was removed from the jar and then a different marble was added, these children judged that the jar again contained 86 marbles. Thus, children appeared to appreciate the inverse relationship between adding and subtracting one object. The study does not reveal, however, whether children understand that the relationship holds for addition and subtraction of quantities larger than one.

A second set of studies focuses on preschool children’s abilities to add and subtract large, approximate nonsymbolic numerosities. Adults and preschool children who are shown an array of dots or a sequence of sounds or actions are able to represent the approximate cardinal value of the set of entities, without verbal counting (e.g. Cordes, Gelman, Gallistel, & Whalen, 2001; van Oeffelen & Vos, 1982). These non-symbolic representations are imprecise, they are subject to a ratio limit on discriminability, and they have been found in educated adults (Barth, Kanwisher & Spelke, 2003; Whalen, Gallistel & Gelman, 1999), preschool children (Lipton & Spelke, 2005), adults in an indigenous Amazonian community lacking any formal education (Pica, Lemer, Izard & Dehaene, 2004), pre-verbal infants (Brannon, 2002; Xu & Spelke, 2000) and non-human animals (Meck & Church, 1983).

Moreover, adults with and without formal education, preschool children, and infants can perform approximate additions and subtractions on non-symbolic stimuli (Pica et al., 2004; McCrink & Wynn, 2004; Barth, La Mont, Lipton & Spelke, 2005; Barth, La Mont, Lipton, Dehaene, Kanwisher & Spelke, 2006). In an experiment that is a direct precursor to the present studies, 5-year-old children were presented with computer-animated events in which an array of blue dots appeared and moved into a box, and then a second set of blue dots moved into the box. Then children saw an array of red dots next to the box, and they judged whether there were more blue dots (hidden in the box) or red dots. Children performed this task reliably though imperfectly, and their performance showed the ratio signature of large approximate number representations (Barth et al., 2005). These studies provide evidence that children have an abstract understanding of addition and subtraction prior to formal mathematics instruction. Recent experiments revealed, moreover, that children with no instruction in symbolic arithmetic can use this understanding to solve approximate addition and subtraction problems presented in symbolic form (Gilmore, McCarthy & Spelke, 2007). No study, however, reveals whether children’s abstract knowledge of addition and subtraction of nonsymbolic quantities supports an understanding of the inverse relationship between these operations, when the operations are applied either to nonsymbolic or symbolic numerical problems.

Here we report three experiments that examine understanding of inversion by children who have not yet begun formal schooling. In the first experiment, we presented children with nonsymbolic, large approximate arithmetic problems similar to those used by Barth et al. (2005). In the second experiment, the same set of approximate arithmetic problems were presented with symbolic representations of number. If children have a general understanding of inversion, they should be able to solve these problems, just as they solve problems involving the successive addition and subtraction of one. In the third experiment we tested whether children used approximate number representations to solve these problems, by presenting problems requiring exact representations of number.

In the critical trials of these experiments, children were given problems in which a quantity y was first added to and then subtracted from a hidden quantity x, and the resultant quantity was compared to a contrasting quantity w (i.e., children answered questions of the form, is x + y − y more or less than w?). It is possible, however, that children would succeed at problems of this form without understanding inversion, in one of two ways. First, children might fail to attend to the addition and subtraction operations and simply compare x to w directly. Second, children may perform two operations of approximate addition and subtraction in succession and succeed in the x + y − y task by this circuitous route. To distinguish among these possibilities, children were presented with problems that involved inversion (x + y − y compared to w) interspersed with control problems that did not (x + y − z compared to w) (after Bisanz & LeFevre, 1990; Bryant et al., 1999; Rasmussen et al., 2003). Some control problems preserved the numerical ordering of x and w, whereas others did not. If children failed to attend to the operations, they should perform correctly on the subset of control problems whose two operations preserve the numerical ordering of x and w, and fail on the other control problems. If children performed two operations in succession, then they should perform above chance on all the control problems. If children understand the inverse relationship of addition and subtraction, in contrast, they should perform reliably better on the inversion problems than on either type of control problem.

Experiment 1

The first experiment tested preschool children’s understanding of inversion with nonsymbolic, approximate numerosities presented as visible arrays of dots.

Method

Participants

Twenty children (9 male), aged 5 years 4 months to 6 years 1 month (mean 5 years 7.4 months) were recruited from a participant database drawn from the greater Boston area.

Task

The children were shown a series of large approximate arithmetical problems (see Table 1). They compared two sets of different numerosities after one set had undergone an addition and subtraction transformation. On inverse trials the quantity added and the quantity subtracted was the same (e.g. 42 + 10 − 10), whereas on control trials the quantity added and the quantity subtracted differed (e.g. 38 + 16 − 12). The comparison set differed from the resultant set by a ratio of 2:3 or 3:2 (e.g. 42 v 63). The same comparisons were used for the inversion and the control trials. The order of operations for both inversion and control trials was always plus-minus, to reduce both the number of trials that each child had to complete and the variety of sequences that they had to remember.

Table 1.

Inverse and non-inverse problems given to children. In Experiments 1 and 2 approximate comparison sets were used for all problems. In Experiment 3 exact comparison sets were used for inverse trials and approximate comparison sets for control trials.

Inverse			Simple uneven		Complex uneven
Problem	Comparison		Problem	Comparison	Problem	Comparison
	Exp 1 & 2	Exp 3
36 + 40 − 40	24	35	41 + 12 − 17	24	45 + 9 − 34	30
20 + 38 − 38	30	21	38 + 13 − 9	63	24 + 38 − 8	36
42 + 10 − 10	63	44	52 + 8 − 12	32	63 + 8 − 43	42
54 + 8 − 8	36	52

The arithmetic problems were presented using non-symbolic stimuli consisting of arrays of dots. For inverse trials, the addend and subtrahend arrays had different arrangements of dots to suggest that different sets of dots were added and removed. The arrays were constructed to ensure that children were using numerosity rather than the correlated continuous variables of dot size, envelope area, or density to make quantity judgments. On half of the trials, the less numerous array had larger dot size, a larger envelope area and a higher density than the more numerous array. The initial set, addend and subtrahend had the same dot size. Thus, children could not accurately predict whether the result set or the comparison set was larger on the basis of correlated continuous variables without considering the numerosity of the sets.

The inversion trials could be solved simply by comparing the initial set and the comparison set. To test whether children were using this strategy, the control trials were structured so that this strategy yielded the correct answer on half of the control problems (simple uneven) and the incorrect answer on the remaining control problems (complex uneven). For example, in the simple uneven problem 41 + 13 − 18 vs. 24, both the result set (36) and the initial set (41) are larger than the comparison set (24) and so children could answer correctly if they simply compared the initial set with the comparison set. In contrast, for the complex uneven problem 45 + 9 − 34 vs. 30, the result set (20) is smaller than the comparison set (30) but the initial set (45) is larger than the comparison set and therefore children would answer incorrectly if they simply compared the initial set with the comparison set.

Children could also base their answers on the relative size of the sets across trials. For example, children might guess that the result set is larger than the comparison set if the initial array or the addend was particularly large, or if the subtrahend or the comparison set was particularly small. The problems were designed so that these strategies would lead to the correct answer on half of the trials and the incorrect answer on the other trials. If children were using this strategy, therefore, we would expect them to perform significantly above chance on the trials where set size was a predictor, and significantly below chance on the trials where set size was not a predictor.

Procedure

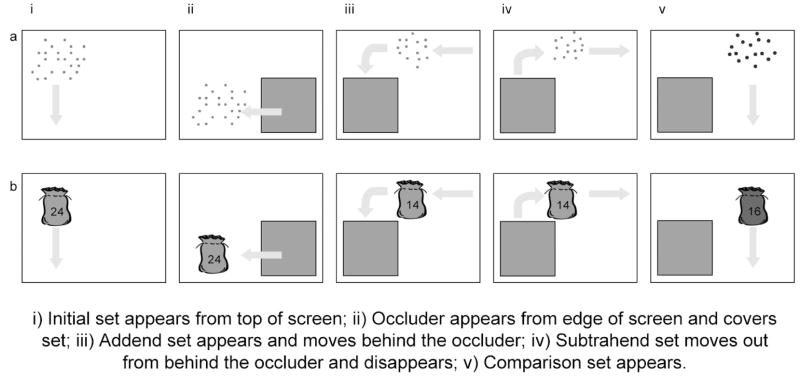
The task was presented on a laptop computer (see Figure 1). In the experimental trials an array of red dots (the initial set) appeared and was covered up by an occluder. A further red dot array (the addend) appeared and moved behind the occluder, then a third red dot array (the subtrahend) moved out from behind the occluder and off the screen. Finally a blue dot array (the comparison set) appeared and moved beside the occluder. The animations were described to children by the experimenter saying “Look! Here come some red dots… They are being covered up… Here come some more red dots, now they are all behind there… Look some of the red dots are coming out and going away… Here come some blue dots. Are there more red dots behind the box or more blue dots?”

Figure 1.

Schematic of animations shown to children with a) non-symbolic stimuli (Experiment 1), and b) symbolic stimuli (Experiment 2 & 3).

The children completed 10 experimental trials consisting of 4 inversion and 6 control trials. Prior to the experimental trials the children completed 6 practice trials. The first two practice trials involved a simple numerical comparison of a red-dot and blue-dot array. The second two practice trials involved a comparison of a red-dot and a blue-dot array after the red set had undergone an addition transformation. The final two practice trials involved a comparison of a red-dot and blue-dot array after the red set had undergone a subtraction transformation.

Results and Discussion

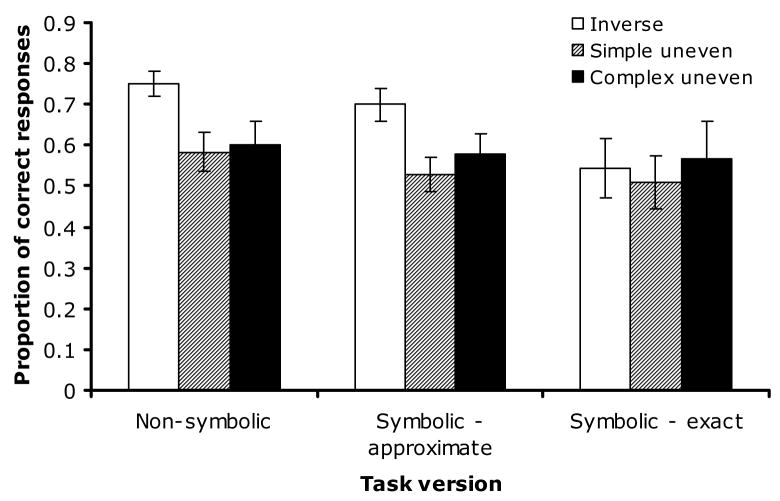
Children performed significantly above chance (50%), both for the inverse trials (75%, t(19) = 7.96, p < .001, d = 1.78) and for the control trials (59.2%, t(19) = 2.77, p = .012, d = 0.62; see Figure 2). Thus, children showed some ability to perform successive operations of addition and subtraction on nonsymbolic, large approximate numerosities. Most important, children performed more accurately on the inverse than on the control trials, (t(19) = 3.30, p = .004, d = 0.78), despite the fact that both these types of problems could be solved correctly by performing successive operations of addition and subtraction. Performance on the inverse trials exceeded performance on the simple control trials (58.3%; t(19) = 2.92, p = .009, d = 0.65), whereas performance on the simple and complex uneven trials (60.0%) did not differ (t(19) =.203, p = .841). Thus, children did not base their answers on a simple comparison between the initial set and the comparison set.

Figure 2.

Mean accuracy (and s.e.m.) on different trial types with non-symbolic stimuli (Experiment 1), symbolic stimuli with approximate comparisons (Experiment 2) and symbolic stimuli with exact comparisons for inverse and approximate comparisons for control problems (Experiment 3).

Children’s scores were analyzed further to determine whether they relied on strategies based on the relative sizes of sets. The children did not make use of the relative size of the initial array/addend (set size predictor 65.8%, set size not predictor 64.0%; t(18) = .298, p = .769). However, they were more accurate on problems where the size of the comparison set predicted the correct response (mean 71.9%) than on problems where the size of the comparison set predicted the incorrect response (54.0%; t(18) = 5.73, p < .001). Although children were not statistically above chance on the problems for which the comparison set predicted the incorrect response (t(18) = 1.37, p = .187), this bias cannot account either for children’s overall above-chance performance or for their superior performance on the inverse problems, since the children scored above 50% on these trials, whereas they would have performed significantly below chance on these trials if they relied on this comparison strategy alone. Finally, the children were biased by the subtrahend in the opposite way to that expected (set size not predictor 76.3%, set size predictor 57.0%; t(18) = −3.76, p = .001): They tended to overestimate the number of red dots remaining after a large number of red dots were taken away. This tendency also cannot account either for children’s overall success or for their superior performance on inverse problems.

There was some evidence that children made more use of the envelope area in their judgments of numerosity than dot size or density. The children were more accurate when the initial, addend and subtrahend arrays had equal density and thus envelope area was correlated with numerosity (71.9%) than when they had equal envelope area and thus density was correlated with numerosity (54.0%; t(18) = 2.73, p = .014). This finding accords with recent research that suggests that envelope area plays a role in adults’ estimates of numerosity (Shuman & Spelke, 2006). Because envelope area was controlled within each type of problem, this effect cannot account for children’s successful performance.

In summary, preschool children can recognize and take advantage of an inverse transformation of large sets when given non-symbolic approximate arithmetic problems. Although children are capable of performing successive operations of addition and subtraction on nonsymbolic numerosities, their performance is reliably enhanced when the two operations are related by inversion. Neither this inversion effect, nor children’s successful performance on problems without inversion, can be explained by numerical comparison strategies or by responses to continuous quantitative variables. Because all the problems involved numbers considerably larger than 4, moreover, children’s success cannot be explained by local knowledge of the inverse relation between addition and subtraction of specific small numbers. Experiment 1 therefore provides evidence for an early-developing, general understanding of the inverse relationship between addition and subtraction that can be applied to abstract nonsymbolic representations of number.

Children’s successful performance in Experiment 1 contrasts with the lack of evidence from previous studies that preschool children have a general understanding of inversion, applicable to problems involving symbolic exact additions and subtractions that they have not yet learned to perform. In the next experiment we begin to explore whether children’s success in Experiment 1 stems from the use of nonsymbolic stimuli or from the use of approximate arithmetic problems. Experiment 2 investigates whether children can identify and use this inverse relationship when they are given large, approximate arithmetic problems involving successive addition and subtraction of symbolic numerical representations.

Experiment 2

Experiment 2 used the method of Experiment 1 with one critical change. Instead of viewing cartoon events involving arrays of visible objects, children viewed cartoon events involving bags of hidden objects whose number was designated symbolically: by a number word and Arabic numeral notation. If children can perform successive addition and subtraction on large, approximate symbolically presented numbers, then children should perform above chance both on inversion problems (x + y − y) and on uneven problems (x + y − z). If children can recognize and exploit the inverse relation of symbolic, approximate addition and subtraction, they should perform reliably better on the inversion problems.

Method

Participants

Thirty-two children (9 male) aged 5 years 2 months to 6 years 3 months (mean 5 years 8.9 months) were recruited from the same database used in Experiment 1.

Task and procedure

The children completed the task used in Experiment 1 with symbolic instead of non-symbolic representations of number. The problems presented were the same as in Experiment 1 and consisted of 6 practice trials (2 comparison, 2 addition, 2 subtraction) and 10 experimental trials (4 inverse, 6 control). The task again was presented on a computer, but the sets were represented by a picture of a bag with an Arabic numeral on the front (see Figure 1). In the experimental trials a red bag (the initial set) appeared and was covered up by an occluder. A further red bag (the addend) appeared and moved behind the occluder, then a red bag (the subtrahend) moved out from behind the occluder and offscreen. Finally a blue bag (the comparison set) appeared and moved beside the occluder. The animations were described to the children by the experimenter saying (e.g.) “Can you help Justin guess if he has more red marbles or more blue marbles… Look he has 42 red marbles… Now they are being covered up… He gets 10 more red marbles… Now they are all behind there… But look, 10 of the red marbles are coming out and going away… Look he has 63 blue marbles… At the end, does he have more red marbles behind the box or more blue marbles?”

Results and Discussion

Children performed significantly above chance on inverse trials (70.0%, t(29) = 4.94, p < .001, d = 0.90) but they were no more accurate than chance on control trials (55.2%, t(28) = 1.47, p = .153; see Figure 2). Children were significantly more accurate on the inverse than on the control trials (t(28) = 3.66, p = .001, d = 0.48). Moreover, children were significantly more accurate on the inverse trials than on the simple uneven trials (52.9%, t(28) = 3.63, p = .001, d = 0.51), and they showed no difference in performance on the simple vs. complex uneven problems (57.8%; t(28) = .724, p = .475). These findings indicate that children’s success on the inverse trials did not depend on an overall strategy to compare only the initial and final arrays.

The children’s responses were examined to determine whether they employed superficial strategies based on the relative size of sets. There was no evidence that children based their answers on the relative size of the initial set/addend or comparison set (initial/addend set size predictor 61.5%, not predictor 59.5%: t(28) = .419, p = .678; comparison set size predictor 63.0%, not predictor 56.0%: t(28) = 1.57, p = .128). There was some evidence that children considered the relative size of the subtrahend in making their judgments. As in Experiment 1, however, this effect was in the opposite direction to that expected: the children were more accurate on trials in which the size of the subtrahend predicted the incorrect answer (69.0%) than on trials on which the size of the subtrahend predicted the correct answer (55.2%; t(28) = −2.69, p = .012).

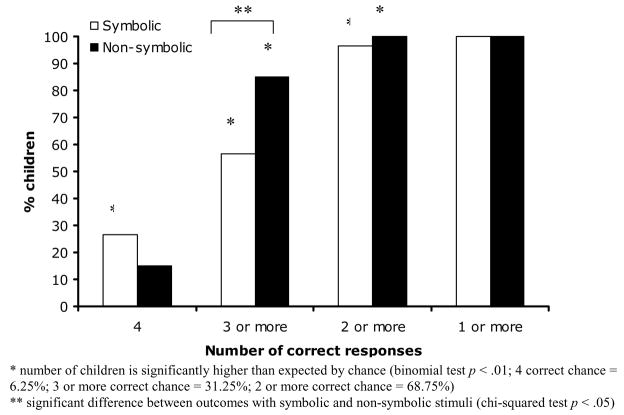
To determine whether understanding of inversion was more widespread and consistent with non-symbolic or symbolic stimuli the data from Experiment 2 were compared with those from Experiment 1. The number of children who answered 1-or-more, 2-or-more, 3-or-more and all 4 inverse trials correctly was examined (see Figure 3). Performance profiles were highly similar across the two studies, and in neither study did the overall results appear to reflect the performance of a small subset of children.

Figure 3.

Percentage of children giving different numbers of correct responses on inverse trials with non-symbolic (Experiment 1) and symbolic (Experiment 2) stimuli.

Experiment 2 provides evidence that preschool children can identify an inverse relationship when they are given large, approximate arithmetic problems involving successive addition and subtraction of symbolic numerical representations. This finding contrasts with the lack of evidence from previous research that preschool children understand the effects of inversion on exact, symbolic representations of large number (Klein and Bisanz, 2000; Rasmussen et al., 2003, Vilette, 2002). Children’s performance in our experiments suggests that they can identify inverse relationships involving approximate representations of large number earlier than they can do so with exact representations of large number.

It is possible, however, that the successful performance of children in Experiment 2 stemmed from the method that we used rather than from the focus on approximate numerical representations. The method used in Experiment 2 differs from those of previous research, because we did not require children to produce an answer, either verbally or by constructing a set. It is possible, therefore, that children would have succeeded in our task even if given problems that required exact number representations. Experiment 3 investigated this possibility by testing children’s understanding of inversion using the method of Experiment 2 with numbers that required exact comparisons.

Experiment 3

Method

Participants

Seventeen children (5 male) aged 5 years 3 months to 6 years 2 months (mean 5 years 10 months) were recruited from the same database used in Experiment 1.

Task and procedure

The task and the procedure were the same as Experiment 2 with only one change: the values of w presented on inverse trials were altered so that inverse trials required exact rather then approximate comparisons. The comparison sets for the inverse trials were ±1 or 2 from the sum (e.g. for the problem 36 + 40 − 40 the comparison set was 35; see Table 1). The comparison sets for the control trials were the same as in Experiment 2.

Results and Discussion

Children performed at chance levels both on inverse trials (54.4%, t(16) = 0.614, p = .548) and control trials (53.9%, t(16) = 0.746, p = .466; see Figure 2). There was no difference between children’s accuracy for the inverse and the control trials (t(16) = 0.047, p = .963) or between accuracy on simple or complex control trials (51.0% vs. 56.9%; t(16) = 0.511, p = .616). These results indicate that children did not recognize and take advantage of an inverse relationship involving large numbers when an exact comparison was required.

Further analyses compared children’s performance in Experiment 3 to their performance in Experiment 2. Children were more accurate on inverse problems in Experiment 2 than Experiment 3 (F(1,46) = 4.194, p = .046), but there was no difference in performance on control problems across the two experiments (F(1,45) = 0.044, p =.834). Children’s contrasting performance in the two experiments provides evidence that children show a general understanding of the inverse relation only when they are presented with problems of approximate nonsymbolic or symbolic arithmetic.

The findings of Experiment 3 provide evidence that children fail to exhibit knowledge of inversion when presented with exact problems involving large numbers. Nevertheless, the experiment does not clarify the reasons for this failure. It is possible that children’s successful performance in Experiment 2 depended on a mapping of each symbolic number in the problem to a nonsymbolic numerosity. Because nonsymbolic number representations are imprecise, the children in Experiment 3 may have failed to discriminate the difference between the initial and final numerosities. Alternatively, children’s contrasting performance in Experiments 2 and 3 may stem from imprecision in children’s memory for the first numerical value. When preschool children are presented with a long inversion problem beginning with one exact large number and ending with another, children may have attempt to compare the initial and final numbers but fail to do so accurately they only remember the initial number’s approximate value. Regardless of whether the limits to preschool symbolic calculation stem from limits to discrimination or memory for numerical magnitudes, Experiments 2 and 3 provide evidence that preschool children master inversion only for approximate large-number problems.

General Discussion

These experiments provide evidence that preschool children with no history of formal instruction in mathematics understand a central logical principle of arithmetic. Moreover, children apply this understanding successfully both to non-symbolic and to symbolic representations of large, approximate number, but not to symbolic representations of large, exact number. Although young children’s ability to calculate and manipulate exact numbers may be restricted to very small number problems (Levine, Jordan & Huttenlocher, 1992), their understanding of logical principles in relation to approximate numbers extends well beyond the small-number range.

Our first experiment replicates previous findings of nonsymbolic numerical abilities in preschool children (e.g., Barth et al., 2003, 2005, 2006; Brannon, 2002; McCrink & Wynn, 2004), and it extends those findings in two ways. First, performance in our studies on problems of the form x + y − z provides evidence that preschool children can perform two successive operations of addition and subtraction on large approximate numerosities presented in nonsymbolic form (as arrays of dots). Second, children’s superior performance on problems of the form x + y − y, relative to the problems involving three discriminably different quantities, provides evidence that children appreciate the inverse relation between these two operations: a fundamental logical principle of arithmetic. These findings add to the considerable evidence that nonsymbolic, approximate number representations are central to human knowledge of mathematics (Dehaene, 1997; Gallistel, 1990).

Recent research provides evidence that preschool children can also operate on symbolic representations of large, approximate numerosity to compare quantities (Lipton & Spelke, 2005) and perform approximate addition and subtraction (Gilmore et al., 2007). The findings of our second experiment suggest that these abilities may be more fragile than abilities to compare, add and subtract non-symbolic numerosities, because the children in the present studies did not reliably solve control problems involving successive addition and subtraction of distinct symbolic numerosities. Nevertheless, children showed robust understanding of the inverse relation between these operations on symbolic, approximate numbers. Thus, a central aspect of the logical structure of arithmetic is used by children spontaneously, not only when they are presented with nonsymbolic numerosities but when they are presented with numbers in symbolic form.

Children’s performance on the symbolic inverse problems in Experiment 2 is striking, because they have had no instruction whatever in symbolic arithmetic. It is possible that children develop understanding of logical principles of symbolic arithmetic through experience with verbal counting and small-number arithmetic (Baroody, 1999; Canobi, 2005). Alternatively, children may develop this understanding out of an earlier understanding of nonsymbolic numerical relationships and operations. Further studies are needed to determine both the developmental relationships among these abilities in preschool children, and the detailed characteristics of children’s understanding of symbolic number in relation to nonsymbolic number (see Gilmore et al., 2007).

Children’s successful recognition and use of inversion for large approximate quantities contrasts with their failure to use inversion for large exact problems. Children’s mastery of the logical structure of arithmetic may therefore be first expressed in contexts involving approximate number representations (whether symbolic or nonsymbolic) and only later extend to the exact arithmetic tasks that children encounter in school. Further work is necessary to establish the developmental order and causal relations between these abilities.

These findings may have implications for arithmetic instruction. At present most instruction in arithmetic focuses almost exclusively on exact symbolic representations of number. Contrary to these approaches, children may benefit from instruction with approximate symbolic and approximate non-symbolic arithmetic problems. These types of problems may allow children to focus easily and spontaneously on the abstract logical principles that underlie arithmetic. Since many children have difficulties acquiring mechanical computation skills, the use of problems similar to those of the present experiments may allow young children to make sense of new and challenging numerical tasks by harnessing their preexisting understanding of the conceptual relations at the core of arithmetic.