The scaling of leaf area and mass: the cost of light interception increases with leaf size

Abstract

For leaves, the light-capturing surface area per unit dry mass investment (specific leaf area, SLA) is a key trait from physiological, ecological and biophysical perspectives. To address whether SLA declines with leaf size, as hypothesized due to increasing costs of support in larger leaves, we compiled data on intraspecific variation in leaf dry mass (LM) and leaf surface area (LA) for 6334 leaves of 157 species. We used the power function LM=α LA^β to test whether, within each species, large leaves deploy less surface area per unit dry mass than small leaves. Comparing scaling exponents (β) showed that more species had a statistically significant decrease in SLA as leaf size increased (61) than the opposite (7) and the average β was significantly greater than 1 (β_mean=1.10, 95% CI 1.08–1.13). However, scaling exponents varied markedly from the few species that decreased to the many that increased SLA disproportionately fast as leaf size increased. This variation was unrelated to growth form, ecosystem of origin or climate. The average within-species tendency found here (allometric decrease of SLA with leaf size, averaging 13%) is in accord with concurrent findings on global-scale trends among species, although the substantial scatter around the central tendency suggests that the leaf size dependency does not obligately shape SLA. Nonetheless, the generally greater mass per unit leaf area of larger than smaller leaves directly translates into a greater cost to build and maintain a unit of leaf area, which, all else being equal, should constrain the maximum leaf size displayed.

1. Introduction

The size of living organisms and their organs mediates a variety of biological processes (Peters 1983; Leonard & Robertson 1994). Terrestrial plants are not an exception. Tree size influences gas exchange rates to such an extent that the decrease of water transport efficiency with size poses a limit to maximum tree height (Koch et al. 2004). At the organ level, size dependency may influence processes as disparate as the evolution of fruit size and dispersal system (Herrera 2002) or the partition of biomass to leaves, stems or roots (Enquist & Niklas 2002). The scaling of leaf mass to leaf area is a particularly relevant relation because it directly impacts the specific leaf area (SLA), the amount of light-capturing surface area that is deployed with a given investment of dry mass. Given the direct relationship between SLA and light interception (Reich et al. 1998), SLA represents a potential revenue stream and hence is analogous to a potential rate of return on dry mass investment in terms of light capture (Westoby et al. 2000). Consequently, SLA is intimately connected to the resource use economy of the plant (Reich et al. 1997, 1998; Wright et al. 2004), its relationships with decomposers and herbivores (Cornelissen et al. 1999) and the way plant species replace each other during succession (Shipley et al. 2006). The understanding of size-related biophysical limitations of SLA is therefore of paramount relevance on physiological and ecological grounds.

Arguments have been made both in favour of and against the idea that larger leaves should require proportional greater investment in support and structure. Some have proposed that mechanical support and dry mass investments per unit leaf area should scale positively with size to compensate for mechanical damage and gravity, since leaf laminas are cantilevered structures (Howland 1962; Grubb 1998). Alternatively, larger leaves may require less investment in support in general, because they reduce the number of leaves that have to be produced per shoot or plant to support a given leaf area (Givnish 1979). Additionally, across temperature gradients, size may decrease and density increase in acclimation to higher temperatures (Givnish 1987; Wright et al. 2005), and as a result leaf mass per unit area would decrease with increasing size.

The empirical evidence from published reports is inconclusive with respect to SLA and leaf size. Several studies have found that larger leaves need more specific support per unit leaf area than smaller ones measured as investment in petioles, lamina dry mass, twig size or venation stiffness (Shipley 1995; Grubb 1998; Gunn et al. 1999; Niklas 1999; Niinemets & Kull 1999; Niinemets et al. 2006). In contrast, Niinemets & Kull (1994) reported that in a comparison of 83 woody temperate species, SLA increased with leaf size. Ackerly & Reich (1999) also showed a significant positive relationship of SLA with leaf size across an alternative set of 85 species of angiosperms.

Thus, there is no consensus among disparate studies regarding whether SLA declines, increases or remains constant with increasing leaf size. However, the studies described above pull together a variety of uncontrolled environmental and phylogenetic sources of variation, which may influence the scaling relations. In fact, several of the previous studies had contradictory results when mixing study scales: Shipley (1995) found that leaf mass scaled allometrically to leaf area when compared across species, but isometrically within species; Fonseca et al. (2000) reported that community-average leaf size-SLA relationships showed opposite trends than across-species patterns; and several papers highlight that SLA changes during plant ontogeny (Thomas & Bazzaz 1999), which may in turn shift the SLA-leaf size allometry if leaf size did not change accordingly at the same rate and in the same direction than SLA (Sack et al. 2002).

Habitat, phylogeny and development may confound the characterization of the leaf size effect on SLA in broad interspecific comparisons. Therefore, we attempted to isolate putative confounding factors as outlined here and fully explained in the methods section. In short, we compiled data from sources where leaf dry mass (LM) and leaf surface area (LA) were measured in at least 10–15 independent replicates per species in a single environment (replicates came from a variable number of individual plants, depending on the original source, see table 1) and at a comparable developmental stage (i.e. fully expanded mature yearly leaves). Then we examined the scaling relationship of LM to LA within each of those species, evaluating LM=α LA^β by log-transforming this function, thus converting the power exponents to linear slope scores, to test the null hypothesis that β=1. The value of β>1 indicates that larger leaves have lower SLA, whereas β<1 means the opposite. If LA and LM scale isometrically, then changes in leaf size have no impact on SLA. We gathered a large data compilation of 157 species, expanding the scope of inference from previous intraspecific studies typically made with far fewer species.

Table 1.

Sources of data used in this compilation. See electronic supplementary material for species-specific data. Growth form categories: T, tree; S, shrub; V, vine; H, herb; G, grass. Leaf habit in parentheses: (d), deciduous; (e), evergreen; (sd), semi-deciduous.

data source	reference	no. of species	sample size per species	no. of plants sampled per species	growth form	ecosystem	region
Baraloto	Ann. For. Sci. in press	35	10–70	3–21	T(e)	tropical forest	French Guiana (S America)
Shipley	New Phytol.153: 359–364	23	10	5	G(d), H(d), S(d), S(e)	grassland	Canada (N America)
Reich1	Ecology80: 1955–1969	20	15–50	10	T(e), S(e)	tropical forest	Venezuela(S America)
Roderick	Ann. Bot.89: 537–542	15	30	—	T(d), T(e), H(d), V(e), H(e)	garden	Australia
Prior	Funct. Ecol.17: 504–515	14	18	6	T(d), T(sd), T(e)	seasonally dry tropical forest	Australia
Reich2	unpublished data	12	10–15	—	G(d), H(d), T(d)	temperate praire-savanna	MN, U.S.A. (N America)
Milla1	unpublished data	9	50	15	S(d), S(e), V(e)	mediterranean	Spain (Europe)
Williams-Linera	Plant Ecol.149: 233–244	7	100	8	T(e), T(d)	tropical forest	Mexico (C America)
Reich3	unpublished data	6	10–15	10–15	T(e), G(e)	Tropical forest	Brazil (S America)
Kudo	Ecoscience6: 439–450	6	20	20	S(e), H(d), S(d)	Tundra	Sweden (Europe)
Reich4	Ecology80: 1955–1969	3	15–25	10	H(d), S(d)	alpine	CO, U.S.A. (N America)
Niinemets	unpublished data	2	60–400	3–5	T(d)	temperate forest	Estonia (Europe)
Roumet	New Phytol.143: 73–81	2	150	39	G(d)	mediterranean	France (Europe)
Castro-Díez	Trees11: 127–134 and unpublished data	2	50	15	S(e)	mediterranean	Spain (Europe)
Milla2	unpublished data	1	34	10	S(e)	alpine	Spain (Europe)

2. Material and methods

(a) Compilation and filtering of data

We aimed to isolate as far as possible the effect of changing leaf size from other confounding factors. To do so, we searched for published papers in which LA and LM were measured independently in at least 10–15 replicates (leaves) per species, per developmental stage of leaves and plants, per canopy position and per location or experimental unit in experimental-gradient studies. We only considered studies of adult plants (no seedlings or saplings). Leaf ontogeny was standardized by including only fully mature current-year leaves. Also, for each individual species, data came from leaves in similar light environs and from a single site or plant community. This allowed us to calculate the scaling exponent of LM=α LA^β for each species separately. In this way, variation in factors such as differences between species or environment was kept as low as possible. This procedure constrained the number of data sources suitable for the compilation, since most multi-species studies had to be discarded due to low sample size per species.

Original, raw data for each measured leaf were obtained from the corresponding authors of published reports, or otherwise were gathered from our own databases or those of colleagues (table 1). When an original database supplied data for the same species in different environmental situations, we extracted the data subset that came from the control treatment in an experiment, the most typical situation in a gradient study, or an arbitrarily chosen condition (e.g. sun leaves instead of shade leaves). However, in case the fit of the regression equations of LM to LA was not tight enough to fit our criteria below, we selected the treatment level or location that yielded the best goodness of fit.

Initially, we compiled data for 194 species from 18 original sources. To obtain a reliable set of β, this initial database was purged so that all species surpass the following filtering criteria: (i) to be included in the final compilation, any species must show a statistically significant relation between (log)LA and (log)LM, and the goodness of fit of that relation should be higher than r²=0.80 and (ii) the range of LA variation should be at least twofold within each species. After applying the above filters, our final compilation comprised 6334 leaves of 157 species coming from 15 original sources (table 1).

(b) Calculations and statistics

Leaf mass (LM, g) and projected one-sided leaf surface area (LA, cm²) were assumed to be related to each other as defined by the following power function:

$$\text{LM}=\alpha {\text{LA}}^{\beta }.$$

To facilitate computation and visualization, we log-linearized the above function, thus converting the power exponents to linear slope scores

$$\text{log}(\text{L}\text{M})=\text{log}(\alpha )+\beta \text{log}(\text{LA}).$$

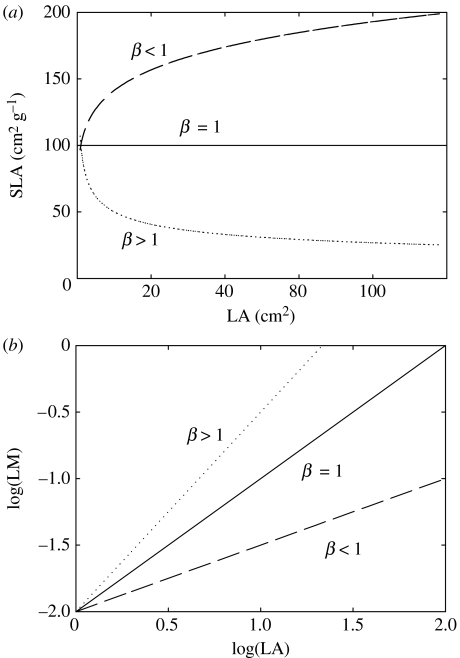
In figure 1, it is shown how a given trend on a LA–SLA scatter plot (figure 1a) translates into a (log)LA versus (log)LM slope (β) (figure 1b). Basically, β>1 indicates that SLA decreases as LA increases, whereas β<1 means the opposite. If LA and LM scale isometrically, then changes in leaf size have no impact on SLA.

Figure 1.

(a) Theoretical relationships between leaf area (LA, cm²) and specific leaf area (SLA, cm² g^-1) assuming three scenarios: (i) SLA is unaffected by leaf size, (ii) SLA increases as leaf size increases, and (iii) SLA decreases as leaf size increases. (b) Reflection of the scenarios depicted in (a) to the scaling of LA to leaf mass (LM, g). β=exponent of the power function LM=α LA^β. See text for further explanations.

To calculate slopes and intercepts of (log)LA versus (log)LM, we used type II linear regression procedures. Type I (least squares) regression calculates regression parameters so that error in the dependent (y) variable is minimized. This assumes no measurement error in the independent (x) variable. Type II, or reduced major axis (RMA), regression minimizes both the error associated to variation in dependent and independent variables. The RMA regression is more appropriate when there is no a priori functional relation of dependency between y and x variables, and when the x variable is subjected to measurement errors (Sokal & Rohlf 1995). We fitted a RMA regression line to the (log)LM versus (log)LA data separately for each species. Also, for each species, a likelihood ratio test was run to evaluate whether β of the RMA line was significantly higher, equal or lower than 1 (Warton & Weber 2002). Moreover, to test the initial hypothesis that β=1 in the complete dataset, we conducted a one sample t-test of the RMA β set against β=1. Given the nature of our hypothesis regarding allocation of mass to mechanical support, we assess LM as a function of LA, but results can easily be examined in the opposite relationship (Niklas et al. 2007). Type II regression procedures were carried out using Smatr (v. I, Falster, D. S., Warton, D. I. & Wright, I. J. http://www.bio.mq.edu.au/ecology/SMATR). Detailed description of the methods for assessing whether β varies with phylogenetic history, plant life form, or ecosystem of origin are provided in the electronic supplementary material.

3. Results

Our 6334 leaves, 157 species dataset covered a range of LA from 0.03 (the smallest leaf of Empetrum hermaphroditum) to 1872 cm² (the largest leaf of Sterculia pruriens). This spans six orders of magnitude and includes most of leaf size variation on Earth. The compilation included representatives of most plant growth form types and major biomes on Earth.

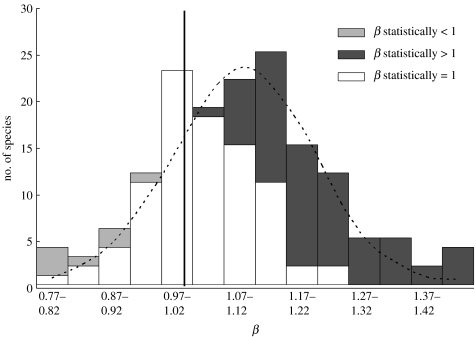
On average, the exponent β for the power function LM=α LA^β averaged 1.10 for the 157 species (figure 2). This average for β was significantly higher than 1 in a one-sample t-test (p<0.001), with the 95% CI for β of 1.08–1.13. Thus, LM tended to increase proportionally faster than LA with each order of magnitude increase in both. Consequently, larger leaves showed lower SLA, on average.

Figure 2.

Frequency distribution of the power exponents of LM=α LA^β encountered in the 157 species of this compilation. Different patterns represent the statistical significance of the likelihood ratio test against β=1 for each species. Reference line: β=1.

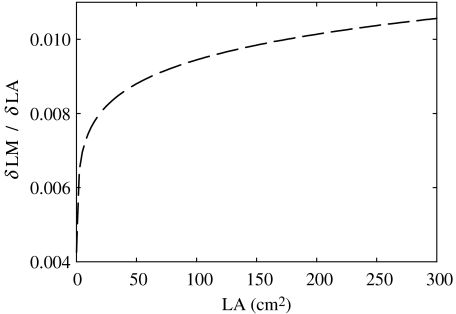
The numerical difference between 1.10 and 1.00 may appear small. To show graphically how small differences in β can translate into large differences in SLA when leaves differ in size, we modelled the rate of variation in LM as a function of LA as the point derivative of LM on LA (δLM/δLA=(a β) LA^(β−1)) for each leaf of the compilation, assuming β=1.10, and LA=LA of the actual leaf. δLM/δLA reflects the instantaneous rate of increase in LM at a given value of LA. In figure 3, we plot δLM/δLA for the whole range of leaf sizes of the study. It can be appreciated how the rate of LM increase per unit increase in leaf area is higher in larger-leaved species.

Figure 3.

Instantaneous rate of change of LM with respect to increasing LA (δLM/δLA) at different ranges of LA. This theoretical relation assumes β=1.10 (β average of the 157 species studied here).

However, it is equally remarkable that β showed a great degree of variability among the species, ranging from 0.776 to 1.764. Of the 157 species, 120 yielded a β score higher than 1, with 61 of those having a statistically higher β when tested separately against β=1 (i.e. lower limit of 95% CI higher than 1), compared with 89 species that were not statistically different than 1 or 7 with β significantly less than 1 (figure 2). Thus, the tendency for SLA to decrease with increasing leaf size is strong, but not obligate.

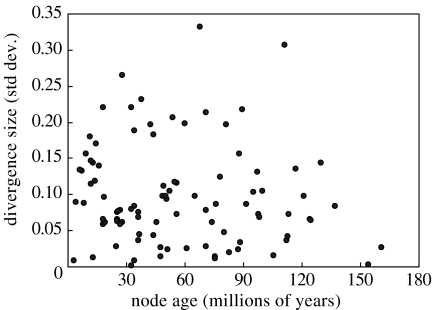
The tendency of phylogenetically related organisms to resemble each other did not translate in this study to similar β scores for related species and/or clades. Tree-wide conservatism of β scores was not significant (p>0.05 for each of the fully resolved 50 trees, results not shown). Moreover, node-level analysis revealed that only 5 out of 94 bifurcating nodes showed significant conservatism of β scores at p=0.05 (results not shown). We did not find any trend towards significant conservatism in older compared to younger nodes, as shown in figure 4 (no regression model fitted the scatter), which also suggests no major influence of phylogenetic inertia on β scores of the study species. Thus, overall, the influence of phylogeny on the slope of LM to LA was negligible.

Figure 4.

Divergence size of β scores (standard deviation of subtended nodes) as a function of node age of the phylogenetic tree of the seed plants, pruned for the study species. No simple regression model explained a significant fraction of the scatter. (see electronic supplementary material for calculations)

The graphs in figure 5 of the electronic supplementary material show how several characteristics of the raw data and of the (log)LM versus (log)LA regression fit affected: (i) the β score obtained for each species, and (ii) the probability of β being significantly different from 1. First, β was neither related to the number of replicates used to infer each species-specific RMA equation nor was it to the range of leaf sizes within a given species (figure 5a,b electronic supplementary material). Additionally, we tested three statistical factors for possible role in causing species' β values to differ significantly from 1: (i) the number of paired-data used to calculate the RMA equation, (ii) the range of variation in the arbitrarily considered independent variable (LA), and (iii) the goodness of fit of the RMA equation to the data. Overall, however, none of those three factors affected the outcome of the statistical test (figure 5c–e electronic supplementary material).

The scaling exponent, β, neither differed among growth forms (p=0.59, not shown) nor between plants showing deciduous, evergreen or semi-deciduous leaf habit (p=0.45, not shown), or between woody and herbaceous species (p=0.73, not shown). Also, β did not differ among species from different ecosystems (p=0.38, not shown). Furthermore, we neither found statistically significant relationships, nor trends, between β and either mean annual temperature or annual rainfall at the study sites (data compiled from papers, or alternatively from national weather services, not shown). Also, we attempted several multiple regression and discriminant MANOVA techniques using the above plant and site traits as factors and β as the dependent variable, but no significant trend arose (not shown).

4. Discussion

Averaging across the 157 species examined here, leaf mass scales disproportionately faster than LA. Large leaves of a given species tend to have higher mass per unit leaf area than small leaves of the same species, for the majority of species. Since LM is a power function of LA, the allometric effect varies at different ranges of leaf size. For instance, for two species sharing the same scaling exponent (β=1.07) but differing in average leaf size, the allometric effect differs in magnitude. A change from a small 96 cm² leaf of Eucalyptus tetrodonta to a large 622 cm² of the same species corresponds to a 22% decrease in SLA. In contrast, Quercus coccifera, which is on average small leaved, also experiences a decrease of SLA with increasing leaf size, though to a lesser extent (9%). The increase with leaf size in leaf mass invested per unit leaf area corresponds directly to increased construction and maintenance costs of displaying a unit of leaf area. Construction costs (energy units) per unit leaf area are directly related to the mass invested per unit leaf area; for instance, construction costs per unit leaf area were strongly correlated and proportionally scaled ≈1 : 1 with the g of dry mass per unit leaf area, based on a re-analysis (log(g glucose per m²)=0.0876+1.04587 (log(1/SLA)); n=121, r²=0.98, p<0.001) of data for 121 plant species (cf. Villar & Merino 2001). Maintenance costs (based on dark respiration rates per unit leaf area) increase linearly with dry mass per unit leaf area within each of 11 plant species (similar re-analysis of data from Lusk & Reich 2000), as is generally the case. Hence, the increase in mass per unit leaf area of larger than smaller leaves directly translates into a greater cost to build and maintain a unit of leaf area, which, all else being equal, should constrain the maximum leaf size displayed.

Our β=1.10, central tendency at the within-species level, is generally in accordance with broad among-species trends worldwide (Niklas et al. 2007) and more limited intraspecific studies of approximately 20 species (Niklas et al. 2007; Price & Enquist 2007). In a comparison of mean values for 1943 species, Niklas et al. (2007) found that overall, large leaves deploy less light-absorbing area per unit of dry mass investment than small leaves, and that additionally suggests that larger leaves require comparatively more nutrients per unit dry mass and thus probably allocate more nutrients to structural support rather than productive tissues. However, the tendency towards low leaf area per unit dry mass in larger leaves was much more muted in the large interspecific comparison (slope of 0.98 for (log)LA versus (log)LM, equivalent to a slope of 1.02 for (log)LM versus (log)LA, as done in our study), and was not observed at all for trees, as a subset of the overall dataset. Hence, the tendency towards diminished leaf area display per g investment in larger leaves is more pronounced as a phenotypic response within species than as a genotypic pattern among species. This is not necessarily surprising, as interspecific patterns (as in Niklas et al. 2007) could result entirely from inverse selection pressures for leaf size and SLA, and would not require any intrinsic phenotypic allometry of LM to LA. Our intraspecific results, therefore, suggest that there are biophysical and physiological consequences of increasing leaf size that are independent of current interspecific differences in multiple leaf trait strategies that may have arisen from selection in the past. Taken together, both reports (Niklas et al. 2007 and our current paper) support the idea of ‘diminishing return’ on mass investment with increasing leaf size using light capture potential as a measure of potential return, due to increased requirement for costly material support for a given leaf area with increasing leaf size.

At this point, it is important to highlight that, in spite of the β=1.10 central tendency, we found a remarkable range of scaling exponents (from β=1.764 to β=0.776) among the 157 study species. Thus, the size-dependent proportional shift in SLA across the observed range of leaf sizes (SLA_VAR, see electronic supplementary material), although generally smaller than 1 (average=0.87), is higher than 1 for a fair amount of species. Surprisingly, this variation was unrelated to leaf habit, growth form, ecosystem of origin or climate, which are typical drivers of differences in plant traits (Wright et al. 2004). Additionally, the range of the LA and SLA spectra that each species occupies was not related to variation in β among species (analyses not shown). It is also important to reflect on the consequences of changing LA on SLA from a quantitative viewpoint. Tripling LA for the leaves of a given species, and assuming β=1.10, produces a 10% decrease in SLA. Small as it may be, this drop in SLA increases constructions costs at the leaf level, which, scaled to the whole-plant level (i.e. multiplied per the number of leaves produced by an individual plant), should imply a significant increase in the pool of resources required to build light capturing leaf area. In conclusion, we found that a given species could possess almost any kind of LM–LA relationship. Nevertheless, there was a significant central tendency for larger leaves to show lower SLA. Hence, more often than not, the biomass (and related construction and maintenance) costs of deploying light-absorbing leaf area are higher for larger than for small leaves.

Supplementary Material

Supplementary materials A–E

A. Explanation of supplementary material C & D. B. Calculations of the effects of phylogeny, life form, and ecosystem of origin on β. C,D. List of study species together with taxonomical and growth form affiliation, and data source provenance. E. Scatter plots of the β RMA slope, and p-value of the likelihood ratio test against β=1, against log-scaled sample size (n), range of leaf area variation (δLA), and goodness of fit (r²)