Abstract
Studies of the end-Permian mass extinction have emphasized potential abiotic causes and their direct biotic effects. Less attention has been devoted to secondary extinctions resulting from ecological crises and the effect of community structure on such extinctions. Here we use a trophic network model that combines topological and dynamic approaches to simulate disruptions of primary productivity in palaeocommunities. We apply the model to Permian and Triassic communities of the Karoo Basin, South Africa, and show that while Permian communities bear no evidence of being especially susceptible to extinction, Early Triassic communities appear to have been inherently less stable. Much of the instability results from the faster post-extinction diversification of amphibian guilds relative to amniotes. The resulting communities differed fundamentally in structure from their Permian predecessors. Additionally, our results imply that changing community structures over time may explain long-term trends like declining rates of Phanerozoic background extinction
Keywords: mass extinction, end-Permian extinction, Karoo Basin, food webs, extinction cascades
1. Introduction
Mass extinctions represent times of severe ecological crisis in the Earth's past. The history of mass extinctions documented in the fossil record is one of the geosciences' crucial contributions to the assessment of human impact on the Earth today (May 2001). Although numerous studies have focused on distinguishing background from mass extinctions, measuring extinction magnitudes, identifying primary abiotic causes, searching for clade-based selectivity and examining biotic recovery (Sepkoski 1996; Solé et al. 2002; Benton & Twitchett 2003; Wang 2003; Lockwood 2004; Jablonski 2005), less attention has been paid to the role of community structure in the propagation of or resistance to perturbative mechanisms. Understanding the influence of community structure on responses to extinction mechanisms is important because many of the species that went extinct during these episodes probably did so in response to cascading secondary effects on their ecological communities (Vermeij 2004; Angielczyk et al. 2005; Roopnarine 2006). Moreover, even if the physical nature of mechanisms that cause mass extinctions varied little during the Phanerozoic, the structures and compositions of affected communities and ecosystems have changed significantly (Vermeij 1977; Bambach 1993; McGhee et al. 2004; Wagner et al. 2006).
The largest mass extinction recorded in the fossil record is the end-Permian mass extinction (approx. 251 Myr ago). It has been estimated that at least 80% of all marine invertebrate animal species and up to 74% of terrestrial animal families disappeared at this time (Erwin et al. 2002; Benton & Twitchett 2003; Benton et al. 2004; Ward et al. 2005), and the post-extinction Early Triassic world was characterized by degraded terrestrial and marine ecosystems (Looy et al. 1999; Pruss & Bottjer 2004). We investigated the potential role of community structure in this event using a numerical network simulation model (cascading extinction on graphs, CEG) to examine the extent to which food-web topology promotes or inhibits the propagation of disruptions through a community (Roopnarine 2006). We measure community resistance as the number of secondary extinctions resulting from a specific disruption or perturbation, with secondary extinction defined as the extinction of a species owing to the elimination of dependencies on at least one other species within the community.
We applied the CEG model to three terrestrial, tetrapod-dominated palaeocommunities from the Late Palaeozoic and Early Mesozoic of the Beaufort Group, Karoo Basin, South Africa: the Middle Permian Eodicynodon, end-Permian Dicynodon and the Early Triassic Lystrosaurus biostratigraphic assemblage zones (Wordian, Changhsingian and Induan–Olenekian stages, respectively; Rubidge 1995, 2005). The Dicynodon and Lystrosaurus zones occur immediately before and immediately after the end-Permian mass extinction, respectively. We focused on bottom-up disruptions of primary productivity for three reasons. First, considerable evidence indicates widespread declines in primary production during several major biodiversity crises, including the end-Permian and Cretaceous–Tertiary extinctions (Zachos et al. 1989; Knoll et al. 1996; Looy et al. 2001). Second, the modern biodiversity crises, comprising primarily the loss of species of high trophic levels owing to habitat destruction or overexploitation, have not yet led to major top-down propagations of secondary extinctions (Vermeij 2004), though the effects of top-down trophic cascades can be demographically significant (Myers et al. 2007). Third, the increasing human exploitation of species at lower trophic levels, our expanding control of photosynthetic resources (Diamond 2005) and the growing risk of bottom-up perturbations driven by climate change (Orr et al. 2005) heighten the need to understand the potential of cascading-up effects.
(a) Metanetwork properties
The first step in applying the CEG model to the palaeocommunities is the construction of an ecologically plausible guild-level representation of trophic relationships within each community, termed a metanetwork. Each guild consists of species with the same potential prey and predators, and links between guilds represent sets of potential trophic interactions (see the electronic supplementary material, table 1). Links were assigned using simple rules based on fundamental ecological principles and morphological characteristics of the organisms in the various communities. In this sense, guilds are estimations of trophic species, a concept used frequently in the reconstruction of modern food webs, and represent sets of species with identical prey and predators (Briand & Cohen 1984; Williams & Martinez 2000). However, our guilds reflect palaeobiological uncertainty in the specification of identical sets of predators and prey to different fossil species.
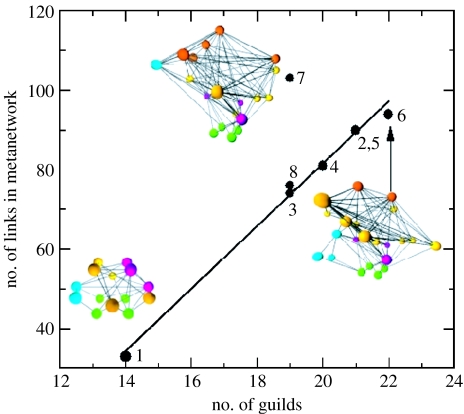
Published connectances for modern communities (connectance measured as the ratio of links between trophic species to the square of trophic species richness) range from 0.026 to 0.315 (Dunne et al. 2002a,b). The connectances of our Karoo metanetworks fall within this range: Eodicynodon, 0.204; Dicynodon, 0.194 and Lystrosaurus, 0.285. We expect our values to be towards the high end of the modern range because metanetwork guilds include more taxa than do trophic species, making community guild richness lower than trophic species richness. Our reconstruction of a highly resolved food web for the modern marine community of San Francisco Bay, comprising 1312 invertebrate and vertebrate species assigned to guilds using the same rules that were applied to the Karoo metanetworks, yields a connectance of 0.192, showing that our methodology generates reasonable food webs when applied to modern data (data available at http://zeus.calacademy.org/SFBaynetwork). The Lystrosaurus zone metanetwork has an anomalously greater connectance compared with other zones in the Beaufort Group (figure 1), primarily owing to the greater representation of amphibian guilds relative to amniote guilds. Since Early Triassic amphibians were closer ecological analogues to extant crocodilians than to most extant lissamphibians, we reconstructed amphibians in all zones as feeding at multiple trophic levels both ontogenetically and as adults, and in freshwater and terrestrial habitats.
Figure 1.
Connectance or density of interguild links for eight Permo–Triassic stratigraphical assemblage zone communities from the Karoo Basin. 1, Eodicynodon (Wordian); 2, Tapinocephalus (Capitanian); 3, Pristerognathus (Capitanian–Wuchiapingian); 4, Tropidostoma (Wuchiapingian); 5, Cistecephalus (Wuchiapingian); 6, Dicynodon (Changhsingian); 7, Lystrosaurus (Induan–Olenekian) and 8, Cynognathus (Olenekian–Anisian). All communities follow a linear relationship (y=7.85x−75.64, r2=0.99), with the exception of Lystrosaurus (which was excluded from the regression). Palaeocommunity metanetworks are illustrated for the Eodicynodon, Dicynodon and Lystrosaurus assemblage zones. Spheres represent guilds: green, primary producers; blue, aquatic (freshwater) taxa; purple, insects; red, amphibians and yellow, amniotes. Insect, amphibian and amniote guilds are divided among herbivorous, carnivorous and omnivorous habits. Links between guilds represent sets of trophic interactions.
(b) Species-level food webs
It is impossible to precisely reconstruct species-level food webs for palaeocommunities due to the incompleteness of the fossil record. We therefore used metanetwork data and link distributions to stochastically generate a large number of possible species-level networks, rather than attempting a single static reconstruction. We thus account for two important sources of uncertainty in our knowledge of actual food webs, as well as their temporal and spatial variability. First, the exact number of trophic interactions that any fossil species would have possessed or the particular species with which it interacted cannot be known, even though we have a good idea of its interactions at the guild level. Second, food-web topologies of specific communities are probably flexible in both time and space because community structures are dependent on environmental and biotic contexts (Thompson 1999b,a).
We derived species-level food webs, or palaeotrophic networks, from the metanetworks using stochastic draws from guild trophic-link distributions. The trophic-link distributions are based on measures of the number of prey per consumer species in Recent communities. Those measures generally define regular decay distributions, most often attributed to exponential or power-law functions. The mixed distributions used in this paper took the form P(r)=exp(−r/ϵ), where ϵ=exp((γ−1)log M/γ), M is the total number of potential prey species or units of productivity available and γ is the power-law exponent that determines the extent to which a species can be a generalist (see the electronic supplementary material, figure 1). Link distributions converge to an exponential distribution of the form described for a variety of modern food webs (Camacho et al. 2002) as γ approaches 1. The factor ϵ reflects the point at which a power-law distribution of exponent γ would yield the minimum number of prey for any consumer species. However, the true algorithmic minimum for the mixed distributions was 1, and the distributions were always truncated to yield no more than M interactions. This process yielded distributions of trophic habits for species within guilds ranging from specialist to generalist feeders, reflecting distributions estimated empirically from modern communities (Camacho et al. 2002; Montoya et al. 2006). All the networks we generated using this procedure possessed link densities within the range observed for modern, species-level and aggregated food webs (Pimm et al. 1991; Havens 1992; Martinez 1992; see the electronic supplementary material, table 2).
(c) Determining secondary extinction
We employed two approaches to determine whether a species' population became secondarily extinct following a perturbation. First, we derived analytical solutions using the network topological approach, in which a population becomes extinct if all the nodes (species) or units of productivity to which it is linked are lost (Dunne et al. 2002b). The topological approach is amenable to the analysis of very diverse and complicated networks, and its application to modern communities has led to a general conclusion that increased connectance among trophic species raises resistance to secondary extinction (Dunne et al. 2002b; Eklöf & Ebenman 2006). Second, since populations that do not become topologically extinct are nonetheless likely to be affected by perturbations to the community, we also employed a dynamic approach that incorporated the demographic properties and interactions of populations. In theory, combined topological and dynamic extinctions could be written in terms of classical interspecific dynamics, but the sheer number of interactions quickly renders this approach intractable for communities of even modest diversity (hundreds of species) and connectance (Montoya et al. 2006; Shipley et al. 2006). We therefore used systems of difference equations and numerical simulations to combine the two approaches.
Individual species populations in the CEG model possess several important network parameters, including an in-degree measuring the number of prey resources and an out-degree measuring the number of predators. Interspecific trophic-link properties include the strengths of biotic interactions and the demographic state of each population. We parameterize consumer in-links using interaction strengths, with individual interaction strengths being inversely proportional to the number of prey links or interactions of the population (Roopnarine 2006). If the state of a population is considered to be a balance between incoming energy and energy lost to predation, then parameterization of the trophic network yields a standardized population size that can be determined for each species. Secondary extinction occurs in a simulation if the population size falls below a threshold level, the minimum viable population size (MVP). MVP sizes were set in the simulations to specify the size at which a population (i) became functionally extinct within the community, (ii) was doomed to extinction owing to environmental or demographic stochasticity (e.g. Allee effects), or (iii) had declined to zero population size. Conceptually, MVP in the CEG model is a function of carrying capacity and is always given as a fraction of standardized carrying capacity at zero perturbation (Roopnarine 2006). MVP size can therefore be set to 0, indicating that the population must decline to 0 individuals for extinction to occur, or set to 1, indicating that the population will become extinct immediately under any conditions, or it can be set to a value between 0 and 1, indicating the fraction of the pre-perturbation population size at which extinction will occur. Different MVP sizes among guilds reflect the greater susceptibility of some guilds of consumers to extinction. For example, larger animals, particularly carnivores, tend to have greater sensitivities to perturbations, and hence greater MVP size, owing to smaller equilibrium population sizes, as well as factors such as greater range requirements (Brown 1995). Those larger consumers, on the other hand, also tend to have broader dietary repertoires as a function of larger size, for example owing to larger and more efficient digestive systems, or the ability to handle a wider array of prey. Large consumers in our model would therefore have higher MVP sizes, but greater numbers of incoming links. Varying MVP sizes did not, however, alter our results significantly.
2. Results
(a) Analytic estimations
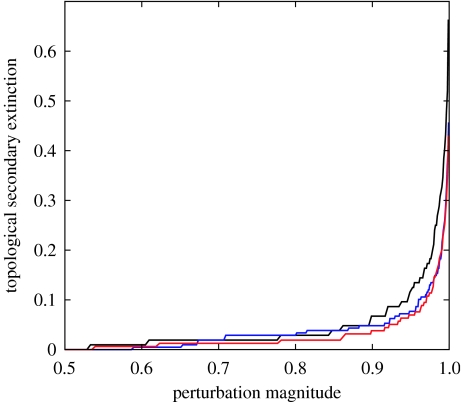
We applied bottom-up disruptions of productivity to Karoo species-level networks by reducing the level of productivity in one or more primary producer guilds. We then used numerical simulations to assess the total effects of the disruptions to the palaeocommunities, including feedback and indirect interactions. We also analytically estimated the expected topological effects of the initial perturbation to the systems. Given the stochasticity in topological specification of the species-level networks, the probability of topological secondary extinction of any consumer population, after the removal or loss of resources, declines as the consumer's in-degree or number of prey species increases (see §4 and the electronic supplementary material, figure 2). A comparison of expected topological secondary extinction for typical Eodicynodon, Dicynodon and Lystrosaurus zone communities suggests that Lystrosaurus zone communities should have been marginally more resistant to secondary extinction than the earlier communities (figure 2). This result is unsurprising given the greater guild-level connectance of the Lystrosaurus metanetwork and expectations of the topological perspective (Dunne et al. 2002b).
Figure 2.
Expected topological secondary extinction for Eodicynodon (black curve), Dicynodon (blue curve) and Lystrosaurus (red curve) assemblage zone communities. Perturbation magnitude (x-axis) is the proportion of primary production removed from the systems, and topological secondary extinction (y-axis) is the proportion of consumer species expected to go extinct as a result. Secondary extinction is summed over all guilds in the community.
Topological secondary extinctions are expected to trigger cascading secondary effects among survivors. These additional impacts stem from the demographic effects of the perturbation on surviving populations. Although the complexity of the interspecific demographic interactions prohibits a thorough analytical treatment, we investigated the impact of the initial perturbation by estimating the number of interactions lost by surviving populations, as well as subsequent changes to the strengths of surviving interactions. Populations survive the perturbation either because they are immune to topological secondary extinction (i.e. their resources exceed the magnitude of the perturbation), or because despite being susceptible, they were statistically lucky. By estimating the number of interactions that are expected to persist in each metanetwork after a perturbation, we found that very few links were lost by populations that survived initial disruptive pulses (see §4). Moreover, the fraction of links lost did not increase linearly or rapidly as perturbation magnitude increased (see the electronic supplementary material, figure 3), although the strengths of remaining interactions did compensate for lost links. Since we model individual interaction strength as the inverse of the number of interactions, as other resources experience secondary extinction, we expect individual species to compensate by increasing interaction strengths with remaining resources. However, the secondary loss of species was more rapid than the loss of interactions by surviving species, and summed interaction strength at the guild level declined in a stepwise fashion as the magnitude of perturbation was increased (see the electronic supplementary material, figure 4). Therefore, even though survivors do respond to the loss of resources from lower trophic levels by increasing the strengths of their remaining interactions, the total interaction strength exerted by one guild on another of lower trophic level decreased as bottom-up perturbation increased and more consumer species experienced secondary extinction.
(b) Numerical simulations
Continued analytical prediction of community behaviour is difficult beyond the initial bottom-up propagation of the perturbation. Surviving consumers compensate, thereby initiating top-down effects, creating the potential for continued and complex secondary interactions and additional extinctions. Furthermore, topological metanetwork features in which members of one or two guilds potentially prey on each other, such as loops and bidirectional links, are difficult to address analytically, yet exist in our metanetworks. We addressed these problems with numerical simulations of bottom-up perturbations, incorporating the full set of metanetwork features, and combined topological and demographic (dynamic) secondary extinctions. We refer to this as combined secondary extinction.
The Karoo communities responded topologically to the initial perturbation, but subsequent dynamic top-down cascades were initiated by surviving consumers, in turn reinforcing bottom-up effects and ultimately generating positive feedback loops. Under these conditions, levels of secondary extinction were greater than those resulting from topological effects alone (figure 3), supporting the position that topological analysis predicts lower levels of secondary extinction than dynamic analysis (Eklöf & Ebenman 2006) and justifying our combined approach.
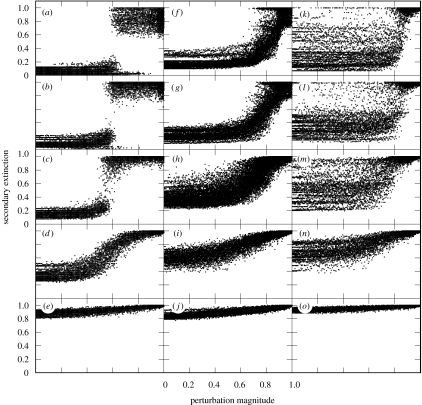
Figure 3.
Levels of secondary extinction resulting from numerical simulations of perturbations to 100 stochastically generated food webs for each palaeocommunity. (a–e) Eodicynodon, (f–j) Dicynodon and (k–o) Lystrosaurus zone networks. Simulations were repeated for networks generated with trophic-link distribution power-law exponents of 1 (e,j,o), 1.5 (d,i,n), 2 (c,h,m), 2.5 (b,g,l) and 3 (a,f,k). Secondary extinction (y-axis) measures the total (topological+dynamic) proportion of species that became extinct in response to the perturbations. Note that the distribution of results for Lystrosaurus zone networks is much broader compared with the other two zones, highlighting the lower predictability of responses of those networks to perturbation. This remains true even as increasing γ values reduce the modes of the distributions of secondary extinction at specific perturbation magnitudes.
Simulations of combined secondary extinction in the Permian Eodicynodon and Dicynodon zone communities using broad trophic-link distributions were quite resistant over a wide range of perturbation magnitudes, exhibiting some secondary extinction but eventually settling to new stable states (figure 3a,f). However, there are perturbation thresholds beyond which secondary extinction rose both rapidly and catastrophically. This result is explained by the topologically triggered loss of highly linked consumers that are immune at lower perturbation levels (Dunne et al. 2002b; Roopnarine 2006), and the transition from a predominance of secondary extinctions caused by external perturbation-driven dynamics to extinctions resulting from internally driven demographic interactions. In contrast, Triassic Lystrosaurus zone communities had highly variable and unpredictable responses, often exhibiting high levels of secondary extinction even at low levels of perturbation (figure 3k).
3. Discussion
(a) Community basis of Early Triassic instability
Do these results imply that Lystrosaurus zone communities were inherently less stable than preceding communities? Such a conclusion would be congruent with observations that the Early Triassic was a time of environmental and ecological instability (deWit et al. 2002; Benton et al. 2004; Pruss & Bottjer 2004; Payne & Kump 2007). If correct, this implies that community structure itself contributed to the instabilities observed in the geological record. The major differences between the Lystrosaurus zone communities and those of the Eodicynodon and Dicynodon zones were their systematic and ecological compositions. Recall that Lystrosaurus zone communities were amphibian‐dominated and possessed more connections per guild compared with the other amniote-dominated communities. The result was a greater connectance of the Lystrosaurus metanetwork (figure 1), and correspondingly greater dynamic amplification of perturbations and feedback among guilds, leading to higher levels of combined secondary extinction.
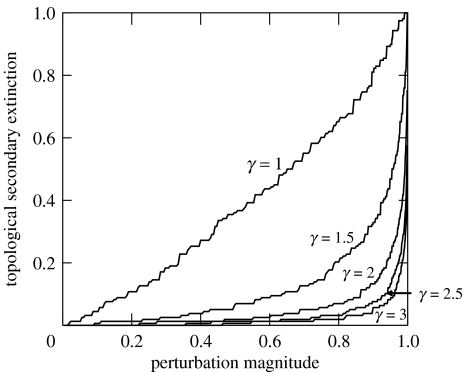
However, the instability of the Early Triassic community can be moderated by manipulating a single set of parameters in the model, namely γ, the power-law exponents of the guild link distributions that control network connectance at the species level. We employed values of 3 for every guild in the initial simulations (figure 3a,f,k), but repeating the simulations over a range of γ values between 1 and 3 for the three zones demonstrated a general trend of increasing resistance to secondary extinction as γ increased (figure 3). Ecologically, increasing γ corresponds to increasing dietary breadth within guilds, leading to greater proportions of generalist species at higher values of γ. Highly connected generalist species have lower probabilities of topological secondary extinction and generate less intense top-down compensatory feedback owing to lower per capita interaction strengths (although they do contribute more significantly to the phenomenon of catastrophic crashes). Therefore, in general, holding the metanetwork topology (relationships among guilds) constant while increasing the proportion of generalist species within guilds produces communities that are more resistant to secondary extinction. This raises the possibility of long-term community-level selection based on the emergent property of species' dietary breadths. Selection for communities that are more resistant to secondary extinction could explain, at least partially, apparent trends such as declining rates of background extinction over the Phanerozoic (Raup & Sepkoski 1982). Selection at this level would also favour communities with guilds increasingly dominated by generalists (and hence greater values of γ). Increasing the proportion of generalists, however, yields diminishing returns as values of γ exceed 2 (figure 4), and any higher-level selection for communities composed increasingly of extreme generalists would probably be offset or overwhelmed by the advantages of population-level selection for dietary specialization and coevolved biotic interactions (Vermeij 2004).
Figure 4.
Expected topological secondary extinction for Lystrosaurus zone communities, applying trophic-link distributions with values of γ ranging from 1 to 3. The level of secondary extinction decreases as γ increases, but by ever diminishing amounts.
We are also led to question the variability of actual Lystrosaurus zone communities. Unlike Eodicynodon and Dicynodon zone communities, whose responses to perturbation are uniform within the range of our stochastic reconstructions, Lystrosaurus zone communities have highly variable responses. This could mean that some real Lystrosaurus zone communities were very unstable and experienced frequent compositional turnover in response to an unstable environment. On the other hand, Lystrosaurus zone communities could have been as stable as their predecessors if only a small fraction of the range of stochastic reconstructions, in the region of low secondary extinctions, was realized in actual communities. If true, this would imply that animals in Lystrosaurus zone communities were significantly more constrained in their trophic habits than were their ecological predecessors because deviations from a limited set of interactions could precipitate the collapse of their communities.
There is a paradox here associated with the hierarchical organization of communities. More highly connected, or generalized, species are more resistant to secondary extinction because they use a greater diversity of resources. More highly connected communities, or metanetworks, however, seem to generate higher levels of secondary extinction and global instability owing to the greater linkage among different sections of the communities. The Lystrosaurus zone metanetwork amplified perturbation effects to a greater degree, in comparison with the Eodicynodon and Dicynodon zones, owing to the greater connectance among its guilds, and regardless of species-level connectances. Perhaps such unstable community topologies cannot normally exist under disruptive conditions, but the unusual ecological and taxonomic conditions present in the aftermath of a mass extinction may provide a window of opportunity, albeit a brief one.
(b) Taphonomic considerations
These observations also raise the question of whether the unusual structure of the Lystrosaurus zone community was a direct result of the effects of the end-Permian mass extinction, or if our reconstructions have been influenced by a taphonomic bias that resulted in a skewed picture of a normally structured community. Although the preservational environment of the Lystrosaurus zone appears to have differed from that of the Permian zones (Smith & Botha 2005), we doubt the significance of taphonomic biases for several reasons. First, collector effort has been spread uniformly across the whole of the Beaufort Group in the Karoo Basin, implying that the unusual faunal composition of the Lystrosaurus zone is not simply the result of inadequate exploration of exposed strata of this age (M. Nicolas 2007, personal communication). Second, recent detailed collecting near the Permo–Triassic boundary has made the lower portions of the Lystrosaurus assemblage zone one of the best-known portions of the entire Karoo sequence (Botha & Smith 2006). The number of fossils collected from the Lystrosaurus zone is also relatively high when compared with other zones (M. Nicolas 2007, personal communication), and the full spectrum of body sizes known from the other communities is present. Finally, although continued collecting has uncovered new species in the Lystrosaurus zone (Modesto et al. 2003), these species generally are members of guilds that were already represented in the assemblage.
(c) Conclusions
In summary, ecological communities are complex adaptive systems (Gell-Mann 1994) whose particular topologies are expected to vary through time and space, even if rules of community assembly remain static. This variability means that we cannot rely on the prediction of specific outcomes from specific perturbations. Instead, we must predict distributions of potential outcomes, as exhibited most dramatically by the Lystrosaurus zone communities. This distinction becomes evermore important as community complexity increases. Whatever the specific topological details of the three Karoo Basin community types might have been, the response of post-mass extinction Lystrosaurus zone communities to disruptions of productivity would have been inherently less predictable and potentially more disastrous. Finally, the application of dynamic community models to palaeoecological data has the potential to yield insight into both the resistance to and recovery from episodes of mass extinction, as well as apparent Phanerozoic trends such as the declining rate of background extinction.
Material and methods
(a) Metanetwork reconstruction
The first step in constructing metanetworks for the communities consisted of compiling a list of vertebrate genera reported from each of the three assemblage zones, based on lists from literature reports (Rubidge 1995; Schoch & Milner 2000; Angielczyk & Kurkin 2003; Modesto et al. 2003; Damiani & Rubdige 2004; Sidor & Smith 2004), and K. Angiekzyk 2002–2006, personal observations. Although the Permian–Triassic transition in the Karoo has received much attention (MacLeod et al. 2000; Ward et al. 2000; Smith & Ward 2001; Retallack et al. 2003; Steiner et al. 2003; De Kock & Kirschvink 2004; Smith & Botha 2005; Ward et al. 2005), precise correlations and detailed faunal lists do not exist for all localities assigned to a particular assemblage zone (although see Kitching 1977). Therefore, all taxa reported from an assemblage zone were treated as a single palaeoecological community. This is a simplification because not all taxa reported from a given zone have stratigraphical or spatial ranges spanning the entire zone (e.g. Rubidge 1995; Smith & Ward 2001; Ward et al. 2005; Botha & Smith 2006). Additionally, it has recently been suggested that it may be possible to further subdivide the Lystrosaurus assemblage zone into a series of temporally successive subcommunities (Botha & Smith 2006). However, the stratigraphical ranges of a number of Lystrosaurus zone taxa are insufficiently well constrained to allow their definite assignment to one or more of these subcommunities at this time.
We next assigned vertebrate genera from each assemblage to series of guilds. These assignments were sometimes simplistic (e.g. all aquatic non-tetrapod vertebrates were assigned to a single fish guild), but they usually were based on body size, inferred diet and phylogeny. Terrestrial tetrapods were divided into herbivore and faunivore guilds on the basis of cranial and dental morphology, with additional consideration of the dietary hypotheses of previous workers (see the electronic supplementary material, table 1). The herbivore and faunivore guilds were further subdivided into five body size classes, using skull length as a proxy: very small (skull length 0–100 mm), small (101–200 mm), medium (201–300 mm), large (301–400 mm) and very large (401 mm and above). This process yielded a total of 10 guilds. Amphibian taxa were divided into the same body size classes, but were placed in separate amphibian guilds, reflecting dietary differences between them and terrestrial tetrapods. The amphibian guilds added another five potential guilds to each community. Not all amphibian or amniote guilds were present in each community.
All tetrapod herbivores fed on one primary producer guild (terrestrial productivity available to tetrapods and insects) that included a potentially large number of producer species and food sources. Treating these producers as a single guild reflects the fact that there are no arboreal or flying tetrapods in any of the communities, which when combined with the generally short stature of Permian and Triassic tetrapods implies that a significant amount of primary productivity was simply out of reach of the terrestrial vertebrates. Terrestrial faunivores were assigned links to terrestrial herbivore and faunivore guilds up to two size classes larger and two size classes smaller than themselves. For example, medium-sized faunivores could feed on very small, small, large and very large terrestrial herbivores and faunivores. This accounts for the fact that any particular faunivore species probably consumed adult individuals of species smaller than itself, and juveniles of species larger than itself. The two smallest terrestrial faunivore guilds also were assigned links to insects and myriapods. Amphibian guilds were given more catholic diets, although all were assumed to be faunivorous. An amphibian guild could feed on other amphibian guilds up to two size classes larger or smaller than itself, terrestrial herbivores and faunivores up to two size classes larger or smaller than itself, fishes and aquatic insects. Given these diets, amphibians link the dry and freshwater components of the communities. The single fish guild in each community had predatory links to one source of primary productivity (aquatic macrophytes), all amphibian and insect guilds (assuming that some members of these guilds had aquatic larval or adult stages) and all aquatic non-insect invertebrates. It is doubtful that any herbivore guilds exhibited significant omnivory because all probably fed only at the primary producer level and do not show obvious specializations for faunivory.
The Middle Permian to Middle Triassic insect fossil record of the Karoo Basin is patchier than the vertebrate fossil record, with no insect fossils reported from most of the assemblage zones (Rubidge 1995). However, a diverse insect fauna has been recovered from a handful of Dicynodon assemblage zone-age localities in KwaZulu–Natal (Riek 1973, 1974, 1976; Anderson & Anderson 1985, 1997; van Dijk 1997; van Dijk & Geertsema 1999; Geertsema et al. 2002; Ponomarenko & Mostovski 2005). Because insect faunas are not known from the Eodicynodon or Lystrosaurus assemblage zones, the Dicynodon zone insect fauna was used for all reconstructed communities. This approach is conservative because including the same insect fauna in each community increases the similarity of the ecological structures of the communities, as well as their responses to perturbation. Excluding the insect fauna completely, or including it only in the Dicynodon assemblage zone, would exaggerate differences between the assemblages. The insect fauna consisted of three guilds: insect herbivores, insect faunivores and insect omnivores (including detritivores). Because nearly all the relevant fossils consisted of isolated wings, it was difficult to assign specific diets for each genus. This problem was addressed by noting to which higher taxon (usually at the ordinal level) a particular genus was assigned, reconstructing the basal feeding strategy for that higher taxon using published information (Rasnitsyn & Quicke 2002; Grimaldi & Engel 2005). This approach provided the best combination of rigor and consistency in the dietary reconstructions. Herbivorous insects were allowed to feed on all four producer guilds. Faunivorous insects were allowed to feed on all insect guilds (including faunivorous insect species), as well as on myriapods (when present). Omnivorous insects were linked to all four sources of primary productivity, all three insect guilds (including themselves) and myriapods.
Few non-insect invertebrates are known from the Middle Permian to Middle Triassic assemblages of the Karoo Basin (van Dijk 1981; Anderson & Anderson 1985; Rubidge 1995). Our metanetworks included a maximum of three non-insect invertebrate guilds: molluscs, conchostracans and myriapods. Molluscs and conchostracans fed only upon aquatic microphytes. The myriapods fed on two sources of primary productivity (terrestrial productivity available to tetrapods and insects and terrestrial productivity available only to insects).
Productivity is difficult to measure in the geological record and is often expressed as the temporal and/or spatial variation of proxy measurements (e.g. δ13C). However, the network nature of the CEG model specifies trophic links of primary consumers to producers. The Karoo Basin has produced well-studied Permian and Triassic fossil floras (e.g. Anderson & Anderson 1985), but correlations between the plant localities and tetrapod-bearing strata, especially with regard to the Permo–Triassic boundary, are not exact (Gastaldo et al. 2005). Therefore, detailed reconstructions of the Karoo producer communities were not attempted. Nevertheless, any palaeocommunity that is preserved in the fossil record must have possessed sufficient levels of primary production to support the consumers, and we can parameterize the model on the basis of initial consumer demand (when perturbation is absent). The number of available units of primary production was thus fixed for all metanetworks as 10 times the maximum species richness of primary consumer guilds, reflecting the thermodynamic scaling of energy transfer among trophic levels (repeating simulations at levels 20, 30 and 40 times, the maximum species richness of primary consumer guilds did not alter results qualitatively). Units of primary production were subdivided into primary producer guilds according to the proportions of primary consumers of particular trophic habits (e.g. aquatic microphytes and suspension/filter feeders versus macrophytes and fishes). We used four producer guilds: terrestrial productivity available to tetrapods and insects, terrestrial productivity available only to insects, aquatic macrophytes and aquatic microphytes. All simulations were run with twice the observed generic consumer diversity present in each guild, implying that each genus comprised two species. We used this assumption to account for taxonomic uncertainty and incompleteness in the fossil record.
(b) Probability of extinction, link loss and interaction strength
The probability of topological secondary extinction, where a consumer loses all of its prey resources, is
| (4.1) |
where r is the consumer's in-degree or number of prey species; M is the total number of potential prey or units of productivity and ω is the magnitude of the perturbation (see the electronic supplementary material, figure 2). The total expected level of extinction within a consumer guild J is therefore
| (4.2) |
where ψ is the level of secondary extinction; p(er) is the probability of extinction of a consumer with r in-links and nr is the expected number of species in J with r in-links and is calculated as a fraction of the total diversity of J (denoted |J|), equivalent to the area under the link distribution curve corresponding to link degree r. Thus,
The probability that a species that survives a perturbation will nonetheless lose q interactions out of r is
| (4.3) |
The expected number of interactions in guild J that therefore survive a perturbation of ω is
| (4.4) |
where LJ is the number of surviving interactions; L0 is the original number of interactions before perturbation; the second term on the right hand side of the equation is the number of interactions lost by immune members of J (where r>ω); the third term on the right hand side of the equation is the number lost by susceptible but surviving members of J (where r≤ω); and p(q) is the probability of losing q interactions out of r (see the electronic supplementary material, figure 3). p(q) is maximized when r=1 (yielding p(q)=r/M). The original number of interactions in J prior to perturbation is
| (4.5) |
The strength of a single interaction of a species with r prey, in the absence of perturbation, is
| (4.6) |
However, when the community is perturbed and secondary extinction occurs, the interaction strength is a function of the probability of the species surviving the perturbation and the expected number of interactions lost by the guild,
| (4.7) |
(c) Demographic interactions
If the state of a population is considered to be a balance between incoming energy and energy lost to predation, then parameterization of the trophic network yields a standardized population size that can be determined for each species as
| (4.8) |
where rj is the number of interactions of consumer species' population j; |Mj| is the number of prey species of j; |N| is the number of species that prey on j; rn is the number of predatory interactions of j's predators and ki,ω are species population sizes in guilds J, M and N after a perturbation of magnitude ω (subscripts simplified on right-hand side of formula).
Acknowledgments
We thank G. J. Vermeij, C. Tang, D. Goodwin and E. Conel for their many helpful comments and discussions. M. Kowaleski and an anonymous reviewer provided many helpful comments and suggestions. M. Olson compiled data on fishes for the San Francisco Bay food web. R. Van Syoc kindly assisted with the compilation of invertebrate data from the Invertebrate Zoology collection at the California Academy of Sciences. This project was supported by grants from NSF (EAR-0313560 to P.D.R and ARC-0530825 to P.D.R. and S.C.W.), the Swarthmore College Research Fund and the Woodrow Wilson National Fellowship Foundation (to S.C.W.), and a Royal Society USA/Canada Research Fellowship (to K.D.A.).
Supplementary Material
Supplemental guild and metanetwork data, as well as supporting figures
References
- Anderson J.M, Anderson H.M. A. A. Balkema; Rotterdam, The Netherlands: 1985. Palaeoflora of southern Africa. Prodromus of South African megafloras, Devonian to Cretaceous. [Google Scholar]
- Anderson H.M, Anderson J.M. Towards new paradigms in Permo–Triassic Karoo palaeobotany (and associated faunas) through the past 50 years. Palaeontol. Afr. 1997;33:11–21. [Google Scholar]
- Angielczyk K.D, Kurkin A.A. Has the utility of Dicynodon for Upper Permian terrestrial biostratigraphy been overstated? Geology. 2003;31:363–366. doi:10.1130/0091-7613(2003)031<0363:HTUODF>2.0.CO;2 [Google Scholar]
- Angielczyk, K. D., Roopnarine, P. D., & Wang, S. C. 2005 Modeling the role of primary productivity disruption in end-Permian extinctions, Karoo Basin, South Africa. In The nonmarine Permian (eds S. G. Lucas & K. E. Zeigler), no. 30, pp. 16–23. New Mexico Museum of Natural History and Science Bulletin.
- Bambach R.K. Seafood through time: changes in biomass, energetics, and productivity in the marine ecosystem. Paleobiology. 1993;19:372–397. [Google Scholar]
- Benton M.J, Twitchett R.J. How to kill (almost) all life: the end-Permian extinction event. Trends. Ecol. Evol. 2003;18:358–365. doi:10.1016/S0169-5347(03)00093-4 [Google Scholar]
- Benton M.J, Tverdokhlebov V.P, Surkov M.V. Ecosystem remodelling among vertebrates at the Permian–Triassic boundary in Russia. Nature. 2004;432:97–100. doi: 10.1038/nature02950. doi:10.1038/nature02950 [DOI] [PubMed] [Google Scholar]
- Botha J, Smith R.M.H. Rapid vertebrate recuperation in the Karoo Basin of South Africa following the end-Permian extinction. J. Afr. Earth Sci. 2006;45:502. doi:10.1016/j.jafrearsci.2006.04.006 [Google Scholar]
- Briand F, Cohen J.E. Community food webs have scale-invariant structure. Nature. 1984;307:264–266. doi:10.1038/307264a0 [Google Scholar]
- Brown J.H. The University of Chicago Press; Chicago, IL: 1995. Macroecology. [Google Scholar]
- Camacho J, Guimerà R, Amaral L.A.N. Robust pattern in food web structures. Phys. Rev. Lett. 2002;88:228102-1–228102-4. doi: 10.1103/PhysRevLett.88.228102. doi:10.1103/PhysRevLett.88.228102 [DOI] [PubMed] [Google Scholar]
- Damiani R.J, Rubdige B.S. A review of the South African temnospondyl amphibian record. Palaeontol. Afr. 2004;39:21–36. [Google Scholar]
- De Kock M.O, Kirschvink J.L. Paleomagnetic constraints on the Permian–Triassic boundary in terrestrial strata of the Karoo Supergroup, South Africa: implications for causes of the end-Permian extinction event. Gondwana Res. 2004;7:175–183. doi:10.1016/S1342-937X(05)70316-6 [Google Scholar]
- deWit M.J, Ghosh J.G, de Villiers S, Rakotosolofo N, Alexander J, Tripati A, Looy C.V. Multiple organic carbon isotope reversals across the Permo–Triassic boundary of terrestrial Gondwana sequences: clues to extinction patterns and delayed ecosystem recovery. J. Geol. 2002;110:227–240. doi:10.1086/338411 [Google Scholar]
- Diamond J. Viking; New York, NY: 2005. Collapse. How societies choose to fail or succeed. [Google Scholar]
- Dunne J.A, Williams R.J, Martinez N.D. Food-web structure and network theory: the role of connectance and size. Proc. Natl Acad. Sci. USA. 2002a;99:12 917–12 922. doi: 10.1073/pnas.192407699. doi:10.1073/pnas.192407699 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunne J.A, Williams R.J, Martinez N.D. Network structure and biodiversity loss in food webs: robustness increases with connectance. Ecol. Lett. 2002b;5:558–567. doi:10.1046/j.1461-0248.2002.00354.x [Google Scholar]
- Eklöf A, Ebenman B. Species loss and secondary extinctions in simple and complex model communities. J. Anim. Ecol. 2006;75:239–246. doi: 10.1111/j.1365-2656.2006.01041.x. doi:10.1111/j.1365-2656.2006.01041.x [DOI] [PubMed] [Google Scholar]
- Erwin, D. H., Rampino, M. R. & Yugan, J. 2002 End-Permian mass extinctions: a review. In Catastrophic events and mass extinctions: impacts and beyond, vol. 356 (eds C. Koeberl & K. G. MacLeod), pp. 363–383. Geological Society of America Special Paper. Boulder, CO: The Geological Society of America.
- Gastaldo R.A, Adendorff R, Bamford M, Labandeira C, Neveling J, Sims H. Taphonomic trends of macrofloral assembalges across the Permian–Triassic boundary, Karoo Basin, South Africa. Palaios. 2005;20:479. doi:10.2110/palo.2004.P04-62 [Google Scholar]
- Geertsema H, van Dijk D.E, van den Heever J.A. Palaeozoic insects of southern Africa: a review. Palaeontol. Afr. 2002;38:19–25. [Google Scholar]
- Gell-Mann M. Complex adaptive systems. In: Cowan G.A, Pines D, Meltzer D, editors. Complexity. Metaphors, models, and reality. Santa Fe Institute studies in the sciences of complexity. vol. XIX. Addison-Wesley Publishing Company; Reading, MA: 1994. [Google Scholar]
- Grimaldi D, Engel M.S. Cambridge University Press; Cambridge, UK: 2005. Evolution of the insects. [Google Scholar]
- Havens K. Scale and structure in natural food webs. Science. 1992;257:1107–1109. doi: 10.1126/science.257.5073.1107. doi:10.1126/science.257.5073.1107 [DOI] [PubMed] [Google Scholar]
- Jablonski D. Mass extinctions and macroevolution. Paleobiology. 2005;31:192–210. [Google Scholar]
- Kitching, J. W. 1977 The distribution of the Karoo vertebrate fauna, no. 1, p. 131. Memoirs of the Bernard Price Institute for Palaeontological Research. Johannesburg, Republic of South Africa: University of the Witwatersrand.
- Knoll A.H, Bambach R.K, Canfield D.E, Grotzinger J.P. Comparative Earth history and Late Permian mass extinction. Geology. 1996;273:452–457. [PubMed] [Google Scholar]
- Lockwood R. The K/T event and infaunality: morphological and ecological patterns of extinction and recovery in veneroid bivalves. Paleobiology. 2004;30:507–521. doi:10.1666/0094-8373(2004)030<0507:TTEAIM>2.0.CO;2 [Google Scholar]
- Looy C.V, Brugman W.A, Dilcher D.L, Visscher H. The delayed resurgence of equatorial forests after the Permian–Triassic ecologic crisis. Proc. Natl Acad. Sci. USA. 1999;96:13 857–13 862. doi: 10.1073/pnas.96.24.13857. doi:10.1073/pnas.96.24.13857 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Looy C.V, Twitchett R.J, Dilcher D.L, Van Konijnenburg-Van Cittert J.H.A, Visscher H. Life in the end-Permian dead zone. Proc. Natl Acad. Sci. USA. 2001;98:7879–7883. doi: 10.1073/pnas.131218098. doi:10.1073/pnas.131218098 [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacLeod K.G, Smith R.M.H, Koch P.L, Ward P.D. Timing of mammal-like reptile extinctions across the Permian–Triassic boundary in South Africa. Geology. 2000;28:227–230. doi:10.1130/0091-7613(2000)28<227:TOMREA>2.0.CO;2 [Google Scholar]
- Martinez N.D. Constant connectance in community food webs. Am. Nat. 1992;139:1208–1218. doi:10.1086/285382 [Google Scholar]
- May R.M. 8th edn. Princeton University Press; Princeton, NJ: 2001. Stability and complexity in model ecosystems. [Google Scholar]
- McGhee G.R, Sheehan P.M, Bottjer D.J, Droser M.L. Ecological ranking of Phanerozoic biodiversity crises: ecological and taxonomic severities are decoupled. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2004;211:289–297. doi:10.1016/j.palaeo.2004.05.010 [Google Scholar]
- Modesto S.P, Damiani R.J, Neveling J, Yates A.M. A new Triassic owenettid parareptile and the mother of mass extinctions. J. Vertebr. Paleontol. 2003;23:715–719. doi:10.1671/1962 [Google Scholar]
- Montoya J.M, Pimm S.L, Solé R.V. Ecological networks and their fragility. Nature. 2006;442:259–264. doi: 10.1038/nature04927. doi:10.1038/nature04927 [DOI] [PubMed] [Google Scholar]
- Myers R.A, Baum J.K, Shepherd T.D, Powers S.P, Peterson C.H. Cascading effects of the loss of apex predatory sharks from a coastal ocean. Science. 2007;315:1846–1850. doi: 10.1126/science.1138657. [DOI] [PubMed] [Google Scholar]
- Orr J.C, et al. Anthropogenic ocean acidification over the twenty-first century and its impact on calcifying organisms. Nature. 2005;437:681–686. doi: 10.1038/nature04095. doi:10.1038/nature04095 [DOI] [PubMed] [Google Scholar]
- Payne J.L, Kump L.R. Evidence for recurrent Early Triassic massive volcanism from quantitative interpretation of carbon isotope fluctuations. Earth Planet. Sci. Lett. 2007;256:264–277. doi:10.1016/j.epsl.2007.01.034 [Google Scholar]
- Pimm S.L, Lawton J.H, Cohen J.E. Food web patterns and their consequences. Nature. 1991;350:669–674. doi:10.1038/350669a0 [Google Scholar]
- Ponomarenko A.G, Mostovski M. New beetles (Insecta: Coleoptera) from the Late Permian of South Africa. Afr. Invertebr. 2005;46:253. [Google Scholar]
- Pruss S.B, Bottjer D.J. Early Triassic trace fossils of the western United States and their implications for prolonged environmental stress from the end-Permian mass extinction. Palaios. 2004;19:551–564. [Google Scholar]
- Rasnitsyn A.P, Quicke D. Springer; London, UK: 2002. History of insects. [Google Scholar]
- Raup D.M, Sepkoski J.J. Mass extinctions in the marine fossil record. Science. 1982;215:1501–1503. doi: 10.1126/science.215.4539.1501. doi:10.1126/science.215.4539.1501 [DOI] [PubMed] [Google Scholar]
- Retallack G.J, Smith R.M.H, Ward P.D. Vertebrate extinction across the Permo–Triassic boundary in Karoo Basin, South Africa. Geol. Soc. Am. Bull. 2003;115:1133–1152. doi:10.1130/B25215.1 [Google Scholar]
- Riek E.F. Fossil insects from the Upper Permian of Natal South Africa. Ann. Natal Museum. 1973;21:513. [Google Scholar]
- Riek E.F. An unusual immature insect from the Upper Permian of Natal. Ann. Natal Museum. 1974;22:271. [Google Scholar]
- Riek E.F. New Upper Permian insects from Natal South Africa. Ann. Natal Museum. 1976;22:755. [Google Scholar]
- Roopnarine P.D. Extinction cascades and catastrophe in ancient food webs. Paleobiology. 2006;32:1–19. [Google Scholar]
- Rubidge, B. S. 1995 Biostratigraphy of the Beaufort Group (Karoo Supergroup) South African Committee for Stratigraphy Biostratigraphic Series, vol. 1, pp. 1–46.
- Rubidge B.S. Geological Society of South Africa; Johannesburg, Republic of South Africa: 2005. Reuniting lost continents: fossil reptiles from the ancient Karoo and their wanderlust. [Google Scholar]
- Schoch, R. R. & Milner, A. R. 2000 Handbuch der Paläoherpetologie Part 3B Stereospondyli. Berlin, Germany: Verlag Dr Friedrich Pfeil.
- Sepkoski J.J. Patterns of Phanerozoic extinctions: a perspective from global databases. In: Walliser O.H, editor. Global events and event stratigraphy. Springer; Berlin, Germany: 1996. pp. 35–53. [Google Scholar]
- Shipley B, Vile D, Garnier E. From plant traits to plant communities: a statistical mechanistic approach to biodiversity. Science. 2006;314:812–814. doi: 10.1126/science.1131344. doi:10.1126/science.1131344 [DOI] [PubMed] [Google Scholar]
- Sidor C.A, Smith R.M.H. A new galesaurid (Therapsida: Cynodontia) from the Lower Triassic of South Africa. Palaeontology. 2004;47:535. doi:10.1111/j.0031-0239.2004.00378.x [Google Scholar]
- Smith R.M.H, Botha J. The recovery of terrestrial vertebrate diversity in the South African Karoo Basin after the end-Permian extinction. C. R. Palevol. 2005;4:623–636. doi:10.1016/j.crpv.2005.07.005 [Google Scholar]
- Smith R.M.H, Ward P.D. Pattern of vertebrate extinctions across an event bed at the Permian–Triassic boundary in the Karoo Basin of South Africa. Geology. 2001;29:1147–1150. doi:10.1130/0091-7613(2001)029<1147:POVEAA>2.0.CO;2 [Google Scholar]
- Solé R.V, Montoya J.M, Erwin D.H. Recovery after mass extinction: evolutionary assembly in large-scale biosphere dynamics. Phil. Trans. R. Soc. B. 2002;357:697–707. doi: 10.1098/rstb.2001.0987. doi:10.1098/rstb.2001.0987 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steiner M.B, Eshet Y, Rampino M.R, Schwindt D.M. Fungal abundance spike and the Permian–Triassic boundary in the Karoo Supergroup. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2003;194:405–414. doi:10.1016/S0031-0182(03)00230-X [Google Scholar]
- Thompson J.N. The evolution of species interactions. Science. 1999a;284:2116–2118. doi: 10.1126/science.284.5423.2116. doi:10.1126/science.284.5423.2116 [DOI] [PubMed] [Google Scholar]
- Thompson J.N. Specific hypotheses on the geographic mosaic of coevolution. Am. Nat. 1999b;153:S1–S14. doi:10.1086/303208 [Google Scholar]
- van Dijk D.E. A study of the type locality of Lidgettonia africana Thomas 1958. Palaeontol. Afr. 1981;24:43. [Google Scholar]
- van Dijk D.E. Insect faunas of South Africa from the Upper Permian and the Permian/Triassic boundary. Palaeontol. Afr. 1997;34:43–48. [Google Scholar]
- van Dijk D.E, Geertsema H. Permian insects from the Beaufort Group of Natal South Africa. Ann. Natal Museum. 1999;40:137–171. [Google Scholar]
- Vermeij G.J. The mesozoic marine revolution. Paleobiology. 1977;3:245–258. [Google Scholar]
- Vermeij G.J. Princeton University Press; Princeton, NJ: 2004. Nature. An economic history. [Google Scholar]
- Wagner P.J, Kosnik M.A, Lidgard S. Abundance distributions imply elevated complexity of post-Paleozoic marine ecosystems. Science. 2006;314:1289–1292. doi: 10.1126/science.1133795. doi:10.1126/science.1133795 [DOI] [PubMed] [Google Scholar]
- Wang S.C. On the continuity of background and mass extinction. Paleobiology. 2003;29:455–467. doi:10.1666/0094-8373(2003)029<0455:OTCOBA>2.0.CO;2 [Google Scholar]
- Ward P.D, Montgomery D.R, Smith R. Altered river morphology in South Africa related to the Permian–Triassic mass extinction. Science. 2000;289:1740–1743. doi: 10.1126/science.289.5485.1740. doi:10.1126/science.289.5485.1740 [DOI] [PubMed] [Google Scholar]
- Ward P.D, Botha J, Buick R, De Kock M.O, Erwin D.H, Garrison G.H, Kirschvink J.L, Smith R. Abrupt and gradual extinction among Late Permian land vertebrates in the Karoo Basin South Africa. Science. 2005;307:709–714. doi: 10.1126/science.1107068. doi:10.1126/science.1107068 [DOI] [PubMed] [Google Scholar]
- Williams R.J, Martinez N.D. Simple rules yield complex food webs. Nature. 2000;404:180–183. doi: 10.1038/35004572. doi:10.1038/35004572 [DOI] [PubMed] [Google Scholar]
- Zachos J.C, Arthur M.A, Dean W.F. Geochemical evidence for suppression of pelagic marine productivity at the Cretaceous/Tertiary boundary. Nature. 1989;337:61–64. doi:10.1038/337061a0 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental guild and metanetwork data, as well as supporting figures