Spatial structure inhibits the rate of invasion of beneficial mutations in asexual populations

Abstract

Populations in spatially structured environments may be divided into a number of (semi-) isolated subpopulations due to limited offspring dispersal. Limited dispersal and, as a consequence, local competition could slow down the invasion of fitter mutants, allowing the short-term coexistence of ancestral genotypes and mutants. We determined the rate of invasion of beneficial mutants of Escherichia coli, dispersed to different degrees in a spatially structured environment during 40 generations, experimentally and theoretically. Simulations as well as experimental data show a decrease in the rate of invasion with increasingly constrained dispersal. When a beneficial mutant invades from a single spot, competition with the ancestral genotype takes place only along the edges of the growing colony patch. As the colony grows, the fitness of the mutant will decrease due to a decrease in the mutant's fraction that effectively competes with the surrounding ancestor. Despite its inherently higher competitive ability, increased intragenotype competition prevents the beneficial mutant from rapidly taking over, causing short-term coexistence of superior and inferior genotypes.

1. Introduction

Adaptation in asexual populations consists of sequential substitutions of beneficial mutations within the same line of descendants via periodic selection (Koch 1974; Levin 1981). Several beneficial mutations that are simultaneously present will compete with each other for fixation (Muller 1932; Gerrish & Lenski 1998). It is expected that the largest beneficial mutation will sweep through the population following exponential dynamics until it is fixed, thereby eliminating pre-existing variation. The substitution rate of beneficial mutations will be lower in a spatially structured environment than in a homogeneous population, where purging is expected to be a relatively rapid process (Gordo & Campos 2005), owing to the slower invasion of beneficial mutations due to limited offspring dispersal and localized competition, i.e. due to spatial constraints of population dynamics (Czárán 1998).

In a spatially structured environment, dispersal will often be limited to a certain degree, causing the population to become structured. Without dispersal, a beneficial mutant will invade as a single growing colony. This has a twofold disadvantage: first, since growth mostly happens at the perimeter of the colony, the radius of a colony increases at a constant rate, which means a quadratic increase in time of the number of cells; although colonies exhibit vertical growth, this is expected to be at least an order of magnitude smaller than radial growth at the centre of a colony (Grimson & Barker 1993). Comparing this with the faster, exponential increase of cells in a well-mixed environment, population structure can be said to slow down the growth of cells, independent of a competitor, due to limited expansion ability. Second, if nutrient diffusion is limited in a spatially structured environment, cells influence the availability of nutrients only for their immediate neighbours. Despite a difference in competitive ability, the mutant/ancestor ratio will change slowly, because most ancestral cells are not affected by the mutant. The mutant essentially limits its own growth, because most competition takes place among mutant clone mates (Pacala 1986; Ives 1988; Hanksi & Cambefort 1991), and it can only take advantage of its competitive superiority at the perimeter of the mutant colony. Moreover, as the invasion process progresses, the invading strain is expected to lower its own fitness due to changes in the ratio of inter- to intraspecific competition. Thus, even though the invading strain has a higher competitive ability, limited dispersal and local resource competition will reduce the invasion rate (Crawley 1990; Burke & Grime 1996).

Owing to the slower dynamics of exclusion, several mutants can coexist temporarily, possibly opening the way for further increase in genetic diversity, e.g. through recombination and/or the appearance of mutants that can coexist with other mutants. With respect to adaptation to changing environments, higher genetic variation may be of great advantage to the populations (Boles et al. 2004). Since most species grow in spatially structured environments and are limited, to different degrees, in their dispersal rate, the implications of our study are not restricted to micro-organisms.

In a previous study, we have demonstrated experimentally that the long-term rate of adaptation slows down due to limited dispersal in a structured environment (Habets et al. 2006). Here, we investigate the reason for this decrease; we study how the rate of invasion and the fitness of a beneficial mutant are affected by dispersal in a structured environment directly, both experimentally and theoretically. This was done by measuring the rate of fixation of two Escherichia coli mutants, each with an approximately 50% fitness advantage relative to its ancestor. To manipulate dispersal, we used a non-motile E. coli strain, which we dispersed to different degrees at the beginning and during the invasion assay. We show both experimentally and theoretically a conspicuous divergence in fixation dynamics as a function of spatial structure, the proximate reason for which is the decline of the mutant fitness due to spatial constraints on population interactions.

2. Material and methods

(a) Bacteria, media and experimental design

The invading strains (representing a beneficial mutant) were obtained in a previous experiment. Thirty-six populations derived from the E. coli B strains REL 606 or REL 607 were propagated for 900 generations in either a homogeneous environment or two spatially structured environments; one where the population structure was kept intact by using velvet to replicate the populations and another where the population was mixed before each daily transfer (Habets et al. 2006). From each structured environment, we isolated a clone from one population at generation 900; these were used for the invasion assays against an ancestral clone. Owing to a difference in the ability to use l-arabinose, ancestral cells grow as red colonies on indicator plates, whereas the invading strains (which originated from an isogenic strain except for the marker) produce white colonies. Indicator plates (tetrazolium arabinose indicator agar) contain per litre 10 g tryptone, 1 g yeast extract, 5 g NaCl, 16 g agar, 10 g arabinose and 1 ml of a 5% stock of tetrazolium (2,3,4-triphenyltetrazolium chloride).

The invading strains competed versus the ancestor for 5 days in an environment identical to the one they had adapted to: Petri plates (diameter 60 mm) containing 10 ml of 1/10 Luria-Broth agar. Prior to the assay, each competitor was pre-conditioned to the same environment they would compete in, to make sure both clones were in the same physiological state. At the beginning of the invasion assay the ancestor (2.5×10⁷ cells) was spread on the agar surface, while the invader (5×10⁴ cells) was introduced in one of three different ways: in the first treatment (A), cells were introduced in one spot in the middle of the plate (1 μl); in the second treatment (B), cells were introduced in 20 different spots (1 μl each); and in the third and fourth treatments (C and M), we uniformly mixed both competitors before spreading them evenly on the plate. The total number of cells of both competitors at the start of the experiment was the same for all treatments: 500 : 1. Every day, the populations were transferred to new plates containing fresh medium; populations of the first three treatments (A, B and C) were transferred using velvet; in the fourth treatment (M) cells were scraped off the plate, diluted and mixed in 10 ml of saline before transfer. Fifty microlitres (containing approx. 2.5×10⁷ cells) of a stationary phase culture was transferred to fresh medium and incubated for 24 h at 37°C. The populations grew approximately 200-fold each day, until they reached a density of about 5×10⁸ cells ml⁻¹, which represents approximately eight generations.

At days 1, 2, 3 and 5 of the invasion assay, the relative frequency of the invader was estimated by plating a dilution of the population on indicator plates. For this, cells were scraped off the plates after the population was transferred, diluted in saline and mixed. Since it is not possible to accurately estimate the frequency at the start of the experiment (because cells cannot be scraped off without ending the experiment), experimental values are represented beginning at generation 8 (day 1).

In order to exclude the possibility that the results would be influenced by pre-adaptation of the evolved clone to the transfer method (velvet versus mixing), invading strains with a fitness advantage of approximately 50% relative to the ancestor were used from each of the structured environments (Habets et al. 2006). Both clones were competed in all four treatments; every treatment was replicated sixfold. No significant differences between clones were found (table 1).

Table 1.

Repeated measures ANOVA testing the effect of four different degrees of dispersal on the rate of invasion of two evolved clones.

source	d.f.	MS	F	p
between subjects
dispersal (treatment)	3	1.820545	418.034	<0.001
invading strains	1	0.001042	0.239	0.628
dispersal×invading strains	3	0.007549	1.733	0.179
error	34	0.004355
within subjects
time	3	2.43519	1165.930	<0.001
time×dispersal	9	0.44386	212.515	<0.001
time×invading strains	3	0.00441	2.112	0.103
time×dispersal×invading strains	9	0.00442	2.115	0.035
error	102	0.00209

(b) Rate of diffusion

Fifty microlitres of a 10-fold diluted stationary phase LB culture of the ancestral clone (approx. 2.5×10⁷ cells) was spread out on an agar plate (100×15 mm) partitioned into 20 ml of nutrient-free agar and 5 ml of concentrated LB agar. The total nutrient concentration was the same as used for the invasion experiment. Cells were spread either on the nutritious agar, in close proximity to the nutritious agar, or at some distance from it. After 24 h, the density of the populations was tested. This was done by scraping the cells off the plate.

(c) Model

We used a simple stochastic cellular automaton (CA) model to imitate the four different treatments of the experiment. The CA space is a 1000×1000 square grid of sites representing the surface of the agar medium in a Petri dish. Each site is assumed to be capable of harbouring a single bacterial cell, so growth is purely two dimensional. Of the 10⁶ sites, 0.5% were inoculated at time 0 by bacteria at a mutant to ancestor ratio of 1 : 500, equal to the experimental design. The ancestral strain was dispersed on the plate at random. For treatment A, the invading cells were clumped into a single spot in the middle of the plate; in B the same number of cells was distributed into 20 spots and the spots spaced out evenly on the plate; in C and M the invaders were dispersed over the plate at random. A generation consists of 10⁶ independent, random updating steps, so that each site is updated once on average every generation. An updating step starts with the random choice of a focal site and one of its neighbouring sites. If the focal site contains a single cell and the neighbouring one is empty, then the cell may put a copy of itself into the empty site with a probability equal to its basic fitness f_i, a parameter of the strain the focal cell belongs to. We used f_ancestor=0.67 and f_mutant=1.00 to maintain a relative fitness of 1.5 for the invader. Every eighth generation, a 0.5% sample of the bacteria present on the plate is transferred to a new plate. In treatments A, B and C, the bacteria in the sample keep their previous site on the new plate; in treatment M, the sample is reshuffled and dispersed on the new plate at random. Using this updating algorithm, we have recorded the relative frequency and the relative fitness of the invading strain over 40 generations (5 days, eight generations per day).

Note that the number of simulated cells is two orders of magnitude smaller than that in bacterial experiments described above, because the fates of enormous numbers of cells are impossible to follow even with the most powerful of recent computers. Therefore, a quantitatively correct simulation of the dynamics on a Petri dish is not feasible; rather the simulation model is intended to provide a qualitative explanation for the experimental data.

3. Results

(a) Rate of invasion in model

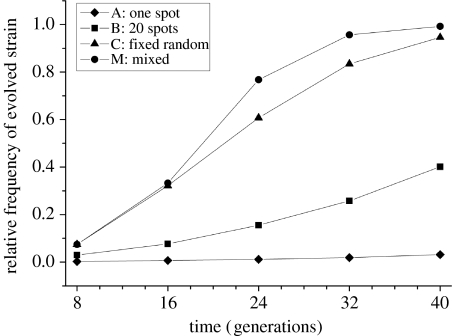
We investigated the rate of invasion of a superior competitor in a spatially structured environment when mixed to different degrees with its well-dispersed ancestor. Simulations show that the superior clone can invade in all four treatments (figure 1), but the rate at which this happens depends on the degree of mixing, with daily mixing (treatment M) leading to the quickest invasion. A rigid spatial population structure with a single invasion centre (treatment A) delays the invasion process considerably. Keeping the rigid spatial structure but increasing the number of invasion centres (in treatments B and C) provides the invader with an additional competitive advantage, so that a relatively short time is sufficient for it to increase towards fixation.

Figure 1.

Simulated relative frequencies of the superior competitor over time. Parameters: basic fitnesses: f_ancestor=0.67, f_mutant=1.00; initial ancestor to mutant frequency ratio: 500 : 1; transfer dilution: 200-fold; transfer frequency: every eighth generation.

(b) Rate of invasion in experiment

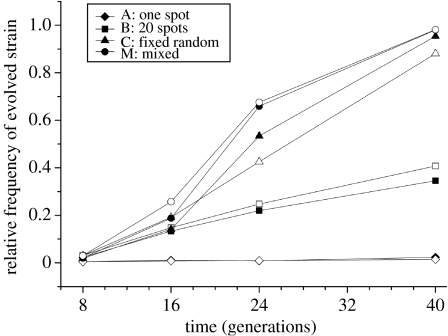
In accordance with the simulations, the experimental results show that the superior competitor invades in all four treatments (figure 2) and that the rate of invasion depends on the degree of mixing (table 1), with daily mixing (treatment M) leading to the fastest invasion.

Figure 2.

Relative frequency over time (generation) of the superior competitor during the competition experiment. Filled symbols represent the clone evolved on the structured plate of our long-term experiment; open symbols represent the clone evolved on the mixed plate. No significant fitness difference is found between the clones. The different treatments represent the different degrees of mixing. The difference in density of the various starting ‘spots’ of the superior competitor is negligible (the density on the plate is everywhere about 8.9×10⁵ cm⁻²) and does not influence the competition.

A potential dissimilarity between simulations and experimental data is a difference in the diffusion rates of nutrients. A difference in diffusion rates would affect the rate of invasion, because diffusion of nutrients, together with the rate of uptake of nutrients by cells, determines the local nutrient concentration in a structured environment. If diffusion of nutrients is fast, cells can exhaust nutrients over a larger area, increasing the impact they have on their environment (Huston & DeAngelis 1994). Whereas no diffusion takes place in the simulations, the dominant competitor in the experiment might rapidly obtain nutrients from a larger area, thereby preventing cells not only in close proximity but also further away from growing. With a high rate of nutrient diffusion, the dynamics of invasion in a spatially structured environment would resemble the dynamics in a well-mixed environment.

We found that the rate of nutrient diffusion was negligible relative to the rate of nutrient uptake, because growth after 24 h differed significantly between cells that grew on nutrients, in close proximity to nutrients or at some distance from the nutrients in a Petri plate that was partly nutrient rich and partly nutrient free (F_2,6=50.975, p<0.001). We can therefore conclude that diffusion was roughly similar for simulation and experimental conditions, consistent with the general similarity in invasion dynamics produced by simulations and experiment.

(c) Fitness of the superior competitor

We next tested whether the rate of invasion of the superior competitor is dependent on its frequency. The previous results suggested that with an increase in the number of invaders, intraspecific competition increases relative to interspecific competition, reducing the rate of invasion. We tested this hypothesis by calculating the fitness of the invading strain, relative to its ancestral competitor, at three different time points during invasion in both the simulation as well as the experimental data. The relative fitness is calculated by the ratio of the Malthusian parameters (m) of the competitors; m=ln[N_i(1)/N_i(0)/1d], where N_i(0) is the density at the start of the competition, N_i(1) the density after 1 day of competition assay and d is the number of days (Lenski et al. 1991).

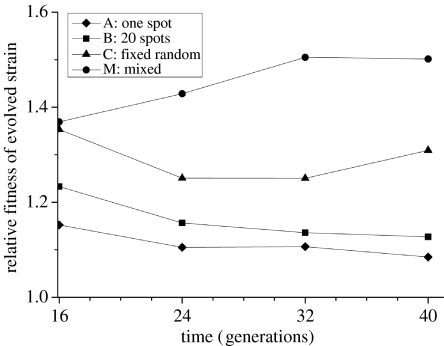
The simulation data show that the fitness of the superior clone depends on two aspects: the initial distribution of the superior competitor and the amount of mixing during invasion (figure 3). Fitness is lowest if the invader is clumped in one spot and highest when mixed at the start of the experiment. If besides mixing at the start, the population is mixed in between transfers (treatment M), an increase in fitness is observed. A conspicuous decrease in the fitness of the invader was found in all other treatments (figure 3). The results of the model confirm the hypothesis that reproduction of the invading cells is constrained by the increasing within-strain aggregation, preventing the bulk of invaders from directly interacting with the inferior competitive ancestral population, and therefore inhibiting their increase in relative frequency. The unexpected increase in fitness in the mixed treatment (M) of the simulations, which we did not see in the experimental data (see figure 4), remains unexplained.

Figure 3.

Relative fitness of the superior competitor over time (generation) in the simulation. Parameters are the same as given in figure legend 1.

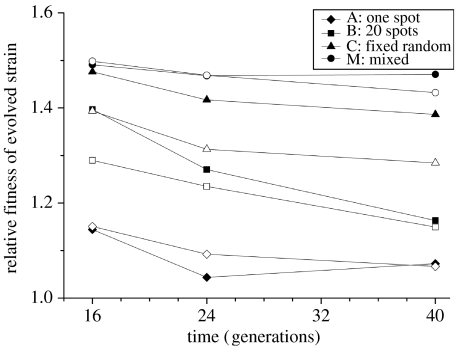
Figure 4.

Relative fitness of the superior competitor over time (generations) during the competition experiment. Filled symbols represent the clone evolved on the structured plate of our long-term experiment; open symbols represent the clone evolved on the mixed plate of our long-term experiment.

The experimental data exhibit the same dependence on both initial distribution of the invader and dispersal during invasion. Like the theoretical results, there is a significant difference in treatments (repeated measures ANOVA for differences in treatments: between subjects F_3,35=80.697; p<0.001); the better the superior competitor is distributed over the plate at the start of the experiment, the higher the fitness at all time points (figure 4).

When the competitors are not mixed daily (treatments A, B and C), there is a significant fitness decrease over time between generations 16 and 40 (figure 4; A: F_2,27=4.449, p=0.021; B: F_2,27=30.981, p<0.001; C: F_2,27=6.923, p=0.004; M: F_2,24=0.466, p=0.386). This fitness decrease is significantly different between the treatments (time–treatment interaction: F_3,35=4.307, p=0.011) and appears to be largest in treatment B. The more dispersed the invader is at the beginning of the experiment, the faster the ratio of inter- to intraspecific competition changes, and thus the larger the predicted fitness decrease; we would therefore expect treatment C to have the largest fitness decrease. However, in treatment C, the invasion progresses faster and towards the end of the invasion experiment, the population mainly consists of mutants with well-dispersed small islands of ancestral cells. This leads to a deceleration of the rate of fitness decline. Since we measure over the same time period for all treatments, this deceleration in fitness decrease leads to a slower overall fitness decrease in treatment C than treatment B, even though all treatments demonstrate this fitness decline over time (figure 4).

4. Discussion

We have assessed the rate of invasion of a beneficial mutant under the spatial constraints of competitive interaction. In a well-mixed environment, the difference in fitness between an ancestral strain and a new beneficial mutant is constant throughout competition, i.e. the mutant can realize its fitness advantage at a maximum level. When population growth occurs in a spatially constrained fashion with limited dispersal and local interactions, however, the fitness of any genotype will depend on the fitness of neighbouring genotypes, since nutrients are limiting in each spot. Moreover, space also counts as a limiting factor for sedentary organisms. Without dispersal, a mutant with higher fitness will not be able to exploit its advantage to the full, because it is mostly in competition with its clone mates. The rate of invasion will consequently be reduced if the dominant competitor is constrained spatially. This finding helps to understand our previous finding that populations evolving in spatially structured environments that were not mixed had a lower rate of adaptation than populations that were mixed regularly (Habets et al. 2006). In contrast to these results, previously published theoretical data show that mixing in a spatially structured environment leads to a decrease in the rate of fixation of beneficial mutations due to an increase in the role of drift (Perfeito et al. 2006). By spatial reshuffling, the mutants are scattered which spoils the protective clumps they would form without mixing, thus increasing the chance that the mutant will be lost by drift. Although a direct comparison with our model cannot be made—since we study the rate of invasion of a single beneficial mutant and not the rate of fixation (the number of beneficial mutants fixed within a certain time frame)—there is a clear difference in the role of demographic stochasticity due to a much larger population size in our study.

Owing to slower invasion of adaptive mutants, we expect not only the ecology but also the evolution of the community to be affected. Since inferior competitors are present in the community for a longer time, they can recombine with other persisting lineages or obtain new mutations, some of which might be beneficial. It is therefore possible that genotypes arise that would not have had the opportunity to emerge in a well-mixed environment. In short, spatial constraints can cause the maintenance of more genetic variation, which might help the population to adapt to changing environments (Boles et al. 2004). In addition, stable coexistence may arise between certain genotypes in a population, because a higher standing genetic variation provides more opportunities for such interactions. Thus, we arrive at the conjecture that by slowing down the exclusion dynamics between competing genotypes, spatial constraints may increase evolutionary diversification in populations.

In an evolution experiment with E. coli in environments with varying degrees of spatial structure, we found support for this view. We observed a lower rate of adaptation and higher maintained diversity in bacterial populations evolved in a spatially structured environment with intact population structure relative to populations evolved in mass action or a structured but regularly mixed environment (Habets et al. 2006). Spatial structure has also been proposed as a crucial factor for the maintenance of diversity (Korona et al. 1994; Rainey & Travisano 1998), particularly where competitive interactions are non-transitive (Czárán et al. 2002; Kerr et al. 2002). The associated slower dynamics that we observe here may be an additional factor causing the short-term coexistence of competitors in such communities.

Our findings show that improving resource competitive ability (i.e. growth rate) in spatially structured environments is not as advantageous as in a well-mixed environment. This suggests the importance of evolving other strategies such as increased dispersal or interference competition to reduce local competition. We are currently exploring these proposals.