Predicting Social Security numbers from public data

Abstract

Information about an individual's place and date of birth can be exploited to predict his or her Social Security number (SSN). Using only publicly available information, we observed a correlation between individuals' SSNs and their birth data and found that for younger cohorts the correlation allows statistical inference of private SSNs. The inferences are made possible by the public availability of the Social Security Administration's Death Master File and the widespread accessibility of personal information from multiple sources, such as data brokers or profiles on social networking sites. Our results highlight the unexpected privacy consequences of the complex interactions among multiple data sources in modern information economies and quantify privacy risks associated with information revelation in public forums.

In modern information economies, sensitive personal data hide in plain sight amid transactions that rely on their privacy yet require their unhindered circulation. Such is the case with Social Security numbers in the United States: Created as identifiers for accounts tracking individual earnings (1), they have turned into sensitive authentication devices (2), becoming one of the pieces of information most often sought by identity thieves. The Social Security Administration (SSA), which issues them, has urged individuals to keep SSNs confidential (3), coordinating with legislators to reduce their public exposure (4).* After embarrassing breaches, private sector entities also have attempted to strengthen the protection of their consumers' and employees' data (7).^† However, the horse may have already left the barn: We demonstrate that it is possible to predict, entirely from public data, narrow ranges of values wherein individual SSNs are likely to fall. Unless mitigating strategies are implemented, the predictability of SSNs exposes them to risks of identify theft on mass scales.

Any third party with internet access and some statistical knowledge can exploit such predictability in 2 steps: first, by analyzing publicly available records in the SSA Death Master File (DMF) to detect statistical patterns in the SSN assignment for individuals whose deaths have been reported to the SSA; thereafter, by interpolating an alive person's state and date of birth with the patterns detected across deceased individuals' SSNs, to predict a range of values likely to include his or her SSN. Birth data, in turn, can be inferred from several offline and online sources, including data brokers, voter registration lists, online white pages, or the profiles that millions of individuals publish on social networking sites (10). Using this method, we identified with a single attempt the first 5 digits for 44% of DMF records of deceased individuals born in the U.S. from 1989 to 2003 and the complete SSNs with <1,000 attempts (making SSNs akin to 3-digit financial PINs) for 8.5% of those records. Extrapolating to the U.S. living population, this would imply the potential identification of millions of SSNs for individuals whose birth data were available. Such findings highlight the hidden privacy costs of widespread information dissemination and the complex interactions among multiple data sources in modern information economies (11), underscoring the role of public records as breeder documents (12) of more sensitive data.

Hypotheses

The first 3 digits of an SSN are called its area number (AN), the next 2 are its group number (GN), and the last 4 are its serial number (SN). The SSA openly provides information about the process through which ANs, GNs, and SNs are issued (1). ANs are currently assigned based on the zipcode of the mailing address provided in the SSN application form [RM00201.030] (1). Low-population states and certain U.S. possessions are allocated 1 AN each, whereas other states are allocated sets of ANs (for instance, an individual applying from a zipcode within New York state may be assigned any of 85 possible first 3 SSN digits). Within each SSA area, GNs are assigned in a precise but nonconsecutive order between 01 and 99 [RM00201.030] (1). Both the sets of ANs assigned to different states and the sequence of GNs are publicly available (see www.socialsecurity.gov/employer/stateweb.htm and www.ssa.gov/history/ssn/geocard.html). Finally, within each GN, SNs are assigned “consecutively from 0001 through 9999” (13) (see also [RM00201.030], (ref.1.)

The existence of such patterns is well known (14), and has been used to catch impostors posing with invalid or unlikely SSNs (15). However, outside the SSA, the understanding of those patterns was confined to the awareness of the possible ANs allocated to a certain state and the GNs issued in a certain year or years. Based on such limited knowledge, SSN inferences described in the literature would start from known SSNs and predict, based on their digits, the possible states and ranges of years when those SSNs could have been issued (15). We conjectured, however, that the functional relationship between the digits of an SSN and the location and time of its application could be reversed, allowing the inference of all of the 9 digits of unknown SSNs starting from their presumptive state and day of application. Empirical observation of SSA's policies—particularly the Enumeration at Birth (EAB) initiative, which started extending nationwide in 1989 (2)—drove the conjecture (the EAB was designed as an antifraud program integrating the application for an SSN into the birth certification process). After EAB, the overwhelming majority of U.S. newborns started obtaining their SSNs shortly after birth (12). Although the assignment process remained inherently noisy, we hypothesized that (i) times and locations of individuals' SSN applications over time have become more correlated with those individuals' times and states of birth; (ii) such correlation may allow a more granular understanding of the SSN assignment scheme and its regularities than what is currently described in the literature; (iii) this more granular understanding, coupled with the increasing correlation between births and SSN applications, may allow the prediction of unknown SSNs entirely from the applicants' birth information.

Analysis

We tested our hypotheses using DMF data—a publicly available file reporting SSNs, names, dates of birth and death, and states of SSN application for individuals whose deaths have been reported to the SSA (see www.ntis.gov/products/ssa-dmf.aspx). (Ironically, one of its applications is fraud prevention, because the DMF can be used to expose impostors who assume deceased individuals' SSNs.) The process of discovery of a more granular understanding of the SSN assignment patterns was iterative: We used public information about the assignment scheme to analyze publicly available data; this allowed us to reinterpret public details about the assignment scheme and analyze the data again under improved lenses. We focused on DMF data for individuals born between January 1973 (after the SSN assignment was centralized to the Baltimore SSA headquarters) and December 2003 (before DMF data get too scarce). We split DMF records into groups by their state of application, and—within each group—sorted them chronologically by birthday. If our hypothesis was correct, we would observe individuals with close birthdays and same state of application display similar SSNs in the rearranged dataset. Thereafter, we would be able to use such regularities to predict unknown SSNs based on birth information.

Pattern Analysis.

After grouping and sorting DMF data by state of assignment and date of birth, we started looking for visual and statistical patterns in the rearranged dataset that proved or disproved the connection between birthdates and SSNs. The analysis confirmed the regularities we expected: As hypothesized, a strong correlation exists between dates of birth and all 9 SSN digits; that correlation increases for individuals born in years after the onset of the EAB program, and in less populous states (where fewer births take place over a given period, determining slower—and more detectable—transitions through the SSN assignment scheme).

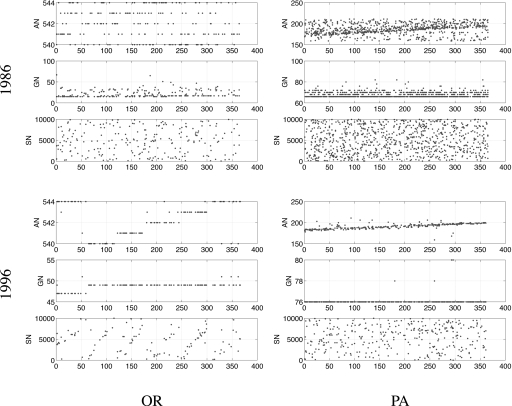
In Fig. 1, we show SSN entries in the DMF as triads of points representing an SSN′s AN, GN, and SN digits. The AN, GN, and SN subplots of Fig. 1 for 2 illustrative states show trends common to all states: Cyclical, chronological (albeit noisy) patterns in the assignment become visible once DMF records are separated by state of assignment and sorted by dates of birth. Regular assignment patterns can be detected across all states over all years of birth, but are more evident for less-populous states (Oregon, versus Pennsylvania) and for years after the state's entry into the EAB program (1996, versus 1986): SSNs assigned in the same state to applicants born on consecutive days are likely to contain the same AN and GN, before the next combination (henceforth, “ANGN”) in the assignment scheme is issued, as well as sequential SNs.

Fig. 1.

SSNs of DMF records sorted by state of assignment and ordered by date of birth for 2 representative states in 1986 and 1996. The x axis represents time: the day of birth, over 365 days in 1986 or 1996, for individuals whose deaths were reported to the SSA and whose SSNs were assigned in Oregon or Pennsylvania. The y axis represents the ANs, GNs, and SNs those individuals were assigned. An imaginary straight vertical line connects each triad of dots in the AN, GN, and SN portions of the figure; each triad represents one DMF record's SSN.

Specifically, GNs transition slowly or remain constant over the years selected for Fig. 1: For instance, excluding the outliers, the GNs assigned in Oregon to individuals born in 1996 transition from 47 to 49; in PA they remain constant at 76.

ANs transition faster than GNs; however, contrary to a commonly held view about their assignment, the same AN is used for 9,999 consecutively assigned SSNs. Under the interpretation of the assignment scheme held outside the SSA, the SSA was believed to rotate through all of a state's ANs for each assigned SN (16). Such scheme would render the AN random for states with multiple ANs, and the predictions we present in this article dramatically less accurate. Instead, Fig. 1 shows an ascending (and, in Oregon, cyclical) trend: For instance, the ANs assigned in Oregon to individuals born in 1996 transition from 544 to 540, then to 541, 542, and 543, before reaching 544 again near year end.

SNs transition faster than either ANs or GNs. The speed at which they change, coupled with the noise and idiosyncracies inherent in their assignment, may suggest that the relationship between dates of birth and SNs is, for practical purposes, random. Indeed, the SSA refers explicitly to “random” assignments at [RM00201.060] (1). However, visual observation of the SN subplots in Fig. 1 evidences a noisy yet visibly (for less-populated states) linear and ascending trend when SNs are sorted by applicants' dates of birth. The steepness of the imaginary line interpolating the SNs is a function of the state's volume of births over a period: At least 5 upward sloping and approximately parallel trend lines emerge in the SN portion of Fig. 1 Left in correspondence to the 5 ANs assigned in 1996.

Based on visual inspection [and statistical analysis presented in supporting information (SI) Appendix], we gained a different and more granular understanding of the regularities in the SSN assignment pattern than what is currently discussed in the literature. We concluded that the combined SSN assignment scheme consists of SNs transitioning first; after 9,999 SNs associated with a certain combination of AN and GN, the next AN in the issuance scheme is assigned; then, when all ANs assigned to a state or territory are exhausted, the next GN in the scheme is assigned. More importantly, we concluded that the linearity in the assignment of SSNs can be publicly observed as a pattern linking applicants' dates of birth to their SSN digits, including their last 4. The assignment patterns that Fig. 1 makes explicit suggest that an individual's SSN may be inferred based on knowledge of the ANs, GNs, and SNs assigned to individuals born around the same day and in the same state as the target.

Algorithm Description.

Our prediction algorithm exploits the observation that individuals with close birthdates and identical state of SSN assignment are likely to share similar SSNs. It employs the DMF as a public source of information about SSNs assigned over time and across states. For each target individual, the algorithm proceeds by first predicting the target's ANGN, and then the SN associated with the predicted ANGN. Specifically:

ANGNs.

We predict a target individual's first 5 SSN digits (that is, his or her ANGN) by choosing the statistical mode of the distribution of ANGN(s) appearing in the set of DMF records whose birthdates are contained within a variable window of days centered around that target individual, excluding the target record from the set. Because the 50 states greatly differ in numbers of births occurring over a given period, they exhibit different transition speeds across the assignment scheme. As described in SI Appendix, we calculated such variable windows of days to account for such differences. Furthermore, various outliers can be found among DMF records (data entry errors or individuals—such as aliens—who received SSNs later than at birth). We describe data-cleansing procedures in SI Appendix, although our prediction accuracy tests also included outliers.

SNs.

We predict a target individual's last 4 SSN digits (that is, his or her SN) using the set of SSNs of all DMF records contained in the variable window of days centered around the target individual's birthdate, and regressing the SNs of those records on their associated birthdates (excluding the target record from the set). The regression model is sketched in Eq. 1:

where SN_i is the SN assigned to individual i, born on day dd and whose record can be found within the window of days vw in a specific year and state; ANGN_i,vw is a vector of dummies for the various ANGNs that can be found associated with the SSN records contained in the DMF within that variable window (the ANGN dummies account for the cyclical pattern of SN issuance); and ε is the regression error. The target individual's date of birth and its predicted ANGN are combined with the β₁ regression coefficient for the day dd_i,vw and the β₂ dummy coefficients for the predicted ANGN_i,vw from the regression conducted over the DMF records included within a window of days around the target's date of birth. For the tests presented below, we used robust regressions. Variations of the algorithm are discussed in SI Appendix.

Results

We evaluated the performance of our prediction algorithm using the DMF as an analysis set to identify assignment patterns, and as a test set to measure the accuracy of SSN predictions based on extrapolated patterns. We predicted ANGNs and SNs for more than half a million DMF records whose SSNs were issued in 1 of the 50 states and whose births reportedly took place between January 1973 and December 2003. Naturally, the analysis set used in the prediction of a given DMF record did not include said record.

We evaluated the results under 2 success metrics: whether we could correctly identify with 1 single attempt an SSN′s first 5 digits (because the last 4 may be discerned elsewhere); and whether we could correctly identify the entire SSN in fewer than x attempts (with x = 10, 100, or 1,000).

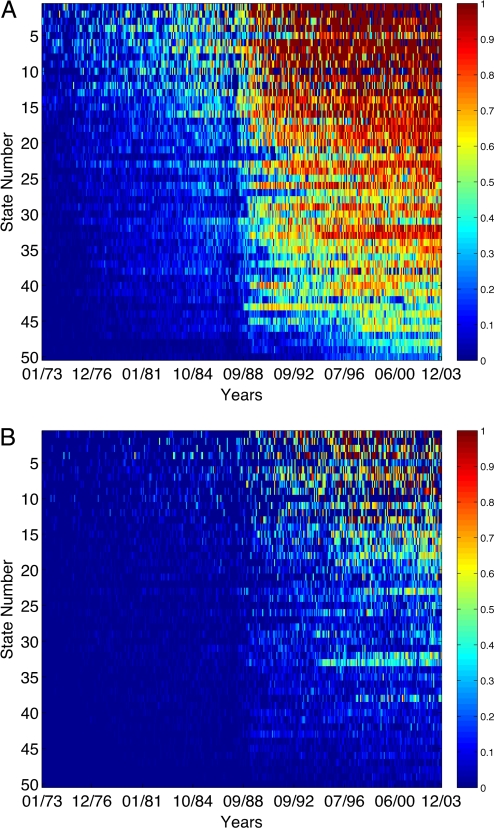
Fig. 2A summarizes the results for our first metric. On average, we matched at the first attempt the first 5 digits for 7% of all records for individuals born nationwide between 1973 and 1988, and 44% for those born after 1988 [means are weighted by the relative numbers of births across years and states obtained from National Center for Health Statistics (NCHS) data]. As hypothesized, although our predictions are already more accurate than random chance by several orders of magnitudes over the 1973 through 1988 period, dramatic and widespread increases in accuracy are especially observable after 1988 (the onset of the nationwide EAB program), particularly for less-populous states. Furthermore, a trend of steady improvements in accuracy is evident over the years across all states, as increasingly larger proportions of newborns receive their SSNs through the EAB program (data scarcity does not determine this result, as discussed in SI Appendix). For instance, we accurately predicted the first 5 digits of 2% of California records with 1980 birthdays, and 90% of Vermont records with 1995 birthdays. If we allow 2 attempts (using the most-frequent and the second most-frequent ANGNs as candidates), the weighted mean prediction accuracy for the first 5 digits of individuals' SSNs raises to 61% for all DMF records issued nationwide with dates of birth between 1989 and 2003: In other words, the first 5 SSN digits of 6 of 10 SSN records in that set can be identified with just 2 attempts.

Fig. 2.

Prediction accuracies for DMF records with January 1973 to December 2003 birthdays across the 50 states. (A) Ratios of ANGNs (first 5 digits) accurately predicted. (B) Ratios of complete SSNs accurately predicted with <1,000 attempts. In each quadrant, columns represent months, and rows represent states (sorted by their 1973 births, lowest to highest). The colors in each cell represent ratios out of monthly SSN counts.

For the last 4 digits, we considered a brute-force matching algorithm where, for each target SSN, the attacker tries out the predicted ANGN and SN combination, before increasing and decreasing the SN by 1-integer steps for the subsequent attempts, while keeping the predicted ANGN constant. Under this algorithm, 10 or fewer attempts per target are sufficient to match the complete SSNs of ≈0.01% of all DMF records with dates of birth between 1973 and 1988, and ≈0.1% of all records with dates of birth between 1989 and 2003. Those are weighted averages; prediction accuracies are as high as 5% for certain years and states (such as Delaware, 1996), corresponding to ≈1 of every 20 SSNs issued in those years and states identifiable with 10 or fewer attempts.

Nationwide, the weighted mean of the percentage of whole SSNs that can be matched with 100 or fewer attempts is 0.08% for records with pre-1989 dates of birth, and 0.9% for those with post-1988 dates of birth. Yearly accuracies rise >10% for some smaller states.

Finally, <1,000 attempts per target are sufficient to match the entire SSNs of 0.8% of all records with dates of birth between 1973 and 1988, and 8.5% of all records with dates of birth between 1989 and 2003 (Fig. 2B). A successful identification of an entire SSN with <1,000 attempts makes that SSN comparable with a 3-digit (and, therefore, highly insecure) financial PIN. For smaller states and recent years, the percentage rises >60%—with some of our predictions matching complete, 9-digit SSNs at the very first attempt.

In practical applications, SSNs are often used as authenticators in inquiries processed by credit reporting agencies (CRAs). Because consumer credit reports contain errors and inconsistencies, CRAs are known to accept as valid even inquiries where just 7 of 9 SSN digits are actually correct (17). This implies that, for some practical purposes, the prediction accuracies we reported may be conservative by 2 orders of magnitude: With just 10 or fewer attempts per target, the inquiries associated with 9.2% of all SSNs issued after 1988 could be accepted as valid by CRAs and 29.1% of those issued in the 25 states with fewer births.

Discussion

The prediction accuracies we have reported pertain to more than half a million DMF records of deceased individuals. However, the same assignment patterns detected over DMF records also apply to the SSNs assigned to alive individuals: Over short periods of time (such as the windows we used in our calculations), mortality rates do not significantly differ by dates of birth (18). This implies that the DMF data are, by and large, a representative subset of the overall SSN-receiving population, and the prediction accuracies we presented also apply to alive individuals whose birth data were available.

Therefore, an alternative way of interpreting our results consists of extrapolating from the prediction accuracies over DMF records for deceased individuals to the US-born population of individuals still alive. In this case, by moving from left to right in both quadrants of Fig. 2, we get a sense of the predictability, by state, of the SSNs of younger and younger individuals. Under the hypothetical assumption of complete availability of birth data, the first 5 digits of 26 million SSNs for individuals born between 1989 and 2003 may be correctly matched at the first attempt (in addition to ≈4 million of those born between 1973 and 1988); and almost 5 million complete SSNs may be matched with <1,000 attempts (in addition to ≈1 million of those born between 1973 and 1988).

Statistical predictions of windows of possible SSNs, however, do not amount, alone, to identity theft. The likelihood that probabilistic inferences can translate to actual SSN identification is a function of several parameters, including the availability of targets' birth data, the availability of services an attacker can exploit for repeated attempts to match the targets' SSNs, and those services' ability to detect and halt such attempts. Inaccurate or unavailable birth information, or the attacker's inability to complete repeated attempts, will reduce the accuracy of the predictions and the number of individuals' SSNs under actual threat compared with the DMF estimations.

Dramatically reducing the range of values wherein an SSN is likely to fall, however, makes identity theft easier to perpetrate. A party who attempted to guess someone's SSN randomly would face poor success odds: Without auxiliary knowledge, the theoretical entropy of an SSN can be estimated at 30 bits (in log₂). The more granular knowledge of the assignment scheme that we have shown to be inferrable significantly decreases that entropy (for some states, down to 11 bits). When 1 or 2 attempts are sufficient to identify a large proportion of issued SSNs' first 5 digits, an attacker has incentives to invest resources into harvesting the remaining 4 from public documents^‡ or commercial services.^§ More importantly, when <10, 100, or 1,000 attempts are sufficient to identify complete SSNs for massive amounts of targets, brute-force attacks replicating the algorithm we presented in the previous section become economically plausible.

Attackers can exploit online services as oracle machines (19), testing subsets of variations predicted by the algorithm to verify which SSN corresponds to an individual with a given birth date [a practice called “tumbling,” consisting of slightly changing numerical details in fraudulent credit applications (such as address numbers and SSNs), has been documented by IDAnalytics (20)].

• “instant” credit approval services [such as plentiful online credit card issuers—including those specifically targeting individuals with poor credit (21); wireless carriers; or instant lending services (22)]. These services require information such as applicants' names, dates of birth, and SSNs to screen credit or service applications, thus offering an attacker a means to verify variations of predicted SSNs;

• sending mass spear phishing emails (23) based on social engineering (24). Such emails would include the target's first 5 or 6 SSN digits to elicit a revelation of the remaining digits;

• the SSA's own SSN Verification Service (www.ssa.gov/employer/ssnv.htm) and the Department of Homeland Security's E-Verify system (www.uscis.gov/e-verify), 2 antifraud initiatives that allow employers to verify large numbers of employees' SSNs at a time. They could be abused if an attacker succeeded in impersonating companies' representatives or self-employed individuals.

Although defense mechanisms to detect repeated abuses are in place at those services [for instance, the SSNVS tracks incorrect attempts at verifying SSNs, and financial institutions blacklist (for various days or months) IP addresses originating 3 or more failed logins or transactions (25)], “botnets” of compromised computers (26) allow attackers to test—cheaply and covertly—vast numbers of variations of targets' SSNs, strategically distributing simultaneous attempts across services, compromised machines, and target accounts. A rational attacker would focus on SSNs issued in states and years with higher prediction accuracies, taking advantage of the lack of a centralized, real-time system for the notification of hits and flags on credit account requests (27), as well as of the fact that, unlike traditional passwords, SSNs cannot be blacklisted after failed attempts, nor changed to avoid future fraud (28).

Consider, for instance, an attacker who rented a small botnet (10,000 IP addresses) to apply for credit cards impersonating 18-year-old West Virginia-born U.S. residents (whose state and dates of birth he has obtained from commercial databases). Assuming that an IP address gets blacklisted by an online credit card issuer after 3 incorrect attempts, that the criminal distributes his or her attacks across 20 issuers and can find birth data for 50% of the potential targets, and that inquiries with the correct first 7 of 9 digits are sufficient for a CRA to answer with a positive match in 50% of the cases, he could harvest credentials at rates as high as 47 per minute, obtaining ≈4,000 credentials within 2 h before his IPs are blacklisted [our estimates are based on the prediction accuracies calculated over DMF records for the corresponding year and state and constrain the number of attempts to stay within 10% of the daily volume of CRA inquiries [estimated at 4 million by the FTC in 2004 (17)]. After that, he could wait for the blacklist period to expire or rent a different set of botnet machines. Estimates for the total number of bots worldwide range from as low as 800,000 (26) to as high as 5 million (29).

The profitability of such operation depends on various factors. Breaching large organizations' databases to harvesting of personal data can produce massive amounts of credentials but often requires significant logistical and technical efforts (for instance, see ref. 30 on the TJ Maxx breach). On the other hand, automated vast-scale cyber-attacks based on distributed computations, or mass-scale harvesting of personal data, are becoming more common (31) because of the availability and affordability of botnets. Botnets are easy to program for repeated online applications, and they are economical: Although estimates vary, controlling 10,000 IPs for a day could cost as little as $1,000 (32). The data necessary for the predictions is, itself, widely available: SSN predictions do not require knowledge of someone's birth zipcode but just his or her state and date of birth. Whereas SSNs are becoming harder to purchase in the open market (8) and less available in public documents (33), mass amounts of birth data for U.S. residents can be obtained or inferred—often for free or at negligible per unit prices—from multiple sources. They include data brokers (such as www.peoplefinders.com, which sells access to birth data and personal addresses for “almost every adult in the United States”); voter registration lists (for most states); online free people searches (such as www.zabasearch.com); as well as social networking sites: Our estimates indicate that at least 10 millions U.S. residents make publicly available or inferrable their birthday information on their online profiles. An attacker may not even need birth data: The rise of synthetic identity theft (where fake names are combined with real SSNs and birthdates) suggests that a correspondence between birthdate and SSN can be sufficient to pass the screening of CRAs, even when names or addresses do not match those in the credit reports (21, 22). Our results show that such correspondence is inferrable even without knowledge of the target's name.

These aspects are further discussed in ref. 34. There, we present an illustrative application of the prediction algorithm in which we infer alive individuals' SSNs based on public information we mined from a social networking site. To illustrate the actual threat of combining public records to infer sensitive information, we used DMF data as the analysis set to extract the most-frequent ANGNs and the SN regression coefficients for the range of states and birthdays corresponding to the alive individuals' birth data. We extracted the birth data from the public profiles of 621 students at a North American university. We then interpolated our sample's birth data with the patterns estimated from DMF records, and then predicted the formers' SSNs. We verified the accuracy of our predictions against the subjects' actual SSN data (from the University Enrollment services), using a secure, IRB-approved protocol that disclosed to us only aggregate predicition accuracy statistics. We found that at parity of year and state of birth (and SSN assignment), the test based on online social network data and the DMF test produced comparable results: we accurately predicted with a single attempt the first 5 digits for 6.3% of our sample, composed mostly of individuals born in populous states before the onset of the EAB program; almost one-third of those predictions (which matched the target's first 5 digits) fell within fewer than 1,000 integers from the target's actual SSN. The DMF test slightly outperforms the social networking site test, since self-reported social network data about hometown and date of birth may be inaccurate or, in fact, misleading. However, these findings confirm that patterns extrapolated from deceased individuals' SSNs in fact can be used to predict the SSNs of living individuals based entirely on public data.

Although inaccurate birth data or inability to run repeated verification attempts are likely to lower prediction accuracies for alive individuals compared with those we obtained for the DMF set, various factors may actually increase prediction accuracies in the real world. Access that criminals have to external data sources with living individuals' SSNs, larger shares of population being born under EAB (and then, inevitably, populating the DMF), and matched predictions or improved prediction algorithms will conspire to augment the DMF analysis set, narrow the group of testable SSN variations, and improve prediction accuracies. Furthermore, the averages we presented above should not befog the finding that the SSN assignment scheme effectively discriminates (in terms of higher identification risks) against younger individuals born in less populous states. More importantly, our extrapolations conservatively focused on individuals born between 1989 and 2003: to those, one should add all individuals born after 2003 who continue to receive SSNs under the current assignment scheme [being a minor is no shield against identity theft (35); some lenders give accounts to individuals with no credit history (21)]. Unlike data breaches, which are local threats (that is, specific to the records contained within a certain database, however large that may be), the predictability we observed is universal, in that applies, in principle, to any current and future SSNs—unless their assignment scheme is modified.

Conclusions

The predictability of SSNs is an unexpected consequence of the interaction between multiple data sources, trends in information exposure, and antifraud policy initiatives with unintended effects. It exposes the privacy tradeoffs of information-disclosure policies (36), reflecting the paradox of information “deemed useful to be publicly available under the old transactions technology” but now too available in a world of wired consumers (37). SSNs were designed as identifiers at a time when personal computers and identity theft were unthinkable; today, abused as authentication devices (38), they enable an “architecture of vulnerability” (39), in which losses are incurred even in absence of fraud, because of costs caused by attempts to defend, and exploit, the system.

A number of mitigating strategies can be considered. In the short term, one of the least costly countermeasures would have the SSA fully randomize the assignment scheme, abandoning the matching of area numbers to states, and the sequential assignment of serial numbers. [The SSA has recently proposed randomizing part of the SSN assignment scheme—but only its first 3 digits (40).] These modifications would eliminate the statistical predictability of newly assigned SSNs. However, they would not do much to protect already existing SSNs.

To address those concerns, various recent legislative initiatives have been focusing on removing SSNs from public exposure or redacting their first 5 digits [see www.ncsl.org/programs/lis/privacy/SSN2007.htm (33, 38)]. However, our results suggest that such initiatives, although well-meaning, may be misguided: Assigned SSNs cannot be revoked to avoid future fraud, exposed data cannot be taken back, and the first 5 digits of an SSNs are those, in fact, easier to infer. This leaves even redacted or truncated SSNs still predictable—and, therefore, still vulnerable. Industry and policy makers may need, instead, to finally reassess our perilous reliance on SSNs for authentication, and on consumers' impossible duty to protect them.