Abstract
Tumour invasion is driven by proliferation and importantly migration into the surrounding tissue. Cancer cell motility is also critical in the formation of metastases and is therefore a fundamental issue in cancer research. In this paper we investigate the emergence of cancer cell motility in an evolving tumour population using an individual-based modelling approach. In this model of tumour growth each cell is equipped with a microenvironment response network that determines the behaviour or phenotype of the cell based on the local environment. The response network is modelled using a feed-forward neural network, which is subject to mutations when the cells divide. With this model we have investigated the impact of the micro-environment on the emergence of a motile invasive phenotype. The results show that when a motile phenotype emerges the dynamics of the model are radically changed and we observe faster growing tumours exhibiting diffuse morphologies. Further we observe that the emergence of a motile subclone can occur in a wide range of micro-environmental growth conditions. Iterated simulations showed that in identical growth conditions the evolutionary dynamics either converge to a proliferating or migratory phenotype, which suggests that the introduction of cell motility into the model changes the shape of fitness landscape on which the cancer cell population evolves and that it now contains several local maxima. This could have important implications for cancer treatments which focus on the gene level, as our results show that several distinct genotypes and critically distinct phenotypes can emerge and become dominant in the same micro-environment.
Keywords: Mathematical model, cellular automaton, tumour invasion, haptotaxis, evolutionary dynamics, clonal evolution, microenvironment
1 Introduction
Cancer cell motility is a crucial aspect of tumour invasion as it facilitates invasion of the healthy tissue in a more efficient way than only cell proliferation can. Cells with motile capabilities can access new nutrient sources and infiltrate the surrounding tissue and this process is instrumental in the formation of metastases, as the cancer cells need to actively move to and from the blood vessels which transport them to new sites in the body. The transition from cancer cells which are predominately proliferative to cells which are motile could therefore be a crucial step in the progression of the disease, and a greater understanding of this process could lead to improved treatment of the disease.
It is an established fact that evolution plays an important role in the development of a tumour (Nowell, 1976; Merlo et al., 2006; Smalley et al., 2005), and the emergence of motile cancer cells therefore has to be viewed from an evolutionary perspective. This view implies that cell motility will only evolve if it confers a selective advantage in the micro-environment in which the tumour grows. It is generally believed that cancer cells cannot move and proliferate simultaneously, a mechanism known as the “go-or-grow” hypothesis (Giese et al., 2003), and this suggests that that the cancer cells are faced with a trade-off: in a harsh low nutrient micro-environment they might be more likely to survive if they migrate, but on the other hand they will be less likely to proliferate and consequently spread their genetic material. Migratory behaviour therefore has a dual effect on the fitness of a cell, it increases the probability that the cell will survive, but at the same time reduces the likelihood that the cell will divide. This suggests that the question of when and how a motile subclone emerges (under the assumption that the initating subclone is non-motile) is far from trivial and is influenced by the complex interactions between the cancer cell population and the micro-environment of the tumour. However, there are many cell types (e.g. fibroblasts, lymphocytes) that have a predominantly motile phenotype and therefore this question is not applicable to them.
In this paper we present a mathematical model aimed at investigating the emergence of cancer cell motility in tumour invasion. The model is based on previous models of solid tumour growth (Gerlee and Anderson, 2007a, 2008, 2009), but is extended here in order to take cell movement into account. In particular we have focused on haptotaxis, cell movement driven up gradients in the extra-cellular matrix density (ECM), which is known to be the dominant mode of movement in tumour invasion (Hood and Cheresh, 2002). In the model the cancer cells are treated as individual entities while extra-cellular factors such as oxygen and the ECM concentration are modelled as continuous quantities, making the model hybrid in nature. In order to capture the fact that tumours are heterogeneous and consist of a large number of subclones competing for space and nutrients, the behaviour of each cell in the model is determined from a response network which is subject to mutations when the cells divide. This means that the behaviour of the cells can change from one generation to the next, and implies that the model has the capability to capture the evolutionary dynamics of tumour growth.
1.1 Biological background
The model presented here will focus on the pre-vascular stages of tumour growth, and we will therefore discuss the structure of the tumour at this stage in detail. Although cancer cells have, due to mutations, escaped normal growth control (Hanahan and Weinberg, 2000), most avascular tumours exhibit a layered structure, which is due to the diffusion limited supply of nutrients (Sutherland, 1988). As the tumour grows, gradients of nutrients (e.g. oxygen, glucose) and waste products (e.g. lactate, hydrogen ions) develop, and when the tumour reaches a critical size, diffusion is insufficient to supply the inner parts of the tumour with nutrients. This leads to cell death or necrosis in the core of the tumour. Outside the necrotic core a rim of quiescent cells is found and further out a thin rim of proliferating cells. The mitotic activity therefore only takes place in a small fraction of the tumour, while the majority of the tumour consists of cells that are either quiescent or dead. It has been established that the limiting nutrient for avascular tumours is oxygen, and that the width of the proliferating rim is determined by the region where the oxygen concentration is in the viable range. Inside the proliferating rim the glucose concentration might still be high, but the usual aerobic metabolism of human cells requires oxygen to produce energy. There is one way for the cancer cells to circumvent this limitation, and that is to utilise the anaerobic metabolic pathway which only uses glucose and does not require any oxygen. In fact this seems to be a ubiquitous feature of solid tumour growth and will be included in the model (Gatenby and Gillies, 2004).
Another important aspect of tumour invasion is the capability of the cancer cells to degrade the surrounding extra-cellular matrix (ECM) (Liotta et al.,1983; Stetler-Stevenson et al., 1993) and to migrate along gradients of ECM, a phenomenon known as haptotaxis (Lawrence and Steeg, 1996).The ECM is a complex mixture of macro-molecules, containing collagens, fibronectin etc., which functions as a scaffold for the cells to grow on. Degradation of the ECM is accomplished by production of matrix-degrading-enzymes (MDEs) by the cancer cells. A large number of different MDEs have been identified, of which matrix metalloproteinases (MMPs) constitute a large family (Ennis and Matrisian, 1993). Most of these are soluble, but it has been shown that a considerable part of matrix degradation is accounted for by membrane anchored MMPs (MT-MMPs) and the plasminogen activator system (Hotary et al., 2000).
The ECM is known to play both a structural and signaling role influencing cell behavior that includes migration, proliferation and survival (Hynes, 1992; Anderson et al., 2006). The mechanical/biological properties of the ECM are multiple and are dynamically modified by cell interactions, via degradation, alignment and production. The movement of cancer cells in the ECM is known to occur in two distinct modes: “path-generation” and “path-finding” (Friedl and Wolf, 2003). In the “path-generating mode” the cell degrades the ECM in the direction of movement and creates a path through the matrix, it then attaches to the matrix at the leading edge using integrins expressed at the cell surface and pulls itself forward. The other mode of movement occurs without degradation of the ECM and the cell instead pushes itself through existing gaps in the matrix and is therefore modulated by the ECM pore size (Zaman et al., 2005, 2006).
Cancer cell migration is tightly linked to metastases, an important step in tumour progression (Sahai, 2007). Metastases are formed from cells that break away from the main tumour mass, and form secondary tumours at new sites in the body. In order for a tumour to metastasise, one or several cancer cells need to go through a series of crucial steps: first the cells needs to migrate away from the primary tumour, and then enter the blood stream through a process known as intravasation. The cell then needs to survive long enough in the blood stream to get the opportunity to exit the vessel via extravasation. The final step in this chain of events is that the cell has to be able to migrate into and proliferate in the new tissue to form a tumour. If the metastases are formed in vital organs such as the liver or intestine this might be fatal. The acquisition of motile capabilities is the first step in this sequence of events and understanding how and why it occurs could lead to improved prevention and treatment of metastases.
1.2 Previous work
Mathematical modelling of tumour growth and invasion has a long history dating back to the work of Burton (1966), who was the first to propose that tumour growth is limited by the diffusion and consumption of nutrients. Subsequent work using a different modelling approach took into account the mechanical properties of the tissue and in particular considered the pressure inside the tumour (Greenspan, 1975). This model introduces a velocity field for the tumour cells which depends on the pressure in the tumour and assumes that the cells flow though the ECM according to Darcy’s law, i.e. just like flow through a porous medium. This model has been further developed by introducing the effect of apoptosis (Byrne and Chaplain, 1996) or different cell types (Breward et al., 2002) and different cell responses (Chaplain et al., 2006). A more recent example of this modelling approach is the model by Cristini et al. (2003) in which they investigate the impact of the microenvironment and show that it plays a significant role in shaping the resulting tumour morphology. For a long time reaction-diffusion models were the dominant modelling approach (see for example Casciari et al. (1992b); Byrne and Chaplain (1997); Anderson et al. (2000); Marchant et al. (2001); Swanson et al. (2003)), but recently individual-based models of tumour growth have gained more attention (Anderson et al., 2007). A wide range of approaches have been used for single-cell modelling such as off-lattice models (Drasdo and Forgacs, 2000; Palsson and Othmer, 2000), cellular Potts models (Stott et al., 1999; Hogeweg, 2000), cellular automata (Deutsch and Dormann, 2005) and hybrid continuous-discrete models (Anderson et al., 1997; Anderson and Chaplain, 1998; Schofield et al., 2005; Anderson, 2005).
Mathematical modelling of the evolutionary dynamics of tumour growth has generally been constrained to models where the fitness of the mutant cells is predefined, and have mostly focused on the modelling of mutational pathways (Iwasa et al., 2006; Nowak et al., 2006; Komarova, 2006). These models have provided useful insight into the evolutionary dynamics of early tumour growth, for example investigating the role of chromosomal instability (Komarova et al., 2003) and the impact of tissue architecture in colon cancer (Michor et al., 2004).
Game theory has also proven to be a suitable tool for investigating evolutionary systems (Nowak and May, 1992), and the evolutionary dynamics of carcinogenesis has been investigated by Gatenby and Vincent (2003), using continuous techniques from game theory and population dynamics. With this approach they identify conditions necessary for invasive growth and suggest that the ordinary cytotoxic treatment of the tumour is often unsuccessful due to the adaptation of the cancer cells to new growth conditions. The evolution of glycolysis and invasion has also been investigated in a game theoretic framework (Basanta et al., 2008b). They show that glycolytic cells are more likely to emerge prior to invasion, which could explain the ubiquitous presence of invasive growth in malignant tumours. The emergence of cancer cell motility was also investigated in a similar model (Basanta et al., 2008a). With this model it was shown that motile phenotypes are more likely to evolve in low oxygen concentrations, and further they suggest that this could have implications for cancer therapy. Game-theory has also been applied to other aspects of tumour growth, such as evolution of cytotoxin production (Tomlinson and Bodmer, 1997) and evolution of cellular interactions (Tomlinson, 1997; Bach et al., 2003).
To this date only a few models have investigated the evolutionary dynamics of tumour growth in a spatial and individual-based setting. One example is the hybrid model introduced in Anderson (2005), which was used for investigating the role of the ECM on tumour growth and evolution. This model is essentially a CA-model, with the difference that it derives the migratory behaviour of the cancer cells from a discretisation of a PDE and that it couples the cell dynamics to continuous fields of oxygen, ECM and matrix degrading enzymes (MDEs). The cells also posses different phenotypes, which are passed on, under mutations, during cell division. Results from this model show that the micro-environment can have a significant impact on both the morphology and phenotypic composition of the tumour, specifically that tumours grown in harsh growth conditions tend to exhibit branched morphologies and contain more aggressive phenotypes. These phenotypes were also particularly motile with decreased cell-cell adhesion and increased haptotaxis.
A similar approach was used in Smallbone et al. (2007), in order to investigate the evolutionary origin of the glycolytic phenotype, but here the phenotypes correspond to boolean (true/false) properties of the cells such as the property of being hyperplastic. Mutations during cell division alter the phenotype of the cells, and in agreement with the Anderson model it exhibits evolution towards more aggressive phenotypes. This builds on previous work by Gatenby and colleagues that has examined both theoretically and experimentally acid-mediated tumour invasion (Gatenby and Gawlinski, 1996; Gatenby and Gillies, 2004; Gatenby et al., 2006). The emergence of mutant subclones has also been investigated in a 3-dimensional cellular automaton using a Voronoi tesselation approach (Kansal et al., 2000). They show that the survival probability of a subclone depends on the growth advantage over other subclones, but they also show that it is non-zero although no growth advantage exists. The evolution of cell motility was investigated in a game theoretic, individual-based setting by Mansury et al. (2006). Assuming that the tumour consists of proliferative and motile genotypes the authors show that the growth dynamics depends on pay-offs for different cell interactions, and further that there exists an optimal pay-off for which the tumour growth rate is maximised.
The model presented in this paper is an extension of two previous models of tumour growth which have been used to investigate the impact of the microenvironment on tumour growth and evolution. The results from the first model revealed that tumours grown in low oxygen concentrations exhibited branched morphologies, but more importantly it also showed that the oxygen concentration has an impact on the evolutionary dynamics (Gerlee and Anderson, 2007a). The low oxygen concentration environment gave rise to tumours with a higher genetic diversity and also containing cells that had evolved further away from the ancestral cell. A subsequent extension of the model which included the effect of the ECM and anaerobic metabolism was used to examine the emergence of the glycolytic phenotype (Gerlee and Anderson, 2008). The results from that study were consistent with the previous observations and further showed that a glycolytic phenotype was most likely to occur in low oxygen concentrations and a dense ECM.
In this paper we focus on the evolution of cell motility and will initially present the modified model, with details on each of the processes and components considered and how they interact. In section 3 we discuss the simulation process and in section 4 we present a suite of results from the model. Finally in section 5 we have an extended discussion about the implications of the model results and conclude in section 6.
2 The Model
We consider a generic tissue which is represented by a two-dimensional grid on which the cancer cells reside. Each point on the grid holds the local concentration of ECM, nutrients and can be either occupied by a cancer cell or be empty. This is of course a highly simplified picture of real tumour-host interactions. The surrounding tissue contains a variety of host cells like fibroblasts, macrophages and blood vessels, all of which have been shown to be important factors in tumourigenesis (Rubin, 2003), but in order to focus on the impact of nutrient concentration and the ECM we have chosen to disregard these aspects of tumour growth. In the current model the vascularity is also modelled in a simplified manner, by incorporating it into the boundary conditions. The model consists of discrete individual tumour cells, continuous chemical fields (oxygen, glucose, hydrogen ions) and ECM density, which interact with one another on the grid via the cellular automaton. We now discuss each of these variables and processes in more detail in the following sections.
2.1 Cell Dynamics
2.1.1 Phenotype
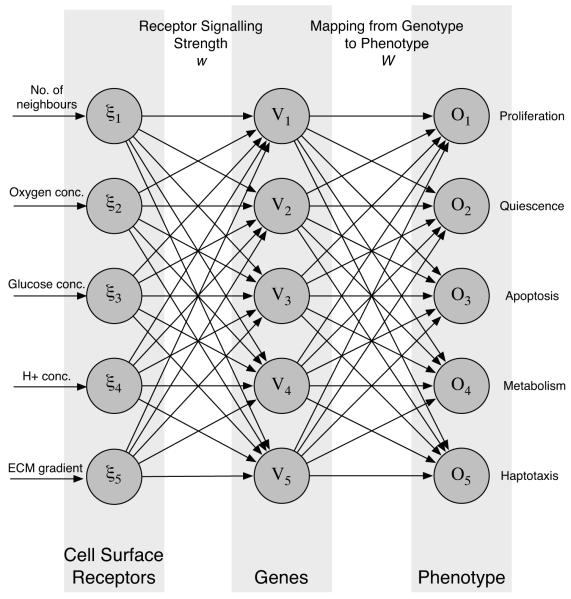
Each cancer cell in the simulation is equipped with a decision mechanism, which determines the behaviour of the cell based on the micro-environment in which it resides. The decision mechanism is modelled using an artificial feed-forward neural network (Haykin, 1999). This neural network approach only serves as an abstract model of cellular behaviour, but still shares some features of the real signaling and regulatory network of the cell. The input layer of the network can be thought of as receptors on the cell surface that interact with extra-cellular molecules. The weight matrix between the input and hidden layer represent the signaling strength of these receptors. The hidden layer functions as regulatory genes that control the behaviour of the cell through the weights of the connection matrix between the hidden and output layer. Finally the output layer can be thought of as the phenotype, as it determines the behaviour of the cell (see fig. 1). With this analogy in mind we can think of changing a connection between the input and hidden layer as changing the expression level of a certain type of receptor and changing a connection between the hidden and output layer as altering the expression level of a regulatory gene.
Fig. 1.
The layout of the response network which determines the phenotype or behaviour of the cancer cells. The micro-environmental variables are fed into the input layer of the network which then processes the information and produces a response at the output layer. The response depends on the network matrices w and W, which are subject to mutations when the cells divide.
In our model the input to the network is the number of neighbours of the cell (n), local oxygen concentration (c), glucose concentration (g), H+ concentration (h) and ECM gradient (∇m). This implies that the input to the network ξ will have five components . The phenotype of the cell is then determined by the output of the network. The output nodes represent the response for proliferation, quiescence, movement, apoptosis and metabolic pathway. As the first four form a group of mutually exclusive behaviours (a cell can not perform these responses simultaneously) the behaviour with the strongest response is chosen from these four, we call this the life-cycle response. If the proliferation node has the strongest response the cell divides and produces a daughter cell and if the quiescence node has the strongest response the cell remains dormant. On the other hand if movement has the strongest response the cell goes into a migratory mode, while if the apoptosis node is strongest then the cell dies via apoptosis. The initial network is designed so that the behaviour of the ancestral cell resembles that of an non-invasive cancer cell (for further details on the decision mechanism and the neural network implementation please consider Gerlee and Anderson (2007a)). A graphical representation of the response network can be seen in fig. 1.
2.1.2 Metabolism
The network modulates the metabolism of the cell in three separate ways: Firstly the strength of the life-cycle response determines the overall energy consumption of the cell, secondly the nutrient consumption is lowered if the cell is quiescent, and finally the network determines the metabolic pathway of the cell. Real cells may rely on a combination of aerobic and anaerobic metabolism (Gatenby and Gillies, 2004), but for simplicity we will let the cells utilise either aerobic or anaerobic metabolism. If the response of the metabolic node is negative the cell uses glycolysis and if the response is positive the normal aerobic pathway is utilised. This choice is modelled by letting the cells utilising the anaerobic pathway consume 18 times more glucose and produce acid whilst not consuming any oxygen.
2.1.3 Mutations
When the cells divide the network parameters are copied to the daughter cell under mutations. The number of mutations that occur in the daughter cell network parameters is chosen from a Poisson distribution with parameter p. These mutations are then distributed equally over the network weights and nodes (see fig. 1 and Gerlee and Anderson (2007a) for further details). The incorrect copying is modelled by adding a normal distributed number s ∈ N(0, σ) to the daughter cell parameter, which means that x → x + s, for those parameters x that are chosen for mutation. The mutations alter the connection strength between the nodes, which in turn changes how the cells responds to the micro-environment. If for example a mutation occurs in a connection which links the ECM gradient with the movement node this may create a subclone with a more motile behaviour.
2.2 Chemical Fields
The metabolism of cancer cells includes a large number of different chemicals that are all needed for maintenance and cell division, but oxygen and glucose concentrations are two key metabolites known to limit the growth of the tumour (Sutherland, 1988). We therefore only choose to focus on these two fields in the model as well as a field for the hydrogen ion concentration, as glycolytic cells produce an excess of acid. For the chemical fields we apply Dirichlet boundary conditions with constant functions, meant to imitate a situation where the tissue is surrounded by blood vessels, with constant nutrient and hydrogen ion concentrations, that supply the tumour with nutrients and remove hydrogen ions from the tissue. The decay rates of the metabolites are known to be considerably smaller than the respective cellular consumption rates and for simplicity we therefore disregard these in the equations. This allows us to develop a minimal model of the chemical fields, similar to those in the models of Patel et al. (2001) and Ferreira et al. (2002). The time evolution of the oxygen (1), glucose (2) and hydrogen ion (3) fields are therefore governed by the following set of partial differential equations,
| (1) |
| (2) |
| (3) |
where Di are the diffusion constants and the are the individual cell consumption or production functions of the chemical i = c, g, h for the cell at position at time t. Note that the hydrogen ion production is only non-zero if the cell relies on glycolytic metabolism. The solution of the chemical field equations are calculated on a grid of the same step size as the cells using an Alternating Direction Implicit (ADI) scheme for both numerical accuracy and efficiency (Press et al., 1996). This choice of space step implies that the consumption and production terms in (1)-(3) are determined by each individual cell. The are thus defined in the following way,
| (4) |
where ri are the base consumption/production rates and is the modulated energy consumption of the individual cell occupying the automaton element at . This modulation of the consumption is introduced in order to take into account the difference in energy consumption between different subclones, and is modelled as
| (5) |
where k determines the strength of the modulation, R is the response of the network and Tr is the target response, corresponding to the response of a normal cell. The use of max(•, 0.25) ensures that the cell has a metabolism which is at least a quarter of the base-line consumption rate (Anderson, 2005). The use of this function implies that a cell with a stronger network response will have a higher nutrient consumption.
2.3 The Extracellular Matrix
The interactions between cancer cells and the surrounding ECM are known to play an important role in carcinogenesis. The ECM is a complex mixture of macro-molecules such as collagens and fibronectin. This fibrous concoction of ECM molecules can be very heterogeneous with cross-linking between the fibres which modulates both the degradability of the ECM as well as the pore sizes contained within it (Zaman et al., 2006). This complexity has been modelled when cell-ECM interactions are considered as the sole focus of the model (Zaman et al., 2006, 2005), or when the ECM degradation (via invadopodia) has been considered in more detail (Enderling et al., 2008). However, due to the complexity of our current model and our motivation for understanding the emergence of a migratory phenotype we will represent the ECM as a single concentration. The ECM will therefore act as a constraint on proliferation and facilitate migration via a minimal modelling approach.
It has been shown that a considerable part of matrix degradation is accounted for by membrane anchored MMPs (MT-MMPs) (Hotary et al., 2000) as well as the plasminogen activator system (Chaplain and Lolas, 2005, 2006). This implies that a majority of the ECM degradation has a very short range and can therefore be approximated by contact degradation (Enderling et al., 2008). We include this effect in the model by letting the ECM be degraded with a rate ec at all grid points adjacent to cancer cells. The ECM also serves as a physical growth restraint of the tumour as cells can not move into regions of the tissue which are too dense, unless they have degraded it sufficiently. This effect is incorporated by introducing a threshold et above which no cells can occupy a grid point. Another mechanism that is included in the model is acid-induced ECM degradation. The exact dynamics of this process is poorly understood, but has been shown to involve stromal cells, e.g. fibroblasts (Rozhin et al., 1994). For simplicity we will assume that the matrix degradation is proportional to the excess acid concentration and model it by letting the ECM be degraded at a rate eh proportional to the excess acid concentration and matrix concentration. In summary the ECM obeys
| (6) |
where is an indicator function that returns the number of cancer cells adjacent to site and h0 is the normal acid concentration in the tissue. In order to avoid lattice anisotropy (favouring a certain direction of growth) the cancer cells alternate between degrading matrix in the immediate neighbouring and diagonal neighbouring sites every time step, which is implemented by letting alternate between orthogonal and diagonal neighbourhoods.
2.4 Cell Movement
Haptotaxis is the directed movement of cells in response to gradients in the ECM. This implies that the cells need to be able to sense the local gradient of ECM and respond to it. It is believed that cancer cells cannot move and proliferate simultaneously (Giese et al., 2003), and therefore the haptotaxis output node will be part of the life-cycle response just like proliferation, quiescence and apoptosis. In other words if the haptotaxis node gets the strongest response the cell will go into a migratory mode and will not be able to proliferate.
The ECM gradient sensed by the cell is chosen to be the larger of the two gradients in the x- and y-direction, which means that for a cell at position (i, j) we calculate the central difference
| (7) |
and
| (8) |
where mi,j is the ECM concentration at position (i, j). We then pick the larger of the two and use it as input to the network. If the haptotaxis node gets the strongest response then the cell will move one grid point in the direction of the largest gradient towards higher ECM concentration. If the grid point is already occupied movement fails and the cell remains stationary. Due to the different time scales operating upon migration, proliferation and chemical diffusion (although this is addressed via the implementation of an ADI numerical scheme) we must ensure the cells migrate on the right timescale. Therefore, in order to modulate the speed of movement, each time the response of the network is haptotaxis, a random number r between 0 and 1 is generated, then if R(ξ, G) · pm > r the cell is allowed to move, if not the cell remains stationary. Here R(ξ, G) represents the output from the network which ranges from 0 to 1, i.e. the value of the movement node (with respect to input ξ and genotype G) and pm is the movement probability. This formulation implies that a cell with a stronger haptotactic response will on average move more often (i.e. faster), and also makes the movement node subject to possible evolutionary change (as mutations to the network can change the strength of the response). Haptotaxis is known to occur through two distinct modes: “path-finding” (where the cell moves between the fibres through the pores of the ECM) and “path-generating” (where the cell creates a path through the matrix by degrading the fibers) (Friedl and Wolf, 2003). Little is known about what determines the mode of movement, and we have therefore decided to focus solely on the “path-finding” mode. This means that the movement of the cells is not subject to the restraint that the ECM poses with respect to cell proliferation, i.e. a cell can move to a neighbouring site although the ECM concentration is higher than the threshold et. The movement through the tissue matrix consumes energy, but on the other hand motile cells do not spend energy on synthesis of DNA and other cell material. We have therefore assumed that the motile cells have a energy consumption lower than that of proliferating cells, and consequently they consume less nutrients.
2.5 Cellular Automaton
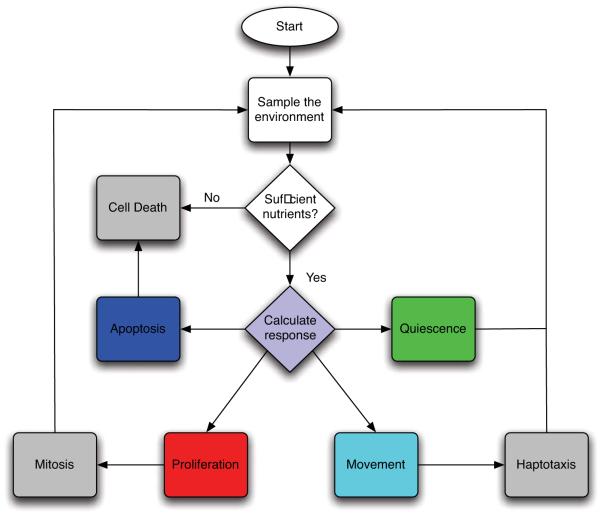
The slice of tissue under consideration is represented by a N × N grid. The spacing of the grid is defined by a grid constant Δx, which determines the size of the cells. The grid points are identified by a coordinate where i, j = 0, 1, ...., N - 1. The chemical concentrations interact with the cells according to cellular production or consumption rates and are given appropriate initial and boundary conditions. Each time step the chemical concentrations are solved using the ADI-scheme and all tumour cells are updated in a random order. Every time step each cell is updated according to the flowchart in fig. 2 and as follows:
The input vector ξ is sampled from the local environment (i.e the grid point where the cell resides).
A response R = R(ξ, G) is calculated from the network.
The cell consumes nutrients according to the action taken and the metabolic pathway chosen. If there is not sufficient nutrients present the cell dies from necrosis.
- The life-cycle action determined by the network is carried out:
- If proliferation (P) is chosen, check if the cell has reached proliferation age and if there is space for a daughter cell. If both are true the cell divides and the daughter cell is placed in a neighbouring grid point, if not the cell does nothing until the next update
- If quiescence (Q) is chosen the cell becomes quiescent.
- If movement (M) is chosen the cell moves one grid point (in the von Neumann neighbourhood) in the direction of the steepest ECM gradient. If the grid point is occupied the movement fails and the cell remains quiescent until next update.
- If apoptosis (A) is chosen the cell dies.
If a cell dies from either apoptosis or necrosis it is no longer updated. If the cell dies by apoptosis the grid point where it resided is considered empty, but if the cell dies from necrosis (starvation) the cell still occupies the grid point. The reason for this is that the two death processes occur in different ways. When apoptosis occurs the cell membrane collapses and the cell shrinks, while when necrosis occurs the cell keeps it shape and thus still occupies physical space (Alberts et al., 1994). In order to account for the activity of the immune system, which removes necrotic debris (Kerr et al., 1994), necrotic cells are removed after a given time tN .
Fig. 2.
The life-cycle of the cancer cells represented as a flowchart.
2.6 Parameters
The initial network, which is used as a “seed” in every simulation, is chosen so that the behaviour of the cell resembles that of an initial cancer cell phenotype which has lost normal growth inhibition. The response of the network therefore has to capture the essential behaviour of real cancer cells. The important features that we want to capture are:
Cells should perform apoptosis if the oxygen concentration falls below a certain threshold cap.
Cells should die if the glucose concentration falls below a certain threshold gap.
Cells should not divide if there is no space for the daughter cell (contact inhibition) i.e if
Cells should perform apoptosis if the acidity is a above a certain threshold hap.
Cells should move in response to the ECM gradient if it is above a value mh, which also depends on the number of neighbours of the cell
Cells should switch to anaerobic metabolism if the oxygen concentration falls below cm
The value of cap is difficult to estimate as it depends on the cell type under consideration, but measurements performed in several types of tumours reveal that the oxygen concentration in the necrotic centre of the tumour is 0.5-30% of the concentration in the surrounding tissue (Brown and Wilson, 2004). We therefore estimate cap to be 15 % of the initial oxygen concentration. For high values this parameter is known to have an effect on the morphology of the tumour (Gerlee and Anderson, 2007b; Anderson et al., 2008), but for the relatively small values we consider this effect is negligible. The threshold for glucose induced necrosis is set to 50% of the normal glucose concentration, below which hypoglycemia occurs (Ganong, 1999). The acidity threshold hap is set to match the critical pH = 7.1 below which normal cells go into apoptosis (Casciari et al., 1992a). As there is a physical limit to the acidity a cell can survive we also introduce another threshold which is the acid concentration at which a cell will go into apoptosis regardless of the network response, this is set to match pH=6.5.
We are interested in studying the emergence of motility and therefore we parametrise the initial network so that it has a weak haptotactic response i.e. the haptotaxis node will only be selected if the ECM gradient is sufficiently large (see section 2.4). Cell movement is also affected by cell-cell adhesion, as a cell which is surrounded by many other cells is less likely to move due to the higher number of adhesive bonds. We take this into account by making the response for haptotaxis a decreasing function of the number of neighbours. This is of course a crude way of modelling cell adhesion, for more detailed models please consider Armstrong et al. (2006) and Gerisch and Chaplain (2008).
The metabolic threshold is set to cm = 0, as we are also interested in the emergence of cells that utilise the anaerobic pathway.
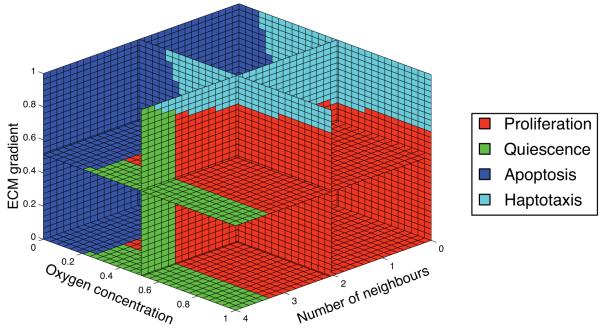
A network which matches the above criteria was constructed by hand and the behaviour of the initial cell with respect to number of neighbours, oxygen concentration and ECM gradient is shown in fig. 3. The ancestral cell is unlikely to move because it requires very steep gradients in the ECM for the haptotaxis node to be selected. A cell at the tumour boundary, which continuously degrades the surrounding ECM creates a gradient, but if this cell has the initial response network it will proliferate before the gradient becomes steep enough to move via haptotaxis. The initial cell therefore has the potential to move, but is more likely to proliferate, however, subsequent mutations to the ancestral network can naturally change this.
Fig. 3.
The life-cycle response of the initial cell as a function of the number of neighbours, oxygen concentration and ECM gradient. The glucose and hydrogen ion concentrations are kept at to their background values.
In order to simplify the analysis and simulations of the model we nondimensionalise the model in the standard way. Time is rescaled by the typical time of the cell-cycle, τ = 16 h (Calabresi and Schein, 1993), and the length by the typical length scale of an early stage tumour and its microenvironment, L = 1 cm. The chemical concentrations are rescaled using background concentrations (see Table 2) and consumption rates are rescaled using a tumour cell density n0 = Δx-2 = 0.0025-2 = 1.6 × 105 cells cm-2 (since the cells reside on a 2-dimensional grid). All cell specific parameters are summarised in Table 1 and we refer to Gerlee and Anderson (2007a) for a more detailed discussion on the parametrisation and non-dimensionalisation of the model.
Table 2.
A summary of the micro-environment specific parameters in the model in dimensional units
| Parameter | Meaning | Value | Reference |
|---|---|---|---|
| Dc | oxygen diffusion constant | 1.8 × 10-5 cm2 s-1 | (Grote et al., 1977) |
| Dg | glucose diffusion constant | 9.1 × 10-5 cm2 s-1 | (Crone and Levitt, 1984) |
| Dc | hydrogen ion diffusion constant | 1.1 × 10-5 cm2 s-1 | (Crone and Levitt, 1984) |
| c0 | oxygen background conc. | 1.7 × 10-8 mol cm-2 | (Anderson, 2005) |
| g0 | glucose background conc. | 1.3 × 10-8 mol cm-2 | (Walenta et al., 2001) |
| h0 | hydrogen ion background conc. | 1.0 × 10-13 mol cm-2 (pH = 7.4) | (Patel et al., 2001) |
| n0 | cancer cell density | 1.6 × 105 cells cm-2 | (Casciari et al., 1992a) |
| tN | necrotic cell removal rate | 5 cell cycles | Estimated |
Table 1.
A summary of the cell specific parameters in the model
| Parameter | Meaning | Value | Reference |
|---|---|---|---|
| rc | base oxygen consumption rate |
2.3 × 10-16 mol cells-1 s-1 |
(Freyer and Sutherland, 1986) |
| aerobic glucose consumption rate |
3.8 × 10-17 mol cells-1 s-1 |
Calculated from (Freyer and Sutherland, 1986) |
|
| anaerobic glucose consumption rate |
6.9 × 10-16 mol cells-1 s-1 |
Calculated from (Freyer and Sutherland, 1986) |
|
| rh | hydrogen ion production rate |
1.5 × 10-18 mol cells-1 s-1 |
(Patel et al., 2001) |
| cap | hypoxia induced apoptosis threshold |
2.5 × 10-9 mol cm-2 |
(Brown and Wilson, 2004) |
| gap | hypoglycemia threshold | 6.5 × 10-9 mol cm-2 | (Ganong, 1999) |
| hap | acid induced apoptosis |
pH = 7.1 | (Casciari et al., 1992a) |
| maximal acid concentration |
pH = 6.5 | (Casciari et al., 1992a) | |
| Ap | proliferation age | 16 h | (Calabresi and Schein, 1993) |
| p | mutation probability | 0.01 | (Anderson, 2005) |
| q | quiescent metabolism factor | 5 | (Freyer et al., 1984) |
| Tr | target response | 0.675 | Model specific |
| k | modulation strength | 6 | Model specific |
| σ | mutation strength | 0.25 | Model specific |
The degradation rates and threshold density of the ECM have not been measured experimentally and we will therefore use non-dimensional estimates for these parameters. In our simulations we will let et be in the range [0.65, 0.9], which corresponds to 35-10% of the ECM requiring degradation before it can be occupied by a cell. Instead of using this threshold as a measure of the density we introduce an effective matrix density E = 1 - et, which will serve as a measure of the growth constraint imposed by the matrix. For a high matrix threshold we will have a low effective matrix density and vice versa. The matrix degradation rate of the cells is set to ec = 0.1, which implies that a cell needs 1-4 cell cycles (corresponding to E = 0.1 - 0.35) to degrade the ECM in a neighbouring grid point to a level below et. The combined effect of acid on the matrix is poorly characterised and we therefore set it to eh = 10-3, considerably smaller than the degradation by the cells, in order to make the growth advantage of acid-producing cells smaller.
The speed at which haptotaxis occurs has not been experimentally determined and depends on many factors such as ECM composition, ECM density andcell type. We estimate the movement probability pm, which controls the speed, to be pm = 0.5. If we assume a maximal response of R = 1, this implies that a cell will on average move 1/2 grid point per time step. The time step in the simulation is set to Δt = 10-1 cell cycles and the space step to Δx = 25μm, which means that the average speed will be approximately 2 × 10-7 cm/s, in agreement with the measurements of Zaman et al. (2006) which range from 3 - 12μm/hr = 5.4 × 10-8 - 3.2 × 10-7cm/s. The nutrient consumption rate of moving cells is assumed to lie in between that of proliferating and quiescent cells and is set to be 2-fold lower than the base consumption rate.
The grid size was set to N = 200, corresponding to a domain of size 0.5 cm2 and which means that we can simulate a tumour of radius 100 cells, which if we assume radial symmetry in a 3-dimensional setting would correspond to a tumour consisting of approximately 1003 or 1 million cells. The time step in the simulation was set to Δt = 10-1 and the space step to Δx = 0.0025.
3 Simulations
In the following suite of simulations we investigate both the impact of cancer cell motility on tumour growth and the micro-environmental conditions in which a motile phenotype is most likely to evolve. We focused on the impact of the oxygen concentration and the ECM density (by varying c0 and E) and examined the dynamics of the model for a range of values of these two factors. The growth dynamics were analysed by measuring the time evolution of the total number of cells and the invasive distance of the tumour, and we also examined the spatial distribution of cancer cells.
The evolutionary dynamics were analysed by measuring the evolution of phenotypes in the population and we also compared the motility of cancer cell populations that had evolved in different oxygen concentrations and ECM densities. To gain further insight into phenotype evolution and the long-term influence of the micro-environment we also performed “reseed”-simulations. In these simulations the most abundant genotype, at the end of the simulation, was used as an ancestor in a new simulation, and this process was then repeated as many times as desired. This technique is similar to selective cell culture experiments where cells are passaged through several assays to select for cells with certain phenotypes (Dairkee et al., 1995).
Each simulation was started with a homogeneous concentration of oxygen, glucose and hydrogen ions at background values , and with the boundary conditions . Variations in the matrix density were accounted for by setting the initial condition for ECM to , where s ∈ [-0.2, 0.2] is a random variable with a uniform distribution, and each simulation was started with a population of 4 cancer cells at the centre of the grid.
Instead of comparing tumours of the same age we decided to compare tumour of the same size, and the duration of each simulation was therefore determined by the time it took the tumour to reach an invasive distance of 0.45N,where the invasive distance is defined as the distance from the center of the tumour to the most distant cancer cell. This is because the evolutionary component of the model makes it difficult to estimate the time it takes a tumour to reach a given size. If for example a mutation, which triggers haptotaxis, occurs early in the simulation the tumour will reach a much larger size compared to a tumour where haptotaxis never emerges in the same amount of time.
4 Results
4.1 Growth Dynamics
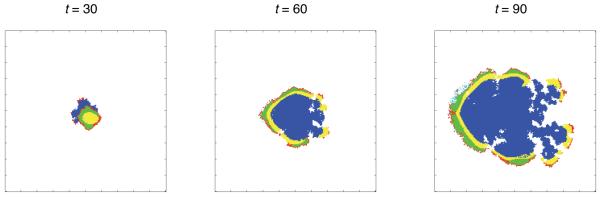
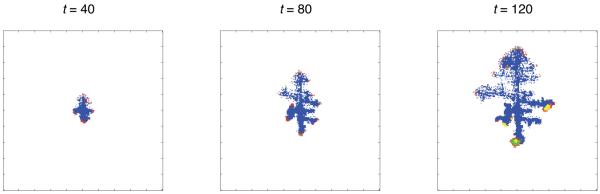
Figure 4 and 5 show two examples of tumour growth where haptotaxis has emerged, both lasting 90 time steps (approximately 60 days). The first figure shows a tumour growing in an intermediate oxygen concentration (c0 = 0.5) and a low density matrix (E = 0.1). In this simulation a motile subclone emerged on the left hand side of the tumour as revealed by the fragmented tumour boundary consisting of motile (cyan coloured) cells at t = 60 and 90. The part of the tumour dominated by motile cells expands at a higher rate compared to the non-motile (right) side, and this leads to an asymmetric morphology where the tumour has grown more towards the left part of the domain.
Fig. 4.
Spatial distribution of the cells at t = 30, 60 and 90 (approx. 20, 40 and 60 days) for c0 = 0.5 and E = 0.1 on a grid of size 200×200. Proliferating cells are shown as red, quiescent cells as green, necrotic cells as yellow, moving cells as cyan, dead cells as blue and empty grid points are white. In this simulation a haptotactic subclone emerges on the left side of the tumour leading to an asymmetric morphology. A supplementary movie of this simulation can be found at: http://www.nbi.dk/~gerlee/Fig4.mov.
Fig. 5.
Spatial distribution of the cells at t = 40, 80 and 120 (approx. 27, 53 and 80 days) for c0 = 0.1 and E = 0.3 on a grid of size 200×200. Proliferating cells are shown as red, quiescent cells as green, necrotic cells as yellow, moving cells as cyan, dead cells as blue and empty grid points are white. Haptotaxis in low oxygen concentration gives rise to a branched tumour morphology although the branches are not as well defined compared to the lower part of the tumour which is dominated by immobile cells. A supplementary movie of this simulation can be found at: http://www.nbi.dk/~gerlee/Fig5.mov
Although some parts of the tumour are exposed directly to the matrix they still exhibit necrosis and this is due to the competition for oxygen and the screening effect which cells closer to the oxygen source exert. At the later stages of the simulation the tumour exhibits a layered structure, with a necrotic core and a viable rim, and is approximately 7-8 mm in diameter. This is larger than avascular tumours normally are found to be (2-3 mm), and the reason for this is our choice of cell size (25 μm), which possibly is a slight over-estimate of the normal tumour cell size.
The second example shows a tumour growing in a harsher micro-environment where the oxygen concentration is low (c0 = 0.1) and the matrix density is high (E = 0.3). In agreement with other models the low oxygen environment gives rise to a branched morphology (Gerlee and Anderson, 2007a; Anderson et al., 2006; Anderson, 2005; Ferreira et al., 2002), but there is an obvious difference between upper and lower parts of the tumour. The lower part exhibits a pattern with compact branches, while the top part on the other hand exhibits a diffuse fingering pattern induced by the haptotactic motility which evolved in this part of the tumour. As with the solid fingers the living cells only reside at the tips of the fingers, although in this case we observe a mix of proliferating, quiescent and motile cells. Both of these types of morphologies have been observed in other models of tumour growth (Macklin and Lowengrub, 2007; Frieboes et al., 2006; Cristini et al., 2005), where the morphological changes are driven by micro-environmental parameters such as the nutrient diffusion rate, matrix stiffness and cell-cell adhesion (via surface tension). In particular, more invasive morphologies are observed under harsh micro-environmental conditions which is in agreement with the authors previous work and others (Rejniak, 2005; Anderson et al., 2008).
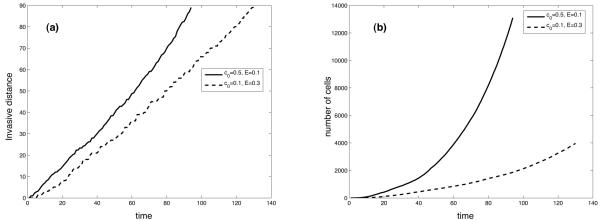
The time evolution of the invasive distance and the number of cells for the two simulations is shown in fig. 6. We see, as expected, that the number of cancer cells grows at a higher rate in a high oxygen concentration, but we can also observe that the difference in the invasive distance is considerably smaller. This is partly due to the fractal morphology (Gerlee and Anderson, 2007b), but is also exacerbated by the non-compact structure of the branches in the motile part of the tumour. These have a lower average density and this means that the tumour consists of a relatively small number of cells while still invading a considerable distance into the healthy tissue. The figure also shows that an increase in ECM density leads to a decrease in invasive distance, which is somewhat unexpected since the cells can migrate regardless of the ECM density, therefore it is probably due to inhibition of proliferation rather than migration. Zaman and co-workers found a more complex relationship between ECM density and migration which was maximal at intermediate concentrations (Zaman et al., 2006), however, we would require a more sophisticated model of cell migration to capture these dynamics which is beyond the scope of this paper.
Fig. 6.
The time evolution of the (a) invasive distance and (b) number of cells for the simulations shown in fig. 4 and 5.
These two examples were particularly chosen to illustrate the impact of cell motility. However, in some simulations haptotaxis does not emerge at all, and the tumour grows only through cell proliferation as in the previous version of the model, and we refer to Gerlee and Anderson (2008) for an in-depth discussion of that growth process.
4.2 Evolutionary Dynamics
The evolution of phenotypes in the population was characterised by measuring the average response vector as a function of time. The response vector measures the fraction of the input space that each of the life-cycle responses (proliferation, quiescence, apoptosis and movement) occupy. Formally we define four sets xi = {ξ ∈ I; R(ξ) = i}, where R(ξ) is the network response to input vector ξ, i = P, Q, M, A and I is the set of all possible inputs to the network. The sizes of these sets are now given by,
| (9) |
where δij is the Kronecker delta (δij = 1 if i = j, 0 otherwise) and B is the volume of the entire 5-dimensional input space. From this the average response vector defined as S = (|xP|, |xQ|, |xM|, |xA|) can be calculated. In order to focus on the impact of the oxygen concentration and ECM density in determining cell behaviour we reduced the input space to 3-dimensions by fixing the glucose and hydrogen ion concentrations to their background values.
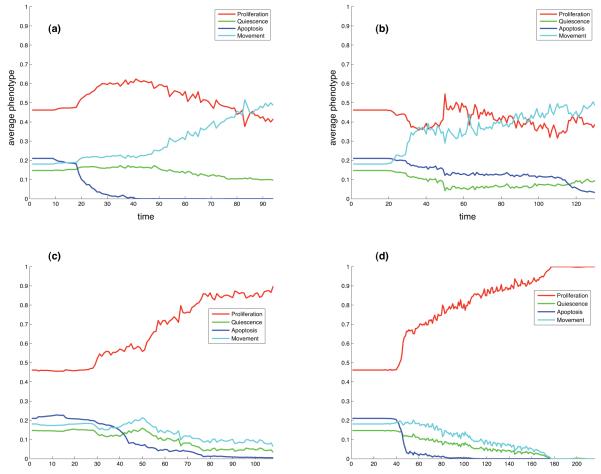
The initial cell has response vector S = (0.46, 0.15, 0.21, 0.18) (compare with fig. 3), while a cell which, for example, has evolved to a state where it proliferates in all possible environmental conditions would have a response vector S = (1, 0, 0, 0). Every time step of the simulation the response vector was calculated for every active cell and averaged over the entire population. This measure is shown in fig. 7a and b for the two simulations discussed in the previous section. In both cases we can observe an increase in the movement potential of the cells. The initial movement potential is only 18 %, but at the end of the simulations it has increased to approximately 50% in both simulations, and this increase in movement has mainly occurred at the expense of quiescence and apoptosis.
Fig. 7.
The time evolution of the average response vector for (a) the simulation shown in fig. 4 and (b) fig. 5. Panel (c) and (d) show the result of two simulations that occurred in identical micro-environmental conditions as (a) and (b) respectively, but instead evolved towards a proliferating population.
In fig. 7c and d as a comparison, we also show the evolution of the average response vector in two simulations where haptotaxis did not emerge. In this case the population instead evolves to a state where the dominant behaviour is proliferation. These simulations occurred in exactly the same micro-environments as (a) and (b) respectively, the only difference coming from the random nature of mutations.
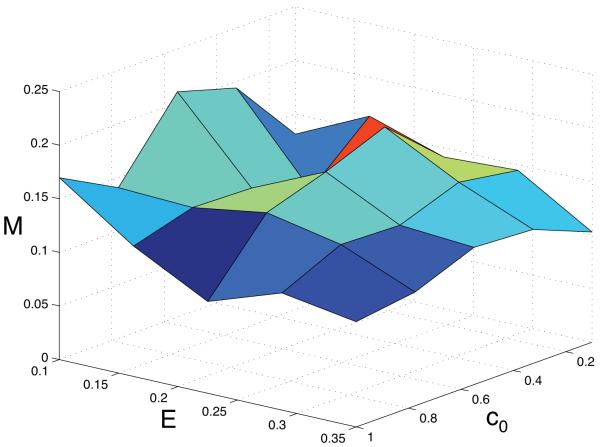
The above simulations are however only four isolated examples of the possible dynamics of the system, and to get a more complete understanding of the emergence of haptotaxis we examined the dynamics of the system for 5 × 5 = 25 different points in the (c0, E)-parameter space. The most straight-forward measure of motility in the population would simply be to calculate the fraction of cells that are in a motile state at the end of the simulation, but this turned out not to be very informative. Such an approach worked well when we considered the emergence of the glycolytic phenotype, and the reason for this is that the cells are glycolytic independent of the life-cycle response. Movement on the other hand only occurs when the cells reside on the tumour boundary, and more so only in certain environmental conditions (crucially they also need to proliferate to spread their genetic material). This implies that the fraction of the population which actually moves is usually small (< 10%) and therefore this is not a useful measure for determining the extent of haptotaxis. Instead we measured the average movement potential (i.e. the fourth component of S) of the cancer cell population at the end of each simulation. This measure ranges from 0 to 1, where 0 corresponds to a population where no cells have the capability to move and 1 corresponds to the (highly unlikely) situation where all the cells in the population only have the capability to move (and not to proliferate). The result of this parameter exploration can be seen in fig. 8, where the results have been averaged over 50 different simulations in each point in parameter space. The surface plot shows that the highest movement potential occurs in intermediate oxygen concentration (c0 = 0.5) and a soft tissue matrix (E = 0.1), where it takes the value M = 0.21. The lowest value of M =0.1 on the other hand occurs in low oxygen concentration (c0 = 0.1) and dense matrix (E = 0.35). The general trend seems to be that M decreases with increasing matrix density, and that it is highest at intermediate oxygen concentrations. But it should be noted that the surface plot is quite rugged, which suggests that the results are not fully conclusive.
Fig. 8.
The average movement potential S4 as a function of the oxygen concentration c0 and the matrix density E.
In order to examine the sensitivity of these results to our choice of the movement parameter (pm, see section 2.4) we did the exact same analysis for a range of values, pm = 0.25, 0.5, 0.75, 1, where pm = 0.5 was the default value used in the above simulations. Intriguingly, the evolutionary dynamics remained unchanged (in relation to fig. 8), with no major increases or decreases in movement potential being observed (data not shown). However, there was a significant change in the growth rate of the tumour with an obvious increase in growth for larger values of pm (as the cells on average move more often). It is worth noting that the evolutionary dynamics will change if we reduce the value of pm considerably, since then the movement and proliferation timescales are the same (if not slower for the movement). This results in suppression of the migratory phenotype as there is no evolutionary advantage to movement, since cells can invade faster purely via proliferation.
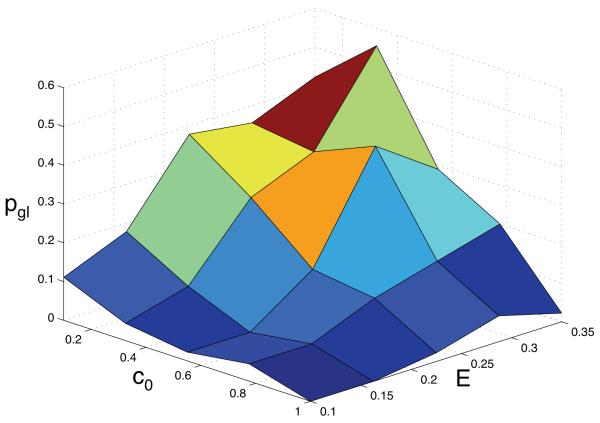
We were also interested in measuring how the introduction of cell motility affects the emergence of the glycolytic phenotype. This was quantified by calculating the probability pgl that the population was dominated by anaerobic cells, i.e. we calculated the fraction of simulations for each point in parameter space where 90 % or more of the cells were glycolytic. The probability was estimated from 50 simulations at each point in the (c0,E)-parameter space and the result can be seen in fig. 9. The general shape of the pgl surface plot is similar to what we observed with our previous model (Gerlee and Anderson, 2008). The highest probability of finding a tumour dominated by glycolytic cells occurs at a low oxygen concentration and within dense tissue matrix, but compared to the previous result the probability is now smaller (pgl ≈ 0.6 vs. 0.8).
Fig. 9.
The probability pgl that the glycolytic phenotype dominates the population. Note that the general shape of the surface is similar to the results obtained in Gerlee and Anderson (2008) where the cells were immobile, but that pgl in this case is smaller.
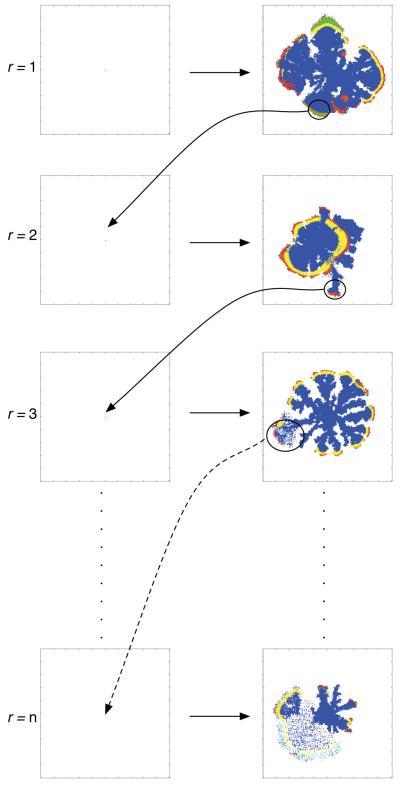
The results obtained so far suggest that the dynamics of the model are variable and that the population can adapt to the micro-environment by either evolving a proliferative or migratory phenotype. Another way of looking at it is to say that the addition of haptotaxis to the model has reshaped the fitness landscape the cancer cell population evolves on, and that multiple local fitness maxima now exist. This hypothesis was tested by performing reseed-simulations which consist of multiple sub-simulations. In these sub-simulations the most abundant genotype (the largest proportion of cells in the population with the same network wiring) at the end of the simulation (when the invasive distance had reached 0.45N) was saved and subsequently used as the genotype of four initiating cells in the next sub-simulation, this process was repeated n times (see fig. 10). Note that the micro-environment was also reset for every sub-simulation i.e. the cells always experience the same initial micro-environment conditions.
Fig. 10.
Schematic of the reseed-simulations. The dominant sublcone (circled) at the end of the first simulation is used as the initial cell in the next step of the simulation. This process is then repeated n times, and the resulting phenotype is usually highly evolved and aggressive.
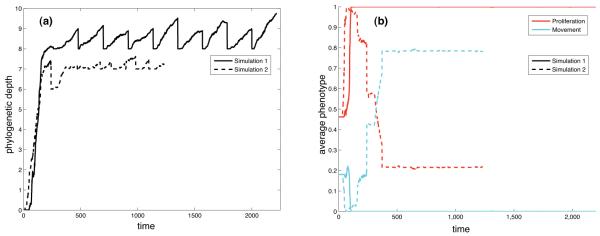
The results of two such reseed simulations can be seen in fig. 11, where n = 10 and the micro-environmental parameters were set to (c0, E) = (0.1, 0.35). The left panel shows the average phylogenetic depth as a function of time, which is the number of mutational steps from the ancestral genotype to each cell in the population. This measure shows how far the population has evolved away from the initial cell and also gives a measure of the rate of evolutionary change. From this plot it is clear that most evolutionary change occurs at the early stages in both simulations. After that the phylogenetic depth seems to stagnate, and the sawtooth pattern seen for t > 500 in the solid line is due to the fact that the dominant genotype, which is used to seed the sub-simulations for t > 500 has a phylogenetic depth of 8. In each sub-simulations new genotypes emerge which have a phylogenetic depth larger than 8, but these never come to dominate the population and therefore the phylogenetic depth returns to 8 at the start of every sub-simulation. A similar behaviour is seen in the other simulation (dashed line) suggesting that the evolutionary dynamics in both cases have converged on a successful subclone, but interestingly the right panel, which shows the evolution of the average response for proliferation and movement, reveals that the dominant phenotypes in the two simulations are very different. In the simulation corresponding to the solid line the dominant phenotype only has the capability to proliferate, while in the other simulation the dominant phenotype is highly motile with approximately 80% of the input space corresponding to haptotaxis. The duration of the reseed-simulation is determined by the total time it takes the tumour to reach an invasive distance of 0.45N in each of the n sub-simulations. If the growth rate of the tumour is high then it will obviously take a shorter time to do this, and this effect can also be seen in the two plots. The duration of the simulation corresponding to the dashed line is shorter, and again this shows that a motile phenotype invades the tissue at a higher rate.
Fig. 11.
The time evolution of the (a) the phylogenetic depth and (b) the proliferation and movement potentials for two different reseed-experiments in the same micro-environment (c0, E) = (0.1, 0.35). In both cases the dominant subclone was reseeded 10 times, but the smaller number of total time steps in one of the simulations (dashed lines) implies that the growth rate in that case was higher.
5 Discussion
From the results presented here we have seen that the emergence of a migratory phenotype is somewhat rare but when it does occur it has the capability to alter the dynamics of the model significantly. In simulations where haptotaxis emerges we observe different tumour morphologies and the tumours also grow at a higher rate due to motile cells invading the surrounding ECM. Tumour growth driven by haptotaxis exhibits both compact and branched morphologies depending on the tissue oxygen concentration, and as in other models normal oxygen concentrations give rise to compact growth while branched growth occurs in low oxygen concentrations. But notable is that motile cells give rise to diffuse morphologies with lower average cancer cell density. Occurring together with branched growth this diffuse morphology allows for a large invasive distance while the number of cells (and therefore also the number of cell divisions) remains low.
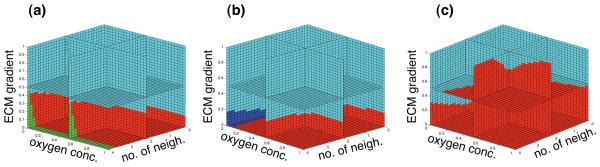
For a motile subclone to spread in the population it has to evolve a mechanism that allows the cells to switch between haptotaxis and proliferation, as a cell which only moves never has the chance to spread its genetic material. This presents an interesting trade-off as cells which are highly motile can access more nutrients and are therefore more likely to survive, but on the other hand are less likely to divide and give rise to daughter cells. Three examples of the life-cycle response from evolved genotypes can be seen in fig. 12. In (a) and (b) we observe the most common mechanism, which is to use the ECM gradient as a switch between movement and proliferation. When the cell senses a sufficiently large gradient in the ECM it moves along it, but when no gradient is present it goes into a proliferative state. This gives rise to a switching behaviour of the cells at the boundary and also implies that the tumour grows at a higher rate than before as the cells can move much faster than they proliferate. The response shown in (c) is a slightly different solution to the problem. Here the behaviour of the cell again is a function of the ECM gradient, but there is also a dependency on the oxygen concentration. When the oxygen concentration is low the ECM gradient required to switch to haptotaxis is smaller, and we can therefore say that this subclone exhibits hypoxia-driven motility.
Fig. 12.
The life-cycle response of three evolved genotypes as a function of the number of neighbours, oxygen concentration and ECM gradient. (a) and (b) utilise the ECM as a switch between proliferation (red) and haptotaxis (cyan), while in (c) the oxygen concentration also influences the choice.
Apart from the ECM gradient the switch between proliferation and hapto-taxis in the initial phenotype also depended on the number of neighbours, a simplified way to include the effects of cell adhesion. For a larger number of neighbours the cell requires a steeper ECM gradient to go into haptotaxis (fig. 3). This effect is diminished in the phenotypes shown in fig. 12, and in particular in fig. 12b where the switch between haptotaxis and proliferation is independent of the number of neighbours, which suggests that selection favours cells with low cell adhesion.
The selection for haptotaxis was investigated by measuring how the average response for movement depends on the micro-environment. Unfortunately the results from that parameter exploration were inconclusive, although there is an indication that a haptotactic phenotype is most likely to emerge in intermediate oxygen concentrations in a soft tissue matrix. One possible explanation for this is that in high oxygen concentrations the micro-environment is relatively mild and consequently the general selection pressure on the population is low. On the other hand in low oxygen concentrations the selection pressure for cells with a large proliferation potential is possibly so strong that it overshadows the selection for motility. The dependency on the ECM seems somewhat harder to explain as the ECM in fact does not impede cell movement. One possible explanation is that non-motile cells grow at a higher density and therefore cooperatively degrade the matrix at a higher rate compared to moving cells which tend to grow at a lower density. This is surprising because in our model although the dense ECM does not pose a direct restraint to the moving cells, a motile subclone is less likely to emerge in a dense tissue matrix. Of course these results could be investigated experimentally, via techniques such as the sandwich assay (Hlatky and Alpen, 1985; Dairkee et al., 1995) where the cells are grown between two cover slips covered in a given substrate which allows for both continuous imaging of the cells and a variable nutrient supply. With this assay it would be possible to grow cancer cells under a range of micro-environmental conditions and continuously measure both phenotypic and genotypic properties of the cells, making a comparison with the model results possible.
When the cell dynamics are restricted to proliferation (quiescence and apoptosis) the most efficient strategy for a subclone is to proliferate whenever there is space to do so (Gerlee and Anderson, 2007a, 2008). Now that the cells also have the capability to move the optimal strategy is no longer obvious. Although the fitness of a cell in this model is not only a function of its genotype, but also of the environment, it can still be instructive to imagine a fitness landscape on which the population evolves. Formally the dimensionality of this landscape is equal to the number of parameters in the network, but we shall rather use it for qualitative reasoning about the evolutionary dynamics. When cells are immobile the most effective way for a cell to spread its genetic material is to proliferate at all times. This means that the fittest cells are those with a response vector S = (1, 0, 0, 0), and we can therefore think of this phenotype as occupying a peak in the fitness landscape. In fact all populations evolve towards this proliferative state, although the micro-environment affects the rate at which this occurs. When we allow the cells to move we alter the structure of the fitness landscape. This is obvious from the evolution of the average response vector (fig. 7), where the population no longer evolves towards an exclusively proliferative state, but rather to a combination between proliferation and haptotaxis, e.g. S = (0.5, 0, 0, 0.5). The implication is that the one peaked fitness landscape driven purely by proliferation has now turned into a multifaceted landscape with multiple local maxima combining both proliferation and migration.
Evidence for this hypothesis can be seen in the results of the reseed-simulations. The two simulations are started with the same ancestral genotype and the populations evolved in identical micro-environments and still the outcomes are very different. In one of the simulations the population becomes completely proliferative, while the other highly motile. The evolutionary trajectories of the simulations have clearly diverged and the populations occupy two separate peaks in the fitness landscape. The stagnation in the phylogenetic depth also highlights this fact and shows that the two evolutionary processes have converged on different phenotypes. The trajectory taken by the system depends on which mutations occur in the population, and because the mutations are random, different peaks maybe traversed in different simulations of the system. This is a well-known property of evolutionary systems, and highlights the importance of contingency (i.e. the dependency on previous events) in evolution (Taylor and Hallam, 1998).
These results also highlight the fact that most of the mutations occur very early in the simulations (as observed in the phylogenetic depth, fig. 11a) implying that all of the key mutations occur early in the tumour development. In an experiment similar to these reseed simulations it was observed that primary breast cancer cells acquired genetic changes (aneuploidy, p53 mutations) and phenotypic changes (CK19-expression) associated with late stage cancer (Dairkee et al., 1995). This occurred after only 10 rounds of reseeding, corresponding to approximately 70 days of evolution, which appears to be consistent with our simulation results.
The evolution of cell motility in cancer has so far only been treated in a few modelling studies. It was for example investigated in a game-theoretic framework by Mansury et al. (2006). They consider a tumour consisting of two genotypes: one highly proliferative and the other highly migratory, where the success of each genotype depends on pay-offs it receives when the cells interact. They show that the tumour can be driven by both proliferative and migratory expansion and that this depends on the pay-off for the interaction between proliferating cells, where the highest rate of tumour invasion occurs for intermediate pay-offs for proliferating cells. The model presented here also exhibits two different modes of tumour growth, and complementary to our analysis their investigation shows that the nature of cell-cell interactions also can influence the evolution of cell motility.
The emergence of a motile subclone was also investigated in a game-theoretic framework by Basanta et al. (2008a,b). They conclude that the appearance of a motile phenotype is more likely in a nutrient starved micro-environment and specifically after the emergence of a glycolytic phenotype. There is some similarity with our results, in that we only see the emergence of both glycolytic and migratory phenotypes after the onset of necrosis (i.e. nutrient starvation). However, the precise order of the emergence in our model is unclear (data not shown) and requires further investigation.
The impact of the micro-environment on tumour evolution and in particular haptotaxis was examined in Anderson et al. (2006). They show, using a hybrid individual-based model, that tumours which grow in harsh micro-environments are more likely to contain aggressive phenotypes. In the context of that model a harsh micro-environment is defined by a heterogeneous tissue matrix and also by low oxygen concentration. A key feature of the aggressive phenotypes which evolved in these conditions was an increase of haptotaxis and a decrease in cell adhesion, which is similar to what we observed in this model. Again this implicates that the selection pressure created by a harsh micro-environment is a driving force in the evolution of cell motility.
Experimental studies have shown that hypoxia is an important factor in the selection for cell motility (Sullivan and Graham, 2007). For example it is known that hypoxia triggers ECM degradation through upregulation of urokinase-type plasminogen activator receptor (uPAR) expression and that it enhances cell motility via hypoxia-induced hepatocyte growth factor (HGF)-MET receptor signaling. Hypoxia also triggers the up regulation of glycolosis via HIF1-α (Gatenby and Gillies, 2004). These mechanisms are present in normal cells, but extended periods of hypoxia selects for subclones in which these pathways, because of specific mutations, are enhanced. The loss of cell-cell adhesion is also a common feature of cancer cells and is thought to be the first crucial step for metastases to form (Cavallaro and Christofori, 2004).
In agreement with these studies our results highlight the importance of tumour cell/micro-environment interactions in driving hypoxia, and subsequent evolutionary dynamics which lead to the emergence of glycolytic and migratory phenotypes. These phenotypes tend to have a lower dependence on the number of neighbouring cells (cf. cell-cell adhesion) and an increased sensitivity to ECM gradients. These steps culminate in the formation of an aggressive tumour capable of invading the surrounding tissue.
6 Conclusions and Outlook
In this paper we have presented an individual-based model of tumour growth aimed at investigating the evolution of cancer cell movement. We focused on haptotaxis, directed movement along ECM gradients in the tissue, and implemented this mechanism in a model which has previously been used for investigating the evolutionary dynamics of tumour growth (Gerlee and Anderson, 2007a, 2008).
Probably the most important conclusion of this paper is that the introduction of cell motility changes the fitness landscape on which the population evolves. Without movement the fitness landscape is single peaked, where exclusively proliferating cells are the most fit, but when cells are allowed to move this makes the fitness landscape more complicated. This was highlighted with reseed-experiments which clearly showed that the population can evolve to different peaks in the fitness landscape under identical conditions. This potentially could have important implications for gene therapy which targets cancer cells on the genotype level and implicitly assumes that there is a specific genetic signature linked to the tumour. Our results on the other hand show that not even a specific phenotype can be associated with a given micro-environment and even less so a particular genotype.
This paper has shown the important role that evolutionary dynamics play in both the development and progression of a growing tumour and how they are modulated by the micro-environemnt. In the future we would like to pursue this relationship further as well as refine certain aspects of the model. In particular a more accurate description of both cell-cell adhesion and cell-ECMadhesion, as well as a more complete model of the ECM incorporating pore size distributions and fibre realignment should be considered. This will allow us to better characterise the mechanical interactions between cells (e.g. cell pushing) and between cells and the ECM (e.g. pore constrained migration), and ultimately produce a more physiologically realistic model of the tumour.
7 Acknowledgments
This work was funded by the National Cancer Institute, Grant Number: U54 CA 113007.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alberts B, Bray D, Lewis J, Raff M, Roberts K, Watson J. The Cell. 3rd Edition. Garland Publishing; New York: 1994. pp. 1173–1175. Ch. 22: Differentiated Cells and the Maintenance of Tissue. [Google Scholar]
- Anderson A, B.D S, Young I, Griffiths B. Nematode movement along a chemical gradient in a structurally heterogeneous environment. 2. theory. Fundamental and applied nematology. 1997;20:165–172. [Google Scholar]
- Anderson A, Rejniak K, Gerlee P, Quaranta V. Micronevironment driven invasion: a multiscale multimodel investigation. J. Math. Biol. 2008 doi: 10.1007/s00285-008-0210-2. In review. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson ARA. A hybrid mathematical model of solid tumour invasion: the importance of cell adhesion. Math. Med. Biol. 2005;22:163–186. doi: 10.1093/imammb/dqi005. [DOI] [PubMed] [Google Scholar]
- Anderson ARA, Chaplain M. Continuous and discrete mathematical models of tumor-induced angiogenesis. Bull. Math. Bio. 1998;6:857–899. doi: 10.1006/bulm.1998.0042. [DOI] [PubMed] [Google Scholar]
- Anderson ARA, Chaplain MAJ, Newman EL, Steele RJC, Thompson AM. Mathematical modelling of tumour invasion and metastasis. J. Theoret. Med. 2000;2:129–154. [Google Scholar]
- Anderson ARA, Chaplain MAJ, Rejniak KA, editors. Single-Cell-Based models in biology and medicine. Birkhauser-Verlag; 2007. [Google Scholar]
- Anderson ARA, Weaver AM, Cummings PT, Quaranta V. Tumor morphology and phenotypic evolution driven by selective pressure from the microenvironment. Cell. 2006;127:905–915. doi: 10.1016/j.cell.2006.09.042. [DOI] [PubMed] [Google Scholar]
- Armstrong NJ, Painter KJ, Sherratt JA. A continuum approach to modelling cell-cell adhesion. J Theor Biol. 2006;243(1):98–113. doi: 10.1016/j.jtbi.2006.05.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bach LA, Sumpter DJT, Alsner J, Loeschcke V. Spatial evolutionary games of interaction among generic cancer cells. Computational and Mathematical Methods in Medicine. 2003;5:47–58. [Google Scholar]
- Basanta D, Hatzikirou H, Deutsch A. Studying the emergence of invasiveness in tumours using game theory. The European Physical Journal B. 2008a;63(3):393–397. [Google Scholar]
- Basanta D, Simon M, Hatzikirou H, Deutsch A. An evolutionary game theory perspective elucidates the role of glycolysis in tumour invasion. Cell Proliferation. 2008b;41:980–987. doi: 10.1111/j.1365-2184.2008.00563.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breward CJW, Byrne HM, Lewis CE. The role of cell-cell interactions in a two-phase model for avascular tumour growth. J. Math. Biol. 2002;45(2):125–152. doi: 10.1007/s002850200149. [DOI] [PubMed] [Google Scholar]
- Brown J, Wilson W. Exploiting tumour hypoxia in cancer treatment. Nature. 2004;4:437–447. doi: 10.1038/nrc1367. [DOI] [PubMed] [Google Scholar]
- Burton AC. Rate of growth of solid tumours as a problem of diffusion. Growth. 1966 Jun;30(2):157–176. [PubMed] [Google Scholar]
- Byrne H, Chaplain M. Modelling the role of cell-cell adhesion in the growth and development of carcinomas. Math. Comput. Model. 1996;24:1–17. [Google Scholar]
- Byrne H, Chaplain M. Free boundary value problems associated with the growth and development of multicellular spheroids. European J, Appl. Math. 1997;8:639–658. [Google Scholar]
- Calabresi P, Schein P. e. Medical Oncology. 2nd edn. McGraw-Hill; New York: 1993. [Google Scholar]
- Casciari JJ, Sotirchos SV, Sutherland RM. Variation in tumour cell growth rates and metabolism with oxygen-concentration, glucose-concentration and extra-cellular ph. J. Cell. Physiol. 1992a;151:386–394. doi: 10.1002/jcp.1041510220. [DOI] [PubMed] [Google Scholar]
- Casciari K, Sotirchos S, Sutherland R. Mathematical modelling of microenvironment and growth in emt6/ro multicellular tumour spheroids. Cell Proliferation. 1992b;25:1–22. doi: 10.1111/j.1365-2184.1992.tb01433.x. [DOI] [PubMed] [Google Scholar]
- Cavallaro U, Christofori G. Cell adhesion and signaling by cadherins and ig-cams in cancer. Nat. Rev. Cancer. 2004;4:118–132. doi: 10.1038/nrc1276. [DOI] [PubMed] [Google Scholar]
- Chaplain M, Graziano L, Preziosi L. Mathematical modelling of the loss of tissue compression responsiveness and its role in solid tumour development. Math. Med. Biol. 2006;23(3):197–229. doi: 10.1093/imammb/dql009. [DOI] [PubMed] [Google Scholar]
- Chaplain MAJ, Lolas G. Mathematical modelling of cancer invasion of tissue: The role of the urokinase plasminogen activation system. Math. Model. Meth. Appl. Sci. 2005;15:1685–1734. [Google Scholar]
- Chaplain MAJ, Lolas G. Mathematical modelling of cancer invasion of tissue: dynamic heterogeneity. Networks Heter. Media. 2006;3:399–439. [Google Scholar]
- Cristini V, Frieboes H, Gatenby R, Caserta S, Ferrari M, Sinek J. Morphologic instability and cancer invasion. Clin. Cancer Res. 2005;11:6772–6779. doi: 10.1158/1078-0432.CCR-05-0852. [DOI] [PubMed] [Google Scholar]
- Cristini V, Lowengrub J, Nie Q. Nonlinear simulation of tumor growth. J. Math. Biol. 2003;46(3):191–224. doi: 10.1007/s00285-002-0174-6. [DOI] [PubMed] [Google Scholar]
- Crone C, Levitt DG. Handbook of Physiology: A critical, comprehensive presentation of physiological knowledge and concepts. American Physiological Society; Bethesda, Maryland: 1984. pp. 414pp. 434–437. Ch. 2: The Cardiovascular System. [Google Scholar]
- Dairkee SH, Deng G, Stampfer MR, Waldman FM, Smith HS. Selective cell culture of primary breast carcinoma. Cancer Res. 1995 Jun;55(12):2516–2519. [PubMed] [Google Scholar]
- Deutsch A, Dormann S. Cellular Automaton Modeling of Biological Pattern Formation. Birkhäuser; 2005. [Google Scholar]
- Drasdo D, Forgacs G. Modeling the interplay of generic and genetic mechanisms in cleavage, blastulation, and gastrulation. Developmental Dynamics. 2000;219(2):182–191. doi: 10.1002/1097-0177(200010)219:2<182::aid-dvdy1040>3.3.co;2-1. [DOI] [PubMed] [Google Scholar]
- Enderling H, Alexander NR, Clark ES, Branch K, Estrada L, Crooke C, Jourquin J, Lobdell NA, Zaman MH, Guelcher SA, Anderson ARA, Weaver AM. Dependence of invadopodia function on collagen fiber spacing and crosslinking: computational modeling and experimental evidence. Biophys. J. 2008;95:2203–2218. doi: 10.1529/biophysj.108.133199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ennis BW, Matrisian LM. Matrix degrading metalloproteinases. Journal of Neuro-Oncology. 1993;18(2):105–109. doi: 10.1007/BF01050416. [DOI] [PubMed] [Google Scholar]
- Ferreira SC, Martins ML, Vilela MJ. Reaction-diffusion model for the growth of avascular tumor. Phys. Rev. E. 2002;65:021907. doi: 10.1103/PhysRevE.65.021907. [DOI] [PubMed] [Google Scholar]
- Freyer JP, Sutherland RM. Regulation of growth saturation and development of necrosis in emt6/ro multicellular spheroids by the glucose and oxygen supply. Cancer Res. 1986;46:3513–3520. [PubMed] [Google Scholar]
- Freyer JP, Tustanoff E, Franko AJ, Sutherland RM. In situ consumption rates of cells in v-79 multicellular spheroids during growth. J. Cell. Physiol. 1984;118:53–61. doi: 10.1002/jcp.1041180111. [DOI] [PubMed] [Google Scholar]
- Frieboes H, Zheng X, Sun C, Tromberg B, Gatenby R, Cristini V. An integrated computational/experimental model of tumor invasion. Cancer Res. 2006;11:1597–1604. doi: 10.1158/0008-5472.CAN-05-3166. [DOI] [PubMed] [Google Scholar]
- Friedl P, Wolf K. Tumour-cell invasion and migration: diversity and escape mechanisms. Nat. Rev. Cancer. 2003 May;3(5):362–374. doi: 10.1038/nrc1075. [DOI] [PubMed] [Google Scholar]
- Ganong W. Review of Medical Physiology. 19th Edition. Appleton & Lange; New York: 1999. p. 329. Ch. 19th. [Google Scholar]
- Gatenby R, Vincent T. Application of quantitative models from population biology and evolutionary game theory to tumor therapeutic strategies. Mol. Cancer Ther. 2003;2:919–927. [PubMed] [Google Scholar]
- Gatenby RA, Gawlinski E, Gmitro A, Kaylor B, Gillies R. Acid-mediated tumor invasion: a multidisciplinary study. Cancer Res. 2006;66(10):5216–5223. doi: 10.1158/0008-5472.CAN-05-4193. [DOI] [PubMed] [Google Scholar]
- Gatenby RA, Gawlinski ET. A reaction-diffusion model of cancer invasion. Cancer Res. 1996;56(24):5745–5753. [PubMed] [Google Scholar]
- Gatenby RA, Gillies RJ. Why do cancers have high aerobic glycolysis? Nat. Rev. Cancer. 2004;4:891–899. doi: 10.1038/nrc1478. [DOI] [PubMed] [Google Scholar]
- Gerisch A, Chaplain MAJ. Mathematical modelling of cancer cell invasion of tissue: local and non-local models and the effect of adhesion. J Theor Biol. 2008;250(4):684–704. doi: 10.1016/j.jtbi.2007.10.026. [DOI] [PubMed] [Google Scholar]
- Gerlee P, Anderson A. A hybrid cellular automaton model of clonal evolution in cancer: The emergence of the glycolytic phenotype. J. Theor. Biol. 2008;250:705–722. doi: 10.1016/j.jtbi.2007.10.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerlee P, Anderson A. Modelling evolutionary cell behaviour using neural networks: Application to tumour growth. Biosystems. 2009;95(2):166–174. doi: 10.1016/j.biosystems.2008.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerlee P, Anderson ARA. An evolutionary hybrid cellular automaton model of solid tumour growth. J. Theor. Biol. 2007a June;246(4):583–603. doi: 10.1016/j.jtbi.2007.01.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerlee P, Anderson ARA. Stability analysis of a hybrid cellular automaton model of cell colony growth. Phys. Rev. E. 2007b;75:051911. doi: 10.1103/PhysRevE.75.051911. [DOI] [PubMed] [Google Scholar]
- Giese A, Bjerkvig R, Berens ME, Westphal M. Cost of migration: invasion of malignant gliomas and implications for treatment. J. Clin. Oncol. 2003 Apr;21(8):1624–1636. doi: 10.1200/JCO.2003.05.063. [DOI] [PubMed] [Google Scholar]
- Greenspan H. Models for the growth and stability of cell cultures and solid tumors. J. Theor. Biol. 1975;56:317–340. doi: 10.1016/s0022-5193(76)80054-9. [DOI] [PubMed] [Google Scholar]
- Grote J, Susskind R, Vaupel P. Oxygen diffusivity in tumor tissue (ds-carcinosarcoma) under temperature conditions within the range of 20-40 degrees c. Pflugers Arch. 1977;372:37–42. doi: 10.1007/BF00582204. [DOI] [PubMed] [Google Scholar]
- Hanahan D, Weinberg R. The hallmarks of cancer. Cell. 2000;100:57–70. doi: 10.1016/s0092-8674(00)81683-9. [DOI] [PubMed] [Google Scholar]
- Haykin S. Neural Networks: a comprehensive foundation. 2nd ed. Prentice Hall; New Jersey: 1999. [Google Scholar]
- Hlatky L, Alpen E. Two-dimensional diffusion limited system for cell growth. Cell Tissue Kinet. 1985;18(6):597–611. doi: 10.1111/j.1365-2184.1985.tb00703.x. [DOI] [PubMed] [Google Scholar]
- Hogeweg P. Evolving mechanisms of morphogenesis: on the interplay between differential adhesion and cell differentiation. J. Theor. Biol. 2000 Apr;203(4):317–333. doi: 10.1006/jtbi.2000.1087. [DOI] [PubMed] [Google Scholar]
- Hood J, Cheresh D. Role of integrins in cell invasion and migration. Nat. Rev. Cancer. 2002;2:91–100. doi: 10.1038/nrc727. [DOI] [PubMed] [Google Scholar]
- Hotary K, Allen E, Punturieri A, Yana I, Weiss SJ. Regulation of cell invasion and morphogenesis in a three-dimensional type i collagen matrix by membrane-type matrix metalloproteinases 1, 2, and 3. J. Cell Biol. 2000;149(6):1309–1323. doi: 10.1083/jcb.149.6.1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hynes R. Integrins: versatility, modulation, and signaling in cell adhesion. Cell. 1992;69(1):11–25. doi: 10.1016/0092-8674(92)90115-s. [DOI] [PubMed] [Google Scholar]
- Iwasa Y, Nowak MA, Michor F. Evolution of resistance during clonal expansion. Genetics. 2006 Apr;172(4):2557–2566. doi: 10.1534/genetics.105.049791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kansal AR, S T, Chiocca EA, Deisboeck T. Emergence of a subpopulation in a computational model of tumor growth. J. Theor. Biol. 2000;207:431–441. doi: 10.1006/jtbi.2000.2186. [DOI] [PubMed] [Google Scholar]
- Kerr JF, Winterford CM, Harmon BV. Apoptosis. its significance in cancer and cancer therapy. Cancer. 1994;73:2013–2026. doi: 10.1002/1097-0142(19940415)73:8<2013::aid-cncr2820730802>3.0.co;2-j. [DOI] [PubMed] [Google Scholar]
- Komarova N, Sengupta A, Nowak M. Mutation-selection networks of cancer initiation: tumor suppressor genes and chromosomal instability. J. Theor. Biol. 2003;223:433–450. doi: 10.1016/s0022-5193(03)00120-6. [DOI] [PubMed] [Google Scholar]
- Komarova NL. Spatial stochastic models for cancer initiation and progression. Bull. Math. Biol. 2006 Oct;68(7):1573–1599. doi: 10.1007/s11538-005-9046-8. [DOI] [PubMed] [Google Scholar]
- Lawrence JA, Steeg PS. Mechanisms of tumor invasion and metastasis. World Journal of Urology. 1996;14(3):124–130. doi: 10.1007/BF00186891. [DOI] [PubMed] [Google Scholar]
- Liotta LA, Rao CN, Barsky SH. Tumor invasion and the extracellular matrix. Lab. Invest. 1983;49(6):636–649. [PubMed] [Google Scholar]
- Macklin P, Lowengrub J. Nonlinear simulation of the effect of microenvironment on tumor growth. J. Theor. Biol. 2007 Apr;245(4):677–704. doi: 10.1016/j.jtbi.2006.12.004. [DOI] [PubMed] [Google Scholar]
- Mansury Y, Diggory M, Deisboeck TS. Evolutionary game theory in an agent-based brain tumor model: exploring the ‘genotype-phenotype’ link. J. Theor. Biol. 2006 Jan;238(1):146–156. doi: 10.1016/j.jtbi.2005.05.027. [DOI] [PubMed] [Google Scholar]
- Marchant B, Norbury J, Sherratt J. Travelling wave solutions to a haptotaxis-dominated model of malignant invasion. Nonlinearity. 2001;14:1653–1671. [Google Scholar]
- Merlo LMF, Pepper JW, Reid BJ, Maley CC. Cancer as an evolutionary and ecological process. Nat. Rev. Cancer. 2006 Dec;6(12):924–935. doi: 10.1038/nrc2013. [DOI] [PubMed] [Google Scholar]
- Michor F, Iwasa Y, Rajagopalan H, Lengauer C, Nowak MA. Linear model of colon cancer initiation. Cell Cycle. 2004 Mar;3(3):358–362. [PubMed] [Google Scholar]
- Nowak M, May R. Evolutionary games and spatial chaos. Nature. 1992;359(6398):826–829. [Google Scholar]
- Nowak MA, Michor F, Iwasa Y. Genetic instability and clonal expansion. J. Theor. Biol. 2006 Jul;241(1):26–32. doi: 10.1016/j.jtbi.2005.11.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowell PC. The clonal evolution of tumour cell populations. Science. 1976;194:23–28. doi: 10.1126/science.959840. [DOI] [PubMed] [Google Scholar]
- Palsson E, Othmer HG. A model for individual and collective cell movement in dictyosteliumdiscoideum. Proc. Natl. Acad. Sci. 2000 Sep;97(19):10448–10453. doi: 10.1073/pnas.97.19.10448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patel A, Gawlinski ET, Lemieux SK, Gatenby RA. A cellular automaton model of early tumor growth and invasion: The effects of native tissue vascularity and increased anaerobic tumor metabolism. J. Theor. Biol. 2001;213:315–331. doi: 10.1006/jtbi.2001.2385. [DOI] [PubMed] [Google Scholar]
- Press W, Teukolsky S, Vetterling W, B.P F. Numerical Recipes in C: The Art of Scientific Computing. Cambridge University; 1996. [Google Scholar]
- Rejniak K. A single cell approach in modeling the dynamics of tumor microregions. Mathematical Biosciences and Engineering. 2005;2:643–655. doi: 10.3934/mbe.2005.2.643. [DOI] [PubMed] [Google Scholar]
- Rozhin J, Sameni M, Ziegler G, Sloane BF. Pericellular ph affects distribution and secretion of cathepsin b in malignant cells. Cancer Res. 1994;54(24):6517–6525. [PubMed] [Google Scholar]
- Rubin H. Microenvironmental regulation of the initiated cell. Adv. Cancer Res. 2003;90:1–62. doi: 10.1016/s0065-230x(03)90001-7. [DOI] [PubMed] [Google Scholar]
- Sahai E. Nat. Rev. Cancer. Vol. 7. 2007. Illuminating the metastatic process; pp. 737–749. [DOI] [PubMed] [Google Scholar]
- Schofield P, Chaplain M, Hubbard S. Evolution of searching and life history characteristics in individual-based models of host-parasitoid-microbe associations. Journal of Theoretical Biology. 2005;237(1):1–16. doi: 10.1016/j.jtbi.2005.03.025. [DOI] [PubMed] [Google Scholar]
- Smallbone K, Gatenby RA, Gillies RJ, Maini PK, Gavaghan DJ. Metabolic changes during carcinogenesis: Potential impact on invasiveness. J. Theor. Biol. 2007 Feb;244(4):703–713. doi: 10.1016/j.jtbi.2006.09.010. [DOI] [PubMed] [Google Scholar]
- Smalley K, Brafford P, Herlyn M. Selective evolutionary pressure from the tissue microenvironment drives tumor progression. Semin Cancer Biol. 2005 Dec;15(6):451–459. doi: 10.1016/j.semcancer.2005.06.002. [DOI] [PubMed] [Google Scholar]
- Stetler-Stevenson WG, Aznavoorian S, Liotta LA. Tumor cell interactions with the extracellular matrix during invasion and metastasis. Annu. Rev. Cell. Biol. 1993;9:541–573. doi: 10.1146/annurev.cb.09.110193.002545. [DOI] [PubMed] [Google Scholar]
- Stott E, Britton N, Glazier J, Zajac M. Stochastic simulation of benign avascular tumor growth using the potts model. Math. Comput. Model. 1999;30:83–198. [Google Scholar]
- Sullivan R, Graham CH. Hypoxia-driven selection of the metastatic phenotype. Cancer Metastasis Rev. 2007;26:319–331. doi: 10.1007/s10555-007-9062-2. [DOI] [PubMed] [Google Scholar]
- Sutherland R. Cell and environment interactions in tumor microregions: The multicell spheroid model. Science. 1988;240:177–184. doi: 10.1126/science.2451290. [DOI] [PubMed] [Google Scholar]
- Swanson KR, Bridge C, Murray JD, Alvord EC. Virtual and real brain tumors: using mathematical modeling to quantify glioma growth and invasion. J. Neurol. Sci. 2003 Dec;216(1):1–10. doi: 10.1016/j.jns.2003.06.001. [DOI] [PubMed] [Google Scholar]
- Taylor T, Hallam J. Replaying the tape: An investigation into the role of contingency in evolution. In: Adami C, Belew R, Kitano H, C T, editors. Replaying the Tape: An Investigation into the Role of Contingency in Evolution. MIT Press; 1998. pp. 256–265. [Google Scholar]
- Tomlinson I, Bodmer WF. Modelling the consequences of interactions between tumour cells. Br J Cancer. 1997;75(2):157–160. doi: 10.1038/bjc.1997.26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomlinson IPM. Game-theory models of interactions between tumour cells. European Journal of Cancer. 1997 Aug;33(9):1495–1500. doi: 10.1016/s0959-8049(97)00170-6. [DOI] [PubMed] [Google Scholar]
- Walenta S, Snyder S, Haroon Z, Braun R, Amin K, Brizel D, Mueller-Klieser W, Chance B, Dewhirst M. Tissue gradients of energy metabolites mirror oxygen tension gradients in a rat mammary carcinoma model. Int. J. Radiation Oncology Biol. Phys. 2001;51:840–848. doi: 10.1016/s0360-3016(01)01700-x. [DOI] [PubMed] [Google Scholar]
- Zaman M, Kamm RD, Matsudaira P, Lauffenburger D. Computational model for cell migration in three-dimensional matrices. Biophys J. 2005 Aug;89(2):1389–1397. doi: 10.1529/biophysj.105.060723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaman M, Trapani L, Sieminski A, Siemeski A, Mackellar D, Gong H, Kamm R, Wells A, Lauffenburger D, Matsudaira P. Migration of tumor cells in 3d matrices is governed by matrix stiffness along with cell-matrix adhesion and proteolysis. Proc Natl Acad Sci U S A. 2006 Jul;103(29):10889–10894. doi: 10.1073/pnas.0604460103. [DOI] [PMC free article] [PubMed] [Google Scholar]