Rate constants rather than biochemical mechanism determine behaviour of genetic clocks

Abstract

Many biological systems contain both positive and negative feedbacks. These are often classified as resonators or integrators. Resonators respond preferentially to oscillating signals of a particular frequency. Integrators, on the other hand, accumulate a response to signals. Computational neuroscientists often refer to neurons showing integrator properties as type I neurons and those showing resonator properties as type II neurons. Guantes & Poyatos have shown that type I or type II behaviour can be seen in genetic clocks. They argue that when negative feedback occurs through transcription regulation and post-translationally, genetic clocks act as integrators and resonators, respectively. Here we show that either behaviour can be seen with either design and in a wide range of genetic clocks. This highlights the importance of parameters rather than biochemical mechanism in determining the system behaviour.

1. Introduction

Timekeeping mechanisms are a fundamental feature of many cell types. The need for accurate timekeeping is found in many different biological settings, from development (Hirata et al. 2002) to circadian (daily) clocks (Young & Kay 2001), to cell-cycle regulation (Kohn 1999) and across many time scales, from the fast firing of neurons to the slow seasonal changes that occur in the bodies of many organisms (Dunlap et al. 2003). The biological clocks that regulate these processes use very diverse biochemical mechanisms. Here we explore how biochemical mechanism affects the behaviour of these systems.

A common motif in many clocks is intertwined with positive and negative feedbacks loops. Genetic clocks typically contain feedback loops involving both activators and repressors. Positive and negative feedbacks can also occur post-translationally by increasing or decreasing protein stability. Neuronal clocks employ a different biochemical mechanism. Sodium channels open in response to increased voltage levels, in turn further increasing the voltage (positive feedback) while potassium channels causing sodium inactivation decrease the voltage (negative feedback). These are, by no means, the only examples of biological systems with positive and negative feedbacks (e.g. population interaction (Hirsch & Smale 1974) and the cAMP system (Goldbeter 1996)).

Summarizing early experimental work on the effect of current on neuronal oscillations, Hodgkin, in 1948, proposed a classification of neurons into two types (Hodgkin 1948). The period of type I neurons is quite sensitive to the strength of the input current and can vary over several orders of magnitude. On the other hand, the behaviour of type II neurons depends less on the strength of the input signal and more on the signal's frequency. This classification also has broad implications for the behaviour of neurons, such as entrainment properties, phase response curves and robustness to noise (Rinzel & Ermentrout 1989; Oprisan & Canavier 2002; Guantes & Poyatos 2006). Rinzel & Ermentrout (1989) have linked this classification to the underlying bifurcation structure of the models. They also show that both types I and II behaviours can be seen in a specific model depending on the choice of rate constants. Thus, the rate constants and the bifurcation structure appear to be more important than the biochemical mechanism in determining whether neuronal oscillators show type I or type II behaviour.

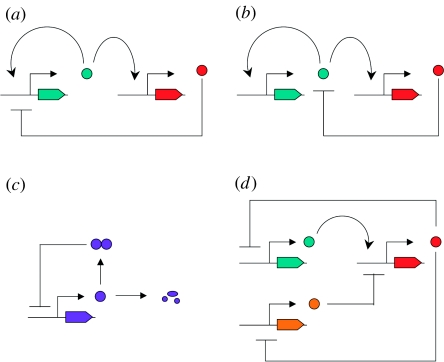
A wide variety of biochemical mechanisms are used in various cellular oscillators that contain both positive and negative feedbacks. For example, negative feedback may occur through the repression of transcription (figure 1a) or by post-translational regulation of the stability of an activator (figure 1b). Positive feedback can also occur through the regulation of dimer formation (figure 1c; see Tyson et al. 1999) or by having two negative feedback steps in serial (figure 1d; see Kuznetsov et al. 2004). Recently, Guantes & Poyatos (2006) suggested that biochemical mechanism may determine whether a genetic clock behaves as a resonator or integrator. We are interested in whether the biochemical mechanism determines the oscillatory behaviour of the system.

Figure 1.

Designs of genetic clocks with both positive and negative feedbacks. (a) Design I: activator (turquoise) stimulates transcription of its own gene and the gene for repressor (red); repressor blocks transcription of the gene for activator. (Similar to design in Atkinson et al. (2003) and Guantes & Poyatos (2006)). (b) Design II: similar to design I, except that repressor promotes the degradation of the activator protein (Guantes & Poyatos 2006). (c) Design III: the unstable regulatory protein is degraded to inactive fragments or forms a stable dimer that represses the transcription of its own gene. This design is similar to a circadian clock model for Drosophila melanogaster proposed by Tyson et al. (1999). (d) Design IV: activator (turquoise) stimulates the transcription of one repressor gene (red) whose product represses transcription of the activator gene as well as the transcription of the second repressor gene (orange). The product of the second repressor gene (orange) inhibits the transcription of the first repressor gene. This design is similar to that studied by Kuznetsov et al. (2004).

2. Examples of genetic clocks with both positive and negative feedbacks

We consider several examples of genetic networks with both positive and negative feedbacks. Each design combines positive and negative feedbacks using a different biochemical mechanism. Guantes & Poyatos (2006) explore models with two genes, one that codes for an activator (x) and the other that codes for a repressor (y). In both designs, the activator binds to both genes to activate transcription. In design I, the repressor inactivates the transcription of the activator's gene whereas, in design II, the repressor promotes the degradation of the activator post-translationally (figure 1). They derived the following model equations for these designs:

$$\frac{\text{d}x}{\text{d}t}=\Delta \left(\xi \frac{1+\rho x^2}{1+x^2+{\sigma }_1{y}^2}-x-{\sigma }_{2}xy\right),\frac{\text{d}y}{\text{d}t}=\Delta ϵ\xi \frac{1+\rho x^2}{1+x^2}-y,$$

where σ₁=0 for design II and σ₂=0 for design I.

Tyson et al. (1999) model post-translational positive feedback inspired by the circadian clock in Drosophila. In this design (figure 1c), there is a negative feedback loop where the PER protein inhibits its own transcription. PER monomers are unstable but are stabilized when PER forms homodimers. At low concentrations of PER, few homodimers are formed and degradation occurs rapidly. As the concentration of PER increases, more homodimers form, further stabilizing PER and creating a positive feedback in the system. The model equations for this design are

$$\begin{array}{l}q=\frac{2}{1+\sqrt{1+8K_{\text{eq}}{P}_{\text{t}}}},\hfill \\ \frac{\text{d}M}{\text{d}t}=\frac{v_{\text{m}}}{1+{(P_{\text{t}}(1-q)/(2P_{\text{crit}}))}^2}-k_{\text{m}}M,\hfill \\ \frac{\text{d}{P}_{\text{t}}}{\text{d}t}=v_{\text{p}}M-\frac{(k_{\text{p}1}q+k_{\text{p}2})P_t}{J_{\text{p}}+P_{\text{t}}}-k_{\text{p}3}{P}_{\text{t}},\hfill \end{array}$$

where M is the concentration of per mRNA and P_t is the total concentration of PER.

Kuznetsov et al. (2004) studied a genetic system with three genes that includes positive and negative feedbacks (figure 1d). One protein (V) represses the transcription of the gene for another protein (U) that in turn represses the gene encoding V. This combination of two repressors produces a positive feedback loop. The third gene encodes a protein (W) that activates the transcription of gene U, and U represses the transcription of gene W, closing a negative feedback loop. The model equations for this design are

$$\frac{\text{d}U}{\text{d}t}=\frac{{\alpha }_1}{1+V^{\beta }}+\frac{{\alpha }_3{W}^{\eta }}{1+W^{\eta }}-U,\frac{\text{d}V}{\text{d}t}=\frac{{\alpha }_2}{1+U^{\gamma }}-V,\frac{\text{d}W}{\text{d}t}=ϵ\left(\frac{{\alpha }_4}{1+U^{\gamma }}-W\right).$$

Parameter values for all models are given in figure 2. Although all the four systems we study contain positive and negative feedbacks, each of them uses different biochemical mechanisms. We were interested in the relationship between the system design and the types of behaviour (type I or II) that may be displayed by the system. We therefore examined the behaviour of the model equations for these systems over a wide range of parameters, and tested for types I and II behaviours.

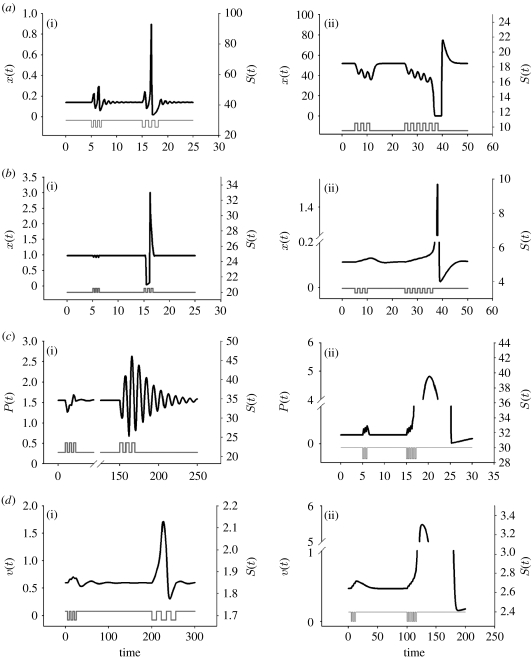
Figure 2.

(a(i)–d(i)) Resonator and (a(ii)–d(ii)) integrator behaviours obtained in all four system designs ((a) I, (b) II, (c) III and (d) IV). For certain parameter values, each design resulted in resonator behaviours (black line, x(t) in (a(i)) and (b(i)), P(t) in (c(i)), v(t) in (d(i))) upon stimulation by an input signal at a particular frequency (grey line, S(t)). For other parameter values, each design resulted in integrator behaviour (black line, x(t) in (a(ii)) and (b(ii)), P(t) in (c(ii)), v(t) in (d(ii))) upon repeated stimulation by an input signal (grey line, S(t)). Resonator parameter values for design I: ϵ=0.05, ξ=1.58, ρ=50, σ₁=1, σ₂=0 and Δ=25.5 or 30, depending on the pulse train. Three pulses (changes to Δ as was done in Guantes & Poyatos 2006) were given at t=5 with a frequency of 0.4 and three pulses were given at t=15 with frequency of 0.63. Design II: same as design I, except that σ₁=0 and σ₂=1 with Δ=20 or 20.5. Three pulses were given at t=5 of frequency 0.25 and three at t=15 of frequency 0.35. Design III: v_m=4, k_m=0.4, v_p=0.5, k_p2=0.03, k_p3=0.1, K_eq=60, P_crit=0.5, J_p=0.05 with k_p1=21 or 23.5. Three pulses (changes in k_p1) were given at t=5 of frequency 1.5 and three at t=150 with frequency 3.8. Design IV: α₂=α₄=3, α₃=1, β=η=γ=3, ϵ=0.1 with α₁=1.68 or 1.72. Three pulses (changes in α₁) were given at t=5 of frequency 4 and three at t=200 of frequency 11. Integrator parameter values for design I: same as design I resonator parameter values, except that Δ=9.5 or 10.5. Three pulses of frequency 1.2 given at t=5 and six at t=25. Design II: ϵ=1, ξ=0.06, ρ=100, σ₁=0, σ₂=0.4 and Δ=3.34 or 3.6. Three pulses of frequency 1 given at t=5 and six pulses at t=25. Design III: same as design III resonator parameter values with k_p1=28.5 or 30. Three pulses of frequency 0.2 were given at t=5 and six at t=15. Design IV: α₂=5.5, α₃=2, α₄=3, β=η=γ=3, ϵ=0.01 with α₁=2.4 or 2.3. Three pulses of frequency 1.5 were given at t=5 and six at t=100. In all cases, at t=0, the system was at steady state.

3. Results

As a qualitative test of whether each of these genetic systems can act as a resonator or an integrator, each model was subjected to pulsatile stimuli and their responses recorded. If repeated pulses at a particular frequency caused a large response, and pulses at shorter or longer frequencies caused a small response, the model was considered a resonator. If the response was, instead, dependent on the total number of pulses, the model was classified as an integrator. Amazingly, all four designs appear to act as integrators or resonators depending on the rate constants (figure 2). This indicates that the rate constants rather than the biochemical mechanism determine which type of behaviour can be seen.

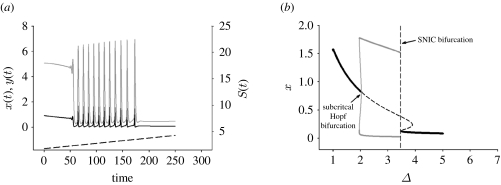
The underlying bifurcation structure has been shown to determine whether oscillators act as resonators or integrators (Rinzel & Ermentrout 1989). Resonator behaviour is typically observed when the system is close to a Hopf bifurcation (HB) where a stable steady state becomes unstable, and integrator behaviour is typically observed when the system is near a saddle node on an invariant circle (SNIC) bifurcation where a stable steady state is lost (Rinzel & Ermentrout 1989). For all four designs, varying just one system parameter results in both Hopf and SNIC bifurcations (figure 3). In fact, if the parameter is incrementally changed, the system proceeds to low-amplitude oscillations after a slight delay related to ‘slow passage’ through the HB (typical of resonators; see Baer et al. 1989) to large amplitude oscillations with increasing period (typical of integrators; figure 3). This provides further evidence that the rate constants determine which type of behaviour is seen. A similar analysis is presented for the other designs in the electronic supplementary material. These simulations also show that the resonator or integrator behaviour can be seen over a large range of parameter values.

Figure 3.

A system design exhibits both resonator and integrator behaviours as a parameter is incrementally varied. This figure studies design II. Other designs can be seen in the electronic supplementary material. (a) For lower values of the varied parameter, low-amplitude oscillations, i.e. resonator behaviour (Baer et al. 1989), was obtained (black line x(t); grey line, y(t); dashed line, S(t)). As the parameter is incrementally increased, the period increases, reflecting integrator behaviour (Rinzel & Ermentrout 1989). Parameter values: ϵ=1, ξ=0.06, ρ=100, σ₁=0, σ₂=0.4, with Δ=1.8+t/100. Initial conditions were x=0.93 and y=5.0668, the steady -state values for Δ=1.8. (b) One parameter (Δ) bifurcation diagram illustrating both a HB (resonator) and a SNIC bifurcation (integrator). x(t) is the activator concentration. Black solid line, stable x^*; dashed line, unstable x^*; thick grey line, stable LC; thin grey line, unstable LC.

It is interesting to note that some models of glycolytic oscillations (Goldbeter 1996; Westermark & Lansner 2003) admit at most one steady state for any given set of parameter values, ruling out the possibility of a SNIC bifurcation. In these models, a HB occurs, which we and others link to resonator behaviour (Rinzel & Ermentrout 1989). This again stresses the point that parameter values (and the associated bifurcation structure) determine whether a genetic system will produce integrator or resonator behaviour.

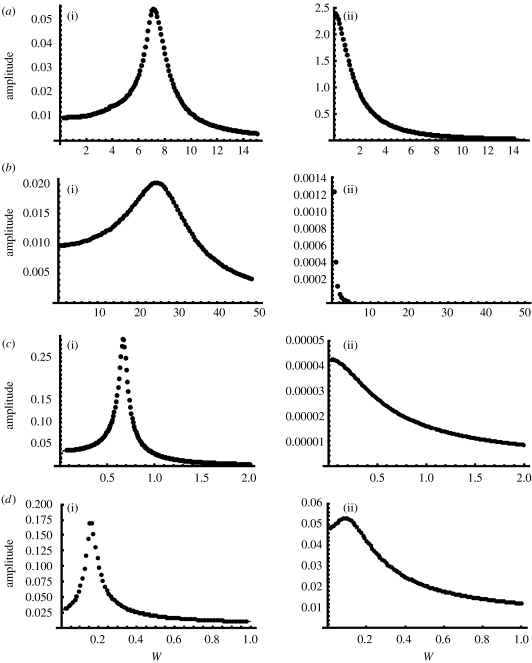
To further demonstrate the resonator and integrator behaviours in these designs, we subjected each design, with resonator or integrator rate constants, to small amplitude sinusoidal stimuli (figure 4). The amplitude of the response of each model was recorded as a function of the input frequency. For resonator designs I–IV, there was a particular frequency that gave the largest response amplitude. For the integrator designs I–III, the response amplitude decreases as a function of the input frequency. We have chosen the rate constants for the integrator design IV so that a small remnant of the resonance behaviour can be seen at low input frequencies. This was done to illustrate that in any design there is a spectrum of behaviours, from resonator to integrator, depending on how close the rate constants are to a SNIC or HB.

Figure 4.

(a–d) Response of designs I–IV to sinusoidal inputs. For each model described in figure 2, we applied a small amplitude sinusoidal stimulus and recorded the model's response amplitude (maximum–minimum of x (designs I and II) M (design III) or U (design IV) after initial transients; (a(i)–d(i)) resonator and (a(ii)–d(ii)) integrator). The rate constants that showed resonance in figure 2 displayed a maximum response amplitude at a particular frequency, w. The response amplitude for integrator models decreased as the frequency increased (with the exception of IV that is discussed in the text). For resonator and integrator design I, Δ=30+sin (wt) or Δ=9.5+0.1 sin (wt), respectively. For resonator and integrator design II, Δ=20+0.1 sin (wt) or Δ=3.6+0.01 sin (wt), respectively. For resonator and integrator design III, k_p1=20+0.1 sin (wt) or k_p1=30+0.1 sin (wt), respectively. For resonator and integrator design IV, α₁=1.72+0.01 sin (wt) or α₁=2.4+0.01 sin (wt), respectively. All other parameters are the same as given in figure legend 2.

4. Similarity of mathematical structure in models for genetic and neuronal oscillators

The Morris–Lecar model of the electrical firing of a neuron also shows both resonator and integrator behaviours, depending on the parameters (Rinzel & Ermentrout 1989). The biochemical mechanisms of this model are very different from any of the designs we studied. The Morris–Lecar model tracks the voltage of the neuron (V) and how much current can pass through channels in the membrane of the cell (w). The model equations are the following:

$$\frac{\text{d}V}{\text{d}t}=-g_{\text{ca}}{m}_{\infty }(V)(V-V_{\text{ca}})-g_{k}w(V-V_k)-g_l(V-V_l),\frac{\text{d}w}{\text{d}t}=\varphi \frac{w_{\infty }(V)-w}{{\tau }_w},$$

$$m_{\infty }(V)=0.5(1+\text{tanh}(V-V_1)/V_2),w_{\infty }(V)=0.5(1+\text{tanh}(V-V_3)/V_4).$$

Although τ_w, the time constant for the gating variable w, is often expressed as a function of voltage, it is sometimes assumed constant and is close enough to be treated so for our purposes.

While the Morris–Lecar model describes a system with quite different biochemical mechanisms from the genetic oscillators of designs I–IV, it turns out that the mathematical structures of the models are related, indicating similar behaviour. In particular, designs I and II and the Morris–Lecar genetic oscillator models can readily be put into the following common form:

$$\frac{\text{d}x}{\text{d}t}=f(x,y)-ax-bxy,\frac{\text{d}y}{\text{d}t}=g(x)-y.$$

For normal physiological ranges of the variables (e.g. −70<V<20, 0<w<1 in the Morris–Lecar model, or x, y>0 in the models for designs I and II), it happens that ∂f/∂x>0 and ∂g/∂x>0 (i.e. x is an activator providing positive feedback) and ∂f/∂y≤0 (i.e. y is an inhibitor providing negative feedback). These models are therefore mathematically quite similar and depend on the rate constants of a particular model. This fact is emphasized by plotting f(x, y) and g(x) (figure S4 in the electronic supplementary material). Given this similarity of mathematical structure, it is not surprising that many of the behaviours of the neuronal model are also seen in the genetic systems.

5. Discussion

Many genetic oscillators contain both positive and negative feedbacks. Circadian clocks in diverse organisms contain positive (e.g. in Drosophila PDP1 activates CLK that activates PDP1) and negative (e.g. in Drosophila, PER and TIM repressing their own transcription) feedback loops (Reppert & Weaver 2000). Cell-cycle regulation also contains positive and negative feedbacks (Csikasz-Nagy et al. 2006). Many theoretical studies have considered biological oscillations with both positive and negative feedbacks (Tyson & Othmer 1978; Tyson & Keener 1988). Here we show, similar to the previous work in neuronal oscillators (Rinzel & Ermentrout 1989), that the rate constants are the key to determining what behaviour is seen in these networks.

One of the central questions in genetic clocks is how they can be robust despite the stochasticity of molecular interactions (Barkai & Leibler 1997). The overall structure of a genetic network can determine how robust or reliable the network is (Brandman et al. 2005; Klemm & Bornholdt 2005). The rate constants play an important role as well by determining the number of molecular interactions that occur (Gonze et al. 2004; Forger & Peskin 2005). Guantes & Poyatos (2006) show that the robustness of these networks with positive and negative feedbacks strongly correlates with whether the network acts as a resonator or an integrator (Guantes & Poyatos 2006). Here we show that these properties depend not on the specific biochemical mechanism but on the values of the rate constants. Thus, in determining whether resonator or integrator behaviour is obtained, rate constants are also important in determining how robust a network will be.

The seminal work of Winfree (2001) showed how the mathematical structure of biological oscillators can be remarkably similar across a wide range of organisms and biochemical mechanisms. Our work and that of Guantes & Poyatos (2006) support this idea; the classification as integrators or resonators developed for neuronal oscillations also applies to oscillations in genetic networks. This implies that the vast literature on the properties of resonators or integrators in neuronal oscillations will also probably apply to genetic clocks. Much future work is needed to test these ideas.

The presence of just negative feedback alone, or even a combination of positive and negative feedbacks, certainly does not guarantee that oscillations will be found. Indeed, oscillations are notoriously difficult to achieve in genetic networks (Tyson & Othmer 1978; Atkinson et al. 2003). However, having both positive and negative feedbacks expands the range of parameters at which oscillations may be obtained (Rinzel & Ermentrout 1989). In general, oscillations occur only when the positive feedback is fast when compared with the negative feedback (see Tyson et al. 1999). Once again, the rate constants are vital to determining behaviour. This has proven to be an essential design principle in constructing synthetic genetic clocks (Atkinson et al. 2003).

These results reveal that a wide range of biological oscillator models can show either resonator or integrator behaviour. Since both the behaviours are possible, there are parameter choices that may exhibit the characteristic of both. Guckenheimer (1983) studied a similar system and found a very rich bifurcation structure. This model contained just two parameters, but yielded over 20 regions of behaviour within this space and several bifurcations not discussed here (e.g. Takens-Bogdanov or degenerate Hopf). The models we study contain many more parameters. While a complete bifurcation analysis of these models would be interesting, it is well beyond the scope of this work. Future work also could develop generic models of genetic clocks. Such generic models are discussed by Fall et al. (2000).

Our work shows, similar to other studies (Tyson 2004), that the network diagram alone does not determine the behaviour of a biological clock employing positive and negative feedbacks. Knowledge of the parameters is required, as a given design can result in very different behaviours. Although we limited our study to a particular class of oscillators (with positive and negative feedbacks), it is probable that other types of oscillators share this property. Surprisingly, few experimental data are available which measure rate constants in genetic networks. Thus, much more experimental work is needed to understand the system behaviour.

Supplementary Material

Supplementary material

Bifurcation diagrams for all designs