Competition of hospital-acquired and community-acquired methicillin-resistant Staphylococcus aureus strains in hospitals

Abstract

Recently, we [E.M.C. D’Agata, G.F. Webb, M.A. Horn, R.C. Moellering Jr., and S. Ruan, Modelling the invasion of community-acquired methicillin-resistant Staphylococcus aureus into the hospital setting, Clin. Infect. Dis. 48 (2009), pp. 274–284] proposed a deterministic mathematical model to characterize the factors contributing to the replacement of hospital-acquired methicillin-resistant Staphylococcus aureus (HA-MRSA) with the community-acquired MRSA (CA-MRSA) and to quantify the effectiveness of interventions aimed at limiting the spread of CA-MRSA in the hospital setting. Numerical simulations of the model strongly suggest that CA-MRSA will become the dominant MRSA strain in the hospital setting. In this companion paper, we provide steady-state analysis and more numerical simulations of the model. It is shown that when no colonized or infected patients enter the hospital, competitive exclusion of HA-MRSA by CA-MRSA will occur with increased severity of CA-MRSA infections resulting in longer hospitalizations and a larger in-hospital reservoir of CA-MRSA. Improving compliance with hand hygiene and decolonization of CA-MRSA carriers are effective control strategies.

1. Introduction

Staphylococcus aureus is a gram-positive bacterium that colonizes the skin and is present in the anterior nares in about a quarter of the population [5]. The bacterium acquires resistance against all classes of antibiotics by either mutation of an existing bacterial gene or horizontal transfer of a resistance gene from another bacterium [5]. Since it was first reported in the 1950s, methicillin-resistant Staphylococcus aureus (MRSA) has been regarded as a healthcare-associated pathogen affecting predominantly the elderly and debilitated [5,14], and MRSA infections are an important clinical and public health problem [6]. It was estimated that deaths in patients with MRSA in the USA in 2005 surpassed those caused by HIV/AIDS in the same year [1,12].

In 1998, a new strain of MRSA emerged in the community setting occurring among young healthy individuals with no exposure to the healthcare setting [9]. Since then, this community-acquired MRSA strain (CA-MRSA) has rapidly spread throughout the world [4, 11,13,23]. Outbreaks of CA-MRSA have been reported among children [9], athletes [16], nurseries [17] and obstetrical wards [20]. With the use of mathematical models, it has been shown that the presence of a community reservoir has a major impact on the control of MRSA in the hospital [2,15,19,20]. It has been suggested that CA-MRSA may be replacing the traditional hospital-acquired MRSA (HA-MRSA) [18].

Recently, we [3] developed a deterministic mathematical model to quantify the temporal patterns of CA-MRSA spread into the hospital setting and its competitive exclusion of HA-MRSA over time. The transmission dynamics of CA-MRSA within the hospital setting and the effectiveness of current infection control strategies were quantified to determine the optimal strategy or a combination of strategies, aimed at preventing the spread of CA-MRSA between patients. The deterministic model describes the transmission dynamics of CA-MRSA within a 400-bed tertiary-care hospital with approximately 25,000 admissions per year. The impact of an increasing influx of CA-MRSA into the hospital setting as a result of the persistent and rising dissemination of CA-MRSA within the community is quantified and the effect of different interventions aimed at limiting the spread of CA-MRSA is analysed and compared. Individuals within the hospital are in five mutually exclusive states: susceptible, colonized with either CA-MRSA or HA-MRSA and infected with either CA-MRSA or HA-MRSA. Individuals enter the hospital in one of these states and exit via death or discharge. Within the hospital, susceptible individuals can become colonized with either CA-MRSA or HA-MRSA and can subsequently become infected with the respective MRSA strain. Transmission of MRSA between individuals occurs through the hands of healthcare workers (HCWs), the main vectors of antimicrobial-resistant bacteria. Control strategies for preventing the spread of MRSA include improving compliance with hand hygiene and placing individuals who are infected with MRSA on contact precautions as per standard Centers for Disease Control and Prevention requirements.

In this companion paper, we provide the steady-state analysis and more numerical simulations of the model. It is shown that when no colonized or infected patients enter the hospital, competitive exclusion of HA-MRSA by CA-MRSA will occur with increased severity of CA-MRSA infections, resulting in longer hospitalizations and a larger in-hospital reservoir of CA-MRSA. Numerical simulations also demonstrate that if some of the patients admitted to the hospital are colonized or infected with HA-MRSA and CA-MRSA strains, then both strains can persist in the hospital in terms of positive equilibria.

2. The model

The patients in the hospital are divided into five compartments:

S(t) = number of susceptible patients at time t.

CC(t) = number of patients colonized with the CA-MRSA strain at time t.

CH(t) = number of patients colonized with the HA-MRSA strain at time t.

IC(t) = number of patients infected with the CA-MRSA strain at time t.

IH(t) = number of patients infected with the HA-MRSA strain at time t.

Patients are admitted at a total rate of Λ per day with the fractions of CA-MRSA colonized, CA-MRSA infected, HA-MRSA colonized and HA-MRSA infected patient admissions = λ_CC, λ_IC, λ_CH, λ_IH, respectively. Susceptible patients have an average length of stay (LOS) = 1/γ_S, and colonized CA-MRSA and colonized HA-MRSA have average LOS = 1/γ_C and 1/γ_H, respectively. The colonization rates of susceptible patients to the colonized CA-MRSA compartment are (1 − η)β_CC/N and (1 − η)β_IC/N and to the colonized HA-MRSA compartment are (1 − η)β_CH/N and (1 − η)β_IH/N. Here η is the compliance with hand washing hygiene (with η = 0 corresponding to 0% compliance and η = 1 corresponding to 100% compliance), β_CC, β_IC, β_CH, β_IH the colonization transmission rates of patients from HCWs contaminated by colonized CA-MRSA, infected CA-MRSA, colonized HA-MRSA and infected HA-MRSA patients, respectively, and N the total number of patients in the hospital. The ratios β_CC/β_CH and β_IC/β_IH are approximately 4/3 because of the more rapid doubling time of CA-MRSA. In the simulations, the average LOS of susceptible patients (γ_S) is adjusted so that the number of patients in the hospital is maintained at N. The rates of infection of colonized CA-MRSA and colonized HA-MRSA patients are φ_C and φ_H, respectively. The cure rates of infected CA-MRSA and infected HA-MRSA patients are τ_C and τ_H, respectively. The death rates of infected CA-MRSA and infected HA-MRSA patients are δ_C and δ_H, respectively. The rates of decolonization of colonized CA-MRSA and colonized HA-MRSA patients are α_CC and α_CH, respectively. Parameter estimates were obtained from the Beth Israel Deaconess Medical Center’s computerized database system, which provides patient and infection control data and from the literature (Table 1).

Table 1.

Variables and parameters of the model [3].

Symbol	Interpretation	Baseline value
N	Total number of patients in the hospital	400
Λ	Total admissions per day	70
λCC	Fraction of colonized CA-MRSA admissions	Varies
λCH	Fraction of colonized HA-MRSA admissions	Varies
λIC	Fraction of infected CA-MRSA admissions	Varies
λIH	Fraction of infected HA-MRSA admissions	Varies
1/γS	Average LOS of susceptible patients	5 days
1/γCC	Average LOS of colonized CA-MRSA patients	5 days
1/γCH	Average LOS of colonized HA-MRSA patients	7 days
1/γIC	Average LOS of infected CA-MRSA patients	10 days
1/γIH	Average LOS of infected HA-MRSA patients	18 days
η	Hand hygiene compliance fraction (0 to 1)	0.6 (60%)
βCC	Colonized/colonized CA-MRSA transmission rate	0.36
βCH	colonized/colonized HA-MRSA transmission rate	0.27
βIC	Infected/colonized CA-MRSA transmission rate	0.09
βIH	Infected/colonized HA-MRSA transmission rate	0.07
δCγIC	Infected CA-MRSA patient death rate	0.033/10 (3.3%)
δHγIC	Infected HA-MRSA patient death rate	0.2/18 (20%)
φCγCC	Colonized CA-MRSA patient infection rate	0.1/5 (10%)
φHγCH	Colonized HA-MRSA patient infection rate	0.1/7 (10%)
τCγIC	Infected CA-MRSA patient cure rate	0.967/10 (96.7%)
τHγIH	Infected HA-MRSA patient cure rate	0.8/18 (80%)
αCγCC	Infected CA-MRSA patient cure rate	0.0/5 (0%)
αHγCH	Infected HA-MRSA patient cure rate	0.0/7 (0%)

Note: LOS, length of stay.

The equations of the basic model are

$$\begin{array}{l}\frac{\text{d}S}{\text{d}t}=\underset{\text{admission}}{\underbrace{\mathrm{\Lambda }(1-{\lambda }_{\text{CC}}-{\lambda }_{\text{CH}}-{\lambda }_{\text{IC}}-{\lambda }_{\text{IH}})}}\\ -\underset{\text{CA}-\text{MRSA}\text{colonization}}{\underbrace{\frac{(1-\eta ){\beta }_{\text{CC}}}{N}S(t)\text{CC}(t)-\frac{(1-\eta ){\beta }_{\text{IC}}}{N}S(t)\text{IC}(t)}}\end{array}\begin{array}{l}\underset{\text{HA}-\text{MRSA}\text{colonization}}{\underbrace{-\frac{(1-\eta ){\beta }_{\text{CH}}}{N}S(t)\text{CH}(t)-\frac{(1-\eta ){\beta }_{\text{IH}}}{N}S(t)\text{IH}(t)}}\\ +\underset{\text{decolonization}}{\underbrace{{\alpha }_{\text{C}}\text{CC}(t)+{\alpha }_{\text{H}}\text{CH}(t)}}-\underset{\text{exit}\text{from}\text{hospital}}{\underbrace{{\gamma }_{\text{S}}S(t)}}\end{array}$$ (1)

$$\begin{array}{l}\frac{\text{dCC}}{\text{d}t}=\underset{\text{admission}}{\underbrace{\mathrm{\Lambda }{\lambda }_{\text{CC}}}}+\underset{\text{CA}-\text{MRSA}\text{colonization}}{\underbrace{\frac{(1-\eta ){\beta }_{\text{CC}}}{N}S(t)\text{CC}(t)+\frac{(1-\eta ){\beta }_{\text{IC}}}{N}S(t)\text{IC}(t)}}\\ +\underset{\text{treatment}}{\underbrace{{\tau }_{\text{C}}\text{IC}(t)}}-\underset{\text{infection}}{\underbrace{{\phi }_{\text{C}}\text{CC}(t)}}-\underset{\text{decolonization}}{\underbrace{{\alpha }_{\text{C}}\text{CC}(t)}}-\underset{\text{death}}{\underbrace{{\gamma }_{\text{C}}\text{CC}(t)}}\end{array}$$ (2)

$$\begin{array}{l}\frac{\text{dCH}}{\text{d}t}=\underset{\text{admission}}{\underbrace{\mathrm{\Lambda }{\lambda }_{\text{CH}}}}+\underset{\text{HA}-\text{MRSA}\text{colonization}}{\underbrace{\frac{(1-\eta ){\beta }_{\text{CH}}}{N}S(t)\text{CH}(t)+\frac{(1-\eta ){\beta }_{\text{IH}}}{N}S(t)\text{IH}(t)}}\\ +\underset{\text{treatment}}{\underbrace{{\tau }_{\text{H}}\text{IH}(t)}}-\underset{\text{infection}}{\underbrace{{\phi }_{\text{H}}\text{CH}(t)}}-\underset{\text{decolonization}}{\underbrace{{\alpha }_{\text{H}}\text{CH}(t)}}-\underset{\text{death}}{\underbrace{{\gamma }_{\text{H}}\text{CH}(t)}}\end{array}$$ (3)

$$\frac{\text{dIC}}{\text{d}t}=\underset{\text{admission}}{\underbrace{\mathrm{\Lambda }{\lambda }_{\text{IC}}}}+\underset{\text{infection}}{\underbrace{{\phi }_{\text{C}}\text{CC}(t)}}-\underset{\text{treatment}}{\underbrace{{\tau }_{\text{C}}\text{IC}(t)}}-\underset{\text{death}}{\underbrace{{\delta }_{\text{C}}\text{IC}(t)}}$$ (4)

$$\frac{\text{dIH}}{\text{d}t}=\underset{\text{admission}}{\underbrace{\mathrm{\Lambda }{\lambda }_{\text{IH}}}}+\underset{\text{infection}}{\underbrace{{\phi }_{\text{H}}\text{CH}(t)}}-\underset{\text{treatment}}{\underbrace{{\tau }_{\text{H}}\text{IH}(t)}}-\underset{\text{death}}{\underbrace{{\delta }_{\text{H}}\text{IH}(t)}}$$ (5)

with initial conditions S(0) = S₀, CC(0) = CC₀, CH(0) = CH₀, IC(0) = IC₀ and IH(0) = IH₀ specified at time 0.

3. Steady-state analysis

In this section, we analyse the steady states of the model. We consider two cases. (i) No colonized or infected patients enter the hospital, that is, λ_CC = λ_CH = λ_IC = λ_IH = 0. In the absence of such admissions, there is a competitive exclusion effect as the two strains compete in the hospital. The strain that dominates has the higher basic reproduction number, which must also be higher than 1. (ii) There are patients colonized with CA-MRSA strain admitted to the hospitals, that is, λ_CC ≠ 0, λ_CH = λ_IC = λ_IH = 0. If colonized or infected patients with CA-MRSA strain are admitted each day, then both strains are more likely to co-exist in the hospital.

The CA-MRSA strain in the absence of the hospital strain has a basic reproduction number defined by

$$R_0^{\text{C}}=\frac{(1-\eta )\mathrm{\Lambda }({\beta }_{\text{CC}}({\tau }_{\text{C}}+{\delta }_{\text{C}})+{\beta }_{\text{IC}}{\phi }_{\text{C}})}{N{\gamma }_{\text{S}}[({\alpha }_{\text{C}}+{\gamma }_{\text{C}})({\tau }_{\text{C}}+{\delta }_{\text{C}})+{\delta }_{\text{C}}{\phi }_{\text{C}}]}$$ (6)

and the HA-MRSA strain in the absence of the community strain has a basic reproduction number defined by

$$R_0^{\text{H}}=\frac{(1-\eta )\mathrm{\Lambda }({\beta }_{\text{CH}}({\tau }_{\text{H}}+{\delta }_{\text{H}})+{\beta }_{\text{IH}}{\phi }_{\text{H}})}{N{\gamma }_{\text{S}}[({\alpha }_{\text{H}}+{\gamma }_{\text{H}})({\tau }_{\text{H}}+{\delta }_{\text{H}})+{\delta }_{\text{H}}{\phi }_{\text{H}}]}.$$ (7)

3.1. No admission of MRSA colonized or infected patients

When λ_CC = λ_CH = λ_IC = λ_IH = 0, the model can have three types of steady states based on $R_0^{\text{C}}$ and $R_0^{\text{H}}$.

3.1.1. $\text{Max}\{R_0^{\text{C}},R_0^{\text{H}}\}<1$: disease-free steady state

When $\text{max}\{R_0^{\text{C}},R_0^{\text{H}}\}<1$, the disease-free steady state

$$E_0=\left(\frac{\mathrm{\Lambda }}{{\gamma }_{\text{S}}},0,0,0,0\right)$$ (8)

exists. In fact, we have the following results.

Theorem 3.1

If S₀, CC₀, CH₀, IC₀, IH₀ ≥ 0, then the solutions are non-negative and remain bounded in the positive cone of R⁵. If $R_0^{\text{C}}<1$ and $R_0^{\text{H}}<1$, then the disease-free steady state E₀ is locally asymptotically stable. If either $R_0^{\text{C}}>1$ or $R_0^{\text{H}}>1$, then E₀ is unstable.

Proof

It is easy to see that the solutions remain in the positive cone if the initial conditions are in the positive cone. Let T (t) = S(t) + CC(t) + CH(t) + IC(t) + IH(t). Then

$$\begin{array}{l}\frac{\text{d}T(t)}{\text{d}t}=\mathrm{\Lambda }-{\gamma }_{\text{S}}S(t)-{\gamma }_{\text{C}}\text{CC}(t)-{\gamma }_{\text{H}}\text{CH}(t)-{\delta }_{\text{C}}\text{IC}(t)-{\delta }_{\text{H}}\text{IH}(t)\\ \le \mathrm{\Lambda }-min\{{\gamma }_{\text{S}},{\gamma }_{\text{C}},{\gamma }_{\text{H}},{\delta }_{\text{C}},{\delta }_{\text{H}}\}T(t).\end{array}$$

Thus, the solutions remain bounded in the positive cone of R⁵ and the system induces a global semiflow in the positive cone of R⁵.

To determine the stability of the disease-free steady state E₀, we use the results in van den Driessche and Watmough [4]. Re-order the components of E₀ as CC = 0, IC = 0, CH = 0, IH =0, S = Λ/γ_S. Set

$$\mathcal{F}=\left[\begin{array}{c}{F}_1\\ F_2\\ F_3\\ F_4\\ F_5\end{array}\right]=\left[\begin{array}{c}\frac{(1-\eta ){\beta }_{\text{CC}}S(t)\text{CC}(t)}{N}+\frac{(1-\eta ){\beta }_{\text{IC}}S(t)\text{IC}(t)}{N}\\ 0\\ \frac{(1-\eta ){\beta }_{\text{CH}}S(t)\text{CH}(t)}{N}+\frac{(1-\eta ){\beta }_{\text{IH}}S(t)\text{IH}(t)}{N}\\ 0\\ 0\end{array}\right]$$

and

$$\mathcal{V}=\left[\begin{array}{c}{V}_1\\ V_2\\ V_3\\ V_4\\ V_5\end{array}\right]=\left[\begin{array}{c}({\phi }_{\text{C}}+{\alpha }_{\text{C}}+{\gamma }_{\text{C}})\text{CC}(t)-{\tau }_{\text{C}}\text{IC}(t)\\ ({\tau }_{\text{C}}+{\delta }_{\text{C}})\text{IC}(t)-{\phi }_{\text{C}}\text{CC}(t)\\ ({\phi }_{\text{H}}+{\alpha }_{\text{H}}+{\gamma }_{\text{H}})\text{CH}(t)-{\tau }_{\text{H}}\text{IH}(t)\\ ({\tau }_{\text{H}}+{\delta }_{\text{H}})\text{IH}(t)-{\phi }_{\text{H}}\text{CH}(t)\\ V_5\end{array}\right],$$

where

$$\begin{array}{l}{V}_5=\frac{(1-\eta )}{N}S(t)[{\beta }_{\text{CC}}\text{CC}(t)+{\beta }_{\text{CH}}\text{CH}(t)+{\beta }_{\text{IC}}\text{IC}(t)+{\beta }_{\text{IH}}\text{IH}(t)]\\ +{\gamma }_{\text{S}}S(t)-{\alpha }_{\text{C}}\text{CC}(t)-{\alpha }_{\text{H}}\text{CH}(t).\end{array}$$

Then

$$\begin{array}{l}F={\left[\begin{array}{llll}\frac{\partial F_1}{\partial \text{CC}}\hfill & \frac{\partial F_1}{\partial \text{IC}}\hfill & \frac{\partial F_1}{\partial \text{CH}}\hfill & \frac{\partial F_1}{\partial \text{IH}}\hfill \\ \frac{\partial F_2}{\partial \text{CC}}\hfill & \frac{\partial F_2}{\partial \text{IC}}\hfill & \frac{\partial F_2}{\partial \text{CH}}\hfill & \frac{\partial F_2}{\partial \text{IH}}\hfill \\ \frac{\partial F_3}{\partial \text{CC}}\hfill & \frac{\partial F_3}{\partial \text{IC}}\hfill & \frac{\partial F_3}{\partial \text{CH}}\hfill & \frac{\partial F_3}{\partial \text{IH}}\hfill \\ \frac{\partial F_4}{\partial \text{CC}}\hfill & \frac{\partial F_4}{\partial \text{IC}}\hfill & \frac{\partial F_4}{\partial \text{CH}}\hfill & \frac{\partial F_4}{\partial \text{IH}}\hfill \end{array}\right]}_{E_0}\\ =\left[\begin{array}{cccc}\frac{(1-\eta ){\beta }_{\text{CC}}\mathrm{\Lambda }}{N{\gamma }_{\text{S}}}& \frac{(1-\eta ){\beta }_{\text{IC}}\mathrm{\Lambda }}{N{\gamma }_{\text{S}}}& 0& 0\\ 0& 0& 0& 0\\ 0& 0& \frac{(1-\eta ){\beta }_{\text{CH}}\mathrm{\Lambda }}{N{\gamma }_{\text{S}}}& \frac{(1-\eta ){\beta }_{\text{IH}}\mathrm{\Lambda }}{N{\gamma }_{\text{S}}}\\ 0& 0& 0& 0\end{array}\right].\end{array}$$

Similarly,

$$V=\left[\begin{array}{cccc}{\phi }_{\text{C}}+{\alpha }_{\text{C}}+{\gamma }_{\text{C}}& -{\tau }_{\text{C}}& 0& 0\\ -{\phi }_{\text{C}}& {\tau }_{\text{C}}+{\delta }_{\text{C}}& 0& 0\\ 0& 0& {\phi }_{\text{H}}+{\alpha }_{\text{H}}+{\gamma }_{\text{H}}& -{\tau }_{\text{H}}\\ 0& 0& -{\phi }_{\text{H}}& {\tau }_{\text{H}}+{\delta }_{\text{H}}\end{array}\right].$$

Therefore,

$$F{V}^{-1}=\left[\begin{array}{cccc}{R}_0^{\text{C}}& \frac{(1-\eta )\mathrm{\Lambda }[{\beta }_{\text{CC}}{\tau }_{\text{C}}+{\beta }_{\text{IC}}({\phi }_{\text{C}}+{\alpha }_{\text{C}}+{\gamma }_{\text{C}})]}{N{\gamma }_{\text{S}}[({\alpha }_{\text{C}}+{\gamma }_{\text{C}})({\tau }_{\text{C}}+{\delta }_{\text{C}})+{\delta }_{\text{C}}{\phi }_{\text{C}}]}& 0& 0\\ 0& 0& 0& 0\\ 0& 0& R_0^{\text{H}}& \frac{(1-\eta )\mathrm{\Lambda }[{\beta }_{\text{CH}}{\tau }_{\text{H}}+{\beta }_{\text{IH}}({\phi }_{\text{H}}+{\alpha }_{\text{H}}+{\gamma }_{\text{H}})]}{N{\gamma }_{\text{S}}[({\alpha }_{\text{H}}+{\gamma }_{\text{H}})({\tau }_{\text{H}}+{\delta }_{\text{H}})+{\delta }_{\text{H}}{\phi }_{\text{H}}]}\\ 0& 0& 0& 0\end{array}\right],$$

which implies that the spectral radius of the matrix F V ⁻¹ is

$$\rho (F{V}^{-1})=max\{R_0^{\text{C}},R_0^{\text{H}}\}.$$

If $R_0^{\text{H}}<1$ and $R_0^{\text{C}}<1$, then ρ(F V ⁻¹) < 1. By Theorem 2 in van den Driessche and Watmough [4], we know that the disease-free steady state E₀ is locally asymptotically stable. E₀ is unstable if $R_0^{\text{H}}>1$ or $R_0^{\text{C}}>1$.

Remark 1

The case when $R_0^{\text{H}}<1$ and $R_0^{\text{C}}<1$ corresponds to the situation that there are no MRSA strains prevailing in the hospital. By using the comparison method, one can show that the disease-free steady state E₀ is indeed globally stable.

3.1.2. $R_0^{\text{C}}<1<R_0^{\text{H}}$: steady state with only the HA-MRSA strain

When $R_0^{\text{C}}<1<R_0^{\text{H}}$, there is a disease steady state with only the hospital MRSA strain

$$E_{\text{H}}=(S_{\text{H}},0,C_{\text{H}},0,I_{\text{H}}),$$ (9)

where

$$S_{\text{H}}=\frac{\mathrm{\Lambda }}{{\gamma }_{\text{S}}{R}_0^{\text{H}}},C_{\text{H}}=\frac{(R_0^{\text{H}}-1)\mathrm{\Lambda }({\tau }_{\text{H}}+{\delta }_{\text{H}})}{R_0^{\text{H}}[{\gamma }_{\text{H}}({\tau }_{\text{H}}+{\delta }_{\text{H}})+{\delta }_{\text{H}}{\phi }_{\text{H}}]},I_{\text{H}}=\frac{{\phi }_{\text{H}}{C}_{\text{H}}}{{\tau }_{\text{H}}+{\delta }_{\text{H}}}.$$

Theorem 3.2

If $R_0^{\text{C}}<1<R_0^{\text{H}}$, then the HA-MRSA strain endemic steady state E_H exists and is locally asymptotically stable.

Proof

Re-order the steady-state E_H as (0, 0, C_H, I_H, S_H). Similarly as in the proof of Theorem 3.1, we have

$$F=\left[\begin{array}{cc}\frac{(1-\eta ){\beta }_{\text{CC}}{S}_{\text{H}}}{N}& \frac{(1-\eta ){\beta }_{\text{IH}}{S}_{\text{H}}}{N}\\ 0& 0\end{array}\right],V=\left[\begin{array}{cc}{\phi }_{\text{C}}+{\alpha }_{\text{C}}+{\gamma }_{\text{C}}& -{\tau }_{\text{C}}\\ -{\phi }_{\text{C}}& {\tau }_{\text{C}}+{\delta }_{\text{C}}\end{array}\right]$$

and

$$\begin{array}{l}F{V}^{-1}=\frac{(1-\eta )\mathrm{\Lambda }}{N{\gamma }_{\text{S}}{R}_0^{\text{H}}[({\alpha }_{\text{C}}+{\gamma }_{\text{C}})({\tau }_{\text{C}}+{\delta }_{\text{C}})+{\delta }_{\text{C}}{\phi }_{\text{C}}]}\\ \times \left[\begin{array}{cc}{\beta }_{\text{CC}}({\tau }_{\text{C}}+{\delta }_{\text{C}})+{\beta }_{\text{IC}}{\phi }_{\text{C}}& {\beta }_{\text{CC}}{\tau }_{\text{C}}+{\beta }_{\text{IC}}({\phi }_{\text{C}}+{\alpha }_{\text{C}}+{\gamma }_{\text{C}})\\ 0& 0\end{array}\right].\end{array}$$

Thus, the spectral radius of F V ⁻¹ is given by

$$\rho (F{V}^{-1})=\frac{R_0^{\text{C}}}{R_0^{\text{H}}}.$$

Since $R_0^{\text{C}}<1<R_0^{\text{H}}$, we have ρ(FV⁻¹) < 1, which implies that E_H is locally asymptotically stable by Theorem 2 in van den Driessche and Watmough [4].

Remark 2

The case when $R_0^{\text{C}}<1<R_0^{\text{H}}$ corresponds to the situation that only the hospital MRSA strain is prevailing in the hospital.

3.1.3. $1<R_0^{\text{C}}<R_0^{\text{H}}$:HA-MRSA strain wins

When $1<R_0^{\text{C}}<R_0^{\text{H}}$, the community MRSA strain disease steady state

$$E_{\text{C}}=(S_{\text{C}},C_{\text{C}},0,I_{\text{C}},0)$$ (10)

exists, where

$$S_{\text{C}}=\frac{\mathrm{\Lambda }}{{\gamma }_{\text{S}}{R}_0^{\text{C}}},C_{\text{C}}=\frac{(R_0^{\text{C}}-1)\mathrm{\Lambda }({\tau }_{\text{C}}+{\delta }_{\text{C}})}{R_0^{\text{C}}[{\gamma }_{\text{C}}({\tau }_{\text{C}}+{\delta }_{\text{C}})+{\delta }_{\text{C}}{\phi }_{\text{C}}]},I_{\text{C}}=\frac{{\phi }_{\text{C}}{C}_{\text{C}}}{{\tau }_{\text{C}}+{\delta }_{\text{C}}}.$$

Notice that the hospital MRSA strain disease steady state E_H still exists in this case. However, the stability of E_H and E_C depends on the relationship between $R_0^{\text{C}}$ and $R_0^{\text{H}}$. We first have the following result regarding the stability of E_H and E_C.

Theorem 3.3

If $1<R_0^{\text{C}}<R_0^{\text{H}}$, then both the HA-MRSA strain steady state E_H and the CA-MRSA strain steady state E_C exist. Moreover, E_H is locally asymptotically stable and E_C is unstable.

Proof

The proof is similar to that of Theorem 3.4, so here we omit it.

Remark 3

In the case when $1<R_0^{\text{C}}<R_0^{\text{H}}$, even the community MRSA strain is introduced into the hospital, it is not strong enough to spread, the hospital MRSA strain is dominant and is prevailing in the hospital.

3.1.4. $1<R_0^{\text{C}}=R_0^{\text{H}}$: Co-existent steady state with both strains

When $1<R_0^{\text{C}}=R_0^{\text{H}}$, there is a co-existent steady state

$$E^{\ast }=(S^{\ast },{\text{CC}}^{\ast },{\text{CH}}^{\ast },{\text{IC}}^{\ast },{\text{IH}}^{\ast })$$ (11)

with both CA-MRSA and HA-MRSA strains, where

$$S^{\ast }=\frac{\mathrm{\Lambda }}{{\gamma }_{\text{S}}{R}_0^{\text{C}}},{\text{IC}}^{\ast }=\frac{{\phi }_{\text{C}}}{{\tau }_{\text{C}}+{\delta }_{\text{C}}}{\text{CC}}^{\ast },{\text{IH}}^{\ast }=\frac{{\phi }_{\text{H}}}{{\tau }_{\text{H}}+{\delta }_{\text{H}}}{\text{CH}}^{\ast },$$

and CC^* and CH^* satisfy the relationship

$$\frac{({\tau }_{\text{C}}+{\delta }_{\text{C}}){\gamma }_{\text{C}}+{\delta }_{\text{C}}{\phi }_{\text{C}}}{{\tau }_{\text{C}}+{\delta }_{\text{C}}}{\text{CC}}^{\ast }+\frac{({\tau }_{\text{H}}+{\delta }_{\text{H}}){\gamma }_{\text{H}}+{\delta }_{\text{H}}{\phi }_{\text{H}}}{{\tau }_{\text{H}}+{\delta }_{\text{H}}}{\text{CH}}^{\ast }=\mathrm{\Lambda }-{\gamma }_{\text{S}}{S}^{\ast }.$$

Remark 4

In the very special case when $1<R_0^{\text{C}}=R_0^{\text{H}}$, both the community and hospital MRSA strains co-exist and prevail in the hospital.

3.1.5. $1<R_0^{\text{H}}<R_0^{\text{C}}$: CA-MRSA strain wins

Finally, if $1<R_0^{\text{H}}<R_0^{\text{C}}$, then we have the following result regarding the stability of E_H and E_C.

Theorem 3.4

If $R_0^{\text{C}}>R_0^{\text{H}}>1$, then both the HA-MRSA strain steady state E_H and the CA-MRSA strain steady state E_C exist. Moreover, E_H is unstable and E_C is locally asymptotically stable.

Proof

For the CA-MRSA strain steady state E_C, following the proof of Theorem 3.2, we have $\rho (F{V}^{-1})=R_0^{\text{H}}/R_0^{\text{C}}<1$ since $R_0^{\text{C}}>R_0^{\text{H}}$. Thus, E_C is locally asymptotically stable.

The Jacobian matrix at the HA-MRSA strain steady state E_H is

$$\begin{array}{l}[\begin{array}{ccc}-K_{\text{H}}-{\gamma }_{\text{S}}& -\frac{(1-\eta ){\beta }_{\text{CC}}\mathrm{\Lambda }}{N{\gamma }_{\text{S}}{R}_0^{\text{H}}}+{\alpha }_{\text{C}}& -\frac{(1-\eta ){\beta }_{\text{CH}}\mathrm{\Lambda }}{N{\gamma }_{\text{S}}{R}_0^{\text{H}}}+{\alpha }_{\text{H}}\\ -K_{\text{H}}& \frac{(1-\eta ){\beta }_{\text{CC}}\mathrm{\Lambda }}{N{\gamma }_{\text{S}}{R}_0^{\text{H}}}-({\phi }_{\text{C}}+{\alpha }_{\text{C}}+{\gamma }_{\text{C}})& 0\\ 0& 0& \frac{(1-\eta ){\beta }_{\text{CH}}\mathrm{\Lambda }}{N{\gamma }_{\text{S}}{R}_0^{\text{H}}}-({\phi }_{\text{H}}+{\alpha }_{\text{H}}+{\gamma }_{\text{H}})\\ 0& {\phi }_{\text{C}}& 0\\ 0& 0& {\phi }_{\text{H}}\end{array}\\ \begin{array}{cc}-\frac{(1-\eta ){\beta }_{\text{IC}}\mathrm{\Lambda }}{N{\gamma }_{\text{S}}{R}_0^{\text{H}}}& -\frac{(1-\eta ){\beta }_{\text{IH}}\mathrm{\Lambda }}{N{\gamma }_{\text{S}}{R}_0^{\text{H}}}\\ \frac{(1-\eta ){\beta }_{\text{IC}}\mathrm{\Lambda }}{N{\gamma }_{\text{S}}{R}_0^{\text{H}}}+{\tau }_{\text{C}}& 0\\ 0& \frac{(1-\eta ){\beta }_{\text{IH}}\mathrm{\Lambda }}{N{\gamma }_{\text{S}}{R}_0^{\text{H}}}+{\tau }_{\text{H}}\\ -{\tau }_{\text{C}}-{\delta }_{\text{C}}& 0\\ 0& -{\tau }_{\text{H}}-{\delta }_{\text{H}}\end{array}],\end{array}$$

where

$$K_{\text{H}}=\frac{(1-\eta )(R_0^{\text{H}}-1)\mathrm{\Lambda }[{\beta }_{\text{CH}}({\tau }_{\text{H}}+{\delta }_{\text{H}})+{\beta }_{\text{IH}}{\phi }_{\text{H}}]}{N{R}_0^{\text{H}}[{\gamma }_{\text{H}}({\tau }_{\text{H}}+{\delta }_{\text{H}})+{\delta }_{\text{H}}{\phi }_{\text{H}}]}.$$

The Jacobian matrix has one eigenvalue $a+\sqrt{a^2+4b}$, where

$$\begin{array}{l}a=\frac{(1-\eta ){\beta }_{\text{CC}}\mathrm{\Lambda }}{N{\gamma }_{\text{S}}{R}_0^{\text{C}}}-({\phi }_{\text{C}}+{\alpha }_{\text{C}}+{\gamma }_{\text{C}}+{\tau }_{\text{C}}+{\delta }_{\text{C}}),\\ b=\frac{R_0^{\text{C}}-R_0^{\text{H}}}{R_0^{\text{H}}}[({\alpha }_{\text{C}}+{\gamma }_{\text{C}})({\tau }_{\text{C}}+{\delta }_{\text{C}})+{\delta }_{\text{C}}{\phi }_{\text{C}}].\end{array}$$

Since b > 0, $a+\sqrt{a^2+4b}>a+\mid a\mid \ge 0$ and this eigenvalue must be positive. Thus, E_H is unstable.

Remark 5

When $R_0^{\text{C}}$ increases to greater than 1 and $R_0^{\text{H}}$ the CA-MRSA strain invades the hospital and eventually overtakes the HA-MRSA strain.

3.1.6. Steady states chart and transcritical bifurcation

The above results on the existence and stability of equilibria are summarized in Table 2.

Table 2.

Steady states chart for the Model when λ_CC = λ_CH = λ_IC = λ_IH = 0.

BRN	E0	EH	EC	E*
$max\{R_0^{\text{H}},R_0^{\text{C}}\}<1$	Stable	Does not exist	Does not exist	Does not exist
$R_0^{\text{C}}<1<R_0^{\text{H}}$	Unstable	Stable	Does not exist	Does not exist
$1<R_0^{\text{C}}<R_0^{\text{H}}$	Unstable	Stable	Unstable	Does not exist
$1<R_0^{\text{C}}=R_0^{\text{H}}$	Unstable	Exists	Exists	Exists
$1<R_0^{\text{H}}<R_0^{\text{C}}$	Unstable	Unstable	Stable	Does not exist

BRN, basic reproduction number.

From Table 2, we can observe the following scenarios. At the beginning when $max\{R_0^{\text{H}},R_0^{\text{C}}\}<1$, there is no MRSA strains prevailing in the hospital. When $R_0^{\text{C}}<1<R_0^{\text{H}}$, the HA-MRSA strain spreads out in the hospital. Now the CA-HRSA strain is introduced into the hospital. When $R_0^{\text{C}}$ increases to be greater than 1 but less than $R_0^{\text{H}}$, that is, when $1<R_0^{\text{C}}<R_0^{\text{H}}$, the CA-MRSA strain does not establish in the hospital and HA-MRSA is still dominant there. In the critical case when $1<R_0^{\text{C}}=R_0^{\text{H}}$, the CA-MRSA strain and HA-MRSA strain co-exist in the hospital. Finally, when $R_0^{\text{C}}$ increases to pass $R_0^{\text{H}}$ so that $1<R_0^{\text{H}}<R_0^{\text{C}}$, the CA-MRSA strain takes over the HA-MRSA strain and dominates the hospital.

From a dynamical system point of view, we can also see that the HA-MRSA strain steady state E_H changes from stability to instability and the CA-MRSA strain steady-state E_C changes from instability to stability when $R_0^{\text{C}}$ passes through $R_0^{\text{H}}$. Therefore, there is a trans-critical bifurcation when $1<R_0^{\text{C}}=R_0^{\text{H}}$.

3.2. With admission of CA-MRSA colonized patients

As the HA-MRSA strain is prevailing in many hospitals, the main concern now is if the CA-MRSA strain will invade the hospital and take over the HA-MRSA strain. In the previous section, we considered the equilibrium points of the model when there is no admission of MRSA colonized or infected patients into the hospital and discussed different possible outcomes. It will be interesting to discuss the model when there is admission of CA-MRSA colonized or/and infected patients into the hospital. For the sake of simplicity, in this section, we analyse the steady states of the model with admission of CA-MRSA colonized patients only. The case when there is admission of CA-MRSA infected patients or of both CA-MRSA colonized and infected patients can also be discussed.

When λ_CC > 0 and λ_CH = λ_IC = λ_IH = 0, there is a co-existent steady state

$$\overline{E}=(\overline{S},\overline{\text{CC}},\overline{\text{CH}},\overline{\text{IC}},\overline{\text{IH}}),$$ (12)

where

$$\overline{S}=\frac{\mathrm{\Lambda }}{{\gamma }_{\text{S}}{R}_0^{\text{C}}},\overline{\text{IC}}=\frac{{\phi }_{\text{C}}}{{\tau }_{\text{C}}+{\delta }_{\text{C}}}\overline{\text{CC}},\overline{\text{IH}}=\frac{{\phi }_{\text{H}}}{{\tau }_{\text{H}}+{\delta }_{\text{H}}}\overline{\text{CH}},$$

and $\overline{\text{CC}}$ and $\overline{\text{CH}}$ are given by

$$\begin{array}{l}\overline{\text{CC}}=\frac{\mathrm{\Lambda }{\lambda }_{\text{CC}}}{({\phi }_{\text{C}}+{\alpha }_{\text{C}}+{\gamma }_{\text{C}})-[(1-\eta )\overline{S}/N({\beta }_{\text{CC}}+{\beta }_{\text{IC}}{\phi }_{\text{C}}/({\tau }_{\text{C}}+{\delta }_{\text{C}}))+{\tau }_{\text{C}}{\phi }_{\text{C}}/({\tau }_{\text{C}}+{\delta }_{\text{C}})]},\\ \overline{\text{CH}}=\frac{{\tau }_{\text{H}}+{\delta }_{\text{H}}}{({\tau }_{\text{H}}+{\delta }_{\text{H}}){\gamma }_{\text{H}}+{\delta }_{\text{H}}{\phi }_{\text{H}}}\left[\mathrm{\Lambda }(1+{\lambda }_{\text{CC}})-{\gamma }_{\text{S}}\overline{S}-\frac{({\tau }_{\text{C}}+{\delta }_{\text{C}}){\gamma }_{\text{C}}+{\delta }_{\text{C}}{\phi }_{\text{C}}}{{\tau }_{\text{C}}+{\delta }_{\text{C}}}\overline{\text{CC}}\right].\end{array}$$

We still need to make sure that $\overline{\text{CC}}>0$ and $\overline{\text{CH}}>0$. Lengthy and tedious calculations show that $\overline{\text{CC}}>0$ if

$$R_0^{\text{H}}>R_0^{\text{C}}.$$ (13)

To have $\overline{\text{CH}}>0$, we assume that

$$\mathrm{\Lambda }(1+{\lambda }_{\text{CC}})>{\gamma }_{\text{S}}\overline{S}+\frac{({\tau }_{\text{C}}+{\delta }_{\text{C}}){\gamma }_{\text{C}}+{\delta }_{\text{C}}{\phi }_{\text{C}}}{{\tau }_{\text{C}}+{\delta }_{\text{C}}}\overline{\text{CC}}.$$ (14)

Remark 6

The existence of a positive steady state $\overline{E}=(\overline{S},\overline{\text{CC}},\overline{\text{CH}},\overline{\text{IC}},\overline{\text{IH}})$ indicates that both the CA- and HA-MRSA strains can co-exist in the hospital if there is admission of CA-MRSA colonized patients into the hospital. However, to have such a positive equilibrium, condition (14) implies that the admission rate λ_CC of CA-MRSA colonized patients into the hospital must be greater than a threshold value, while condition (13) demonstrates that the basic reproduction number for the HA-MRSA strain must be greater than that for the CA-MRSA strain. This is reasonable and agrees with the observation in the previous section: since there are new cases of CA-MRSA colonized patients admitted into the hospital everyday, the HA-MRSA strain has to be stronger (i.e. $R_0^{\text{H}}>R_0^{\text{C}}$) in order to co-exist with the CA-MRSA strain in the hospital. Otherwise, it will be overtaken by the CA-MRSA strain.

4. Numerical simulations and discussion

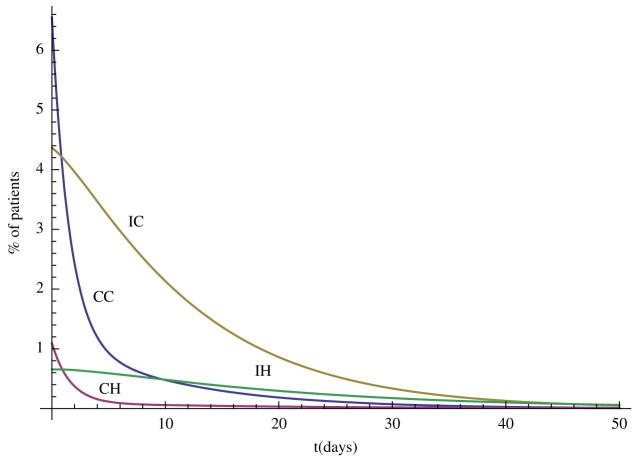
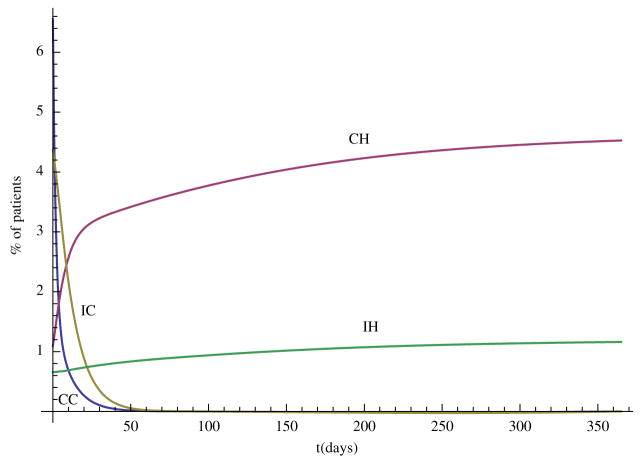
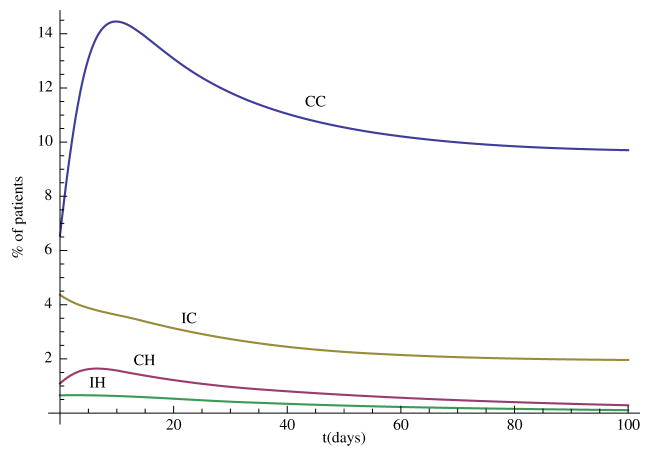
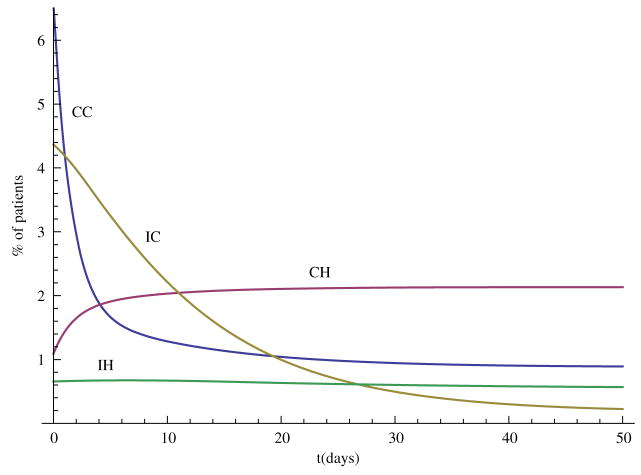
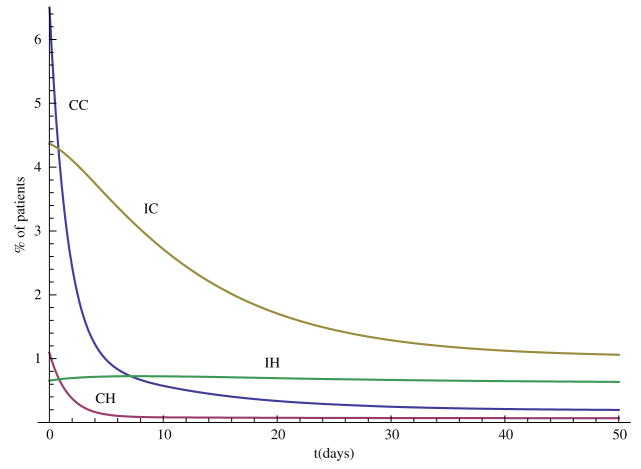
In this section, we carry out some numerical simulations to illustrate the results obtained in the previous section. Choose parameter as follows: Λ = 70, N = 400, η = 0.6, β_CC = 0.36, β_CH = 0.27, β_IC = 0.09, β_IH = 0.07, α_C = 0.6, α_H = 0.6, γ_S = 0.2, γ_C = 0.2, γ_H = 0.1429, τ_C = 0.0967, τ_H = 0.0444, φ_C = 0.02, φ_H = 0.0143, δ_C = 0.0033, δ_H = 0.0111. We can see that $R_0^{\text{H}}=0.1652<1$ and $R_0^{\text{C}}=0.1352<1$, so the disease-free steady state E₀ = (0.88, 0, 0, 0, 0) is stable (Figure 1). Now change some parameter values as follows: β_CH = 0.71, β_IH = 0.17, η = 0.3, α_H = 0.3, then $R_0^{\text{H}}=1.035>1>R_0^{\text{C}}=0.2891$ and the hospital MRSA strain steady-state E_H is stable (Figure 2). Finally, choose β_CC = 0.87 and β_IC = 0.19, we have $R_0^{\text{C}}=1.111>R_0^{\text{H}}=1.029>1$, and the community MRSA strain drives out the hospital MRSA strain (Figure 3).

Figure 1.

When $R_0^{\text{H}}<1$ and $R_0^{\text{C}}<1$, the disease-free steady state E₀ is stable.

Figure 2.

When $R_0^{\text{H}}>1>R_0^{\text{C}}$, the hospital MRSA strain steady state E_H is stable.

Figure 3.

When $R_0^{\text{C}}>R_0^{\text{H}}>1$, the community MRSA strain takes over.

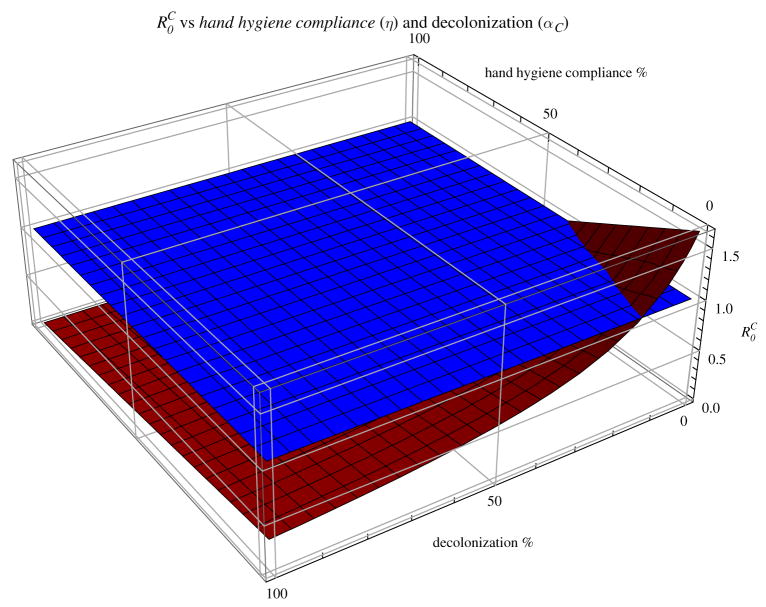
Hand hygiene and decolonization are both efficient interventions. Figure 4 shows that, when there is no entry of new cases, combining hand hygiene and decolonization can reduce the basic reproduction number for CA-MRSA to less than 1.

Figure 4.

Basic reproduction number $R_0^{\text{C}}$ for the community MRSA strain with baseline parameter values as in Table 1, except that the hand hygiene % and decolonization % vary from 0 to 100.

The above simulations were carried out with the assumption that no colonized or infected cases enter the hospital, that is, λ_CC = λ_CH = λ_IC = λ_IH = 0. If there are colonized or infected cases entering the hospital, then the outcomes are completely different. For example, if λ_CC = 0.03, λ_CH = 0.07, that is, some patients admitted to the hospital are colonized with HA-MRSA and CA-MRSA strain, respectively, then both strains will co-exist in the hospital (Figure 5). Similarly, if λ_IC = 0.005, λ_IH = 0.0017, that is, some patients admitted to the hospital are infected with HA-MRSA and CA-MRSA strain, respectively, then once again both strains will co-exist in the hospital (Figure 5).

Figure 5.

When λ_CC = 0.03, λ_CH = 0.07 and λ_IC = λ_IH = 0, both HA-MRSA and CA-MRSA strains establish in the hospital.

Entry of new cases into the hospital is crucial for the spread and control of both HA-MRSA and CA-MRSA strains. The simulations in Figures 5 and 6 strongly support the suggestion of screening for MRSA at hospital admission for colonized and infected cases [7,8]. However, screening requires action and compliance with infection control precautions. If HCWs do not comply with hand hygiene and other contact precautions when a patient is identified with MRSA through screening, then this intervention would not prevent the spread of MRSA. It also indicates that, when λ_CC, λ_CH, λ_IC and λ_IH are not all zero, the modal can have positive steady states with the endemicity of both HA-MRSA and CA-MRSA strains.

Figure 6.

When λ_CC = λ_CH = 0, λ_IC = 0.005 and λ_IH = 0.0017, there is a stable positive endemic steady state with both HA-MRSA and CA-MRSA strains in the hospital.