Extraction of Configurational Entropy from Molecular Simulations via an Expansion Approximation

Abstract

A method is presented for extracting the configurational entropy of solute molecules from molecular dynamics simulations, in which the entropy is computed as an expansion of multi-dimensional mutual information terms, which account for correlated motions amongst the various internal degrees of freedom of the molecule. The mutual information expansion is demonstrated to be equivalent to estimating the full-dimensional configurational probability density function (pdf) using the Generalized Kirkwood Superposition Approximation (GKSA). While the mutual information expansion is derived to the full dimensionality of the molecule, the current application uses a truncated form of the expansion in which all fourth- and higher-order mutual information terms are neglected. Truncation of the mutual information expansion at the nth-order is shown to be equivalent to approximating the full-dimensional pdf using joint pdfs with dimensionality of n or smaller by successive application of the GKSA. The expansion method is used to compute the absolute (classical) configurational entropy in a basis of bond-angle-torsion internal coordinates for several small molecules as well as the change in entropy upon binding for a small host-guest system. Convergence properties of the computed entropy values as a function of simulation time are investigated and comparisons are made with entropy values from the second generation Mining Minima software. These comparisons demonstrate a deviation in -TS of no more than about 2 kcal/mol for all cases in which convergence has been obtained.

I. INTRODUCTION

The total entropy of a molecule in solution can be separated into two parts, a solvent entropy associated with solvent motions, and a solute, or configurational, entropy associated with solute motions¹. Changes in the latter are thought to make substantial contributions to important biochemical processes like protein folding and molecular association. As a consequence, methods of quantifying the configurational entropy could help explain how biomolecules function, and methods of controlling it could be valuable for molecular design.

In recent years, it has become possible to estimate changes in configurational entropy from NMR data^2-7. This approach has yielded remarkable insights; for example, binding in at least two systems appears to be associated with reduced local entropy in the binding site of a protein, balanced by increased local entropy far from the binding site^8,9. However, NMR methods of assessing entropy currently rely upon assumptions regarding the orientational distributions underlying observed order parameters, and are not yet able to account for motional correlations. It is thus of interest to seek further insight by other means.

Computer modeling can be used to study the configurational entropy of a solute molecule, and have the potential to provide a more detailed look at the nature and biological roles of configurational entropy. For example, the Mining Minima (M2) method has provided evidence that configurational entropy is an important determinant of affnities for host-guest and protein-ligand binding¹⁰. However, M2 is not immediately applicable to a molecule as complex as a protein. Also, Mining Minima might be expected to underestimate entropy because it focuses on local energy wells, rather than explicitly including higher energy conformations as in the case of Monte Carlo or molecular dynamics simulations. Another approach, the hypothetical scanning method, can be used to determine the entropy associated with a specified microstate of a molecular system^11,12, and has been used to compare the entropy of a helical and a hairpin conformation of a peptide. However, both hypothetical scanning and M2 require specialized software, and a method of extracting configurational entropy from conventional molecular dynamics (MD) or Monte Carlo simulations would be of considerable interest.

The quasiharmonic approximation¹³ is perhaps the best known method of extracting the configurational entropy from a molecular simulation. It involves diagonalizing the covariance matrix of the atomic coordinates and approximating their probability distribution function (pdf) as a multidimensional Gaussian distribution with variances equal to its eigenvalues. The configuration integral of this pdf can then be obtained analytically. Perhaps the chief drawback of the quasiharmonic approximation is that it can substantially overestimate the entropy for systems with multimodal pdfs; i.e., with multiple occupied energy minima.^14,15. Also, when applied to a trajectory in Cartesian coordinates, it requires that the snapshots be rotationally and translationally superimposed so that a reasonable covariance matrix may be calculated, and different results can be obtained depending upon how the superposition is done.

Other simulation-based approaches also deserve mention. For example, histogramming methods can be used to compute entropies via the density of states^16,17, and have been successfully applied to the solvation of small molecules¹⁸. They have also been applied to peptides^19,20, though convergence properties in these applications have not yet been reported. An intriguing approach based upon covariance analysis of torsion angles in the complex plane has recently been presented²¹. Methods of calculating entropy differences from simulations are further addressed in a helpful recent review and analysis by Peter et al²².

The present paper describes a new approach to computing configurational entropy based on superposition approximations to the full-dimensional probability density in terms of one-dimensional, two-dimensional, three-dimensional, and higher-order pdfs. Such superposition approximations are well known in the theory of homogeneous fluids^23-29 with references too numerous to fully enumerate here, and have previously been used to establish entropy expansions for liquids^30-34. More recently entropy expansion methods have been applied to signal processing³⁵ and more general complex systems, such as frustrated spin systems³⁶. Despite the rich body of work in this area, these density-based entropy expansions have not, to our knowledge, been applied to configurational entropy of a solute molecule.

We follow in particular a formulation in which the entropy is expressed in terms of pairwise and higher-order mutual information terms³⁶, where an nth-order mutual information captures the degree to which the n-dimensional correlation influences the entropy. This mutual information expansion can be directly related back to a superposition approximation of the pdf, as demonstrated in the Theory section. The accuracy of the computed entropy should in principle increase as higher order terms in the series are included. However, the computations become more difficult because of the rapid increase in the number and the order of the multi-particle pdfs that need to be analyzed. Here, calculations at the pairwise level are found to yield remarkably good agreement with independent M2 calculations for model systems, and it is proposed that the pairwise level provides a favorable balance of accuracy and efficiency.

II. THEORY

Although the concepts employed here are not new, they have not previously been applied to the calculation of the configurational entropy of a molecule from a simulation, to our knowledge, and therefore are detailed here in connection with configurational entropy for the sake of clarity and specificity.

A. Partial molar configurational entropy

The standard chemical potential of a molecule in solution can be written as³⁷

$${\mu }^{\mathrm{o}}=-RT\ln \left(\frac{8{\pi }^2}{C^{\mathrm{o}}}Z\right)$$ (1)

where R is the gas constant, T is absolute temperature, C^o is standard concentration, and Z is the configuration integral

$$Z\equiv \int e^{-\beta E\left(\mathbf{r}\right)}d\mathbf{r}.$$ (2)

Here β = (RT)^-1 and the integration is performed over a set of Cartesian internal coordinates, r that define the molecular conformation, such as Anchored Cartesian coordinates^38,39. This expression omits a Jacobian determinant contribution that is nearly constant across thermodynamically accessible conformations (in Ref. 38, see Equation (13) and associated text). For a molecule in the gas phase, E(r) is the vacuum potential energy as a function of conformation, U(r) ⁴⁰. For a molecule in solution, the potential energy is supplemented by the solvation energy as a function of conformation: E(r) = U(r)+W(r) ³⁷. The factor of $\frac{8{\pi }^2}{C^{\mathrm{o}}}$ in effect accounts for the rotational and translational freedom of the molecule in solution^37,41 at standard concentration.

The partial molar configurational entropy S^o is given by¹

$$-T{S}^{\mathrm{o}}={\mu }^{\mathrm{o}}-\langle E\rangle ,$$ (3)

where the angle brackets are used to indicate an ensemble average. By introducing the concept of the full-dimensional pdf, ρ(r), over the configuration space of the molecule, the partial molar configurational entropy can be rewritten in the form (see Appendix A)

$$-T{S}^{\mathrm{o}}=-RT\ln \frac{8{\pi }^2}{C^{\mathrm{o}}}+RT\int \rho \left(\mathbf{r}\right)\ln \rho \left(\mathbf{r}\right)d\mathbf{r}.$$ (4)

The negative of the integral in Equation (4) is the Shannon entropy associated with the pdf ρ(r)⁴² and is closely related to the Gibbs H-function^43,44. This quantity, when multiplied by the gas constant, becomes a physical entropy associated with the distribution in the configuration space. We will denote this as $S=-R\int \rho \left(\mathbf{r}\right)\ln \rho \left(\mathbf{r}\right)d\mathbf{r}$, such that one can write

$$-T{S}^{\mathrm{o}}=-RT\ln \frac{8{\pi }^2}{C^{\mathrm{o}}}-TS.$$ (5)

The quantity - ln ρ(r) is called the information, or self-information, associated with a measurement on the distribution ρ(r)^45,46. It is of interest to note that, in a statistical thermodynamic sense, the quantity S is itself an ensemble average of the information associated with the pdf; that is S = R⟨-ln ρ(r)⟩, where the gas constant is used to set the units.

B. Bond-angle-torsion coordinates

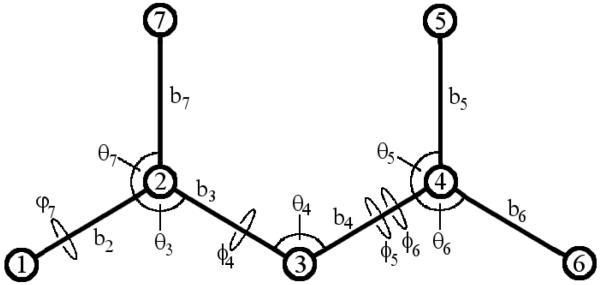
The present method uses an internal coordinate system comprising bond-lengths, bond-angles, and dihedrals, rather than Cartesian coordinates^{38,39,41,47-49}. For a molecule with N atoms, a system of 3N - 6 bond-angle-torsion (BAT) coordinates can be defined as follows (see Figure 1). Three atoms connected by serial bonds (atoms 1, 2, 3 in Figure 1) are chosen as root atoms. Assuming no external field, the internal energy of the molecule is independent of origin. Therefore, one can define the position of atom 1 as the origin of the internal coordinate system, thus eliminating three external degrees of freedom. Additionally, the overall orientation of the molecule does not affect the energy. For this reason, one may define the bond between atoms 1 and 2 to lie along the z-axis of the internal frame, eliminating the azimuthal and polar angles of atom 2 with respect to the origin. Finally, the plane formed by atoms 1, 2, and 3 can be identified as the xz-plane of the internal coordinate system. This eliminates the polar angle that defines atom 3 relative to the z-axis. Fixing the orientation of the molecule in such a manner results in the removal of an additional three external degrees of freedom. These six external degrees of freedom will not be dealt with further here.

FIG. 1.

Schematic representation of the 3N - 6 bond-angle-torsion (BAT) coordinates for a small molecule. Atoms 1, 2, and 3 are chosen as the root atoms. The symbol ϕ denotes a proper torsion and the symbol φ denotes an improper torsion.

The internal coordinates are then constructed in a tree, starting with the root atoms, where the coordinates of atom i are given by its bond-length, bond-angle, and dihedral angle with respect to a series of three other atoms closer in the tree to the root atoms. When the dihedral angles of two atoms are defined with respect to the same three prior atoms (e.g., atoms 5, 6 in Figure 1), they can be defined independently as ϕ_i and ϕ_j. Alternatively, one can be defined as a phase angle with respect to the other⁴⁹: ${\varphi }_j^{\prime }={\varphi }_j-{\varphi }_i$. In this way, the torsion of one methyl hydrogen will range from 0 to 2π, but the torsions of the other two will have tight probability distributions around $\frac{2\pi }{3}$ and $\frac{4\pi }{3}$. For a receptor-ligand complex, a pseudo-bond is formed between one atom of the receptor and one atom of the ligand; this leads to incorporation of pseudo-bond length, 2 pseudo-bond angles, and 3 pseudo-bond torsions.

Transforming from Cartesian to BAT coordinates {b, θ, ϕ} requires multiplying the volume element of the integral by a Jacobian determinant of the form $J(b,\theta )=b_2^2{\prod }_{i=3}^N{b}_i\sin {\theta }_i$, where b_i is the bond length between atoms i - 1 and i and θ_i is the bond angle defined by atoms i - 2, i - 1 and i³⁹. Hence,

$$S=-R\int J(\mathbf{b},\theta )\rho (\mathbf{b},\theta ,\varphi )\ln \rho (\mathbf{b},\theta ,\varphi )d\mathbf{b}d\theta d\varphi .$$ (6)

The Jacobian determinant can often be omitted when calculating a unimolecular entropy change, because it depends only upon bond-lengths and bond-angles, which are rather rigid. However, for a binding reaction, the density of the free ligand is expressed in units of length^-3, so a correct calculation of the change in translational entropy requires including the Jacobian terms that convert the pseudobond coordinates (previous paragraph) into units of length^-3. Furthermore, the present study compares the entropy expansion results with M2 calculations, which include bond-stretch and angle-bend coordinates with a full Jacobian, so the full Jacobian is included in all data reported here.

C. First order entropy approximation

To simplify notation {b, θ, ϕ} is now replaced by x ≡ (x₁, · · · , x_m), where m = 3N - 6, N being the number of atoms. Likewise, J(x_i, x_j, x_k), for example, now symbolizes those parts of the Jacobian determinant associated with variables x_i, x_j, x_k. Thus, if x_i = b₃, x_j = θ₅ and x_k = ϕ₄, then $J(x_i,x_j,x_k)=b_3^2\sin {\theta }_5$. The total configurational entropy for this molecule is then

$$S(x_i,\cdots ,x_m)=-R\int J(x_1,\cdots ,x_m)\rho (x_1,\cdots ,x_m)\ln \rho (x_1,\cdots ,x_m)d{x}_1\cdots d{x}_m.$$ (7)

Although the m-dimensional pdf could in principle be determined by means of a simulation, through histogramming or via parametric or non-parametric density estimators, achieving adequate convergence is not practical for most systems of chemical or biological interest. As a result, an approximation must be employed.

Prior to establishing the first order approximation to the m-dimensional entropy, it is necessary to develop a consistent notation for use in the subsequent derivations. In this work, the exact form of a marginal or joint density, entropy, or mutual information of a specific dimensionality will be identified using a subscript equal to the dimensionality. For example, the three-dimensional joint probability density of x₃, x₄, and x₅ will be denoted as

$${\rho }_3(x_3,x_4,x_5)\equiv \int J(x_1,x_2,x_6,\cdots ,x_m)\rho (x_1,\cdots ,x_m)d{x}_{1}d{x}_{2}d{x}_6\cdots d{x}_m.$$ (8)

Further, when a quantity is approximated at a particular order, this will be denoted using a superscript with the order of the approximation in parentheses. As an example, the third order approximation to the full-dimensional entropy will be expressed as S⁽³⁾.

One may begin by considering the approximation that motions along the m degrees of freedom are completely uncorrelated with each other, as previously noted⁵⁰. This assumption allows the pdf to be estimated to first order as

$${\rho }^{\left(1\right)}(x_1,\cdots ,x_m)\approx \prod _{i=1}^m{\rho }_1\left(x_i\right)$$ (9)

where ρ₁(x_i) is the marginal probability density for x_i; e.g.,

$${\rho }_1\left(x_1\right)\equiv \int J(x_2,\cdots ,x_m)\rho (x_1,\cdots ,x_m)d{x}_2\cdots d{x}_m.$$ (10)

Substituting ρ⁽¹⁾(x₁, · · · , x_m) for ρ(x₁, · · · , x_m) within the logarithm in Equation (7) allows one to separate the entropy into a sum of integrals of the form

$$S_1\left(x_i\right)\equiv -R\int J\left(x_i\right){\rho }_1\left(x_i\right)\ln {\rho }_1\left(x_i\right)d{x}_i.$$ (11)

The integral in Equation (11) is the marginal entropy associated with x_i. From this, the first order approximation to the full-dimensional entropy becomes the sum of the marginal entropies,

$$S^{\left(1\right)}=\sum _{i=1}^m{S}_1\left(x_i\right)$$ (12)

Thus, the assumption that the degrees of freedom are uncorrelated allows simplification from an intractable m-dimensional pdf to m far more tractable one-dimensional pdfs. However, the resulting first-order approximation to the entropy is inaccurate when correlations exist. More particularly, it is an upper bound which applies in the limit of completely uncorrelated motions^36,50.

D. Approximate factorizations of the probability density

In order to account for correlations among the various degrees of freedom, it is desirable to approximate the full-dimensional density at a higher order. This is a well developed method in the field of liquid theory^23-29, and the connection between the approximated density and the expansion approximation of the entropy has been previously investigated^30-36. The derivation of the mutual information expansion in this section follows these works.

In a series of papers, Kirkwood sought to formulate a general theory of molecular distributions in liquids^23,24, which led to the approximation of a three-point distribution in the liquid as a superposition of contributions from two-point distributions; i.e., to the Kirkwood Superposition Approximation (KSA)²⁵. The Kirkwood approximation was later shown to be a specific case of more general expansions which allow an n-point distribution to be estimated using corresponding (n - 1)-point distributions^26-29,35. This estimation is called the Generalized Kirkwood Superposition Approximation (GKSA). Reiss²⁸ and Singer²⁹ demonstrated that the KSA and the GKSA are, from a variational standpoint, the optimal approximations of an n-particle distribution for n ≥ 3.

We employ the GKSA to approximate the full-dimensional pdf for the internal coordinates of a molecular species. We then demonstrate that the full-dimensional entropy can be approximated using a mutual information expansion obtained by substituting the GKSA-estimated pdf inside the logarithm of the entropy integral. This approximation allows one to expand the logarithm as a summation, and permits the entropy integral to be separated into a sum of lower-dimensional terms.

We begin by returning to the m-dimensional pdf, ρ(x₁, x₂, ..., x_m). If the pdf spans a space of dimension larger than three, one may approximate it using the GKSA: ρ^(m-1)(x₁, x₂, ..., x_m) ≈ ρ(x₁, x₂, ..., x_m). The Kirkwood approximation for the three-dimensional pdf is^25,29,35,36

$${\rho }^{\left(2\right)}(x_1,x_2,x_3)=\frac{{\rho }_2(x_1,x_2){\rho }_2(x_1,x_3){\rho }_2(x_2,x_3)}{{\rho }_1\left(x_1\right){\rho }_1\left(x_2\right){\rho }_1\left(x_3\right)}.$$ (13)

This can be expressed in a shortened notation as

$${\rho }^{\left(2\right)}(x_1,x_2,x_3)=\frac{{\prod }_{C_2^3{\rho }_2}}{{\prod }_{C_1^3{\rho }_2}},$$ (14)

where ρ₂ denotes a two-dimensional joint pdf, and the product notation ${\prod }_{C_n^m}$ indicates that all of the possible $\left(\begin{array}{c}\hfill m\hfill \\ \hfill n\hfill \end{array}\right)$ unique combinations of the given subsets of degrees of freedom must be included in the product.

One can then insert the KSA-approximated density of Equation (14) into the logarithm of the full-dimensional entropy expression in Equation (7) and expand the argument of the logarithm with product and quotient rules for logarithms, into the form

$$S^{\left(2\right)}(x_1,x_2,x_3)=-R\int J(x_1,x_2,x_3)\rho (x_1,x_2,x_3)[\ln {\rho }_2(x_1,x_2)+\ln {\rho }_2(x_1,x_3)+\ln {\rho }_2(x_2,x_3)-\ln {\rho }_1\left(x_1\right)-\ln {\rho }_1\left(x_2\right)-\ln {\rho }_1\left(x_3\right)]d{x}_{1}d{x}_{2}d{x}_3.$$ (15)

This separates into 6 integrals that can be evaluated individually. In each integral, one can integrate out the degrees of freedom that are not included inside the logarithm, thus reducing the full three-dimensional pdf in front to a lower dimensional marginal pdf. The result is

$$\begin{array}{cc}\hfill S^{\left(2\right)}(x_1,x_2,x_3)=& -R\int J(x_1,x_2){\rho }_2(x_1,x_2)\ln {\rho }_2(x_1,x_2)d{x}_{1}d{x}_2\hfill \\ \hfill & -R\int J(x_1,x_3){\rho }_2(x_1,x_3)\ln {\rho }_2(x_1,x_3)d{x}_{1}d{x}_3\hfill \\ \hfill & -R\int J(x_2,x_3)\rho (x_2,x_3)\ln {\rho }_2(x_2,x_3)d{x}_{2}d{x}_3\hfill \\ \hfill & +R\int J\left(x_1\right){\rho }_1\left(x_1\right)\ln {\rho }_1\left(x_1\right)d{x}_1\hfill \\ \hfill & +R\int J\left(x_2\right){\rho }_1\left(x_2\right)\ln {\rho }_1\left(x_2\right)d{x}_2\hfill \\ \hfill & +R\int J\left(x_3\right){\rho }_1\left(x_3\right)\ln {\rho }_1\left(x_3\right)d{x}_3.\hfill \end{array}$$ (16)

Each integral in Equation (16) is now just a marginal or pairwise joint entropy:

$$S^{\left(2\right)}(x_1,x_2,x_3)=S_2(x_1,x_2)+S_2(x_1,x_3)+S_2(x_2,x_3)-S_1\left(x_1\right)-S_1\left(x_2\right)-S_1\left(x_3\right).$$ (17)

The above equation can be simplified by introducing the pairwise joint mutual information⁴⁵

$$I_2(x_i,x_j)\equiv S_1\left(x_i\right)+S_1\left(x_j\right)-S_2(x_i,x_j),$$ (18)

which is a measure of correlation between two degrees of freedom that relates the amount of information about x_j that is gained by fully characterizing x_i⁵¹. Using this definition, Equation (17) can be rewritten in the form

$$S^{\left(2\right)}(x_1,x_2,x_3)=S_1\left(x_1\right)+S_1\left(x_2\right)+S_1\left(x_3\right)-I_2(x_1,x_2)-I_2(x_1,x_3)-I_2(x_3,x_2).$$ (19)

This approximate expression equals the first order approximation of Equation (12), corrected for pairwise correlations by including the pairwise joint mutual information. This offers a conceptually intuitive method of approximating the full-dimensional entropy, by first summing the individual contributions from each degree of freedom, then correcting for correlations among higher order terms. One may generalize this mutual information expansion to higher dimensionality.

For higher dimensionality, the GKSA allows one to approximate an m-dimensional pdf using the form^29,35,36

$${\rho }^{(m-1)}(x_1,x_2,\cdots ,x_m)=\frac{\prod _{C_{m-1}^m}{\rho }_{m-1}}{\frac{\prod _{C_{m-2}^m}{\rho }_{m-2}}{\frac{⋮}{\frac{\prod _{{C_2^m}^{{\rho }_2}}}{\prod _{{C_1^m}^{{\rho }_1}}}}}},$$ (20)

where, as before, the term ρ_n represents a specific n-dimensional joint pdf and the products are over all unique combinations of the indicated dimensionality.

Returning to the definition of the entropy given in Equation (7), one can expand the logarithm term by approximating the argument of the logarithm using the GKSA of Equation (20),

$$S^{(m-1)}=-R\int J(x_1\cdots ,x_m)\rho (x_1\cdots ,x_m)\ln {\rho }^{(m-1)}(x_1\cdots ,x_m)d{x}_1\cdots d{x}_m.$$ (21)

Following the derivation of the three-dimensional case (generalized in Appendix B), the m - 1 order approximation to the full-dimensional entropy can be written as

$$S^{(m-1)}=\sum _{n=1}^{m-1}{(-1)}^{m-n+1}\sum _{C_n^m}{S}_n.$$ (22)

Using the definition of higher-order joint mutual information³⁶, it can be shown that Equation (22) can be written as

$$S^{(m-1)}=\sum _{i=1}^m{S}_1\left(x_i\right)-\sum _{C_2^m}{I}_2(x_i,x_j)+\sum _{C_3^m}{I}_3(x_i,x_j,x_k)-\sum _{C_4^m}{I}_4(x_i,x_j,x_k,x_l)+\cdots .$$ (23)

This is the mutual information expansion offered by Matsuda³⁶.

Looking at Equation (23) from a computational standpoint, it becomes clear that one has not eliminated the sampling and storage issues that plague the computation of the full-dimensional entropy: instead of having to populate one m-dimensional histogram, one must populate m different m - 1 dimensional histograms. Further, there is an insurmountable combinatorial explosion of the lower dimensional histograms to be constructed, for a system of any size. What Equation (23) does offer is a systematic method for including higher order corrections to the approximated full-dimensional entropy. This expansion can be truncated at any level desired, allowing the entropy to be computed using a maximum dimensionality of the histograms to be constructed that is suitable for a given molecular system and available computational resources. Note that it is unnecessary ever to form a representation of the full-dimensional pdf by multiplying these lower dimensionality histograms; the low-dimensionality histograms themselves are all that is needed to compute the terms of the entropy expansion. However, it is of interest to discern the relation between the order of truncation and the level of approximation of the density in the GKSA.

E. Truncating the mutual information expansion: the connection to density

The GKSA can now be used as justification for a particular level of approximation to the entropy, providing a meaningful connection between estimation of the density at a given dimensionality and the highest order correction included in the truncated mutual information expansion. Suppose that one desires to limit the dimensionality of the joint pdfs to a small number such as two or three. One may then apply the GKSA successively to obtain an approximation of the m-dimensional pdf using joint pdfs of the desired maximum dimensionality. The simplest example occurs when one approximates a four-dimensional pdf using one- and two-dimensional joint pdfs only. This is done by first applying the GKSA to the four-dimensional pdf^26,28,29,35,

$${\rho }^{\left(3\right)}(x_1,x_2,x_3,x_4)=\frac{{\rho }_3(x_1,x_2,x_3){\rho }_3(x_1,x_2,x_4){\rho }_3(x_1,x_2,x_5){\rho }_3(x_2,x_3,x_4)}{\frac{{\rho }_2(x_1,x_2),{\rho }_2(x_1,x_3){\rho }_2(x_1,x_4){\rho }_2(x_2,x_3){\rho }_2(x_2,x_4){\rho }_2(x_3,x_4)}{{\rho }_1\left(x_1\right){\rho }_1\left(x_2\right){\rho }_1\left(x_3\right){\rho }_1\left(x_4\right)}}.$$ (24)

Into this expression, one may substitute the Kirkwood approximation for each of the three-dimensional joint pdfs. After some simplifying algebra, the new approximation becomes

$${\rho }^{\left(2\right)}(x_1,x_2,x_3,x_4)\approx \frac{{\rho }_2(x_1,x_2){\rho }_2(x_1,x_3){\rho }_2(x_1,x_4){\rho }_2(x_2,x_3){\rho }_2(x_2,x_4){\rho }_2(x_3,x_4)}{{\left[{\rho }_1\left(x_1\right){\rho }_1\left(x_2\right){\rho }_1\left(x_3\right){\rho }_1\left(x_4\right)\right]}^2}.$$ (25)

Substitution of Equation (25) into the logarithm of Equation (7) and subsequent integration yields the expression

$$\begin{array}{cc}\hfill S^{\left(2\right)}(x_1,x_2,x_3,x_4)=& S_2(x_1,x_2)+S_2(x_1,x_3)+S_2(x_1,x_4)+S_2(x_2,x_3)+S_2(x_2,x_4)\hfill \\ \hfill & +S_2(x_3,x_4)-2[S_1\left(x_1\right)+S_1\left(x_2\right)+S_1\left(x_3\right)+S_1\left(x_4\right)].\hfill \end{array}$$ (26)

By using the definition of the joint pairwise mutual information, this can be rewritten as

$$\begin{array}{cc}\hfill S^{\left(2\right)}(x_1,x_2,x_3,x_4)=& S_1\left(x_1\right)+S_1\left(x_2\right)+S_1\left(x_3\right)+S_1\left(x_4\right)-I_2(x_1,x_2)-I_2(x_1,x_3)\hfill \\ \hfill & -I_2(x_1,x_4)-I_2(x_2,x_3)-I_2(x_2,x_4)-I_2(x_3,x_4).\hfill \end{array}$$ (27)

which is equivalent to applying Equation (23) to a four-dimensional pdf and truncating the expansion after the second order corrections. From this it is clear that truncation of the mutual information expansion of the entropy at the pairwise level is equivalent to approximating the density by the GKSA using only one- and two-dimensional joint pdfs.

In general, one can estimate an m-dimensional pdf using only one-and two-dimensional joint pdfs by successive application of the GKSA. The general approximation takes the form

$${\rho }^{\left(2\right)}(x_1\cdots ,x_m)\approx \frac{{\prod }_{C_2^m}{\rho }_2}{{\left[{\prod }_{C_1^m}{\rho }_1\right]}^{m-2}},$$ (28)

and the corresponding entropy expansion takes the form

$$\begin{array}{cc}\hfill S^{\left(2\right)}(x_1,\cdots ,x_m)& \approx \sum _{C_2^m}{S}_2-(m-2)\sum _{C_1^m}{S}_1\hfill \\ \hfill & =\sum _{C_1^m}{S}_1-\sum _{C_2^m}{I}_2.\hfill \end{array}$$ (29)

This expansion is identical to the general mutual information expansion in Equation (23) but truncated at the pairwise level of correlation. This can be easily extended to include three-dimensional joint pdfs as well. The general form of the density approximation is now

$${\rho }^{\left(3\right)}(x_1\cdots ,x_m)\approx \frac{{\prod }_{C_3^m}{\rho }_3}{\frac{{\left[{\prod }_{C_2^m}{\rho }_2\right]}^{m-3}}{{\left[{\prod }_{C_1^m}{\rho }_1\right]}^{C_2^m-2}}}.$$ (30)

The associated expansion of the entropy becomes

$$\begin{array}{cc}\hfill S^{\left(3\right)}(x_1,\cdots ,x_3)& \approx \sum _{C_3^m}{S}_3-(m-3)\sum _{C_2^m}{S}_2+C_2^{m-2}\sum _{C_1^m}{S}_1\hfill \\ \hfill & =\sum _{C_1^m}{S}_1-\sum _{C_m^2}{I}_2+\sum _{C_m^3}{I}_3.\hfill \end{array}$$ (31)

Again, this is the same as the expression given in Equation (23) truncated at the level of three-fold correlations. While one can generalize this approximation to any desired level, we will not extend beyond three dimensions in this paper.

It is worth noting that, assuming an nth order approximation of the density,

$$S^{\left(n\right)}=R\langle -\ln {\rho }^{\left(n\right)}\rangle =-R\int \rho \ln {\rho }^{\left(n\right)}dx,$$ (32)

where the angle brackets imply that -ln ρ⁽ⁿ⁾ is averaged over the true pdf ρ rather than ρ⁽ⁿ⁾. The quantity S⁽ⁿ⁾ provides a measure of the amount of information we gain about the true distribution ρ by analysis of the approximate distribution ρ⁽ⁿ⁾. This measure is closely related the Kullback-Leibler (K-L) divergence, or relative entropy, which provides a measure of di erence between the true and approximate pdfs⁴⁶. It is clear from the above analysis that the information about ρ that is lost by assuming ρ⁽ⁿ⁾ (i.e., the K-L divergence between ρ and ρ⁽ⁿ⁾) is precisely contained in the mutual information terms of order n+1 and larger.

F. Computational Details

The dynamical trajectories were all generated using the University of Houston Brownian Dynamics computer code⁵². The stochastic dynamics module was employed, along with a distance dependent dielectric model, D_ij = 4r_ij, where r_ij is the distance in Angstroms between atoms i and j. The program Quanta⁵³ was used to type the atoms and generate CHARMm22⁵⁴ force parameters.

Each trajectory was run for a minimum simulated time of 50 ns with a time-step of 0.001 ps, and was recorded at a rate of 10⁵ snapshots for each ns of simulated time. The output trajectories were then converted into BAT coordinate files. The mutual information expansion method was applied through a computer code called the Algorithm for Computing Configurational ENTropy from Molecular Mechanics (ACCENT-MM), in which all pdfs were generated by histograming. Marginal and pairwise joint histograms were constructed for all combinations of bond-length, bond-angle, and torsional degrees of freedom, with 120 bins used for each dimension. Threefold joint histograms were constructed only for torsional degrees of freedom. For computing the threefold mutual information associated with the torsions, 60 bins were used for each dimension, as this was found to produce the most stable numerical results. For the host-guest complex, the BAT coordinate system included a pseudobond that connected an atom in the guest molecule to an atom in the host molecule, as noted in the Theory section.

The results obtained using the entropy expansion method were compared with secondgeneration Mining Minima (M2) calculations¹⁰ for the same molecules and the same energy model. The M2 calculations yield not only the chemical potential of the molecule but also the average energy, allowing one to calculate the configurational entropy using Equation (3). In the entropy expansion method, the average energy obtained from the dynamical trajectories was combined with the configurational entropy computed by the ACCENT-MM software to yield the chemical potential, again using Equation (3). Comparison with M2 offers cross-validation of the entropy expansion results against a tested methodology that relies on different computation formalisms.

Corrections for internal symmetries must be made before the ACCENT-MM results can be compared with those from M2. The M2 code utilizes a symmetry filtering algorithm that prevents overcounting of the energy minima by including only a single representative of each distinct configuration⁵⁵. This is accomplished by finding all configurations that can be made to superimpose through motions along rotational or internal coordinates and removing duplicates. This becomes an issue for methyl rotations, for which M2 reduces three configurations to one, so that the ACCENT-MM entropy values must be correspondingly reduced by ln 3 for each methyl group present in the molecule, since the dynamics simulations allow each methyl to rotate 0 - 2π radians. In the case of cyclohexane, M2 includes a single instance of the thermodynamical prodominant chair configuration, while the MD simulations include two. Therefore, the ACCENT-MM entropy is reduced by ln 2 for comparison. It should be noted that chosing to use phase angles for constructing torsional pdfs does not reduce the configurational symmetry, and therefore the same corrections apply.

III. RESULTS

A. Hydrogen Peroxide

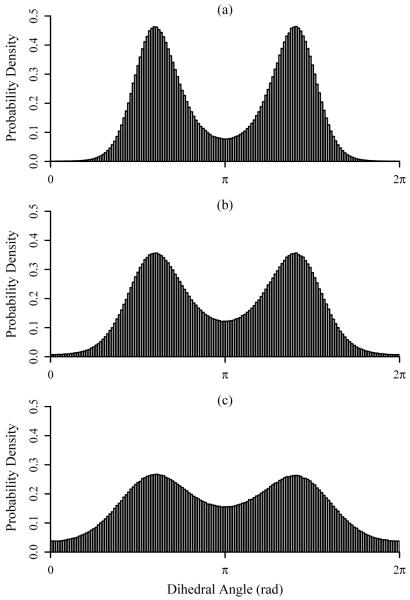
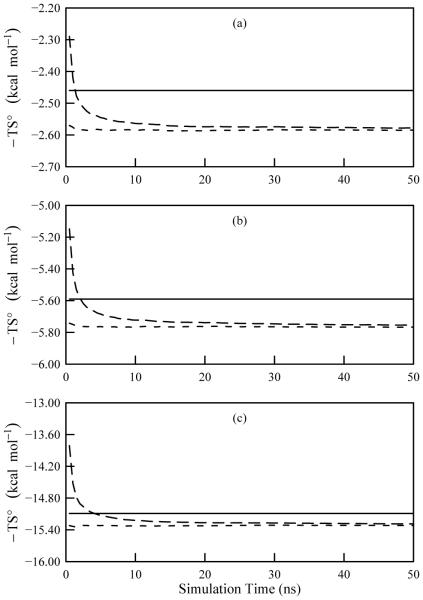
The simplest system that was investigated here is the hydrogen peroxide molecule. With four atoms, hydrogen peroxide has six internal degrees of freedom: three bonds, two angles, and one dihedral. Figure 2 demonstrates the structures of the pdfs for the H-O-O-H dihedral at 300, 500, and 1000 K, and Figure 3 documents the convergence of the first- and second-order approximations to the total entropy, S⁽¹⁾ and S⁽²⁾, respectively, for all three simulation temperatures. Table I compares the average potential energies, temperature weighted standard entropies, and standard chemical potentials with the corresponding M2 results. The first- and second-order entropy values are very similar and agree well with the M2 results. Furthermore, the mean energies from the simulations and from M2 are comparable. As a consequence, the chemical potentials computed using the two methods agree favorably.

FIG. 2.

Plots of the ACCENT-MM probability density functions for the H-O-O-H dihedral angle in hydrogen peroxide for simulation temperatures of (a) 300 K, (b) 500 K, and (c) 1000 K.

FIG. 3.

Convergence plots of the temperature weighted entropy for hydrogen peroxide as computed using ACCENT-MM for simulations at (a) 300 K, (b) 500 K, and (c) 1000 K. The data include the first-order approximation to the total entropy (short dash) and the second-order approximation to the total entropy (long dash). The solid line shows the value obtained using M2.

TABLE I.

Thermodynamic quantities for hydrogen peroxide computed with ACCENT-MM as compared with M2. All values are in kcal/mol

			ACCENT-MM
		M2	(1)a	(2)b
300 K	⟨E⟩	11.94	11.98	11.98
	-TSo	-2.46	-2.58	-2.58
	μo	9.48	9.40	9.40
500 K	⟨E⟩	13.13	13.14	13.14
	-TSo	-5.59	-5.77	-5.75
	μo	7.54	7.37	7.39
1000 K	⟨E⟩	16.11	15.89	15.89
	-TSo	-15.09	-15.32	-15.29
	μo	1.02	0.57	0.60

^aFirst-order approximation to the entropy

^bSecond-order approximation to the entropy

B. Methanol

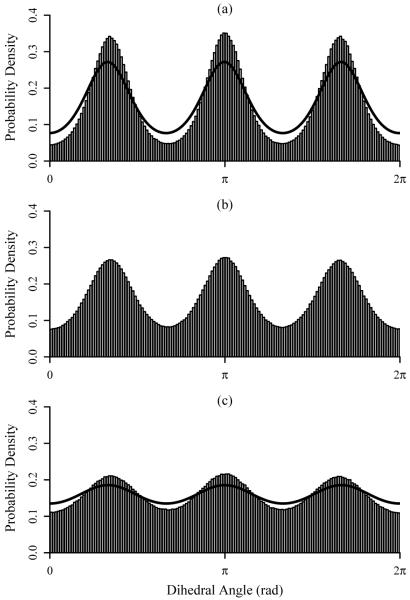
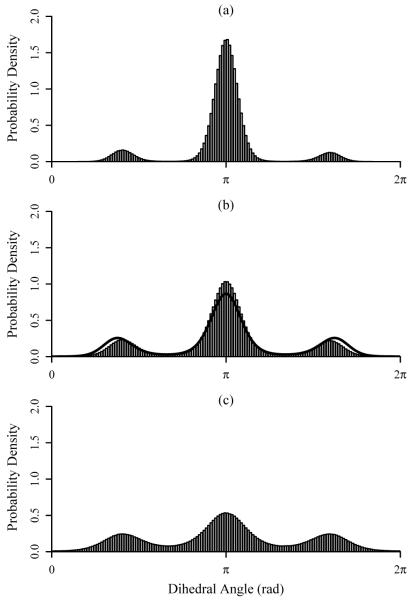
Methanol is the simplest system investigated that includes strongly coupled torsional degrees of freedom, those for the three methyl hydrogens. The plots in Figure 4 demonstrate the marginal pdfs for a single H-O-C-H dihedral at 300, 500, and 1000 K. The pdfs of the torsions corresponding to the remaining two methyl hydrogens are essentially identical to the first, as expected for a well-converged simulation, and are therefore not shown here. Table II compares the entropies computed using ACCENT-MM at the first-, second-, and third-order with M2 results; chemical potentials and mean energies are again included. The first- and second-order approximations to the entropy do not agree well with the M2 results, deviating by as much as 9 kcal/mol. However, including the third-order mutual information terms bring the expansion results within 0.5 kcal/mol of the M2 entropies.

FIG. 4.

Plots of the ACCENT-MM probability density functions for a single H-O-C-H dihedral angle in methanol for simulation temperatures of (a) 300 K, (b) 500 K, and (c) 1000 K. The solid lines demonstrate pdfs generated by Demchuk and Singh⁵⁶.

TABLE II.

Thermodynamic quantities for methanol computed with ACCENT-MM using the “full torsion” pdfs as compared with M2. All values are in kcal/mol

			ACCENT-MM
		M2	(1)a	(2)b	(3)c
300 K	⟨E⟩	11.95	12.01	12.01	12.01
	-TSo	3.09	-0.49	4.66	3.24
	μo	15.04	11.52	16.67	15.25
500 K	⟨E⟩	14.34	14.32	14.32	14.32
	-TSo	2.12	-3.34	4.52	2.32
	μo	16.46	10.98	18.84	16.64
1000 K	⟨E⟩	20.29	19.95	19.95	19.95
	-TSo	-3.88	-13.02	0.28	-3.44
	μo	16.41	6.93	20.23	16.51

^aFirst-order approximation to the entropy

^bSecond-order approximation to the entropy

^cThird-order approximation to the entropy

We conjectured that the large magnitudes of the third-order mutual informations resulted from the strong—and foreseeable—coupling of the three methyl hydrogens. This suggested that the importance of the third-order terms could be reduced by treating the torsions associated with two of the hydrogens as phase angles relative to the first (see the BAT coordinate discussion in the Theory section). These phase angles display tight distributions centered at $\frac{2\pi }{3}$ and $\frac{4\pi }{3}$, respectively (data not shown). Repeating the calculations with this phase angle approach leads to excellent agreement between the second-order ACCENT-MM entropies with M2, with deviations no greater than 0.2 kcal/mol (Table III). In addition, the third-order mutual information values all drop to nearly zero, as evidenced by the equality of S⁽²⁾ and S⁽³⁾. The present analysis shows that a suitably chosen coordinate system can markedly reduce the importance of higher-order terms in the entropy expansion. The use of phase angles in effect builds an important part of the correlation information into lower-order joint pdfs. We observed similar results for other molecular species. As a consequence, the remainder of this paper uses only the phase angle treatment of coupled torsional angles.

TABLE III.

Thermodynamic quantities for methanol computed with ACCENT-MM using the “phase angle” pdfs as compared with M2. All values are in kcal/mol

			ACCENT-MM
		M2	(1)a	(2)b	(3)c
300 K	⟨E⟩	11.95	12.01	12.01	12.01
	-TSo	3.09	2.36	3.01	3.01
	μo	15.04	14.37	15.02	15.02
500 K	⟨E⟩	14.34	14.32	14.32	14.32
	-TSo	2.12	1.17	2.05	2.06
	μo	16.46	15.49	16.37	16.38
1000 K	⟨E⟩	20.29	19.96	19.96	19.96
	-TSo	-3.88	-5.16	-3.70	-3.70
	μo	16.41	14.80	16.26	16.26

^aFirst-order approximation to the entropy

^bSecond-order approximation to the entropy

^cThird-order approximation to the entropy

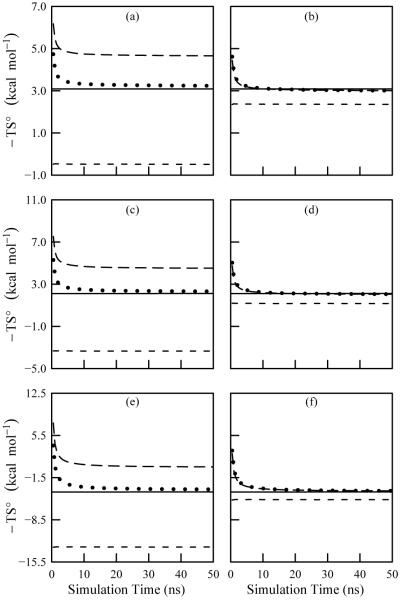
Figure 5 demonstrates the convergence of the temperature weighted standard entropy as a function of simulation time for the temperatures investigated. The plots on the left hand side are for the “full torsion” data in which each torsion was treated independently, while those on the right hand side are from the “phase angle” approach. Excellent convergence appears to have been attained using both approaches.

FIG. 5.

Convergence plots of the temperature weighted entropy for methanol computed with ACCENT-MM. Frames (a) and (b) are for a simulation temperature of 300 K using the “full torsion” and “phase angle” methods, respectively. Frames (c) and (d) are the same, but at 500 K. Frames (e) and (f) are the same, but at 1000 K. The data include the first-order approximation to the total entropy (short dash), the second-order approximation to the total entropy (long dash), and the third-order approximation to the total entropy (dotted). The solid line shows the value obtained using M2.

Torsional contributions to the configurational entropy of methanol have previously been investigated by Demchuk and Singh⁵⁶. They performed Monte Carlo simulations on ensembles of methanol molecules at 300 and 1000 K using AMBER-style force field parameters, and constructed marginal pdfs using parameterized trimodal von Mises fitting functions⁵⁶. Figures 4a and 4c offer direct comparison between the histograms constructed using ACCENT-MM with the von Mises functions generated by Demchuk and Singh. The two sets of pdfs have similar shapes, but those from the prior study are less sharply peaked, presumably due to differences in the force fields employed. The study by Demchuk and Singh yielded average values of 1.744 and 1.831 for the unitless quantity S₁(ϕ)/R associated with the methyl torsions at 300 K and 1000 K, respectively. For comparison, the corresponding marginal pdfs from this study yield values of 1.626 and 1.815 for the same respective temperatures. The two sets of data are quite similar, though the previous calculations resulted in slightly higher entropies, consistent with the flatter pdfs shown in Figure 4.

C. 1,2-dichloroethane

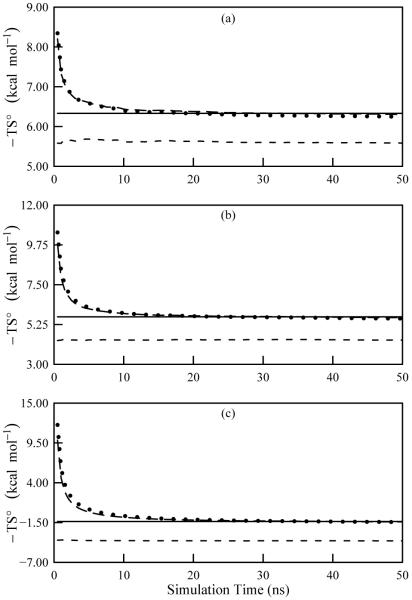
The BAT coordinates for 1,2-dichloroethane include five torsional angles, four of which can be defined as narrowly distributed phase angles with respect to the fifth. The fifth torsion, chosen to be the Cl-C-C-Cl torsion, is allowed to vary through the full range of 0 to 2π, as evident from its pdf (Figure 6). The value of S⁽²⁾ again agrees well with the M2 results, as shown in Table IV. As in the case of methanol when phase angles were employed, the third-order mutual information terms for this molecule contribute little to the entropy. Also, the mean energies again demonstrate good agreement with the M2 values, so the chemical potentials compare favorably. Finally, Figure 7 documents good convergence for the three temperatures over the course of the 50 ns simulations.

FIG. 6.

Computed probability density functions for the Cl-C-C-Cl dihedral angle in 1,2-dichloroethane, for simulation temperatures of (a) 300 K, (b) 500 K, and (c) 1000 K. The solid line shows the pdf generated by Hnizdo et al⁵⁷.

TABLE IV.

Thermodynamic quantities for 1,2-dichloroethane computed with ACCENT-MM as compared with M2. All values are in kcal/mol

			ACCENT-MM
		M2	(1)a	(2)b	(3)c
300 K	⟨E⟩	5.72	5.77	5.77	5.77
	-TSo	6.33	5.58	6.30	6.31
	μo	12.05	11.35	12.07	12.08
500 K	⟨E⟩	9.51	9.62	9.62	9.62
	-TSo	5.69	4.37	5.64	5.67
	μo	15.20	13.99	15.26	15.29
1000 K	⟨E⟩	18.68	18.77	18.77	18.77
	-TSo	-1.36	-4.03	-1.41	-1.30
	μo	17.32	14.74	17.36	17.47

^aFirst-order approximation to the entropy

^bSecond-order approximation to the entropy

^cThird-order approximation to the entropy

FIG. 7.

Convergence plots of the temperature-weighted entropy for 1,2-dichloroethane computed with ACCENT-MM for simulations at (a) 300 K, (b) 500 K, and (c) 1000 K. The data include the first-order approximation to the total entropy (short dash), the second-order approximation to the total entropy (long dash), and the third-order approximation to the total entropy (dotted). The solid line shows the value obtained using M2.

Hnizdo and co-workers⁵⁷ studied the torsional entropy of 1,2-dichloroethane using Monte Carlo dynamics at 500 K with the OPLS force field. The marginal pdf for the Cl-C-C-Cl torsion was fit to a Fourier series expansion. As shown in Figure 6, their pdf agrees well with that obtained here, given the use of two different energy models. To compare the entropy values, we computed the Shannon entropy associated with the Fourier series expansion provided in the previous paper. The resulting value of S₁(ϕ)/R was found to be 1.19, compared to 1.01 in the present work.

D. Alkanes

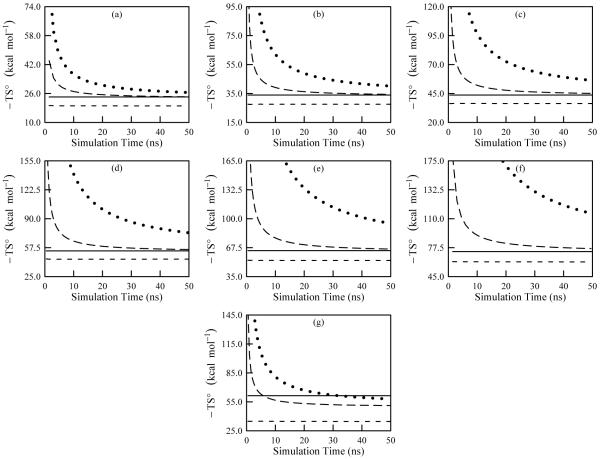
In this section, we present data for ACCENT-MM computations on seven straight-chain and cyclic alkanes in order to evaluate convergence properties and accuracy for larger molecules. The compounds investigated are butane, pentane, hexane, heptane, octane, nonane, and cyclohexane, all simulated at 1000 K to promote conformational sampling. The results of 50 ns simulations of these alkanes are summarized and compared with M2 results in Table V. The first-order entropies deviate from the M2 results by more than 10 kcal/mol, but the second-order corrections improve the ACCENT-MM results to within about 2 kcal/mol of the M2 values for the straight-chain species. Convergence graphs in Figure 8 show that the second-order entropies are relatively well converged after 50 ns (long dash curves in Figure 8). The cyclohexane entropies converge faster than the hexane entropies (compare Figures 8c and 8g), as might be expected given the reduced volume of torsional space accessible to this cyclic molecule. This also coincides with the lower entropy displayed by the cyclohexane in comparison to hexane.

TABLE V.

Thermodynamic quantities for various alkanes computed at 1000 K with ACCENT-MM as compared with M2. All values are in kcal/mol

			ACCENT-MM
		M2	(1)a	(2)b	(3)c
Butane	⟨E⟩	38.90	38.92	38.92	38.92
	-TSo	24.09	19.13	23.62	24.51
	μo	62.99	58.05	62.54	63.43
Pentane	⟨E⟩	48.60	48.33	48.33	48.33
	-TSo	33.69	27.59	34.41	40.14
	μo	82.29	75.92	82.74	132.37
Hexane	⟨E⟩	54.95	54.71	54.71	54.71
	-TSo	43.67	36.34	45.08	56.30
	μo	98.62	91.05	99.79	111.01
Heptane	⟨E⟩	67.84	67.35	67.35	67.35
	-TSo	53.89	44.65	55.41	74.21
	μo	121.73	112.00	122.76	141.56
Octane	⟨E⟩	77.37	76.89	76.89	76.89
	-TSo	64.22	53.11	65.98	94.62
	μo	141.59	130.00	142.87	171.51
Nonane	⟨E⟩	86.85	86.11	86.11	86.11
	-TSo	73.08	61.55	73.64	88.53
	μo	159.93	147.66	159.75	174.64
Cyclohexane	⟨E⟩	61.99	61.86	61.86	61.86
	-TSo	61.38	34.74	51.17	57.93
	μo	123.37	96.60	113.03	119.79

^aFirst-order approximation to the entropy

^bSecond-order approximation to the entropy

^cThird-order approximation to the entropy

FIG. 8.

Convergence plots of the temperature weighted entropy for alkanes as computed using ACCENT-MM for a simulation temperature of 1000 K. The frames are: (a) butane; (b), pentane; (c), hexane; (d), heptane; (e), octane; (f), nonane; and (g), cyclohexane. The data include the first-order approximation to the total entropy (short dash), the second-order approximation to the total entropy (long dash), and the third-order approximation to the total entropy (dotted). The solid line shows the value obtained using Mining Minima.

The third-order entropies for the straight-chain alkanes deviate from M2 more than the second-order entropies (Table V). However, these deviations must be interpreted in light of the convergence plots (dotted curves in Figure 8), which indicate that the third-order entropies are not well converged at 50 ns, yet are approaching the M2 results. Thus, the fully converged third-order results may well be similar to the second-order values. As for the previous systems, the average energies from M2 agree with the simulations to within 1 kcal/mol (Table V). Consequently, the chemical potentials obtained from M2 and from ACCENT-MM at the second-order agree to within about 2 kcal/mol.

Correlations contribute more strongly to entropy for cyclohexane than for the linear alkanes, as might be expected for this fairly stiff ring. This is apparent from the fact that the first-order approximation to the entropy deviates more from the M2 entropy for cyclohexane than for the straight-chain alkanes (Figure 8g and Table V). Moreover, whereas for the linear alkanes the second-order approximation converges to near the M2 results, the second-order entropy for cyclohexane deviates from M2 by more than 10 kcal/mol. This indicates that the second-order approximation still overestimates the total entropy of cyclohexane, presumably due to pronounced higher-order correlations. Accordingly, Figure 8g indicates that the third-order approximation is converging to a number close to the M2 value. It is concluded that correlations above second-order are modest but non-negligible in the case of cyclohexane.

The convergence properties were more fully examined for butane and nonane, the smallest and largest alkanes investigated here. Figure 9 shows the convergence of these two molecules for 150 ns of simulation. By 150 ns, the butane results have converged at all orders of approximation (Figure 9a). For nonane, although the second-order results have converged, the third-order approximation is still unconverged after 150 ns (Figure 9b). Despite the lack of convergence, one can make a comparison between the M2 values and an extrapolated prediction of the third-order entropy for these systems. We fit the third-order convergence data using a function of the form $S^{\left(3\right)}\left(t\right)=a{t}^{-b}+S_{\infty }^{\left(3\right)}$, where t is the simulation time in ns and a, b, and $S_{\infty }^{\left(3\right)}$ are adjustable parameters. This functional form has been previously shown to offer good estimation of configurational entropy convergence data¹⁵. The benefit of using this functional form is that the parameter $S_{\infty }^{\left(3\right)}$ is the optimal value of the third-order entropy for an infinite simulation time and can be used as an estimation of the true third-order entropy. The parameters a, b, and $S_{\infty }^{\left(3\right)}$ were optimized using standard linear least squares (LLS) techniques.

FIG. 9.

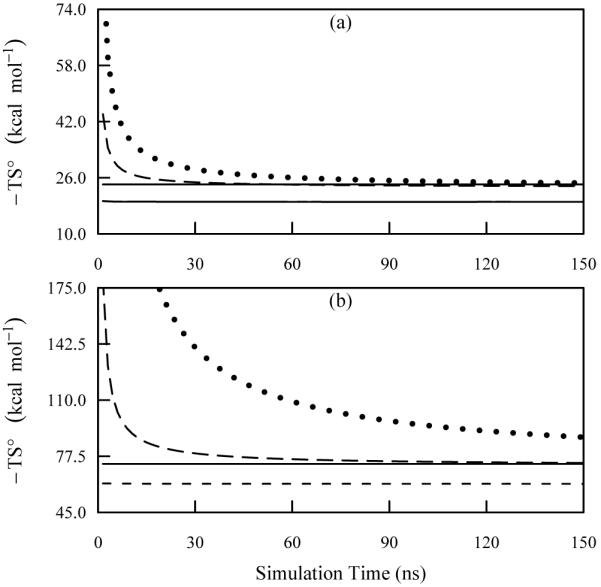
Convergence plots of the temperature weighted entropy for butane and nonane 150 ns of simulation as computed using ACCENT-MM for a simulation temperature of 1000 K. The data include the first-order approximation to the total entropy (short dash), the second-order approximation to the total entropy (long dash), and the third-order approximation to the total entropy (dotted). The solid line shows the value obtained using M2.

The LLS optimization for the butane simulation data yielded values of a = 92.6702, b = 0.8342, and $S_{\infty }^{\left(3\right)}=23.0329$ kcal/mol. Thus the extrapolated third-order entropy is within about 1 kcal/mol of both the second-order approximation and the M2 value and differs from the reported third-order entropy at 150 ns by about 1.5 kcal/mol, indicating that good convergence has been achieved for butane. For the nonane data, the LLS optimized parameters were found to be a = 1202.0011, b = 0.8205, and $S_{\infty }^{\left(3\right)}=67.9114$ kcal/mol. The extrapolated estimation of the third-order entropy for nonane is about 20 kcal/mol less than the reported value at 150 ns. However, the estimated value the third-order entropy for nonane is in deviation from the M2 results by only about 5 kcal/mol, confirming that the third-order entropy appears to be converging to a value similar to that obtained using M2.

E. Urea Receptor

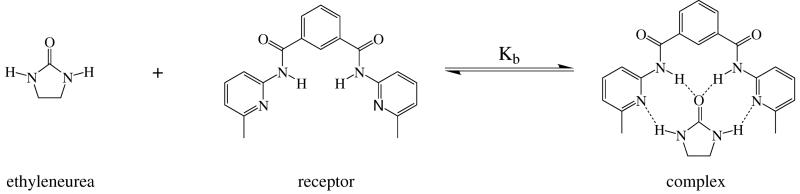
As a final example, we report the computed entropy changes upon binding for a simple host-guest complexation system, a dimethyl-substituted variant of a synthetic barbiturate receptor^58,59, which binds ethyleneurea via four hydrogen bonds^14,58 (Figure 10).

FIG. 10.

Complexation reaction for ethyleneurea with a synthetic receptor. Only those hydrogen atoms that participate in hydrogen bond interactions are shown explicitly, as dashed lines.

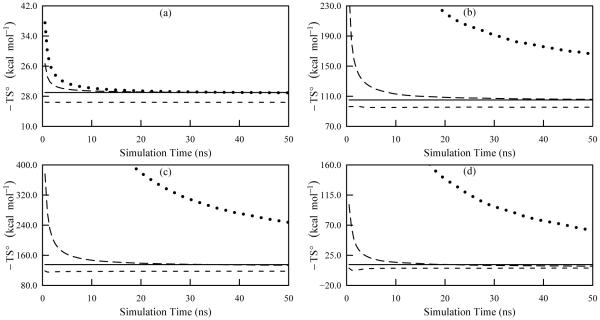
Table VI provides the thermodynamic quantities computed using both the ACCENT-MM and M2 methods. The absolute second-order entropies for the ligand and the receptor agree with M2 almost exactly, while differing by about 1.6 kcal/mol for the complex. Furthermore, as with the other systems studied here, the average energies from M2 agree closely with those from the simulations. The final result is that the change in chemical potential at second-order deviate from the M2 values by less than 1.2 kcal/mol. Figure 11 demonstrates convergence of the second-order approximations to the entropy (long dash curves). These are relatively well converged after the 50 ns simulation time. The third-order approximations do not compare as favorably with the M2 results (Table VI) but, as with the alkanes, their deviation appears to be attributable in large part to incomplete convergence of the third-order mutual information contributions (Figure 11).

TABLE VI.

Thermodynamic quantities computed for the complexation reaction at 300 K using ACCENT-MM as compared with M2. All values are in kcal/mol

			ACCENT-MM
		M2	(1)a	(2)b	(3)c
Ligand	⟨E⟩	-9.64	-9.64	-9.64	-9.64
	-TSo	19.00	16.40	18.98	18.92
	μo	9.36	6.76	9.34	9.28
Receptor	⟨E⟩	16.15	15.57	15.57	15.57
	-TSo	105.12	95.45	105.87	166.28
	μo	121.27	111.02	121.44	181.85
Complex	⟨E⟩	-9.96	-9.33	-9.33	-9.33
	-TSo	135.25	117.73	133.61	247.43
	μo	125.29	108.40	124.28	238.10
Net	⟨E⟩	-16.47	-15.26	-15.26	-15.26
	-TΔSo	11.13	5.88	8.76	62.23
	ΔGo	-5.34	-9.38	-6.50	46.97

^aFirst-order approximation to the entropy

^bSecond-order approximation to the entropy

^cThird-order approximation to the entropy

FIG. 11.

Convergence plots of the temperature weighted entropy for the complexation as computed using ACCENT-MM at a simulation temperature of 300 K. The frames are: (a) ethyleneurea; (b), receptor; (c), complex; (d), change on binding. The data include the first-order approximation to the total entropy (short dash), the second-order approximation to the total entropy (long dash), and the third-order approximation to the total entropy (dotted). The solid line shows the value obtained using Mining Minima.

IV. DISCUSSION

This study demonstrates the theoretical and practical application of a rigorous entropy expansion to flexible molecules and complexes. The first level of the expansion neglects all correlations and therefore provides an upper limit of the entropy. The second level accounts in addition for pairwise correlations and always yields a lower entropy than the first-order approximation. Successive levels correct for tertiary, quaternary and higher-order correlations and can either raise or lower the entropy, depending on the nature of the correlation³⁶. At all levels, correlations are conceptualized and incorporated through pairwise and higher-order mutual information terms. It is furthermore shown that the entropy approximation at each order is a cross-entropy between the factorization approximation of the pdf at that order and the true pdf. For example, the second-order entropy approximation is based upon an approximation of the full pdf in terms of first- and second-order marginal pdfs; and higher order approximations of the entropy correspond to factorizations incorporating higher-order marginal pdfs.

The well-defined hierarchy of approximations in the present approach is appealing because it provides a clear path, though not always an easy one, to improving the quality of entropy calculations. In this sense, the expansion approach puts simulations on a similar footing to quantum chemical calculations, for which the incorporation of higher-order correlations also represents a systematic path of improvement.

¡¡MKG: edited this paragraph in light of corrected cyclohexane results.¿¿ The central issues of convergence and accuracy are addressed in practical terms here by the simulation studies. In all cases the first-order entropy appears to converge promptly, while the second-order entropy typically converges adequately within ∼50 ns. Convergence to third order is considerably harder to achieve. It is thus encouraging that second-order approximations of the entropy agree well with reference results from the very different M2 method, except for the highly coupled cyclohexane ring, for which agreement appears improved by including third-order information. These observations arguably support the validity of both the M2 and the entropy expansion approaches. It is also encouraging to note that previous investigations of homogeneous liquids have demonstrated that third- and higher-order corrections are modest, even if non-trivial: it appears that, in the case of simple fluids, more than 80% of the total entropy can be accounted for by including the second-order (i.e., two-particle) densities^31,33. It thus seems likely that the second order approximation will, in many cases, provide a good balance of accuracy and computational speed.

It is important to use a suitable coordinate system with the entropy expansion method. For example, it is found that treating each hydrogen of a methyl group as having an independent torsion pushes substantial correlation into the third-order terms and therefore makes the calculation more complex. This particular problem can be avoided by treating two of the hydrogen torsions as phase angles relative to the other hydrogen torsion. More generally, it is likely that using Cartesian coordinates instead of BAT coordinates would make the entire methodology intractable. Conversely, there may exist some sets of collective coordinates that will make the method more tractable.

The entropy expansion method should be useful for systems of biological and chemical interest, and such an application is currently being pursued by the present authors. Although the calculations are computationally taxing because they involve large systems, it seems likely that adequate convergence can still be achieved at the second order and that this level of approximation will be instructive. In fact, the present results already are relevant because they indicate that second-order correlations make remarkably large contributions to the configurational entropy. This is evident from comparisons of the first- and second-order entropy data in the Results tables. Even for the simple host-guest system studied here, the second-order mutual information terms reduce the binding entropy penalty by several kcal/mol. This observation raises interesting questions regarding the interpretation of NMR-derived configurational entropies, which currently do not account for correlations. It is also worth noting that the present methodology can provide a structural picture of the origins of entropy changes, a capability of potential value for insight and design. It is not clear that the density of states approaches enable so detailed an analysis.

For densely packed molecules like proteins or systems containing flexible rings (such as cyclohexane above), third-order correlations may become more important and should be addressed by efforts to compute third-order mutual information terms. The nearest-neighbor entropy method^15,60-62 is likely to be particularly valuable for this purpose because it appears to make better use of the available simulation data than the histogramming approach taken here, and thus may speed convergence. Hnizdo et al have employed the nearest-neighbor method for computing configurational entropy of dihedral angles¹⁵, while Kraskov and coworkers have applied the method to more general systems^61,62. In addition, the theory presented here provides a clear basis for formulating mixed levels of approximation in the entropy expansion or, equivalently, the pdf, where highly correlated degrees of freedom would be treated at third order, say, while others would be treated only at second order. Such an approach could be of considerable value in the study of challenging molecular systems. Thus, a range of enhancements and applications of the present expansion approach can readily be envisioned.

APPENDIX A

For a molecule with a potential energy E(r) that is dependent only upon generalized position coordinates, the probability density of the spatial coordinates is given by⁶³

$$\rho \left(\mathbf{r}\right)=\frac{e^{-\beta E\left(\mathbf{r}\right)}}{\int e^{-\beta E\left(\mathbf{r}\right)}d\mathbf{r}},$$ (A1)

such that normalization is imposed in the form $\int \rho \left(\mathbf{r}\right)d\mathbf{r}=1$. This expression is obtained through the assumption of separability of the Hamiltonian into momentum and spatial parts within the Gibbs’ distribution⁶³. The corresponding momentum probability will not be dealt with here. In accordance with probability theory, the average value for an observable X(r) over a continuous distribution is defined as⁶⁴

$$\langle x\left(\mathbf{r}\right)\rangle \equiv \int X\left(\mathbf{r}\right)\rho \left(\mathbf{r}\right)d\mathbf{r}.$$ (A2)

The configurational entropy is related to the standard chemical potential and average energy through the expression in Equation (3)

$$-T{S}^{\mathrm{o}}={\mu }^{\mathrm{o}}-\langle E\rangle .$$ (A3)

Into this one can substitute the definition of the average energy and the definition of μ^o to obtain

$$-T{S}^{\mathrm{o}}=-RT\frac{8{\pi }^2}{C^{\mathrm{o}}}-\left[RT\ln (\int e^{-\beta E\left(\mathbf{r}\right)}d\mathbf{r})\right]\int \rho \left(\mathbf{r}\right)d\mathbf{r}-\int E\left(\mathbf{r}\right)\rho \left(\mathbf{r}\right)d\mathbf{r},$$ (A4)

where the definition of μ^o has been multiplied by the normalization constraint. The term in square brackets above is constant for a given temperature, and can be taken inside the normalization integral. This allows the last two terms on the right hand side to be combined as a single integral,

$$-T{S}^{\mathrm{o}}=-RT\frac{8{\pi }^2}{C^{\mathrm{o}}}-RT\int \rho \left(r\right)[\ln (\int e^{-\beta E\left(\mathbf{r}\right)}d\mathbf{r})+\beta E\left(\mathbf{r}\right)]d\mathbf{r}.$$ (A5)

The second term in the square brackets can be written in the form of a logarithm, such that

$$-T{S}^{\mathrm{o}}=-RT\frac{8{\pi }^2}{C^{\mathrm{o}}}-RT\int \rho \left(r\right)[\ln (\int e^{-\beta E\left(\mathbf{r}\right)}d\mathbf{r})-\ln e^{\beta E\left(\mathbf{r}\right)}]d\mathbf{r}.$$ (A6)

Finally, the logarithms can be combined to yield the expression

$$-T{S}^{\mathrm{o}}=-RT\frac{8{\pi }^2}{C^{\mathrm{o}}}+RT\int \rho \left(\mathbf{r}\right)\ln \left(\frac{e^{-\beta E\left(\mathbf{r}\right)}}{\int e^{-\beta E\left(\mathbf{r}\right)}d\mathbf{r}}\right)d\mathbf{r},$$ (A7)

which becomes

$$-T{S}^{\mathrm{o}}=-RT\frac{8{\pi }^2}{C^{\mathrm{o}}}+RT\int \rho \left(\mathbf{r}\right)\ln \rho \left(\mathbf{r}\right)d\mathbf{r},$$ (A8)

as was to be shown.

APPENDIX B

Equation (20) shows the GKSA for a general m-dimensional pdf. Substitution of this approximate pdf into the logarithm of the entropy integral found in Equation (7) results in Equation (21). One may use the product rule of logarithms to expand this expression (with special attention to the sign of the terms) to obtain

$$S^{(m-1)}=-R\int J(x_1,\cdots ,x_m)\rho (x_1,\cdots ,x_m)\left\{\sum _{n=1}^{m-1}{(-1)}^{m-n+1}\ln \left[\prod _{C_n^m}{\rho }_n\right]\right\}d{x}_1\cdots d{x}_m$$ (B1)

The summation can be taken outside of the integral and the negative sign absorbed into the exponent, yielding the expression

$$S^{(m-1)}=\sum _{n=1}^{m-1}{(-1)}^{m-n+2}R\int J(x_1,\cdots ,x_m)\rho (x_1,\cdots ,x_m)\ln \left[\prod _{C_n^m}{\rho }_n\right]d{x}_1\cdots d{x}_m.$$ (B2)

Each logarithm is a product of $C_n^m$ different n-dimensional joint pdfs. The logarithm of each product of n-dimensional joint pdfs can be expanded using the product rule,

$$S^{(m-1)}=\sum _{n=1}^{m-1}{(-1)}^{m-n+2}R\int J(x_1,\cdots ,x_m)\rho (x_1,x_2\cdots ,x_m)\sum _{C_n^m}\left[\ln {\rho }_n\right]d{x}_{1}d{x}_2\cdots d{x}_m,$$ (B3)

where, as before, the summation can be taken outside of the integral,

$$S^{(m-1)}=\sum _{n=1}^{m-1}{(-1)}^{m-n+2}\sum _{C_n^m}R\int J(x_1,\cdots ,x_m)\rho (x_1,x_2\cdots ,x_m)\ln {\rho }_{n}d{x}_{1}d{x}_2\cdots d{x}_m.$$ (B4)

As any given n-dimensional joint pdf depends on exactly n of the m degrees of freedom, one may integrate over the remaining m - n dimensions independently of the logarithm terms. This integration will result in the reduction of the full m-dimensional pdf to the corresponding n-dimensional joint pdf, ρ_n. If one defines dτⁿ as the differential element of volume corresponding to the n dimensions that remain to be integrated (including the remaining portions of the Jacobian determinant), the entropy can now be written as

$$S^{(m-1)}=\sum _{n=1}^{m-1}{(-1)}^{m-n+1}\sum _{C_n^m}\{-R\int {\rho }_n\ln {\rho }_{n}d{\tau }^n\}.$$ (B5)

The term in braces is exactly the nth-order joint entropy associated with a specific set of n degrees of freedom. Thus, one has the final form of the expansion

$$S^{(m-1)}=\sum _{n=1}^{m-1}{(-1)}^{m-n+1}\sum _{C_n^m}{S}_n.$$ (B6)