Abstract
Using functional genomic and protein structural data we studied the effects of protein complexity (here defined as the number of subunit types in a protein) on gene dispensability and gene duplicability. We found that in terms of gene duplicability the major distinction in protein complexity is between hetero-complexes, each of which includes at least two different types of subunits (polypeptides), and homo-complexes, which include monomers and complexes that consist of only subunits of one polypeptide type. However, gene dispensability decreases only gradually as the number of subunit types in a protein complex increases. These observations suggest that the dosage balance hypothesis can explain gene duplicability of complex proteins well, but cannot completely explain the difference in dispensabilities between hetero-complex subunits. It is likely that knocking out a gene coding for a hetero-complex subunit would disrupt the function of the whole complex, so that the deletion effect on fitness would increase with protein complexity. We also found that multi-domain polypeptide genes are less dispensable but more duplicable than single domain polypeptide genes. Duplicate genes derived from the whole genome duplication event in yeast are more dispensable (except for ribosomal protein genes) than other duplicate genes. Further, we found that subunits of the same protein complex tend to have similar expression levels and similar effects of gene deletion on fitness. Finally, we estimated that in yeast the contribution of duplicate genes to genetic robustness against null mutation is ~ 9%, smaller than previously estimated. In yeast, protein complexity may serve as a better indicator of gene dispensability than do duplicate genes.
Keywords: Protein complex, Gene deletion, Fitness effect, Duplicate gene, Protein domain, Whole genome duplication
1. Introduction
Previous studies have suggested that most genes (~80%) of the budding yeast (Saccharomyces cerevisiae) are nonessential under laboratory conditions (Winzeler et al., 1999; Glaever et al., 2002; Steinmetz et al., 2002). Two mechanisms have been proposed for explaining this phenomenon. The first is the existence of duplicate genes (e.g., Nowak et al., 1997; Gu et al., 2003; Conant and Wagner, 2004; Kafri et al., 2005); that is, the loss of function in one copy can be compensated by the other copy or copies. The second mechanism stems from alternative metabolic pathways, regulatory networks, and so on (Wagner, 2000). Papp et al. (2004) used an in silico metabolic flux model of the yeast metabolic network to address the dispensability issue. They estimated that up to 68% of “dispensable” genes might actually be important, but under conditions yet to be examined in the laboratory, 15–28% of dispensable genes are compensated by a duplicate, while only 4–17% are buffered by flux reorganization of the metabolic network.
In this study, we pursue the gene dispensability issue from the viewpoint of protein complexity. The number of domains in a polypeptide (He and Zhang, 2005) and the number of subunits in a protein complex (Yang et al., 2003) have been used to describe gene complexity and protein complexity, respectively. Here we define “domain complexity” as the number of domains in a polypeptide and “protein complexity” as the number of different subunit types in a protein complex. Although the number of protein interactions has been shown to correlate with protein deletion lethality (Jeong et al., 2001), we have four reasons to investigate protein complexity. First, the protein-protein interaction study was based on high-throughput data, which may have high false positive and false negative rates (von Mering et al., 2002). Second, subunits in a large complex without direct physical interactions to each other may not be detected by yeast two-hybrid analyses. Third, the number of protein interactions may reflect the number of functions or reactions that a polypeptide is involved, while a large complex may have only one specific function. Fourth, we are also interested in comparing monomers and homo-multimers, which is not feasible from protein interaction data.
Utilizing data on the fitness of heterozygotes for knockouts of essential genes in yeast, Papp et al. (2003) found a greater decrease in heterozygote fitness if the gene is involved in a protein complex than if it is not, supporting the dosage balance hypothesis (Veitia, 2002, 2003). However, homozygous gene deletion of a complex subunit may disrupt the protein function, which may be difficult to compensate by duplicated genes or alternative pathways if the function is cooperatively performed by multiple subunits. Further, Phadnis and Fry (2005) showed a negative correlation between homozygous effects and dominance of mutations (the ratio of heterozygous to homozygous effects) for all major categories of genes, which implies heterozygous and homozygous gene deletions may not have the same trend of fitness effect. It is therefore interesting to investigate whether the fitness effect of homozygous gene deletion increases with protein complexity and domain complexity.
The second purpose of this study is to reexamine the issue of the effect of protein complexity on gene duplicability. Although Papp et al. (2003) and Yang et al. (2003) have shown that protein complexity is an important determinant of gene duplicability, the relationship between protein complexity and gene duplicability is still not very clear. This is particularly so with respect to the question of whether homo-complexes tend to have a higher gene duplicability than hetero-complexes; although Yang et al. (2003) considered this question, their data was not sufficiently large to draw a clear conclusion.
A duplication involving one or a few genes and a duplication of the whole genome may be under different selection pressures because whole genome duplication (WGD) may not create a dosage imbalance. Our third purpose is therefore to investigate whether duplicate genes derived from WGD in the yeast (Wolfe and Shields, 1997; Dietrich et al., 2004; Kellis et al., 2004) and non-WGD duplicate genes show different relationships among protein complexity, duplicability, and dispensability. He and Zhang (2006) found that a less severe fitness consequence of deleting a duplicate gene than deleting a singleton gene is at least in part due to the reason that duplicate genes are intrinsically less important than singleton genes. We wish to obtain a better estimate of the contribution of duplicate genes to gene dispensability in the yeast genome because the estimate by Gu et al. (2003) did not subdivide duplicate genes into WGD and non-WGD genes and did not consider the possibility of different gene duplicabilities for homo- and hetero-complexes.
Finally, we are also interested to compare how protein complexity and domain complexity correlate with gene dispensability and gene duplicability, and to investigate whether subunits in a protein complex share similar gene dispensability and expression level. In this study, for simplicity, we include monomers, which consist of a single polypeptide, in the class of homo-complexes because, as will be seen later, monomers and homo-complexes show small differences in both gene dispensability and gene duplicability.
2. Materials and Methods
2.1. Identification of duplicate genes and singletons
An all-against-all FASTA (Pearson and Lipman, 1988) search was conducted for the whole set of S. cerevisiae protein sequences to obtain the list of singleton (single-copy) and duplicate genes as described in Gu et al. (2003). A singleton gene is defined as a protein that does not hit any other proteins in the FASTA search with E = 0.1. Duplicate genes are defined using the following two criteria: (1) their amino acid sequence similarity is ≥ I (I = 30% if L ≥ 150 amino acids but I = 0.01n + 4.8L−0.32(1 + exp(−L/1000)) if L < 150 amino acids, where n = 6 and L is the length of the alignable region), and (2) the length of the alignable region between the two sequences is ≥ 50% of the longer protein. We obtained a whole genome duplication dataset from the genes listed in either Kellis et al. (2004) or Dietrich et al. (2004). Although some gene pairs in the WGD dataset are quite diverged and may not satisfy the duplicate gene definition, we still use them in our analysis. The genes that did not satisfy the criteria for being singletons or duplicate genes were classified as twilight zone genes. The proportion of singleton families, P, was calculated as the number of singletons divided by the sum of the number of singletons and the number of duplicate gene families; 1 - P is used as a measure of gene duplicability.
2.2. Data on fitness effect of gene deletion
The growth rates of each yeast single-gene-deletion strain under various conditions were obtained from Steinmetz et al. (2002) (YDPM, http://www-deletion.stanford.edu/YDPM/YDPM_index.html) with five growth media: YPD, YPDGE, YPG, YPE and YPL; and from Glaever et al. (2002) with six extra conditions: YPGal, Minimal, Ph8, NaCl, Sorbitol and Nystatin. Each strain contains the precise homozygous diploid deletion of one ORF in the yeast genome. Genes annotated as essential in MIPS (Mewes et al., 2002) (http://mips.gsf.de/) or in YDPM were removed from this growth rate dataset because there is a possibility that an essential strain could be detected due to cross hybridization of a tag from another non-essential strain. The remaining genes were used and we calculated the fitness values (f) as the extent of survival and reproduction of the deletion strain relative to the pool of all strains grown and measured collectively (Gu et al., 2003). Essential genes annotated in both MIPS and YDPM were sequentially included, and their fitness values were assumed to be 0. All genes were subdivided into four groups according to their f values: (1) the deletion has a weak or no fitness effect in all conditions studied if fmin ≥ 0.95, where fmin is the smallest f value among all 11 growth conditions; (2) the deletion has a moderate effect if 0.8 ≤ fmin < 0.95; (3) the deletion has a strong effect if 0 < fmin < 0.8; and (4) the deletion is lethal and we set f = 0. To avoid including pseudogenes and erroneously predicted genes, only ORFs with gene names in MIPS, YDPM or SGD (http://www.yeastgenome.org/) were kept for further analyses. Dispensable genes are defined as genes with a weak or no deletion fitness effect, i.e., fmin ≥ 0.95.
Similar to Papp et al. (2003), we only used the growth rates of heterozygous strains obtained on YPD substrate from Steinmetz et al. (2002) to estimate their haplosufficiency. Only genes with two measurements from repeat experiments were retained, and average growth rates were calculated. Relative heterozygous fitness was calculated as the relative growth rate to the pool of all strains.
2.3. Collection of protein complexity data
Domain complexity data is obtained from Deng et al. (2002). Protein complexity is defined here as the number of different polypeptide types in a protein complex, not as the number of polypeptide subunits as defined in Yang et al. (2003). The information of protein complexity was assembled from the complex or subunit descriptions in Swiss-Prot/TrEMBL (http://us.expasy.org/sprot/), MIPS, and SGD. A protein was regarded as a complex only when the descriptions of all components agreed with each other. A careful manual survey of published papers was made to verify these annotations. For example, in MIPS category 100, calcineurin B includes three entries; however, they do not form a hetero-trimer, but, instead, a regulatory subunit and two catalytic subunits form two kinds of hetero-dimers. We also used each gene name and several keywords to find literature on PubMed (http://www.ncbi.nlm.nih.gov/) and Google Scholar (http://scholar.google.com/) to increase the dataset. Homo-complexes (each composed of only one polypeptide type) were divided into monomers, homo-dimers, and homo-multimers, while hetero-complexes (each composed of more than one gene type) were classified according to the number of subunit polypeptide types. Polypeptides appearing in more than one complex were classified as multi-complex subunits, and the largest complex that a protein is involved was designated for the polypeptide. Cytoplasmic and mitochondrial ribosomal proteins were treated separately from other proteins because their unusual properties, such as extremely high expression, and their large numbers of subunits may cause sampling bias.
2.4. Fitness values and expression levels among complex subunits
Since a protein complex is a functional unit, its components should have similar deletion fitness effects. To test this hypothesis, hetero-complex genes, not including ribosomal and multi-complex proteins, were subdivided into dispensable (i.e., with a weak or no gene deletion effect) and indispensable, or lethal and nonlethal to examine if subunits of the same complex tend to have the same effect. We also wish to know, after excluding those dispensable and lethal genes, whether the fitness values of the subunits of a protein complex are still more similar than random gene pairs. For this purpose, we only keep genes with a strong or moderate deletion effect. The mean fitness difference between complex subunits is calculated and compared with the distribution of mean difference between randomly selected gene pairs. This random selection was repeated 107 times. For comparison, the fitness difference between duplicate genes (Gu et al., 2003) is also examined using the present method.
Similar procedures were applied to compare protein expression levels among complex subunits. TAP-tagged protein abundance data (Ghaemmaghami et al., 2003) were obtained from Yeast GFP Fusion Localization Database (http://yeastgfp.ucsf.edu/). Codon adaptation index (CAI) values, each of which indicates the strength of codon usage bias, were from MIPS.
3. Results
3.1. Protein complexity and gene dispensability
Previous studies used either only complex/non-complex dataset (Ge et al., 2001; Papp et al., 2003; Poyatos and Hurst, 2004; Teichmann and Veitia, 2004; Phadnis and Fry, 2005) or used proteins of no recorded interaction as monomers (Yang et al., 2003). We collected a more extended and reliable protein complex dataset, so that an analysis of different protein complexities is feasible. Table 1 shows the fitness effects of gene deletions for subunits of homo-complexes and subunits of hetero-complexes. The proportions of genes with weak (or lethal) fitness effect of deletion for monomers, homo-dimers, and homo-multimers are not significantly different from one another (Fisher’s exact test, p > 0.1). Thus, the number of subunits in a homo-complex protein, including monomers, does not seem to affect gene dispensability significantly. In contrast, subunits of a hetero-complex tend to have a lower dispensability than subunits of a homo-complex, especially when the number of subunit types becomes larger than 2. This trend is also observed for the proportion of genes with lethal deletion effect (Table 1).
Table 1.
Relationships between protein complexity and fitness effect of gene deletion or gene duplicability
| Protein structure a | Total# of genes | Proportions (numbers) of genes with lethal, strong, moderate and weak deletion effect on fitness |
Proportions (numbers) of duplicate, twilight zone, and singleton genes |
Proportion of singleton families, P | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Lethal | Strong | Moderate | Weak | WGD Duplicate | Non-WGD Duplicate | Twilight | Singleton | |||
| Monomer | 109 | 19% (21) | 22% (24) | 18% (20) | 41% (44) | 26% (28) | 14% (15) | 30% (33) | 30% (33) | 54% |
| Homo-dimer | 127 | 20% (26) | 17% (22) | 20% (26) | 42% (53) | 20% (26) | 22% (28) | 23% (29) | 35% (44) | 54% |
| Homo-multimer | 83 | 16% (13) | 24% (20) | 17% (14) | 43% (36) | 18% (15) | 30% (25) | 19% (16) | 33% (27) | 49% |
| Hetero-complex (2) | 166 | 25% (41) | 22% (37) | 19% (32) | 34% (56) | 12% (19) | 13% (22) | 39% (65) | 36% (60) | 75% |
| Hetero-complex (3~4) | 219 | 37% (81) | 24% (52) | 18% (40) | 21% (46) | 10% (23) | 7% (16) | 31% (67) | 52% (113) | 85% |
| Hetero-complex (5~8) | 190 | 59% (112) | 15% (29) | 12% (23) | 14% (26) | 10% (19) | 11% (20) | 36% (69) | 43% (82) | 80% |
| Hetero-complex (9~) | 213 | 58% (124) | 28% (60) | 8% (18) | 5% (11) | 3% (7) | 13% (28) | 30% (63) | 54% (115) | 91% |
| Cytoplasmic ribosome | 126 | 13% (17) | 29% (37) | 45% (57) | 12% (15) | 80% (101) | 5% (6) | 5% (6) | 10% (13) | 21% |
| Mitochondrial ribosome | 62 | 3% (2) | 84% (52) | 5% (3) | 8% (5) | 0% (0) | 0% (0) | 16% (10) | 84% (52) | 100% |
The number in the parentheses for hetero-complexes indicates the number of subunit types.
3.2. Protein complexity and gene duplicability
To reveal the relationships between protein complexity and gene duplicability, we compared the proportions of singleton, duplicate, and twilight zone genes for homo- and hetero-complex subunits (Table 1). The proportion of duplicate genes (including WGD and non-WGD duplicates) is consistently higher than 40% for all homo-complex proteins; the differences between monomers and homo-dimers or homo-multimers are not significant (Fisher’s exact test, p > 0.1). In contrast, subunits of hetero-complexes have a much lower proportion of duplicate genes; the proportion decreases from 25% to 16% as the number of complex subunit types increases from 2 to ≥ 9, though this difference is not statistically significant (Fisher’s exact test, p > 0.05). In terms of the proportion of singleton families (P), the P value increases from 75% to 91% as the number of subunit types in a hetero-complex increases from 2 to ≥ 9. Note that the differences in gene duplicability between subunits of homo-complexes (monomers, homo-dimers, or homo-multimers) and subunits of hetero-complexes (subdivided according to their subunit types) are all significant (Fisher’s exact test, p < 0.01). Yang et al. (2003) showed that complex proteins are less duplicable than monomers. Our present result further indicates that in terms of gene duplicability the major distinction is between homo-complexes and hetero-complexes. It is likely that only duplication of a gene for a subunit in a hetero-complex may cause dosage imbalance.
To include protein dosage for further analysis, we compared the proportion of haploinsufficient genes (heterozygous deletion fitness value obtained on YPD substrate < 0.99) among indispensable genes (homozygous deletion fitness value obtained on YPD substrate < 0.95) for homo-complex subunits. We found that homo-multimers are significantly more haploinsufficient (7/24) than homo-dimers + monomers (6/73, Fisher’s exact test, p < 0.05), which suggests that maintaining a sufficient protein dosage is more essential for homo-multimers (Kondrashov and Koonin, 2004). This result implies that many duplicates of genes for homo-multimer subunits were possibly retained due to protein dosage requirement. Compared to monomers, most duplicates of genes for homo-multimer subunits were from non-WGD events (Fisher’s exact test, p < 0.05, Table 1). This result supports the above observation because unlike WGD, which occurs rarely, non-WGD duplication can occur more frequently and duplicate genes can be retained if there is an increased requirement of protein dosage. We also found that the low duplicability of subunits of large hetero-complexes (composed of 9 or more subunit types) is largely due to their small number of WGD duplicates (Fisher’s exact test compared to other hetero-complexes, p < 0.001, Table 1).
3.3. Ribosomal proteins
Ribosomes are the largest protein complexes in the yeast proteome. The WGD duplicates have been retained for most of the cytoplasmic ribosome proteins, but not for mitochondrial ones (Table 1). This phenomenon might be explained (1) by the dosage theory (Kondrashov and Koonin, 2004), i.e., after the WGD event a larger dosage would be required in the cytoplasm than in the mitochondria, because WGD immediately double the number of nuclear genes but cause no increase in the number of mitochondrial genes, and (2) by the dosage balance hypothesis (Veitia, 2002, 2003), i.e., similar concentrations of subunits in the same protein complex are selectively preferred; otherwise, the imbalanced dosage of subunits may significantly reduce the final concentration of the protein complex. When a singleton cytoplasmic ribosomal subunit is deleted, its function cannot be compensated and the whole ribosome is not functional (10 out of 13 singleton genes have a lethal deletion effect), whereas deletion of a subunit with duplicates may only cause dosage deficiency and imbalance, but may not be lethal (91 out of 107 duplicate genes have strong or moderate deletion effects, but only 3 of them are lethal). Interestingly, most mitochondrial ribosome subunits are not essential (only with strong deletion effects), despite the fact that they are singleton genes.
3.4. Sequence similarity and gene dispensability
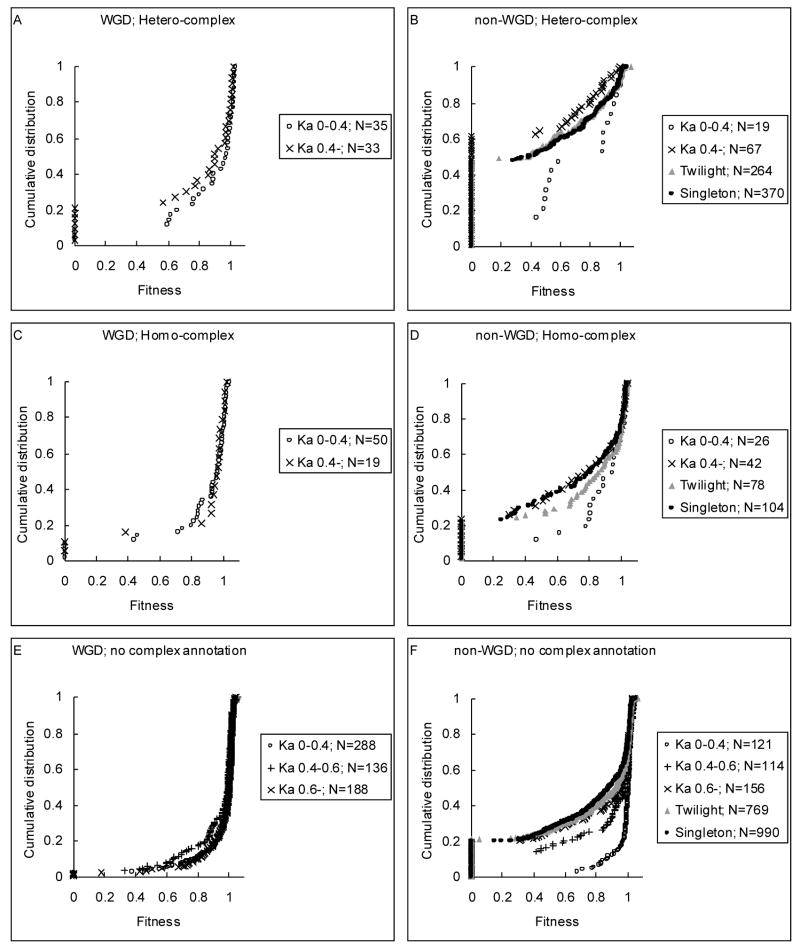
Duplicates with higher sequence similarity were believed to have higher chance of functional compensation (Gu et al., 2003). We subdivided our dataset into WGD and non-WGD sets, and also homo-complexes, hetero-complexes, and proteins without complex annotation (excluding ribosomal proteins). These genes were further subdivided according to the KA of each gene to its most similar paralogue in the genome. Their cumulative distributions of fitness effect of gene deletion were compared (Fig. 1). Surprisingly, the correlation between gene deletion fitness effect and KA is weak, especially for WGD genes (Kolmogorov-Smirnov (KS) test, p > 0.1), though this correlation was considered as strong evidence of functional compensation among duplicates (Gu et al., 2003). On the other hand, non-WGD hetero-complex subunits with KA < 0.4 are more dispensable than subunits with KA > 0.4 (KS test, p < 0.001, Fig. 1B); however, subunits with KA > 0.4 are less dispensable than twilight zone and singleton genes (KS test, p < 0.001). For non-WGD homo-complex subunits, genes with KA > 0.4 have similar fitness distributions (Fig. 1D), while genes with KA < 0.4 are more dispensable (KS test, p < 0.05). Similar results are found for non-WGD genes without protein complex annotations (Fig. 1F). In this case, gene dispensability is increased when KA is < 0.6 (KS test, p < 0.05).
Fig. 1.
Cumulative fitness distribution of gene deletions of WGD (A, C, E) and non-WGD (B, D, F) duplicate genes for hetero-complexes (A, B), homo-complexes (C, D), and proteins without complex annotation (E, F). Duplicate genes are further subdivided according to the KA of each gene to its most similar paralogue in the genome. N indicates gene number.
Because protein complexity is an important determinant of gene duplicability (Papp et al., 2003; Yang et al., 2003), one may suspect that the higher dispensability of subunits of a homo-complex protein is mainly due to a higher proportion of duplicate genes for subunits of homo-complex proteins in the genome. Figure 1 indicates that when the distance of each gene to its most similar paralogue is controlled, homo-complex subunits still are much more dispensable than hetero-complex subunits, especially for non-WGD genes. This result suggests that the higher dispensability for homo-complex subunits is not due to their abundance of duplicate genes. We further analyzed gene dispensability with protein complexity for hetero-complex subunits. When we removed duplicate genes to regenerate the relationships between fitness effect of gene deletion and protein complexity (Fig. 2), the observation that gene dispensability decreases as the number of subunit types in a protein complex increases (Table 1) still holds, except that the dispensability of homo-complex subunits is slightly decreased. Therefore, we suggest that the higher dispensability of genes coding for subunits of small hetero-complexes (or homo-complexes) cannot be attributed to functional compensation of duplicated genes. On the other hand, protein complexity may serve as a better indicator of gene dispensability than does gene duplication, as will be discussed later.
Fig. 2.
Fitness distribution of gene deletions after exclusion of duplicate genes. Homo-complexes include monomers, homo-dimers, and homo-multimers. The number in the parentheses for hetero-complexes indicates the number of subunit types. N indicates gene number.
3.5. Domain complexity and protein complexity
Since a protein domain may be the functional unit, one may expect multi-domain polypeptides to have lower dispensability. Indeed, Figure 3 shows that multi-domain polypeptides (with ≥2 domains) are significantly less dispensable than single-domain polypeptides. This difference is more significant when polypeptides for which no domain information is available are included in single-domain polypeptides. We found that 43% of hetero-complex subunits and 55% of homo-complex subunits are multi-domain polypeptides (Fisher’s exact test, p < 0.001). This result suggests that the proportion of multi-domain polypeptides cannot explain the low dispensability of hetero-complex subunits. On the other hand, one may suspect that the larger number of domains in the homo-complex avoids the need for a hetero-complex, implying that it might be the total number of domains of all the subunits of a protein complex that is a determinant of gene duplicability. To test this hypothesis, we only consider subunits of homo-complex or hetero-complex for which the summation of domain numbers in a complex is 2~4. Duplicate genes are excluded. Our result indicates that hetero-complex subunits are still less dispensable than homo-complex ones (51 genes out of 192 genes with weak deletion fitness effects for hetero-complex subunits; 30 genes out of 70 genes for homo-complex subunits; Fisher’s exact test, p < 0.05). Among these genes, hetero-complex subunits should have fewer domains than homo-complex subunits. Therefore, we suggest protein complexity should be a more important determinant of gene dispensability than domain complexity.
Fig. 3.
Fitness distribution of gene deletions for polypeptides subdivided according to their domain annotation after exclusion of duplicate genes. Single-domain polypeptides are, on average, more dispensable than multi-domain polypeptides (proportion of weak effect genes, p < 0.05; proportion of lethal genes, p < 10−6), while polypeptides with 2 or > 2 domains have similar dispensability (p > 0.1). N indicates gene number.
Previous studies showed that domain complexity (He and Zhang, 2005) and protein complexity (Papp et al., 2003; Yang et al., 2003) both are important determinants of gene duplicability. Therefore, it is interesting to investigate whether these two factors correlate with each other since homo-complex subunits have a higher proportion of multi-domain polypeptides. Table 2 reveals that when the domain number in a polypeptide increases from one to > 2, its gene duplicability (1 - P) also increases from 35% to 64% for homo-complex subunits (Fisher’s exact test, p < 10−2), and from 10% to 45% for hetero-complex ones (Fisher’s exact test, p < 10−9). Moreover, homo-complex subunits are more duplicable than hetero-complex subunits when the number of domains is controlled (Fisher’s exact test, p < 10−7 for single-domain polypeptides; p < 10−3 for polypeptides with 2 domains; the difference is not significant for polypeptides with > 2 domains due to the small sample size). Our result suggests domain complexity and protein complexity are largely independent with respect to gene duplicability.
Table 2.
Relationships between protein complexity, domain complexity and gene duplicability
| Protein structure | Proportions (numbers) of duplicate, twilight zone, and singleton genes |
Proportion of singleton families, P | ||
|---|---|---|---|---|
| Duplicate | Twilight | Singleton | ||
| Homo-complex subunits with one domain | 31% (44) | 25% (36) | 44% (63) | 65% |
| Homo-complex subunits with 2 domains | 49% (48) | 23% (23) | 28% (27) | 47% |
| Homo-complex subunits with > 2 domains | 47% (36) | 34% (26) | 19% (15) | 36% |
| Hetero-complex subunits with one domain | 12% (54) | 27% (120) | 61% (273) | 90% |
| Hetero-complex subunits with 2 domains | 19% (33) | 44% (77) | 37% (64) | 79% |
| Hetero-complex subunits with > 2 domains | 28% (47) | 51% (86) | 21% (35) | 55% |
One-domain polypeptides include polypeptides for which no domain information is available.
3.6. Similar dispensabilities and expression levels for the subunits of a complex
To clarify whether subunits of a complex share similar dispensability, complex subunits were subdivided into dispensable (i.e. with a weak or no gene deletion effect) and indispensable, or into lethal and nonlethal genes (Table 3). The proportions of each combination of subunit pairs found in the same complex and those of randomly selected gene pairs were compared. We found that the observed number of subunit pairs with the same fitness effect category is much higher than expected. Therefore, complex subunits tend to display similar fitness effects of gene deletion. It has been reported that proteins in the same interaction module also have similar dispensability (Poyatos and Hurst, 2004). Because most genes are distributed at the two extreme ends of fitness effect of gene deletion, it is interesting to ask whether the above conclusion still holds if we consider only genes with strong or moderate deletion effects. The answer is yes, no matter which growth condition is considered (Table 4). Although duplicated genes may have a chance to compensate each other’s function (Gu et al., 2003), we found that under most conditions duplicate gene pairs are not as similar to each other in gene deletion effect on fitness as the subunits of a complex. The reason might be that many duplicated genes have already functionally diverged, whereas the subunits of a complex usually play the same functional role.
Table 3.
Expected and observed proportions (numbers) of pairwise fitness combinations for hetero-complex subunits
| Expected proportion (all possible pairwise combinations) | Observed proportion (combinations found in the same complex) | p value (Fisher’s exact test) | |
|---|---|---|---|
| Dispensable vs. Dispensable | 3.2% (9045) | 4.4% (71) | 8.7 × 10−3 |
| Dispensable vs. Indispensable | 29.5% (83295) | 12.2% (197) | 5.1 × 10−62 |
| Indispensable vs. Indispensable | 67.3% (190036) | 83.4% (1350) | 7.6 × 10−49 |
| Lethal vs. Lethal | 19.8% (55945) | 45.4% (735) | 2.2 × 10−120 |
| Lethal vs. Nonlethal | 49.5% (139695) | 18.6% (301) | 1.1 × 10−147 |
| Nonlethal vs. Nonlethal | 30.7% (86736) | 36.0% (582) | 6.2 × 10−6 |
The numbers of dispensable, indispensable, lethal, and nonlethal genes are 135, 617, 335, and 417, respectively.
Table 4.
The mean value of fitness difference between randomly selected gene pairs and between complex subunits or duplicate gene pairs
| Conditions | Complex subunits/random pairs |
Duplicate genes/random pairs |
||
|---|---|---|---|---|
| Mean of fitness difference | p value | Mean of fitness difference | p value | |
| YPD | 0.116/0.142 | 3.6 × 10−6 | 0.120/0.147 | 3.7 × 10−4 |
| YPDGE | 0.105/0.141 | < 1 × 10−7 | 0.109/0.141 | 3.3 × 10−6 |
| YPG | 0.136/0.232 | < 1 × 10−7 | 0.156/0.230 | < 1 × 10−7 |
| YPE | 0.140/0.245 | < 1 × 10−7 | 0.169/0.247 | < 1 × 10−7 |
| YPL | 0.131/0.209 | < 1 × 10−7 | 0.130/0.206 | < 1 × 10−7 |
| YPgal | 0.105/0.133 | 3.0 × 10−5 | 0.099/0.129 | 3.0 × 10−4 |
| Minimal | 0.138/0.158 | 7.3 × 10−3 | 0.123/0.173 | 6.6 × 10−6 |
| Ph8 | 0.132/0.176 | < 1 × 10−7 | 0.142/0.161 | 2.6 × 10−2 |
| NaCl | 0.111/0.135 | 5.4 × 10−4 | 0.112/0.140 | 1.1 × 10−3 |
| Sorbitol | 0.100/0.122 | 7.5 × 10−5 | 0.124/0.127 | 3.7 × 10−1 |
| Nystatin | 0.115/0.145 | 4.2 × 10−5 | 0.117/0.139 | 8.9 × 10−3 |
Only genes with strong or moderate deletion effect on fitness are included.
Under the dosage balance hypothesis, complex subunits should have similar protein expression levels. Using the same method described above, i.e., comparing with randomly selected gene pairs, we find that similarity indeed exists for protein expression levels of complex subunits. The mean logarithm difference of TAP-tagged protein abundance values between hetero-complex subunits is significantly less than the mean difference between random gene pairs (p ≪ 10−7). For proteins that do not have abundance data (~one third of the genes), the codon adaptation index (CAI) was used to infer the expression level (Sharp and Li, 1987; Coghlan and Wolfe, 2000). We found that the mean difference in CAI values between subunits of a protein complex is only half of the mean difference between random gene pairs (p ≪ 10−7). This result is comparable to Ge et al.’s (2001) finding that genes encode interacting proteins tend to have similar expression profiles.
4. Discussion
4.1. Different trends of dispensability and duplicability for hetero-complexes
We noted above that although subunits of hetero-complexes composed of 2 subunit types are less dispensable compared with subunits of homo-complexes (Fig. 2), the difference is not significant (Fisher’s exact test, p > 0.1). In contrast, the dispensability of hetero-complexes composed of 3~4 subunit types is significantly lower (Fisher’s exact test, p < 0.01). In other words, when the number of subunit types increases, gene dispensability decreases gradually, instead of a sharp difference between homo- and hetero-complexes. On the other hand, although gene duplicability (1 - P) correlates with protein complexity, the difference in gene duplicabilities between subunits of hetero-complexes composed of 2 and > 9 subunit types is not significant. Although the insignificance could be due to a small sample size, both duplicabilities are significantly less than the duplicability of homo-complex subunits. The duplicability dramatically decreases from 46% ~ 51% for homo-complex subunits to 9% ~ 25% for hetero-complexes subunits (Table 1). The reason might be only duplication of a gene for a hetero-complex subunit may cause serious dosage imbalance. This observation suggests that the dosage balance hypothesis can explain gene duplicability of complex proteins well (Papp et al., 2003; Yang et al., 2003), but cannot completely explain the difference in dispensabilities between hetero-complex subunits.
It is likely that knocking out a gene coding for a hetero-complex subunit would disrupt the function of the whole complex. This viewpoint is supported by the above result that subunits in the same complex tend to have similar deletion fitness effects. If the function of a protein complex is determined by most or all of its subunits, to compensate its lost function may need another complex either from duplicated genes or from alternative pathways. This effect may be more harmful than a complex concentration reduction derived from subunit duplication or heterozygous deletion (dosage imbalance). On the other hand, the formation of a large protein complex may take a long time in evolution. These protein complexes may play important roles in the organism, so that the complexes can be retained and can accumulate subunits during the evolutionary process. Therefore, losing the function of a large complex may be more severe than losing the function of a small one. This might explain why the dispensability of hetero-complexes decreases with protein complexity.
4.2. Functional compensation by duplicate genes
We subdivided non-WGD genes into hetero-complexes, homo-complexes, and genes without complex annotations (Fig. 1), and estimated the contribution of duplicate genes using Gu et al.’s method (2003). Our result indicates that the dispensability of 1, 10, and 106 genes out of 104, 93, and 1086 dispensable genes might be attributed to gene duplication for these three categories, respectively. The proportion of the contribution of duplicate genes to genetic robustness is thus estimated to be 9% (117/1283) for non-WGD genes. He and Zhang (2006) found that less important genes tend to have a higher gene duplicability than important genes and suggested that this difference can partly account for a less severe fitness effect of deleting a duplicate gene than deleting a singleton gene. In our case, the high dispensability of non-WGD genes with KA < 0.4 may partly be due to recent duplications of less important genes, rather than all from functional compensation by duplicates. Therefore, the contribution of duplicate genes to dispensability may not be as high as previously estimated (23%, Gu et al., 2003).
It is worth noting that, except for ribosomal proteins, most of the ~400 WGD gene pairs that have been retained are dispensable (Fig. 1). For genes with the same protein complexity and with the same range of KA to their most similar paralogues in the genome, WGD genes are consistently more dispensable than non-WGD duplicate genes. The difference is statistically significant for hetero-complexes, for homo-complexes with KA > 0.4, and for genes without complex annotation and with KA > 0.6 (KS test, p < 0.05). This result implies that in the majority of cases the dispensability of WGD genes may not be due to functional compensation from their duplicates, because functional compensation should have similar effects for WGD and non-WGD duplicates. An alternative explanation is that dispensable genes might have a higher chance to be retained than indispensable genes following the WGD event. This result echoes the previous observation that dispensable (less important) genes have a higher duplicability (He and Zhang, 2006). The reason Gu et al. (2003) overestimated the contribution of duplicate genes to dispensability is likely because their singleton dataset includes many hetero-complex subunits, while duplicate gene dataset includes many homo-complex subunits and WGD genes, which are dispensable intrinsically.
Another set of WGD genes are cytoplasmic ribosomal proteins, which, as mentioned earlier, tend to be indispensable. Our result shows that while deletion of a singleton cytoplasmic ribosomal subunit usually has lethal effect, deletion of a ribosomal subunit with duplicates may only cause dosage deficiency and imbalance (strong or moderate effect), but may not be lethal (Table 1). This fact suggests functional compensation exist for these WGD ribosomal proteins. However, although deletion of a ribosomal subunit with duplicates may not be lethal, such deletion is still evolutionarily deleterious. It is likely that their duplicates are retained mainly due to dosage requirement, but not due to functional compensation.
Acknowledgments
We thank two reviewers for comments and Z. Gu, M. Bradley and A. Prachumwat for suggestions and help. The work was supported by grants from National Science Council (NSC 094-2917-I-009-015 to Y. -S. Lin and NSC 093-3112-B-009-001 to J. -K. Hwang) and NIH grants to W. -H. Li. We thank the Structural Bioinformatics Core at the National Chiao Tung University for hardware and software support.
Abbreviations
- WGD
whole genome duplicate
- CAI
codon adaptation index
- KS test
Kolmogorov-Smirnov test
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Coghlan A, Wolfe KH. Relationship of codon bias to mRNA concentration and protein length in Saccharomyces cerevisiae. Yeast. 2000;16:1131–1145. doi: 10.1002/1097-0061(20000915)16:12<1131::AID-YEA609>3.0.CO;2-F. [DOI] [PubMed] [Google Scholar]
- Conant GC, Wagner A. Duplicate genes and robustness to transient gene knock-downs in Caenorhabditis elegans. Proc R Soc Lond B Biol Sci. 2004;271:89–96. doi: 10.1098/rspb.2003.2560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deng M, Mehta S, Sun F, Chen T. Inferring domain-domain interactions from protein-protein interactions. Genome Res. 2002;12:1540–1548. doi: 10.1101/gr.153002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dietrich FS, et al. The Ashbya gossypii genome as a tool for mapping the ancient Saccharomyces cerevisiae genome. Science. 2004;304:304–307. doi: 10.1126/science.1095781. [DOI] [PubMed] [Google Scholar]
- Ge H, Liu Z, Church GM, Vidal M. Correlation between transcriptome and interactome mapping data from Saccharomyces cerevisiae. Nat Genet. 2001;29:482–486. doi: 10.1038/ng776. [DOI] [PubMed] [Google Scholar]
- Ghaemmaghami S, Huh WK, Bower K, Howson RW, Belle A, Dephoure N, O’Shea EK, Weissman JS. Global analysis of protein expression in yeast. Nature. 2003;425:737–741. doi: 10.1038/nature02046. [DOI] [PubMed] [Google Scholar]
- Glaever G, Chu AM, Ni L, Connelly C, Riles L, Veronneau S, Dow S, Lucau-Danila A, Anderson L, Andre B, Arkin AP, Johnston M. Functional profiling of the Saccharomyces cerevisiae genome. Nature. 2002;418:387–391. doi: 10.1038/nature00935. [DOI] [PubMed] [Google Scholar]
- Gu Z, Steinmetz LM, Gu X, Scharfe C, Davis RW, Li WH. Role of duplicate genes in genetic robustness against null mutations. Nature. 2003;421:63–66. doi: 10.1038/nature01198. [DOI] [PubMed] [Google Scholar]
- He X, Zhang J. Gene complexity and gene duplicability. Curr Biol. 2005;15:1016–1021. doi: 10.1016/j.cub.2005.04.035. [DOI] [PubMed] [Google Scholar]
- He X, Zhang J. Higher duplicability of less important genes in yeast genomes. Mol Biol Evol. 2006;23:144–151. doi: 10.1093/molbev/msj015. [DOI] [PubMed] [Google Scholar]
- Jeong H, Mason SP, Barabasi AL, Oltvai ZN. Lethality and centrality in protein networks. Nature. 2001;411:41–42. doi: 10.1038/35075138. [DOI] [PubMed] [Google Scholar]
- Kafri R, Bar-Even A, Pilpel Y. Transcription control reprogramming in genetic backup circuits. Nat Genet. 2005;37:295–299. doi: 10.1038/ng1523. [DOI] [PubMed] [Google Scholar]
- Kellis M, Birren BW, Lander ES. Proof and evolutionary analysis of ancient genome duplication in the yeast Saccharomyces cerevisiae. Nature. 2004;428:617–624. doi: 10.1038/nature02424. [DOI] [PubMed] [Google Scholar]
- Kondrashov FA, Koonin EV. A common framework for understanding the origin of genetic dominance and evolutionary fates of gene duplications. Trends Genet. 2004;20:287–291. doi: 10.1016/j.tig.2004.05.001. [DOI] [PubMed] [Google Scholar]
- Mewes HW, Frishman D, Guldener U, Mannhaupt G, Mayer K, Mokrejs M, Morgenstern B, Munsterkotter M, Rudd S, Weil B. MIPS: a database for genomes and protein sequences. Nucleic Acids Res. 2002;30:31–34. doi: 10.1093/nar/30.1.31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowak MA, Boerlijst MC, Cooke J, Maynard Smith J. Evolution of genetic redundancy. Nature. 1997;388:167–171. doi: 10.1038/40618. [DOI] [PubMed] [Google Scholar]
- Papp B, Pal C, Hurst LD. Dosage sensitivity and the evolution of gene families in yeast. Nature. 2003;424:194–197. doi: 10.1038/nature01771. [DOI] [PubMed] [Google Scholar]
- Papp B, Pal C, Hurst LD. Metabolic network analysis of the causes and evolution of enzyme dispensability in yeast. Nature. 2004;429:661–664. doi: 10.1038/nature02636. [DOI] [PubMed] [Google Scholar]
- Pearson WR, Lipman DJ. Improved tools for biological sequence analysis. Proc Natl Acad Sci USA. 1988;85:2444–2448. doi: 10.1073/pnas.85.8.2444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phadnis N, Fry JD. Widespread correlations between dominance and homozygous effects of mutations: Implications for theories of dominance. Genetics. 2005;171:385–392. doi: 10.1534/genetics.104.039016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poyatos JF, Hurst LD. How biologically relevant are interaction-based modules in protein networks. Genome Biol. 2004;5:R93. doi: 10.1186/gb-2004-5-11-r93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp PM, Li WH. The codon adaptation index - a measure of directional synonymous codon usage bias, and its potential applications. Nucleic Acids Res. 1987;15:1281–1295. doi: 10.1093/nar/15.3.1281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinmetz LM, Scharfe C, Deutschbauer AM, Mokranjac D, Herman ZS, Jones T, Chu AM, Giaever G, Prokisch H, Oefner PJ, Davis RW. Systematic screen for human disease genes in yeast. Nat Genet. 2002;31:400–404. doi: 10.1038/ng929. [DOI] [PubMed] [Google Scholar]
- Teichmann SA, Veitia RA. Genes encoding subunits of stable complexes are clustered on the yeast chromosomes: An interpretation from a dosage balance perspective. Genetics. 2004;167:2121–2125. doi: 10.1534/genetics.103.024505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veitia RA. Exploring the etiology of haploinsufficiency. Bioessays. 2002;24:175–184. doi: 10.1002/bies.10023. [DOI] [PubMed] [Google Scholar]
- Veitia RA. Nonlinear effects in macromolecular assembly and dosage sensitivity. J Theor Biol. 2003;220:19–25. doi: 10.1006/jtbi.2003.3105. [DOI] [PubMed] [Google Scholar]
- von Mering C, Krause R, Snel B, Cornell M, Oliver SG, Fields S, Bork P. Comparative assessment of large-scale data sets of protein-protein interactions. Nature. 2002;417:399–403. doi: 10.1038/nature750. [DOI] [PubMed] [Google Scholar]
- Wagner A. Robustness against mutations in genetic networks of yeast. Nat Genet. 2000;24:355–361. doi: 10.1038/74174. [DOI] [PubMed] [Google Scholar]
- Winzeler EA, Shoemaker DD, Astromoff A, Liang H, Anderson K, Andre B, Bangham R, Davis RW. Functional characterization of the S. cerevisiae genome by gene deletion and parallel analysis. Science. 1999;285:901–906. doi: 10.1126/science.285.5429.901. [DOI] [PubMed] [Google Scholar]
- Wolfe KH, Shields DC. Molecular evidence for an ancient duplication of the entire yeast genome. Nature. 1997;387:708–713. doi: 10.1038/42711. [DOI] [PubMed] [Google Scholar]
- Yang J, Lusk R, Li WH. Organismal complexity, protein complexity, and gene duplicability. Proc Natl Acad Sci USA. 2003;100:15661–15665. doi: 10.1073/pnas.2536672100. [DOI] [PMC free article] [PubMed] [Google Scholar]