PROBABILITY DISCOUNTING OF GAINS AND LOSSES: IMPLICATIONS FOR RISK ATTITUDES AND IMPULSIVITY

Abstract

Sixty college students performed three discounting tasks: probability discounting of gains, probability discounting of losses, and delay discounting of gains. Each task used an adjusting-amount procedure, and participants' choices affected the amount and timing of their remuneration for participating. Both group and individual discounting functions from all three procedures were well fitted by hyperboloid discounting functions. A negative correlation between the probability discounting of gains and losses was observed, consistent with the idea that individuals' choices on probability discounting tasks reflect their general attitude towards risk, regardless of whether the outcomes are gains or losses. This finding further suggests that risk attitudes reflect the weighting an individual gives to the lowest-valued outcome (e.g., getting nothing when the probabilistic outcome is a gain or actually losing when the probabilistic outcome is a loss). According to this view, risk-aversion indicates a tendency to overweight the lowest-valued outcome, whereas risk-seeking indicates a tendency to underweight it. Neither probability discounting of gains nor probability discounting of losses were reliably correlated with discounting of delayed gains, a result that is inconsistent with the idea that probability discounting and delay discounting both reflect a general tendency towards impulsivity.

Risk-taking is a complex construct that can be defined as voluntary participation in behaviors that have probabilistic outcomes. The development of instruments for examining attitudes related to risk-taking is important in understanding the processes involved in potentially harmful behavior. Although self-report scales have traditionally been used to assess risk attitudes (e.g., Zuckerman & Kuhlman, 2000), more recently the probability discounting task has been used to quantify risk attitudes based on behavior observed in the laboratory (e.g., Shead, Callan, & Hodgins, 2008). This article examines the relation between probability discounting of gains and losses in order to test predictions that follow from different definitions of risk attitudes.

Probability Discounting

Probability discounting refers to the observation that a probabilistic gain is usually considered to be worth less than the same amount of gain available for certain. As the probability of receiving a specific gain decreases, the subjective value of that gain decreases and it becomes less likely that the probabilistic gain will be chosen from among alternatives. When probability is expressed as “odds against” (Rachlin, Raineri, & Cross, 1991), the preceding statement can be changed to read, “as the odds against receiving a gain increase, the subjective value of the gain decreases…” (i.e., the value of the probabilistic gain is discounted). In the probability discounting paradigm, participants are asked to choose between sets of certain and probabilistic gains in order to determine an indifference point corresponding to the subjective value of the probabilistic gain. That is, the subjective value of a probabilistic gain is the point at which a certain gain (e.g., $25) and a probabilistic gain (e.g., 25% chance of $100) would be chosen equally as often (Mellers, Schwartz, & Cooke, 1998).

Green, Myerson, and Ostaszewski (1999) have shown that discounting of probabilistic gains is well described by the function:

1

where V is the subjective value of the probabilistic gain, A is the amount of the probabilistic gain, Θ is the odds against receiving the probabilistic gain, h reflects the rate at which the value of the probabilistic gain is discounted, and the exponent s is a scaling parameter that provides an index of sensitivity to odds against winning. The odds against winning are the average number of losses expected before a win on a particular gamble (Rachlin et al., 1991) and may be expressed mathematically as:

2

where Θ is the odds against and p is the probability of winning a gamble. Note that when s  =  1.0, the above function is reduced to a simple hyperbolic function:

3

Risk and Probability Discounting

Risk attitudes can be conceptualized in two ways. In the first conceptualization, which has long been used in economics and finance, the risk associated with a given set of choices is defined by the variance of the possible outcomes such that a probabilistic outcome is always riskier than a certain outcome (Markowitz, 1952). From this perspective, risk attitudes are attitudes toward uncertainty. An attitude of risk-seeking involves placing relatively less weight on the uncertainty (in the sense that one does not know what will actually happen when outcomes are probabilistic) and more on the amounts involved, regardless of whether the outcomes are gains or losses, whereas an attitude of risk-aversion involves placing relatively more weight on the uncertainty and less on the amounts.

A second way to conceptualize risk attitudes is in terms of the probability of an undesirable outcome. According to this conceptualization, it is the relative weight that an individual puts on the most undesirable outcome that tends to remain constant across situations. Consider how this latter conceptualization of risk attitudes relates to probabilistic gains and losses. Note that a probabilistic gain involves either a gain or receiving nothing, and a probabilistic loss involves either a loss or losing nothing. For probabilistic gains, those averse to risk want to avoid the lowest value outcome, getting nothing (and are willing to forgo a chance of getting a large, probabilistic gain), whereas those who are risk-seeking are willing to take more chances to get more (and will tolerate possibly ending up with nothing). For probabilistic losses, those averse to risk want to avoid the chance of losing more (and are willing to forgo the chance of losing nothing) whereas those who are risk-seeking are willing to take more chances in order to possibly lose nothing (and will tolerate the possibility of losing more).

A more formal way of describing this conceptualization of risk attitudes is to consider individual preferences relative to the expected value of a probabilistic event. The expected value (EV) of a gamble can be expressed as:

4

where A is the nominal value of the outcome (either a gain or loss) and p is the probability of that outcome occurring. For example, if there is a 30% chance of winning $50, the expected value of that gamble is .30 times 50, or $15.

Returning to Equation 3, it can be shown that when s  =  1.0 and h  =  1.0, the subjective value of a probabilistic outcome is equal to the expected value.1 That is, EV  =  pA  =  A/(1 + Θ). When the expected value of a probabilistic outcome is plotted as a function of the odds against the outcome occurring, the riskiness associated with different rates of probability discounting can be evaluated graphically. This is illustrated in the top panel of Figure 1, in which the curved line represents the expected value of a $10 gain as a function of the odds against receiving it. This line represents the degree of probability discounting that is considered risk-neutral. Any deviation from the expected value of the probabilistic outcome reflects some degree of risk-aversion or risk-seeking because more or less weight is being placed on the most undesirable outcome relative to the most desirable outcome. When the degree of discounting is shallower than the expected value, data points fall above the EV line. In other words, a lower degree of probability discounting (higher subjective values) is associated with risk-seeking choices. When the degree of discounting is steeper than the expected value, data points fall below the EV line. In other words, a higher degree of probability discounting (lower subjective values) is associated with risk-averse choices.

Fig 1.

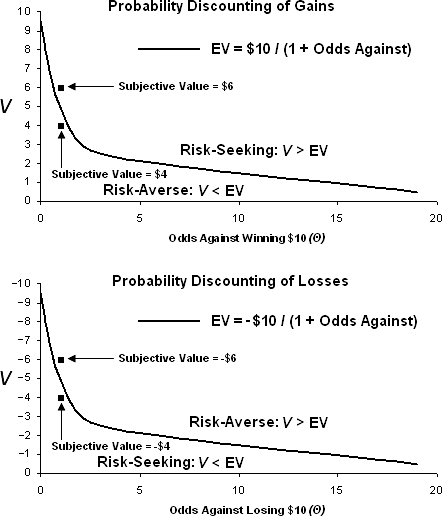
Expected value as a function of odds against receiving or losing $10. For probabilistic gains (top panel), the EV function divides the space into two domains: risk-seeking, when subjective value is greater than EV, and risk-averse, when subjective value is less than EV. For probabilistic losses, the EV function again divides the space into two domains: risk-seeking, when subjective value is less than EV, and risk-averse, when subjective value is greater than EV. Examples of subjective values that deviate from EV are plotted at Θ  =  1 (EV  =  +/−$5).

The bottom panel of Figure 1 depicts the expected value function (i.e., the curved line) for probabilistic losses. As illustrated, when probabilistic losses are discounted, lower subjective values indicate risk-seeking choices. This makes intuitive sense because someone who is risk-seeking is more likely to choose the possibility of losing nothing, while taking the risk of possibly losing the entire larger amount, rather than incur a smaller, certain loss. In other words, risk-seeking individuals show steep discounting of probabilistic losses. Meanwhile, a risk-averse individual is more likely to incur the smaller, certain loss rather than risk losing the larger, probabilistic amount. Such individuals show shallow discounting of probabilistic losses and are willing to lose more to avoid the possibility of losing a larger amount.

As an example of how risk attitudes are quantified by degree of discounting relative to EV, consider the flipping of a coin. Suppose someone is told that a coin will be flipped, and she will win $10 if it lands on heads but will win nothing if it lands on tails. The risk-neutral subjective value for a probabilistic gain of $10 with a probability of 0.5 (Θ  =  1) corresponds to the EV  =  $10(.5)  =  +$5. In this scenario, preferring to get $4 for sure rather than flipping a coin to see whether or not you win $10 is risk-averse and would be reflected in steeper discounting of the probabilistic $10 gain, whereas preferring a coin flip over $6 for sure is risk-seeking and would be reflected in shallower discounting (see the top panel of Figure 1). Now suppose the same person is told that a coin will be flipped, and she will lose $10 if it lands on heads but will lose nothing if it lands on tails (EV  =  −$5). In this instance, preferring to pay $6 rather than flipping a coin to see whether one has to pay $10 or nothing at all is risk-averse and would be reflected in shallower discounting of the probabilistic $10 loss, whereas preferring to flip a coin rather than pay $4 is risk-seeking and would be reflected in steeper discounting (see the bottom panel of Figure 1).

Thus, using this working definition of risk attitudes, risk-seeking individuals exhibit shallower discounting of gains because they overweight the possibility of a large gain while underweighting the possibility of gaining nothing. For losses, risk-seeking individuals exhibit steep discounting because they overweight the outcome of losing nothing while underweighting the possibility of losing a large amount. Correspondingly, risk-averse individuals discount gains steeply because they overweight the possibility of gaining nothing while underweighting the possibility of a large gain; and they discount losses shallowly because they overweight the possibility of losing a large amount and underweight the possibility of a small loss.

The distinction between risk-seeking and risk-aversion used here is reminiscent of that between optimists and pessimists: those who are risk-taking are more controlled by the best that could happen; those who are risk-averse are more controlled by the worst that could happen. What is important for the present study is that this distinction predicts a negative correlation between discounting of gains and losses. That is, risk-seeking individuals who prefer larger, probabilistic gains over smaller, certain gains (and hence show shallow probability discounting of gains) should also prefer larger, probabilistic losses over smaller, certain losses (and hence show steep probability discounting of losses). In contrast, risk-averse individuals should show steep probability discounting of gains but shallow probability discounting of losses.

Delay Discounting

Many behavior analysts favor a definition of impulsivity that includes an inability to delay gratification, as evidenced by preference for smaller, more immediate gains over larger, delayed gains and higher rates of delay discounting (Rachlin, Brown, & Cross, 2000). This has led some researchers to use delay discounting as a measure of impulsivity (e.g., Crean, de Wit, & Richards, 2000). Delay discounting refers to the tendency for delayed gains to be considered worth less compared to the value of immediate gains (Ainslie, 1975; Bickel & Marsch, 2001). As the length of time until receipt of a gain increases, the subjective value of that gain decreases and it becomes less likely that the delayed gain will be chosen among current alternatives. In the delay discounting experimental paradigm, participants usually are presented with choices between a gain (e.g., money) that is available immediately and a gain that is available after a specified delay. The amount of the immediate gain is adjusted to identify the subjective value of the delayed gain. This subjective value, or indifference point, represents the point at which an immediate gain and a delayed gain would be chosen equally as often.

Both human and nonhuman preference between immediate and delayed gains is well described by a hyperboloid function:

5

where V is equal to the subjective value of a delayed gain, A is equal to the amount of the delayed gain, D is equal to the length of the delay before A is received, k is equal to the individual rate at which the value of the delayed gain is discounted, and the exponent s is a scaling parameter that provides an index of sensitivity to delay (for a review, see Green & Myerson, 2004). As rates of discounting increase, the value of k increases and the discounting curve becomes steeper. Steeper discounting curves describe individuals who prefer smaller, more immediate gains over larger, delayed gains. The s parameter modifies the form of the original hyperbolic function so that when s is less than 1.0, it flattens the curve, causing it to level off as the length of delay increases. Note that the simple hyperbolic discounting function (Mazur, 1987):

6

represents the special case of Equation 5 when s  =  1.0.

A number of studies have compared the discounting rates of groups that are assumed to differ in impulsivity (Baker, Johnson, & Bickel, 2003; Crean et al., 2000; Kirby, Petry, & Bickel, 1999; Mitchell, 1999; Petry, 2001a, b; Petry & Casarella, 1999; Reynolds, Karraker, Horn, & Richards, 2003; Reynolds, Richards, Horn, & Karraker, 2004). Results show that groups composed of putatively more impulsive individuals demonstrate higher rates of delay discounting than groups composed of less impulsive individuals. Heroin addicts, for example, are described as impulsive because they cannot control the urge to use drugs even though the long-term health and financial consequences are quite negative, and Kirby et al. showed that heroin addicts had higher discount rates for delayed gains than control participants.

Present Investigation

Several studies have reported positive correlations between rates of probability and delay discounting of gains (Mitchell, 1999; Myerson, Green, Hanson, Holt, & Estle, 2003; Richards, Zhang, Mitchell, & de Wit, 1999). Myerson et al. suggested that such results are inconsistent with the notion that there is a general impulsiveness trait that underlies both an inability to delay gratification and a tendency to gamble and take risks. However, Richards et al. argued that impulsive individuals (i.e., those with higher k values) may indeed take more risks, but only when there is the possibility of a negative outcome occurring. If so, then examining the discounting of probabilistic losses would be of particular relevance to our understanding of risky behavior in the real world, where most forms of risky activities, such as gambling, involve both the possibility of gaining something (probabilistic gains) and the possibility of losing something (probabilistic losses).

Estle, Green, Myerson, and Holt (2006) recently compared the discounting of delayed and probabilistic hypothetical gains and losses. They found that delayed gains are discounted significantly more steeply than delayed losses, but only at smaller amounts, whereas probabilistic gains are discounted significantly more steeply than probabilistic losses, but only at larger amounts. However, they did not examine correlations among rates of discounting on the various tasks, perhaps because the number of participants was relatively small for a correlational study.

The present study expands on this work by examining the correlations among discounting of probabilistic losses, probabilistic gains, and delayed gains. Examining the correlation between discounting of probabilistic gains and losses is particularly important because it allows for a comparison between two alternative ways of thinking about risk— either as the possibility of an unfavorable outcome or as uncertainty regarding the outcome. Each alternative has different implications for risk attitudes and traits such as risk-aversion and risk-seeking. The relation between delay discounting and probability discounting of gains and losses is also of considerable importance, given that it is often assumed that impulsivity is a trait affecting choices involving probabilistic outcomes as well as choices involving delayed outcomes. Thus, clarifying the relation between delay and probability discounting may have important implications for understanding impulsivity.

METHOD

Subjects

All of the participants (14 males and 46 females), aged 18 to 28 (M  =  21.0), were students at the University of Calgary and received psychology course credit as well as monetary compensation for their participation.

Apparatus

Each participant completed three computerized discounting tasks: (1) delay discounting of gains, (2) probability discounting of gains, and (3) probability discounting of losses. These tasks were programmed using PsyScope software (Cohen, MacWhinney, Flatt, & Provost, 1993).

Procedure

Upon arriving at the laboratory, participants read and signed a consent form describing the study. At this point they received $20.00, and it was explained that they would be able to keep at least a portion of this money at the conclusion of the experiment. Next, participants were told that they would be asked to make a series of choices between two monetary amounts, and that there would be three types of choice tasks. It was also explained that their performance on these tasks would affect the amount of money that they would receive for participating in the study.

More specifically, participants were told that one question from each of the three discounting tasks would be randomly selected at the end of the session and their responses to those questions would be used to determine how much of the $20.00 provided at the beginning of the study they would be allowed to keep. The purpose of this procedure was to encourage participants to make every choice as though the outcome they selected was one they would actually receive (Kirby & Herrnstein, 1995). Instructions for the three discounting tasks (see Appendix A) were delivered verbally, followed by a practice trial for each type of task. After completion of the practice trials, the experiment began. The order in which the three types of tasks were completed was counterbalanced across participants.

In the two probability discounting tasks, participants answered six questions in each block of questions at each of six different probabilities. For probability discounting of gains, each question asked participants to choose between a certain amount and a larger, probabilistic amount ($10.00) that could be received with one of six different probabilities (shown on the computer monitor as the percent chance of receiving the gain). These probabilities were presented in the following order: 95, 90, 75, 50, 25, and 5%; using Equation 2, the odds against receiving these probabilistic gains can be calculated to be .053, .111, .333, 1.0, 3.0, and 19.0, respectively.

At each of the six probabilities, a block of six questions was presented on the computer screen. The first block of questions consisted of choices between a certain gain and $10.00 with a probability of 95%, the second block of questions consisted of choices between a certain gain and $10.00 with a probability of 90%, and so on. The amount of the certain gain was adjusted across successive questions within each block, based on the participant's response to the previous question. For example, the first question in each block asked the participant to make a choice between a probabilistic gain ($10.00) and a certain gain whose amount was half that of the probabilistic gain ($5.00). If a participant chose the certain gain, then its amount was decreased on the next choice; if a participant chose the probabilistic gain, then the amount of the certain gain was increased on the next choice.

The size of the adjustment decreased with successive choices in order to rapidly converge on the individual's indifference point at each probability. Each adjustment was half the difference between the probabilistic and certain gains from the previous question. Thus, the second question in each block consisted of a certain gain of $7.50 or $2.50, depending on the participant's response to the first question. If a participant chose a 75% chance of $10.00 over a certain gain of $5.00 on the first question, the second question would ask the participant to choose between a 75% chance of $10.00 and a certain gain of $7.50 ($5.00 + $2.50  =  $7.50). Alternatively, if the participant chose a certain gain of $5.00 over a 75% chance of $10.00, the second question would ask the participant to choose between a 75% chance of $10.00 and a certain gain of $2.50 ($5.00 − $2.50  =  $2.50). For subsequent questions, the adjustment was half of the previous adjustment. For example, on the second question, if the participant chose a 75% chance of $10.00 over a certain gain of $2.50, then the next question would ask the participant to choose between a 75% chance of $10.00 and a certain gain of $3.75 (i.e., $2.50/2  =  $1.25 + $2.50  =  $3.75).

This procedure was repeated until the participant answered all six questions in the block for the given probability. The certain amount that would have been presented on a seventh trial, had there been one, was used as an estimate for that participant's indifference point for the given probability. Six indifference points, each indicating the subjective value of the probabilistic gain at a different probability, were obtained for each participant.

For the probability discounting of losses task, the procedure was similar except that each question asked participants to choose between an amount that was certain to be lost and a larger, probabilistic amount that could be lost with a stated probability. The probability of losing nothing was also stated in parentheses to clarify the difference between the two types of probability discounting tasks. The decision-making process was assumed to be somewhat analogous to deciding whether to pay a small fixed fee to park your car in a parking lot or temporarily park your car illegally at no cost but at the risk of incurring a large fine.

The probabilistic loss was always $10.00 and the probabilities were 95, 90, 75, 50, 25, and 5%. The adjusting-amount procedure was similar to that used in the probability gain discounting tasks; however, the amount of the certain loss was adjusted across questions within each block according to the reverse rule used to adjust gains. That is, if a participant chose the certain loss, then the amount of the certain loss was increased (instead of decreased) on the next question; if a participant chose the probabilistic loss, then the amount of the certain loss was decreased (instead of increased) on the next question. Six indifference points, indicating the subjective value of the probabilistic loss, were obtained for each participant.

In the delay discounting task, an adjusting-amount procedure analogous to the one use for probabilistic gains was employed. Each question asked participants to choose between a gain that was available immediately and a gain that was delayed by a specified period of time. The delayed gain was always $10.00 and was available after one of six delays (1, 7, 30, 90, 180, or 365 days). At each delay, six questions were presented sequentially on the computer screen. Each block of six questions required participants to choose between an immediate gain and $10.00 at a fixed delay that increased across blocks. The amount of the immediate gain was adjusted across questions within each block. The adjusting-amount procedure was the same as that used in the probability discounting task for gains. Again, six indifference points were obtained for each participant indicating the subjective value of the delayed gain.

To safeguard against participants making errors that could lead to inaccurate estimates of their indifference points, two programming features were included in all three discounting tasks. First, if at any point participants made a choice they were not happy with, they could push a key labelled “restart” which would take them back to the start of the current block of questions. Second, because participants' first choice in a block of questions (i.e., the choice between an immediate/certain outcome of $5.00 and delayed/ probabilistic outcome of $10.00) had the most influence on their subsequent choices (i.e., whether all immediate/certain outcomes would be above or below $5.00), a confirmation procedure was used in which participants were required to confirm their choice between the immediate/certain outcome of $5.00 and delayed/ probabilistic outcome of $10.00 at two finer increments of amount before proceeding.

For example, if a participant chose $5.00 immediately over $10.00 in 30 days, the next choice would be between $4.99 immediately and $10.00 in 30 days. If they then chose $4.99 immediately, their next choice would be between $4.97 immediately and $10 in 30 days. If they again chose the immediate amount, their next choice would be determined by the adjusting-amount procedure (i.e., $2.50 immediately or $10.00 in 30 days). Similarly, if a participant chose $10.00 in 30 days over $5.00 immediately, their next two choices would have an immediate gain of $5.01 and $5.03, respectively. If a participant were to make inconsistent choices on one of these “confirmation” trials (e.g., choose $5.00 immediately for the first question but then choose a delayed $10.00 over $4.99 immediately), the procedure would revert to the first question in the block.

Data Analysis

Hyperboloid discounting functions (Equations 1 and 5) were fitted to the data for individual participants and to the group medians for each discounting task using nonlinear least squares regression implemented by Microsoft® Excel's SOLVER Add-In (Brown, 2001). In addition, degree of discounting was measured by calculating the area under the discounting curve (AUC: Myerson, Green, & Warusawitharana, 2001; note that smaller AUCs reflect steeper rates of discounting). The resultant AUCs then were used in correlational analyses.

RESULTS

The top panel in Figure 2 shows the group median subjective value of a probabilistic $10 gain plotted as a function of the odds against receiving that gain. The curved line represents the best-fitting hyperboloid model (Equation 1). The proportion of variance accounted for (R²) was .990 (h  =  4.45 and s  =  0.44). The middle panel shows the group median subjective value of a probabilistic $10 loss as a function of the odds against losing the $10. Once again, the hyperboloid model fit the group data well. The proportion of variance accounted for was .990 (h  =  2.36 and s  =  0.55). The bottom panel shows the group median subjective value of a delayed $10 gain as a function of the delay until receiving the $10. The curved line represents the fit of the hyperboloid model (Equation 5). The proportion of variance accounted for was .993 (k  =  0.00014 and s  =  27.20).

Fig 2.

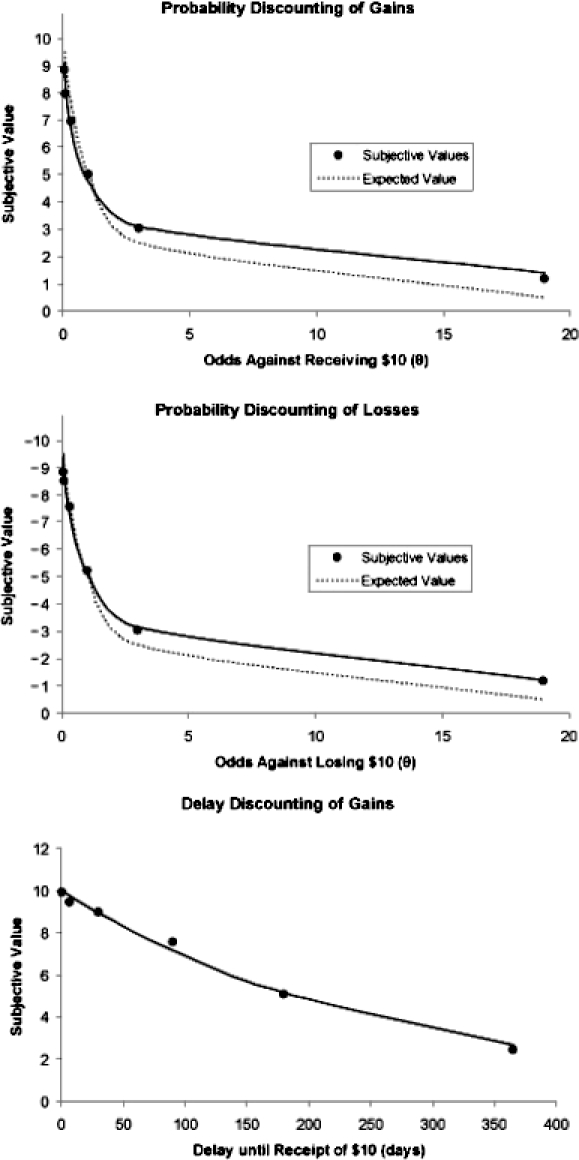
Group discounting functions for the three discounting tasks. Data points represent the group median indifference points. For probabilistic gains (top panel), the solid line represents the best-fitting hyperboloid discounting function, where h  =  4.45, s  =  .44, R²  =  .990; the broken line represents the expected value. For probabilistic losses (middle panel), the solid line represents the best-fitting curve for the hyperboloid discounting function, where h  =  2.36, s  =  .55, R²  =  .990; the broken line represents the expected value. For delayed gains (bottom panel), the solid line represents the best-fitting hyperboloid discounting function, where k  =  .00014, s  =  27.20, R²  =  .993.

These results indicate that the hyperboloid function provided an excellent model for fitting group discounting data. In order to discern whether this model was adequate for fitting individual discounting data, individual coefficients of determination, R², were examined. For the probability gain discounting task, the median of the R²s for the fits of Equation 1 to the individual participants' indifference points was .94 when the probabilistic outcome was a gain and .93 when the probabilistic outcome was a loss. For the delay discounting task, the median of the R²s for the fits of Equation 5 to the individual participants' indifference points was .89. Taken together, these results indicate that the hyperboloid function provides a good description of individual as well as group discounting data.

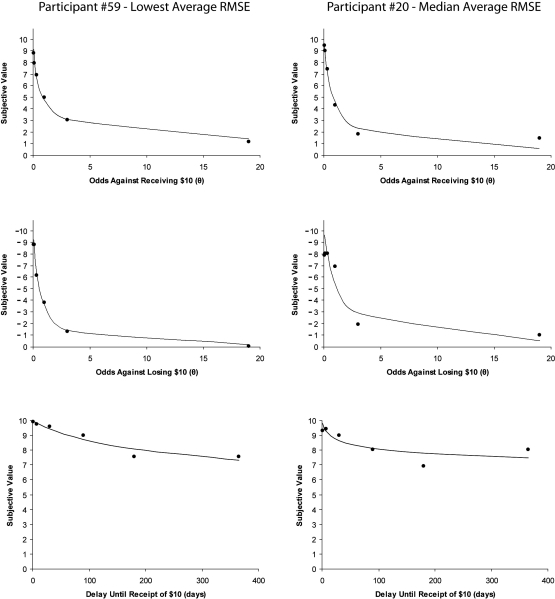
Examples of fits to individual data are shown in Figure 3. The figure depicts individual discounting functions for the participant with the lowest average root mean squared error (RMSE) across the three discounting tasks (i.e., the best fit) and the participant whose average RMSE corresponded to the group median. Individual R², RMSE, and AUC for all 60 participants for each of the three discounting tasks are reported in Appendix B.

Fig 3.

Individual discounting functions for participants whose average RMSEs across the three discounting tasks correspond to the lowest average RMSE (left panels), and the median average RMSE (right panels). In each instance, the top graph represents the individual participant's subjective values and best-fitting curve for probabilistic gains, the middle graph represents probabilistic losses, and the bottom graph represents delayed gains.

The R²s for individual data were used to determine whether a participant's data were included in the subsequent correlational analyses. That is, if any individual's data were not well described by the hyperboloid model (as indicated by a low R²), then the discounting task data for that individual were excluded from the analysis. A low R² suggests that the individual's decisions on the particular task were highly irregular compared to other participants. For example, low R²s could result from exclusive responding to one alternative. Multiple switches between immediate and delayed gains, such as choosing $5.00 now over $10.00 in 30 days and then choosing $10.00 in 90 days over $5.00 now, would lead to an increase in subjective value of delayed gains over time. Such a pattern cannot be described by the model and suggests a lack of understanding of the discounting task.

Individual participants' data were excluded from correlational analyses if their R² was equal to zero or was an extreme outlier based on a boxplot analysis. Extreme cases were determined by multiplying the interquartile range of R² values by three and then subtracting that value from the value of the R² at the first quartile (25^th percentile). Any R²s lower than the resulting value were deemed extreme cases and excluded from analyses examining data from that discounting task. For probability discounting of gains, 2 participants were excluded (Participants 24 and 47), which made the lowest R²  =  .55 (Participant 18) among the remaining sample. For probability discounting of losses, 5 participants were excluded (Participants 1, 18, 47, 51, and 57), making the lowest R²  =  .73 (Participant 35) among the remaining sample. For delay discounting, 4 participants were excluded (Participants 26, 33, 36, and 47), which made the lowest R²  =  .32 (Participant 51) among the remaining sample.

When the correlations among the AUCs for the different discounting tasks were examined, there was little evidence of a relation between delay discounting and discounting of either probabilistic gains or losses. The correlation between delay discounting and probability discounting of gains was not significant, r(53)  =  .15, p  =  .268. The probability of replication, p_rep, defined as the proportion of times the sign of the obtained correlation was replicated in 2000 resamples (Killeen, 2005) was .88. The correlation between delay discounting and probability discounting of losses also was not significant, r(50)  =  .16, p  =  .274, with p_rep  =  .88.

The only correlation of AUC measures that approached significance was that between discounting of probabilistic gains and discounting of probabilistic losses, r(52)  =  −.26, p  =  .062, with p_rep  =  .97. This result suggests that individuals who discounted probabilistic gains more steeply tended to show relatively shallow discounting of probabilistic losses, whereas those who showed shallow discounting of probabilistic gains showed relatively steep discounting of probabilistic losses. These results are consistent with the present view of risk attitudes, which implies that risk-averse individuals will discount probabilistic gains at high rates and losses at low rates whereas risk-seeking individuals will show the opposite pattern.

Further evidence for this view was provided by an analysis that focused specifically on the probability discounting data and the difference between subjective values and expected values. For this analysis, each participant's subjective values for the six probabilities on each probability discounting task were compared to the corresponding expected values, and the difference between subjective values and corresponding expected values were summed, resulting in two scores (one for gains and one for losses) that quantified an individual's deviations from expected value.

The key finding was a significant negative correlation between the scores for the two probability discounting tasks, r(54)  =  −.451, p  =  .001. According to the present view of risk attitudes, subjective values for probabilistic gains that are lower than expected values are indicative of risk-averse choices, whereas subjective values higher than expected values are indicative of risk-seeking choices. The opposite is true for probabilistic losses: subjective values that are lower and higher than expected values reflect risk-seeking and risk-averse attitudes, respectively. Thus, the observed negative correlation reflects the fact that those who tended to be risk-averse on one probability discounting task tended to be risk-averse on the other task as well, and those who tended to be risk-seeking on one task tended to be risk-seeking on the other task, too.

Finally, based on their AUCs, approximately half (54%) of the participants showed steeper discounting of probabilistic gains than of probabilistic losses. To determine whether participants discounted probabilistic gains and losses to significantly different degrees, we compared AUCs using a paired samples t-test. The results of this analysis revealed that there was no significant difference in the degree to which participants discounted probabilistic $10 gains (M  =  .289, SD  =  .145) and probabilistic $10 losses (M  =  .286, SD  =  .152), t(53) < 1.0, p  =  .922.

DISCUSSION

The major goal of the present study was to examine the pattern of correlations among discounting of probabilistic gains, probabilistic losses, and delayed gains, and to consider the implications of this pattern for the nature of risk attitudes and their relation to impulsivity. An additional goal was to test whether a hyperboloid function (Equation 1) describes probability discounting of gains and losses when participants' choices affect their remuneration for participating.

With respect to the form of the probability discounting function when participants' choices lead to real gains and losses, results showed that indeed, probability discounting was well described by the hyperboloid function. This was true for both group and individual probability discounting functions and for both gains and losses. These results replicate and extend Estle et al.'s (2006) findings with hypothetical monetary gains and losses. In the present study, participants knew that the total amount of money they would receive after the session depended on the choices they had made, yet probabilistic gains and losses were discounted to the same degree. This result is consistent with Estle et al., who found that hypothetical losses are discounted more steeply than hypothetical gains only when relatively large amounts were involved (i.e, greater than $100; see Experiment 4 in Estle et al.).

With respect to the pattern of correlations among discounting of probabilistic gains, probabilistic losses, and delayed gains, the degree to which delayed gains were discounted (as measured by the AUC) was not correlated with the degree to which probabilistic gains or probabilistic losses were discounted. The important finding was a negative correlation (r  =  −.26) between degree of probability discounting of gains and probability discounting of losses which had a high probability of replication, p_rep  =  .97, indicating that the correlation between probability discounting of gains and losses would be negative in 97 out of 100 replications of the preset study. Indeed, in a recent study of university students who reported that they gambled “in some form at least twice per month” (Shead et al., 2008), we found an even stronger negative correlation, r  =  −.54, between discounting of probabilistic gains and losses.

Taken together, these findings suggest that individuals who discount probabilistic gains at lower rates tend to discount probabilistic losses at higher rates, and vice versa. Although the observed negative correlation would bear further replication, the present results clearly are inconsistent with an interpretation of risk attitudes based on an “uncertainty” hypothesis. Such a hypothesis predicts a positive correlation because risk-seeking individuals should shallowly discount probabilistic outcomes and risk-averse individuals should discount such items steeply, regardless of whether the outcomes are gains or losses.

Rather, the results support an interpretation of risk attitudes according to which riskier choices are associated with overvalued gains and undervalued losses and/or overestimation of the odds of experiencing a gain and underestimation of the odds of experiencing a loss. That is, individuals who discount probabilistic gains to a lesser degree are taking greater risks to obtain them (preferring a chance at a larger gain over a smaller, certain gain) than those who discount probabilistic gains more shallowly. Similarly, individuals who discount probabilistic losses to a greater degree are taking greater risks to avoid a loss altogether (preferring a chance of no loss versus an “insurance policy” of a smaller, certain loss). Therefore, risk-seeking individuals should have a tendency to overweight the highest-valued outcome, regardless of whether the outcomes are gains or losses. Consistent with this interpretation, participants in the present study who took more risks when making decisions involving probabilistic gains (preferred larger, probabilistic gains over smaller, certain gains) also took more risks when making decisions involving probabilistic losses (preferred larger, probabilistic losses over smaller, certain losses), as indicated by the negative correlation between probability discounting of gains and losses.

Also of interest is the present finding that the correlation between delay discounting and discounting of probabilistic gains was not significant. This latter result is not consistent with some previous research that has found significant positive correlations between rates of delay and probability discounting of gains (e.g., Holt, Green, & Myerson, 2003; Mitchell, 1999; Richards et al., 1999), but is consistent with Myerson et al. (2003). Myerson et al. studied two larger than usual samples (both Ns > 100) using both smaller and larger amounts of reward and found that although the correlations between discounting of delayed and probabilistic gains were never negative, they were sometimes significant and sometimes not. The presence of a correlation between the two probability discounting tasks and the absence of a correlation between delay and probability discounting tasks has at least two important theoretical implications. First, it reinforces the notion that separate processes underlie the discounting of delayed and probabilistic outcomes (Green & Myerson, 2004), and second, it suggests that there are fundamental similarities in the processes that underlie decisions involving probabilistic gains and decisions involving probabilistic losses.

Our finding of a negative correlation between probability discounting of gains and losses has important implications for an interpretation of individual differences based on prospect theory (Kahneman & Tversky, 1979). According to prospect theory, the subjective value of a probabilistic outcome is the product of a probability weighting function and a value function. The probability weighting function is assumed to be the same for gains and losses, but gains and losses are associated with separate value functions. Thus, if individual differences in probability discounting primarily reflect individual differences in the probability weighting function, then the degree to which probabilistic gains and losses are discounted should be positively correlated. However, if individuals differ more in their value functions than in their weighting functions, then the correlation between the two types of discounting will be primarily dependent on the former. From the perspective of prospect theory, therefore, the observed negative correlation argues that individual differences in value functions are more important than individual differences in probability weighting functions in determining the degree of discounting.

It should be noted, however, that individual differences in value functions, in principle, could give rise to either negative or positive correlations between probability discounting of gains and losses depending on the nature of the covariation between the value functions for gains and losses. Prospect theory (Kahneman & Tversky, 1979) is moot on this point. It is also possible that the assumption that the probability weighting function is unaffected by the nature of the probabilistic outcome is incorrect. Further research is needed that examines the basis for the negative correlation between probability discounting of gains and losses from various theoretical perspectives.

The sample used in this study limits our ability to generalize to other populations. Most participants were college students in their twenties. Previous discounting research has shown that delay discounting rates change as a function of age (Green, Fry, & Myerson, 1994), and it is not unlikely that probability discounting rates do so, too. Future research should examine probability discounting of losses with samples of individuals from a broader population. In addition, it would be informative to examine group differences in probability discounting of gains and losses, and given the inherent risk involved in gambling behavior, it would be especially interesting to examine discounting of probabilistic losses among problem gamblers.

As noted earlier, several studies have found that problem gamblers discount delayed gains at higher rates than controls (Petry, 2001a, b; Alessi & Petry, 2003). However, another study (Holt et al., 2003) in which the participants were all college students found no differences in the discounting of delayed gains between those who gambled and those who did not, although the gamblers did discount probabilistic gains less steeply than the nongamblers. Only one study, Shead et al. (2008), has examined probability discounting of both gains and losses in gamblers. Surprisingly, problem gambling severity was unrelated to either type of discounting, although it should be noted that the participants were university students who gambled, rather than individuals who met clinical diagnostic criteria. Based on the results of the current study, it might be expected that problem gamblers would be more risk-taking with respect to both probabilistic gains and losses than non-problem gamblers, and research on probability discounting with clinical samples is needed to test this hypothesis.

Conclusions

The present study is the first to examine the relations between delay discounting of gains and probability discounting of both gains and losses. A negative correlation between the probability discounting of gains and losses was observed, consistent with the idea that individuals' choices on probability discounting tasks reflect their general attitude towards risk, regardless of whether the outcomes are gains or losses. One important implication of this finding is that risk attitudes reflect the weighting of the value and/or the likelihood of the lowest-valued outcome rather than the uncertainty or variability of the outcome. More specifically, risk-aversion reflects a tendency to overweight both the possibility of getting nothing when a probabilistic gain is involved and the possibility of actually losing when a probabilistic loss is involved, whereas risk-seeking reflects the tendency to underweight these possibilities. Neither probability discounting of gains nor probability discounting of losses were reliably correlated with discounting of delayed gains, a result that is inconsistent with the idea that probability discounting and delay discounting both reflect a general tendency towards impulsivity.

Appendix A

The following instructions were read aloud to each participant:

Now I am going to ask you to make some choices involving money. You are to make decisions about which of two consequences you prefer. There will be three types of questions. One set of questions will have you choose between different amounts of money available immediately or after different delays. For example, you may be asked the following: Which option do you prefer? (a) $2 at the end of this session, or (b) $10 in 30 days. A second set of questions will have you choose between different amounts of money available for sure or with a specified chance. For example, you may be asked the following: Which option do you prefer? (a) $7 for sure at the end of the session, or (b) a 25% chance of receiving $10. A third set of questions will have you choose between different amounts of money that must be paid for sure or with a specified chance of being paid. For example, you may be asked the following: Which option do you prefer? (a) $4 to be lost for sure at the end of the session, or (b) a 70% chance of losing $10 (30% chance of losing nothing).

These questions will appear on the computer screen and you will be asked to indicate your preference by pressing the corresponding key on the keyboard (i.e., [a] or [b]). At the end of the session, one question from each of these three sets of questions will be selected at random and you will receive/lose whatever you chose in response to those 3 questions. For the set of questions involving delayed amounts, if on that trial you selected an immediate amount of money [option (a)], you will keep that amount of the $20 given to you at the onset of the session. If you selected the delayed amount of money [option (b)], you will be required to forfeit that amount of the $20 given to you and it will be placed in an envelope with your name on it and it will be available to you when the time has elapsed. For the set of questions involving certain/uncertain amounts to be received, if on that trial you selected a certain amount [option (a)], you will keep that amount of the $20 given to you at the beginning of the study. If on that trial you selected a chance of winning $10 [option (b)], you will select a token from a bag containing “win $10” tokens and “win $0” tokens in the proportion that reflects the probability. For example, if the trial you selected was $10 with a 25% chance, you will select one token from a bag containing 1 “win $10” token and 3 “win $0” tokens. You will keep that amount of the $20 given to you at the onset of the session if you draw a “win $10” token and you will forfeit $10 of the $20 if you draw a “win $0” token.

For the set of questions involving certain/uncertain amounts to be lost, if on that trial you selected a certain loss [option (a)] you will forfeit that amount of the $20. If on that trial you selected an uncertain payment [option (b)], again you will select one token from a bag with “lose $10” and “lose $0” tokens and either forfeit $10 or $0, depending on which token you pick. If it turns out that you lose more money than you are allowed to keep, you will not be required to pay any money. You will be entitled to a minimum of $5 of the $20 provided to you at the beginning of the study. Remember that each of these three questions will be randomly selected so please answer each question during this task according to your actual preferences.

Appendix B

Proportion of Explained Variance (R²) and Root Mean Squared Error (RMSE) for the Best-fitting Hyperboloid Functions and the Area Under the Empirical Discounting Curve (AUC) for Individual Participants.

Participant	Delay (gains)			Probability (gains)			Probability (losses)
	R2	RMSE	AUC	R2	RMSE	AUC	R2	RMSE	AUC
1	.981	.523	.526	.939	.607	.480	.000a	2.082	–b
2	.988	.303	.636	.949	.596	.330	.942	.722	.333
3	.968	.391	.148	.939	.853	.168	.980	.571	.220
4	.793	1.076	.677	.625	1.442	.522	.776	1.944	.285
5	.810	1.866	.616	.974	.635	.215	.892	1.037	.390
6	.980	.590	.433	.893	1.282	.174	.915	.764	.468
7	.596	.585	.823	.971	.597	.205	.956	.699	.339
8	.919	.783	.627	.989	.393	.128	.926	1.043	.246
9	.959	.755	.564	.957	.344	.182	.902	.538	.557
10	.948	.783	.485	.995	.194	.366	.980	.444	.335
11	.923	.897	.535	.876	.560	.558	.941	.718	.171
12	.865	1.409	.146	.961	.669	.226	.961	.677	.234
13	.920	1.188	.418	.946	.503	.393	.914	1.060	.244
14	.641	1.000	.719	.908	1.053	.174	.934	.902	.379
15	.954	.567	.611	.947	.700	.227	.956	.647	.205
16	.846	1.209	.445	.892	1.370	.586	.955	.806	.369
17	.967	.834	.260	.925	.932	.122	.984	.473	.354
18	.761	1.222	.092	.553	1.318	.352	.557	2.460	.500
19	.872	1.155	.457	.952	.666	.396	.898	1.304	.301
20	.682	.604	.781	.978	.591	.207	.864	1.348	.212
21	.585	.439	.829	.990	.278	.314	.846	.814	.409
22	.977	.576	.285	.858	1.075	.208	.958	.436	.547
23	.945	.420	.778	.942	1.053	.145	.972	.640	.184
24	.648	1.945	.794	.450	2.922	.361	.987	.425	.368
25	.358	.074	.983	.966	.785	.183	.849	1.296	.315
26	.000a	.066	–b	.839	1.178	.514	.903	1.361	.057
27	.949	.494	.707	.958	.731	.507	.979	.620	.060
28	.987	.583	.109	.965	.836	.089	.982	.568	.121
29	.927	.582	.697	.937	.816	.351	.963	.776	.164
30	.847	1.025	.562	.928	1.081	.302	.913	1.347	.104
31	.890	.309	.875	.859	1.194	.585	.936	.876	.081
32	.872	.953	.561	.967	.801	.206	.930	1.198	.145
33	.000a	.074	–b	.797	.910	.527	.932	1.000	.121
34	.936	.260	.777	.970	.523	.178	.831	1.253	.293
35	.646	1.279	.578	.689	.888	.510	.727	1.795	.116
36	.039	.893	.942	.989	.306	.327	.836	.650	.539
37	.546	1.325	.149	.751	1.457	.417	.921	1.134	.310
38	.896	1.044	.178	.682	.750	.136	.923	.917	.360
39	.806	.411	.867	.946	.645	.156	.876	.656	.549
40	.893	1.042	.678	.820	1.038	.080	.927	.913	.426
41	.943	.824	.579	.856	1.185	.559	.970	.647	.194
42	.969	.579	.100	.969	.636	.118	.926	1.016	.272
43	.834	1.139	.370	.973	.424	.199	.910	1.080	.166
44	.971	.187	.884	.945	.840	.311	.966	.595	.196
45	.950	.829	.507	.939	.843	.098	.997	.171	.500
46	.801	1.713	.477	.837	1.318	.298	.957	.875	.162
47	.091	.478	.932	.000a	2.194	–b	.634	1.256	.475
48	.446	.073	.981	.974	.568	.419	.975	.679	.489
49	.979	.697	.329	.996	.215	.400	.931	.941	.152
50	.939	.341	.731	.976	.488	.319	.973	.607	.247
51	.318	2.050	.211	.865	1.084	.332	.287	3.488	.369
52	.926	.438	.766	.852	.868	.382	.931	.417	.633
53	.917	1.553	.259	.872	1.907	.162	.919	1.553	.044
54	.420	2.833	.461	.852	.697	.179	.898	1.164	.233
55	.789	1.651	.639	.862	.979	.173	.954	.821	.473
56	.887	1.303	.606	.960	.665	.276	.954	.834	.363
57	.892	.344	.586	.970	.463	.397	.454	2.466	.289
58	.863	1.283	.301	.701	2.083	.228	.752	1.797	.125
59	.928	.326	.821	.995	.271	.221	.994	.325	.118
60	.872	1.536	.537	.882	.819	.345	.912	.802	.522

^aR² of .000 indicates that the mean accounted for as much of the variance as the best-fitting hyperboloid function.

^bThe value of AUC is omitted because the poor fit made the measure meaningless (see above).