System theoretical investigation of HER mediated signaling

Abstract

The partitioning of biological networks into coupled functional modules is being increasingly applied for developing predictive models of biological systems. This approach has the advantage that predicting a system level response does not require a mechanistic description of the internal dynamics of each module. Identification of the input-output characteristics of the network modules and the connectivity between the modules provide the necessary quantitative representation of system dynamics. However, determination of the input-output relationships of the modules is not trivial; it requires the controlled perturbation of module inputs and systematic analysis of experimental data. In this report, we apply a system theoretical analysis approach to derive the time-dependent input-output relationships of the functional module for the human epidermal growth factor receptor (HER) mediated Erk and Akt signaling pathways. Using a library of cell lines expressing endogenous levels of EGFR and varying levels of HER2, we show that a transfer function-based representation can be successfully applied to quantitatively characterize information transfer in this system.

INTRODUCTION

A module based approach where the network is partitioned into functional modules at a coarse-grained level is being increasingly applied in biological problems successfully [1-9]. For system level analysis of a modular network, each module can be treated as a black box whose internal mechanisms do not have to be explicitly represented or even known. Molecular interactions within a module are only important with respect to their effect on how the module converts an input to an output; they can otherwise be ignored in analyzing the system properties [10, 11]. Identification of the input-output characteristics of the network modules and the analysis of the quantitative relationships among the inputs and outputs of the modules can facilitate understanding of the design principles of the network [12-14]. Once such characterization is in place, the impact of altering the input-output behavior of specific modules or changing the topology of the network, i.e., reengineering, on the overall system behavior can be predicted. Separation of a network into modular components also helps with identifying the observation points that would serve as critical reporters of the network state and with making investigation of particular subsections of the system computationally more tractable.

However, characterizing the input-output relationships of the modules is not trivial; it requires data collected under conditions where the system properties are altered in a controlled fashion. The key to success in this type of analysis is the access to the correct type of datasets, and this aspect has to be built into the design of the experimental studies. Unfortunately, lack of such data often imposes a severe restriction on the use of module based approaches in biological problems. In this study, using the data that we have collected for the Erk and Akt signaling pathways stimulated through the human epidermal growth factor receptor (HER) family in a library of cloned cell lines, we show that a linear transfer function-based systems analysis method can be successfully applied to extract the temporal input-output relationship of biological modules. We note that our findings may not be valid under conditions that are far removed from the ones employed in our experimental study. In this respect, we carefully temper our conclusions based on the amount and content of the data that was used for our analysis.

The HER (also known as ErbB) family of receptor tyrosine kinases consists of four members, EGFR/HER1 and HER2-4 [15]. The HER family is arguably the most important receptor system in the context of development and tumorigenesis [16-18]. In addition to their normal physiological role in growth, proliferation, and differentiation of epithelial cells, HER receptors play a key role in transformation and tumor progression [19-23].

Ligand binding induces dimerization of the HER receptors and their subsequent phosphorylation, and various homo- and hetero-dimer combinations can be formed [24-26]. There is considerable evidence to suggest that the important determinants of cellular response to HER signaling are the types of dimers formed among the family members [26-29]. It has been reported that the specific tyrosine sites on the cytoplasmic tail of a receptor that get phosphorylated can depend on its dimer partner [30]. This implies that each dimer type may be capable of engaging a unique complement of cell signaling pathways.

Signal transduction initiated by the phosphorylation of HER receptors leads to the activation of the downstream elements MAPK/MEK/Erk and PI3K/PKB/Akt [31-34], which are widely accepted as the dominant mitogenic and pro-survival pathways, respectively. Expression of constitutively active forms of Erk-activating kinases causes transformation of fibroblasts and production of tumors in nude mice [35, 36]. Whereas prolonged Erk activation has been shown to correlate with neurite outgrowth, agents that induce transient Erk activation do not show this effect [36-39]. The serine/threonine-specific protein kinase Akt promotes cellular survival by blocking apoptosis, which it achieves by binding and regulating many downstream effectors; e.g., NF-κB, Bcl-2 family proteins, and MDM2 [40, 41]. Akt has been implicated in many types of cancers because of its possible role in inducing protein synthesis and in angiogenesis and tumor development [42-44].

In this study we utilize a modular approach to quantitatively investigate the Erk and Akt signal transduction pathways when activated through EGFR and HER2 receptors. The cell lines used in this study have distinct HER2 expression levels, and consequently display distinct EGFR and HER2 activation profiles. We obtained the data representing independent input-output pairs by pairing HER and Erk/Akt activation in these cell lines. Collected datasets enabled us to derive the transfer function of the signal transduction module with a higher degree of confidence. Our results support the hypothesis that the HER dimer identity is a critical determinant of downstream signaling. Further, we find that even though Erk and Akt activation are mainly driven by fast processes, slower responses with memory effects are also present.

METHODS

Experimental data collection

We measured the activation levels of EGFR, HER2, Erk and Akt in a library of four human mammary epithelial cell (HMEC) lines that express endogenous levels of EGFR and different levels of HER2. The parental cell line (Par) was originally provided by Martha Stampfer (Lawrence Berkeley Laboratory, Berkeley, CA) as HME cell line 184A1L5. It expresses approximately 200,000 molecules of EGFR, very low levels of HER2 (∼30,000), and non-detectable HER3 and HER4 [45]. This cell line was transduced with the HER2 gene and subcloned to establish three HER2 expressing clones; a low (17L; 179K EGFR and 113K HER2), a medium (24H; 158K EGFR and 600K HER2), and a high (A11H; 298K EGFR and 1,472K HER2) HER2 expresser [46]. Cells were maintained in DFCI-1 medium supplemented with 12.5 ng/ml EGF (PeproTech, Rocky Hill, NJ) as described in [47]. At about 70-80% cell confluency, the medium was replaced with DFCI-1 medium lacking all supplements but containing 0.1% BSA. Cells were then quiesced for 12-18 hours before treatment. To activate cells through EGFR, 100 ng/ml EGF was added into the culture medium and cells were incubated at 37°C for fixed amounts of time from 5 to 120 min. At least two independent 2-hour time-course experiments were performed, with two technical replicates in each experiment, for every treatment condition. Samples were collected at 9 time points (0, 5, 10, 20, 30, 45, 60, 90, and 120 min) after ligand addition.

To prepare samples for receptor mass and phosphorylated receptor detection, cells were solubilized with ice cold lysis buffer (1% NP-40, 20mM pH 8.0 Tris buffer, 137mM NaCl, 10% glycerol, 2mM EDTA, supplemented with 1mM heat activated sodium orthovanadate and 1% protease inhibitor cocktail III (Calbiochem, La Jolla, CA)) for 20 min. A different cell lysis buffer (1mM EDTA, 0.5% Triton X-100, 5mM NaF, 6M urea, 2.5mM activated sodium orthovanadate, 1% protease inhibitor cocktail III, 100μM PMSF and 2.5mM sodium pyrophosphate, in PBS, pH 7.2-7.4) was used to prepare samples for phospho-Erk (pErk) and phospho-Akt (pAkt) detection. Collected cell lysates were stored at −80°C until needed.

ELISA assays [48] were employed to quantify receptor phosphorylation, and Erk and Akt phosphorylation levels. In all reported experiments, R&D DuoSet IC ELISA kits (R&D Systems Inc., Minneapolis, MN) were used and manufacturer's protocols.

Model description

We envision the process of HER mediated signaling as occurring in two serially connected stages. The first receptor activation stage converts the environmental cue, i.e., ligand and receptor availability information to a particular distribution of phosphorylated HER dimers [46]. The second signal transduction stage that is investigated here converts this receptor activation information into the activation patterns of the signaling molecules Erk and Akt. Whereas the outputs of the signal transduction module – Erk and Akt phosphorylation – are well-defined, the specific features of receptor activation that serve as the module inputs need to be elucidated. Here, we measured the aggregate phosphorylation levels of the EGFR and HER2 receptors, and the phosphorylation levels of Erk and Akt as readouts for the inputs and outputs of the signal transduction module in the investigated cell lines to obtain four pairs of independent input-output measurements (Fig. 1; I_exp and O_exp). We first analyzed the relationships between these experimentally measured inputs and outputs using a transfer function based approach. We refer to this model formulation as a phosphorylation-based model. This model, which uses the raw input and output data in the analysis yielded poor fits for both Erk and Akt activation (see Supplementary Material). Hence, we explored alternate strategies for defining the system inputs.

Figure 1.

Input (HER phosphorylation) and output (Erk and Akt phosphorylation) time-series for the studied HME cell lines: A) Parental, B) 17L C) 24H and D) A11H. In each of these panels, I_exp refers to the receptor phosphorylation levels measured in the ELISA experiments for EGFR (solid line) and HER2 (dashed line) - the inputs to the phosphorylation-based model. I_total refers to the total abundances of phosphorylated EGFR (solid) and HER2 (dashed) - the inputs to the total-based model. I_dimer refers to the abundances of EGFR-EGFR (solid), EGFR-HER2 (dashed) and HER2-HER2 (dash-dotted) dimers - the inputs to the dimer-based model. O_exp refers to the system outputs: Erk (solid) and Akt (dashed). I_exp, I_dimer and I_total are each expressed in units of 1000s of molecules. The outputs are expressed in a normalized form. Note that some of the subplots in panel D have different y-scales compared to the corresponding subplots in panels A-C.

It should be noted that I_exp represents the total phosphorylation level of EGFR and HER2, and combines information about the dimer types that contribute to these levels and the extent of phosphorylation of these dimers. In order to evaluate the relative ability of various receptor dimers to activate Erk and Akt we need to obtain the abundances of the HER dimers in these cell lines. These dimer abundances are difficult to measure experimentally. We have recently estimated the dimer abundances in the cell lines by using a mathematical model of EGFR and HER2 dimerization and trafficking to analyze experimental data on EGFR and HER2 receptor mass and phosphorylation [46].

To investigate whether a receptor-dimer based representation is necessary, we performed our analysis using two types of metrics to quantify the module input: a) the abundances of phosphorylated EGFR–EGFR (pR₁₁), EGFR–HER2 (pR₁₂) and HER2–HER2 (pR₂₂) dimers and ii) the total abundances of phosphorylated EGFR (pR₁ = 2pR₁₁ + pR₁₂) and HER2 (pR₂ = 2pR22 + pR₁₂) molecules. These inputs are labeled I_dimer and I_total (Fig. 1), and we refer to the associated models as dimer-based and total-based models respectively in the remainder of the paper.

Figure 1 summarizes the inputs and the outputs that were used in our modeling studies. Collected experimental data was interpolated at equally spaced (T=2.5 min) time points using cubic splines to obtain the time series that were used in the numerical computations. As the measured Erk and Akt phosphorylation levels are in arbitrary units, the relative levels among the four cell lines are the more relevant quantities. Therefore, we normalized the outputs of the module to the [0-1] range for computational convenience.

Input-output relationships in dynamic networks

In linear response theory, time-dependent input-output relationship of a dynamical module can be expressed using the convolution integral [49]

$$O_i\left(t\right)=\underset{j}{\Sigma }{\int }_0^t{f}_{\mathit{ij}}(t-\tau )\cdot I_j\left(\tau \right)d\tau$$ Eq. (1)

The transfer function f(t) defines the internal module dynamics; convolution with the transfer function (TF) filters the input I(t) to yield the output O(t) of the module. For N inputs and M outputs, the TF matrix contains M×N elements (each element connects one input to one output). The convolution integral in Eq. (1) becomes a simple multiplication, $O_i\left(s\right)={\Sigma }_j{f}_{\mathit{ij}}\left(s\right)\cdot I_j\left(s\right)$ in the dual Laplace space where x(s) denotes the Laplace transform of the function x(t) [49].

In most instances, biological experiments utilize discrete observation time points, which make methods developed for discrete time systems more suitable for their investigation. For simplicity, we assume that the system is observed with equal time intervals T. Use of unequal observation intervals is quite common in biological systems but, as done in this report, collected results can be converted to equal interval time-series data for computational convenience. The complex form of the Laplace transform, the z-transform is more suitable for dealing with discrete time series data [49].

In principle, one can simply take the numerical transforms of the input and output functions and compute the TFs as a ratio. However, as numerical transforms can be very susceptible to fluctuations and cutoff effects, unavoidable uncertainties and the finite time-span of the experimental data may cause erroneous features when calculating numerical transformations. Therefore, instead of computing the TFs by numerically transforming the observables, we assume specific forms for the TFs and fit their parameters to increase the reliability of our derivations. To test if the used forms impose any unwarranted restrictions, we also employed a “free form” TF with 21 degrees of freedom and show that our chosen analytical TF forms are sufficient to model the investigated system.

Transfer function determination

We determined the TF of the signal transduction module by fitting Eq. (1) to the experimental data (O_exp) collected for the four cell lines. We investigated various specific expressions for the TF in this study. Parameters of the TFs were determined using non-linear least squares regression by fitting the model output predictions to the experimental pErk and pAkt measurements using the MATLAB nlinfit routine. Given a TF form, the filter routine of the MATLAB program was used to compute the outputs by filtering (convoluting) the inputs with the transfer function. The four input-output pairs obtained from the four cell lines were simultaneously fit to obtain a single set of TF parameters. Hence, we implicitly assume that the inherent characteristics of the signal transduction module remain unchanged across the cell lines. The initial guesses for the fitted parameters were chosen at random, and at least 1,000 optimization runs were performed for every discussed TF form. In most cases, the runs converged to a single optimal parameter set. When there were multiple optimal solutions, we chose the ones with the lowest residuals. We also visually inspected the results to ensure their quality.

As there are no cross terms connecting them in our model, we derived the TFs for Erk and Akt activation separately in our analysis. Therefore, our models had a single output, either the Erk or Akt phosphorylation level, and the fitted TF matrices respectively contained 2, 2 and 3 elements depending upon whether a phosphorylation-, total- or dimer-based model was used, since these models had two, two and three input time-series, respectively (see I_exp, I_dimer and I_total in Fig. 1).

RESULTS

Table 1 presents the z-transforms of the TF terms that were used in this study. An impulse (delta function) term Bδ(t) in the TF corresponds to an instantaneously relaxing response where the output at a given time is related only to the input value at the same instant of time. In contrast, an exponentially decaying term Ae^−at with a>0 connects the system response to the past input values as well, and the time span of the relevant input points and weights of their contributions are characterized by the decay rate of the exponential. When the decay rate is much faster than the sampling frequency, i.e. a >>1/T, the response relaxes to a large extent before the next discrete observation point. At this limit, the exponential term becomes effectively equivalent to an impulse function. As the shapes and positions of the maxima in the receptor phosphorylation, and Erk and Akt activation profiles are very similar (Fig. 1), the TFs for the signal transduction module can be expected to have a large impulse function component. Our results discussed below support this expectation. We therefore started our investigation at the simplest level by assuming impulse transfer functions for the Erk and Akt activation and added additional terms to the TFs as necessary to improve the fits.

TABLE 1.

The z-transforms of simple functions

x(t)	x(z)
Impulse/delta function δ(t)	1
Delayed delta function δ(t−kT)	z−k
Exponential function e−at	z/(z−e−aT)
Decaying oscillatory exponential function e−at cos(ωt+ϕ)	[z2 cos ϕ − z e−aT cos(ωT−ϕ)] / [z2 − 2 z e−aT cos(ωT) + e−2aT]

Transfer functions for Erk activation

Table 2 presents the parameter values for the optimized TFs obtained using the Erk activation data from the four investigated cell lines. Let TF(pR_ij→pErk) denote the TF for the activation of Erk through dimer type ij. Similarly, TF(pR_i→pErk) is the TF for the activation of Erk through receptor type i in the total-based model.

TABLE 2.

Transfer functions for Erk activation

Form	Element	Expression§	RMS Error
Dimer based models
1E1D	pR11 → pErk	14.13 δ(t) − 6.36 exp(−0.487 t)	0.0028
	pR12 → pErk	2.66 δ(t) + 0.53 exp(−0.073 t)
	pR22 → pErk	−5.46 δ(t) − 2.32 exp(−0.224 t)
2E1D	pR11 → pErk	9.78 δ(t) − 2.36 exp(−0.124 t) cos(0.167 t − 0.170)	0.0016
	pR12 → pErk	4.16 δ(t) + 0.16 exp(−0.020 t) cos(0.023 t + 0.099)
	pR22 → pErk	−11.48 δ(t) + 0.68 exp(−0.120 t) cos(0.530 t − 0.048)
21D	pR11 → pErk	Series Σ Ak 8(t−kT) with 21 elements (k=0 to 20) for each dimer pair. Obtained series are plotted in Figure 3.	0.0023
	pR12 → pErk
	pR22 → pErk
Total based model
2E1D	pR1 → pErk	5.13 δ(t) − 1.42 exp(−0.105 t) cos(0.072 t + 0.783)	0.0085
	pR2 → pErk	−2.57 δ(t) + 0.32 exp(−0.083 t) cos(0.137 t − 0.390)

^§Reported expressions are for the transfer functions per 100,000 activated receptors or receptor dimers. The output Erk activation is computed by convoluting the phosphorylation profile of the 100 K receptor dimers (or receptors) of a type with its respective transfer function. The z-transforms of the utilized transfer functions can be expressed as a ratio of polynomials in z⁻¹ using the transforms listed in Table 1.

We first analyzed the data using the dimer-based model. Model fits to the experimental data and the obtained transfer functions for the three dimer types are presented in the top plots of the panels in Figs. 2 and 3, respectively. When the TFs for all three dimer types were impulse functions B_ij δ(t), the quality of the fit was poor (not shown). We supplemented these simplest TFs by adding single exponential terms of the form A_ij exp(−a_ijt) to the transfer functions (1E1D model). This resulted in a substantial improvement in the fits. All possible combinations were tried, with exponentials being added to one or more of the transfer functions for the three dimer types. The best fit TF parameters for this model contain exponential terms with significant amplitude, with TF(pR₁₂→pErk) showing the slowest exponential decay (Table 2).

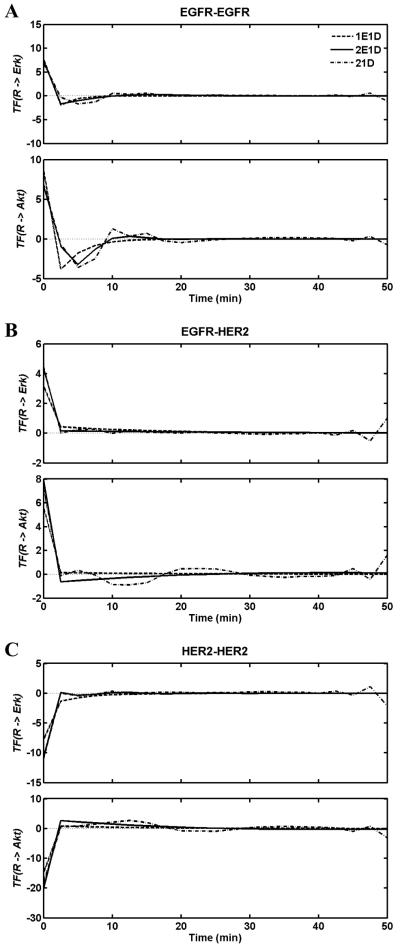
Figure 2.

Transfer function fits for Erk and Akt activation in the four studied cell lines. Cell lines for the panels are as in Fig. 1. Circles with experimental error bars represent the experimental results. Dimer-based model predictions using the 1E1D model (dashed), 2E1D model (solid) and 21D model (dash-dot); and total-based model predictions using the 2E1D model (dotted) are shown. The dimer-based 2E1D model (solid line) yields the best overall fit to the experimental data.

Figure 3.

Transfer functions relating the abundances of each of the three dimer types: A) EGFR-EGFR homodimers, B) EGFR-HER2 heterodimers and C) HER-HER2 homodimers to Erk (top plots) and Akt activation (bottom plots). Transfer functions derived using the 1E1D (dashed), 2E1D (solid) and 21D (dash-dot) models are shown. The continuous transfer functions shown in Tables 1 and 2 are plotted at uniform sampling points with an interval of 2.5 min.

We extended our analysis by including a second exponential term; i.e., dimer TFs contained two exponential terms and an impulse function (2E1D model). In this scenario, depending upon the poles, the TF in the time-domain can be expressed as the sum of two exponential decays with distinct rates A_ij,1 exp(−a_ij,1t)+A_ij,2 exp(−a_ij,2t) with a_ij,2≠a_ij,2 or as a damped oscillation A_ij exp(−a_ijt) cos(ω_ijt+φ_ij). Solutions with sustained oscillations (i.e., no damping, a_ij=0) were not observed. Theoretically, with two exponential terms, two equal real roots with solution (A₁+ tA₂) exp(−at) can also occur, but none of our fits resulted in this type of solution. Inclusion of a second exponential term improved the fits, particularly for the parental cell line (Fig. 2, solid lines). The best fits involved oscillatory TFs for all three dimers, but the oscillations were damped and subtle, with the impulse function term dominating all three TFs (Table 2, Fig. 3).

In order to investigate whether using analytical TF forms restricts our analysis and introduces artifacts, we also employed a “free form” TF with 21 degrees of freedom (21D model) by expressing the TF as a series of impulse functions, ${\mathit{TF}}_{\mathit{ij}}={\Sigma }_{k=0}^{20}{B}_{\mathit{ij},k}\delta (t-\mathit{kT})$. The 21 terms in the series correspond to using a time window of 50 min, given our sampling interval of 2.5 min. Fits with this free form TF (Fig. 2, dash-dotted lines) were very similar to those obtained with the 2E1D model, but this TF captures and reproduces the finer details in the data (Fig. 3). The TFs for the 1E1D, 2E1D, and 21D models agree well (Fig. 3), which indicates that our analytical model selection is not biasing the computations in a significant way. Interestingly, the 2E1D model with an analytical TF form produces fits with better optimization scores than the 21D free form model (Table 2). The same conclusion also applies to the Akt activation discussed in the next section. This is most likely due to the fact that the 21D model is trying to over-fit the data and the optimization is affected by noisy features in the data. This is also evident in the fluctuations in the TFs near the cutoff times (Fig. 3), which are most likely artifacts of the noise in the experimental data. These are typical characteristics of unconstrained over-fitting in parameter optimization. In contrast, the analytical forms are able to average out such noise by fitting through the mean patterns.

When the magnitudes of the t=0 contributions (i.e., immediate response contribution) to Erk activation are compared using the 2E1D model, we observe that the ratio EGFR–EGFR:EGFR–HER2:HER2–HER2 is roughly 1.7:1:2.5 (Table 2, Fig. 3). Therefore, our analysis predicts that the immediate Erk response to receptor signaling is more sensitive to the variations in the receptor homodimer levels. The shapes of the TFs indicate that the responses decay relatively fast. The decay rate of the exponential terms defines the delays (i.e., memory effects) in the Erk activation induced by the dimers. When the decay rates are compared, we observe that the decay is slowest for the EGFR-HER2 heterodimer. This suggests that HER2 may play a role in lengthening Erk activation in cell types that co-express EGFR and HER2.

To investigate whether a receptor-dimer based analysis is necessary, we repeated our computations using the total abundances of phosphorylated EGFR and HER2 (I_total) as module inputs (total-based model, see Methods). As in the dimer-based case, the best fit was obtained with a 2E1D model, but the quality of the fit was significantly worse than the dimer-based model as reflected by a larger error score (Table 2) and visibly poorer fit (Fig. 2, dotted lines). As the total-based model has lesser number of free parameters for the same TF form, we tested whether this was the cause of the low fit quality and added more exponential terms to the TFs to equalize the number of parameters. The fit quality was still quite poor. Use of the free form 21D model with multiple impulse terms did not improve the fits, either (not shown). These observations, and the poor results for the phosphorylation-based model which uses the raw input and output data (see Methods section and Supplementary Material), indicate that receptor-dimer distribution profiles provide a better representation for describing Erk activation through the HER signaling pathway in HME cell lines. This supports the existing evidence that the dimerization pattern is a critical determinant of the cellular response to HER signaling [26-30].

Transfer functions for Akt activation

Our analysis of Akt activation paralleled the Erk investigation. Table 3 lists the parameters of the fitted TFs. Model fits to the experimental data and the obtained transfer functions for the three dimer types are presented in the bottom plots of the panels in Figs. 2 and 3, respectively. The quality of the fit was very poor when the TF for each dimer pair contained only an impulse term. Addition of one exponential term to each of the TFs (1E1D model) resulted in reasonable fits (Table 3, Fig. 2). As in the Erk activation case, we repeated the calculations using the 2E1D and 21D models (Fig. 2). The 21D model particularly improved the fits for the 24H cell line but the resulting Akt activation predictions (Fig. 2, dash-dotted lines) and the obtained TFs (Fig. 3, dash-dotted lines) contained sizeable fluctuations, which is most likely due to the reproduction of the noisy features in the Akt data..

TABLE 3.

Transfer functions for Akt activation

Form	Element	Expression§	RMS Error
Dimer based models
1E1D	pR11 → pAkt	16.95 δ(t) − 8.24 exp(−0.307 t)	0.0033
	pR12 → pAkt	5.49 δ(t) + 0.15 exp(−0.048 t)
	pR22 → pAkt	−15.89 δ(t) + 1.01 exp(−0.082 t)
2E1D	pR11 → pAkt	−5.97 δ(t) +15.88 exp(−0.301 t) cos(0.417 t + 0.650)	0.0018
	pR12 → pAkt	8.68 δ(t) − 0.81 exp(−0.037 t) cos(0.049 t + 0.432)
	pR22 → pAkt	−23.31 δ(t) + 3.16 exp(−0.051 t) cos(0.052 t + 0.152)
21D	pR11 → pAkt	Series Σ Ak 8(t−kT) with 21 elements (k=0 to 20) for each dimer pair. Obtained series are plotted in Figure 3.	0.0021
	pR12 → pAkt
	pR22 → pAkt
Total based model
2E1D	pR1 → pAkt	8.66 δ(t) + 0.16 exp(−0.053 t) − 3.66 exp(−0.258 t)	0.0151
	pR2 → pAkt	−5.76 δ(t) + 0.01 exp(−0.015 t) + 2.54 exp(−0.273 t)

^§Meanings of the parameters and other details are as in Table 2.

When the t=0 contributions to Akt activation are compared using the 2E1D model, the ratio EGFR–EGFR:EGFR–HER2:HER2–HER2 is roughly 1:1.2:3.0 (Table 3, Fig. 3). These values indicate that, in contrast to Erk activation, EGFR homodimers are relatively less potent than EGFR HER2 heterodimers in activating Akt. EGFR is known to be a stronger stimulator of Erk than of Akt [50]. However, the Akt pathway is known to be activated strongly when the EGFR is co-expressed with other members of the HER family [50, 51]. Our results support these observations.

We obtained fits to the Akt activation data using a total-based model formulation (Fig. 2, dotted lines). As was the case for Erk activation, this formulation had a larger error score compared to fits obtained using the dimer-based model (Table 3). This further supports the conclusion that receptor dimers are better predictors of HER-mediated signaling than the total abundances of phosphorylated EGFR and HER2.

Based on these results, we conclude that, with the right data, it is possible to extract a transfer function which can successfully explain the temporal input-output relationships between the HER receptor and Erk/Akt activation patterns.

SUMMARY and DISCUSSION

Using the experimental data collected for Erk and Akt activation mediated by EGFR and HER2, we have shown that a module based analysis of the dynamical properties of biological networks is feasible, and that it can be an informative approach to understand the inherent dependencies in the experimental data. Our analysis indicates that, even though delayed temporal effects are present in this system, the activation patterns of Erk and Akt upon stimulation by HER receptors can be explained to a large degree using impulse transfer functions that relate the outputs at a given time to the inputs at the same instant of time. In other words, the EGFR and HER2 phosphorylation information is immediately transmitted and converted into Erk and Akt activation patterns in HME cells.

The sampling period of the experiments sets an upper bound on the resolution of the extracted quantities. The shortest time interval in our measurements was 5 min, which dictates that the time step used in our analysis has to be larger than half of this, i.e. the condition T≥2.5 has to be satisfied (Nyquist rate condition). Noting that our sample collection was actually done using unequal time intervals, the bound may have to be even larger. Therefore, our analysis cannot capture the dynamics between HER and Erk/Akt activations that occur on a time-scale smaller than 2.5 min.

In our analysis, the impulse term can also be thought of as an exponential function with a very large decay constant, which nullifies the response by time T. Thus, the 1E1D and 2E1D TF models effectively are second and third order response functions, respectively. Since the data fits with these models and the free form 21D model agree rather well (Fig. 2), and since the obtained TF shapes do not seem to depend on the employed model (Fig. 3), we conclude that the signaling module for HER mediated Erk and Akt signaling is a low order system under the studied conditions. As seen in Tables 2 and 3, optimizations that employed simple analytical expressions for the TFs in fact resulted in fits with lower errors compared to the free form 21D model. These observations validate our choice of simple analytical forms with a minimal number of adjustable parameters for the modeled TFs.

Signal transduction in general and Erk signaling in particular are known to be non-linear phenomena. Hence, there are several caveats in applying linear systems theory to analyze these systems. In our analysis, the first implication of the linearity assumption is that the inputs are connected to the outputs on a one-to-one basis; i.e., the output is merely the summed response of independent channels. This is a reasonable assumption in the investigated problem because once receptor dimers are formed they are unlikely to alter each other's signaling dynamics directly.

Another implication of linear response theory is the omission of non-linear input-output relationships in the individual signaling channels, for e.g. in the channel from EGFR homodimers to Erk. Such relationships can still be accommodated in the framework described here by defining input/output metrics that are non-linear functions of the measured variables. Although not pursued in detail in this report, one can envision a scenario where the output is related to an exponent of the receptor phosphorylation level. In other words, rather than using O=f(I), it can be assumed that O=f(Iα) with α>1. However, since it introduces additional fit parameters, ensuring reliable parameter estimation in this expanded analysis requires that more data be available. As the size of our data was limited (yet it was a larger set than usually available for similar studies), we have opted to limit ourselves to linear analysis in this report.

Use of linear response theory to analyze nonlinear systems has an implicit shortcoming that equally applies to our analysis: The results are only valid in the vicinity of the conditions that they are derived from, and their range of validity is problem dependent. In our experiments, we have measured the receptor and Erk/Akt activation as a response to relatively high ligand dosages and only for a single dose treatment condition. Therefore, our results and derived transfer functions may not be reliable for conditions that are significantly different than what was used in our analysis. For example, they cannot be assumed to be valid for a large range of ligand doses - derivation of the transfer functions from dose-response studies would require access to the correct type of data and possibly a non-linear analysis method. In this respect, the transfer functions that we derive in this study should be considered as characterizing the system under treatment conditions that lead to robust phosphorylation patterns in epithelial cells. We are currently expanding our experimental data sets, which will make it possible to address the possible non-linearity issues.

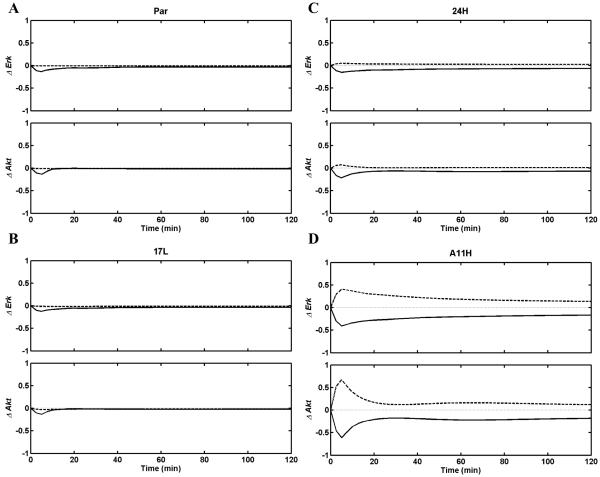
Derived transfer functions reported in Tables 2 and 3 indicate that some of the TFs, particularly the TF for the HER2 homodimers, have negative parts. This is a reflection of the trend in the data where we see a substantial decrease in Erk and Akt activation in the A11H cell line which has the largest HER2 expression level (Fig. 1). The negative TF needs to be examined in the context of the region of validity of our analysis. As discussed above, we cannot extrapolate our results to a scenario where only HER2 homodimers are present and conclude that these homodimers would inhibit Erk and Akt activation compared to a control. The only conclusion that can be derived is that, near the conditions of our study, an incremental increase in the active HER2 homodimers would decrease Erk and Akt activation, while EGFR homodimers and EGFR-HER2 heterodimers would counter this effect. It should also be noted that the levels of a particular dimer type cannot be changed arbitrarily. The kinetics of dimer formation patterns among receptor types is interlinked. For example, if the HER2 expression level is decreased in a cell line, one can expect that the number of both HER2 homo- and EGFR-HER2 hetero-dimers would decrease while the number of EGFR homodimers increases. Therefore, a more reasonable way to interpret the meaning of the TFs is to predict how the responses would change when the system is realistically manipulated. For example, one can compute how Erk and Akt activation would change if the expression levels of the EGFR or HER2 receptors were altered. Our cell lines are a testament to the fact that these manipulations can be implemented. Figure 4 presents the predictions for the decrease in the Erk and Akt activation levels when EGFR or HER2 expression levels are lowered by 10% in the dimer-based model. For these prediction calculations, we lowered the expression level of the respective receptor type by 10%, and recomputed the dimer abundances using our kinetic model [46]. We then used these dimer abundances as inputs to the TFs of the 2E1D models to predict the changes in the Erk and Akt responses. As seen in Fig. 4, a decrease in either receptor type lowers the Erk and Akt activation when HER2 expression levels are comparable to EGFR levels (17L cell line). When HER2 expression is much higher than EGFR expression (24H and A11H cell lines), a decrease in HER2 numbers enhances Erk or Akt activation. This simple analysis reported in Figure 4 demonstrates the quantitative predictive power of the transfer function models derived here.

Figure 4.

The change in Erk (ΔErk; top) and Akt (ΔAkt; bottom) activation when the EGFR expression level is reduced by 10% (solid) or the HER2 expression level is reduced by 10% (dashed) in each of the studied cell lines. Cell lines for the panels are as in Fig. 1. Note that panel D has different y-scales compared to panels A-C.

Although it was not pursued in this study, module based analysis can also be applied to investigate possible feedback relationships between Erk and Akt and with their upstream effectors. Using a purely theoretical analysis, Kholodenko has predicted that negative feedback in the Erk pathway may lead to sustained oscillations in Erk phosphorylation [52]. Although the oscillations seen in our TFs could be due to the noise in the measurements, our results may in fact point to the existence of real oscillations in our system. It is interesting that the time period of oscillations in our derived TFs (Figure 3) is in the same order of magnitude as that predicted by Kholodenko [52]. While our current results are not conclusive in this regard, our recent single-cell imaging experiments have shown the existence of sustained oscillations in nuclear Erk translocation upon EGF stimulation of HME cells (Ippolito et al., to be submitted).