The Limits of Fine-Scale Mapping

Abstract

When a novel genetic trait arises in a population, it introduces a signal in the haplotype distribution of that population. Through recombination, that signal’s history becomes differentiated from the DNA distant to it, but remains similar to the DNA close by. Fine-scale mapping techniques rely on this differentiation to pinpoint trait loci. In this study, we analyzed the differentiation itself to better understand how much information is available to these techniques. Simulated alleles on known recombinant coalescent trees show the upper limit for fine-scale mapping. Varying characteristics of the population being studied increase or decrease this limit. The initial uncertainty in map position has the most direct influence on the final precision of the estimate, with wider initial areas resulting in wider final estimates, though the increase is sigmoidal rather than linear. The θ of the trait (4Nμ) is also important, with lower values for θ resulting in greater precision of trait placement up to a point—the increase is sigmoidal as θ decreases. Collecting data from more individuals can increase precision, though only logarithmically with the total number of individuals, so that each added individual contributes less to the final precision. However, a case/control analysis has the potential to greatly increase the effective number of individuals, as the bulk of the information lies in the differential between affected and unaffected genotypes. If haplotypes are unknown due to incomplete penetrance, much information is lost, with more information lost the less indicative phenotype is of the underlying genotype.

INTRODUCTION

Through recombination, the history of sites surrounding a novel genetic trait become distinct from the history of the sites distant from that trait. The variation in the genetic sequences of individuals with and without the trait can allow researchers to distinguish sites with similar histories from sites with dissimilar histories, allowing the trait to be mapped, and, hopefully, revealing the genetic basis for the observed trait. This similarity in genetic history between causative alleles and nearby alleles is reflected in linkage disequilibrium, and has been used to map a wide variety of human genetic diseases [Weiss and Terwilliger, 2000]. Modern studies often use genome-wide linkage disequilibrium to map the diverse causes of complex diseases [Badano and Katsanis 2002], but even here, each contributory allele is discovered through an analysis of nearby SNPs, an analysis that works because of the shared genetic history of the SNP and the causative allele. Ideally, one would use SNPs ascertained from the sampled individuals, but imputed SNPs from panels can also be used. The only difference is that the ascertainment scheme for imputed SNPs is often more complex, and determining an appropriate correction is difficult [Kuhner, et al. 2000].

The strongest signal for the trait in both simple and complex diseases is, of course, the causative allele itself. If it is known that this allele has been sequenced, the genetic history of the sampled population becomes irrelevant, and association studies can be applied directly to the sequence data [Felsenstein, in prep]. But if that allele has not been sequenced, or if it is unknown whether it has been sequenced, the surrounding polymorphisms can be used to extrapolate the genetic history of the sampled individuals, and we can look for the signal in the patterns of co-inheritance. The pattern of co-inheritance is codified explicitly and completely in the recombinant coalescent tree, or ancestral recombination graph. In this study, we elected to study that tree itself, rather than reconstructions of it, to determine the maximum amount of information any measure of co-inheritance could provide. Figure 1 illustrates one such very simple tree, and shows how mapping can be performed directly on the tree instead of using SNPs. All mapping methodologies, from basic linkage disequilibrium to the more complex methods discussed below, are ways to get at the information present in this true tree.

Figure 1.

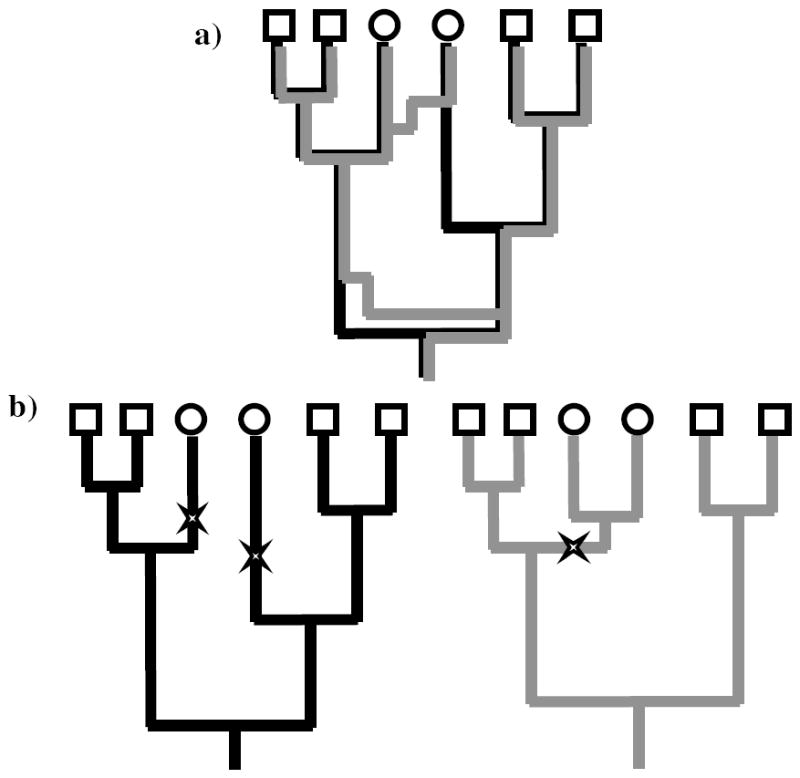
In a), we see a simple recombinant coalescent tree (ancestral recombination graph) with the black history separated from the grey history by two recombination events. In b), these have been separated into two ‘interval trees’. The observed data (squares and circles) are more likely to be observed on the right (grey) tree than the left (black) tree, since only one mutation event is needed to explain the data, not two.

Many mapping analyses begin with linkage analysis of families to identify chromosomal regions that are associated with the trait. These studies typically narrow the area where the trait locus must be to a region several centimorgans in size, which may contain hundreds of genes. To further pinpoint the location of the trait locus, fine-scale mapping techniques must be used. The simplest, oldest, and most common fine-scale mapping technique is to use linkage disequilibrium measures. The efficacy of various traditional disequilibrium measures was reviewed by Devlin and Risen [1995]. These measures are point estimates of how closely a particular genetic polymorphism matches the polymorphism of the phenotype. Haplotype Data Mining [Toivonen et al. 2000], available as the program TreeDT, looks for recurrent marker patterns in the data, and other programs are available that similarly look for other patterns of coinheritance. CLADHC [Durrant et al. 2004] collects patterns of variance into cladograms to look for association in that way.

Other techniques and programs are available that take a more genealogical approach to fine-scale mapping. McPeek and Strahs [1999] refined the basic disequilibrium measures for use in multilocus studies by modeling the decay of haplotype sharing (DHS), implemented in the program DHSMAP. Other algorithms have followed, each with different models of the underlying process and using different techniques to extract the process from the given data. COLDMAP [Morris, et al. 2000; 2002] and GeneRecon [Mailund et al. 2006] use the ‘Shattered Coalescent’ to estimate allele locations. BLADE [Liu et al. 2001] uses a Bayesian analysis that allows for multiple ancestral haplotypes. DLME+ [Rannala and Reeve 2001; Reeve and Rannala 2002] models a variety of data types (including RFLPs) and uses the annotated human genome sequence to construct a prior for allele location. LATAG [Zöllner and Pritchard 2005] performs interval-based coalescent reconstructions which are recombination-aware, but do not have to model the entire recombinant coalescent tree. Several of the approaches above are reviewed by Molitor et al. [2004].

On a larger scale, the program ‘Margarita’ [Minichiello and Durbin 2006] collects plausible recombinant coalescent trees for large amounts of data for entire chromosomes. This resembles the fine-scale mapping programs above in its attempt to reconstruct plausible genetic histories for the trait alleles, but applies this to the question of large-scale instead of fine-scale mapping.

All these methods rely on the genetic history of the trait being studied, though some address this reliance directly and some only indirectly. Linkage disequilibrium is an observable result of the same genetic process that is the ultimate cause of the present-day distribution of trait alleles. As such, it can be a very useful tool to use to track down the location of those alleles. (For a review that delves into more detail on this, see Nordborg and Tavaré [2002].)

When the causative allele itself has not been sequenced, all remaining evidence is indirect: nearby sequenced polymorphisms provide information about the ancestral pattern of genetic inheritance, and that pattern provides information about the most likely site for the trait locus. The accuracy of all fine-scale mapping analyses relies on two factors: whether the technique accurately recovers the pattern of inheritance, and whether that pattern distinguishes between the potential locations. Some techniques perform both steps at once, and do not include explicit reconstructions, but even these, by necessity, are limited by these two factors. The pattern of inheritance is codified explicitly and completely in the recombinant coalescent tree. Our use of known trees with known trait alleles simulates a ‘perfect’ technique, able to completely capture the inheritance pattern. The power of this tree to map the trait gives an upper limit to the precision any technique can achieve, and thus provides a ‘gold standard’ by which any method from the simple linkage disequilibrium estimates to the more complicated tree-based methods may be judged.

In addition, we examine how characteristics of the population being studied can influence this upper limit. Our results will help researchers determine beforehand if attempting to map a particular trait in a particular population is hopeless or promising, and what data collection strategy will be most effective.

MATERIALS & METHODS

Simulations

Recombinant coalescent trees were simulated via algorithms first developed for the program Recombine [Kuhner et al. 2000], under a variety of simulation parameters. The number of sites (l), the number of haplotypes sampled, the values of θ, and recombination rate (r) were all varied systematically. Population parameters were defined as follows: θ=4Nμ, with N the effective population size and μ the mutation rate in mutations per generation for the trait alleles. r=C/μ, with C the number of recombination events per pair of adjacent sites per generation. We found that the summary statistic θrl = 4NCl, a map length parameter scaled by the population size, was helpful when comparing different analyses. We therefore present results using this statistic divided by 400, which corresponds to distances in centimorgans for humans. Results for other organisms can be obtained by multiplying these results by the ratio of the other organism’s effective population size to the effective population size of humans, assumed here to be 10,000.

Simulation of the alleles at the trait locus was performed by one of three methods. In the first method, a site and an ancestral state were chosen for the trait at random and then allowed to mutate using a symmetrical two-state model. If this resulted in invariant or nearly-invariant data (defined as having less than three samples with the minority allele), the data set was discarded and simulated again at the same site on the same tree.

In the second method, used in the case/control analyses, trees of 40-100 tips were simulated under various parameter values and trait data were simulated on them as above. If the tree happened to have exactly 20 tips with the minority allele, it was saved; otherwise, the entire tree was discarded. The 20 minority allele tips (the cases) and a randomly-selected 20 majority allele tips (the controls) were saved, the data from the remaining tips were discarded, and the resulting data sets were analyzed. A given set of trees modeled the case where the minority allele was found at a given frequency in the general population, but for which an equal number of cases and controls were collected.

In the third method, used in the penetrance analyses, DNA was first simulated at all sites under the F84 model [Kishino and Hasegawa 1989] for DNA mutation with equal base frequencies and a transition/transversion ratio of 2.0. A site was chosen at random from the variable sites where the minority allele(s) had a total frequency of at least three samples. The majority allele was then marked as a single state, and all other alleles were assigned to the other state. The remaining simulated data were not used; since the true tree was known, there was no need for tree inference.

In all these methods, we assume that while a trait may be caused by multiple events, the locations of these events were not separated by recombination in the history of the sampled population. For analyses with penetrance models, pairs of samples were randomly combined into individuals, who were then assigned a phenotype based on their simulated genotype. When individuals with a single genotype could potentially exhibit multiple phenotypes, a phenotype was chosen at random based on the penetrance model.

Likelihood calculation

To map the simulated trait alleles, the likelihood that the data (either known alleles or known phenotypes) would be produced on the known tree at a given site (the ‘data likelihood’) was calculated for each candidate trait locus position using a symmetrical two-state data model with peeling algorithm of Felsenstein [1981]. This model was used instead of a DNA mutation model to more closely imitate traits for which a variety of mutational events might cause the trait. We used this model for all experiments, including those where the trait data was created by converting simulated DNA to two states. Assuming a uniform prior probability over all candidate positions allowed us to convert these likelihoods to posterior probabilities. The sites with the highest probability of containing the trait were then collected until the total inferred probability that the true site had been collected was 95%. (These sites were not required to be contiguous.) The number of sites in this collection measures the precision of the mapping attempt.

To calculate the likelihood for ambiguous data (for individuals whose phenotypes allowed more than one genotype, or unphased haplotypes), the probabilities of all possible haplotypes were summed (Appendix A). For data sets with more than one individual displaying an ambiguous phenotype, each combination of resolved haplotypes had to be summed. This method goes beyond most previous fine-mapping analyses, where either the data is computationally phased by a program such as PHASE [Stephens and Donnelly 2003] before the mapping analysis, or different resolutions of the ambiguous data are sampled during the analysis [Kuhner et al. 2000]. Our method is more precise, but computationally intensive, particularly in cases with many unphased individuals. The number of calculations that must be performed is proportional to S^N, where S is the number of ambiguous states, and N is the number of individuals with ambiguous phenotypes. We found a novel method to reduce this computational burden by ‘collapsing’ haplotypes so that the maximum number of ambiguous states for diploid individuals is two. This method is described in detail in Appendix A.

Amount of recombination

The number of expected recombination events in a tree depends on a complex interaction between the recombination rate, the number of sites under consideration (minus one), and the number of tips in the tree. The equation for the simplest case (two tips and two sites) is presented in Appendix B. The solution for more complicated cases is sufficiently arcane (the two-tip three-site case involves equilibria between 16 states instead of just three), that we approximated it using Monte Carlo simulation of trees with different values for r, l, and number of samples. Trees were simulated using an implementation of Hudson’s simulator [Hudson 1983] (a recombinant coalescent tree simulator). This simulator is ‘final coalescent’ aware, meaning that recombination events that only affect lineages whose common ancestor has been reached are ignored (as they cannot affect the present-day data).

Software

For experimental conditions where the summary statistic 4NCl was 20 or less (0.05 cM), a modified version of the LAMARC program [Kuhner 2006] was used to create trees, simulate data on those trees, and calculate the likelihood of the simulated data. For experiments involving 4NCl greater than 20, for efficiency a series of programs were used in concert—an algorithm based on the Hudson simulator [Hudson 1983] to create trees, an external simple program to generate trait data on those trees, the PHYLIP program ‘dnamlk’ [Felsenstein 2005] to calculate data likelihoods, and a Perl script to perform the final mapping analysis. These two implementations produced identical results from the same starting conditions, and both followed the same underlying algorithms.

Analysis

1000 replicate experiments were performed for each analyzed parameter combinations, with trees constructed, data simulated, and likelihoods assessed. When multiple differently-penetrant trait models were compared under the same conditions (population size, recombination rate, etc.), the same trees and simulated data were used for both, differing only in the assignment of phenotypes to the simulated genotypes.

Each replicate experiment resulted in a set of the most probable locations of the trait in question which collectively had a 95% probability of including the truth (the ‘final map length’). The more informative the data, the smaller the final map length. The average number of sites included over the 1000 experiments is therefore an estimate of the amount of information present. These results are given in centimorgans (cM), scaled to a population with an effective size of 10,000 (such as humans).

RESULTS

Within each 1000-replicate study, results varied widely. Even under the least-informative conditions, the final map length was sometimes small, and even under the most-informative conditions, it was sometimes large. One practical message is that the success of a mapping attempt is not guaranteed even under optimal conditions, nor is failure guaranteed by non-optimal ones.

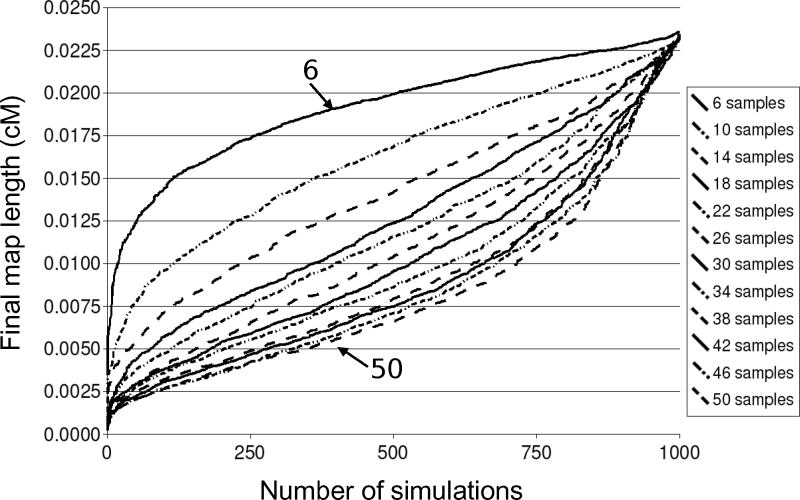
Figure 2 shows a graph of a representative experiment where the increase in information from adding more samples was tested. Each point on a line shows the number of replicate experiments whose final map length was the given distance or shorter. Each line starts close to zero (representing the most informative simulation of the 1000) and goes to 95% of the original map length (0.025), representing simulations with no information at all (one can be 95% certain of including the correct site by simply excluding a random 5% of the sample). The differences between experimental conditions can be seen in how fast the line changes from being very informative to being minimally informative. In some of our simulations, the shape of this distribution deviated from the typical ‘vibrating string’ seen in Figure 2, but when it did not, the average map length is reported.

Figure 2.

Simulation results from experiments with 1000 replicates. Each line tracks the number of simulations whose final estimate of the location of the trait allele contained greater than or equal to the given percentage of sites. Simulations were performed with r=0.015, Θ=1.0, and l=1000, and results are displayed assuming 4N=40,000.

Different experimental conditions can therefore be compared to see which contain more information about the location of the trait. As a result, knowing the population parameters that influenced the history of a trait can give us a fair idea of how successful we might be in mapping it. The parameters studied here are map distance, θ, the length of the stretch of DNA where the locus might reside, the number of individuals sampled, and the effect of systematic oversampling of cases versus controls.

Map distance

Without recombination, disequilibrium mapping would be impossible. The total amount of recombination over the region to be mapped strongly influences how much power is available to map any trait. A mapping study with a large map distance to search has more information available to pinpoint the location. However, this information is spread out over a longer distance, which results in longer final map distances. Figure 3 shows the correlation between initial map distance and the final map distance in centimorgans. For low numbers of samples, the correlation is roughly linear (on a log-log plot), but somewhat sigmoidal for more samples.

Figure 3.

The effect of increased map distance in the simulated trees on fine mapping precision. Data collected with Θ=1.0 and l=1,000,000, varying r. Results are shown assuming N= 10,000.

θ and l were kept constant for these experiments at 1.0 and 1,000,000, respectively. Decreasing l to 1,000 and increasing r by a factor of 1,000 (leaving the total map distance constant) produced nearly identical results for all conditions tested (data not shown).

Population size and mutation rate

θ is a measure of the genetic diversity present in a population, increasing with larger populations and with higher mutation rates. The θ for the trait itself, which we use here, may be different from the θ for the markers in the same genomic region if the mutation rates differ. For example, a disease whose alleles are active and inactive forms of a gene may have a much higher mutation rate than a single base pair, since there are many different ways to inactivate a gene. Similarly, a trait solely caused by a deletion event may have a lower mutation rate than the single-base substitution rate.

In this study, we considered only the informativeness of the underlying trait genealogy, and therefore considered only the trait θ. Marker θ will of course affect the success of attempts to infer the genealogy. Our results assume perfect inference and therefore represent an upper bound on mapping precision.

In trees with the same amount of expected recombination (the same number of samples and same recombination distance), a lower θ for the trait meant a narrower confidence interval, to a point. This effect followed a sigmoidal pattern, seen in Figure 4. Shown are plots of final map distances vs. θ for trees of 10 samples (squares) and 18 samples (triangles), calculated from an initial map distance of 0.025 cM. All points are averages of 1000 replicates.

Figure 4.

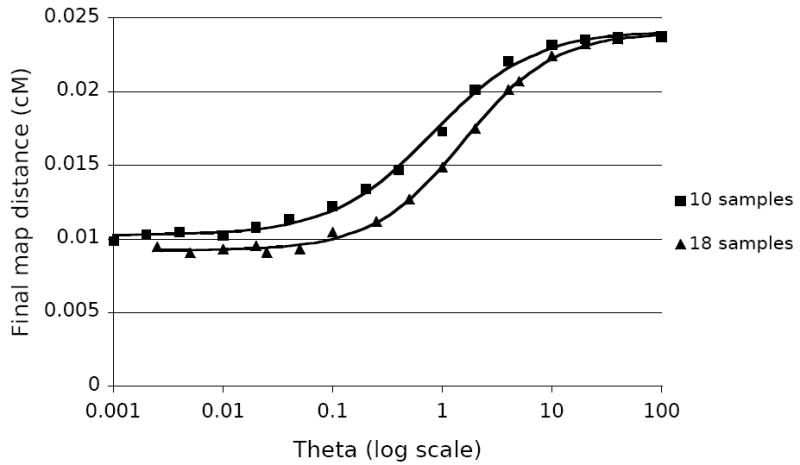
The effect of Θ on fine mapping precision. Data collected with l=1000, and r chosen for each point such that the total map distance was 0.025 cM, assuming N= 10,000. Displayed curves are the best fit sigmoidal curves for the given data.

Number of samples

Collecting data from more individuals is one obvious tactic to try to gain precision, given that most other factors that influence the amount of information in the sample are outside the researcher’s control. Figure 5 shows the same simulation results as Figure 3, this time with the with the final map distance plotted against the number of samples, for several different values of the original map distances. More samples increase precision, with the effect more pronounced when the original map length is greater.

Figure 5.

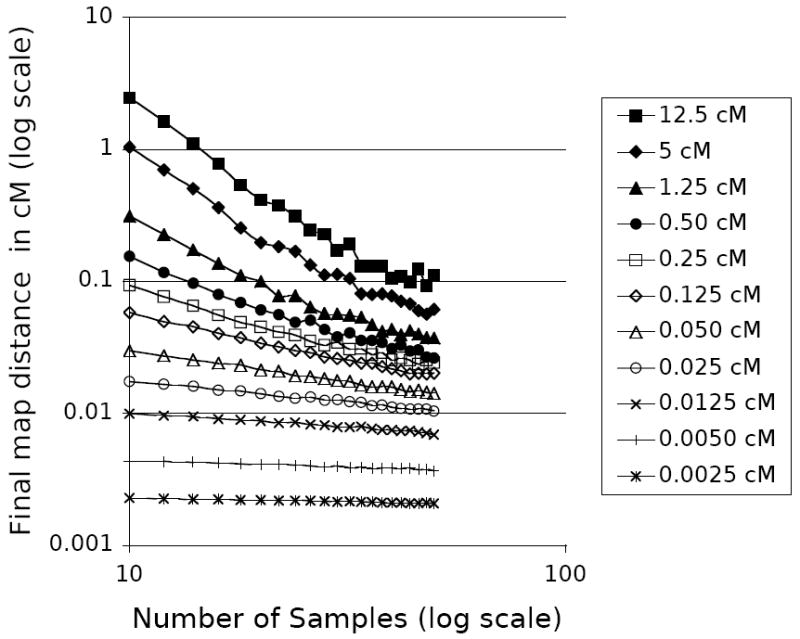
The effect of the number of samples on fine mapping precision. Data reproduced from Figure 3.

However, we have already seen that increasing recombination events increases the precision of the estimate, and we know that adding samples will increase the number of recombination events. How much of the added precision with increased samples is due to the increased number of recombination events, and how much is due to the new information contained in the new samples?

To separate these two conditions, we performed simulations with the initial map length chosen such that the expected average number of recombination events remained constant (between 50.3 and 50.5) for each tested number of samples, as determined by Monte Carlo simulation using the Hudson simulator. Figure 6 shows the results of these simulations, and compares these results to the previous experiment where the initial map length remained constant as the number of samples changed. (An initial map distance of 0.0125 cM with 10 samples results in approximately 50.4 average expected recombinations.) As can be seen, the additional recombinations present in a tree with more samples accounts for about 15% of the increase in precision, leaving 85% due to the added information present in the increased number of samples.

Figure 6.

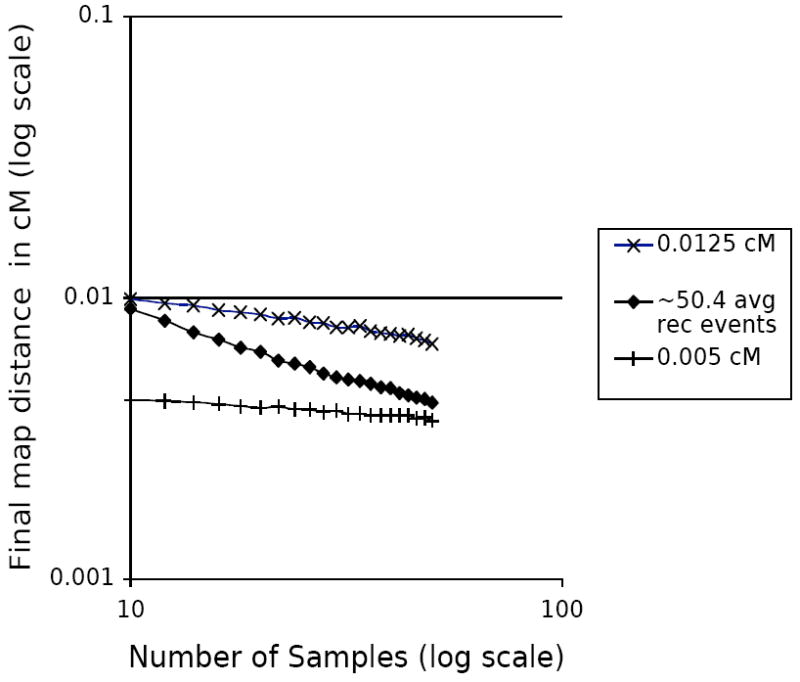
The effect of the number of recombination events on fine mapping precision. The 0.0125 cM and 0.005 cM data are repeated from Figure 5, and for the diamonds, the total cM for each point was chosen such that the expected number of recombinations for that number of samples with Θ=1.0 and l=1000 was ~50.4 (determined by Monte Carlo simulation using Hudson’s tree generator).

Oversampling

However, many researchers do not collect randomly sampled data from the population at large, but instead collect a given number of cases and controls irrespective of the allele frequency in the general population. To study the effect of this methodology, we performed a series of mapping simulations where 20 cases and 20 controls were collected from a population under a range of minor-allele frequencies in the general population, under a range of initial map distances. These results are shown in Figure 7, and show a mapping precision increase with the increase of minor allele frequency. The variability of these results was smaller than for the analyses where all the simulated data was examined (variance data not shown). Computational limits prevented us from simulating minor allele frequencies lower than 20%.

Figure 7.

The effect of the minor allele frequency on the final map distance for trees with 20 cases (samples with the minor allele) and 20 controls (samples with the major allele). Data collected with Θ=1.0 and l=1,000,000, varying r. Results are shown assuming N= 10,000.

In addition, we also analyzed our case/control trees with the original data, i.e. with the same 20 cases, but using all the controls instead of just the 20 we randomly sampled (in the 40-tip case, these are identical to the case/control analysis). These represent a study where samples were chosen until 20 cases were found, and then analyzed. A comparison of the two methods is shown in Figure 8, which shows the difference in accuracy between the two methods in centimorgans.

Figure 8.

Comparison of results from a case/control study of data where only 20 cases and 20 controls were chosen from a randomly-generated (as shown in Figure 7) to analysis of the same data with all samples included. Data collected as in Figure 7.

As can be seen, the difference in accuracy between the two measures is relatively small (~0.006 cM even in the worse case), though inversely correlated with the frequency of the minor allele.

Penetrance

All the experiments thus far have assumed that all trait alleles are fully haplotyped. In reality, this is seldom the case. Even if all homozygotes and heterozygotes have unique phenotypes (the codominant case) or are otherwise distinguishable from one another (as through pedigree studies), the phase of the heterozygote can seldom be determined. There is also the issue of incomplete penetrance. These phenomena clearly cause loss of information; the question is: how much?

We studied a variety of penetrance cases, and compared how increasing sample size (N) affected the results. Unfortunately, with computational complexity increasing as 2^N, we were only able to obtain results for 1,000 replicates up to the case where N=32. Figure 9 shows the results for several partially-penetrant cases as compared to the fully-haplotyped case. Eight cases contain results for simulations with varying degrees of multiplicative penetrance. Eight more contain results where only the heterozygote was partially penetrant, in order to get a handle on where information is encoded in the data.

Figure 9.

The effect of different penetrance models on fine mapping precision. The numbers in the legend indicate the penetrance of one phenotype for homozygous-common, heterozygous, and homozygous-uncommon individuals, respectively. The top eight cases follow multiplicative penetrance, while the next seven are for cases where only the heterozygote is partially penetrant. Data collected with Θ=0.1, r=0.1 , and l=1000 (0.025 cM, assuming N= 10,000).

All tested penetrance cases with a multiplicative penetrance model lost the vast majority of their mapping precision (92-99% in the 80:60:20 case). The less extreme models where only the heterozygote was partially penetrant did better, but still lost precision (25-62% in the 100:20:0 case).

DISCUSSION

At the most basic level, any site that has always been co-inherited with a candidate site throughout the history of our sampled sequences cannot be distinguished from it as a potential candidate for the location of the trait allele. (We will refer to the coalescent tree for a set of co-inherited sites uninterrupted by recombination anywhere in the complete ancestral recombination graph as an ‘interval tree’.) This means that the minimum mappable length is the length of the interval tree containing the trait allele. As uncertainty increases, more intervals must be included, decreasing the precision of our estimates and increasing the final map length. (The researcher’s ability to accurately reconstruct the interval trees goes down with the number of variable sites in each interval, as there is less data to work with. This is an important consideration for real-world analyses, but is beyond the scope of this study.)

We can compare how probable it is that the observed pattern of data (i.e. which individuals display which traits) would be produced by each interval tree, and thereby distinguish the best interval trees from the worst. The extent to which this ‘data likelihood’ distinguishes the interval trees from one another ultimately determines how precise the estimate of the trait location will be. This means that the true interval tree must be sufficiently distinct from the other interval trees, and that the mutation(s) that caused the trait differentiation must have arisen within a part of that interval tree with a unique set of descendants when compared to other interval trees.

Interval tree width, interval tree distinctiveness, and the specifics of mutational events all contribute to the amount of signal available in the tree. The total map distance, the trait-locus θ, the amount and type of data collected, and the penetrance of the causative allele all affect these constraints in different ways.

Map distance

Higher recombination rates and longer map distances produce more recombination events, which means a greater number of interval trees, and more distinctiveness between interval trees. This increase in information can potentially compensate for the added uncertainty involved in mapping a trait with a long initial map length. Figure 3 shows that the length of the final map distance increases as the initial map distance increases, but that for a sufficient number of samples, the increase is moderate. Results are shown scaled for a human-like population of N= 10,000, but can be scaled for populations of any size. All recombinant coalescent trees with the same number of samples and the same average number of recombination events will contain, on average, the same amount of information. (The number of markers available for tree reconstruction may differ; again, this is beyond the scope of this paper.)

The presence of recombination hot spots can affect the tree’s information content. The clustering of recombination events at the same site can cause ‘loss’ of interval trees due to recombination events occurring at the same locations. However, a similar loss was not seen to affect the final map distance: identical results were found over 5 cM with a total length of 1000 sites and a high recombination rate as 1,000,000 and a low recombination rate (data not shown). The lower number of sites results in fewer interval trees due to the increased probability of multiple recombination events at the same site; the same phenomenon that happens with recombination hot spots. However, significantly lower number of interval trees could increase the variance of the mapping analysis, making predicting the mapping precision of a nascent study less certain. In addition, if only a small number of hot spots are expected, the areas between them have a very high ratio of sites to recombination events, and while the final map distance will have the same distance in centimorgans, this may represent a much larger number of sites than in a region where recombination events are more evenly distributed.

Population size and mutation rate

A large population size means a larger θ for both the marker data and for the trait data, which will result in more recombination events and observed mutations. The increased number of mutations in the marker data means that there will be more information (variable markers) from which to reconstruct the true tree. However, this is counterbalanced by the fact that a large θ for the trait allele makes multiple trait mutation events more likely. This tends to cause the data likelihoods of all interval trees to regress to the mean, making them harder to distinguish from each other. This effect can be examined on its own by comparing simulations in which θ for the trait is decreased while simultaneously increasing the recombination rate by the same factor, resulting in trees with the same number of expected recombination events. As seen in Figure 4, the analysis with the lower trait θ is more precise.

When estimating the θ for a trait for which the phenotype is the result of a gene dysfunction, one must consider not the mutation rate of DNA in general, but rather the cumulative rate for all mutations that could potentially cause dysfunction. As calculated by Pritchard [2001], the effective θ for disease-causing mutations in a typical gene in humans might be in the range 0.1 to 5.0. This is based on an estimated human θ of about 0.001 [Li and Sadler 1991; Cargill et al. 1999], a typical gene length of around 1,500 bp [Eyre-Walker and Keightley 1999], and an average of 100-1000 potential survivable non-synonymous mutations. This would make the value of θ for human diseases not ideal but in a plausible range for fine-scale mapping.

This analysis does ignore potential asymmetry between forward- and back-mutations. For example, the rate at which mutations cause a normal gene to be disrupted is much larger than the rate at which mutations cause a disrupted gene to be repaired. This effect will lower the probability of compensatory mutations in the same lineage, and thereby further distinguish interval trees from each other. Ignoring it is conservative, however, and in the case of low trait θ values, will not make much difference.

Two phenomena explain the two ends of the sigmoidal curves in Figure 4. At extremely high values of θ, the trait mutations saturate the tree, randomizing the observed alleles and making all data sets equally likely. As θ decreases, the data becomes less randomized and more structured, fitting some interval trees much better than others. Finally, at very low values of θ, data sets that would be produced with exactly one mutation are reasonably likely, while data sets that would be produced with more mutations are not. At that point, further decreases of θ do not appreciably affect mapping accuracy. The ascertainment used here prevents us from including cases with no trait-locus mutations.

Number of samples

Sampling data from more individuals will increase the number of recombination events and make for more complicated trees, increasing interval tree divergence. However, the amount of information per individual decreases logarithmically as more individuals are added. The reason for this decrease is that the coalescent histories of the added individuals are highly correlated with those already sampled, so as more samples are added, fewer and smaller branches are added to the known tree. As seen in Figure 5, additional tips have a significant effect if the initial map distance is large, but this effect disappears at more than about 40 samples, or 20 diploid individuals. A similar effect has been seen in a variety of coalescent-based analyses of population parameters, such as those by Pluzhnikov and Donnelly [1996] and Felsenstein [2006]. This is important, because the complexity of tree-space increases much faster than exponentially as we add samples, making analyses that rely on searching through possible trees take much longer to finish.

Computational limitations restricted our simulations to a maximum of 50 sampled individuals, and a maximum map distance of 12.5 cM. Both of these values are unfortunately much lower than is typical for an association study. Fortunately, many of the trends we observe vary with the log of both the number of individuals and the map distance, so extrapolations of our simulations to more realistic cases are not unreasonable. In a growing population, less information is generally available from an equivalent sample size from a static population, but information content per individual does not drop off as quickly as it does in static populations. In growing populations, therefore, roughly similar results should be obtained by collecting data from more individuals.

If the analysis does rely on a thorough search of tree-space, but more data are readily available, one could theoretically use the new data in a replicate analysis and average the resulting probabilities. Averaging the results gives the new analysis the same weight as the first analysis, as if the analysis was merely repeated using the same data. This is conservative, but appropriate, since the two sets of data will be highly correlated, and share the majority of their respective ancestral histories.

Analyses that do not rely on a searching tree-space, such as disequilibrium measures, may use all the data at their disposal, but the amount of information gained per individual decreases as more are added. If a locus is difficult to map, exponential increases in sample size will be needed to substantially improve results.

The results from our case/control analysis (Figure 7) are encouraging in this regard. As expected, traits with minority alleles at low frequency are shown to be harder to map than those with high frequency. However, causative alleles hiding in a wide range of initial map distances (0.125 to 5 cM) were all able to be discovered within a final map distance window of about 0.02 cM. Furthermore, from Figure 8 we see that even for the rarest minority allele studied (at 20%) these map distances were all less than 0.008 cM worse than they would have been had 60 more controls been added, enough to make the relative frequency of the alleles in the sample match that in the population. In effect, by collecting 20 cases and 20 controls, one reaps the benefit of collecting 100 samples.

Figure 5 cannot be compared directly to Figure 7, since the number of minority alleles was only constrained to be three or more in the former, but constrained to be exactly 20 in the latter, making the simulations in Figure 7 have more cases on average than those in Figure 5. (This is confirmed by the fact that the variance in the unconstrained simulations was greater than that in the case/control simulations.) As a result, Figure 7 shows systematically more accurate results than Figure 5. Using Figure 5 to extrapolate to ~100 samples, however, one can imagine the final map distances for 0.125 and greater converging even in the unconstrained case, as they do in Figure 7.

From this we conclude that the majority of the information in a recombinant coalescent tree remains even when data for many of the tips containing the majority allele are discarded (or never collected in the first place). It should be stressed, however, that this is the information in the true tree, and one’s ability to accurately reconstruct or estimate the true tree may be significantly compromised given sampled cases and controls instead of individuals sampled at random from the population. The task of accurate reconstruction of trees given cases and controls should therefore be of paramount importance to software and algorithm designers who wish to provide tools for genetic mapping.

Penetrance

When we observe phenotypes in diploid individuals, mapping traits becomes a more difficult proposition because the underlying genotype is often not known, and even if it is, when an individual is heterozygous one rarely knows how to properly resolve the haplotypes. One interesting conclusion from the data in Figure 9 is that data with heterozygote ambiguity (the codominant case) is nearly as informative as fully-phased data. Thus, if we are studying a codominant trait or can distinguish the heterozygotes from the homozygotes through family studies, the resulting estimate of the trait location has the potential to be almost as precise as if full haplotype information were known. The probable explanation is that it is unlikely for the true tree to contain an interval tree whose data likelihood is increased by having two tips simultaneously incorrectly placed. As a result, the correctly placed trait alleles dominate the data likelihood function.

However, traits with only two phenotypes lose a significant amount of signal. As Figure 9 illustrates, in the case of multiplicative penetrance when all genotypes can display both phenotypes, nearly all the information content is lost (92-99% for the 80:60:20 case). The contribution of partial penetrance of the heterozygote to this information loss can be seen in the middle cases in Figure 9, where the penetrance of the homozygotes was kept fixed at 100%. In these cases, an appreciable but less drastic amount of information was lost (25-62% in the 100:20:0 case). These losses are attributable to the fact that the more possible haplotype resolutions are available, the more likely it is that an incorrect resolution will happen to match an incorrect interval tree, and receive a high data likelihood. In the multiplicative penetrance case, all tips of the tree might have either of the two alleles on it (albeit with different probabilities), making an erroneous match much more likely, and more able to mask the correct fit.

If genotype resolution is impossible, collecting more data is the only remaining option, and modern searches for disease-causing alleles have expanded to collecting data from hundreds if not thousands of individuals. Unfortunately, these simulations are limited by the 2^N limit in computational complexity for increasing sample sizes, so it is difficult to extrapolate to these higher values from the available simulations. The information content in the partially-penetrant cases does approach that of the non-penetrant case as the number of samples increases, perhaps indicating that at particularly high numbers of samples, some information lost due to incomplete penetrance might be regained. However, just as the search space for trees increases with the number of samples, the number of possible haplotype resolutions also increases, making a complete search clearly impossible, and requiring the researcher to rely on sampled searches or summary statistics, which both will again decrease information content.

In the cases of partial penetrance solely in the heterozygote, the best estimates came from the case where a heterozygote would display the uncommon phenotype 80% of the time. This precision steadily decreased as the simulated penetrance changed, until the worst estimates were seen when the heterozygote displayed the uncommon phenotype only 20% of the time. This corresponds to the decrease in the number of individuals (on average) displaying the minority phenotype (though not the number of minority haplotypes). This means that, given an unequal distribution of alleles, the more evenly split the phenotypes in the population, the more power there will be to map the corresponding trait alleles. Interestingly, this means that the precision does not rely on the uncertainty of heterozygotes penetrance—if it did, cases where the heterozygote was equally likely to display either phenotype would have been the worst.

In some cases, the penetrance model itself is not known. Unfortunately, a simulation study that tried to model this case would need to choose a prior over all reasonable penetrance models in order to properly combine the estimates from each. Such a prior has not been defined, and would almost certainly be controversial. Our research does show that it would be inadequate to simply average the fully-dominant and fully-recessive cases, hoping to include the intermediate partially-penetrant cases by proxy. As seen in Figure 9, both the dominant and recessive cases contain more information than several partially-penetrant cases, and estimates that ignored this would be inappropriately narrow.

Conclusions

While individual results will vary, fine mapping studies of any sort will be on average more effective for trait alleles unlikely to have arisen more than once, for traits with alleles that are close to equally frequent in the population. When genotypes are known, enough information is present in 20 randomly-sampled diploid individuals that one must sample exponentially more individuals to significantly affect the limit of one’s potential mapping precision. When genotypes are not known, sampling more individuals (and/or doing case-control studies) will help only insofar as they add information that would otherwise be contained in the genotype data. If the trait genotypes are differentially penetrant, much information can be recovered if the homozygotes and heterozygotes can be distinguished by pedigrees or additional studies. Further effort spent phasing the heterozygotes will not add appreciably to the total amount of information available. This result mirrors similar results from the COLDMAP program [Morris et al, 2004] which showed that phasing SNP data when mapping provided only minimal improvement, and in one case analyzed using DMLE+ [Reeve and Rannala, 2002], where the addition of phase information for the DTD mutation that causes diastrophic dysplasia also did not appreciably narrow the confidence window. These other studies suggest that one’s ability to reconstruct the true tree will also be largely unaffected by phase information.

This analysis also explains why, once the data was collected, the gene that causes Cystic Fibrosis (CFTR) was able to be mapped fairly straightforwardly [Rommens et al. 1989]. The disease is the most common fatal recessive single-gene disorder in people of European descent, with a mutant allele frequency of approximately 0.022 among Caucasians [Kerem et al. 1989]. The gene contains a coding region of approximately 6500 nucleotides, and with over 500 reported CFTR mutants, the θ for dysfunctional CFTR alleles is probably fairly high. However, over 70% of the dysfunctional alleles are the same 3-nucleotide deletion (ΔF508) [Kerem et al. 1989], which has an estimated age of at least 580 generations, and could possibly be much older [Wiuf 2001]. The high frequency and long history together ensure a larger number of relevant recombination events, as well as a higher number of cases in general. Because heterozygous individuals can be easily discovered through their affected offspring, this nearly mimics the codominant case, which we have seen to be the most informative of the tested cases.

As most simple genetic diseases like CF have been successfully mapped at this point, attention is turning to mapping complex diseases. Our results indicate that diseases in populations with a common disease allele with high penetrance should be more easily mapped than those with rare alleles with incomplete penetrance. Collecting data from more individuals can help, and while randomly sampling individuals would increase the precision only with the log of the number of individuals, performing case/control data collection will increase the effective sample size significantly. However, incomplete penetrance (or worse, having an unknown penetrance model) is likely to lose much of the information that might be present in the population, and this information cannot be regained through any mapping study.

To predict the precision of a nascent mapping effort, one must measure or estimate the trait θ and the distance to be mapped in centimorgans. For example, a study of a human disease might use a trait θ of 1.0 (from Pritchard’s estimation of human disease θ), and be attempting to map within a 5 cM region. From Figure 5, we would expect that the recombinant coalescent history of 20 or more diploid individuals would contain on average enough information to map the causative allele in the best-case scenario to slightly less than 0.1 cM. A case/control analysis could decrease this further (Figure 7), to around 0.02 cM, depending on the frequency of the trait allele in the population. Other factors could increase the range again: attempting to map a complex disease with incomplete penetrance, having incomplete or inconclusive surrounding data that make it difficult to accurately reconstruct the true tree, or even the simple bad luck of happening to choose a disease whose alleles shared a common heritage with a large portion of the surrounding genome.

In humans, 0.02 cM would be about 20 kilobases, which seems a bit long for an absolute minimum. Several factors may explain why studies have been seen to contain more information than this. First of all, while our simple case/control analysis showed it to be quite effective at distilling information from the population at large, it may be that collecting even more case and controls (into the hundreds, in many cases) could increase mapping efficiency faster than the slow logarithmic rate at which adding randomly-sampled individuals would. Luck combined with a publication bias may explain more—0.02 cM is just an average, and the variance is large (Figure 2). If only the more successful studies are published, mapping will appear to be more effective than it actually is. Pritchard’s estimate of human disease θ (1.0) may also be high, or again, publication bias may have selected for mapping studies with a lower trait θ. Our assumption of equal rates of forward and back mutation rates will also contribute to a wider estimate than is found in actual studies, since allowing back mutations can artificially increase the fit of the data to inappropriate interval trees. Recombination hot spots in real data are unlikely to increase mapping precision, although their presence could have systematically increased the variance of possible analyses and increased the effect of the publication bias.

It is our hope that by knowing the odds before attempting a mapping project, researchers will be able to direct their efforts towards those studies with the highest chance of success, and collect the right kind of data for the projects they choose to embark on.

APPENDIX A

Fundamental to coalescent analysis is the ability to calculate the likelihood of observing a set of data given a particular coalescent tree. Calculating this ‘data likelihood’ for a set of unambiguous data using a ‘peeling’ algorithm has been described in Felsenstein [1981]. This is the likelihood that alleles evolving on the tree in question would have resulted in the given observed data.

The peeling algorithm involves iteratively considering each coalescent node on the tree, and calculating the likelihood that, given all possible starting alleles, one would end up with the likelihoods at the Upward nodes. The ‘tips’ of the tree that correspond to the present observations will have very simple likelihoods: If the observed allele is H, the likelihood of the observation if the true allele is H is 100%, and the likelihood of the observation if the true allele is h is 0%. We can use the vector [1, 0] to store this information for ease of access at the tip, with the first position the likelihood of H, and the second position the likelihood of h. These likelihoods are then used to calculate the likelihoods at each rootward node via the peeling algorithm. If there is no definitive observation of the data for a particular tip, the likelihood of that observation if the true allele was H is 100%, and the likelihood if the true allele is h is also 100%. Unknown data (‘?’) can therefore be represented by the vector [1, 1] at the tip.

In the case where an observation is ambiguous, such as an observed phenotype which might arise from different genotypes, we must consider all possible unambiguous haplotype resolutions that fit our observations. The data likelihood becomes:

$$\mathrm{P}(\mathrm{O}|\mathrm{G})=\sum _i\mathrm{P}(\mathrm{O}|{\mathrm{D}}_{\mathrm{i}})\mathrm{P}({\mathrm{D}}_{\mathrm{i}}|\mathrm{G})$$ (Eq A1)

where O is the set of observations, D_i is a particular haplotype arrangement, and G is the genealogy. (The general form P(x|y) is the probability of x given y.) In the case of an ambiguous phenotype, there is more than one possible haplotype arrangement, so each must be calculated and summed. If there are two or more individuals each displaying an ambiguous phenotype, each combination of haplotype arrangements must be considered, so, for example, if there are two heterozygotes with unknown phase, the four possible configurations of data would be HhHh, HhhH, hHHh, and hHhH.

Figure Al illustrates one such case with two individuals, one displaying a dominant phenotype, and the other displaying a recessive phenotype. Since there are three possible ways to arrange data on the tips in the dominant individual, all three must be considered. However, two of these cases share the same data at one of the tips, and only differ at the second. These two cases can be mathematically reduced to a single case, as shown on the right side of the figure, with a [1, 0] at the first tip and a [1, 1] at the second. The likelihood of observing the dominant phenotype in the first individual and the recessive phenotype in the second individual given this particular tree is therefore the sum of the data likelihood of the two cases.

The situation becomes more semantically challenging when we consider penetrance, but remains mathematically simple. The penetrance of a genotype is used to determine P(O|D) from Equation Al. Mathematically, we can include this term in the peeling algorithm by assigning the penetrance of a genotype to either tree-tip in our analysis. We can further use the ‘collapsing’ trick above to combine tips with different penetrance values, as illustrated in Figure A2.

If the homozygote hh had (say) a 10% penetrance for our phenotype, we could collapse this case with the hH case, and still maintain only two different resolutions. The first case would enumerate the probabilities when the first allele was an H, while the second case would enumerate the probabilities when the first allele was an h.

Following these methods, we can collapse all possible penetrance conditions with two alleles in a diploid individual to two cases. This can reduce our search time considerably: in a case with N diploid individuals displaying the dominant phenotype, we reduce the total number of cases from 3^N to 2^N.

Figure A1.

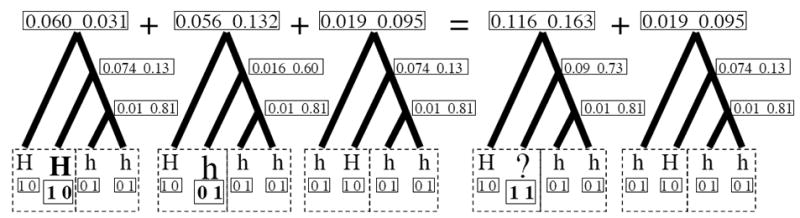
Calculating the probability of unhaplotyped data on coalescent trees. In this example, the left two boxed tips come from an individual displaying the dominant phenotype, and the right two boxed tips from an individual displaying the recessive phenotype. The total data likelihood on the tree is therefore the sum of the data likelihoods of the left three trees. The data likelihood of the first two of these trees can be ‘collapsed’ into the first of the two trees on the right, using ‘H?’ as the haplotype. The data likelihoods are calculated assuming a tree with a total length of three, evenly divided by coalescent events, where the likelihood of an allele remaining the same along a branch of length one is 90%.

Figure A2.

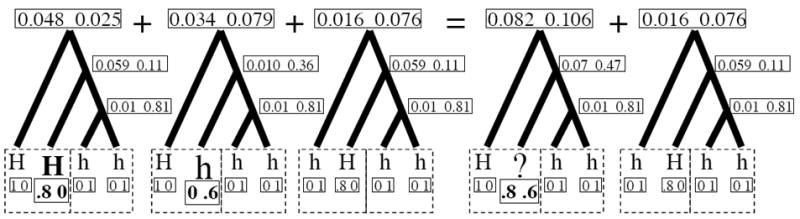
Calculating the probability of unhaplotyped, differently penetrant data on coalescent trees. In this example, HH individuals have a 80% chance of displaying the dominant phenotype, Hh individuals have a 60% chance of displaying the dominant phenotype, and hh individuals have a 100% chance of displaying the recessive phenotype. As in Figure A1, the left two boxed tips come from an individual displaying the dominant phenotype, and the right two boxed tips from an individual displaying the recessive phenotype. The ‘?’ tip on the right is a combination of the data likelihoods of the bolded tips on the left. The data likelihoods are calculated as in Figure A1.

APPENDIX B

Determining the average number of recombination events present in a recombining coalescent tree for a given set of parameters is not trivial. Unfortunately, one may not simply use the formula:

$$(\mathrm{s}­\mathrm{1})\mathrm{r}\mathrm{\theta }\sum _{k=\mathrm{1}}^{n-\mathrm{1}}\frac{\mathrm{1}}{k}$$ (Eq B1)

where s is the number of sites, r is the recombination rate, θ is four times the effective population size times the mutation rate, and n is the number of tips in the tree. This formula fails to take into consideration two things. First, the addition of a recombination event to the tree moving backwards in time changes the probability of the next recombination event being added to the same tree, due to a increase in the number of lineages with fewer ‘active sites’ (sites with a present-day sampled descendant from the given lineage) in each. Second, coalescent events between lineages with distant active sites create new lineages with a greatly increased number of potential locations for new recombination events.

Instead, we can consider the tree as a series of states with transitions between the states marked by recombination and coalescence. Going backward in time, we consider how the recombination rate and population size affect the rates between the different states. First, we calculate the expected time until all but one of the sites have coalesced using the formula:

$$T_i=\mathrm{1}+\sum _{k=\mathrm{1}}{P}_{\mathit{ij}}{T}_j$$ (Eq B2)

where T_i is the expected time we want, starting from state i, and P_ij is the probability of changing to state i when starting in state j, or Prob(i|j) [Feller, 1950].

We can extend the equation for the expected time until the first coalescence to calculate the number of expected recombination events that will occur during that time with the equation:

$$R_i=\sum _j{P}_{\mathit{ij}}(a_{\mathit{ij}}+R_j)$$ (Eq B3)

where R_i is the number of expected recombinations between state i and the final state, and a_ij is the number of recombinations encountered when moving from state i to state j.

For example, if we take the simplest case that has any recombination (two tips and two sites), we have three states with rates between and away from them, illustrated in the system of equilibria in Figure B1. In this system, the upper three states all have potential recombination events that make a difference to the tree, while the lower three states do not. Even if only one of the two sites has coalesced, further recombination will not affect the coalescence of the single site remaining.

This system of equilibria can be simplified by multiplying everything by 2N, as illustrated in Figure B2.

We can set this up as a matrix to give us a system of equations. The a_ij matrix is almost all 0’s, with two exceptions (going from state 1 to 2, and from state 2 to 3), giving us:

$$R_1=(\mathrm{4}\mathrm{NCdt})+(\mathrm{1}­4\mathrm{NCdt}-\mathrm{1}\mathrm{dt}+\mathrm{4}\mathrm{NCdt}+\mathrm{0})(R_1)$$ (Eq B4)

$$R_2=(\mathrm{2}\mathrm{NCdt})+(\mathrm{1}\mathrm{dt}+\mathrm{1}­\mathrm{2}\mathrm{NCdt}-\mathrm{3}\mathrm{dt}+\mathrm{2}\mathrm{NCdt})(R_{\mathrm{2}})$$ (Eq B5)

$$R_3=(\mathrm{0})+(\mathrm{0}+\mathrm{4}\mathrm{dt}+\mathrm{1}­\mathrm{6}\mathrm{dt})(R_{\mathrm{3}})$$ (Eq B6)

In each equation, the R_i’s cancel, letting us further cancel the dt’s and solve the system of equations for R₁:

$$R_{\mathit{1}}=\frac{\mathrm{1}+\frac{\mathrm{6}\mathrm{NC}}{\mathrm{9}+\mathrm{2}\mathrm{NC}}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}\mathrm{NC}}-\frac{\mathrm{3}}{\mathrm{9}+\mathrm{2}\mathrm{NC}}}$$ (Eq B7)

In the case where 4NC equals one, R₁is then 11/16. We confirmed this number with an implementation of Hudson’s recombinant tree simulator [Hudson 1983], a final-coalescent aware tree generator. The average number of recombinations present in 10,000 trees generated with 4NC=1.0 (θ=1.0 and r=l.0) was 0.6862, well in line with the expected 0.6875.

Beyond this simplest case, however, the complexity increases rapidly. Rather than working out the analytical solution to the number of expected recombinations, values were estimated using 10,000 replicates of the Hudson simulator.

Figure B1.

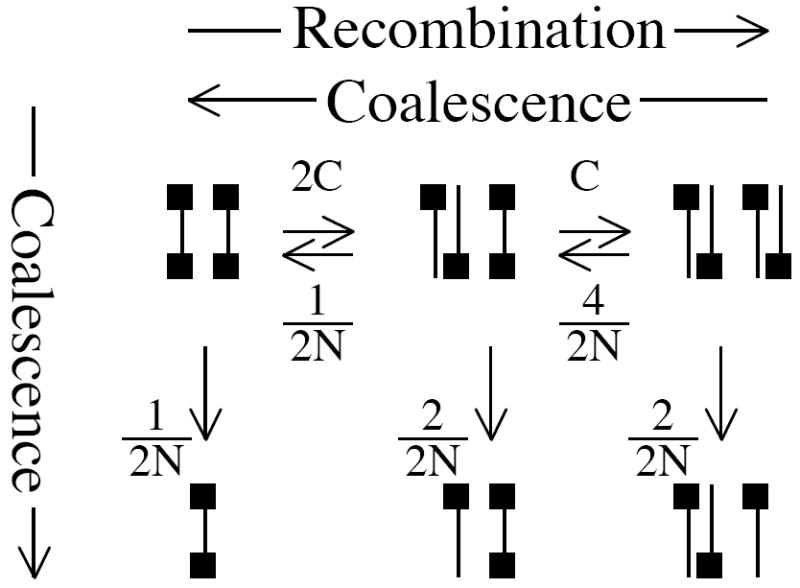
The equilibria between possible states of a two-tip, two-site coalescent tree. Black squares represent ‘active’ sites--sites whose direct descendants have been sampled.

Figure B2.

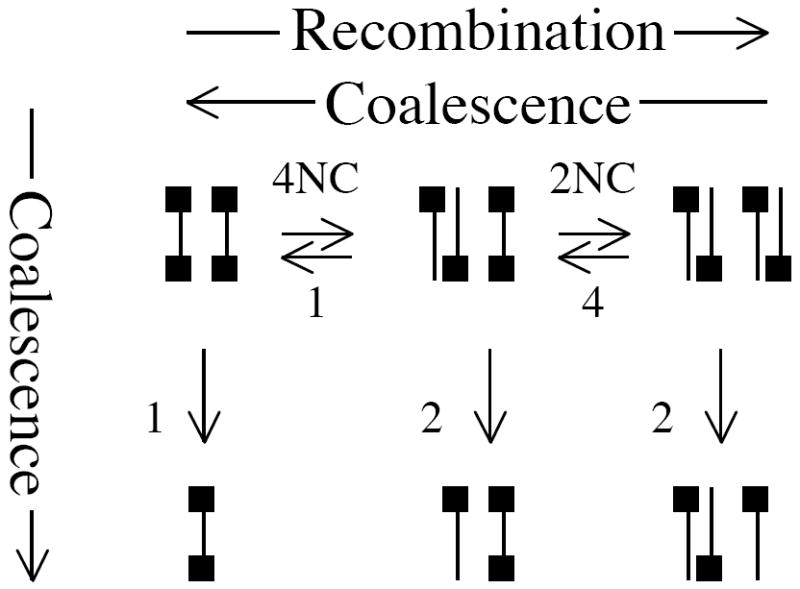
The equilibria between possible states of a two-tip, two-site coalescent tree (modified). The equilibria from Figure B1 here have been multiplied by 2N.