Abstract
‘Loss to follow-up’ can be substantial in substance abuse clinical trials. When extensive losses to follow-up occur, one must cautiously analyze and interpret the findings of a research study. Aims of this project were to introduce the types of missing data mechanisms and describe several methods for analyzing data with loss to follow-up. Furthermore, a simulation study compared Type I error and power of several methods when missing data amount and mechanism varies. Methods compared were: Last Observation Carried Forward, Multiple Imputation, Modified Stratified Summary Statistics and Mixed Effects Models. Results demonstrated nominal Type I error for all methods; power was high for all methods except LOCF. MEM, Modified SSS and MI are generally recommended for use; however, many methods require that the data are missing at random or missing completely at random (i.e., “ignorable”). If the missing data are presumed to be non-ignorable, a sensitivity analysis is recommended.
Keywords: Substance Abuse Clinical Trial, Loss to Follow-up, Treatment Effect, Hypothesis Tests, Longitudinal Data
1. Introduction
In substance abuse clinical trials, much of the missing data are due to losses to follow-up; i.e., individuals who drop-out of the study after randomization to treatment and whose data are lost thereafter. This type of ‘drop-out’ is differentiated from individuals who may discontinue treatment (clinical drop-out) but who are followed throughout the duration of the study, a scenario common with intention-to-treat analyses, or individuals who are lost but later located for future or follow-up assessment (intermittent missing data). In this paper, we discuss the impact of losses to follow-up on hypothesis tests of the treatment effect where missing data are prevalent in outpatient substance abuse clinical trials. This is particularly warranted given that many substance abuse treatment clinical trials demonstrate substantial losses to follow-up after the first dose of treatment with missing data percentages ranging from 10% to 50% (Dutra et al., 2008; Edwards & Rollnick, 1997; Higgins & Budney, 1997; Howard, Cox, & Saunders, 1990; Mattson et al., 1998; McRae, Hedden, Carter, Malcolm, & Brady, 2006; Nich & Carroll, 2002).
This high percentage of loss to follow-up in substance abuse research may interfere with the evaluation of treatment programs and could call into question the validity of study findings. Furthermore, extant research suggests that individuals who are lost to follow-up tend to have poorer functioning compared to individuals who complete treatment; thereby, biasing treatment outcome (Sobell, Sobell, & Maisto, 1984). Traditional methods of longitudinal data analysis such as data deletion (complete case analysis) or single imputation, may be biased or otherwise invalidated in the presence of substantial missing data (Figueredo, McKnight, McKnight, & Sidani, 2000). Furthermore, the performance of various statistical methods for missing data needs to be evaluated in the presence of different missing data scenarios, and in particular, in scenarios involving substantial losses to follow-up, as seen in substance abuse clinical trials.
Therefore, the aim of this study is to describe the types of missing data mechanisms that may occur in substance abuse clinical trials, as well as various methods used to test hypothesis of the treatment effect when missing data are present. Methods extensively described in this paper include but are not limited to stratified summary statistics, imputation and mixed effect models. Further, a Monte Carlo simulation study is performed to compare several of the methods described in terms of their Type I error and power. We end with recommendations for the analysis of longitudinal data in the presence of loss to follow-up.
The primary purpose of this manuscript is to inform the substance abuse researcher of the various types of missing data that may occur in substance abuse clinical trials as well as describe various methods which may be used for various missing data scenarios. We do this, in order to aid researchers in applying modern and appropriate longitudinal analysis when individuals are lost to follow-up.
1.1 Missing Data Mechanisms
Subjects who miss a study visit in substance abuse research are often lost thereafter. This complete ‘loss to follow-up’ gives rise to the probability that the missing data mechanism is not random and may be dependent upon observed and unobserved values of the outcome. Several missing data mechanisms defined by their dependence on observed and unobserved data points, including the outcome, have been classified by Rubin (1987). The specific case of missing data mechanisms for data that are lost to follow-up in the longitudinal setting has been further described by Schafer and Graham (2002) and is similarly expressed below.
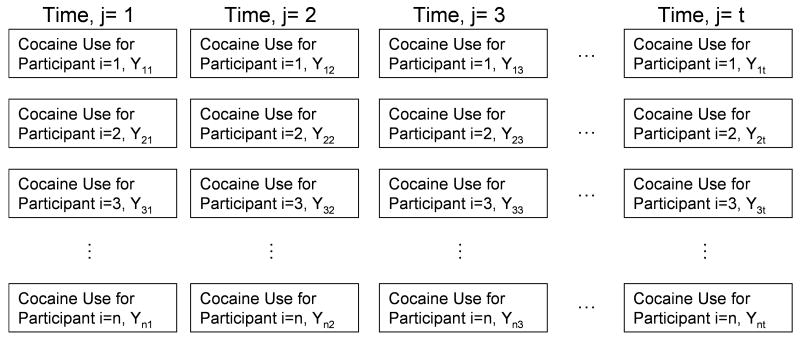
To describe missing data mechanisms, some notation and illustrations are helpful. Assume that the outcome variable (e.g., amount of cocaine used) can be measured on each participant repeatedly over the course of the study. In mathematical notation, let Yij represent the jth j = 1,…,t, measurement of the outcome variable for the ith participant, i = 1,…,n. Figure 1 demonstrates this notation for a longitudinal study for n individuals over t points in time. This illustrates serves as the framework from which all missing data mechanisms will be discussed.
Figure 1. Representation of a Complete Longitudinal Dataset for, n, Individuals and, t, Time Points.
It should be noted that Figure 1 demonstrates the case where all individuals' outcomes are measured at all points in time, i.e. a complete dataset. However, should an individual miss a visit this can also be defined. A missed visit, m, can be defined as the time at which a subject drops out of a study and does not return, j=m.
Missing data can further be classified by its dependence on observed and/or unobserved outcomes; that is, a missing data mechanism may be defined. The most ideal missing data scenario occurs when data are missing completely at random (MCAR). This occurs when the missing data is independent of any outcome variables and any covariates of interest (Rubin, 1987; Schafer & Graham, 2002). For example, suppose a participant is followed continuously through the first (m-1) visits, but fails to return to the study starting at visit m. In this setting, the values for the outcome variables are unobserved from week m to the end of the study, t (i.e., Yim,…,Yit are all unobserved). For this missing data to be MCAR, the missing outcome data must be not be associated with any observed or unobserved data point. A practical example of such scenario is when a participant changes location during the course of the study for reasons completely unassociated with the study and or disease (e.g., work transfer, military deployment, etc).
The second most common missing data mechanism is missing at random (MAR). MAR occurs when the missing outcome is dependent on any of the observed outcomes, Yi1,…,Yi(m−1), or observed covariates until the time of the missed visit but independent of any unobserved data (Schafer & Olsen, 1998). The key here is that the missingness is not related to the data that are unobserved. A situation in which this may occur would be if missingness was dependent on the covariate depression where depressed individuals were more likely than non-depressed individuals to fail to complete a clinical trial. That is the missingness is not randomly distributed across the entire sample of individuals, depressed and not depressed. However, for the missing data to be MAR, the missing data within each sub-sample is randomly distributed. In practice, data are more likely MAR than MCAR.
Finally, data that are missing not at random (MNAR) occur when the missed outcome is dependent on any outcome not observed due to missed visits; the missing data may be dependent on any of the unobserved outcomes, Yim,…,Yit. This scenario may occur in a relapse prevention study. Suppose a participant has negative urine drug screens for the study up until the point in time when the first missed visit occurred (at week m). If it is known that the participant was positive at this missed visit and the reason for the missed visit was because he or she knew his urine drug screen would be positive, the missed visit would be classified as MNAR.
In summary, the three missing data mechanisms can be contrasted using the following example. In clinical trials involving cocaine dependent participants, the primary outcome is often defined as use of cocaine. Missing data are MCAR if the cocaine dependent patient misses a visit to the clinic and the reason for the missed visit is in no way related to their outcome (use of cocaine) or covariates at any point in the trial. If the cocaine dependent patient misses a visit and the missed visit is directly related to the response from previous visits (for example if a relapse is observed prior to the missed visit and relapse is the reason for the missed visit) or is related to covariates (for example, if persons with concurrent use or comorbidity as related to their cocaine use are more likely to be lost to follow-up) then the missing data are classified as MAR. Finally, an example of missing data which is MNAR can occur when, in addition to the prior visit's observations affecting missingness, the cocaine dependent person would miss a visit due to relapse although the relapse is not observed.
1.2 Identification of the Missing Data Mechanism
Several methods have been proposed to aid in the identification of missing data mechanism. For example, Diggle and colleagues describe methods for testing whether missing data in longitudinal trials are not MCAR (Diggle, 2003). Specifically, they test whether the probability that an individual drops out at a particular point in time, j=m, is independent of previously observed responses, Yi1,…,Yi(m−1). First, a function of the observed responses, denoted as hk, for each individual is determined. For example, the function could be defined as the latest observed measurement, i.e. hk (y1,…,yk) = yk. Using the latest observation in substance abuse trials may have validity since, much of the dropout observed may be due to relapse or no change in response. Other functions could include the slope, mean or other linear combination of the observed responses.
Second, a binary variable is defined for each time point indicating whether an outcome is missing or not. Logistic regression models are then used whereby the dependent variables are the indicators for missingness at each time point. The previously defined function of the observed responses, hk, is then used as an independent variable in the logistic regression model. The probability that an individual is lost to follow-up, pk may then be defined, and the logit is as follows: , where α is the intercept and β is the slope of the logit. Rejection of the null hypothesis, Ho : β = 0, rejects the assumption that the missing data mechanism is MCAR; i.e. rejects the assumption that the missing data is not a function of the previously observed outcomes. Further descriptions of this method are described elsewhere (Diggle, 2003).
Unfortunately, whether missing data are MAR versus MNAR may not be empirically differentiated (Molenberghs, Thijs, Jansen, & Beunckens, 2004). That is, formal tests can not be used to determine whether missing data is MAR versus MNAR. In order to distinguish between MAR and MNAR, it would need to be determined whether an association exists between the unobserved data and the missed outcome. Although MAR may not be empirically distinguished from MNAR, a sensitivity analysis is one technique used when missing data is suspected to be MNAR (Molenberghs et al., 2004). Section 1.8 describes various methods of analysis which may be used when it is suspected that the missing mechanism is MNAR.
1.3 Stratified Summary Statistic Methods for Longitudinal Data Analysis with Missing Data
The summary statistic method of longitudinal data analysis is a technique by which each individual's multivariate longitudinal outcome is reduced to a single summary measure (Frison & Pocock, 1992). For example, suppose skin conductance is used as a measure of craving in a clinical trial. The mean conductance level over a period of time may be used as an overall indication of ‘craving’. Other common summary statistics include the area under the curve, time to peak response, rate of change over time (i.e,. slope). Summary statistics may include linear combinations, nonlinear functions, order statistics and survival functions. The defining attribute of each of these measures is that they effectively consolidate the repeated measurements into a single value that can be analyzed using standard univariate analytical techniques (Dawson, 1994; Dawson, 1994; Dawson & Lagakos, 1991; Frison & Pocock, 1992; Matthews, Altman, Campbell, & Royston, 1990; Pocock, 1983).
As with any type of longitudinal data analysis, the summary statistic approach may need to be modified in the presence of losses to follow-up. Dawson and Han (2000) have studied the effect of the missing data mechanism on summary statistics. For example, when the slope is used as a summary statistic and the missing data mechanism is considered to be completely random (MCAR) the variance of the slopes may vary dependent on the amount of outcome data available (Dawson & Han, 2000). However, if the missing data mechanism is missing at random (Schafer & Olsen) or nonignorable (MNAR) and/or the trend is nonlinear then the mean of the slopes may vary dependent upon the amount of data available per individual.
If the missing data patterns differ between treatment arms, then the summary test statistic approach may be invalid (Wu & Bailey, 1989). Therefore a stratified summary statistic approach may be appropriate for this case whereby each individual's summary response is stratified according to their missing data pattern (Dawson, 1994; Dawson, 1994; Dawson & Han, 2000; Dawson & Lagakos, 1991). This method has been deemed Stratified Summary Statistic (SSS) because one conditions or stratifies the analysis according to missingness patterns. This ‘stratification by missingness pattern’ may be appropriate when the mean and/or variance of the summary statistic is dependent upon the amount or timing of the outcome (Dawson, 1994; Dawson, 1994; Dawson & Han, 2000; Dawson & Lagakos, 1991). Brief steps of the SSS method are described below. A more comprehensive review of these methods are described in existing literature (Dawson, 1994; Dawson, 1994; Dawson & Han, 2000; Dawson & Lagakos, 1991, 1993; Hedden, Woolson, & Malcolm, 2008).
First, individuals are stratified according to their missing data pattern; e.g. individuals with 2 observations over time are in one stratum whereas individuals with 3 observations over time are in another stratum. Then a summary statistic (e.g. mean or slope) may be calculated for each individual over time. For each stratum, the average summary statistic for each treatment group is calculated and the groups compared using an independent t-test. Next each individual t-test statistic is weighted and combined into an aggregate statistic. Dawson proposes a stratum weight, wS, that increases with the number of individuals within stratum and with the number of observations per person in a given stratum (1994). The aggregate statistic in equation (a) is a weighted sum of the stratum specific test statistics. The test statistic, ts is a t-test or a z-test statistic for each stratum, s. This aggregate statistic is then compared to a standard normal distribution (Dawson, 1994).
| (a) |
where s indexes the t strata formed by the observed missing data patterns.
1.4 Modified SSS
The SSS aggregate statistic as contributed by Dawson (Dawson, 1994) may need to be slightly modified when a t-test rather than a z-test is chosen for the stratum specific test (Hedden et al., 2008). That is, the aggregate statistic may need to adjust for the degrees of freedom for each stratum specific t-test.
This aggregate statistic is as follows:
| (b) |
The variable vs is the degrees of freedom associated with each stratum specific test statistic.
Stratified summary statistic approaches have the advantage of simplicity compared to other complex modeling methods. Also, since SSS conditions on the missing data pattern it may be used in instances when the missing data mechanism is suspected to be MNAR. However, SSS is mainly used for hypothesis testing of the treatment effect. If the estimation of the treatment effect is of primary concern, other modeling methods may be used; e.g., mixed effect or pattern mixed effect models.
1.5 Imputation
Imputation methods for missing data include single value imputation and multiple imputation. Last observation carried forward (LOCF) is a single value imputation method in which each subject's last observation is carried forward until the end of the trial. LOCF assumes that observations do not change over time after the last observation observed (Little & Yau, 1996). Therefore, LOCF should be reserved for instances when outcomes are not expected to change over time during the period of imputation. Any imputation method ‘incorporates an assumption about the predictive distribution of the missing values given the observed data’ (Little & Yau, 1996). LOCF may not be a plausible choice in substance abuse research when the outcome variable is hypothesized to steadily decrease over time; e.g. when cocaine use is expected to decrease over time.
Finally and most importantly, Lavori (1992) has aptly illustrated how LOCF can seriously bias study outcomes, i.e. it has the potential to distort the estimated treatment effect in a systematic manner. That is, the statistical method used to contend with attrition, such as LOCF, may have a profound result on the conclusions drawn from a study (Lavori, 1992). Although, LOCF has many pitfalls it is still a widely used method for missing data in substance abuse research. Indeed, in spite of its limitations LOCF results are often presented to FDA Advisory Committees. We include LOCF for comparisons due to its widespread utility.
1.6 MI: The regression method for monotone missing data
A variety of multiple imputation methods have been proposed in the literature (Rubin, 1996, 1987; Schafer, 1999; Schafer & Olsen, 1998). These methods assume that the missing data mechanism is MAR. Some appropriate methods of MI for multivariate normal data with loss to follow-up include the parametric regression method (Rubin, 1987). The regression method for MI fits a regression model for each outcome variable with missing data where the independent variables of the model are the previously observed outcome variables.
Using this model, the estimates of the regression parameters and estimates of the covariance matrices may be computed. Given the parameter estimates of the fitted model, a fresh regression model is simulated using the posterior predictive distribution of the regression parameters. This new model is then used to impute the missing data for each outcome variable (Rubin, 1987).
The dataset is imputed multiple times, i.e. each missing value is replaced by multiple imputed values creating multiple datasets. Each imputed dataset is analyzed using standard methods and parameter estimates for each analysis are then combined. Rules for combining estimates of the regression parameters from multiply imputed datasets are described in the literature (Rubin, 1987). In summary, hypothesis tests of the treatment effect for MI are based on the mean of the estimates computed from the multiply imputed datasets and take into account the uncertainty due to missingness.
1.7 Mixed Effect Models
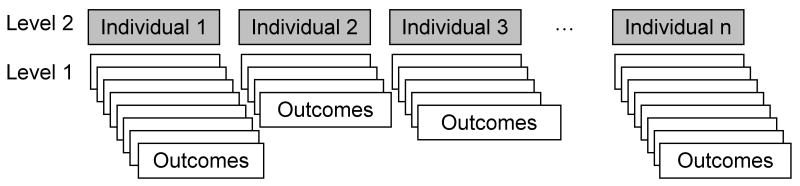
Rather than imputing missing data, mixed effect model (MEM) analysis is a method that uses all of the observed data for analysis (Laird & Ware, 1982). MEM assumes that the missing data mechanism is either MAR or MCAR (Little & Yau, 1996). The mixed effect model for random slopes and intercepts may be expressed in a hierarchical set of regression equations at two levels as described by Singer (1998). This model “explores whether variation in intercepts and slopes is related” to treatment (Singer, 1998). In its simplest form, a two level approach expresses the observation level outcome,Yij, at the observation level (level 1) and at the individual level (level 2). For example, figure 2 demonstrates the longitudinal observations within individuals where individual one has eight observations and individual two has four observations, etc.
Figure 2. Representation of a 2-Level Hierarchical Model for Longitudinal Data.
The two sets of regressions equations for the MEM is presented as Figure 3. For the level 1 regression equations, the observation level outcome (Yij) is expressed as the sum of the participant-specific intercept, pi0, a covariate that represents the time since a reference date (i.e., baseline or randomization) and a random error associated with the jth observation for the ith individual. The level 2 (between individual) model expresses the random effects or the variation in parameters unrelated to individual-level covariates. In Figure 3, the main effect of the randomized treatment (tx) is included in the level 2 equations since it is at the ‘individual’ level.
Figure 3. Two Level Representation of a Random Slope and Intercept Mixed Effects Model.
These level 1 and 2 models may be combined into the following model which expresses both fixed and random components; hence the name, ‘mixed’ effect model.
| (c) |
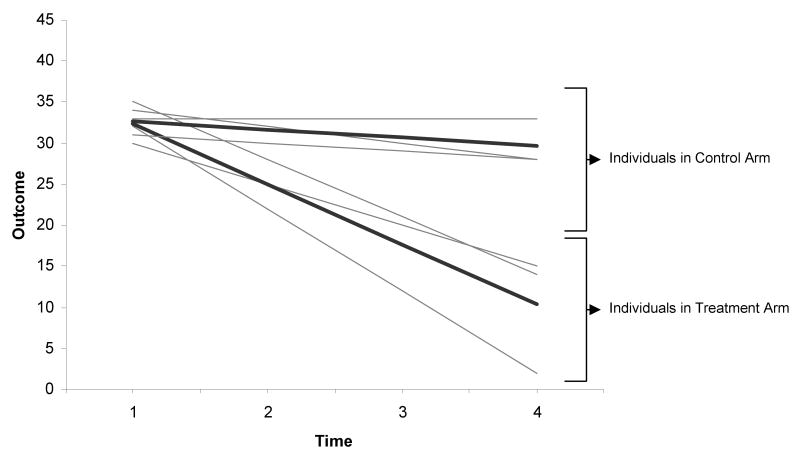
These models assume that an individual's intercepts and/or slopes have a distribution, or deviate from average. For example, figure 4 demonstrates an example of two treatments and three individuals per treatment who differ in the baseline outcome (intercepts) as well as their change in outcome levels over time (slopes.). The darker lines indicate the average response for each treatment over individuals. This figure demonstrates the paradigm when both the intercepts and slopes are random, i.e., both individual intercepts and slopes deviate from average.
Figure 4. Representation of Random Intercepts and Random Slopes for Two Treatment Arms over Four Time Points.
Using our cocaine use paradigm, random intercepts assume that baseline cocaine use differs for each individual. Instead of estimating separate intercepts for each individual, MEM estimates the average intercept and the variance of the intercepts over individuals (Twisk, 2006). Random slopes indicate that the linear trajectory of cocaine use over time varies; hence, the average slope and the variance of the slopes are estimated.
In equation (c), the parameters β00 and β10 indicate the intercept and slope of the average trajectory of individuals on placebo; whereas, (β00 + β01) and (β10 + β11) indicate the intercept and slope of the average trajectory of individuals on treatment. When the treatment by time interaction (indicated as the parameter β11) is not zero, ‘the slopes of the change trajectories differ’ according to the treatment value; that is, the change over time differs dependent on the treatment (Singer & Willett, 2003). A Wald test may be used to test the treatment*time interaction. This may be done by testing that the null, Ho:β11=0. If the null is rejected, the outcome over time is said to differ with treatment.
1.8 Methods for MNAR
Methods described previously such as MEM or MI are most appropriate under the assumption that the missing data mechanism is MAR or ignorable. In substance abuse clinical trials, some of the missing data may be MNAR or non-ignorable. On the other hand, SSS which stratifies by the missing data pattern is a method for use in the instance of non-ignorable missing data (Dawson, 1994; Hedden et al., 2008). However, special cases of MEM or MI can used to account for non-ignorable missing data mechanisms by controlling for missing data patterns, e.g. pattern mixture models. Furthermore, when missing data are indeed MNAR extant literature has suggested that a sensitivity analysis comparing several methods (both MAR and MNAR methods) may be appropriate (Molenberghs et al., 2004).
When the missing data mechanism is largely assumed to be MNAR, several methods of analysis include SSS, pattern mixed effect models or selection models (Dawson, 1994; Diggle & Kenward, 1994; Hedden et al., 2008; Hedeker & Gibbons, 1997). The pattern MEM uses the same methods of an MEM except participants are divided into groups based on their missing data pattern. The missing data pattern groups are then used as an independent variable in the mixed effect model (Hedeker & Gibbons, 1997). Similar procedures may be used for MI. However for MI, the missing data pattern is used as a covariate in the regression model used to impute the missing data.
Selection models may also be used if the missing data mechanism is MNAR (Diggle & Kenward, 1994; Diggle, 2003; Hedeker & Gibbons, 1997). Selection models may be described briefly in two parts. The first step for implementing a selection model includes fitting a logistic regression model to the data in order to estimate the probability that an individual is lost to follow-up. The dependent variable of the model is an indicator for whether or not an individual was lost to follow-up. Independent variables in the logistic regression model include functions of observed outcomes or covariates. The second step involves using the estimated probabilities that an individual is lost to follow-up (estimated using the logistic regression model) as an independent variable in an analysis of the treatment effect.
Although missing data methods that assume MNAR have been developed, they have strong assumptions about the missing data which when wrong could seriously affect the interpretation of the treatment effect for a clinical trial (Molenberghs et al., 2004). That is, MNAR methods make strong assumptions about data that are not actually observed. Rather than ignoring the possibility that data is MNAR and reverting to data deletion of single imputation methods or ‘blindly shifting’ to an analysis that assumes that missing data are MNAR, it has been suggested that a sensitivity analysis may be conducted to determine whether various missing data methods of analysis result in similar findings (Molenberghs et al., 2004). For example, hypothesis tests of the treatment effect using MAR methods such as MEM or MI may be compared to hypothesis tests of the treatment effect using MNAR methods such as SSS, pattern MEM and/or a selection model to determine whether incorporating the missing data pattern into the analysis is informative. That is, comparisons of MAR and MNAR methods will determine whether adding the missing data pattern to the analysis changes the hypothesis tests and/or estimates of the treatment effect (Hedeker & Gibbons, 1997).
2. Materials and Methods
2.1 Monte Carlo Simulation
A Monte Carlo study incorporating the general design of outpatient substance abuse clinical trials was used to assess the Type I Error and power of hypothesis tests of the treatment effect. Assumptions of the simulated dataset were as follows: the outcome followed a multivariate normal distribution and within unit (individual) variation was assumed to follow a compound symmetry structure. A common correlation coefficient of .6 was estimated from the complete cases of previous substance abuse clinical trials (Malcolm et al., 2005). Outcome was assumed to follow a linear trend, with individuals in both treatments groups having similar outcomes at the beginning of the study and then decreasing over time. For simulations of power, the treatment effect was assumed to increase over time. Also, the simulated data had 2 treatment groups and 8 points in time for 100 individuals. The eight time points were chosen, given the typical design of a substance abuse clinical trial whereby individuals are provided treatment for 8 to 12 weeks (Carroll, 1998; Higgins & Budney, 1997; Malcolm et al., 2005). Since this is a study of longitudinal data analysis, each individual was assumed to have at least two measurements.
Missing data patterns were assumed monotonic; i.e. each subject was observed and data were recorded until withdrawal from the study and those who withdrew were not observed for the remainder of the study. Also, missing data was considered either MCAR or MAR with respect to outcome. Missing data in substance abuse trials are unlikely to be Missing Completely at Random; however, this mechanism is included for statistical comparison. In order to simulate the missing data mechanism, the probability of loss to follow-up was assumed to follow a logistic regression model (Diggle, 2003; Ridout, 1991; Shih & Quan, 1998). Particular methods of the missing data simulation have been described previously (Hedden et al., 2008).
Two thousand simulations were preformed for each method for the missing data percentages of 10% and 40%. In order to meet the standards of computation-based analysis, the optimal number of simulations was calculated using the coverage probability of 95% around the estimated Type I error probability of .05 (Hoaglin, 1975). Using this method, the simulation sample size was approximately 2,000.
2.2 Statistical Analysis
General statistical analysis methods of modified SSS, LOCF, MI and MEM were applied to each simulated data set. For modified SSS, the summary statistic distributions were expected to vary with respect to type and amount of missing data; therefore, slopes were analyzed conditionally on missingness patterns (Dawson, 1994; Dawson, 1994). Stratum specific t-test statistics were weighted and combined into an aggregate statistic which was compared to the standard normal distribution.
The LOCF imputation analysis involved imputing missing data using LOCF. Then the slope was calculated for each individual. Average slopes were compared for each treatment group using an independent t-test.
The method of MI described is available in SAS version 9.1, 2003 under the PROC MIANALYZE statement for MI. For this study, SAS PROC MIANALYZE defaults were used for the multiple imputations.
Mixed effect models were used to analyze the incomplete data sets. Specifically, SAS PROC MIXED was used to test the treatment by time interaction for each simulation. A Wald hypothesis test was used to test the treatment*time interaction, determining whether the slopes over time differed between treatments (Dawson & Han, 2000; Singer & Willett, 2003).
For each of the 2000 simulated datasets simulated under the null and alternative hypothesis, data were analyzed using Modified SSS, LOCF, MI or MEM. Type I error was determined by the percent of times that the null hypothesis was rejected given that data was simulated for no treatment effect, i.e. the null hypothesis. Power was similarly determined using data simulated under the assumption of an existing treatment effect; i.e. the alternative hypothesis. Type I Error and Power were calculated for different missing data percentages of 10% and 40% and different missing data mechanisms of MCAR and MAR. Methods with Type I Error near .05 and methods with maximum power were considered most favorable.
A complete dataset was also simulated and analyzed using a summary statistic method; the simulated power for the complete dataset was approximately 84%. The power of the complete analysis was compared to that of missing data methods for both 10% and 40% missing data and missing data mechanisms of MCAR and MAR. A power ratio was computed by taking the simulated power of the various missing data scenarios and methods and dividing it by the simulated power of the complete summary statistic analysis.
3. Results
Table 1 demonstrates the Type I error probability under a variety of missing data percentages and mechanisms for Modified SSS, LOCF, MI and MEM. Results demonstrate Type I error probabilities around .05 for MEM, Imputation and Modified SSS under a variety of assumptions. Little variation in Type I error was demonstrated for the different missing data percentages and/or mechanisms.
Table 1. Comparing Type I Error and Power of Methods for Missing Data Percentages of 10% and 40% and Missing Data Mechanisms of MCAR and MAR.
| Type I Error | Power | ||||
|---|---|---|---|---|---|
| Method | Mechanism | 10% missing | 40% missing | 10% missing | 40% missing |
| Modified SSS (Dawson weight) | MCAR | 0.0615 | 0.0525 | 0.8165 | 0.4445 |
| Last Observation Carried Forward | 0.0615 | 0.0565 | 0.7565 | 0.3685 | |
| Multiple Imputation | 0.0570 | 0.0555 | 0.8910 | 0.4810 | |
| Mixed Effect Model | 0.0565 | 0.0550 | 0.9095 | 0.5415 | |
| Modified SSS (Dawson weight) | MAR | 0.0580 | 0.0520 | 0.9000 | 0.3755 |
| Last Observation Carried Forward | 0.0540 | 0.0570 | 0.4750 | 0.0515 | |
| Multiple Imputation | 0.0520 | 0.0520 | 0.9609 | 0.3820 | |
| Mixed Effect Model | 0.0550 | 0.0575 | 0.9940 | 0.5305 | |
Data simulated for 2 treatment arms, 8 points in time and 100 individuals
Power for each test differed dependent on the method used as well as the missing data percentage and mechanism assumed. Table 1 demonstrates the power of each test under the missing data percentages of 10% and 40% and missing data mechanisms of MCAR and MAR for a variety of methods. Modified SSS, MEM and MI were more powerful compared to LOCF. When the missing data percentage is 10% and the missing mechanism is MCAR, then MEM, Modified SSS and MI have approximately 5-10% more power than LOCF. MEM, Modified SSS and MI are also more powerful than imputation methods when the missing data percentage is greatly increased to 40%. Although MEM, Modified SSS and MI do perform better than LOCF under all missing data percentages and mechanisms, the power of the tests are greatly decreased for a 10% versus a 40% missing data percentage. In general, power fluctuations were observed for each missing data mechanism.
Table 2 demonstrates the ratio of power of the hypothesis test of the treatment effect for Modified SSS, LOCF, MI and MEM with missing data percentages of 10% and 40% and missing data mechanisms of MCAR and MAR compared to the summary statistic analysis of a complete dataset. Power for the complete analysis was approximately 84% using a summary statistic method of analysis. For example, given 10% missing data and a missing data mechanism of MCAR the Modified SSS methods has approximately 73% of the power of a summary statistic analysis of a complete dataset. Overall results demonstrate higher power for Modified SSS, MEM and MI compared to LOCF as well as highly diminished power for 40% compared to 10% missing data percentage.
Table 2. Power ratio of an Incomplete Dataset Analysis versus a Complete Dataset Analyses.
| 10% Missing | 40% Missing | |||
|---|---|---|---|---|
| Method | MCAR | MAR | MCAR | MAR |
| Modified SSS (Dawson Weight) | 0.7342 | 0.7247 | 0.3799 | 0.1897 |
| LOCF | 0.6546 | 0.2444 | 0.3270 | 0.0149 |
| Multiple Imputation | 0.8139 | 0.8730 | 0.3847 | 0.1617 |
| Mixed Effect Models | 0.8353 | 1.0184 | 0.4732 | 0.2152 |
Data simulated for 2 treatment arms, 8 points in time and 100 individuals
Power for a complete data using a Summary Statistic analysis method as a standard for comparison was 84%
4. Discussion
Given the cumulative results for this simulation study and extant literature, recommendations for analysis of substance abuse clinical trials may be established. According to the simulation study in which the assumption that the missing data mechanisms were considered MCAR all methods appear to perform well in terms of both Type I Error and power when missing data percentages are small. Power was not as greatly affected for smaller missing data percentages and a missing data mechanism of MCAR. In this instance, any of the methods discussed may be an appropriate choice.
When the missing data mechanism was MAR and the missing data percentage was 10% power decreased for LOCF. LOCF may not be an appropriate for substance abuse research where data are assumed to change over time after loss to follow-up. When relapse occurs before loss to follow-up, LOCF will assume that the subject will continue to relapse for the duration of the study, making the results conservative as in the case of this simulation study. On the other hand if relapse occurs but is not observed, LOCF results may indicate that individuals are performing better than in reality. Substance abuse is rife with intervals of both relapse and remission; therefore, methods which assume no change in time after loss to follow-up (such as LOCF) may not be valid.
Although Type I Error probabilities were not affected by the amount of missing data, the power of the test differed for each method dependent on the amount of missing data. Therefore, choices of an appropriate method of analysis are further complicated by the amount of missing data. Power of the hypothesis test of the treatment effect varied for each method dependent on both the missing data percentage and mechanism. Given that the missing data percentage is small (<10%), power was not greatly affected utilizing any of the methods of analysis assuming that the mechanism is MCAR. However, given missing data mechanism of MAR and/or missing data percentages of 40%, MEM was the optimal method of analysis in terms of power. Modified SSS and MI demonstrate much greater power compared to LOCF. Also, the Modified SSS procedure has the advantage over MEM and MI; it is a computationally simple method. Furthermore, Modified SSS has been demonstrated to be robust in instances when the missing data is not MCAR or MAR; that is, when the missing data is non-ignorable (Dawson & Han, 2000; Hedden et al., 2008)
In general, Modified SSS, MEM and MI produced tests with Type I Error near .05 and good power. Therefore, these methods are recommended for use in the analysis of substance abuse clinical trials over single imputation methods such as LOCF or traditional methods such as complete case analysis. Future simulation studies may want to focus on differences in power and Type I Error of hypothesis tests as well as bias and efficiency of treatment effect estimates for a variety of missing data percentages, patterns (intermittent or a combination of intermittent and monotonic missing data) or mechanisms for both MAR and MNAR methods. That is, further comparisons of various methods of missing data analysis such as pattern mixture and selection models in terms of size and power of the test of the treatment effect should be assessed (Hedeker & Gibbons, 1997).
Given that losses to follow-up in substance abuse clinical trials often impacts statistical tests and estimates of the treatment effect, appropriate steps should be taken to minimize the amount of loss to follow-up. For example, substance abuse clinical trial investigators should include design elements that reduce the occurrence of missing data such as behavioral platforms; e.g. contingency management (CM) (Higgins, Wong, Badger, Ogden, & Dantona, 2000; Petry & Simcic, 2002). Although retention has been demonstrated to increase using CM, the amount of missing data reported in substance abuse clinical trials still warrants concern and losses to follow-up should also be taken into consideration when in the plan for analysis.
Finally, this article demonstrates the impact that attrition can have on several of the statistical methods that may be used in the substance abuse setting. It should be noted, that the analysis of substance abuse trials should not be limited to these methods. Furthermore, if it is expected that the missing data mechanism is largely non-ignorable a sensitivity analysis may be conducted (Molenberghs et al., 2004).
Missing data due to losses to follow-up are a particular problem in substance abuse clinical trials. Due to the probability that the missing data are dependent on observed and/or unobserved outcomes, methods of analysis that assume that the missing data mechanism is MCAR such as data deletion and single imputation may not be appropriate for this research paradigm. When missing data are assumed to be MAR several methods of analysis including MEM and MI have been demonstrated to perform well. Missing data in substance abuse clinical trials may be a mixture of both MAR and MNAR; however, the two missing data assumptions can not be empirically differentiated. Missing data that is MNAR are a particular problem due to the uncertainty of the missing value. That is, analytical methods which assume that missing data are MAR, treat missing data as if they are similar to the observed data. However, when missing data are non-ignorable, the observed values may not be similar to the unobserved values and therefore methods of analysis that assume MAR may be biased in this instance. However, existing literature suggests that one should not automatically choose an MNAR methods of analysis because they can be highly sensitive to the incorporation of the missing data pattern (Molenberghs et al., 2004). Therefore, when MNAR is suspected, a good choice would be to analyze the data in a variety of ways (a sensitivity analysis) with methods that make various assumptions about the missing data mechanism (methods that assume MAR versus MNAR). For example, a Summary Statistic method and an SSS method or a MEM and a pattern MEM may be selected and compared. Furthermore, results from both of the analyses selected may be reported.
Acknowledgments
The authors would like to acknowledge NIDA 1 R01 DA016368 and NCRR RR01070. The authors would also like to acknowledge Brent Mancha and Courtenay Cavanaugh for their critique of the manuscript.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Carroll KM. A cognitive-behavioral approach: Treating cocaine addiction. Therapy Manuals for Drug Abuse: Manual 2. 1998 from http://www.drugabuse.gov/TXManuals/CBT/CBT1.html.
- Dawson JD. Comparing treatment groups on the basis of slopes, areas-under-the-curve, and other summary measures. Drug Information Journal. 1994;28:723–732. [Google Scholar]
- Dawson JD. Stratification of summary statistic tests according to missing data patterns. Statistics in Medicine. 1994;13(18):1853–1863. doi: 10.1002/sim.4780131807. [DOI] [PubMed] [Google Scholar]
- Dawson JD, Han SH. Stratified tests, stratified slopes, and random effects models for clinical trials with missing data. Journal of Biopharmaceutical Statistics. 2000;10(4):447–455. doi: 10.1081/BIP-100101977. [DOI] [PubMed] [Google Scholar]
- Dawson JD, Lagakos SW. Analyzing laboratory marker changes in aids clinical trials. Journal of Acquired Immune Deficiency Syndromes. 1991;4(7):667–676. [PubMed] [Google Scholar]
- Dawson JD, Lagakos SW. Size and power of two-sample tests of repeated measures data. Biometrics. 1993;49(4):1022–1032. [PubMed] [Google Scholar]
- Diggle P, Kenward MG. Informative drop-out in longitudinal data analysis. Applied Statistics. 1994;43(1):49–93. [Google Scholar]
- Diggle PJ, Heagerty P, Liang KY, Zeger SL. Analysis of longitudinal data. second. New York: Oxford University Press; 2003. [Google Scholar]
- Dutra L, Stathopoulou G, Basden SL, Leyro TM, Powers MB, Otto MW. A meta-analytic review of psychosocial interventions for substance use disorders. American Journal of Psychiatry. 2008;165(2):179–187. doi: 10.1176/appi.ajp.2007.06111851. [DOI] [PubMed] [Google Scholar]
- Edwards AG, Rollnick S. Outcome studies of brief alcohol intervention in general practice: The problem of lost subjects. Addiction. 1997;92(12):1699–1704. [PubMed] [Google Scholar]
- Figueredo AJ, McKnight PE, McKnight KM, Sidani S. Multivariate modeling of missing data within and across assessment waves. Addiction. 2000;95(3):S361–380. doi: 10.1080/09652140020004287. [DOI] [PubMed] [Google Scholar]
- Frison L, Pocock SJ. Repeated measures in clinical trials: Analysis using mean summary statistics and its implications for design. Statistics in Medicine. 1992;11(13):1685–1704. doi: 10.1002/sim.4780111304. see comment. [DOI] [PubMed] [Google Scholar]
- Hedden SL, Woolson RF, Malcolm RJ. A comparison of missing data methods for hypothesis tests of the treatment effect in substance abuse clinical trials: A monte-carlo simulation study. Journal of Substance Abuse Treatment Prevention and Policy. 2008;3(13) doi: 10.1186/1747-597X-3-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hedeker D, Gibbons RD. Application of random effects pattern mixture models for missing data in longitudinal studies. Psychological Methods. 1997;2(1):64–78. [Google Scholar]
- Higgins ST, Budney AJ. From the initial clinic contact to aftercare: A brief review of effective strategies for retaining cocaine abusers in treatment. NIDA Research Monograph. 1997;165:25–43. [PubMed] [Google Scholar]
- Higgins ST, Wong CJ, Badger GJ, Ogden DE, Dantona RL. Contingent reinforcement increases cocaine abstinence during outpatient treatment and 1 year of follow-up. Journal of Consulting and Clinical Psychology. 2000;68(1):64–72. doi: 10.1037//0022-006x.68.1.64. [DOI] [PubMed] [Google Scholar]
- Hoaglin DC, Andrews DF. The reporting of computation-based results in statistics. The American Statistician. 1975;29(3):122–126. [Google Scholar]
- Howard KI, Cox WM, Saunders SM. Attrition in substance abuse comparative treatment research: The illusion of randomization. NIDA Research Monograph. 1990;104:66–79. [PubMed] [Google Scholar]
- Laird NM, Ware JH. Random-effects models for longitudinal data. Biometrics. 1982;38(4):963–974. [PubMed] [Google Scholar]
- Lavori PW. Clinical trials in psychiatry: Should protocol deviation censor patient data? Neuropsychopharmacology. 1992;6(1):39–48. [PubMed] [Google Scholar]
- Little R, Yau L. Intent-to-treat analysis for longitudinal studies with dropouts. Biometrics. 1996;52(4):1324–1333. [PubMed] [Google Scholar]
- Malcolm R, LaRowe S, Cochran K, Moak D, Herron J, Brady K, et al. A controlled trial of amlodipine for cocaine dependence: A negative report. Journal of Substance Abuse Treatment. 2005;28(2):197–204. doi: 10.1016/j.jsat.2004.12.006. [DOI] [PubMed] [Google Scholar]
- Matthews JN, Altman DG, Campbell MJ, Royston P. Analysis of serial measurements in medical research. British Medical Journal. 1990;300(6719):230–235. doi: 10.1136/bmj.300.6719.230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattson ME, Del Boca FK, Carroll KM, Cooney NL, DiClemente CC, Donovan D, et al. Compliance with treatment and follow-up protocols in project match: Predictors and relationship to outcome. Alcoholism Clinical and Experimental Research. 1998;22(6):1328–1339. [PubMed] [Google Scholar]
- McRae A, Hedden S, Carter R, Malcolm R, Brady K. Characteristics of cocaine- and marijuana-dependent subjects presenting for medication treatment trials. Addictive Behaviors. 2006;32(7):1433–1440. doi: 10.1016/j.addbeh.2006.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molenberghs G, Thijs H, Jansen I, Beunckens C. Analyzing incomplete longitudinal clinical trial data. Biostatistics. 2004;5(3):445–464. doi: 10.1093/biostatistics/5.3.445. [DOI] [PubMed] [Google Scholar]
- Nich C, Carroll KM. Intention-to-treat meets missing data: Implications of alternate strategies for analyzing clinical trials data. Drug & Alcohol Dependence. 2002;68(2):121–130. doi: 10.1016/s0376-8716(02)00111-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petry NM, Simcic F., Jr Recent advances in the dissemination of contingency management techniques: Clinical and research perspectives. Journal of Substance Abuse Treatment. 2002;23(2):81–86. doi: 10.1016/s0740-5472(02)00251-9. [DOI] [PubMed] [Google Scholar]
- Pocock SJ. Clinical trials: A practical approach. New York: Wiley; 1983. [Google Scholar]
- Ridout MS. Testing for random dropouts in repeated measurement data. Biometrics. 1991;47(4):1617–1619. [PubMed] [Google Scholar]
- Rubin D. Multiple imputation after 18+ years. Journal of the American Statistical Association. 1996;91:473–489. [Google Scholar]
- Rubin D, editor. Multiple imputation for nonresponse in surveys. New York: John Wiley & Sons; 1987. [Google Scholar]
- Schafer JL. Multiple imputation: A primer. Statistical Methods in Medical Research. 1999;8(1):3–15. doi: 10.1177/096228029900800102. [DOI] [PubMed] [Google Scholar]
- Schafer JL, Graham JW. Missing data: Our view of the state of the art. Psychological Methods. 2002;7(2):147–177. [PubMed] [Google Scholar]
- Schafer JL, Olsen MK. Multiple imputation for multivariate missing-data problems: A data analyst's perspective. Multivariate Behavioral Research. 1998;33(4):545–571. doi: 10.1207/s15327906mbr3304_5. [DOI] [PubMed] [Google Scholar]
- Shih WJ, Quan H. Stratified testing for treatment effects with missing data. Biometrics. 1998;54(2):782–787. [PubMed] [Google Scholar]
- Singer J, Willett J. Applied longitudinal data analysis: Modeling change and event occurrence. New York: Oxford University Press Inc.; 2003. [Google Scholar]
- Singer JD. Using sas proc mixed to fit multilevel models, hierarchiacal models, and individual growth models. Journal of Educational and Behavioral Statistics. 1998;24(4):323–355. [Google Scholar]
- Sobell LC, Sobell MB, Maisto SA. Follow-up attrition in alcohol treatment studies: Is ‘no news’ bad news, good news or no news? Drug & Alcohol Dependence. 1984;13(1):1–7. doi: 10.1016/0376-8716(84)90027-9. [DOI] [PubMed] [Google Scholar]
- Twisk JWR. Applied multilevel analysis. New York: Cambridge University Press; 2006. [Google Scholar]
- Wu MC, Bailey KR. Estimation and comparison of changes in the presence of informative right censoring: Conditional linear model. Biometrics. 1989;45(3):939–955. [PubMed] [Google Scholar]