Sensitivity Measures for Oscillating Systems: Application to Mammalian Circadian Gene Network

Abstract

Vital physiological behaviors exhibited daily by bacteria, plants, and animals are governed by endogenous oscillators called circadian clocks. The most salient feature of the circadian clock is its ability to change its internal time (phase) to match that of the external environment. The circadian clock, like many oscillators in nature, is regulated at the cellular level by a complex network of interacting components. As a complementary approach to traditional biological investigation, we utilize mathematical models and systems theoretic tools to elucidate these mechanisms. The models are systems of ordinary differential equations exhibiting stable limit cycle behavior. To study the robustness of circadian phase behavior, we use sensitivity analysis. As the standard set of sensitivity tools are not suitable for the study of phase behavior, we introduce a novel tool, the parametric impulse phase response curve (pIPRC).

I. Introduction

Biological entities, such as living cells, are dynamical systems comprised of a complex network of interacting components [1]. Highly evolved control mechanisms produce robust physiological behaviors, e.g. the time-keeping ability of circadian clocks. Systems biologists reverse-engineer such systems by identifying the components and studying the dynamics of their interactions [2]. Mathematical models, often formulated as ordinary differential equations (ODEs), are used to formalize the system kinetics. Model simulation and analysis, coupled with experimentation, elucidate biological design principles. Our interest lies in model analysis, for which system-theoretic tools are natural candidates [1], [3].

The principle of robustness provides a clear connection between biological and systems theory [4]. A key property of biological systems is robust performance in the presence of environmental variation - a specific functionality is maintained despite the presence of specific perturbations [5]. Both biological and engineered systems will be robust to expected disturbances, but fragile to rare, or unexpected disturbances. Robustness such as that displayed by biological systems is accompanied by increased complexity [6], thus eliminating the use of intuition as an effective means of elucidating design principles. The systems must be subjected to formal systems analysis tools.

In the case of ODE models, robustness is generally studied in the context of parametric uncertainty via properties such as robust stability [7] and response to perturbation. Although there is no standard quantitative measure of robustness [5], [8], a common thread in the literature relates robustness to parametric sensitivity. Parameters whose perturbation causes undesirable changes (either qualitative or quantitative) in some output identify processes with fragility [9]. The sensitivity of a system to its parameters may be determined using global [10] or local [11] methods. Our interest is in the latter, utilizing formal sensitivity analysis to quantify the local robustness properties of a system.

Sensitivity analysis has been used to study the response of a state variable (such as a component concentration) to a stimulus or perturbation to a parameter (such as a rate constant). High sensitivity (i.e. large changes in state values) to parametric perturbation indicates fragility, whereas low sensitivity indicates robustness [11]. In works such as [11] and [12], the regulatory processes have been rank-ordered from those with the least sensitivity to those with the highest sensitivity. In all cases, it was found that the rank-ordering was dependent on network structure, rather than on a particular choice of parameters. This strongly suggests that studying the sensitivity properties of a model does, in fact, aid in the analysis of the robustness properties of the biological system itself.

Oscillators form a class of biological systems that requires special attention. Many rhythmic processes such as the cell division cycle, the periodic firing of pacemaker neurons, and the daily sleep/wake cycle are regulated at the cellular level. Complex regulatory networks form the mechanisms for robust endogenous oscillations. For oscillators, maintenance under perturbation of oscillation properties such as amplitude or period may be expected. In the case of the circadian clock - the pacemaker governing daily rhythms - the maintained behavior is significantly more sophisticated. Organisms across the kingdoms possess the highly conserved circadian clock. This clock was designed not to maintain perfect 24 hour rhythms, but rather to maintain approximately 24-hour rhythms and to coordinate its internal time (phase) with the environment (external time). A circadian clock responds robustly to corrective signals such as light. This enables entrainment, by which the clock anticipates the arrival of dawn, and light arrives at the appropriate internal time to correct its mismatch with the environment. To study this phenomenon in vivo, phase response curves (PRCs) have been collected [13], describing a clock's phase-dependent response to short-lived stimuli such as pulses of light.

The goal of the present work is to provide a semi-analytical means to study the robustness properties of the phase behavior of a mathematical model of an oscillator. Standard sensitivity measures fail to capture the phase sensitivity [14] (and, therefore, the robustness properties of phase), motivating us to develop phase-based sensitivity measures. We expand the set of sensitivity measures to include the parametric impulse phase response curve (pIPRC), which characterizes the phase behavior of any limit cycle system and its response to stimuli.

To illustrate the derivation and demonstrate the utility of the pIPRC, we analyze a model of the circadian clock in an isolated cell of the mammalian master clock. In Section III we develop a theoretical basis for the study, and in Section IV, we demonstrate the relationship between theory and numerical experiment. In our study, we find that even though the pIPRC is a local measure, it is a powerful predictor for large perturbations.

Although the present work studies the response of a single oscillator to a stimulus, future work will utilize pIPRCs to study a collection of coupled oscillators that communicate via intercellular signals (which ultimately manifest as parametric modulation). Synchronization (as the result of such signaling) has recently presented itself as an important area of circadian research. Evidence is mounting that the circadian clock in a mouse is composed of a collection of sloppy cellular oscillators that use intercellular signaling to synchronize and create a coherent oscillation [15]. Without using parametric-based signaling, the study of weakly connected neural oscillators has led to a well-developed theory of interactions [16], [17]. The pIPRC provides an entrée into this related, but not otherwise directly applicable, theory.

II. Mathematical Model of Circadian Oscillator

A. Limit Cycle System

The analysis methods presented in this work apply to any oscillatory system that can be represented as a system of ODEs exhibiting limit cycle behavior.

Consider a set of autonomous nonlinear ordinary differential equations

$$\dot{\mathbf{\text{x}}}(t)=\mathbf{\text{f}}(\mathbf{\text{x}}(t,\mathbf{\text{p}}),\mathbf{\text{p}})$$ (1)

where x ∈ 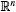is the vector of states and p ∈ 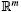is the vector of (constant) parameters. Assume there is a hyperbolic, stable attracting limit cycle γ. Let x^γ(t,p) be the solution to (1) on the limit cycle. It is τ-periodic, meaning x^γ(t,p) = x^γ(t + τ,p). In the interest of succinct notation, in the remainder of this paper we will be writing x(t,p) as a function of the independent variable, t, only.

B. Circadian Clock Model

The molecular mechanism of the circadian clock in a mouse resides in the cells of the suprachiasmatic nucleus of the hypothalamus in the brain. The clockworks in each cell are comprised of genes, mRNA, and proteins, forming a complex network of transcriptional feedback loops [18]. As in engineered systems, interlocking negative and positive feedback loops allow for stable oscillations.

We use the single cell model presented in [19]. Genes with redundant roles - the cryptochrome and period genes Cry1, Cry2, Per1, and Per2 - are combined into a single entity (Per/Cry). Per/Cry mRNA and protein are involved in an auto-regulatory negative feedback loop. An additional gene, Bmal1 codes for the BMAL1 protein, which promotes transcription of Per/Cry. PER/CRY protein, in turn, promotes Bmal1 transcription, forming the positive feedback loop (Figure 1). To study the effects of light, we utilize the light input gate added in [20]. The response to light is similar to the experimental phase response recorded for nocturnal animals [21]. The light input is modeled using parameter L. The gate allows for light input to up-regulate Per/Cry transcription in a phase-dependent manner - it prevents light from entering the system when the nuclear PER/CRY (PCn) is in its trough, which is in the middle of the daytime.

Fig. 1.

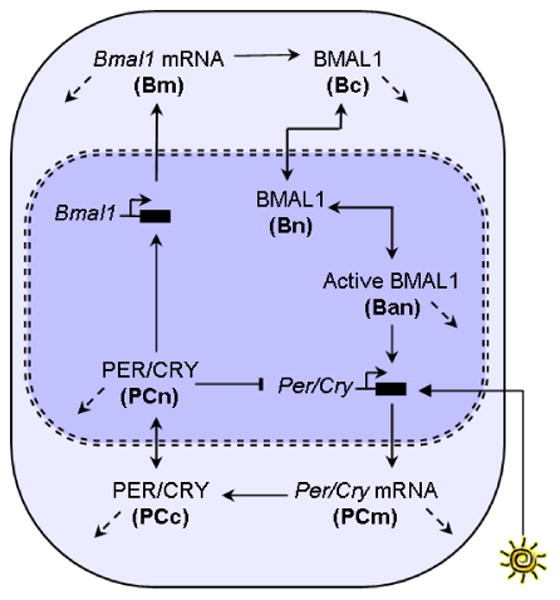
Circadian clock model network. The diagram is adapted from Fig 1 in (Geier et al, 2005). The bold letters denote the states. The solid arrows indicate positive influence. For example, greater concentration (up regulation) of Bmal1 mRNA causes greater concentration of cytoplasmic BMAL1. The flat-headed arrows indicate negative influence. For example, nuclear PER/CRY inhibits the transcription of Per/Cry mRNA . The dashed arrows indicate degradation. There is a negative feedback loop formed by the mRNA and protein versions of Per/Cry. Interlocked with it is a positive feedback loop involving Bmal1 mRNA, BMAL1 protein, and Per/Cry. Light enters the system by modulating the transcription rate of Per/Cry mRNA (PCm). In this study, we use the gating function associated with nocturnal animals.

$$\text{light\_input}=0.2L{\left(\frac{\mathbf{\text{PCn}}}{max(\mathbf{\text{PCn}})}\right)}^{10}.$$

The model is given by

$$\begin{array}{l}\frac{d}{dt}\mathbf{\text{PCm}}=f1-k1d\cdot \mathbf{\text{PCm}}+\text{light\_input}\\ \frac{d}{dt}\mathbf{\text{PCc}}=k2b\cdot {\mathbf{\text{PCm}}}^q-k2d\cdot \mathbf{\text{PCc}}-k2t\cdot \mathbf{\text{PCc}}+k3t\cdot \mathbf{\text{PCn}}\\ \frac{d}{dt}\mathbf{\text{PCn}}=k2t\cdot \mathbf{\text{PCc}}-k3t\cdot \mathbf{\text{PCn}}-k3d\cdot \mathbf{\text{PCn}}\\ \frac{d}{dt}\mathbf{\text{Bm}}=f2-k4d\cdot \mathbf{\text{Bm}}\\ \frac{d}{dt}\mathbf{\text{Bc}}=k5b\cdot \mathbf{\text{Bm}}-k5d\cdot \mathbf{\text{Bc}}-k5t\cdot \mathbf{\text{Bc}}+k6t\cdot \mathbf{\text{Bn}}\\ \frac{d}{dt}\mathbf{\text{Bn}}=k5t\cdot \mathbf{\text{Bc}}-k6t\cdot \mathbf{\text{Bn}}-k6d\cdot \mathbf{\text{Bn}}+k7a\cdot \mathbf{\text{Ban}}\\ -k6a\cdot \mathbf{\text{Bn}}\\ \frac{d}{dt}\mathbf{\text{Ban}}=k6a\cdot \mathbf{\text{Bn}}-k7a\cdot \mathbf{\text{Ban}}-k7d\cdot \mathbf{\text{Ban}}\end{array}$$

where Per/Cry mRNA transcription is down-regulated by nuclear PER/CRY and up-regulated by active nuclear BMAL1 (Ban) according to

$$f1=v1b\cdot \frac{\mathbf{\text{Ban}}+c}{k1b(1+{\left(\frac{\mathbf{\text{PCn}}}{k1i}\right)}^p)+\mathbf{\text{Ban}}+c}$$

and Bmal1 mRNA transcription is up-regulated by nuclear PER/CRY according to

$$f2=v4b\cdot \frac{{\mathbf{\text{PCn}}}^r}{k4b^r+{\mathbf{\text{PCn}}}^r}.$$

The parameter values are set as in [20], resulting in a period of oscillation τ of 23.3 hours.

For the purposes of the current investigation, we consider constant darkness (L = 0) to be the nominal configuration for the system. We study the endogenous oscillations, which have a period τ = 23.3 hours. In Figure 2, the oscillations are plotted as a function of time t. In the remaining figures, we plot the results using “circadian time”. It is common practice to scale data (particularly phase response curves) to show a period of 24 hours [13]:

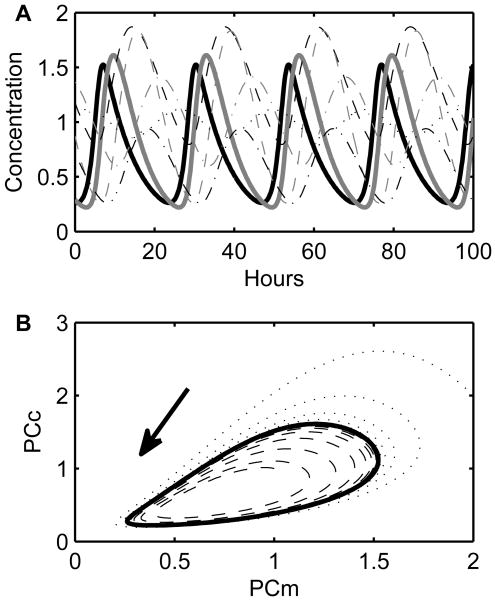
Fig. 2.

Circadian clock model dynamics. (A) A simulation in constant darkness is shown as a function of time. Per/Cry mRNA (PCm) and cytoplasmic PER/CRY (PCc) are shown with the thick lines. (B) The same simulation is shown in phase space (solid line). The dotted and dashed lines represent additional simulations with initial conditions off the periodic orbit (limit cycle). They evolve to the limit cycle, demonstrating that the system has a stable attracting limit cycle.

$$1\text{ circadian hour}=\frac{\tau \text{ hours}}{24}.$$

In addition, we generate all figures such that time 0 corresponds to the internal time associated with dawn. The definitions of internal time (phase) and dawn will be discussed in more detail in Section III-B; briefly, dawn is equivalent to the position on the nominal limit cycle that is passed 7 hours before Per/Cry mRNA peaks. Because there is no light in the nominal system, there is no “daytime” or “nighttime”, and we refer to subjective day (0 to 12 circadian hours after dawn) and subjective night (12 to 24 circadian hours after dawn).

III. Phase Sensitivity Measures

The phase sensitivity measures presented in this section provide a unified framework within which an oscillatory system such as the circadian clock can be studied.

A. Classical Sensitivity Analysis

Classical sensitivity analysis considers the effect at time t on a state value x_i of perturbing (at time 0) a parameter p_j. The matrix S(t) = (S_ij(t)) ∈ 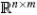of sensitivity coefficients $S_{ij}(t)=\frac{\partial x_i(t)}{\partial p_j}$ is computed by solving the ODE system

$$\frac{d}{dt}\mathbf{\text{S}}\left(t\right)=\mathbf{\text{J}}\left(\mathbf{\text{x}}\left(t\right)\right)\mathbf{\text{S}}\left(t\right)+\frac{\partial \mathbf{\text{f}}}{\partial \mathbf{\text{p}}}\left(\mathbf{\text{x}}\left(t\right)\right)$$

where J(x(t)) ∈ 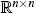is the Jacobian, $J_{ki}=\frac{\partial f_k}{\partial x_i}$ [22].

The sensitivity coefficients capture the dynamics of the response to parametric perturbation. The information contained in S involves the overall sensitivities. For oscillatory systems, this means that S contains information about the change in amplitude, change in limit cycle shape, change in period, and change in phase behavior. Discriminating between the sensitivity of each feature is an important endeavor. Contributions in the form of limit cycle shape, amplitude, period, and phase sensitivities have been made in [23], [24], [25], [26], [27], and [14]. Here, we build on the work in [24] and [27] where the authors capitalize on dynamical systems theory.

We consider the sensitivity of the system on the limit cycle. In later derivations, we will use the sensitivity coefficient

$$S_{ij}^{\gamma }\left(t\right)=\frac{\partial x_i^{\gamma }}{\partial p_j}\left(t\right).$$

To assess the time-keeping ability of a limit cycle clock, we examine the sensitivity of its phase to parametric and state perturbations. In the circadian pacemaker, the phase identifies the time of day of the internal clock. Before we can venture further, a precise definition of phase is required.

B. Phase

To display and analyze experimental data, the phase of a biological oscillator is determined by associating a specific phase to a specific event, such as the electrical spike of a firing neuron, or the peak of concentration of Per mRNA in the circadian clock. To study such a system as a limit cycle, we use a similar approach. Each position x^γ along the limit cycle γ is associated with a phase φ. The mapping is constructed so that progression along γ (in the absence of perturbation) produces a constant increase in φ [28]. Thus, the standard definition for φ is expressed in terms of its evolution through time, via a differential equation [16], [28], [29]. For an unperturbed system, the phase on the limit cycle is the solution to the initial value problem,

$$\frac{d\mathrm{\phi }({\mathbf{\text{x}}}^{\gamma }(t,\mathbf{\text{p}}),t)}{dt}=1,\mathrm{\phi }({\mathbf{\text{x}}}_0^{\gamma })=0$$ (2)

where ${\mathbf{\text{x}}}_0^{\gamma }$ is a reference position on the limit cycle γ [16], [28]. For a more in-depth discussion of φ defined in the presence of perturbations, see [16].

As written, the solution to (2) will grow unbounded with time. In this sense, it is a function of both time and position. For example, $\mathrm{\phi }({\mathbf{\text{x}}}_0^{\gamma },k\tau )=0+k\tau$ where k ∈ 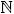. It is, however, common practice to bound phase such that φ ∈ [0,τ). When the bounds are applied, phase and position have a one-to-one relationship and the phase is a function of position only, i.e. φ((x^γ(t,p))). For the derivation of the sensitivity measures in the following sections, we leave phase unbounded.

Remark 1: We note that some other researchers choose the righthand side of (2) to be a constant other than 1. This simply leads to a scaled φ. If bounded, its image is in another interval, such as [0,2π).

Consider a neighborhood U containing γ within its basin of attraction. To define phase within U, we use the concept of isochrons [30].

Definition 1 (Isochron): Let x^γ(0) be a point on the periodic orbit. The isochron associated with x^γ(0) is the set of all initial conditions η(0) such that

$$\underset{t\to \infty }{lim}\Vert {\mathbf{\text{x}}}^{\gamma }(t)-\mathrm{\eta }(t)\Vert =0.$$

An isochron is a “level set” [16] or “same-time locus” [30]; all points on a single isochron will approach the same position on the limit cycle, and therefore all share the same phase. In an n-dimensional system, an isochron will be an (n − 1)-dimensional hyper-surface [30], [31]. Therefore, it is helpful to use small systems to visualize isochrons. Figure 3 shows two isochrons in a 2-state circadian clock model [32]. They intersect the limit cycle at the peak of the first state, and at the position encountered 7 hours later. For any solution x(t) ∈ U to (1), x(t) is on some isochron η(t). The phase of x(t) is defined by the phase of the position on the limit cycle sharing the same isochron; that is, if x₁ = η(t) ∩γ, then φ(x(t),t) ≡ φ(x₁,t). Clearly, if φ is bounded by the period, then φ is a function of position only and φ(x(t)) ≡ φ(x₁). Because all solutions on the same isochron share the same phase (modulo the period), we can rewrite (2) in terms of x ∈ U

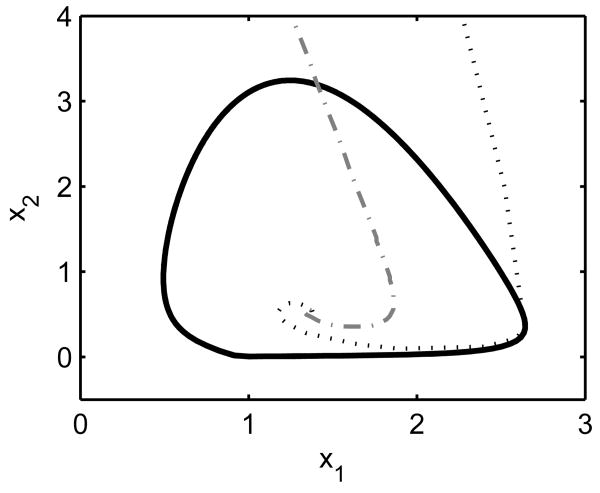
Fig. 3.

Limit cycle with isochrons. The limit cycle is for a 2-state system in which a solution will move around the limit cycle in a counter-clockwise direction. The isochron represented by the dotted line intersects the limit cycle at the peak of state x₁. The isochron represented by the dashed-dotted line intersects the limit cycle at a position encountered 7 hours later, i.e if the first isochron is η(t₁), then this isochron is η(t₁ + 7). Any initial conditions chosen along the same isochron will approach the same position on the limit cycle as time evolves.

$$\frac{d\mathrm{\phi }(\mathbf{\text{x}}(t,\mathbf{\text{p}}),t)}{dt}=1.$$ (3)

For the circadian clock model under investigation, phase is defined such that φ is 7 at the peak of Per/Cry mRNA's oscillation $(\mathrm{\phi }({\mathbf{\text{x}}}_{\mathit{\text{PM peak}}}^{\gamma }(t_1))=7)$ [33]. Dawn is defined such that φ is 0, and is associated with the position on the limit cycle encountered 7 hours earlier $(\mathrm{\phi }({\mathbf{\text{x}}}_0^{\gamma })=\mathrm{\phi }({\mathbf{\text{x}}}_{\mathit{\text{PM peak}}}^{\gamma }(t_1-7))=0)$.

C. Phase Sensitivity to State Perturbations

If the nominal system is disrupted, then its phase evolution will depart from the nominal. We begin by considering a perturbation to a state value $x_k^{\gamma }$ at time t; the perturbed solution may jump off the isochron η(t), incurring a phase shift [16]. As time progresses, the solution will approach the limit cycle, but the phase shift will cause it to be at a different position along the limit cycle than it would have been if it had remained unperturbed. To measure the phase shift caused by an infinitesimal perturbation, we use the state impulse phase response curve (sIPRC). It is a vector equation sIPRC = (sIPRC_k), where

$${\text{sIPRC}}_k({\mathbf{\text{x}}}^{\gamma }(t))=\frac{\partial \mathrm{\phi }}{\partial x_k^{\gamma }}({\mathbf{\text{x}}}^{\gamma }(t))$$

The sIPRC appears in the literature associated with weakly connected neural networks, where it is most commonly referred to as z. There are multiple derivations of the curve's formula. Summarizing the derivation in [24], [27], we begin with the adjoint Green's function

$$\frac{d}{dt}{\mathbf{\text{K}}}^{†}(t,T)+{\mathbf{\text{K}}}^{†}(t,T)\mathbf{\text{J}}({\mathbf{\text{x}}}^{\gamma }(t))=0,$$

where J is the system Jacobian evaluated on the limit cycle. It is integrated backwards from final time t = T to time t = 0 from initial conditions

$${\mathbf{\text{K}}}^{†}(T,T)=\mathbf{\text{I}}.$$

The solution to the adjoint Green's function converges to a unique, stable limit cycle (periodic with the same period as (1)) ξ as T → ∞ [24], [29]. It represents the sensitivity of the final state values to perturbations in previous state values. We express this interpretation in the form of partial derivatives, with the pertubation as the denominator and the observed effect in the numerator:

$${\text{K}}_{ik}^{†}(t,T)=\frac{\partial x_i^{\gamma }(T)}{\partial x_k^{\gamma }(t)}.$$

The key insight presented in [24] is that the phase shift, which in their terminology is ∂tˆ, depends upon earlier state values. This dependence is determined by any one row of the adjoint variable $K_{i\ast }^{†}$ [16], [24], according to

$$\begin{array}{l}\frac{\partial \widehat{t}}{\partial x_k^{\gamma }}(t)=\underset{T\to \infty }{lim}{K}_{ik}^{†}(t,T)/\left(\frac{d{x}_i^{\gamma }(T)}{d\widehat{t}}\right)\\ =\underset{T\to \infty }{lim}{K}_{ik}^{†}(t,T)/f_i({\mathbf{\text{x}}}^{\gamma }(T)).\end{array}$$ (4)

Because $K_{ik}^{†}(t,T)/f_i({\mathbf{\text{x}}}^{\gamma }(T)=K_{ik}^{†}(t+\tau , T)/f_i({\mathbf{\text{x}}}^{\gamma }(T)$ when T ≫ t, we know that $K_{ik}^{†}(t,T)/f_i({\mathbf{\text{x}}}^{\gamma }(T))$ is τ-periodic in the limit as T → ∞. Therefore, $\partial \widehat{t}/\partial x_k^{\gamma }$ is truly a function of position and should be written as such. Intuitively, this is clear because the phase response is dependent upon the position ${\mathbf{\text{x}}}_k^{\gamma }(t)$ along the system limit cycle γ at which the perturbation occurs. Thus, the equation is more precisely expressed as

$$\frac{\partial \widehat{t}}{\partial x_k^{\gamma }}({\mathbf{\text{x}}}^{\gamma }(t))=\underset{T\to \infty }{lim}{K}_{ik}^{†}(t,T)/f_i({\mathbf{\text{x}}}^{\gamma }(T)).$$

To write the sIPRC in our notation, we use (2), i.e.

$$\frac{\partial \mathrm{\phi }}{\partial x_k^{\gamma }}({\mathbf{\text{x}}}^{\gamma }(t))=\frac{\partial \widehat{t}}{\partial x_k^{\gamma }}({\mathbf{\text{x}}}^{\gamma }(t)).$$

The formula for the sIPRC to the k^th state [24] is therefore

$${\text{sIPRC}}_k({\mathbf{\text{x}}}^{\gamma }(t))=\underset{T\to \infty }{lim}{K}_{ik}^{†}(t,T)/f_i({\mathbf{\text{x}}}^{\gamma }(T)).$$

This formula is best interpreted by an examination of flow through the isochrons. Suppose that at time t (when the state value is on isochron η(t)), an instantaneous infinitesimal change is made to x^γ(t). The solution to the perturbed system (x^γ(t) + ∂x) will advance to isochron η(t̃). If t̃ ≠ t, then the system will have incurred a phase shift (t̃ > t is an advance and t̃ < t is a delay). If the system is not subject to any further perturbation, this phase shift (t̃ – t) will be locked in because dφ/dt = 1 in the neighborhood U. It can then be “measured” in the limit as the state trajectory reaches the limit cycle [16]. Recall that ${\mathbf{\text{K}}}_{i\ast }^{†}(t,T)$ predicts the change in state value at final time T. In the limit as ∂x^γ(T) → 0, f_i(x^γ(T)) will accurately describe the speed of the trajectory as it travels from $x_i^{\gamma }(T)$ to $x_i^{\gamma }(T)+\partial x_i(T)$. Dividing the distance dx_i(T) by the speed f_i(x^γ(T)) produces the travel time, our phase shift.

Remark 2: In practice, the limit (T → ∞) can be approximated. Typically, it takes fewer than three periods for the adjoint solution to converge to its limit cycle.

Remark 3: In [24] a negative sign is introduced to (4). We leave it out in order to maintain consistency with the circadian literature. Phase response curves are plotted such that phase advances are positive [13], and a positive value in the sIPRC (as we have presented it) predicts a phase advance.

Remark 4: The computation can be handled efficiently. Because only one row $K_{i\ast }^{†}(t,T)$ of the adjoint solution is required, we solve a vector, rather than matrix equation. This solution can be computed using a standard solver, but effort will be reduced if a package such as the DASPKAdjoint is used [34], [35].

Figure 4 shows the results of a numerical experiment in which a small perturbation is made to the state representing Per/Cry mRNA (PCm) in the clock model. We use the fact that

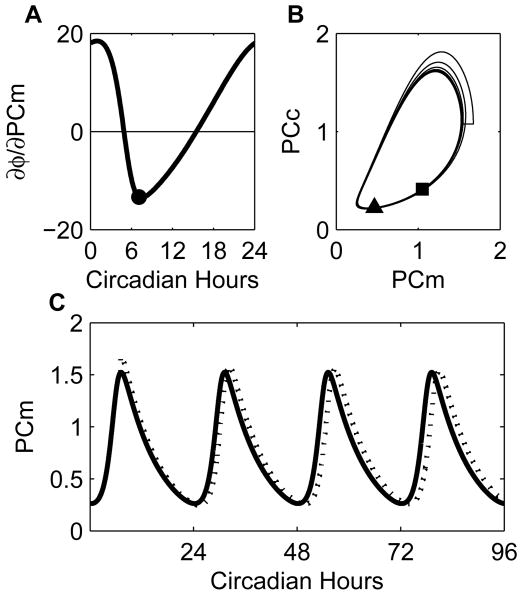
Fig. 4.

System under a state perturbation. (A) The state IPRC for the state representing Per/Cry mRNA (PCm) shows early morning advances and midday delays. To illustrate its utility we perform a numerical experiment using the prediction of the phase shift due to a perturbation in PCm at CT7.1 (circle). Since ∂φ/∂PCm = −13.351 at CT7.1, we predict that a positive perturbation of 0.15 in PCm at CT7.1 will cause a phase shift Δφ ≈ −13.351 · 0.15 = −2.0027, which means there will be a 2-circadian hour delay. (B) In phase space, we show the concentrations of PCm and cytoplasmic PER/CRY (PCc) to show the limit cycle behavior of the numerical experiment. There is a clear deviation from the limit cycle when the perturbation is introduced. The square marks the position of the unperturbed system at CT293 while the triangle marks the position of the perturbed system at the same time. Since the flow about the limit cycle is counter-clockwise, this indicates the perturbed system is lagging. (C) Here we show the same data, but as a function of time. The concentration of PCm in the perturbed system (dotted line) peaks after that in the unperturbed system (solid line) and we observe a 1.9-circadian hour delay.

$$\text{Δ}\mathrm{\phi }\approx \frac{\partial \mathrm{\phi }}{\partial \mathbf{\text{x}}}\mathrm{\Delta }\mathbf{\text{x}}$$

to illustrate the predictive power of the sIPRC. For ΔPCm = 0.15 (which is about 7% of the amplitude of PCm's oscillation) administered at φ = 7, the prediction is a delay of 2 circadian hours, while the observed delay is 1.89 circadian hours. For a highly non-linear system, the error of prediction is quite good. When we consider parametric perturbations, we find that the state values themselves are not changed much. This is, in part, due to the fact that the model under consideration is generally robust to parametric perturbation (the classical sensitivity coefficients are small) (data not shown). The consequence is that we can consider large parametric perturbations and find that predictions are very accurate.

D. Phase Sensitivity to Parametric Perturbations

Predicting the phase change incurred by a parametric perturbation involves a complicating factor - the isochrons are altered in the perturbed vector field. In this section, we continue to use isochrons in the nominal system as the reference for phase behavior. For this to be a legitimate approach, we must therefore consider the state of the system after a parametric perturbation has ceased and the system has returned to the nominal flow. We begin by predicting the response to a sustained perturbation, move to a short, but finite duration perturbation, and finish by considering an impulse perturbation.

1) Cumulative Phase Sensitivity

Applying the chain rule to the phase variable produces

$$\frac{d\mathrm{\phi }}{d\mathbf{\text{p}}}(t)=\mathbf{\sum }_{k=1}^n\frac{\partial \mathrm{\phi }}{\partial x_k^{\gamma }}\frac{\partial x_k^{\gamma }}{\partial p_j}(t).$$

The phase sensitivity is measured in reference to the isochron η(t) of the nominal system. To interpret the formula, we examine the terms from right to left. The $\frac{\partial x_k^{\gamma }(t)}{\partial p_j}$ term is the classical sensitivity coefficient, which describes the effect upon state x_k at time t due to a constant parametric perturbation to parameter p_j initiated at time 0. The $\frac{\partial \mathrm{\phi }}{\partial x_k}$ term is simply the sIPRC_k, which describes the effect that a state perturbation has upon the phase. If the parametric perturbation is lifted at time t, then the vector field will return to its nominal configuration, and the formula will predict the incurred phase shift. Therefore, the phase sensitivity at time t predicts the phase shift incurred by a parametric perturbation sustained until time t. As time progresses, the phase changes accumulate, so we refer to the curve as the cumulative phase sensitivity.

The behavior is best explained in terms of isochrons. Consider a system with initial conditions ${\mathbf{\text{x}}}_0^{\gamma }(0)$. Under the nominal flow, it will be on isochron η(t₁) at time t₁. If a parameter is perturbed (beginning at time 0), then the trajectory will deviate from the nominal trajectory and the system will be on an isochron η(tˆ₁) (with respect to the nominal system). The perturbed system is then t₁ − tˆ₁ time units phase-shifted from the nominal system. If the perturbation is released at that moment (time t₁), then the flow will return to nominal and the phase shift will be locked in (because $\frac{d\mathrm{\phi }}{dt}=1$). For a graphical illustration, see Figure 2 in [24] or Figure 3 in [27].

Figures 5A and B show the cumulative phase sensitivity to the parameter associated with light (L). Within each period, light has varying effects, with maximal delays in the early subjective evening (see Figure 5B). The overall effect during a single period is to slow down the system (dφ/dL(τ) < dφ/dL(0)). Over multiple periods, the effect accumulates, resulting in larger delays, as shown by the negative trend in Figure 5A.

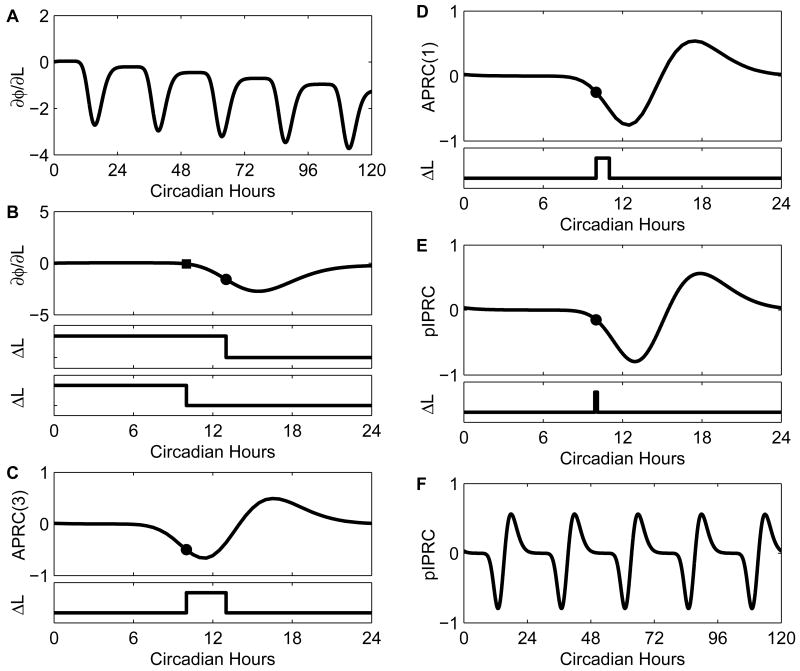
Fig. 5.

Relationship between parametric phase sensitivity, analytical phase response curves (APRCs), and parametric impulse PRCs (pIPRCs). (A) The parametric phase sensitivity to infinitesimal perturbations in light (L) grows with time. Each point on the phase sensitivity curve can be used to predict the delay or advance that will be incurred due to the release of a sustained perturbation in the parameter L. The overall negative slope indicates that, in general, the longer L remains perturbed, the more delayed the system will be. (B) We show the parametric phase sensitivity over the first period. The values at CT10 (filled square) and CT13 (filled circle) predict the accumulated phase shifts between CT0 and CT10, and between CT0 and CT13, respectively. The corresponding perturbation shapes are illustrated in the lower panels. We observe that the phase changes accumulated between CT10 and CT13 can be predicted by subtracting dφ/dL(13) − dφ/dL(10). (C) The analytical PRC, APRC(t,3), predicts the shift due to a 3-circadian hour pulse. To compute APRC(t,3), we subtract dφ(t + 3)/dL − dφ(t)/dL and divide by 3. The lower panel shows the trace of the L perturbation (the signal) to which the APRC at CT10 predicts the response. (D) APRC(1) is the analytical PRC to a 1-circadian hour pulse. The pulse starting at CT10 is highlighted. As the pulses get shorter in duration, the APRC approaches the slope of the phase sensitivity. (E) The IPRC is the slope of the phase sensitivity and it predicts the phase shift in response to an impulse perturbation - a pulse that is infinitesimal in both duration and magnitude. The prediction associated with an impulse at CT10 is highlighted and the pulse shape is shown in the lower panel. (F) The parametric IPRC is periodic.

2) Phase Sensitivity and Square Pulse Perturbations

For oscillating systems in general, and the circadian clock in particular, a more useful measure is the response not to a sustained, or step, perturbation, but to a pulsatile perturbation. There is a rich history of biological experimentation in which animal circadian clocks are studied by subjecting the animals (otherwise kept in constant darkness) to square pulses of light [13]. To supply an analytical curve predicting the response to a square pulse perturbation, Gunawan and Doyle made the observation that the cumulative phase sensitivity curve, evaluated at the pulse onset and offset, provides the necessary information [27]. By subtracting the phase shift accumulated before the pulse onset, we compute the shifts accumulated during the pulse.

Definition 2 (APRC): The analytical phase response curve (APRC) is a function of the time of the pulse onset t and pulse duration d:

$$\mathbf{\text{APRC}}(t,d)=\frac{\frac{d\mathrm{\phi }}{d\mathbf{\text{p}}}(t+d)-\frac{d\mathrm{\phi }}{d\mathbf{\text{p}}}(t)}{d}.$$

Figure 5C and D illustrates the APRC to light (APRC_L) for pulse durations of 3 and 1 circadian hours, respectively. The shape corresponds very closely to that of experimental data, showing the so-called “deadzone” during the subjective day, with delays early in the subjective evening and advances in late subjective evening [36].

3) Phase Sensitivity and Impulse Perturbations

When d approaches 0, the APRC approaches the slope of the phase sensitivity:

$$\begin{array}{l}\frac{d}{dt}\frac{d\mathrm{\phi }}{d\mathbf{\text{p}}}(t)=\underset{d\to 0}{lim}\frac{\frac{d\mathrm{\phi }}{d\mathbf{\text{p}}}(t+d)-\frac{d\mathrm{\phi }}{d\mathbf{\text{p}}}(t)}{d}\\ =\underset{d\to 0}{lim}\mathbf{\text{APRC}}(t,d).\end{array}$$

This means the slope of the phase sensitivity will predict the behavior change caused by an impulse perturbation to a parameter.

Definition 3 (pIPRC): The parametric impulse phase response curve (pIPRC) is

$$\mathbf{\text{pIPRC}}(t)=\frac{d}{dt}\frac{d\mathrm{\phi }}{d\mathbf{\text{p}}}(t).$$ (5)

Proposition 1 (Computation of the pIPRC): The pIPRC can be computed by taking the full time derivative of the phase sensitivity, resulting in an expression involving terms that are relatively easy to compute:

$$\mathbf{\text{pIPRC}}(t)=\mathbf{\sum }_{k=1}^n{\text{sIPRC}}_k({\mathbf{\text{x}}}^{\gamma }(t))\frac{\partial f_k}{\partial p_j}({\mathbf{\text{x}}}^{\gamma }(t)).$$

Because each term on the righthand side is a function of position, the pIPRC is a function of position, i.e.

$$\mathbf{\text{pIPRC}}({\mathbf{\text{x}}}^{\gamma }(t))=\mathbf{\sum }_{k=1}^n{\text{sIPRC}}_k({\mathbf{\text{x}}}^{\gamma }(t))\frac{\partial f_k}{\partial p_j}({\mathbf{\text{x}}}^{\gamma }(t)).$$

For the proof, see the appendix.

The pIPRC is τ-periodic when evaluated on the limit cycle. We noted earlier that the sIPRC is τ-periodic. Clearly, $\frac{\partial \mathbf{\text{f}}}{\partial \mathbf{\text{p}}}({\mathbf{\text{x}}}^{\gamma }(t))$ is periodic, because x^γ(t) is periodic (see Figure 5F). It follows that, like the sIPRC, the pIPRC is a function of position and can therefore be written as a function of phase. We will do so in future sections.

In addition to periodicity, there is a striking similarity between the pIPRC and the sIPRC. They both predict the phase response to an impulse perturbation, under the assumption that the system was in its nominal configuration immediately preceding and immediately following the impulse. This will be important in Section III-F, when we present the phase evolution equation under parametric perturbation. It reformulates the phase evolution equation commonly used to track the phase behavior of a system under state velocity perturbation [16], [17], [28], [29], [37].

The pIPRC to light (pIPRC_L) is shown in Figure 5E and F. The curve in this case is unique in that it serves to characterize the system itself - not simply the response to a specific signal. A signal can be viewed as a modulation over time of a parameter, and the pIPRC can be used to predict the response to that signal. Figure 5E illustrates that, regardless of the shape and strength of the light signal, if it arrives during the subjective day the clock does not phase shift. A signal arriving in early subjective evening will cause a phase delay, and a signal arriving in late subjective evening will cause a phase advance. Later, we will use the pIPRC to predict the response to arbitrary signals.

Remark 5: A related curve, the infinitesimal response curve (IRC) to the period is developed in [38], [39]. As part of a wider ranging set of response curves, the period IRC is the same function as the pIPRC, but its derivation is distinctly different. One notable difference is that its computation does not rely directly on the sIPRC.

E. Period Sensitivity

A sustained parametric perturbation changes the freerunning period τ. The period sensitivity $\frac{\partial \tau }{\partial \mathbf{\text{p}}}$ predicts the change in τ and is expressed analytically by the APRC for an infinitesimal perturbation of duration τ; the timing effects accumulated over one period produce a change in the period [24].

Proposition 2 (Period Sensitivity): The period sensitivity is given by

$$\frac{\partial \tau }{\partial \mathbf{\text{p}}}=-\mathbf{\text{APRC}}(t_1,\tau )\tau ,$$

where the APRC can be evaluated at any time t₁ (as long as the system is not in transient) [24], [27].

The period sensitivity can be used to predict the period in a perturbed system. The negative sign is introduced to make the formula for prediction intuitive:

$${\tau }_{\mathit{\text{perturbed}}}\approx \tau +\frac{\partial \tau }{\partial p_j}\mathrm{\Delta }{p}_j.$$

The relationship between phase response curves and the effects of light upon the period has long been of interest to circadian researchers [13], [21]. For that reason, we explore the relationship between the period sensitivity and the pIPRC. Recall that

$${\text{APRC}}_j(t_1,\tau )\tau =\frac{d\mathrm{\phi }}{d{p}_j}(t+\tau )-\frac{d\mathrm{\phi }}{d{p}_j}(t).$$

Because pIPRC_j is the derivative of the cumulative phase sensitivity, we know

$$\begin{array}{l}{\text{APRC}}_{\mathit{\text{j}}}(t_1,\tau )\tau ={\int }_0^{t_1+\tau }{\text{pIPRC}}_j(t)dt-{\int }_0^{t_1}{\text{pIPRC}}_j(t)dt\\ ={\int }_{t_1}^{t_1+\tau }{\text{pIPRC}}_j(t)dt.\end{array}$$

Thus, there is a direct relationship between the period sensitivity and the area under the pIPRC,

$$\frac{\partial \tau }{\partial p_j}=-{\int }_{t_1}^{t_1+\tau }{\text{pIPRC}}_j(t)dt.$$

F. Phase Evolution Under Parametric Perturbation

A powerful technique, pioneered by Malkin [29] and Winfree [37], and developed further by Kuramoto [28] and others [16], [17], [29] is that of phase reduction. Instead of simulating an entire system, the system is reduced to a single phase variable. The phase model is an ordinary differential equation, which we refer to as the phase evolution equation. In the absence of a signal, it is simply (3).

There are many variants of the phase evolution equation, some of which are designed to follow a single oscillator, with others designed to follow the behavior of multiple, weakly coupled oscillators. The signal term also differs in its independent variable. We choose one that includes variables for both external and internal time, t and φ, respectively. Equation 2.6 in [16], written in our notation becomes

$$\frac{d\mathrm{\phi }}{dt}=1+\mathbf{\text{sIPRC}}(\mathrm{\phi })\cdot \mathbf{\text{G}}(\mathrm{\phi },t)$$ (6)

where G is the vector of “stimulus effects”. The natural initial condition is φ(0) = 0. Under the assumptions that the limit cycle is normally hyperbolic, and that |G| is bounded by a number small enough for the linear approximation to be sufficiently accurate, this equation is valid in the neighborhood U of γ.

In the context of the models examined in [16], it is the sIPRC (referred to as z in [16]) that characterizes the response to a stimulus represented by G. However, we can separate G into two terms such that

$$G_i(\mathrm{\phi },t)=\frac{\partial f_i}{\partial p_j}(\mathrm{\phi })g_j(\mathrm{\phi },t)$$

where g_j is a time-varying perturbation to the j^th parameter. Now, we can rewrite (6) as

$$\begin{array}{l}\frac{d\mathrm{\phi }}{dt}=1+\mathbf{\text{sIPRC}}(\mathrm{\phi })\cdot \mathbf{\text{G}}(\mathrm{\phi },t)\\ =1+\mathbf{\text{sIPRC}}(\mathrm{\phi })\cdot \frac{\partial \mathbf{\text{f}}}{\partial p_j}(\mathrm{\phi })g_j(\mathrm{\phi },t)\\ =1+{\text{pIPRC}}_j(\mathrm{\phi })g_j(\mathrm{\phi },t).\end{array}$$

The result is a phase evolution equation involving the pIPRC and a signal that modulates a parameter. That signal can be a function of phase or external time. In the present work, we use it as a function of external time only, and define the phase evolution equation as

$$\frac{d\mathrm{\phi }}{dt}=1+{\text{pIPRC}}_j(\mathrm{\phi })g_j(t)$$ (7)

where φ(0) = 0. It is now apparent that the pIPRC serves to characterize the timing behavior of the system apart from the signal. It is also apparent the pIPRC can be intrepreted as a velocity response curve. Since p and t are independent, (5) can be rewritten as

$$\mathbf{\text{pIPRC}}(t)=\frac{d}{dt}\frac{d\mathrm{\phi }}{d\mathbf{\text{p}}}(t)=\frac{d}{d\mathbf{\text{p}}}\frac{d\mathrm{\phi }}{dt}(t).$$

Our approach will be valid in the same neighborhood with the same assumptions listed above (from [16]) with one major caveat - a perturbation in parameters alters the vector field. The pIPRC is computed assuming the vector field is about to return to the nominal configuration. If the perturbation continues or changes, then the pIPRC's prediction may be incorrect. However, we have observed that the results are qualitatively correct, and often quantitatively correct (Figure 7). We benefit from the tendency for isochrons to remain nearly fixed despite changes to the vector field.

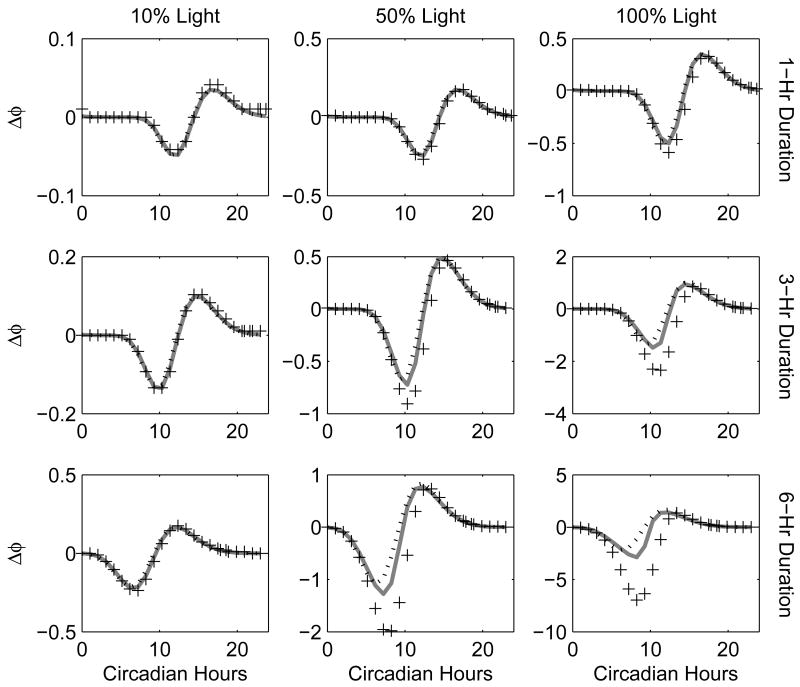
Fig. 7.

Numerical experimental PRCs. Each plot contains the phase shifts for the numerical experimental PRC (pluses), pIPRC_L-predicted PRC (solid gray line), and APRC_L-predicted PRC (dotted black line). The signal is sinusoidal and its active part lasts 1 hour for the first row, 3 hours for the second row, and 6 hours for the third row. The signal maximum is at 10%, 50%, and 100% of full light, respectively. Notice the different scales on the y-axes.

IV. Phase Response Curves

The curves presented in the previous section can be used to predict the outcome of numerical experiments, which in turn are used to mimic in vivo experiments. Such experiments have been used to collect phase response curves - a phase response curve (PRC) describes the response of the system to a particular signal. The traditional method of computation is simple numerical experimentation; send the signal, then observe the result. In this section, we illustrate the relationship between the APRC, pIPRC, and numerical experimental PRC by considering the model's response to light. We outline various methods for predicting the response first to a square pulse signal, then to an arbitrary signal.

We begin by discretizing time over one period, t_disc = {t₁,t₂,…,t_a} and we compute the PRC at the phase associated with each timestep, Φ = {φ(x^γ(t₁)),φ(x^γ(t₂)),…φ(x^γ(t_a))}. The signal must be expressed as a modulation of a parameter, i.e. g_j(t) = Δp_j(t).

A. Square Pulse Response Curves

Standard practice for in vivo biological experiments is to subject an animal to a square pulse of light. A natural in silico approach is to subject the model to the same square pulse. To compute the analytical predictions for such a numerical experiment, we use the APRC and pIPRC.

1) Direct Method

The direct method is straightforward. S is simply a pulse of magnitude mag beginning at time t₁ of duration d, i.e.

$$\mathrm{\Delta }{p}_j(t)=\{\begin{array}{l}\mathit{\text{mag}},t\in [t_1,t_1+d]\\ 0,t\notin [t_1,t_1+d]\end{array}$$ (8)

All simulations will end at time T, which must be chosen to ensure a perturbed system will resettle to the nominal limit cycle. The algorithm we suggest is:

1. Simulate the system in constant dark to create a nominal (reference) limit cycle.

2. Choose a phase marker for the system, such as the peak of state x_i. Record the time t_b when that marker occurs in the last period of simulation (T − τ, T).

3. Choose the time of pulse onset as a marker for the signal, g_onset.

4. For each t ∈ t_disc and its associated φ ∈ Φ,

   1. Run a simulation, sending the signal such that g_onset occurs at time t.

   2. Measure the time t_c of the system marker in the last period of simulation (T − τ,T).

   3. Compute the phase shift Δ(φ) = t_b − t_c.

2) Predictive Method

The APRC is designed for precisely this purpose - to predict the response to square pulses. It does so under the assumption that the linear approximation holds for finite Δp_j.

For each t ∈ t_disc and associated φ ∈ Φ,

$$\text{Δ}\mathrm{\phi }(\mathrm{\phi })\approx {\text{APRC}}_j(t,d)d\text{Δ}{p}_j(t).$$

The pIPRC can be used in the same manner as the APRC, but is, theoretically, less reliable - the pIPRC is valid in the limit not only as Δp_j → 0, but also as Δt → 0. We recommend the APRC for estimating PRCs, but include the pIPRC formula because it is instructive for the purposes of interpretation.

For each t ∈ t_disc and associated φ ∈ Φ,

$$\text{Δ}\mathrm{\phi }(\mathrm{\phi })\approx {\text{pIPRC}}_j(\mathrm{\phi })d\text{Δ}{p}_j(t).$$

If the signal is of magnitude and duration 1 (Δp_j = 1, d = 1), then the pIPRC itself is an estimate for the PRC. This relationship eases interpretation - rather than attempting to envision a curve that is a rate of change in two variables, we have a concrete meaning. Additionally, for relatively short (circa 1 circadian hour) pulses, the numerical results are nearly identical to those of the APRC. We note also that the pIPRC is most accurate when the middle of the pulse time is used for the prediction. In Section IV-B.2 we describe a better pIPRC method, which uses (7).

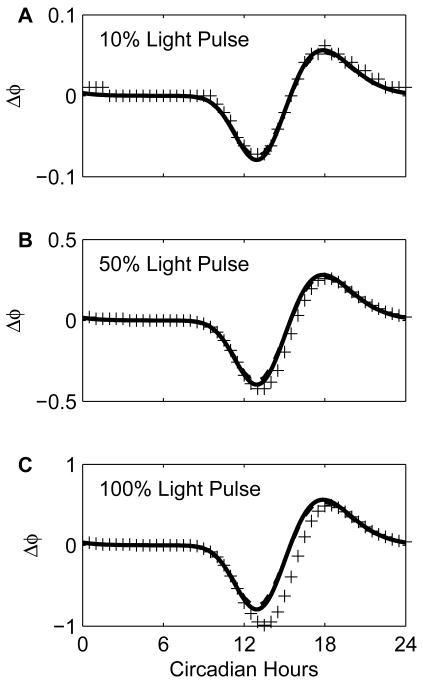
Figure 6 contains the numerical experimental PRC, APRC_L-predicted PRC, and pIPRC_L-predicted PRC for a pulse lasting 1 circadian hour with strengths ΔL = 0.1,0.5,1.0. The figure illustrates that for a relatively short pulse of light the predictions are qualitatively correct, and quantitatively good. For 1-circadian hour pulses of 10%, 50%, and 100% light, the predictions are within 0.01, 0.25, and 0.5 circadian hours of the numerical experimental PRC, respectively. This figure illustrates the utility of the various methods. For large perturbations, the numerical experimental method is the most accurate because all nonlinearity is accounted for. However, for small perturbations, the numerical experimental method loses accuracy. Computation of the phase shift is limited both by the step size of the simulation and by the simulation accuracy. Because long simulations are required, a gradual drift is observed, and measurement of the time-difference between peaks in the nominal and perturbed systems is less reliable. The APRC method does rely on numerical solution, but is not as susceptible to either of these problems.

Fig. 6.

Numerical experimental PRC's. We plot the phase shifts contains the numerical experimental PRC (pluses), pIPRC_L-predicted PRC (solid line), and APRC_L-predicted PRC (dashed line). Each phase shift is plotted for the time at the center of the light pulse. (A) Numerical experimental PRC for 1 Circadian Hour-Pulses of light at 10% strength. For each plus in the numerical experiment, a simulation was performed in which the light parameter L was 0.1 during the light pulse and 0 otherwise. After one week was simulated, we compared the time of the peak in the perturbed system to that of the peak of PCm in the nominal system. The time-step resolution and, therefore, the accuracy of this computation is, at best, 0.01 hour. (B) Numerical experimental PRC for pulse of light at 50% strength. (C) Numerical experimental PRC for pulse of light at 100% strength (L = 1).

B. Arbitrary Signal Response Curves

Square pulse signals alone are insufficient to study the circadian clock's timing behavior. For example, the light-signaling pathway is now understood to be composed of gates [36] which modulate the signal shape. As the models become more mechanistic, we must study the response to signals displaying properties such as attenuation and continuous (rather than discrete) transitions. Additionally, as modelers turn to coupled networks of oscillators, the intercellular signaling mechanisms produce curved signals [40], [41].

In this section, we present three methods for computing the PRC to an arbitrarily shaped signal (parametric perturbation). The first method, the direct method, captures all non-linearity in the system but is the most expensive to compute. The second method (pIPRC method), which uses the phase evolution equation (7) is less accurate, but also less expensive computationally. The third method, which uses the APRC is the least accurate and the least expensive. We recommend use of the direct method for large perturbations and the pIPRC for smaller perturbations. The APRC method is included to complete the set of approaches and to illustrate the dynamical nature of phase behavior. Numerically, it is reasonably accurate, but there is seldom any reason to reject the pIPRC method in favor of the APRC method.

For all methods, we choose a marker for the signal, g_onset(t) such that the signal first becomes active (non-zero) at time t.

1) Direct Method

Use the same method presented in Section IV-A.1.

This is the most accurate method for larger signals, because it captures all non-linear behavior. It is also the most expensive - every point in the PRC requires the simulation of an n-dimensional system of ODEs over several periods. As models increase in size, the direct method becomes much more expensive.

2) pIPRC Method

For each t_s ∈ t_disc and associated φ_s ∈ Φ, simulate the phase evolution equation

$$\frac{d\mathrm{\phi }}{dt}=1+{\text{pIPRC}}_j(\mathrm{\phi })g_j(t)$$

from initial condition φ(t_s) = t_s. We begin the simulation not from time t, but from the time of the onset of the signal, and end the simulation at time t_e when the signal becomes inactive (is identically zero). The phase shift is Δφ(φ_s) ≈ φ(t_e) − t_e.

This method captures the phase shifts caused by the signal as it arrives, but relies on the linear approximation of the trajectory with respect to parameter p_j. The pIPRC was derived with the assumption that it would be evaluated on the limit cycle. When the system is under perturbation, it is not necessarily on the limit cycle. The phase evolution equation is valid under the assumption that the phase determines the pIPRC even when not on the limit cycle. We have found that this method is most useful for small magnitude signals, but will provide qualitatively good results for larger signals. Computationally, each point requires the simulation of a one-dimensional ODE system for the duration of the signal. This cost is independent of the size of the original model.

3) APRC Method

The basis of this method is to discretize the signal into finite square pulses, and then sum up the phase shifts computed using the APRC for each square pulse. The algorithm is as follows:

1. Compute APRC_j for pulses lasting only one timestep Δt, APRC_j(t, Δt).

2. Discretize the signal using the same timestep.

3. For each t_s ∈ t_disc and associated φ_s ∈ Φ, sum the effects over the duration of the signal:

   $$\text{Δ}\mathrm{\phi }({\mathrm{\phi }}_s)\approx \mathbf{\sum }_{k=1}^{\mathit{\text{Nsig}}}{\text{APRC}}_j(t_s+t_k,\text{Δ}t)g_j(t_k)\text{Δ}t$$

   where Nsig is the number of timesteps required to cover the active signal.

This method does not capture the phase shifts caused by the signal as it arrives; it makes the assumption that g_j (t) will arrive when the internal time is also t. In other words, we compute the response to each pulse as if it is the first to arrive (i.e., each pulse is independent from the others). It also relies on the linear approximation of the trajectory with respect parameter p_j. Computationally, this method is remarkably fast; each point requires only addition and multiplication operations (no simulation aside from the computation of the APRC itself) and the cost is independent of the size of the original model.

Figure 7 contains the numerical experimental PRC, pIPRC_L-predicted PRC, and APRC_L-predicted PRC to a half-sinusoidal light signal (identical to that in [42]). The signal is generated such that, if t₁ is the time of signal onset, then

$$L(t)=\{\begin{array}{l}\mathit{\text{mag}}sin\left(\frac{\pi (t-t_1)}{d}\right),\\ 0,\end{array}\begin{array}{l}t\in [t_1,t_1+d]\\ t\notin [t_1,t_1+d]\end{array}.$$

PRCs are collected for durations d = 1, 3, and 6 hours and magnitudes mag = 0.1, 0.5, and 1 (i.e. 10%, 50%, and 100% of full light). The plots are organized so that the magnitude is increased from left to right and the duration is increased from top to bottom. In general, we observe that smaller magnitude and smaller durations allow the predictors to be more accurate (the upper lefthand plot shows the best agreement while the lower right shows the worst). The two predicted curves are similar, although the pIPRC_L is slightly more accurate (this is most apparent for pulses of 6-hour duration). Both predictors under-estimate the delays. However, the pIPRC method correctly captures the phase of the trough of the PRC. This is a direct consequence of the phase evolution equation. Dynamical tracking of the phase behavior is an important aspect of accurate prediction.

V. Conclusion

We have presented the derivation and intepretation of a novel sensitivity measure, the pIPRC, which both characterizes the phase behavior of an oscillator and provides the means for computing the response to an arbitrary signal (in the form of parametric perturbation). The pIPRC and other isochron-based sensitivity measures presented herein comprise a uniform framework within which the various timing properties are related. The relationship between the period sensitivity and the pIPRC is of particular interest. Circadian researchers have postulated a direct correlation between the area under the phase response curve and the effects of constant light on the period [21]. This work confirms the mathematical relationship.

The PRCs and infinitesimal PRCs presented in this work provide quantifiable measures of robustness for oscillators acting as pacemakers. In these systems, robust performance involves proper maintenance of phase behavior. In the case of the circadian clock, this means that the PRC to light must have not only the proper shape, but also the correct magnitude. The model and light gate considered here match observed biological data. In previous work [12], we invalidated a model of the circadian clock in the plant Arabidopsis thaliana, because the pIPRC had neither the proper shape nor the proper magnitude. In that case, the model's pIPRC predicted an ultra-sensitivity to light, which was verified via simulation - the system was reset to dawn whenever light arrived.

Biographies

Stephanie R. Taylor received a B.S. in mathematics and computer science from Gordon College (Wenham, Massachusetts) in 1998. From 1998 to 2003, she worked as a software engineer at JEOL, USA (Peabody, MA), where she developed and implemented software associated with a nuclear magnetic resonance spectrometer. She is currently pursuing a Ph.D. in computer science at the University of California Santa Barbara. As an NSF IGERT (Integrative Graduate Education and Research Traineeship) fellow in the Computational Science and Engineering program, her research involves the mathematical modeling and analysis of biological oscillators.

Dr. Rudiyanto Gunawan received the B.S. degree in chemical engineering and mathematics from the University of Wisconsin, Madison, in 1998, and the M.S. and Ph.D. degrees in chemical engineering from the University of Illinois, Urbana-Champaign, in 2000 and 2003, respectively. In July 2006, after a 3-year postdoctoral fellowship at the University of California, Santa Barbara, he joined the Department of Chemical and Biomolecular Engineering in National University of Singapore, where he is currently an Assistant Professor.

Dr. Linda R. Petzold received the B.S. degree in mathematics/computer science from the University of Illinois at Urbana-Champaign (UIUC) in 1974, and the Ph.D. degree in computer science from UIUC in 1978.

After receiving her Ph.D., she was a member of the Applied Mathematics Group at Sandia National Laboratories in Livermore, California until 1985, when she moved to Lawrence Livermore National Laboratory, where she was Group Leader of the Numerical Mathematics Group. In 1991 she moved to the University of Minnesota as a Professor in the Department of Computer Science. In 1997, she joined the faculty of the University of California Santa Barbara, where she is currently Professor in the Departments of Mechanical Engineering and Computer Science.

Prof. Petzold is a member of the US National Academy of Engineering, and a Fellow of the AAAS. She was awarded the Wilkinson Prize for Numerical Software in 1991, the Dahlquist Prize in 1999, and the AWM/SIAM Sonia Kovalevski Prize in 2003.

Dr. Francis J. Doyle III holds the Suzanne and Duncan Mellichamp Endowed Chair in Process Control at the University of California, Santa Barbara in the Department of Chemical Engineering, in 2002. He received his B.S.E. from Princeton (1985), C.P.G.S. from Cambridge (1986), and Ph.D. from Caltech (1991), all in Chemical Engineering. After graduate school, he was a Visiting Scientist at DuPont in the Strategic Process Technology Group, and held appointments at Purdue University; the University of Delaware; and the Universität Stuttgart. His research interests are in the areas of systems biology and nonlinear process control, with applications ranging from gene regulatory networks to complex particulate process systems. He is the recipient of several research awards including: National Science Foundation National Young Investigator; Office of Naval Research Young Investigator; Alexander von Humboldt Research Fellowship (2001-2002); and AIChE CAST Division Computing in Chemical Engineering Award (2005). He is the author of 3 books, and over 150 journal articles.

Appendix: Derivation of the pIPRC

Here, we derive the formula for computation of the pIPRC

$$\begin{array}{l}\frac{d}{dt}\frac{d\mathrm{\phi }}{d\mathbf{\text{p}}}({\mathbf{\text{x}}}^{\gamma }(t))=\frac{d}{dt}\left(\mathbf{\sum }_{k=1}^n{\text{sIPRC}}_k({\mathbf{\text{x}}}^{\gamma }(t))\frac{\partial x_k^{\gamma }}{\partial p_j}(t)\right)\\ =\frac{d}{dt}\left(\mathbf{\sum }_{k=1}^n\frac{\partial \mathrm{\phi }}{\partial x_k^{\gamma }}\frac{\partial x_k^{\gamma }}{\partial p_j}(t)\right)\\ =\mathbf{\sum }_{k=1}^n\frac{\partial \mathrm{\phi }}{\partial x_k^{\gamma }}\frac{\partial f_k}{\partial p_j}({\mathbf{\text{x}}}^{\gamma }(t)).\end{array}$$

Recall that

$$\frac{\partial \mathrm{\phi }}{\partial x_k^{\gamma }}({\mathbf{\text{x}}}^{\gamma }(t))=\underset{T\to \infty }{lim}{K}_{ik}^{†}(t,T)/fi({\mathbf{\text{x}}}^{\gamma }(T)),$$

where the limit can be ignored in practice. With that in mind, and for the sake of conciseness, we will leave out the limit in the derivation. To simplify notation, $K_{ik}^{†}=K_{ik}^{†}(t,T)$.

Using summation notation,

$$\begin{array}{l}\frac{d}{dt}\frac{d\mathrm{\phi }}{d\mathbf{\text{p}}}=\frac{d}{dt}\left(\mathbf{\sum }_{k=1}^n\frac{\partial \mathrm{\phi }}{\partial x_k^{\gamma }}{S}_{kj}\right)\\ =\frac{d}{dt}\left(\mathbf{\sum }_{k=1}^n\left(K_{ik}^{†}/f_i({\mathbf{\text{x}}}^{\gamma }(T))\right)S_{kj}\right)\\ =\frac{1}{fi({\mathbf{\text{x}}}^{\gamma }(T))}\frac{d}{dt}\left(\mathbf{\sum }_{k=1}^n{K}_{ik}^{†}{S}_{kj}\right).\end{array}$$

Applying the chain rule, we find

$$\begin{array}{l}\frac{d}{dt}\frac{d\mathrm{\phi }}{d\mathbf{\text{p}}}=\frac{1}{f_i({\mathbf{\text{x}}}^{\gamma }(T))}\mathbf{\sum }_{k=1}^n(\frac{d{K}_{ik}^{†}}{dt}{S}_{kj}\\ +K_{ik}^{†}\frac{d{S}_{kj}}{dt})\end{array}$$ (9)

The adjoint equation can be expressed in summation notation as

$$\begin{array}{l}\frac{d}{dt}{\text{K}}_{ik}^{†}={\left(-{\mathbf{\text{K}}}^{†}\mathbf{\text{J}}\right)}_{ik}\\ =\mathbf{\sum }_{h=1}^n\left(-K_{ih}^{†}{J}_{hk}\right).\end{array}$$ (10)

The classical sensitivity coefficient is $S_{kj}(t)=\frac{\partial x_k^{\gamma }(t)}{\partial p_j}$, and the sensitivity differential equation is

$$\begin{array}{l}\frac{d}{dt}(S_{kj}{)=(\mathbf{\text{JS}})}_{kj}+\frac{\partial f_k}{\partial p_j}\\ =\mathbf{\sum }_{h=1}^n\left(J_{kh}{S}_{hj}\right)+\frac{\partial f_k}{\partial p_j}.\end{array}$$ (11)

Substituting (10) and (11) into (9), we have

$$\begin{array}{l}\frac{d}{dt}\frac{d\mathrm{\phi }}{d\mathbf{\text{p}}}=\frac{1}{f_i({\mathbf{\text{x}}}^{\gamma }(T))}\mathbf{\sum }_{k=1}^n(\mathbf{\sum }_{h=1}^n\left(-K_{ih}^{†}{J}_{hk}\right)S_{kj}\\ +K_{ik}^{†}\left(\mathbf{\sum }_{h=1}^n\left(J_{kh}{S}_{hj}\right)+\frac{\partial f_k}{\partial p_j}\right))\\ =\frac{1}{f_i({\mathbf{\text{x}}}^{\gamma }(T))}\mathbf{\sum }_{k=1}^n(\mathbf{\sum }_{h=1}^n\left(-K_{ih}^{†}{J}_{hk}\right)S_{kj}\\ +K_{ik}^{†}\mathbf{\sum }_{h=1}^n\left(J_{hk}{S}_{hj}\right)\\ +K_{ik}^{†}\left(\frac{\partial f_k}{\partial p_j}\right))\end{array}$$

Further expansion of the terms shows

$$\begin{array}{l}\frac{d}{dt}\frac{d\mathrm{\phi }}{d\mathbf{\text{p}}}=\frac{1}{f_i({\mathbf{\text{x}}}^{\gamma }(T))}(\mathbf{\sum }_{k=1}^n\left(\mathbf{\sum }_{h=1}^n-K_{ih}^{†}{J}_{hk}{S}_{kj}\right)\\ +\mathbf{\sum }_{k=1}^n\left(K_{ik}^{†}\mathbf{\sum }_{h=1}^n\left(J_{kh}{S}_{hj}\right)\right)\\ +\mathbf{\sum }_{k=1}^n\left(K_{ik}^{†}\frac{\partial f_k}{\partial p_j}\right))\\ =\frac{1}{f_i({\mathbf{\text{x}}}^{\gamma }(T))}(-\mathbf{\sum }_{k=1}^n\mathbf{\sum }_{h=1}^n{K}_{ih}^{†}{J}_{hk}{S}_{kj}\\ +\mathbf{\sum }_{k=1}^n\mathbf{\sum }_{h=1}^n{K}_{ik}^{†}{J}_{kh}{S}_{hj}+\mathbf{\sum }_{k=1}^n{K}_{ik}^{†}\frac{\partial f_k}{\partial p_j}).\end{array}$$

Careful observation reveals that the first and second terms cancel. The h and k labels simply need to be reversed in one of the terms. Reversing the labels in the second term,

$$\begin{array}{l}\frac{d}{dt}\frac{d\mathrm{\phi }}{d\mathbf{\text{p}}}=\frac{1}{f_i({\mathbf{\text{x}}}^{\gamma }(T))}(-\mathbf{\sum }_{k=1}^n\mathbf{\sum }_{h=1}^n{K}_{ih}^{†}{J}_{hk}{S}_{kj}\\ +\mathbf{\sum }_{k=1}^n\mathbf{\sum }_{h=1}^n{K}_{ih}^{†}{J}_{hk}{S}_{kj}+\mathbf{\sum }_{k=1}^n{K}_{ik}^{†}\frac{\partial f_k}{\partial p_j})\\ =\frac{1}{f_i({\mathbf{\text{x}}}^{\gamma }(T))}\mathbf{\sum }_{k=1}^n{K}_{ik}^{†}\frac{\partial f_k}{\partial p_j}\\ =\mathbf{\sum }_{k=1}^n\frac{\partial \mathrm{\phi }}{\partial x_k^{\gamma }}\frac{\partial f_k}{\partial p_j}.\end{array}$$