Optimal photosynthetic use of light by tropical tree crowns achieved by adjustment of individual leaf angles and nitrogen content

Abstract

Background and Aims

Theory for optimal allocation of foliar nitrogen (ONA) predicts that both nitrogen concentration and photosynthetic capacity will scale linearly with gradients of insolation within plant canopies. ONA is expected to allow plants to efficiently use both light and nitrogen. However, empirical data generally do not exhibit perfect ONA, and light-use optimization per se is little explored. The aim was to examine to what degree partitioning of nitrogen or light is optimized in the crowns of three tropical canopy tree species.

Methods

Instantaneous photosynthetic photon flux density (PPFD) incident on the adaxial surface of individual leaves was measured along vertical PPFD gradients in tree canopies at a frequency of 0·5 Hz over 9–17 d, and summed to obtain the average daily integral of PPFD for each leaf to characterize its insolation regime. Also measured were leaf N per area (N_area), leaf mass per area (LMA), the cosine of leaf inclination and the parameters of the photosynthetic light response curve [photosynthetic capacity (A_max), dark respiration (R_d), apparent quantum yield (ϕ) and curvature (θ)]. The instantaneous PPFD measurements and light response curves were used to estimate leaf daily photosynthesis (A_daily) for each leaf.

Key Results

Leaf N_area and A_max changed as a hyperbolic asymptotic function of the PPFD regime, not the linear relationship predicted by ONA. Despite this suboptimal nitrogen partitioning among leaves, A_daily did increase linearly with PPFD regime through co-ordinated adjustments in both leaf angle and physiology along canopy gradients in insolation, exhibiting a strong convergence among the three species.

Conclusions

The results suggest that canopy tree leaves in this tropical forest optimize photosynthetic use of PPFD rather than N per se. Tropical tree canopies then can be considered simple ‘big-leaves’ in which all constituent ‘small leaves’ use PPFD with the same photosynthetic efficiency.

INTRODUCTION

Within an individual plant, the availability of light (photosynthetic photon flux density, PPFD) declines exponentially with cumulative leaf area index, resulting in strong gradients of PPFD within the canopy (Monsi and Saeki, 1953). Due to their sessile nature, most plants have a high capacity for developmental plasticity and acclimation that allows them to modify the form and function of their leaves to accommodate PPFD gradients within their crown. Adjustments in the physiology of leaves to the PPFD regime (where ‘regime’ is a measure of cumulative PPFD availability over many days or weeks) occurs through changes in leaf mass per area (LMA), leaf anatomy and the differential allocation of nitrogen (N) to carboxylation, electron transfer and light-harvesting processes (Björkman, 1981; Evans, 1989; Hikosaka and Terashima, 1995; Niinemets and Tenhunen, 1997; Oguchi et al., 2003). The principles that organize these adjustments to light availability have been well studied because they are central to our ability to scale photosynthesis from leaf to ecosystems. Over the last 30 years, a theory of optimal nitrogen allocation (ONA; Mooney and Gulmon, 1979; Field, 1983; Farquhar, 1989) based on economic principles has provided valuable explanations of why and how leaf properties should change along light gradients within plant canopies.

The ONA theory is based on the idea that leaf N is a measure of investment in photosynthetic machinery (Field, 1983) because photosynthetic proteins are the dominant fraction of total leaf protein (Evans, 1989). The theory assumes that there are costs and benefits that result from investing a certain amount of N in a leaf and the optimal N invested should depend on the opportunity for carbon gain in the particular micro-environment where a leaf is found (Mooney and Gulmon, 1979; Field, 1983). For instance, ONA predicts that leaves in the sun should have higher N content than leaves in the shade because the opportunity for carbon gain increases with insolation. Several empirical studies have demonstrated such variation of foliar N along PPFD gradients yet not in a perfect match with the theoretical predictions (Field, 1983; Hirose and Werger, 1987a; Evans, 1993; Hollinger, 1996; Dang et al., 1997; Friend, 2001; Kull, 2002; Meir et al., 2002; Wright et al., 2006). In particular, ONA predicts that N allocation is optimal when leaf N changes as a monotonic first degree function of PPFD (Farquhar, 1989); since leaf photosynthetic capacity (A_max) is generally linearly related to leaf N (Field and Mooney, 1986), the same prediction can be applied to changes in leaf A_max along PPFD gradients (e.g. Sands, 1995). Yet, the gradient of N (or A_max) along PPFD gradients in a canopy is often less steep than expected. In general, leaves exposed to a high PPFD regime typically have lower N content than the hypothetical optimum, while leaves in the shade have a higher N content than optimum (Evans, 1993; Hollinger, 1996; Dang et al., 1997; Friend, 2001; Kull, 2002; Meir et al., 2002; Wright et al., 2006). This discrepancy has prompted various explanations consistent with the ONA perspective.

It has been shown that an important assumption of ONA is that both the direct and indirect costs per unit N (i.e. marginal N costs) are the same independent of leaf position in the canopy (Mooney and Gulmon, 1979; Field, 1983; Hirose, 2005). Direct costs such as leaf mass per area (LMA, a measure of construction costs per area) or leaf dark respiration (R_d, a measure of maintenance costs per area) tend to change linearly with both leaf N per area and A_max (e.g. Hirose and Werger, 1987b; Ellsworth and Reich, 1993; Raulier et al., 1999), which supports this ONA assumption. However, there are reasons to question the assumption that indirect marginal costs of N are constant. For instance, when leaf N content increases, the risk of herbivory may increase, which means that indirect costs (i.e. loss of photosynthetic yield because of herbivore damage) may be higher at high rather than low N content (Mooney and Gulmon, 1979; Stockhoff, 1994). Variable marginal costs may also be generated by gradients of abiotic stress within plant canopies (e.g. evaporative demand, temperature and wind) that will not necessarily exactly parallel gradients of light (Niinemets and Valladares, 2004). Incorporating these variable marginal costs in the calculation of net photosynthesis is conceivable in principle (Mooney and Gulmon, 1979; Hollinger, 1996), but difficult in practice.

A second, perhaps more critical, consideration is that optimization of resources other than N may be of greater importance. If N is abundant, then the costs of acquiring it from the environment will be low and plants may ‘prioritize’ either by using other limiting resources optimally or co-optimizing different resources (e.g. Wright et al., 2006). Although N availability is generally expected to be low in temperate and boreal ecosystems, N-availability in the lowland tropics is usually above plant demand (Martinelli et al., 1999; Amundson et al., 2003; Ometto et al., 2006). Several studies have shown that productivity of many tropical forests may be limited by availability of light during the rainy season (Wright et al., 1999; Graham et al., 2003; Nemani et al., 2003; Myneni et al., 2007). Ideally, plants should optimize both N and PPFD use (Haxeltine and Prentice, 1996; Terashima et al., 2005), but there is evidence of possible trade-offs between PPFD and N use at the plant (Hirose and Bazzaz, 1998) and at the leaf scale (Hikosaka et al., 1999). Thus, it is conceivable that tropical canopy trees evolved to optimize the use of light rather than to optimize the use of N.

A third consideration is the role of adjustments in branch and leaf angles along PPFD gradients, which are often treated as fixed constants and not directly considered in ONA theory. A leaf can potentially alter its cost–benefit relationships by changing its spatial configuration without any change in its N content. For instance, a leaf blade can be oriented to intercept more PPFD (Ehleringer and Forseth, 1980; Forseth and Ehleringer, 1982; Galvez and Pearcy, 2003) or, conversely, to intercept less PPFD and hence reduce photoxidative, temperature or water stresses associated with high irradiance (Forseth and Ehleringer, 1982; Kao and Forseth, 1992; Feng et al., 2002; Galvez and Pearcy, 2003; Jiang et al., 2006; Kadioglu and Terzi, 2007). In addition, leaf orientation can homogenize the gradient of PPFD in the crown through an influence on self-shading (Terashima and Hikosaka, 1995). Thus, leaf orientation may help explain deviations between observed and expected N_area and A_max distributions.

Considering the points raised in the preceding paragraphs as well as many published empirical data (Evans, 1993; Hollinger, 1996; Dang et al., 1997; Bond et al., 1999; for a review see Kull, 2002), it was expected that in the present study system of tropical trees, N_area and A_max vs. PPFD might not strictly follow the 1 : 1 relationship predicted by ONA theory. Given the overall importance of light limitation during the rainy season on tropical tree canopies, we hypothesized that light-use efficiency may be of greater priority than N-use efficiency. To avoid potential bias from estimating PPFD due to variations in leaf angle, the ONA predictions were tested using incident PPFD in situ on leaves in their natural orientation. Optimal light use was then evaluated by looking at the relationship between average leaf daily photosynthesis (A_daily) and the average daily PPFD incident on individual leaves over the day (i.e. PPFD regime). The A_daily is a measure of time-integrated photosynthesis that incorporates the effects of both leaf angle and foliar physiology. Thus, a 1 : 1 relationship between A_daily and incident PPFD regime would suggest that leaf angle and physiology are co-ordinated to optimize light use. If the optimization of light use and N are in fact simultaneous, then a linear relationship between leaf A_max and N_area with the PPFD regime would be expected. Under the assumption of constant direct marginal costs in ONA theory, it would also be expected that leaf R_d and LMA would scale linearly with N_area. To evaluate all these possibilities, we studied how N_area, LMA, A_max, R_d, apparent quantum yield (ϕ), curvature (θ) and the cosine of leaf angle changed along vertical PPFD regimes within the canopy of individual tropical canopy trees; the PPFD regime was estimated as average daily PPFD incident on the adaxial surface of leaves over periods between 9 and 17 d. The overarching goal of the study was to assess possible explanations for the difference between observed and expected N and A_max distributions along PPFD gradients in the crown of tropical canopy trees.

MATERIALS AND METHODS

Study site

The study was conducted in Parque Natural Metropolitano, a reserve located on the Pacific coast of the Republic of Panama, near Panama City (9°04′N, 79°23′W, 100 m a.s.l.). This 265-ha reserve protects a 75–150-year-old tropical dry forest. The dry season occurs between January and April and the wet season between June and November; May and December are transition months. The forest canopy was reached via a 42-m free-standing construction crane with a 52-m-long jib (Parker et al., 1992). A tubular one-man gondola (diameter approx. 0·7 m) was used to access the inside of tree crowns. The small size of the gondola allowed repeated and non-destructive access to leaves in a broad range of microenvironments within tree crowns.

Species

Two adult canopy trees of Ficus insipida Willd (Moraceae), two of Castilla elastica Sessé (Moraceae), and one of Luehea seemannii Planch. & Triana (Tiliaceae), were sampled. The tops of all trees were fully exposed to sunlight and were situated at or near the upper edge of the forest canopy. Ficus insipida is a fast-growing, early-successional species (Croat, 1978) that has the highest reported leaf A_max of any tree (Zotz et al., 1995). Ficus insipida has an open crown with a leaf area index (LAI) between 2 and 4. Castilla elastica is also an early-successional species, but has a denser crown than F. insipida, with an LAI ≈ 5·0. Luehea seemannii is a secondary- to late-successional tree, with an LAI ≈ 4·0, and has leaves with pronounced heliotropic movements (E. A. Graham, University of California, Los Angeles, CA, unpubl. res.). Castilla elastica drops its leaves in the dry season, while both F. insipida and L. seemannii are evergreen.

Procedure

All measurements were made during the wet season of 2000, between early June and mid-November. Within each tree, 15 leaves were randomly selected from a broad range of PPFD regimes. Approximately one-third of the leaves were fully exposed to direct sunlight, one-third to intermediate light conditions, and one-third to shaded micro-environments. Each leaf was marked at emergence and measurements were made on young, fully developed leaves. During the observations, all measured leaves remained in a micro-environment similar to that during their development.

PPFD on the adaxial leaf surface at natural leaf orientation was measured with small G1118 GaAsP (gallium arsenide phosphide) photodiodes (Hamamatsu Corp., Bridgewater, NJ, USA), which operate in a broad range of temperatures with minimum drift (Fielder and Comeau, 2000). All sensors were calibrated every 1–2 months under a large range of natural daylight conditions against LI-190SA quantum sensors (Li-Cor, Lincoln, NE, USA). To determine the effect of changes in spectral quality, calibration constants for 18 sensors in the open (R : FR = 1·13) and under a leaf canopy (R : FR = 0·58) were compared. No significant effect of changes in the spectra on the calibration constants was found (t = 0·362, P = 0·722), although a small 3·2 % drift in the response has been reported for measurements made in the forest understorey (Pearcy, 1989; Fielder and Comeau, 2000). Although cosine errors can occur when direct beam PPFD is incident near the ‘horizons’ of the plane of the GaAsP sensors, this type of error is small for solar angles greater than 15° (Pearcy et al., 1990). Additionally, this study was carried out during the wet season when above-canopy, direct-beam PPFD only occurred 16·2 % of the time, while fully diffuse PPFD regimes (including overcast conditions plus early mornings and late afternoons) were the most common, occurring 46·9 % of the time. The remaining 36·8 % corresponded to intermediate conditions, when the sky was partially overcast and some direct beam PPFD was still present. The sensor, which weighs only 0·13 g, and its connector caused no visible effect on leaf orientation. The sensors were connected to a data logger (23X; Campbell Scientific Instruments, Logan, UT, USA), with cables 10–20 m long. Instantaneous PPFD was measured simultaneously for 15 leaves within the same tree and data were recorded every 2 s for 9–17 d. A few leaves were lost to herbivory or disease, or were torn during the photosynthesis measurements but the final sample size was between 10 and 14 leaves per tree. Daylength was calculated assuming a sun trajectory of 182°, which included PPFD when the sun was 1° below the horizon at sunrise and sunset.

Leaf orientation was measured just before the beginning of the PPFD measurements. Two angle measurements were made to estimate the inclination of the leaf lamina. The first was the angle between the leaf mid-vein and the horizontal plane (i.e. a completely horizontal mid-vein had an angle of 0°). The second was the rotational angle of the leaf lamina around the mid-vein, measured such that a leaf lamina that was parallel to the direction of gravity had an angle of 90°. After the PPFD measurements were completed, in situ net CO₂ fixation rates were measured as a function of instantaneous PPFD (A-PPFD curves) for each leaf with a portable infrared gas analyser (LI-6400, Li-Cor Instruments) with red-blue light-emitting diodes (6400-02B, Li-Cor). Leaf temperature, CO₂ concentration, and flow rate were maintained constant at 29 °C, 370 µmol mol⁻¹, and 500 ml min⁻¹, respectively. To obtain A-PPFD curves, leaves were first induced at 500–750 µmol m⁻² s⁻¹ for 5–10 min. Secondly, net photosynthesis was briefly measured at 2000 µmol m⁻² s⁻¹ and then PPFD was progressively decreased to 1500, 1000, 750, 500, 250, 100, 50 and 0 µmol m⁻² s⁻¹. Net photosynthesis was allowed to stabilize at each value of PPFD and a complete photosynthetic light curve (including induction time) was obtained in 25–45 min. Relative humidity in the leaf chamber was controlled manually to ≈70–80 % during measurements. Most leaves were measured in the morning to prevent photoprotection or midday stomatal closure, although a few shade leaves were measured around noon on very cloudy/rainy days.

After the A-PPFD curves were completed, leaves were collected and brought back to the laboratory to measure their different properties. The leaf section used to measure photosynthesis (approx. 8–12 cm²) was cut and its exact area was measured with a leaf area meter. Next, these leaf sections were oven dried at 60 °C until they reached constant mass. Nitrogen content (gN g⁻¹ leaf dry mass) was measured with an elemental analyser (ECS 4010, Costech Technologies, Inc., Valencia, CA, USA).

Data analysis

Data processing was done with the package MathCad Plus 6·0 (Mathsoft, Cambridge, MA, USA, 1996) and R (R Development Core Team, 2006). Photosynthetic light response curves were fitted to a non-rectangular hyperbola (Thornley, 1976). Parameters of the photosynthetic light response curve were estimated with Photosyn Assistant (Dundee Scientific, Dundee, Scotland, UK). The non-rectangular hyperbola function is given by

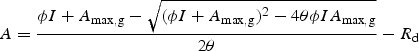where A is net CO₂ assimilation, I is instantaneous PPFD incident on the leaf, ϕ is the apparent quantum yield, A_max,g is the light saturated rate of gross assimilation, θ is the curvature, and R_d is dark respiration. In this study, A_max values correspond to the maximum rate of net assimilation, which was calculated as A_max,g – R_d. To estimate A_daily, the PPFD measurements and the photosynthetic light response curves of leaves were used and it was assumed that leaf assimilation rate was a function of instantaneous PPFD throughout the day. Since these curves were measured under optimal conditions and no stress factors were included in the calculations, A_daily was a measure of potential carbon fixation. The assumption of no-stress was reasonable as previous measurements done on the same F. insipida trees reported here showed that there was little mid-day stomatal closure during the wet season (Zotz et al., 1995). An important consideration when calculating A_daily was whether the PPFD regime above the canopy was different among trees, since each individual tree was measured at a different time during the rainy season. No differences were found in average above-canopy daily PPFD among periods of measurements (n = 5 periods, F = 0·952, P = 0·440).

Leaf mass per area was calculated as the ratio between the dry mass (g) of the leaf section used to measure photosynthesis and its area (m²). Leaf nitrogen per unit area (gN m⁻²) was calculated as the product between leaf nitrogen content (gN g⁻¹ leaf dry mass) and LMA (g leaf dry mass m⁻²). The cosine of leaf inclination was calculated by taking the product of the cosines of the two leaf angle measurements.

The data were fitted to linear and exponential models and the parameters estimated analytically using minimum least squares. An analysis of covariance was used to test for significant differences between slopes and intercepts of the relationship between A_daily and PPFD regime among trees (Zar, 1996). A hyperbolic model with two parameters and zero intercept was used to describe changes in several leaf functional traits as a function of the PPFD regime

where y is a leaf trait, x is the PPFD regime and a and b are parameters. The parameters of the hyperbolas were estimated with an iterative Gauss–Newton method with step halving implemented in JMP (JMP 5·0; SAS Institute, Inc., NC, USA, 2002). To determine the significance of the parameters, likelihood profiles were used to estimate 95 % confidence limits for each individual parameter. The models (linear, exponential, hyperbolic) were selected based on their applicability to all individual trees, the distributions of their residuals and their r² value.

RESULTS

Leaf A_max and leaf N_area were positively correlated in all trees. The correlations were highly significant (highest P < 0·004) and the coefficient of correlation (r) varied between 0·85 and 0·96. The same was observed for the correlation between leaf A_max and LMA (highest P < 0·03; r between 0·69 and 0·97) and between N_area and LMA (highest P < 0·0004; r between 0·91 and 0·99). The relationship of leaf R_d with the other traits was generally positive but more variability was observed in the data set. Leaf R_d was positively correlated with A_max in both C. elastica (minimum P < 0·002, r between 0·76 and 0·95) and L. seemannii (P < 0·001, r = 0·84) but was not significantly correlated to A_max in either F. insipda tree (P = 0·088 for F. insipida-1 and P = 0·363 for F. insipida-2). Leaf R_d was positively correlated to leaf N_area in all trees (highest P < 0·003; r between 0·84 and 0·86) except F. insipida 2 (P = 0·121, r = 0·55). Similarly, R_d was positively correlated to LMA in all trees (highest P < 0·001; r between 0·81 and 0·94) but F. insipida-2 (P = 0·198, r = 0·45). Overall, these different correlations suggest that A_max, N_area, LMA and R_d covaried linearly, so that an increment in any one of these traits was related to a proportional increment in the other traits.

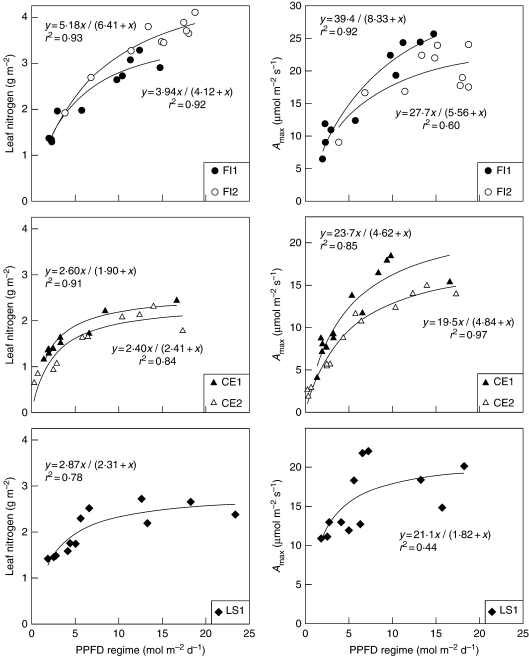
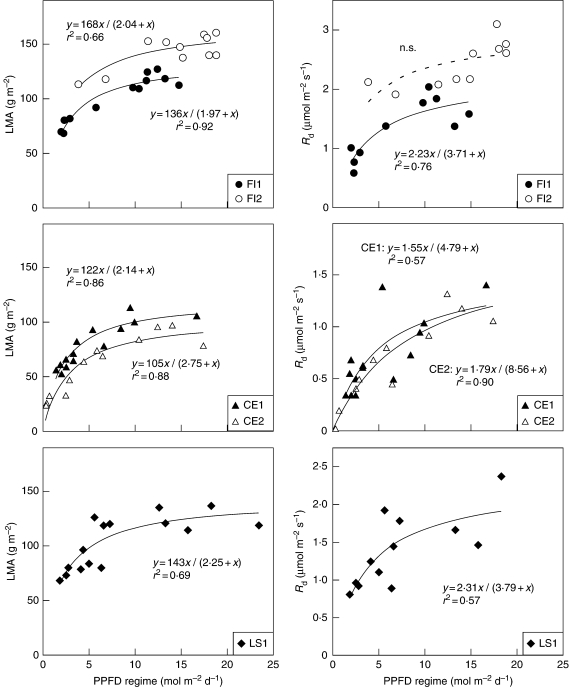
In contrast, leaf N_area and leaf A_max changed as a hyperbolic function of the PPFD regime (Fig. 1). All hyperbola parameters were positive and their 95 % confidence intervals did not include zero. The curvature of the hyperbola was similar between trees, species and traits, and showed that the rate of change in these traits decreased with increasing PPFD regime. Above a PPFD of approx. 10 mol m⁻² s⁻¹, the change in the traits was relatively small. In contrast, the most important changes in trait values occurred in leaves exposed to a PPFD regime below approx. 5–7 mol m⁻² d⁻¹. The hyperbolic relationships explained a very large proportion of the variability in N_area along the PPFD regime gradients in F. insipida (92–93 %), C. elastica (84–91 %) and L. seemannii (78 %). Similarly, most of the variation in A_max was described by a hyperbola in F. insipida (60–92 %) and in C. elastica (85–97 %), while in L. seemannii leaf A_max was more variable and PPFD explained less variation (44 %). The traits related to the construction and maintenance costs, LMA and R_d, respectively, also changed as a hyperbolic function of the PPFD regime and the shape of the curvatures were comparable to that of N_area and A_max (Fig. 2). A large proportion of the variation in LMA along the PPFD gradient was also explained by the hyperbolic model in F. insipida (66–92 %), C. elastica (86–88 %) and L. seemannii (69 %). The relationship between leaf R_d and PPFD was not significant for F. insipida-2 because the leaves had similar R_d and no leaves were sampled in the most shaded portions of the crown. Yet, the hyperbola explained 76 % of the variation in R_d in F. insipida-1, between 57 and 90 % of the variation in C. elastica and 57 % of the variation in L. seemannii. Simple linear regressions were also fitted to these four traits but the linear models were less appropriate than the hyperbolas due to curvature in the residuals. Also, the hyperbolic models explained considerably more variability in N_area (14·4 % more on average), A_max (10·3 %), LMA (13·9 %) and R_d (15·2 %) relationships than the linear models. The relationship between the apparent quantum yield (ϕ) and the PPFD regime was not significant in any tree (data not shown). The relationship between the curvature (θ) parameter and the PPFD regime was not significant for all trees but C. elastica-2 for which θ decreased linearly with PPFD (P = 0·008, r² = 0·52) (not shown). Overall, the results for N_area, A_max, LMA and R_d indicate that there was great consistency in how these traits change along PPFD regime gradients. These traits did not change much in the upper parts of the crown where PPFD availability was higher while leaf phenotypic change was more pronounced in the lowest and shadier parts of the crown.

Fig. 1.

Relationships between leaf nitrogen content (g m⁻²) of individual leaves vs. PPFD regime (mol m⁻² d⁻¹; left-hand panels) and leaf photosynthetic capacity (A_max, μmol m⁻² s⁻¹) of individual leaves vs. PPFD regime (right-hand panels) in five tropical canopy trees. The PPFD regime was calculated as average daily PPFD incident on the adaxial surface of individual leaves at their natural orientation. The continuous lines correspond to two-parameter hyperbolas with both parameters significantly different from zero. ‘FI’ refers to Ficus insipida (individuals 1 and 2), ‘CE’ to Castilla elastica (individuals 1 and 2) and ‘LS’ to Luehea seemannii.

Fig. 2.

Relationships between leaf mass per area (LMA, g m⁻²) of individual leaves vs. PPFD regime (mol m⁻² d⁻¹; left-hand panels) and leaf dark respiration (R_d, μmol m⁻² s⁻¹) vs. PPFD regime (right-hand panels) in five tropical canopy trees. The continuous lines show the best fit to a two-parameter hyperbola with both parameters significantly different from zero, while the dashed line is for relationships with at least one parameter not different from zero. See Fig. 1 for species’ names.

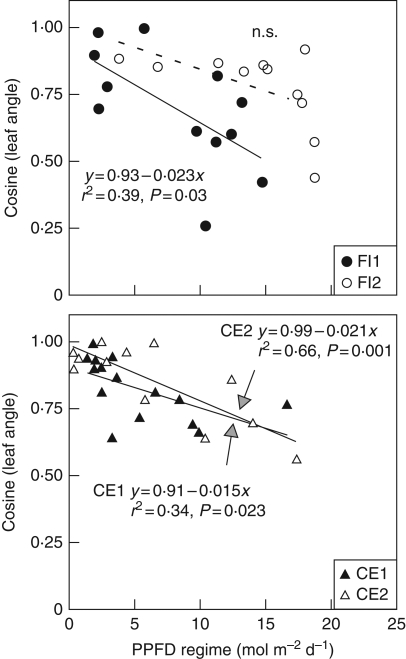
In contrast to the above traits, the cosine of leaf angle decreased proportionally to the PPFD regime in F. insipida-1 and both C. elastica (Fig. 3). The cosine of leaf angle corresponded to the proportion of the leaf surface (one-sided) that was projected on a horizontal plane, i.e. equivalent to the shade cast by a leaf on a horizontal plane if the leaf illumination comes from a source placed vertically above it. Under low PPFD regime the values were near 1, which indicated that leaves were oriented horizontally. The monotonic linear decrease in the cosine of leaf angle shows that leaves were gradually becoming more inclined as PPFD incident on their adaxial surface increased. The amount of variation explained by the PPFD regime varied between 34 % and 66 % and for F. insipida-2 the relationship was not significant. Results were not reported for L. seemannii as this species presents heliotropic leaf movements with leaves changing their angle within a time scale of minutes (E. A. Graham, unpubl. res.).

Fig. 3.

Relationships between cosine of leaf angle and PPFD regime (mol m⁻² d⁻¹) of individual leaves vs. PPFD regime in five tropical canopy trees. Cosine of leaf angle was calculated by taking the product of the cosine of the angle of rotation and the cosine of the angle of inclination of the leaf blade (see Materials and Methods). Leaves with a cosine of 1·0 were horizontal while leaves with a cosine of 0·0 were fully vertical. Continuous lines correspond to statistically significant least square linear regressions. The dashed line is for a non-significant relationship. See Fig. 1 for species’ names.

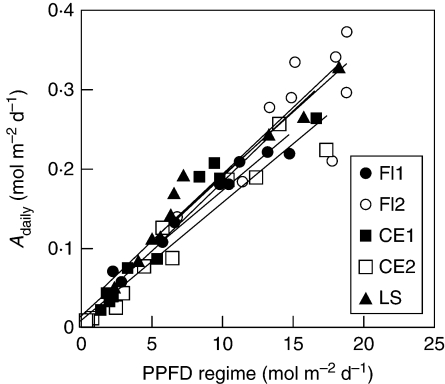
It was found that leaf A_daily was proportional to the PPFD regime on leaves in all trees (Fig. 4). This result is in contrast with the hyperbolic change that was observed between A_max and the PPFD regime (Fig. 1). Most of the variation in A_daily was explained by the linear relationship with the PPFD regime in F. insipida (75–94 %), C. elastica (94 % for both trees) and L. seemannii (94 %). Moreover, an analysis of covariance could not detect a difference between slopes (F = 0·51, P = 0·72) or elevations (i.e. intercepts; F = 2·00, P = 0·11) when comparing the different individual trees; the common slope was 0·016 and was highly significant (t = 21·89, P < 0·001). The common intercept was 0·017 mol m⁻² d⁻¹ and was significant (t = 2·45, P = 0·018), although its absolute value was close to zero. The common linear relationship indicated that there was a strong convergence in photosynthetic leaf light use efficiency (calculated as the ratio between leaf A_daily and PPFD regime) for all sampled leaves in this forest.

Fig. 4.

Linear regressions between the PPFD regime (mol m⁻² d⁻¹) of individual leaves and average daily net leaf photosynthesis (A_daily, mol m⁻² d⁻¹) for five tropical canopy trees. Regression slopes and intercepts did not differ among the five trees (see Results). Each point corresponds to an individual leaf for which average daily net photosynthesis was calculated for the period of PPFD measurements (between 9 and 17 d). See Fig. 1 for species’ names.

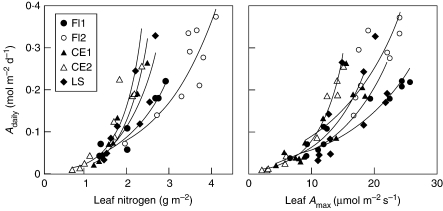
When comparing leaf N_area with leaf A_daily, the relationship was best described with an increasing exponential function (Fig. 5). These exponential relationships were highly significant (P < 0·001) and they explained between 81·4 % and 92·2 % of the variation. These plots demonstrate that the ratio A_daily:N was lower for shaded leaves at the lower positions in the crown than for sunnier leaves. The relationship between leaf A_max and leaf A_daily followed a similar type of increase. All exponential relationships were significant (highest P < 0·010) and explained between 51·2 % and 97·5 % of the variation. It was also found that the relationships between A_daily vs. N_area and A_max could be fitted to linear relationships. However, the average fit was better with the exponential model and it explained more variation (3·13 % better for the A_daily–N_area relationship and 5·33 % better for the A_daily–A_max relationship).

Fig. 5.

Relationship between leaf nitrogen content (g m⁻²) and leaf daytime carbon gain (A_daily, mol m⁻² d⁻¹; left panel) and between leaf photosynthetic capacity (A_max, μmol m⁻² s⁻¹) and A_daily (right panel). The continuous lines correspond to statistically significant least square exponential regressions. See Fig. 1 for species’ names.

DISCUSSION

The prediction from ONA theory that there should be a monotonic first-order increase in A_max or N_area with PPFD regime is not generally supported by empirical data (e.g. Evans, 1993; Hollinger, 1996; Dang et al., 1997; Bond et al., 1999; for a review see Kull, 2002). In earlier studies and here as well, shaded leaves lower in the canopy exhibit higher N_area or A_max than expected while sun leaves in the upper canopy exhibit lower trait values than expected. In several studies, linear models have been fitted to the relationships between N_area, A_max or carboxylation capacity (V_cmax) vs. PPFD regime, and these regressions had elevations higher than zero in the majority of cases (Kull, 2002). Although linear models were also fitted to the present data and significant positive intercepts were found in all trees (data not shown), pattern in the residuals indicated a simple linear model was not statistically valid for the trees studied. Because of the broad range of PPFD regimes assessed (16-fold on average and up to 39-fold), it was observed that changes in N_area and A_max were ascending at low PPFD regime and tended towards an asymptote at intermediate and high PPFD regimes.

Several assumptions of ONA theory hold in the present data, and canopy leaves do partition N in the direction predicted by ONA, albeit imperfectly. There is a positive correlation between N_area and A_max, which supports the assumption that leaf N_area is a valid measure of investment in the photosynthetic enzymes. This agrees with earlier reports for many species of plants (e.g. Field and Mooney, 1986; Hirose and Werger, 1987a; Field, 1991; Ellsworth and Reich, 1993; Anten et al., 1995). Also there are linear correlations between N_area and LMA and between N_area and R_d, which show that the present measures of construction (LMA) and maintenance costs (R_d) changed in direct proportion with N, in accord with the assumption of constant marginal costs (i.e. constant cost per unit N). Positive linear N_area–LMA and N_area–R_d relationships also have been commonly reported (e.g. Hirose and Werger, 1987b; Ellsworth and Reich, 1993; Raulier et al., 1999). There are, however also some assumptions that are not satisfied in the present data and that may account for the imperfect fit to ONA predictions.

There is reason to question the assumption that indirect marginal costs are the same for all leaves irrespective of their N content or position in the canopy. Indirect marginal costs may well be higher for leaves with high N content because these leaves are usually found in exposed parts of the canopy where environmental stresses are higher (e.g. Niinemets and Valladares, 2004). Similarly, indirect marginal costs may be higher if herbivores show preferences for leaves with a higher N content (e.g. Mooney and Gulmon, 1979; Stockhoff, 1994). The present study was not designed to measure how indirect costs changed as a function of leaf N_area or with the physical location of a leaf in the crown. However, part of the key cost–benefit relationship in the ONA theory was directly evaluated (Hirose, 2005) – how gains (i.e. A_daily) changed with allocation to N_area. It was found that A_daily scaled as an exponential function of N_area or A_max indicating that marginal gains were higher in the upper part of the tree crowns, where the highest leaf A_max and N_area were also found; in other words, photosynthetic N-use efficiency (PNUE, photosynthetic gains per unit N) was higher in the sunnier than in the shadier parts of the trees. Since this disproportionate increase in marginal benefits could compensate, or even exceed, any increase in indirect marginal costs, variable indirect marginal costs may not necessarily explain the hyperbolic change in N_area and A_max with PPFD regime.

It should therefore be considered that deviations from ONA predictions may arise simply because the most fundamental assumption in the theory is violated. Perhaps N is not the focus of optimization, particularly in many tropical forests. In lowland tropical forests isotopic fractionation of N indicates that N availability is generally above plant demand (Martinelli et al., 1999; Amundson et al., 2003; Ometto et al., 2006) and that some of these forests may be in a non-Liebig condition where multiple nutrients co-limit productivity (Kaspari et al., 2008). Under these conditions, natural selection may not be able to favour the evolution of mechanisms that allow tropical plants to maximize the efficient use of one mineral resource over another. On the other hand, there is evidence that the productivity of lowland tropical forests is limited by PPFD availability during the cloudy, rainy seasons (Wright et al., 1999; Graham et al., 2003; Nemani et al., 2003; Myneni et al., 2007). The strong convergence of variation in leaf function within the canopy among three species varying in canopy architecture and leaf display patterns suggests that the tropical tree species studied evolved to use PPFD efficiently, not N. The monotonic first-order function between leaf A_daily and PPFD regime that were observed shows that all leaves in the crown used PPFD with the same photosynthetic efficiency (ε_leaf), which was calculated as the ratio between leaf A_daily and leaf PPFD regime (Rosati and DeJong, 2003). This proportionality was maintained because most photosynthetic activity was concentrated on the ascending portion of the photosynthetic light response curves of leaves (Monteith, 1994; Rosati and DeJong, 2003) and, in particular, in the section of the curves where photosynthetic PPFD use efficiency was maximal (J. M. Posada, unpubl. res.), i.e. constant ε_leaf was also related to maximum PPFD-use efficiency. A 1 : 1 relationship between leaf A_daily and the PPFD regime has also been observed in cultivated plants in temperate latitudes (Rosati and DeJong, 2003; Rosati et al., 2004), suggesting that optimization of ε_leaf may be a more widespread phenomenon than previously acknowledged.

Although one might expect plants to use both N and light efficiently (Haxeltine and Prentice, 1996; Terashima et al., 2005), it may be impossible to simultaneously achieve perfect optimization of both (Hirose and Bazzaz, 1998; Hikosaka et al., 1999; Terashima et al., 2005). Here, it was not directly evaluated whether the observed leaf N_area deviated from the N content that would maximize PNUE (e.g. Hikosaka et al., 1999). However, the lack of support for the 1:1 N_area vs. PPFD relationship as well as the exponential A_daily vs. N_area relationship strongly suggested that maximum PNUE was not attained by the entire crown in these trees. It was also emphasized that leaf A_max was not in simple proportionate relationship to the time-integral of leaf A_daily. Leaf A_max is a measure of the maximum instantaneous C-gain, while A_daily incorporates both the physiology and the modulating effect of leaf angle on the PPFD environment. The present data therefore suggest that the spatial arrangement of leaves played a central role in the optimization of PPFD-use and should be explicitly considered when establishing a mechanistic link between the allocation to N_area or A_max and the time-integral of leaf carbon gain.

It was found that the cosine of leaf angle declined monotonically along the entire PPFD gradient for the three of our four study trees that had no heliotropic leaf movements. Above the mid-range of PPFD regime, where N_area and A_max changed little, leaf angle appeared to play a central role in maintaining A_daily proportional to the PPFD regime, while at low PPFD regime both leaf angle and leaf physiology changed. This suggests that leaves optimized their photosynthetic use of PPFD thanks to a leaf-level mechanism that co-ordinated their spatial orientation and their physiology. Previous studies also have long recognized the contribution of leaf angle to an efficient use of PPFD as tilted leaves allow greater sharing of light within the plant canopy (Boysen-Jensen, 1932; Monsi and Saeki, 1953; Monteith, 1994; Terashima and Hikosaka, 1995; Terashima et al., 2005). Also recognized in large canopy tree crowns is the importance of not only leaf-angle variations, but also shoot and branch architecture on light gradients generated by self-shading (Kitajima et al., 2005). Several studies have included, with different levels of complexity, the effect that canopy architecture has on within-canopy PPFD gradients and optimal resource allocation (e.g. Hirose and Werger, 1987b; Gutschick and Wiegel, 1988; Hikosaka et al., 1999; Schieving and Poorter, 1999). It is possible that a relatively small gain in whole plant carbon gain through perfect ONA, or perfect carbon allocation that is reflected in LMA (Gutschick and Wiegel, 1988), are less important than increased leaf area index in maintaining competitiveness with neighbouring plants (Gutschick and Wiegel, 1988; Schieving and Poorter, 1999). This has been considered as an explanation for retaining lower shade leaves in trees despite their low N-use efficiency and small contribution to whole-canopy photosynthesis (Monsi and Saeki, 1953; Kitajima et al., 2005). In herbaceous canopies, models that consider the dynamics of leaf production and death generate more realistic leaf trait distributions in the canopy (Franklin and Ågren, 2002; Hikosaka, 2003, 2005). However, in crowns of many canopy trees, lower shade leaves develop simultaneously with higher sun leaves, unlike sequential development of leaves typical in herbaceous canopies.

Finally, the observed convergence in optimal PPFD use has important implications for the scaling of photosynthesis from leaves to canopy (Dewar, 1996; Haxeltine and Prentice, 1996). Estimating overall ε_leaf as the linear slope between A_daily and the PPFD regime, no significant differences were found in slopes among the study trees. There was a strong convergence in daily photosynthetic light-use efficiency despite substantial species differences in canopy architecture, life history and successional status. These results were particularly surprising for L. seemannii, which has heliotropic leaves that can change their angle in a matter of minutes (E. A. Graham, unpubl. res.). The common slope value, 0·016 mol CO₂ · mol photons⁻¹, was well within the range estimated in cultivated plants, although higher values were reported during cloudy days (Rosati and DeJong, 2003; Rosati et al., 2004). The maintenance of this constant ε_leaf supports the use of ‘big-leaf’ models to simulate whole plant or canopy photosynthesis. Big-leaf models consider the canopy as a single leaf and, due to their simplicity, they have been used extensively (e.g. Amthor, 1994; Dang et al., 1997; Friend, 2001). These models generally assume that leaf A_max changes in a 1 : 1 ratio with the PPFD gradients, which, as shown in this and other studies, is usually not the case (e.g. Friend, 2001; Kull, 2002; Wright et al., 2006). The present results suggest that it is possible to use an even simpler big-leaf approach where the A_max–PPFD gradients can be ignored. The constant ε_leaf means that all leaves, regardless of their position along the PPFD gradient or taxonomic identity, used light with the same efficiency. This constancy also indicates that ε_leaf is equal to the light-use efficiency of the whole forest canopy (ε_canopy). Although the common elevation was statistically significant, its absolute value was close to zero suggesting that this approximation is reasonable. Hence, it should be possible to estimate net photosynthesis of a forest canopy (A_canopy) by combining ε_canopy with measures of PPFD absorbed (PPFD_A) by leaves using the simple equation:

1

This equation is analogous to the well-know relationship between plant growth and absorbed photosynthetic radiation (APAR) where growth is proportional to ε_g · APAR (Monteith, 1977; Monteith, 1994); in this equation ε_g is a constant defining the light-use efficiency of biomass production. The two equations cannot be compared directly because growth (i.e. biomass production) is the result of plant gross photosynthesis minus plant respiration. The results of the present study, however, show how leaf-level optimization of light use can help explain the proportional relationship between biomass production and APAR. This conclusion agrees with previous predictions (Monteith, 1994; Dewar, 1996; Haxeltine and Prentice, 1996) and empirical data for cultivated plants (Rosati and DeJong, 2003; Rosati et al., 2004). An advantage of eqn (1) is that it can be used to estimate tree and forest net photosynthesis as well as gross primary production by taking a few gas exchange measures at leaf level.

In summary, it was found that individual leaves optimized the photosynthetic use of light along PPFD regime gradients in the crown of tropical trees. We suggest that this optimization was possible through unidentified mechanisms that co-ordinate the angle and the physiology of individual leaves so that most instantaneous PPFD incident on a leaf is concentrated on the ascending part of the A–PPFD curve (Rosati and DeJong, 2003; J. M. Posada, unpubl. res.). Although the leaves exhibit variation in the direction of ONA, they did not exhibit a perfect match to the prediction of a 1:1 relationship between N_area or A_max with the PPFD regime. In contrast, daily photosynthetic light-use efficiency exhibited convergent constancy among leaves in a manner to achieve optimization of light use for the whole crown. In other words, N allocation was a subordinate response driven by leaves within the plant canopy using PPFD efficiently. The present study provides evidence of a strong convergence towards the optimization of ε_leaf, which potentially can simplify the scaling of photosynthesis from leaves to plants and ecosystems. The generality of the results should be tested, especially in systems where insolation may not be the primary factor limiting productivity but where plants still present non-optimal leaf N distributions along PPFD gradients.