OptGraft: A computational procedure for transferring a binding site onto an existing protein scaffold

Abstract

One of the many challenging tasks of protein design is the introduction of a completely new function into an existing protein scaffold. In this study, we introduce a new computational procedure OptGraft for placing a novel binding pocket onto a protein structure so as its geometry is minimally perturbed. This is accomplished by introducing a two-level procedure where we first identify where are the most appropriate locations to graft the new binding pocket into the protein fold by minimizing the departure from a set of geometric restraints using mixed-integer linear optimization. On identifying the suitable locations that can accommodate the new binding pocket, CHARMM energy calculations are employed to identify what mutations in the neighboring residues, if any, are needed to ensure that the minimum energy conformation of the binding pocket conserves the desired geometry. This computational framework is benchmarked against the results available in the literature for engineering a copper binding site into thioredoxin protein. Subsequently, OptGraft is used to guide the transfer of a calcium-binding pocket from thermitase protein (PDB: 1thm) into the first domain of CD2 protein (PDB:1hng). Experimental characterization of three de novo redesigned proteins with grafted calcium-binding centers demonstrated that they all exhibit high affinities for terbium (K_d ∼ 22, 38, and 55 μM) and can selectively bind calcium over magnesium.

Introduction and Background

Natural selection has crafted an astounding array of proteins with a remarkable repertoire of functionalities ranging from catalysis, signaling, recognition, and regulation to compartmentalization and repair. Despite this wide range of functionalities, many biotechnological tasks would benefit from individual proteins having properties not required in nature. A number of success stories regarding the use of computations to drive protein design have recently been reported.^1–12 These advances in rational protein design were focused on redesigning an existing protein structure to introduce a new function or enhance an existing property, such as catalytic rate or affinity for a cofactor, substrate, or ligand. This can be accomplished by modifying an existing binding pocket or active site (i.e., redesign),^7,8,13 or by rationally engineering a completely new function into target protein scaffold.^1–3,11,12 In both cases, access to detailed structural information is critical for success. In Ref.7, we introduced a computational procedure for redesigning an existing protein for altered specificity by systematically favoring the binding of a targeted ligand while suppressing the binding energy of competing molecules. In this article, we focus instead on the computation-driven introduction of a new binding site onto an existing protein fold. A number of experimental techniques and computational tools have been proposed to aid the incorporation of new functions into existing protein scaffolds.^5,14–19 Most of the earlier efforts in constructing new protein binding sites focused on the creation of metal-binding sites into proteins with known structures.^{14,15,20–24} It is hoped that these efforts will eventually lead to techniques for the ab initio introduction of more sophisticated functions such as catalytic activity and biosensing onto protein scaffolds.

Earlier efforts relied on visual inspection and local structural homology between donor and binding site acceptor proteins to graft simple metal-binding sites.²⁵ Some of the earliest systematic methods include MetalSearch and Dezymer, which are structure-based computational search procedures designed to guide metalloprotein design based on geometric principles.^14,15 MetalSearch requires the backbone coordinates as input and generates lists of four-residue clusters that should form tetrahedral sites upon replacement with cysteine or histidine. The only criterion evaluated by MetalSearch is tetrahedral site formation, which is frequently a required geometry in metal-binding protein sites.¹⁵ Alternatively, Dezymer identifies backbone positions to introduce new residues to form a new binding site emulating the geometry of the natural ligand-binding site without explicit consideration of binding energies.¹⁴ Upon identification of appropriate residues to create a new binding site, Dezymer predicts whether additional changes in the surrounding area are necessary to optimize steric hindrance and reduce potential clashes. Both of these programs have been used successfully to design tetrahedral metal binding.^15,20 Dezymer was successful in designing more complex functions such as molecular recognition and biosensing.^2,26 More recently, Zanghellini et al.⁵ introduced new algorithms for computational enzyme design that employ hashing techniques to search for the optimal places for catalytic site residues in the correct orientation in large numbers of protein scaffolds. Quantum mechanical calculations are employed to locate transition structures of the substrate in preexisting pockets of protein scaffolds, and in the next step, the surrounding residues are optimized to further stabilize the transition state. This algorithm has been successfully used to design novel biocatalysts for Kemp elimination¹² as well as new Retro-aldolase enzymes.¹¹

In contrast to protein redesign for improving or altering existing functions, the de novo design of new function into existing protein scaffolds is still in its infancy with relatively few success stories.^{2,3,11,12,16,20,23,24,26,27} Key challenges include the ability to computationally explore all potential locations to place the constellation of new residues that confer the new function and to assess the impact of the mutated residues on the overall protein stability and shape retention. In response to these challenges, in this article, we put forth an integrated computational procedure OptGraft for grafting a new binding site onto an existing protein scaffold and ensuring that the geometry of the transferred binding site is retained. The proposed algorithmic procedure consists of two steps (see Fig. 1). In the first step, OptGraft uses geometric criteria to exhaustively identify and rank the best possible locations to place the new binding site. In the second step, OptGraft identifies for the most promising designs whether additional mutations in the neighboring residues are needed to better accommodate the imposed structural changes (e.g., alleviate steric clashes or improve favorable interactions). OptGraft is employed to introduce metal-binding sites onto existing protein scaffolds; however, it is versatile enough to handle the design of binding pockets and active sites for more complex ligands.

Figure 1.

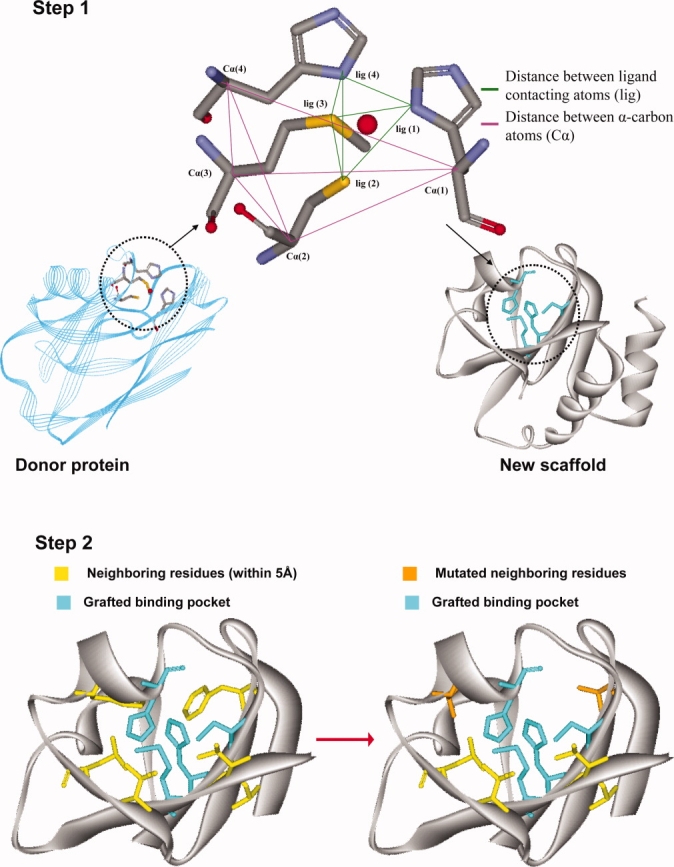
A schematic presentation of OptGraft. Step 1 identifies where the binding pocket should be grafted on the acceptor protein. Step 2 determines what residue modifications are required in the surrounding region (shown in yellow) to ensure that the correct binding pocket geometry is preserved.

In this article, we describe the algorithmic details of OptGraft and introduce the globally convergent Mixed-Integer Linear Program that drives residue redesign. We next benchmark OptGraft against a case study from the literature¹⁴ involving the creation of new copper-binding site, demonstrating the ability of the method to efficiently generate multiple designs with promising geometries. We next use OptGraft to transfer the calcium-binding pocket found in thermitase protein (PDB: 1thm) onto the first domain of the non-calcium-binding CD2 (PDB: 1hng) protein. The creation of a new calcium-binding pocket is tested experimentally by monitoring the fluorescence response to binding the calcium analog terbium for three selected binding pockets, involving mutations at residues 78, 80, 89, and 91 of the protein scaffold. All three designed binding pockets exhibit high affinities for terbium (K_d ∼22, 38, and 55 μM), and calcium acts as a strong competitor of terbium binding. The grafted binding sites also exhibit selectivity toward calcium over magnesium. These results also demonstrate that the geometry score of the grafted binding pocket is a reasonable surrogate for the binding constant (i.e., design with lower geometry score has higher metal affinity). We conclude by discussing the implications of our results for introducing new functions onto existing folds and future plans to design for more complicated functions such as enzymatic catalysis.

Results

OptGraft predictions

We first benchmarked OptGraft predictions against the results available in the literature for the blue copper protein system.^14,20 This tested the efficacy of OptGraft to reproduce existing designs and suggest new ones with more promising geometries.

De novo design of a copper-binding pocket

The Dezymer program was employed by Hellinga and Richards to engineer a blue copper (i.e., type I copper) site in thioredoxin.¹⁴ In the type I copper center, a mononuclear copper ion is coordinated by two histidines (ND), one cysteine (SG), and one methionine (SD) arranged in a distorted tetrahedron and shielded from solvent by the protein scaffold.^28–30 Using the geometry of the copper-binding sites found in plastocyanin (PDB:1pcy), azurin (PDB:2aza), and cupredoxin (PDB:1paz), Dezymer was used to insert an analogous metal center in the hydrophobic core of the E. coli thioredoxin (PDB:2trx).^14,20 After two rounds of search and refinement, five sites were identified that could potentially accommodate the appropriate residues to mimic the overall geometry of the natural blue copper site. The design with the best binding pocket geometry score contained four coordinating residue mutations (L7C, F12H, V16H, and L58M) and was selected for experimental verification. The redesigned protein accommodated a CysHis₂Met high affinity metal-binding center (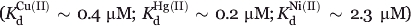). The engineered variant of thioredoxin shared similar properties as the wild-type protein, suggesting that the mutations did not cause major structural perturbations.²⁰

In our computational study, the Azurin copper-binding site was grafted into the hydrophobic core of the thioredoxin scaffold (see Fig. 2). Cartesian coordinates from the crystal structure of the donor protein (i.e., Azurin) were used to tabulate the geometric parameters of the native metal-binding center. The six pairwise distances between α-carbon atoms and between copper-contacting atoms of the four amino acids in the native metal-binding center are listed in Table I. Each individual pair of copper-binding site residues was computationally added to the thioredoxin hydrophobic core, and the relevant distances between mutated residue pairs (i.e., distances between Cα atoms and copper contacting atoms) were calculated. Step 1 of OptGraft was then employed to identify locations that can accommodate the new binding pocket residues to satisfy the predefined geometrical criteria. Solutions are ordered by their corresponding geometry score values, which reflect the degree of similarity between the geometry of the grafted binding pocket and that of the native binding pocket. Lower values indicate improved preservation of the overall pocket geometry. For the ideal grafting case, the value of the geometry score becomes equal to zero.

Figure 2.

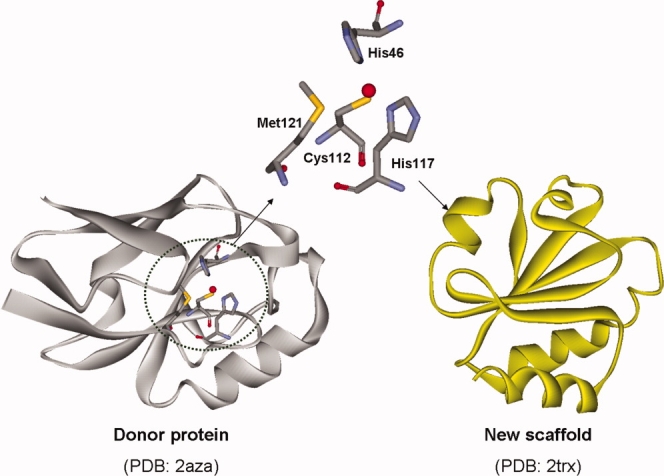
The native copper-binding center in Azurin (left). Copper is bound to different atoms of residues H46, H117, C112, and M121. The structure of the scaffold protein (thioredoxin) is also depicted. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Table I.

Geometric Description of the Copper Site Residues in Azurin

Residues		Distance (Å)
Distance between Cα atoms
46H	112C	5.92
46H	117H	8.23
46H	121M	9.20
112C	117H	5.69
112C	121M	5.57
117H	121M	5.68
Distance between copper contacting atoms
46H (ND1)	112C (SG)	3.88
46H (ND1)	117H (ND1)	3.15
46H (ND1)	121M (SD)	3.39
112C (SG)	117H (ND1)	3.60
112C (SG)	121M (SD)	4.32
117H (ND1)	121M (SD)	3.81

Letters in parentheses represent atoms.

Results after step 1 (see Table II) suggest that there exists many possible ways to introduce a copper-binding pocket into the thioredoxin scaffold. Many solutions are similar in terms of both location within the hydrophobic core and geometry score. In fact, the two solutions with the lowest score have the same four positions mutated and differ only by two amino acids that have exchanged positions (see Table II). Notably, for many solutions, different permutations of the binding site amino acids populate the same candidate locations. Although a large fraction of our predicted designs are similar to those found by Dezymer (e.g., many involve mutating the same four residue positions 7, 12, 16, and 58), many others were found with substantially lower geometry scores alluding to the presence of potentially more promising redesigns. OptGraft identified as many as 119 solutions with geometry scores less than 85.8 corresponding to the score of the best Dezymer solution according to our geometric score. Notably, the top 30 predicted designs by OptGraft have scores ranging from 16.1 to 49.0.

Table II.

OptGraft-Generated Mutations (Step 1) for Constructing the Copper Binding Site in Thioredoxin

	Geometry score		Mutations			Distancea (Å)
1	16.1	16V→H	23I→C	25V→H	56A→M	3.91
2	20.1	16V→H	23I→C	25V→M	56A→H	3.91
3	30.1	16V→H	19A→M	23I→C	25V→H	3.80
4	34.0	7L→C	12F→H	16V→M	58L→H	4.02
5	35.8	7L→H	25V→H	56A→C	58L→M	3.73
6	36.4	7L→H	16V→H	56A→C	58L→M	3.71
7	38.1	5I→C	7L→H	15D→H	56A→M	4.05
8	38.5	7L→M	25V→H	56A→C	58L→H	3.64
9	39.3	4I→H	46A→M	55V→C	57K→H	3.62
10	41.7	16V→H	19A→M	23I→C	56A→H	3.89
11	42.7	4I→H	42L→M	46A→H	55V→C	3.59
12	43.2	16V→H	23I→C	54T→M	56A→H	3.71
13	43.8	4I→H	42L→M	55V→C	57K→H	3.66
14	44.1	5I→M	7L→H	16V→H	56A→C	3.73
15	44.2	4I→M	42L→H	46A→H	55V→C	3.59
16	44.4	16V→H	25V→H	56A→C	58L→M	3.85
17	44.9	4I→M	26D→H	42L→H	55V→C	3.58
18	44.9	45I→H	49Y→M	53L→C	55V→H	3.53
19	45.3	7L→H	16V→M	25V→H	56A→C	4.12
20	45.6	7L→H	16V→H	25V→M	56A→C	4.12
21	46.1	7L→M	16V→H	25V→H	56A→C	4.12
22	46.1	7L→H	16V→H	25V→C	56A→M	4.12
23	46.4	7L→H	12F→C	16V→H	58L→M	3.81
24	46.6	5I→C	7L→H	16V→H	56A→M	3.99
25	47.4	26D→H	42L→H	55V→C	57K→M	3.58
26	48.1	5I→M	7L→H	25V→H	56A→C	3.92
27	48.6	5I→M	23I→H	54T→C	56A→H	3.67
28	48.7	7L→H	25V→M	56A→C	58L→H	3.76
29	48.8	16V→C	19A→M	23I→H	25V→H	3.81
30	49.0	16V→C	19A→H	23I→H	56A→M	3.61

^aDistance between the copper and the nearest Cα atom in the protein backbone. The vdw radii for copper and carbon are 1.15 and 1.55 Å, respectively.

We next sought to eliminate designs that may contain severe steric clashes between the ligand and protein backbone. Designs were eliminated from consideration if the distance between the copper atom and the closest Cα atom of the protein (listed in Table II) was lower than the sum of their corresponding Van der Waals (vdw) radii. No such major atomic clashes were revealed for this case study.

Step 2 of OptGraft was next used to identify what mutations in the neighboring residues may be needed to stabilize the conformation of the grafted binding pocket for the top five solutions. Excluding the grafted residues, all residues within a 5Å distance from the metal were considered as design positions for mutation. The suggested mutations are listed in Table III. Note that for the fourth solution (i.e., 7C, 12H, 16M, and 58H), none of the positions considered for redesign are mutated away from the wild-type amino acids. This result is similar to the Dezymer predictions, where for the same location, no additional mutations are necessary in the adjacent amino acids.²⁰ In all other four cases, the predicted neighboring residue mutations tend to involve switching to smaller residues to reduce steric hindrance and consequently improve the grafted binding pocket's geometry score.

Table III.

OptGraft-Predicted Mutations (Step 2) in Neighboring Residues (Within 5 Å Distance from the Copper Atom) for the Top Five Redesigned Thioredoxin Variants

Designs	Original geometry score	Mutations in neighboring residues	New geometry score
1	16.1	5I→ V, T	15.9
		7L→ V, T, A
		12F, 24L, 54T, and 81F are kept as wild-type
2	20.1	5I→ V, T	20.0
		7L→ A, V
		12F, 24L, 54T, and 81F are kept as wild-type
3	30.1	7L→ A, V, T	29.8
		12F→ L, H, I
		81F→ L, I
		15D, 54T, and 56A are kept as wild-type
4	34.1	8T, 25V, 27F, and 66T are kept as wild-type	34.1
5	35.8	81F→ L, I	35.7
		12F, 16V, 26D, 27F, 57K, and 66T are kept as wild-type

This first study demonstrated that OptGraft is capable, with relatively modest computational costs (e.g., total execution time for identification of top 30 designs is 118.33 s using a 3.00-GHz Xeon CPU/8GB RAM) to exhaustively generate a ranked list of promising locations for grafting the candidate binding site that share the same features and in many cases involve substantially better geometry scores than the ones developed and tested by Hellinga et al.^14,20 Motivated by these results, we next deployed OptGraft to drive the redesign of a new calcium-binding pocket into a protein with known structure.

De novo design of a calcium-binding pocket

The objective here is to computationally design a new calcium-binding pocket into the first domain of non-calcium-binding rat cell adhesion protein CD2 (PDB: 1hng). The computational predictions are tested experimentally to assess the efficacy of OptGraft. The crystal structure of the extracellular region of this protein reveals that it consists of two domains connected by an interdomain flexible linker.³¹ The D1 domain is a typical immunoglobulin β-sheet protein that consists of 99 amino acids. This domain has been extensively used as a platform for different protein design endeavors, and it has been shown that it can accommodate different configurations of calcium-binding pockets.^32–35 Ye et al. employed glycine linkers to fuse calcium-binding loop III from calmodulin at three different locations in the first domain of CD2 protein.³⁴ The results indicated that the redesigned protein gained calcium-binding centers while at the same time the overall conformation of the host protein was minimally disturbed. Using the Dezymer algorithm, this domain has also been subjected to de novo design of calcium-binding pockets.^32,33,35

A calcium-binding pocket is usually located within a loop of 10–15 contiguous residues, with calcium coordinated by oxygen donors from the side-chain carboxylate and hydroxyl groups as well as peptide carbonyl oxygen atoms and water molecules.³⁶ In non-EF-hand-type calcium-binding proteins, which include proteins stabilized by calcium ions, the metal center is usually located on flexible Ω-shape surface loops between protein β-strands. On the other hand, binding pockets of EF-hand calcium-binding proteins have a recognizable structural signature which consists of two helices that flank a highly conserved loop. Reversible binding of calcium to EF-hand proteins enables proteins of this group to participate in biological functions such as calcium transduction and signal modulation.^37,38

In this study, we computationally transfer one of the non-EF-hand calcium-binding pockets found in thermitase protein (PDB: 1thm). This protein contains three calcium-binding sites, and all three contribute to the protein's thermal stability.^39,40 The second calcium site was chosen as the subject for computational grafting because of its lowest structural complexity. This pocket is located near one periphery of the central β-sheet in the loop composed of residues 57 to 67. Five oxygen atoms from the side chains of residues Asp57(OD2), Asp62(OD1 and OD2), Thr64(O), and Gln66(OE1) participate in this calcium-binding site^36,39,40 (see Fig. 3). The geometric description of the pocket defined as carbon–carbon and calcium-contacting atom distances of the residues in the binding pocket are listed in Table IV. These distances encode the target geometry required for calcium-binding for this non-EF-hand site and are employed as input for OptGraft.

Figure 3.

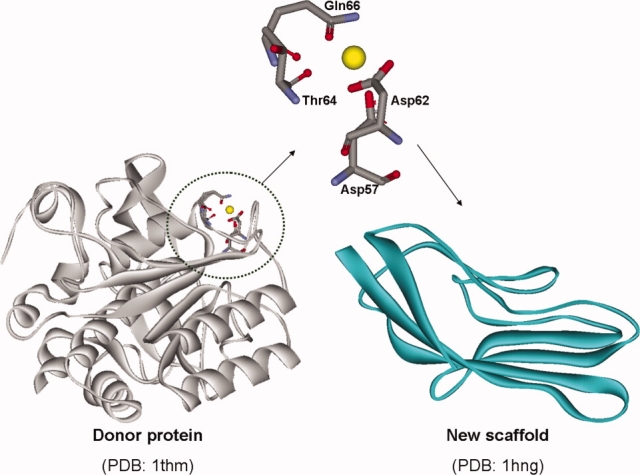
The natural calcium-binding pocket in thermitase (left). Different oxygen atoms of the residues D57, D62, T64, and Q66 form the calcium-binding center. On the right, the structure of the first domain of CD2 protein that was used as a new scaffold is shown. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Table IV.

Geometric Description of the Calcium Site Residues in Thermitase

Residues		Distance (Å)
Distance between Cα atoms
57D	62D	5.24
57D	64T	6.04
57D	66Q	7.94
62D	64T	5.64
62D	66Q	9.98
64T	66Q	5.61
Distance between calcium contacting atoms
57D(OD2)	62D(OD)a	3.55
57D(OD2)	64T(O)	3.40
57D(OD2)	66Q(OE1)	3.39
62D(OD)	64T(O)	3.70
62D(OD)	66Q(OE1)	4.66
64T(O)	66Q(OE1)	2.62

Letters in parentheses represent atoms.

OD represents the average coordination of OD1 and OD2 atoms in Asp62.

Starting with step 1 of OptGraft, the most suitable locations to incorporate the new calcium-binding pocket are identified (Table V). Similar to the pervious study, OptGraft generated many geometrically plausible solutions, which are ranked according to their geometry scores. The geometry scores are significantly influenced by small conformational perturbations in the overall geometry of the predicted pockets. For example, the best predicted solution lies on two anti-parallel β-strands between residues 78 and 91 and has a score of 18.7. However, different arrangements of calcium-binding sites occupying the same subset of positions (i.e., 78, 80, 89, and 91) slightly poorer geometry scores were found with (solutions 9 and 18) (see Fig. 4). Interestingly, the location of these three designs shares four positions with the CD2.Ca1 redesigned protein constructed using Dezymer,³³ where a different set of mutations was introduced in a cluster of five amino acid positions (i.e., 21, 78, 80, 89, and 91) to construct a single calcium-binding center on the same protein scaffold.

Table V.

OptGraft-predicted Mutations (Step 1) Required for Constructing the Calcium Binding Site into the First Domain of CD2

	Geometry score		Mutations			Distancea (Å)
1	18.7	78V→T	80V→D	89L→D	91K→Q	4.00
2	27.3	54A→D	65I→D	67N→T	69T→Q	3.32
3	27.7	8G→D	9A→T	68L→Q	97I→D	2.80
4	28.3	27I→D	29E→D	81Y→T	88I→Q	2.60
5	30.2	54A→D	66K→D	67N→T	69T→Q	2.75
6	30.4	6V→D	76Y→Q	93L→T	95L→D	2.90
7	30.5	54A→D	65I→D	67N→T	68T→Q	4.06
8	31.5	15N→D	16L→D	58L→Q	63L→T	2.03
9	31.8	78V→T	80V→Q	89L→D	91K→D	4.45
10	32.1	8G→D	9A→T	12H→Q	97I→D	2.67
11	32.2	6V→Q	76Y→D	93L→D	94D→T	3.04
12	32.8	28D→T	29E→D	44R→Q	81Y→D	2.55
13	33.3	16L→Q	58L→D	62D→D	63L→T	0.77
14	33.5	33E→T	39V→Q	76Y→D	77N→D	0.85
15	33.8	6V→D	16L→D	76Y→Q	93L→T	3.97
16	33.9	6V→D	76T→Q	94D→T	95L→D	2.85
17	34.2	27I→D	28D→D	81Y→T	88I→Q	2.84
18	34.3	78V→D	80V→Q	89L→T	91K→D	4.25
19	34.8	50L→D	51K→D	52S→T	54A→Q	3.22
20	34.8	32W→D	33E→T	39V→D	77N→Q	2.04
21	35.4	4G→Q	78V→D	91K→D	92A→T	1.99
22	35.7	32W→T	39V→Q	76Y→D	77N→D	1.79
23	36.0	8G→D	68L→T	72D→Q	97I→D	4.79
24	36.2	9A→D	12H→T	14I→Q	68L→D	3.93
25	36.3	8G→D	12H→T	14I→D	68L→Q	3.61
26	36.7	29E→D	31R→Q	79T→T	81Y→D	4.30
27	36.8	32W→Q	38L→D	40A→T	49F→D	2.37
28	37.43	32W→D	38L→D	40A→T	49F→Q	2.10
29	37.51	16L→D	58L→Q	62D→D	63L→T	2.95
30	37.55	9A→T	12H→D	68L→D	98L→Q	2.46

^aDistance between the calcium and the nearest Cα atom in the protein backbone. The vdw radii for calcium and carbon are 1.95 and 1.55 Å, respectively.

Figure 4.

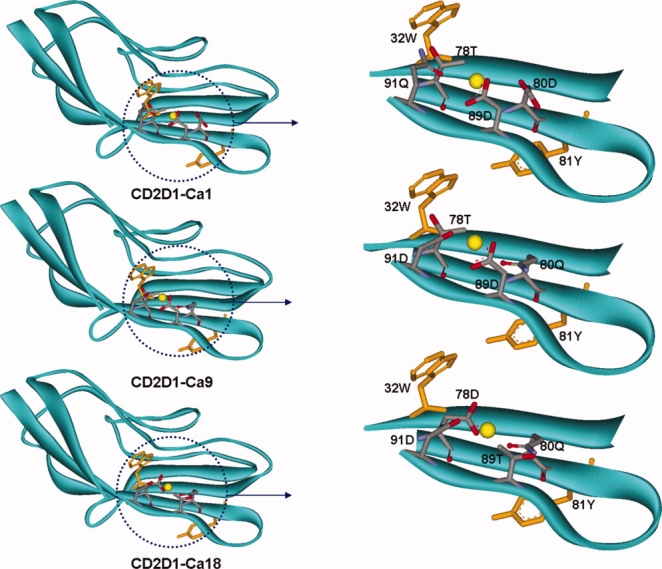
The modeled structures of selected redesigns of CD2D1 variants. Different arrangements of calcium-binding pockets are constructed by permutations of amino acids Asp, Asp, Gln and Thr among residue positions 78, 80, 89, and 91. The calcium atom is shown in yellow. The adjacent Trp and Tyr residues are also depicted.

The next step involved the elimination of predicted binding site placements that are inaccessible by the calcium ion. This was achieved by computationally constructing the protein structure models of the top 30 binding site placement candidates and subsequently introducing the calcium atom in the designed metal centers. We found that the shortest distance between the calcium atom and the nearest Cα atom is less than the sum of the vdw radii of carbon and calcium atoms (equal to 3.5 Å) for 21 out of 30 redesigns. The remaining nine solutions were then scrutinized further under step 2.

All residue positions that are located within 5 Å distance from the ligand, other than the four residues participating in the binding site, were considered for redesign. Interestingly, for solutions 1, 9, 15, 18, 24, 25, and 26, no additional mutations in the design positions are required. This suggests that for these solutions, new calcium-binding sites can be constructed with minimal disturbance in the overall protein fold. On the other hand, for solutions 7 and 23, while many design positions are kept as wild-type, smaller amino acids are commonly preferred for the rest of the positions (see Table VI). Having a smaller amino acid at position Phe55 and Asp72 in design 7 and positions Thr69 and Leu95 in design 23 reduces the magnitude of steric hindrances caused by introducing the binding site residues. These additional mutations lowered the geometry scores for solutions 7 and 23 by 5.2% and 3.1%, respectively.

Table VI.

OptGraft-Predicted Mutations (Step 2) in Neighboring Residues (Within 5 Å Distance from the Calcium Atom) for Nine Redesigned CD2D1 Variants

Designs	Original geometry score	Mutations in neighboring residues	New geometry score
1	18.7	18I, 21F, 30V, 79T, and 90N are kept as wild-type	18.7
7	30.5	55F→ M. L	29.9
		72D→ T, S, A
		66K and 68L are kept as wild-type
9	31.8	18I, 21F, 30V, 79T, and 90N are kept as wild-type	31.8
15	33.7	32W, 94D, and 95L are kept as wild-type	33.7
18	34.3	18I, 21F, 30V, 79T, and 90N are kept as wild-type	34.3
23	36.0	69T→ S, A	34.9
		95L→ V, N, T
		14I, 65I, 73S, and 76Y are kept as wild-type
24	36.2	8G, 10L, 11G, 13G, and 97I are kept as wild-type	36.2
25	36.3	9A, 13G, 65I, 95I, and 97I are kept as wild-type	36.3
26	36.7	30V, 41E, and 80V are kept as wild-type	36.7

Out of the retained nine solutions, we selected the one with lowest geometry score (i.e., solution 1) and solutions 9 and 18 that correspond to different binding site placement orientation in the same location of the protein scaffold (i.e., residues 78, 80, 89, and 91, Fig. 4) to construct and subsequently experimentally test. The three mutant proteins are named CD2D1-Ca1, CD2D1-Ca9, and CD2D1-Ca18. These selections were constructed to explore the effect of different arrangements of the grafted metal-binding center on calcium binding.

Experimental testing

Lanthanides are commonly used to probe calcium-binding sites because of their similar ionic radii and metal coordination chemistry.^41–43 Direct binding of lanthanides can be monitored via FRET interactions between the metal and aromatic residues. Terbium fluorescence has been shown to serve as a suitable surrogate calcium-binding site probe in CD2 mutants Ca.CD2,³⁵ CD2.Ca1,³³ and DEEEE³² designed for calcium binding. The protein scaffold used in this study (i.e., the first domain of CD2 protein) contains Trp32 and Tyr81 residues that are located in the proximity of the grafted binding pockets, and their fluorescence emissions can excite the bound terbium. The distances between the metal-binding sites in our designed versions of CD2 and the native Trp and Tyr amino acids in the protein scaffold are listed inTable VII. Occupancy of the designed binding pockets by terbium can, therefore, be detected by monitoring the resulting fluorescent emission spectrum.

Tabel VII.

The Distances Between Calcium and Native Trp and Tyr Residues in the Protein Scaffold for Different Designs

	Distance (Å)
	Trp7	Trp32	Tyr76	Tyr81
CD2D1-Ca1	23.48	6.88	15.41	9.21
CD2D1-Ca9	22.97	6.61	15.14	9.76
CD2D1-Ca18	23.44	7.17	15.74	9.83

Figure S1 (in supporting information) depicts the fluorescence emission spectra for terbium in the presence of increasing concentrations of wild-type or mutant CD2D1 proteins. Figure S2 shows the increase in terbium fluorescence peak area as a function of protein concentration. Although the fluorescence change on the addition of wild-type CD2D1 is relatively low, all three mutants cause significant increases in terbium fluorescence, with emission peaks at 544 nm. In general, the fluorescence responses are linear with protein concentration. Differences in peak intensities for the different mutants may reflect differences in binding site proximity to excited aromatic residues (Table VII).

Figure 5 depicts terbium binding curves, presented as the fractional change in fluorescence as a function of different terbium concentrations in equilibrium with the CD2D1 mutants. These data were fitted to Eq. (2), and the fitted lines are shown with the data in Figure 5. R² values for the fitted equations are given in parentheses next to each protein. The corresponding terbium K_d values were calculated and listed in Table VIII. Notably, binding pockets with better geometric characteristics (i.e., lower geometry scores) have lower terbium dissociation constants.

Figure 5.

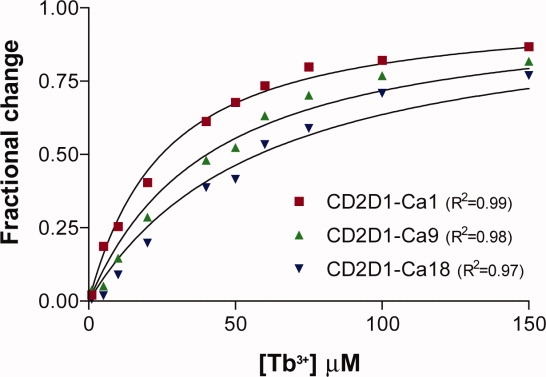
Fractional change in protein–terbium fluorescence with increasing concentrations of terbium in the presence of 4 μM of CD2D1 mutants. Protein–terbium complexes were excited at 282 nm. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Table VIII.

Experimentally Determined Metal Dissociation Constants for the Designed CD2D1 Mutants

	Geometry	Dissociation constants (μM)
	score	Tb(III)	Ca(II)	Mg(II)
CD2D1-Ca1	18.7	22 ± 1	59 ± 2	3362 ± 194
CD2D1-Ca9	31.8	38 ± 2	124 ± 6	5979 ± 308
CD2D1-Ca18	34.3	55 ± 4	220 ± 9	10040 ± 628

Binding competition between terbium and calcium or magnesium was next monitored to obtain relative dissociation constants for calcium and magnesium. The ability of these metals to displace bound terbium on addition to saturated and equilibrated protein–terbium complexes is quantified by the decrease in the terbium fluorescent emission. The fractional drop in fluorescence as a function of calcium or magnesium concentration is shown in Figure 6. The dissociation constants for the competing metal ions (listed in Table VIII) were determined by fitting the competitive binding data to Eq. (3) (the fitted lines are shown in Fig. 6). The calculated K_d values for the competing metal ions vary over almost two orders of magnitude, demonstrating the presence of highly selective sites for calcium over magnesium.

Figure 6.

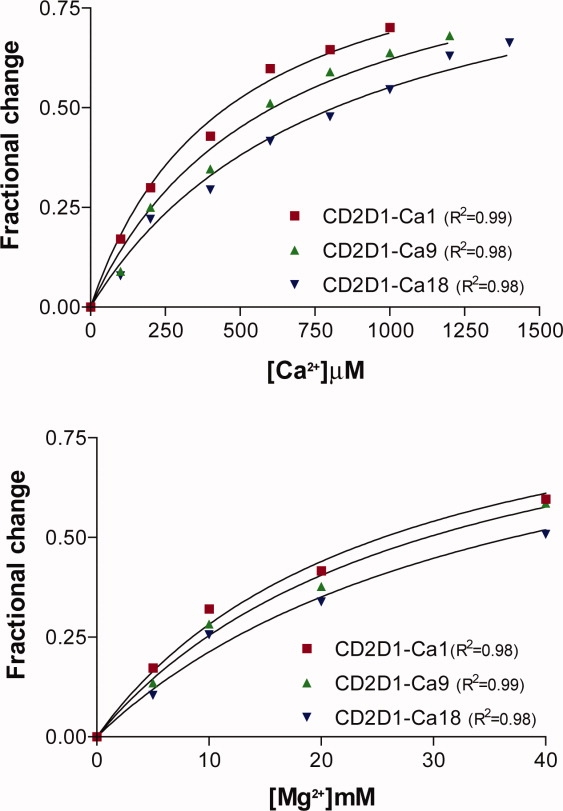
Fractional changes in protein–terbium fluorescence in the presence of increasing concentrations of competing metal ions (i.e., calcium and magnesium). ([Tb³⁺] = 150 μM, [Protein] = 4 μM). [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Summary and Discussion

In this article, we introduced OptGraft, a systematic computational framework for grafting a new binding pocket into a protein with known structure. OptGraft uses integer optimization to exhaustively explore every possible binding pocket placement combination on the protein scaffold and generates a ranked list of the designs that most faithfully match the native binding pocket geometry and orientation. The impact of the new grafted site on the protein structure is systematically assessed and potential distortions are ameliorated by allowing for mutations in neighboring residues. OptGraft was used to redesign a calcium-binding center in the first domain of CD2, one of the rat cell adhesion proteins. All three redesigns predicted by OptGraft selectively bound terbium or calcium over magnesium. Notably, the measured affinities exhibited an increasing trend with improving geometry scores (see Table VIII).

The calculated dissociation constants show that the affinities of the redesigned proteins for terbium are at least two-fold higher than those for calcium. This has been reported in other studies of calcium-binding pockets and is attributed to the added charge on terbium.^33,44 The calcium dissociation constant for the Dezymer-redesigned protein CD2.Ca1 was reported to be 40 ± 10 μM,³³ which is similar to the calcium dissociation constant of 59 ± 2 μM for the best-redesigned OptGraft protein. Despite some position similarities between our designs and CD2.Ca1, the structural characteristics of these designs are distinctively different. The Dezymer-designed calcium-binding site (i.e CD2.Ca1) involves five mutations composed of four negatively charged amino acids. This site is constructed on three different sequence regions of the protein scaffold (F strand, G strand, and flexible BC loop). The creation of this calcium-binding pocket requires mutating the wild-type residues Phe21, Val78, Val80, Ile89, and Lys91 to Glu, Asn, Glu, Asp, and Asp, respectively. In contrast, the three calcium-binding pockets designed using OptGraft are composed of four new amino acids with a total of two negatively charged amino acids located on two sequence regions of the protein scaffold (F strand and G strand). As a positive control, we measured the terbium dissociation constant of Dezymer-redesigned protein Ca.CD2 (PDB: 1t6w).³⁵ Although the K_d for terbium for this mutant was reported to be 6.6 ± 1.6 μM,³⁵ in our hands the experimentally determined K_d was 20 ± 1 μM. Variability in experimental procedures makes accurate quantitative comparisons between proteins difficult, but it is clear that all three OptGraft solutions tested yielded functional grafted calcium-binding pockets comparable with others reported.

The current implementation of OptGraft can be used to introduce only binding (not catalytic) pockets onto existing protein scaffolds as all the geometry optimization/energy minimization steps are performed only at the ground state. In principle, the OptGraft framework can be extended to redesign proteins not just for affinity but also for a desired catalytic function by taking into account the structure and energetic barriers of the transition state. Given an accurate model of the enzyme transition state as well as thorough knowledge of the mechanism and chemistry of the chosen reaction, OptGraft could be modified to perform geometry/energy optimization steps at both ground and transition states. Even though there exists a few computationally-driven de novo enzyme redesign success stories,^11,12 this remains a formidable and largely open challenge.

Methods

OptGraft computational procedure

The first step in OptGraft involves the identification of the most promising locations to graft the new binding pocket into the protein fold. This challenge gives rise to a high dimensional search problem, which we tackle using combinatorial optimization. The objective of this step is to retain the geometry and orientation of the residues in the binding site by minimizing the sum of the squared deviations between carbon–carbon and ligand contacting atom distances of the residues in the binding pocket before and after placement in the protein scaffold (see Fig. 1). By penalizing departures in the distances between atoms forming the binding site, the overall shape and orientation of the binding site is preserved upon grafting in the new location. The combinatorial optimization formulation for the geometry matching problem requires the definition of a number of sets, variables, and parameters needed to describe and evaluate various design choices.

We first define two sets that label amino acid residues in the binding site and protein backbone, respectively.

Set k enumerates all residues composing the binding site, and set i denotes all candidate locations for placing any of the k residues in the protein scaffold. Next, a set of parameters is defined to provide a geometric description of the residues in the binding pocket and target protein scaffold using pair-wise atom distances.

Parameters 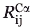and 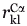store the Cα-Cα carbon distances between backbone locations i, j in the protein and locations k, l in the binding site, respectively. The next two parameters 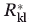, 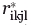quantify the distances between the atoms contacting the ligand in the original binding site and protein respectively (see also Fig. 1). This collection of distances can be augmented with various angles or any other metric in response to the specifics of the design challenge. By imposing a sufficiently large number of pair-wise distances (and bond angles), the preferred geometry of the binding site and the one on grafting onto the new protein scaffold is fully specified. Binary variable set Y_ik encodes the binding site placement decisions made by solving the optimization formulation. They assume value of one only if residue k of the binding site is placed at residue location i in the protein scaffold.

Binary variable

All residues k forming the binding site must be placed somewhere in the new scaffold implying the following equality constraint:

In addition, every position i in the protein scaffold can receive up to one binding site residue k which is encoded by using the following set of inequalities:

The objective function whose minimization drives the placement of the binding site entails the minimization of differences between the geometry of the residues in the protein scaffold and those in the binding pocket. This minimization step recapitulates the arrangement of the amino acids in the target protein scaffold and ensures that the footprint of the constellation of the residues in the grafted binding site remains the same as that in the donor protein. The objective function summation spans over all possible combinations of placing binding site residues k → i and l → j and cumulatively sums the corresponding Cα-Cα and ligand contacting atom distance differences. All terms are multiplied by the product of binary variables Y_ik.Y_jl that is equal to one only if atom k is placed at location i and atom l is placed in location j. This product acts as a “filter” that only allows the summation of the relevant squared distance differences implied by the choice of Y_ik.

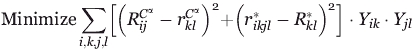(1)

The presence of the nonlinear products precludes the use of efficient mixed-integer linear programming solvers such as CPLEX⁴⁵ to solve for the binding site placement choices encoded using variable Y_ik that globally minimize the objective function. Therefore, the nonlinear products are recast into an equivalent linear form, as follows, at the expense of introducing a set of continuous variables W_ikjl which are equal to one only if both variables Y_ik and Y_jl are equal to one:

Continuous variable

The linearly recast objective function along with the above described constraints give rise to the OptGraft Mixed Integer Linear Programming (MILP) optimization formulation which is solved by accessing solver CPLEX through the GAMS programming environment.

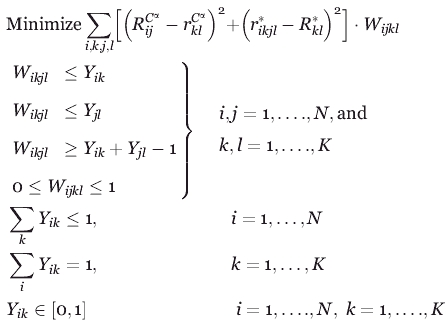The versatility of the adopted MILP modeling description enables the incorporation of additional geometrical characteristics such as angles and different distances. By using integer cuts⁴⁶ and resolving the problem, all promising locations within a prespecified objective function cut-off can be exhaustively generated. Specifically, a previously found binding site placement encoded by Y can be excluded from consideration and a new one can be identified by resolving the problem for a prespecified number of iterations on the addition of the following integer cut:

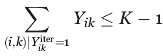The MILP optimization formulation identifies the optimal placement of the appropriate side chains in the backbone of the target protein scaffold to mimic the natural geometry of the binding pocket. However, the designed pocket may not be accessible for the ligand because of steric hindrances caused with the protein backbone or other residues not part of the binding pocket. Therefore, on the generation of the top N (where N is typically equal to 30) binding site placements by the MILP formulation, we systematically filter out the ones that introduce severe steric overlaps between the ligand and protein backbone. This is achieved by first computationally generating the 3D structure of the top N predicted designs and placing the ligand in the designed pockets. Subsequently, the distance between the ligand and the nearest Cα atom of the residues in the protein backbone is measured. Binding site placements leading to ligand-Cα carbon distances less than the sum of their corresponding vdw radii are rejected.

The MILP formulation denoted as step 1 of the OptGraft procedure assumes that the protein structure will remain “rigid” on the addition of the new binding site. However, this structural perturbation may appreciably distort the protein structure and correspondingly the pocket geometry. Step 2 of OptGraft aims to remedy this by systematically testing through energy minimization whether for any of the identified binding site placements the structure is unfavorably perturbed. The geometric criterion of the sum of differences in pairwise distances is recalculated after the structure is relaxed through energy minimization upon the addition of the new residues forming the binding pocket. If the pocket geometry is adversely affected, we proceed with the search for mutations in the binding pocket vicinity that restore the correct geometry of the binding site. In essence, we identify what mutations, if any, are needed to ensure that the minimum energy conformation of the binding pocket coincides with the configuration desired for function. The modified version of protein redesign framework IPRO provides the backbone of the computational environment for the second phase of this study.⁴⁷ The systematic optimization procedure of IPRO iterates between sequence design and backbone optimization (see Fig. 7), and it involves five main steps as follows:

Figure 7.

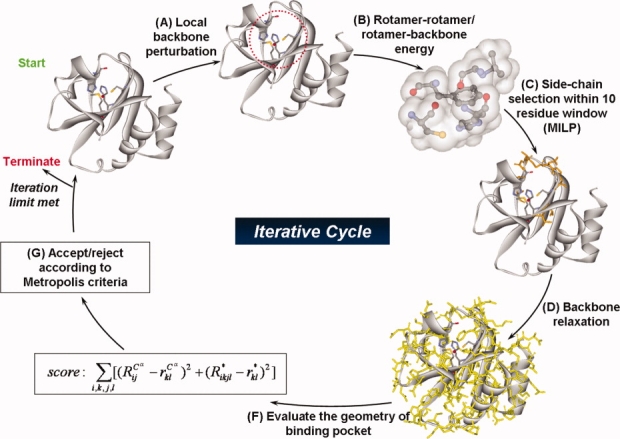
The modified version of protein redesign framework IPRO provides the backbone of the computational environment for the second phase of this study. During each iteration, a local backbone perturbation window (i.e., 1–5 residues) is randomly selected, and a perturbation of the backbone is imposed. An optimization step is carried out globally using an MILP model within a local perturbation window to identify new residues (i.e., mutations) and corresponding rotamers. This optimization step is followed by backbone relaxation. If the redesign and corresponding structural modifications lead to an improved energy of the system while maintaining and/or lowering the overall geometry score, then the perturbation is accepted; otherwise, a simulated annealing step is used to accept or reject the residue redesigns associated with each backbone perturbation step. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

1. Backbone perturbation: Different backbone conformations are sampled out by iteratively perturbing small regions of the backbone that are randomly chosen during each cycle along the length of the sequence.

2. Rotamer–rotamer/rotamer–backbone energy tabulations: Given the backbone conformations determined in step i and the rotamers and rotamer combinations permitted at each position, this step involves the calculation of the interaction energies of all rotamer–backbone and rotamer–rotamer combinations using CHARMM energy function.⁴⁸

3. Side-chain/sequence optimization: This step optimizes the amino acid choices and conformations (rotamers) for the given backbone structure over a 10–15 residue window that includes the perturbation positions and five residue positions flanking it on either side. Specifically, the design positions within the perturbation region are permitted to change amino acid type while the flanking residue positions (five residues on either side) can only change rotamers but not the residue type. This entails two discrete decisions: (1) identifying the choice of amino acid at any given position and (2) selecting the rotamer of the chosen amino acid that minimizes the selected surrogate objective function. IPRO draws on (MILP) optimization model formulations that use binary variables to mathematically represent these discrete decisions.

4. Backbone relaxation: The optimization step described earlier may lead to a number of new residues and/or rotamers for the protein structure. These new side-chains and/or conformations may no longer be optimally interacting with the previous backbone. To remedy this, a backbone relaxation step is included here allowing for dihedral angles to vary while the bond lengths and angles are constrained to their original values

5. Accepting/rejecting moves: Following the relaxation step, the total energy of the system and the geometrical objective function [relation (1)] are calculated. If the redesign and corresponding structural modifications lead to an improved energy of the system while maintaining and/or lowering the overall geometry score, then the perturbation is accepted. Otherwise, it is accepted/rejected based on the Metropolis criterion.⁴⁹ The procedure is repeated for 1000 iterations in the same fashion until an ensemble of redesigns are generated for different design positions.

On completion, IPRO provides a set of low energy solutions and associated mutations in the protein structure that can better accommodate the grafted binding site. All computational studies listed in this article were performed on a Linux PC cluster using a 3.00-GHz Xeon 3160 CPU/8GB RAM.

Experimental procedures

Protein mutagenesis, production, and purification

The redesigned proteins (i.e., CD2D1-Ca1, CD2D1-Ca9, and CD2D1-Ca18) were constructed using standard site-directed mutagenesis techniques⁵⁰ using the first domain of the wild-type CD2 gene cloned into vector pGEX-PKT, which includes an N-terminal fusion to a poly-Gly linker and glutathione S-transferase (GST) protein (plasmid pGEX-PKT was a gift from Dr. H. Godwin).⁵¹ The GST fusion protein were purified from bacterial lysates by affinity chromatography using immobilized glutathione agarose matrix, which can capture the GST moiety. Subsequently, the impurities are removed by washing, and the protein of interest is cleaved and released using a site-specific protease.

All sequences were verified by DNA sequencing. Proteins were expressed in E. coli BL21 as follows: protein expression was induced with 1.0 mM IPTG from BL21 cells harboring plasmids pPCC441-443 and grown in LB broth with ampicillin to mid-log phase (OD₆₀₀ ∼ 0.8). Cells were then pelleted by centrifugation at 3200 g for 20 min, resuspended in 5 mL of ice-cold lysis buffer, lysed in a French press, and centrifuged at 3200 g for 20 min. The recombinant GST fusion proteins in the supernatant were extracted and purified using glutathione-Sepharose 4B, and the cleavable GST tag was subsequently digested by PreScission protease (overnight at 4°C with 50 units of enzyme).⁵² Protein production and purity were qualitatively assessed by SDS-polyacrylamide gel electrophoresis, and Bradford assay was employed to determine the protein concentration. The proteins of interest were highly purified with concentrations in a range of 20–40 μM.

Terbium fluorescence

FRET interactions between protein aromatic residues and terbium were used to probe calcium binding, as described previously.^33,35,41,42 Terbium solutions were freshly prepared from a 15 mM stock of TbCl₃, the concentration of which was confirmed by EDTA microtitration using Xylenol Orange as indicator.⁵³ All solutions were stored at 4°C to avoid precipitation. The binding of terbium to the soluble proteins was measured according to the procedure of Yang W et al.³⁵ In a typical binding experiment, one solution contained 4.0 μM protein in 50 mM Tris-HCl at pH 7.0, 1 mM DTT, and 150 mM NaCl. Another solution contained the same concentration of protein with various amounts of TbCl₃. These two solutions were mixed and equilibrated for 45 min before measuring terbium fluorescence. The dissociation constants for calcium and magnesium were calculated in competition studies with terbium, which were performed in a manner similar as the terbium assays. A typical metal competition experiment was performed by preparing a solution of 4 μM protein and 150 μM TbCl₃ (equilibrated for 14 h at 4°C) and then adding a solution having the same concentrations of protein and terbium (equilibrated), also containing a known concentration of CaCl₂ or MgCl₂.

Fluorescence measurements were recorded on a Fluorolog 3-21 fluorescence spectrometer (Horiba Jobin Yvon, Edison NJ) using a quartz cell with a 1.0-cm path length at room temperature. Terbium was excited indirectly by energy transfer from a tryptophan residue, which was excited at 282 nm. Excitation and emission slit widths were 8 and 12 nm, respectively. A cutoff filter (320 nm) in the emission beam was used to eliminate secondary Raleigh light scattering. For each sample, the fluoresce assays were performed multiple times (at least twice) and averaged to monitor the emission spectra of terbium between 530 and 560 nm (maximum intensity at 544 nm), and the extent of terbium binding was measured by calculating the area under this emission peak. Background emission spectra of protein plus buffer were subtracted from the spectra of FRET samples. Following the generation of terbium-binding curves based on the increase in fluorescence area with increasing terbium concentration, the following equation was used to calculate the terbium dissociation constant ():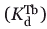

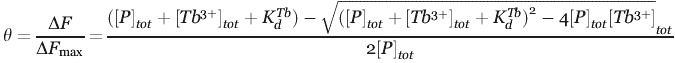(2)

where θ is the fractional change in fluorescence, ΔF denotes the observed fluorescence change of the bound terbium, and ΔF_max is the maximum observed change in the fluorescent intensity of the saturated protein-terbium complex. [P]_tot and [Tb]_tot are the concentrations of the total protein and terbium in the solution, respectively.

Dissociation constants for metals (calcium and magnesium) were determined in terbium-binding competition studies.^33,54,55 In these experiments, the competing metal ion displaces bound terbium from an equilibrated, saturated protein–terbium complex ([protein] = 4 μM and [Tb³⁺] = 150 μM), resulting in a decrease in the terbium FRET emission. This can be modeled by the following equation derived for an independent binding site model^54,55:

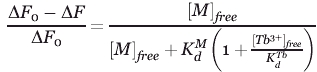(3)

where ΔF₀ and ΔF are the observed changes in the fluorescent emissions in the absence and presence of competing metal ions respectively. 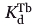denotes the terbium dissociation constant, which is calculated form relation (2), and 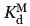is the dissociation constant of the competing metal. [M]_free and [Tb³⁺]_free are the free concentrations of the competing metals and terbium in the solution. In these competition experiments the concentration of protein (4 μM) is significantly lower than the concentration of either metal ([Tb³⁺] = 150 μM, [Ca²⁺] ≥ 100 μM and [Mg²⁺] ≥ 5 mM). Therefore, the free concentration of metals can be approximated as their total initial concentrations.^33,54,55