Synergistic drug combinations improve therapeutic selectivity

Abstract

Prevailing drug discovery approaches focus on compounds with molecular selectivity, inhibiting disease-relevant targets over others in vitro. However in vivo, many such agents are not therapeutically selective, either because of undesirable activity at effective doses or because the biological system responds to compensate. In theory, drug combinations should permit increased control of such complex biology, but there is a common concern that therapeutic synergy will generally be mirrored by synergistic side-effects. Here we provide evidence, from 94,110 multi-dose combination experiments representing diverse disease areas and large scale flux balance simulations of inhibited bacterial metabolism, that multi-target synergies are more specific than single agent activities to particular cellular contexts. Using an anti-inflammatory combination, we show how multi-target synergy can achieve therapeutic selectivity in animals through differential target expression. Synergistic combinations can increase the number of selective therapies using the current pharmacopeia, and offer opportunities for more precise control of biological systems.

Achieving therapeutic selectivity has been a major obstacle in drug discovery¹, leading to disappointing returns despite a surge in research and development spending². Drugs for infectious diseases often achieve selectivity by modulating pathogenic proteins with no human counterparts, but the treatment of cancer, metabolic, or inflammation disorders must rely on targets that are present in both healthy and diseased tissues. This requires precise target modulation, which can be thwarted by the compensatory mechanisms available to complex biological systems^3–5. Overcoming this compensation often requires high drug doses that can induce unwanted effects in other tissues^6,7. Thus, although the prevailing target-based drug design paradigm efficiently finds candidate drugs that are selective in a molecular sense, an alarming fraction have side effects in vivo that prevent their use at effective doses¹.

Synergistic combinations of two or more agents can overcome toxicity and other side effects associated with high doses of single drugs, by either countering biological compensation, sparing doses on each compound, or accessing context-specific multi-target mechanisms^8–10. Therapeutically promising multi-target effects can be identified using experimental^11–16 and theoretical^17–20 techniques. Because they actually make use of biological complexity, combinations are among the most promising avenues towards treating multi-factorial diseases¹.

One empirical method for finding potential multi-target therapies is to seek synergistic responses to combined perturbing agents, like drugs, using phenotypes that integrate across cellular functions²¹. However, synergies between phenotypic perturbers that exceed expectations from the single agents’ activities²² are relatively rare^14,18,23,24, and searching the vast space of combinations can only be fruitful if potential therapies do not also have synergistic side-effects²⁵. We are using our high-throughput combination platform to systematically test combinations of ~3,000 approved drug ingredients, emerging therapeutics, and research probes, against cellular phenotypes representing diverse disease areas¹¹. Here we analyze drug combinations from thirteen phenotypic screens relevant to six disease areas, and flux balance analysis simulations of chemically inhibited metabolism in E. coli bacteria, to show that synergies do indeed operate in more narrow biological contexts than single drugs. We also present examples of how therapeutic selectivity can arise from the multi-target cooperativity underlying most phenotypic synergy.

Results

We performed synergy and selectivity analyses for fourteen large sets of combination data, derived from simulations and experimental screens. Each combination was represented as dose matrices (Fig. 1) in “test” and “control” phenotypes, each with inhibitions Z = (1−T/V) calculated from drug-treated samples with a measured response T relative to vehicle-treated samples with a median level V. The usual drug activity and combination analyses, which focus on positive inhibition values, can be generalized to account for both inhibitors and activators of the measured phenotype. However, because the preponderant majority of our experimental drug activities are inhibitory, we will focus for now on to the simpler, unidirectional analyses.

Figure 1.

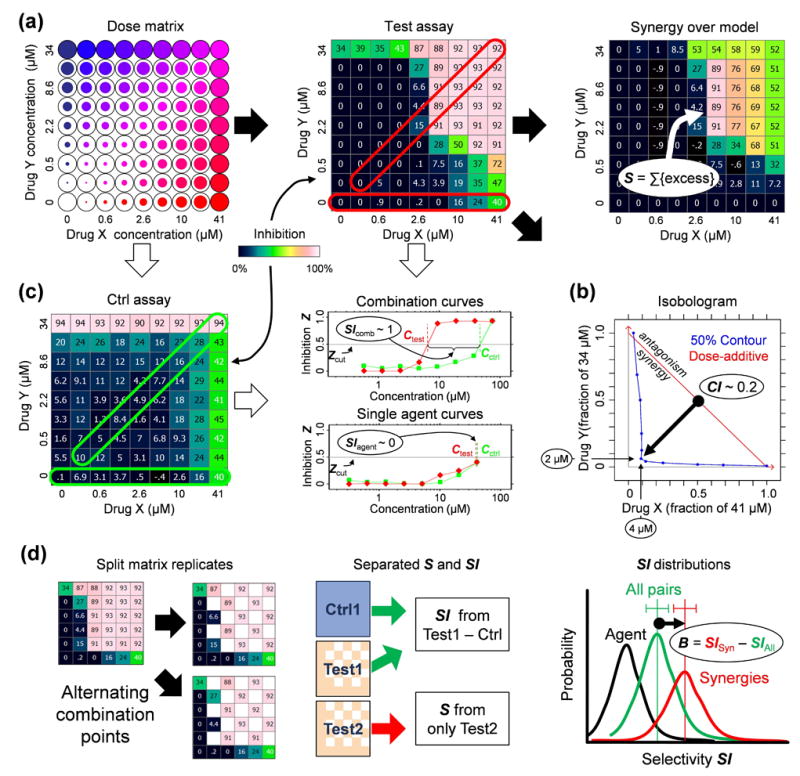
Measuring the selectivity bias. (a) Determining synergy using dose matrix data. A factorial dose matrix samples all mixtures of two serially-diluted single agents’ concentrations. Phenotypic measurements, like inhibition Z relative to vehicle-treated samples, can be visualized over the matrix using a color scale, and each data point be compared to expected values via a null model (e.g., the highest-single-agent²⁴ or dose-additive⁴⁷ model, see Methods) derived from the single agent data along the left and bottom edges of the matrix. The synergy score S = ln f_X ln f_Y Σ_doses max(0,Z_data) (Z_data − Z_model) sums up the excess inhibition over the HSA model with weights to account for drug dilution factors f_X,f_Y, and favor synergy at high inhibition levels. (b) Synergy can also be described using an isobologram, which compares the doses along an equal-effect contour (in blue) for a chosen inhibition level Z_cut (here 50%) to the contour (red) for dose-additivity. The combination index²⁹ CI = (C_X/IC_X) + (C_Y/IC_Y) measures the fractional shift (black arrow) between the most potent mixture’s doses C_X,C_Y and the single agents’ inhibitory concentrations IC_X,IC_Y. In this example, to reach 50% inhibition, only 4 μM of Drug A and 2 μM of Drug B were required in combination, compared to >41 μM and >34 μM for the single agents. (c) Selectivity is determined from the responses in two assays (“test” and “ctrl”). Single agent (horizontal frames) and fixed dose ratio combination curves (diagonal frames) are extracted from both dose matrices. For Z_cut, effective concentrations C_test,C_ctrl (top dose if agents don’t reach Z_cut) are determined in both assays (colors match frames in matrices) for all extracted curves, and the selectivity index SI = log₁₀(C_ctrl/C_test) measures potency shifts between assays, where SI = 1 implies a tenfold potency ratio favoring the test assay. The synergistic selectivity for a single combination can be described using ΔSI = SI_comb − SI_agent or ΔCI = CI_ctrl − CI_test based on the most selective diagonal curve and the most effective single agent in the test assay. (d) The selectivity bias was determined by comparing SI shifts across many combinations. To avoid spurious correlations due to noise, each test matrix was split into independent copies (see Methods), one to calculate SI and the other for S. The SI distributions across the screen were compared for all combinations (green distribution) and those with S > S_cut (green), and the selectivity bias B is measured as the difference between the mean SI values for the two distributions. For reference, we also show the SI distributions of the more effective single agent in black.

Measuring synergy and selectivity

For the test phenotype we determined synergy over a null interaction model determined by the single agent response curves. A number of such models are in use^22,26, the most common being: Loewe dose-additivity²⁷, which is the expected response if both agents inhibit the same molecular target via the same mechanism; Bliss independence²⁸, the multiplicative probability derived for statistically independent target eliminations; and Gaddum’s non-interaction²⁶, or “Highest Single Agent” (HSA), which is simply the higher of the two single agent effects at corresponding concentrations. Synergy was measured using a score S calculated from the volume between the measured combination and HSA response surfaces, and dose-shifting relative to Loewe additivity was measured using a combination index²⁹ CI (Fig. 1).

Selectivity for single agents or combinations was measured by comparing their potency in the test and control assays, via a standard selectivity index SI that represents the logarithmic shift in effective concentration between the test and control phenotypes at a chosen level of inhibition (Fig. 1). SI was measured separately for the single agents and for fixed-ratio combination curves extracted from the test and control dose matrices (Fig. 1). The synergistic selectivity of individual combinations can be described using a differential selectivity index ΔSI between the combination and single agent curves, or a differential synergy ΔCI between the test and control assays (Fig. 1).

The selectivity bias B was measured for each data set as the difference between the average SI of those combinations with S exceeding a cutoff S_cut, and that of the unfiltered combinations. Separate replicates were used when calculating S and SI to correct for statistical correlations due to noise (Methods), and the significance of B was estimated in two ways: (1) calculating the standard error of B, assuming normal SI statistics; and (2) generating histograms for both sets of SI values and determining the likelihood of their being drawn from the same distribution based on Poisson counting statistics within each bin³⁰ (Methods). Simulated combination screens with Gaussian random noise confirm that this approach does not lead to spurious B detections from noise alone (Suppl. Note 1), and simulations with defined synergy and selectivity signals demonstrate that this approach reliably detects introduced selectivity biases without excessive dependence on screen design parameters or the chosen analysis cutoffs (Suppl. Note 1).

Simulated bacterial metabolism

To demonstrate the selectivity bias in a comprehensive biologically-relevant data set, we simulated combined inhibition of bacterial growth via a flux-balance analysis (FBA) model of Escherichia coli metabolism³¹. The FBA model comprises ~950 enzymes or transporters (Methods) that are organized into ~44 distinct metabolic pathways or processes (Suppl. Note 1). Reaction fluxes throughout the network were optimized for growth under two conditions, minimal aerobic acetate media³² and minimal glucose fermentation³³, chosen to activate very different pathways in the network.

Drug effects were simulated by restricting the flux of target enzymes with differing factors to model drug concentrations, at each dose using minimization of metabolic adjustment¹⁸ to model growth responses (Suppl. Note 2). The effective concentrations for each target were used to define dosing ratios for 111,389 pairwise combinations, each of which was simulated as a fixed-ratio dosing series (Methods).

Using fermentation as the test and aerobic growth as the control, S and SI were measured for each combination and averages were calculated across all combinations in 136 mechanism groups derived from combinations of 16 mechanistic classes for FBA model targets. The resulting multi-target selectivity profiles highlight pathways that distinguish fermentation from aerobic metabolism (Fig. 2), and the bias (B ~ 0.6) for the top 1% of synergistic combinations corresponds to almost a fourfold increase in potency over the single agents.

Figure 2.

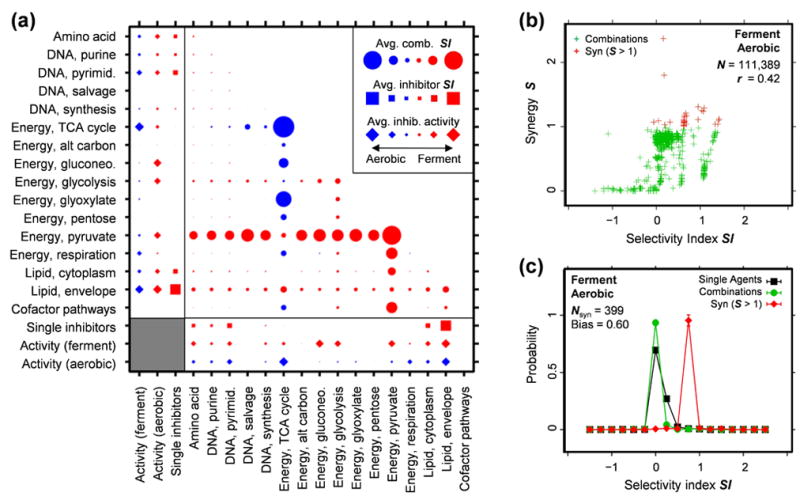
Simulations of selective synergies in Escherichia coli metabolism, averaged by functional category. (a) E. coli growth was simulated under aerobic (minimal acetate) and fermentation (minimal glucose) conditions. Inhibitors were applied by restricting the maximum flux rate through target enzymes, over a series of six concentrations chosen to sample each inhibitor’s transition to activity. The average inhibitor responses for each pathway are shown for each condition (diamonds), along with the average SI (squares) between both conditions. Combinations were simulated as a fixed-ratio series by summing the concentrations of each constituent inhibitor, and the average SI at Z_cut = max(Z_test)/2 is displayed for each pair of pathways (circles). The combinations selectively highlight the citric acid cycle for aerobic conditions and pyruvate metabolism under fermentation. (b) A plot of S vs. SI shows a correlation between synergy and selectivity with the most synergistic combinations (S > 1) having higher-than-average SI values. (c) Comparing the SI distributions of the most synergistic combinations (red) to all combinations (green) and the selectivity distribution of the more selective inhibitor in each combination (black) shows a strong bias towards more selectivity for the synergies. This selectivity bias B is quantified as the difference between the average SI values for synergistic and unfiltered combinations. The value found here, B_fwd = 0.596±0.005, with B_rev = 0.894±0.007 for the “reverse” aerobic – ferment comparison (Suppl. Note 2), represents a fourfold potency increase for the top ~1% of synergies.

Experimental combination screens

For experimental validation, we analyzed thirteen sets of combination data comprising 94,110 dose matrices, drawn from screens in six different disease areas (Fig. 3; Suppl. Note 2). The data sets vary considerably in design (number of drugs, aspect ratio of drug lists, sampling density for each combination, choice of assays), as well as in choice of agents (mechanistic coverage, activity in one or selectivity across multiple assays). Some of these resulted from screens aimed at testing for therapeutic selectivity, by comparing disease-related phenotypes to models of healthy cell viability, while the others investigated mechanistic selectivity, where differential response profiles across phenotypes can highlight particular mechanisms. There were up to four phenotypes tested in each screen, resulting in 2–6 possible assay pairings, only some of which could be considered aligned with a therapeutic selectivity objective.

Figure 3.

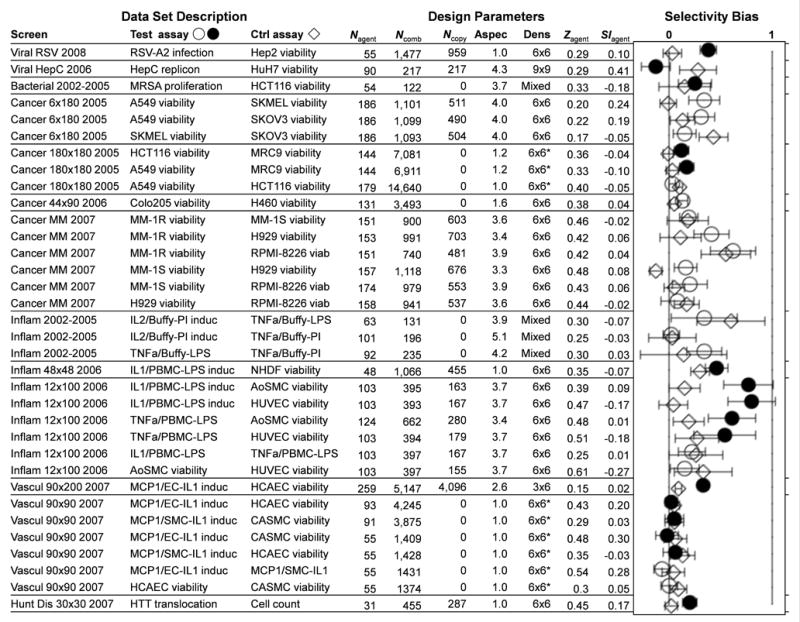
Selectivity bias for thirteen sets of combination data focused on six disease areas. The table shows the “test” and “control” assays corresponding to each comparison, the number of single agents N_agent or combinations N_comb tested, the number N_copy of combinations with independent replicates, and the aspect ratio “Aspec” of the agent lists that were combined. Also shown are the sampling “Dens” (dose matrix size, * when sparse), with the average activity Z_agent and selectivity index SI_agent across the single agents. For each screen, all pairs of assays were compared, in “forward” (circles, filled when aligned with a therapeutic objective) and “reverse” (diamonds) order relative to the assay designations listed. Each combination’s SI value was calculated at Z_cut = max(Z_test)/2, and the top 5% of synergies for each test assay were used to determine a selectivity bias. Error bars represent 95% confidence with a sequential multiple hypothesis adjustment⁴⁸ to account for all assay comparisons in each screen. Weighted by these errors, the consensus selectivity bias is 0.104±0.010 (0.214±0.021 for therapeutically aligned pairs). The synergistic combinations have statistically more positive selectivity, with some screens showing more than threefold potency shifts.

Representing therapeutic selectivity, our viral, bacterial, inflammation, and cardiovascular screens compared disease-relevant assays to human cell line proliferation as toxicity models (Suppl. Note 3). Most showed visible shifts towards positive SI for the synergistic combinations (Fig. 3), in some cases with substantial selectivity biases approaching a 2–3 fold increase in potency over the single agents. The strongest biases occurred with the “Inflam 12×100” and RSV screens, which compared single protein readouts to broad cell viability assays. The other assay pairs aligned with therapeutic objectives also produced significant B (p < 0.05) usually not matched in the reverse comparison. The main exceptions are the viral HepC screen, where extremely selective single agents and a high incidence of pro-viral effects in the replicon assay led to skewed selectivity distributions, and the “Vascul 90×90” screen, where the strong single agent selectivity left little room for additional selectivity gains.

A clear example of a therapeutically-aligned selective combination is the antibacterial synergy between ribavirin, a metabolism inhibitor, and disulfiram, a metabolic drug used for alcohol avoidance therapy. The combination has almost no effect on human cell viability (Fig. 4). Similarly, the antiviral synergy of cepharanthine, an anti-inflammatory drug with antiviral potential³⁴, and benzamil, a potent inhibitor of ion transport channels³⁵, shows no detectable synergy against host cell viability (Suppl. Note 4). Finally, the anti-inflammation synergy between prednisolone and nortriptyline against secretion of tumor necrosis alpha (TNF-α) from stimulated peripheral blood mononuclear cells (PBMC) shows no corresponding increase in toxic effects as measured by PBMC metabolic viability (Fig. 5). In all cases the synergy increases the likely safe treatment window for potential therapies.

Figure 4.

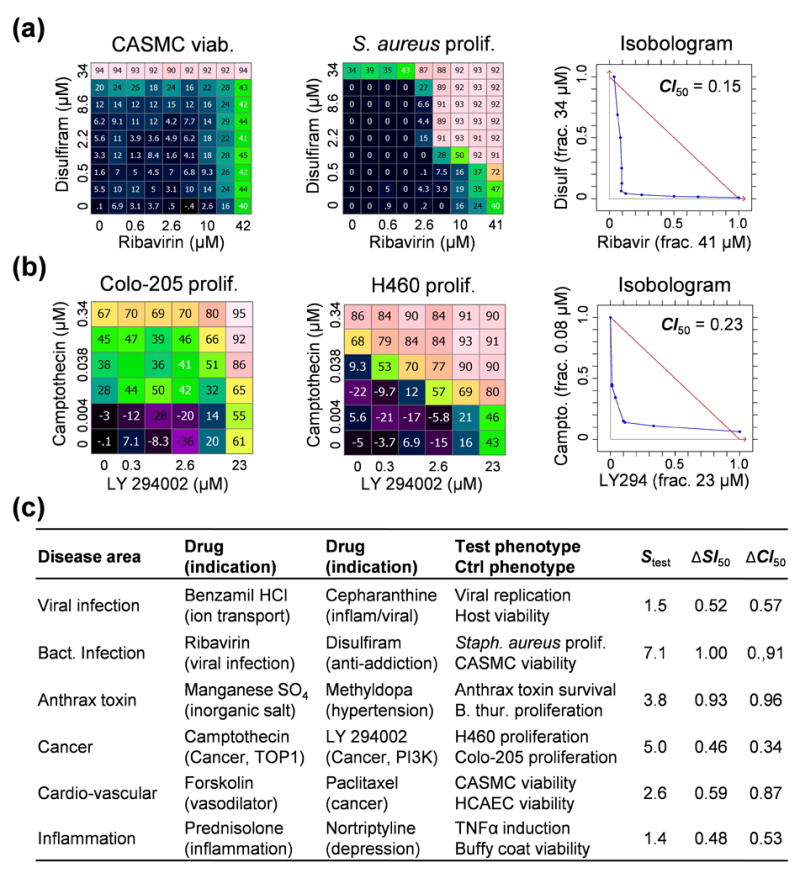
Examples of therapeutically and mechanistically selective synergies, showing the control (left) and test (center) matrices, along with the test isobologram (right). Selectivity is measured using ΔCI and ΔSI at 50% effect. (a) Ribavirin and disulfiram are each active on metabolic targets (inosine monophosphate dehydrogenase for ribavirin, and mitochondrial aldehyde dehydrogenase 2 for disulfiram) at high doses in both primary smooth muscle cell viability and Staphylococcus aureus proliferation assays, but the strong antibacterial synergy is completely absent in the human cell toxicity model. (b) In cancer cell lines, the synergy between camptothecin and LY 294002 (b) is stronger against lung-derived H460 than Colo-205 colon cells. In the screen from which this combination was drawn, we found evidence of synergy in H460 for 21/32 TOP + PI3K (targeting topoisomerase with phosphoinositide 3 kinase) combinations tested, 12 of which had similar levels of selectivity over Colo-205 (data not shown), suggesting that the synergy results from coordinated activity on each drug’s primary target. (c) For all of our example combinations, the single drugs have unrelated indications or modes of action, suggesting that multi-target mechanisms predominate. The remaining examples are detailed in Suppl. Note 4.

Figure 5.

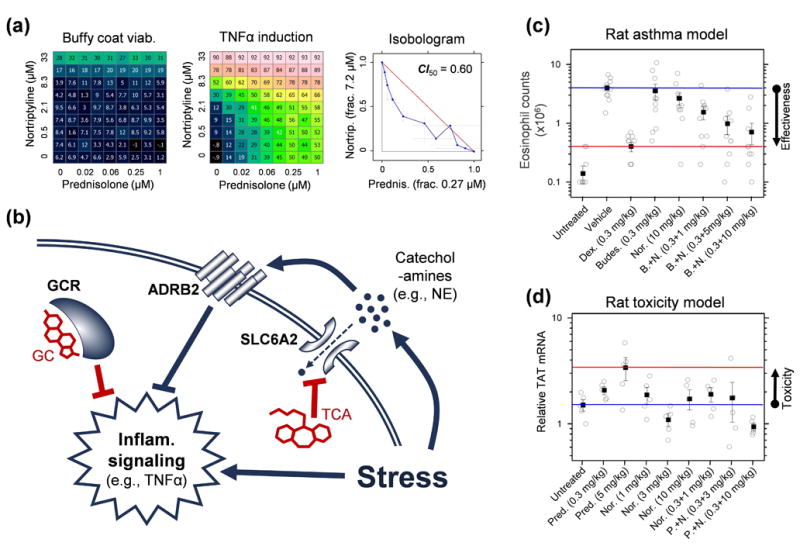
Selective synergy between glucocorticoids (GC) and tricyclic anti-depressants (TCA). (a) The synergy against TNFα secretion in PBMCs remains when related drugs are substituted (Suppl. Note 4), so the synergy operates via the primary drug targets. Moreover, 59 of 63 combinations we have tested in this assay on these targets at sufficient concentrations were also synergistic (S > 5 standard errors, data not shown). (b) Mechanistically, GCs activate the glucocorticoid receptor (GCR) which suppresses inflammatory signaling. In response to stress, lymphocytes secrete catecholamine hormones, such as norepinephrine (NE), which suppress inflammatory signaling via beta-adrenergic receptors (ADRB2)³⁹. TCAs block NE transporters (SLC6A2), which increases extracellular NE levels, with a synergistic anti-inflammatory effect when combined with GCs⁴⁰. Directly adding NE and modulating ADRB2 in combination with GC confirms the role of this pathway in the GC-TCA synergy (Suppl. Note 4). The in vivo therapeutic selectivity arises because while GCR, SLC6A2 and ADRB2 are co-expressed in lymphoid cells, ADRB2 is expressed 3–10 fold lower⁴¹ in tissues such as liver and pituitary that mediate major GC-associated adverse effects⁴², weakening the NE-mediated pathway and attenuating the GC-TCA synergy. In rats, the combination of nortriptyline with another GC that is widely used for asthma treatment, budesonide, was tested in an asthma model via ovalbumin challenge (c). The combination at individually sub-therapeutic doses was able to restore lung infiltration by eosinophils to levels seen with high-dose dexamethasone or unchallenged rats (ANOVA p < 0.05 over single agents). Anti-inflammatory synergy with prednisolone was also confirmed in a rat pain model (Suppl. Note 4). By contrast, rat liver toxicity (d), modeled by a corticosteroid side effect marker tyrosine aminotransferase (TAT), showed elevated expression only for high dose prednisolone (ANOVA p < 0.05), while the effects at doses showing anti-inflammatory synergy were consistent with or lower than negative controls. In vivo data are detailed in Tab. S8.

Considering mechanistic selectivity, the anti-cancer screens in Figure 3 were designed with that goal in mind (Suppl. Note 3), and comparisons between very similar assays in the other screens also provide mainly mechanistic information. While most of these assay pairs yield significantly positive shifts, their B tend to be weaker than those from therapeutically aligned assay pairs. The main exceptions are in the multiple myeloma screen, where substantial selectivity shifts occur between glucocorticoid-resistant MM-1R and the sensitive cell lines.

Individual mechanistically selective synergies (Fig. 4) provide insights into the biology relevant to the tested phenotypes. The strong synergy between LY 294002 and camptothecin in lung-derived H460 compared to colon-derived Colo-205 cells reveals an interaction between phosphoinositide 3 kinase and DNA topoisomerases that occurs only in some cancer contexts. Also, potential post-infection treatments for anthrax that work through host targets are suggested by the synergy between manganese sulfate and the hypertension drug methyldopa in a toxin survival assay that shows no antibacterial activity (Suppl. Note 4). Finally, from our cardiovascular screens, the anticancer microtubule inhibitor paclitaxel and the vasodilator forskolin synergistically inhibit smooth muscle cell proliferation while sparing toxicity on endothelial cells (Suppl. Note 4), pointing to possible uses for reducing the risk of thrombosis with drug-eluting stents³⁶. Information of this kind can be used to guide the design of cotherapeutic treatments or to prioritize indications for candidate therapies.

General findings

Across all of our experimental data sets, the selectivity distributions showed consistently positive bias for synergistic combinations (Fig. 3). The SI values for unfiltered combinations were similar to those of their single agents (Suppl. Note 3), both having a positive skew owing to the more effective compound being used in the SI calculation. When synergy cutoffs were applied, however, the SI distributions of the most synergistic 5% shifted substantially towards more selectivity, with typically 15–40% of the synergies having SI > 0.5 (threefold dose shift), compared to 6–10% for unfiltered combinations and single agents (Suppl. Note 3).

The experimental selectivity biases exceeded levels found for simulated combination screens with random noise high levels (Suppl. Note 1), and were well above levels found in “null” comparisons between replicates of the same assay (Suppl. Note 3), but compared well to those observed for simulated screens with introduced synergy and selectivity signals (Suppl. Note 1). Although the selectivity bias was strongly influenced by screen design parameters, such as the number of compounds used and the individual activity or selectivity of single agents in the screen, B depended only weakly on the chosen synergy cutoff or whether split matrices were used to separate the S from the SI measurements (Suppl. Note 3). Finally, selectivity biases were often asymmetric when the assay order was reversed (Fig. 3), especially for the therapeutically-aligned assay pairs which compared a single protein expression phenotype to a broad measure of cell viability.

Overall, after correcting for multiple assay comparisons in each screen, the consensus B was significantly positive (Fig. 3), and its magnitude increased substantially for assay pairs that were aligned with clear therapeutic objectives. All of this suggests that the selectivity bias arises not from stochastic effects but from biological context specificity, where synergistic combination effects require a narrower set of biological conditions than do single agent activities.

Discussion

There is growing enthusiasm for combination therapy^1,5,10, specifically because greater selectivity is anticipated^1,9. Nevertheless, there are concerns that synergistic therapies would usually be mirrored by synergistic toxicity²⁵, as would indeed happen if side-effect mechanisms are too closely related to those involved with drug efficacy. The arguments on both sides of this question have to date been heuristic, and this manuscript presents the first large-scale study to our knowledge that establishes the selectivity of combination approaches. Our experiments and simulations show a statistical bias towards greater selectivity for synergies, the strength and consistency of which cannot be attributed to stochastic noise or analysis parameter choices. This shows that synergies are more specific to particular cellular phenotypes than are single drugs, in agreement with the recent finding that synthetic lethal genetic interactions are less conserved between species than are single mutant lethalities³⁷.

This selectivity bias for synergistic combinations may be understood in terms of the complexity of biological systems, where cooperative activity operates only in some cellular contexts but not others. The rarity of self-crosses in our screens and the disparate drug mechanisms or indications underlying each of the example combinations point to the synergies being largely explained by multi-target interactions, as is the case for synergistic responses in theoretical studies^17,24. Because multi-target mechanisms require their targets to be available for coordinated action, one would expect synergies to occur in a narrower range of cellular phenotypes given differential expression than would the activities of single agents. Moreover, one would expect this specificity to narrow further as the combination order increases, until a limit is reached determined by the complexity of the biology relevant to a phenotype³⁸.

The anti-inflammatory synergy between prednisolone and nortriptyline provides an illustration of how multi-target activity can lead to therapeutic selectivity (Fig. 5). For the lymphocytes in our PBMC assays, the synergy results from coordinated activity on each drug’s primary target (Suppl. Note 4), prednisolone activating glucocorticoid receptors (GCR) and nortriptyline inhibiting a separate autocrine pathway via norepinephrine transporters (SLC6A2) and beta-adrenergic (ADRB2) receptors^39,40 (Fig. 5). Because the ADRB2 receptors are more highly expressed in lymphocytes⁴¹ than in the liver and pituitary cells⁴¹ that mediate major glucocorticoid toxicities⁴², we would expect the synergy with tricyclic antidepressants to increase the therapeutic window of a glucocorticoid over those toxicities (Suppl. Note 4). Indeed, the amplification of anti-inflammatory effect seen in rodents with this combination does not show a corresponding rise in glucocorticoid-associated toxicity in rats at similar doses (Fig. 5; Suppl. Note 4), as has also been seen with a related anti-inflammatory synergy, prednisolone with the cardiovascular agent dipyridamole^43,44. These combinations represent a multi-target approach towards the long-sought “dissociated steroid”, where the anti-inflammatory activity of glucocorticoids can be separated from chronic side effects⁴⁵.

The increased specificity of combinations over single agents has implications for drug discovery and bioengineering. In medical contexts, the selectivity bias reinforces the potential of chemical combinations for network polypharmacology^1,8 by reducing concerns that synergistic side-effects would make selective combinations too rare²⁵. For example, given performance typical for our screens (Fig. 3), a disease with ~100 useful chemical agents would be expected to have ~2–5 that are >3× selective between two assays, but the ~250 pairwise combinations representing the top 5% of synergies would be expected to yield 40–80 more treatments with similar or increased selectivity (Suppl. Note 3). For bioengineering, selective synergies provide opportunities for optimizing conditions in reactors producing fuels, synthetic materials or pharmaceutical products⁴⁶, for example by introducing combinations of chemical ingredients and comparing phenotypic measurements that track metabolic production of a desired chemical and toxic byproducts that limit a reactor’s performance. There is much to be gained by expanding the notion of a target from a single biomolecule to the right set of nodes in a complex biological network.

Methods

Chemical handling and quality control

The chemical library was archived in robotically-accessible vials, to which diluent (dimethyl sulfoxide or water) was added in preparation for addition to 384-well master plates by a Tecan Freedom liquid-dispensing robot. Liquid transfers to dilution and assay plates were handled using a Perkin-Elmer MiniTrak station adapted for the combination high throughput procedure. Each 384-well assay plate contained multiple dose matrix blocks, with serial dilutions at fixed ratios from the top concentration for each agent. Additional wells were reserved for transfer and untreated control wells. Compound mixtures were then added to the biological assay.

The contents of each plate were tracked in an automated laboratory information management system, using integrated barcode scanners in the liquid handling equipment, and stored in an Oracle database. Plates lacking transfers or with insufficient dynamic range (usually SNR < 5 between untreated controls and a cell-free background) were rejected and repeated. The remaining plates were inspected using custom quality control software. Individual wells that fell outside the expected range for normal assay readouts, or which were discontinuous with their neighbors, were marked for exclusion. Finally, the single agent wells in each combination block were visually inspected for consistency across the experiment, and combination blocks containing the most discrepant single agents were marked for exclusion.

Measuring synergy and selectivity

Dose matrices were assembled from replicate combination blocks on experimental plates. Some of the data showed systematic variations across the plate, most likely due to temperature or humidity gradients during incubation. Raw phenotype measurements T from each treated well were converted to inhibitions Z = (1−T/V) relative to the median V of 10–20 vehicle-treated wells arranged around the plate. Positive modulators of a measured endpoint would best be represented by alternative expressions for Z (eg, log(T/V) for growth or fitness), but as the vast majority of our chemical agents are inhibitors of our measured endpoints we have limited the analyses in the present work to inhibitions. Standard error estimates σ_Z for each median inhibition were also calculated, based on the quadrature sum of a minimum acceptable 3% error, the median absolute deviation (MAD) of the corrected vehicle data on each plate normalized to their median, and the MAD between replicate inhibition data between plates, using an empirical conversion from MAD to standard deviations⁴⁹.

Synergy is determined by comparing the combination’s response to those of the single agents^22,26. A key consideration for clinical combinations is whether a mixture is more potent than the drug-with-itself “Loewe additivity” level²⁷, the point at which there is some benefit over simply increasing component drug doses. Comparisons are made using an Isobologram and a Combination Index²⁹, for example CI₅₀ = (C_X/IC50_X) + (C_Y/IC50_Y), where (C_X/IC50_X) for a mixture is the ratio of the X compound’s concentration C_X in a 50% effective mixture to its 50% inhibitory concentration IC50_X when applied alone. If a single agent does not reach the chosen effect level, we set the effective concentration to the top tested dose, and all CI values become upper limits. The combination index is best suited for analyzing fixed dose-ratio combination curves. For our therapeutic screens with complete dose matrices, we often measure the synergy using a “Synergy Score” S = ln f_X ln f_Y Σ_doses max(0,Z_data) (Z_data−Z_Loewe), between measured effects Z_data and a Loewe additive surface Z_Loewe derived from the single agent curves⁴⁷. This synergy score is a positive-gated, effect-weighted volume over Loewe additivity, adjusted for variable dilution factors f_X,f_Y. Other combination reference models can be used to calculate S, and in this work we are referring all synergy scores to the “Highest Single Agent” Z_HSA = max(Z_X,Z_Y), the maximum single agent response at corresponding concentrations²⁴. Combinations with strong synergies above the reference model that also occur at high effect levels score well, and regions of negative synergy on a surface do not cancel out those with positive synergy. It is worth noting that S does not have a natural scale, so it is only useful for relative comparisons within a screen, rather than as an absolute measure of strong synergy.

Selectivity is calculated by comparing across dose matrices for different measured endpoints. The “selectivity index” SI compares the potency of an agent or combination at the same effect level for two assays (Fig. 1). Given a pair of response matrices for the “test” and “control” assays, we measure inhibitions Z_test and Z_ctrl, and define a fixed cutoff level Z_cut. We then find the effective concentrations C_cut at level Z_SI = 0.5*max(Z_test) for each of the single agents and for fixed-ratio curves of the combination, where the combined concentration in molar units is taken as the sum of the component concentrations, and define a selectivity index SI = log₁₀(C_ctrl/C_test). If a single agent does not reach the chosen effect level, we set the effective concentration to the top tested dose, and SI values become lower limits. Each fixed ratio curve is extracted from diagonals in the test matrix, using bilinear interpolation to determine the corresponding control responses. For each test-control pairing, SI is reported for the most selective diagonal with more than two dose samples covered by both matrices. We also report the differential selectivity ΔSI = SI_comb − SI_best between the combination and the more effective single agent, and a combination index difference ΔCI = CI_ctrl − CI_test.

Measuring selectivity bias and its significance

To measure the selectivity bias for synergistic combinations, we compared distributions of selectivity index SI between populations of combinations for each assay pair in a screen. The synergistic combinations were chosen to be those with a synergy score S in excess of a chosen cutoff S_cut (usually capturing the top 5% of the synergies). Their SI distribution was compared to that of the overall set of combinations via a selectivity bias B (Fig. 1).

Because the B can be subject to regression-to-the-mean effects, where stochastic noise generates meaningless selectivity for synergistic combinations, we calculated the synergy and selectivity using distinct replicate matrices (Fig. 1, more details in Suppl. Note 3). By doing this, stochastic noise in one copy will not affect the selectivity calculation in the other. While most of our screens had replicates, some screens collected only one. To ensure consistency, we analyzed all screens by separating each combination into distinct matrices using with alternate dosing points from the consensus data, and used the true replicates to confirm the accuracy of this approach.

For each pair of assays in a screen, we compared four SI distributions: (1) the synergies with S_cut > S_cut, all combinations without synergy filtering, and most selective single agent from each combination (Fig. 1). For each pairwise comparison of assays, we report B with its 95% range (2 σ_B), and a confidence P-value from Poisson statistics³⁰ representing the probability that chi-squared differences as large as those between the SI distributions for the synergistic and unfiltered combinations are indistinguishable.

When analyzing the significance of selectivity bias measurements across all the screens (Fig. 3), we accounted for the number of pairwise comparisons using a sequential Bonferroni correction⁴⁸ to adjust the error bars. Each screen’s B estimates were assigned an integer rank with increasing signal-to-noise ratio B/σ_B, and then each σ_B was increased by a factor corresponding to 95% confidence after adjusting for multiple tests equal to their rank. In doing this, the strongest bias values are given the largest correction to account for their being the best of all of the assay pairs, while the weakest B retains the 95% confidence error bars corresponding to its standard error from the SI distribution.

In-vitro cell-based assay protocols

Hepatitis C assays

Huh7 cells expressing a sub-genomic RNA replicon of Con1 (genotype 1b) sequence origin and expressing the reporter enzyme luciferase were obtained from ReBLikon, GmBH. Antiviral assays were performed by seeding 4,000 cells/well in a 384-well plate in a total volume of 30 μl/well and incubating at 37°C, 5% CO₂ overnight. Pre-diluted compounds were added at a 10× concentration to each well to achieve the desired final concentration. Assay plates were than incubated for 48 hours or 37°C, 5% CO₂. In order to equilibrate plates to room temperature, assay plates were removed from the incubator for 30 min to 1 hour prior to the addition of 25 μL/well of SteadyLite luciferase assay reagent from Perkin Elmer. Cells were incubated with SteadyLite reagent, for 10 minutes prior to collecting data with a luminometer (Perkin-Elmer Envision). Antiviral activity is quantified by the inhibition of luciferase activity. For the antiproliferation assay Huh7 parental cells which do not express HCV replicon RNA are treated similarly to the above replicon cells; briefly, seed cells on a 384-well plate at 4,000 cells/well, as described above. Compounds are added the following day and, after subsequent 48-hour incubation at 37°C, 5% CO₂, 15 μl/well of ATPlite (Perkin Elmer) is added after plates have been equilibrated at room temperature. The ATPlite assay provides a quantitative measure of the levels of ATP in the cell cultures in each well, where higher levels of ATP correlate with greater cellular viability.

Respiratory Syncytial Virus (RSV) assays

HEp-2 cells were obtained from Diagnostic Hybrids, Inc., and maintained in DMEM (Dulbecco’s Modified Eagle Medium) modified with 10% FBS (Fetal Bovine Serum), 1% P/S (Penicillin/Streptomycin), and 1% GlutaMAX-1. Antiviral assays were performed by seeding 3,000 cells/well in a 384-well plate in a total volume of 30ul (in DMEM modified with 2% FBS and 1% GlutaMAX-1) and incubating at 37°C, 5% CO₂ overnight. Pre-diluted compounds were added at a 10× concentration to each well to achieve the desired final concentration. RSV was added to each well (save 12 no virus added wells per plate) at 50 TCID₅₀. Assay plates were than incubated for 96 hours at 37°C, 5% CO₂. In order to equilibrate plates to room temperature, assay plates were removed from the incubator for 45 min prior to the addition of 25 μL/well of ATPlite assay reagent from Perkin Elmer. Cells were incubated with ATPlite reagent, for 10 minutes prior to collecting data with a luminometer (Perkin-Elmer Envision). Antiviral activity was quantified by comparing the host cell viability in the presence of virus and drug treatment to uninfected cells. For the antiproliferation assay, HEp-2 cells were treated the similarly to the above conditions, without the addition of virus. The antiproliferation assay provides a quantitative measure of the levels of ATP in the cell cultures in each well, where higher levels of ATP correlate with greater cellular viability.

Bacterial proliferation

Methicillin-resistant Staphylococcus aureus (ATC #33591) bacteria were cultured in flasks with Basic Mueller Hinton broth overnight in a 37°C shaker at 250 rpm. On the next day, the cultures were further diluted into Basic Mueller Hinton broth to have an absorbance equivalent to 50% of McFarland standard, corresponding to a density of ~10⁸ CFU/mL, and transferred with automated dispensers into 384-well assay plates (35 μl wells containing media and test compounds) to yield ~10⁶ CFU/ml. The plates were incubated in the presence of drugs and media at 37°C for 18 hours (~30 doublings). Upon completion, cell populations were measured at a single time point, with a turbidity (laser scattering) readout using a BMG Labtech Nephelometer. For the anthrax selectivity example, Bacillus Thuringiensis (ATCC# 10792) was grown as above, but activity was determined by the addition of basic Mueller Hinton media containing 10% Alamar Blue fluorescence dye. Following a 4 hour incubation at 37°C, bacterial populations measurements were made at a single time point using a Perkin-Elmer Victor II plate reader (excitation at 535/590 nm emission).

Anthrax toxicity

Raw 264.7 cells were plated on 384-well plates at a density of 15,000 cells/well and are incubated overnight at 37°C, with 5% CO_2. Next, 4.5 μl of diluted compound was added to each well followed by the addition of 10 μl of anthrax lethal toxin (500 ng/ml PA-63 and 500 ng/ml LF from List Biological Laboratories). Assay plates were than incubated for 4.5 hours at 37°C, with 5% CO_2. Following this incubation, cell cytotoxicity was determined by the release of lactose dehydrogenase (LDH) using a fluorescent CytoTox-One assay (Promega). Assay plates were allowed to equilibrate at room temperature for 30 minutes. After plates had equilibrated, 30 μl/well of CytoTox reagent were added and assay plates were incubated for 10 minutes. Following this incubation, 15 μl/well of Stop Solution was added to assay plates and the amount of LDH released was measured using Perkin-Elmer Envision.

Cancer proliferation

A549 (#CLL-185), Colo 205 (#CLL-222), H929 (#CRL-9068), HCT116 (ATCC #CCL-247), NCI-H460 (#HTB-177), SK-MEL-28 (#HTB-72), SKOV-3 (#HTB-77), RPMI-8226 (#CCL-155), MM.1R and MM.1S (kindly provided by Dr. Steven Rosen, Northwestern University) were cultured in RPMI-1640 media Supplemented with 10% FBS for between 2 and 20 passages, drawing test populations along the way. Cells were seeded into 384-well plates at a density of 1,500 cells per well in 35 μl media using automated dispensers. Plated cells were incubated at 37°C, with 5% CO₂ overnight, after which the compounds were added and the plates were incubated again for 72 hours (~1–2 doublings). Post incubation, cells were assayed for viability by measuring relative ATP levels using ATPLite 1Step (Perkin Elmer, Chicago, IL #6016739) as per the manufacturer’s instructions or 10.5% Alamar Blue fluorescence dye (in 40μl media) was added and plates were incubated for 6 hours. Cell viability measurements were taken at a single time using a Perkin Elmer Envision plate reader.

Cardiovascular HTRF assays

Human coronary artery endothelial cells (HCAEC, Cell Appl. #300-05a) or smooth muscle cells (HCASMC, Cell Appl. #350-05a) were seeded into 384-well plates at a density of 1,500 cells/well in 35 μl Supplemented media using automated dispensers. Cells were incubated at 37°C, 5% CO₂ overnight to allow the cells to adhere, treated with compound, and stimulated with IL-1β (BD Biosciences #554602) one hour later at 3 ng/ml. The plates were incubated again for 24 h, after which 9 μl of cell supernatant were transferred into a corresponding low-profile 384-well plate containing 9 μl of pre-mixed HTRF reagents (Functional Grade Purified anti-human MCP-1 antibody, Clone: MD3-F7 eBioscience #16-7099-85, custom labeled with Eu-cryptate by CisBio, at a f.c. of 0.88 nM; Biotin anti-human MCP-1 antibody, Clone: 2H5, eBioscience #13-7096-85, at 3.35 nM f.c.; Streptavidin labeled XL-665, CisBio #610SAXLB, at 16.75 nM f.c.). HTRF signal was read from the low-profile plates following an overnight incubation at RT using the LANCE-HTRF Eu/APC Dual protocol on Perkin Elmer Envision plate reader. To assess viability based on ATP levels after removing the supernatant for the HTRF assay, the cell culture plate was treated with ATPLite 1Step reagent, and the luminescence for each well was read on the Envision plate reader.

Cardiovascular anti-proliferative assays

Adult Normal Human Dermal Fibroblast (NHDF, Lonza# CC-2511), human aortic smooth muscle cells (AoSMC, ATCC #CC-2571), or human umbilical vein endothelial cells (HUVEC, ATCC #CRL-1730) cells were cultured in Fibroblast Basal Media with provided Supplements and growth factors (Lonza #CC-4126) for 2 to 10 passages. Test populations were seeded at 250 cells/well in 384-well plates and allowed to recover overnight at 37°C with 5% CO₂. Diluted compounds were added to the cells and incubated at 37°C with 5% CO₂ for 72 hours. Cells were then assayed for viability by measuring relative ATP levels as described above.

IL-1β ELISA assay

The inhibitory effect of certain compounds or combinations on the secretion of IL-1β was assayed using the standard sandwich ELISA. Assay plates were prepared by adding lipopolysachharide (LPS) stimulated complete RPMI media into 384-well plates. Master plates were appropriately diluted into assay plates and purified PBMC (20,000 cells/well) were added. Plates were incubated at 37°C, 5% CO₂ overnight and spun to clear the supernatant, which was transferred to ELISA plates coated with IL-1β capture antibody. After a 2h incubation at RT, plates were washed with 1× PBS, 0.1% Tween 20, and a second IL-1β antibody and the detection agent (Eu-labeled Streptavidin) were added. Plates were incubated again for 1h at RT, and after several washes, enhancement solution was added. Following an overnight incubation at 4°C, plates were read on a Perkin Elmer Envision plate reader.

Inflammation assays

The ability of compounds or combinations to suppress the secretion of pro-inflammatory cytokines was assayed as follows. Compound stocks dissolved in DMSO (or H2O as appropriate) were serially diluted on master plates using liquid-handling automation. Master plates were diluted into plates with aqueous media, stimulants (phorbol-12-myristate 13-acetate and ionomycin) and serum. Human buffy coat was obtained fresh daily from the blood bank and diluted in Supplemented media prior to addition to the assay plates. Plates were incubated overnight at 37°C and 5% CO₂ and spun to pellet the cells. After transferring the supernatant to an ELISA plate coated with a capture antibody specific for the target cytokine, plates were washed and probed with a second antibody and detection reagent. Data were read from the ELISA plate using Perkin Elmer Envision readers.

Htt protein translocation assay

Immortalized striatal cells derived from mutant huntingtin (Htt) knockout STHdhQ111 mice were seeded at 8,000 cells/well in a collagen I coated 384-well plate (BD Biosciences). Compounds were added and cells were grown overnight in 33°C incubator with 5% CO₂. Cells were fixed with formaldehyde, permeabilized with 0.5% Triton X-100, blocked with 0.5% BSA and stained with 1F8 antibody from Main Biotechnology Services (1:2000). Nuclei were defined by Hoechst staining. Htt localization used a Cy3-labeled anti-mouse secondary antibody followed by PBS wash. Images were acquired using Cellomics AssayScan VTi 5.0 under a 10× or 20× objectives, using automatic focus every other well. Peri-nuclear staining was quantified using the Compartmental Analysis BioApplication and “RingSpotTotalInten” as endpoint. Cell viability and cell numbers were quantified using the Compartmental Analysis BioApplication and “ObjectPerField” as endpoint.

Norepinephrine induction assay

For the NE experiment (Suppl. Note 4), purified human T-cells were cultured as triplicate samples for each condition. First, an inflammatory response was stimulated with αCD3 and αCD28 antibodies for 30 minutes, after which cells were treated with drugs as indicated. After incubating for 18 hours at 37°C with 5% CO₂, supernatants were collected and TNFα was quantitated using cytometric bead-arrays.

In-vivo assay protocols

Rat asthma model

Brown Norway rats (n = 10/cohort) were sensitized with intraperitoneal ovalbumin (OVA) given on days 0, 7 and 14. Animals were treated with test agents by oral gavage 1 hour prior to intranasal ovalbumin (OVA) challenge for 1 hour on day 21. Lungs were lavaged 72 hours after exposure of OVA to quantitate total leukocytes and specific cell populations in bronchoaveolar lavage fluid.

Rat Pain Assay

Male Sprague Dawley rats (200–225 g) were dosed with drugs three times (2 days, 1 day, and 30 min) prior to the pain induction. Cohorts of 8 rats were treated for each treatment level, along with vehicle and diclofenac (positive control, 25 mg/kg) cohorts. After administering carrageenan, the average retraction force in response to a pain stimulus for the injected and uninjected hind paws was measured with Von Frey filaments at 20, 40, 60, 80, and 120 min post injection. The data for both hind paws were averaged after subtracting a baseline for each animal from measurements on Day -2, and the area under the curve was integrated over the full time range.

Rat toxicity model

Cohorts of 5 male Sprague Dawley rats (Charles River Laboratories), with average starting body weight 178–186g, were given intraperitoneal doses for 10 days, the final dose given 2 hours prior to humane euthanization. Livers were removed and stored in an RNAlater (Ambion, Austin, TX) at 4°C. Samples were homogenized using TissueRuptor (Qiagen) and total RNA was isolated using the RNeasy-Plus Mini kit (Qiagen). Equal amounts of total RNA were used for one step RT-PCR (QuantiTect Probe, Qiagen). Taqman Gene Expression Assays, Applied Biosystems reagents were used for detection of TAT and beta-actin (endogenous control) mRNA using the Applied Biosystems 7300 Real-Time PCR System. The TAT expression values were calculated using the formula relative expression = 2^ΔTAT/2^ΔArbp, where Δgene is the difference between the drug- and vehicle-treated Ct levels for that gene.

Supplementary Material

1. SUPPLEMENTARY MATERIAL.

Suppl. Note 1: Simulated synergy and selectivity.

Suppl. Note 2: Flux balance simulations of bacterial metabolism.

Suppl. Note 3: Experimental screening results and statistics.

Suppl. Note 4: Details and follow-up for selective synergy examples.

Suppl. Data 1: Statistical results from the simulated screens.

Suppl. Data 2: Gene and pathway annotations for the FBA simulations.

Suppl. Data 3: Single inhibitor activities for the FBA simulations.

Suppl. Data 4: Synergy and selectivity data for the FBA simulations.

Suppl. Data 5: Chemical agents used in the experimental screens.

Suppl. Data 6: Synergy and selectivity data for the experimental screens.

Suppl. Data 7: Statistical results from the experimental screens.

Suppl. Data 8: Follow-up data for the example selective synergies.

Suppl. Data 9: In vivo data for the glucocorticoid-TCA synergy.