Temperature, ordering, and equilibrium with time-dependent confining forces

Abstract

The concepts of temperature and equilibrium are not well defined in systems of particles with time-varying external forces. An example is a radio frequency ion trap, with the ions laser cooled into an ordered solid, characteristic of sub-mK temperatures, whereas the kinetic energies associated with the fast coherent motion in the trap are up to 7 orders of magnitude higher. Simulations with 1,000 ions reach equilibrium between the degrees of freedom when only aperiodic displacements (secular motion) are considered. The coupling of the periodic driven motion associated with the confinement to the nonperiodic random motion of the ions is very small at low temperatures and increases quadratically with temperature.

The meaning of temperature and equilibrium and how these relate to ordering apparently are not well studied in classical systems with rapid time-varying fields, with the rate of variation in the Hamiltonian faster than the natural periods for the characteristic motion of the system. This is the case for charged particles in radio frequency (rf) traps.

The confinement of charged particles in a high-frequency quadrupole electric field has been studied since the work of Paul and Raether (1) and Langmuir and coworkers (2) (see also ref. 3). With the development of laser cooling, clouds of trapped ions form ordered crystalline patterns that are characteristic of internal temperatures much lower than would correspond to their kinetic energies in the high-frequency motion.

In the following we consider rf traps with the confining field given by

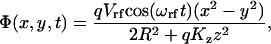where Φ is the potential energy, q is the ion charge, V_rf the applied peak rf voltage at frequency ω_rf, R is the smallest distance from the trap axis to the electrodes, and K_z is constant, characterizing the electric field in the direction where there is no rf field. This potential is appropriate to the linear Paul trap (4, 5), when the effect of the axial potential in the radial direction is neglected, although in the present case K_z was chosen sufficiently large for the restoring force to be the same as in the rf directions, and thus to produce a spherical cloud.

For stable trapping, the frequency of the confining rf field must be substantially greater than the characteristic frequency of the motion of the particle in the average field of the trap, the secular frequency (6, 7). The time variation of the external force results in high-frequency motion of the confined particles. This periodic motion apparently is decoupled from what may be considered random thermal motion. The transition from order to chaos in such ion traps has been studied for few ions in both experiment and simulation (6, 7). For somewhat larger numbers the behavior of up to 512 ions had been studied in such fields, and the stability of the systems was explored (8) (the parameter q_z of ref. 8 is the ratio of frequencies multiplied by 4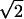). More generally, there has been an understanding that for a large ion cloud rf heating (9), which is the coupling of the rf motion into random motion, will present a limit, because the larger the cloud, the larger the amplitude of the motion in the rf field.

Although an infinite one-component plasma, with no confining field, settles into an ordered (bcc) solid (10), finite cold large clouds form a series of layered structures, spherical, spheroidal, or cylindrical, as found in simulations (11, 12), and in experiments (13) in Penning traps, where confinement is achieved through rotation in a magnetic field. Such systems have been observed to be ordered into up to 20 or so shells in both experiments and simulations. For larger systems the bcc structure characteristic of infinite Coulombic matter is expected to form in the center of the plasma cloud. This has been observed in Penning traps with several hundred thousand ions (14). In rf traps, layered structures also have been observed with increasingly large clouds (15, 16). The purpose of the present work is to investigate the role of the above effective temperature in more detail, and its relevance to ordering phenomena and rf heating.

Simulations

Simulations using the technique of molecular dynamics were carried out with an isotropically confined system. The effective time-averaged confining force in the quadrupole (x,y) directions was taken as equal to the confining force in the non-rf (z) direction to produce a cloud whose time-averaged shape was spherical. The parameters for the simulation are given in Table 1 in dimensionless units in which mass and charge are equal to 1. Very roughly speaking, these could correspond to a realistic trap if the time unit were on the order of ms and the distance unit on the order of mm.

Table 1.

Parameters in simulation

Quantity	Description	Value
N	Number of ions	1,000
4qVrf/ωrf2R2	Trapping parameter q	0.37113
qKz	Coefficient along axis	120,000
ωrf	rf frequency	5,280
Ωr⩵Ωz⩵ωplasma/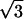	Secular frequency	346.4
ωrf/Ω	Ratio of rf to secular frequencies	15.24
δt	Time step in simulation	0.00001
2π/ωrf	rf period	0.00119 (119 time steps)
aSW	Seitz-Wigner radius in cold system	0.0195
T0	Target temperature in units of 1/Γ	0.0002

The simulations were carried out on a Silicon Graphics (Mountain View, CA) Origin 200 4-processor parallel computer. For a 1,000-ion system, close to one million iterative time steps could be carried out in 1 day, with each time step requiring the computation of the Coulomb force between each pair of particles. This system was cooled only in the axial (nonquadrupole) direction (as in laser cooling; ref. 16). This was accomplished by reducing the axial component of the velocity by a factor determined by the ratio of the summed kinetic energies in this direction to the energy corresponding to the intended temperature. The natural dimensionless unit of kinetic energy, or temperature, is in terms of the parameter Γ, Γ ≡ (q²/a_SW)/kT. In other words, temperatures are in units of q²/a_SW, and for the present case Γ = 1 corresponds roughly to 0.1 K. (Here a_SW is the Seitz-Wigner radius, the radius of the volume element occupied by one ion in the cold plasma.)

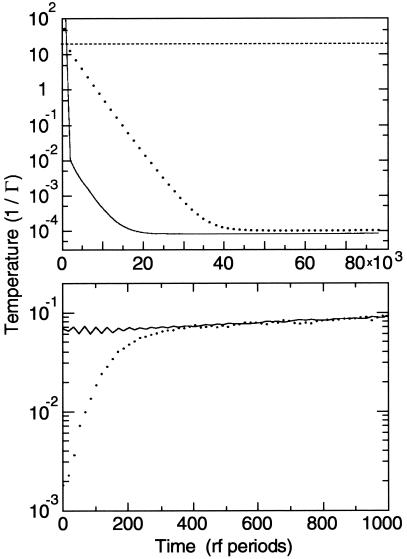
A 1,000-particle system subjected to the sinusoidally varying field was followed in the simulations as the cooling proceeded. The average kinetic energies in the axial z-direction gradually approached the targeted value in about 25,000 rf periods. The kinetic energies associated with the x and y directions are huge in comparison, because of the time variation of the confining field, some 7 orders of magnitude greater than the target temperature. Because of the time-varying confining force, the x and y components of energy are not going to be reduced. Instead, following ref. 8, we define an effective temperature in this direction that uses velocities computed from displacements between times that differ by a complete rf period, in other words motion that is not periodic with the rf voltage. The components of this effective temperature reduce more slowly in these dimensions and require about 50,000 rf periods (roughly 50 ms) to reach the target value, as is illustrated in Fig. 1. We find that this random component of kinetic energy works remarkably well as a practical measure of temperature; indeed for a cold system with the cooling in the simulation turned off, complete equilibration persists between the z-component of kinetic energy and the nonperiodic part of the motion associated with the x,y dimensions that undergo the rf oscillations. There appears to be no dependence of the aperiodic kinetic energy on the distance from the z axis, whereas the periodic motion is proportional to this distance.

Figure 1.

(Upper) The cooling process, with the solid line indicating the axial temperature that is gradually cooled, and the dots indicating the effective radial temperature computed from the part of the motion that is not periodic in the rf field. The temperature is in units of q²/a_SW, and the time is in rf periods. (Lower) The axial and radial temperatures attaining equilibrium after a phase shift in the rf field has been introduced in the simulation.

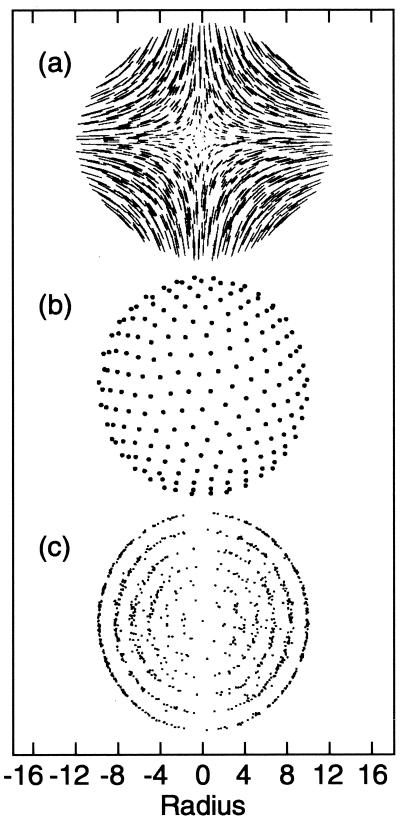
The target temperature, corresponding to Γ = 5,000, is well beyond that (Γ > 170) at which an ionic system confined in a time-independent field becomes ordered. Indeed, as is shown in Fig. 2, an ordered system was obtained. The density in the interior shows a series of spherical shells.

Figure 2.

(a) The amplitude of the motion of particles in the applied rf field. (b) The time-averaged positions of ions in half the outermost shell for the cooled 1,000-ion system. (c) The r-z projection of these positions for all ions. The distance scale shown is in units of a_SW, the Seitz-Wigner radius for the cold system.

A system so cooled was allowed to propagate in the simulation for a time corresponding to another 50,000 rf periods with no cooling, that is, no temperature control applied. No transfer of energy from the rf motion to the random thermal motion was seen in either the aperiodic motion in the x and y directions or the motion in the axial z direction. The limit that may be placed on the rate at which energy was transferred from the periodic motion in the confining field is estimated at <3 parts in 10¹¹ per rf cycle.

This process of propagation without cooling was repeated with the system prepared at higher temperatures. To reach such higher temperatures in a controlled way without having to go through the long preparation, it was found that a controlled shift in the phase of the time dependence of the rf field effectively raised the temperature, by causing a controlled increase in the nonperiodic motion in the transverse directions, which then equilibrates with random motion in the axial direction in a few hundred periods. The magnitude of this shift in phase (a few degrees) determines the temperature that is reached.

Discussion

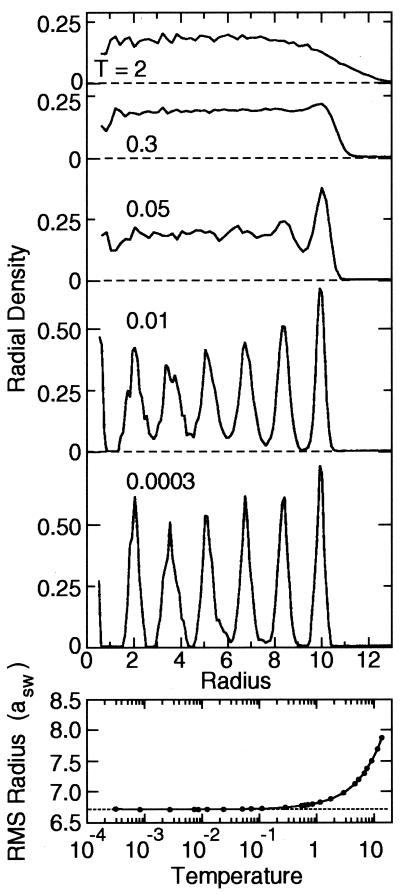
The fact that the effective temperature is related to ordering is shown in Fig. 3, where the radial densities for systems heated to different temperatures are plotted. The dependence on the effective temperature is very similar to the temperature dependence seen for constant confining potentials: there is no sharp phase transition; the shell structure gradually broadens and then disappears as the temperature becomes higher than the value corresponding to Γ of about 170. The spherical radius of the cloud (with coordinates averaged over an rf period) increases with temperature in a way similar to that predicted for static confinement by Dubin (17).

Figure 3.

(Upper) The average radial densities of the spherical 1,000-ion system at various effective temperatures. The radial scale is the distance from the z axis, in units of a_SW, the density is in terms of ions/a_SW³ and the temperatures in units of q²/a_SW. (Lower) Plot indicates the rms (spherical) radius of the cloud as a function of effective temperature, in units of 1/Γ.

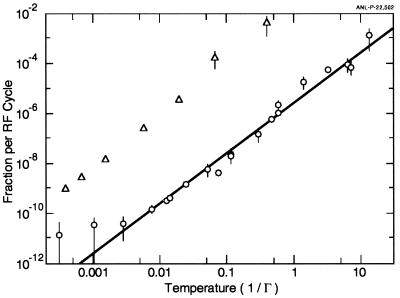
In these simulations, with the system equilibrated at higher temperatures, the rate at which energy from the periodic motion is coupled into random motion becomes discernible in the simulations as is shown in Fig. 4. The strength of the coupling depends on the temperature of the system rather sharply: the line shown in the figure represents a quadratic temperature dependence. For T < 0.01 (Γ > 100), where the shell structure appears unperturbed, the coupling is undetectable in the simulations. This limit would correspond to time constants on the order of an hour, from this source of heating, in real traps operating at trap frequencies of several MHz. The limit set by collisions is likely to be shorter. The accuracy of these limits is hampered, in some measure, by the fact that the motion in the cloud can include excitations of normal modes (18) of the cloud that are not necessarily coupled into axial motion and thus can persist without being affected by the axial cooling. A small amount of such residual motion can persist and sets the uncertainties shown in Fig. 4. It should be noted that a quadratic temperature dependence of the coupling leads directly to an analytic form for the total lifetime of a cold plasma cloud after cooling is turned off, that is proportional to the reciprocal of the initial temperature.

Figure 4.

The coupling between the kinetic energy in the periodic motion of trapped ions into aperiodic, thermal motion is shown. The fraction of the kinetic energy in the periodic motion that is mixed into heat per rf period is plotted as a function of effective temperature in units of Γ = q²/a_SW. The line represents a quadratic temperature dependence of this coupling. The error bars represent an estimate in the uncertainty in determining this coupling from the simulations, caused by the fluctuations in a finite system. For the lowest points, the bars show the limits that can be set for this coupling. ○, The bulk of simulations with the ratio of rf to the frequency of secular motion of 15.5. ▵, simulations with this ratio reduced to 4.7.

Because Prestage et al. (8) had investigated systems with different ratios of the secular to the rf frequencies, some simulations were tried with such variations. The results for one case, a ratio of rf to secular frequencies of 4.7 (instead of 15.2) are shown in Fig. 4 as open triangles. A system having a ratio smaller than 4.7 would not settle into a cold state with the present cooling algorithm. Prestage et al., using 64 and 128 particles, found instabilities when the ratio of frequencies was about 7.07 (q = 0.8), but were able to cool a system to where it apparently remained stable for a ratio of about 18.8 (q = 0.3) and a temperature in our units on the order of a few times 0.001. The number of time steps in the molecular dynamics simulation per rf period was 119 in the present work compared with 20 (8). Although 20 steps per rf period may be a reasonable approximation for most purposes, it may not be sufficiently accurate when the ratio of frequencies becomes this small. However, the results of ref. 8 appear to be consistent with the trends in the present investigations.

It is possible that the pattern seen in rf heating is the origin of some of the phenomena connected to the reported sharp phase transition between chaotic and ordered motion in rf traps with a few ions (6, 7) and the apparent hysteresis effects in such systems. Indeed, sharp transitional behavior is observed in current experiments with larger numbers of ions.

Our results show that the definition of an effective temperature in terms of the nonperiodic motion is valid in a system where the distances between particles are continually changing because of external forces. How to justify the thermodynamic description of such a system is not clear. The very small coupling, corresponding to very low viscosity, between the driven motion and the random thermal excitations is surprising and qualitatively consistent with the successes in getting crystallization for large clouds in such ion traps (15, 16). The quadratic dependence of this coupling on temperature is evident, but not understood at present. This dependence is consistent with the qualitative results of ref. 8 and also with those of recent simulations setting limits for crystalline beams (19). Much work remains in gaining a better understanding of such systems for ion traps, for ordered beams in accelerators, and more generally.

Abbreviation

rf

radio frequency