Formation of harmful algal blooms cannot be explained by allelopathic interactions

Abstract

Many planktonic microalgae produce a range of toxins and may form harmful algal blooms. One hypothesis is that some toxins are allelopathic, suppressing the growth of competitors, and it has been suggested that allelopathy may be one important mechanism causing algal blooms. In a metaanalysis of recent experimental work, we looked for evidence that allelopathy may explain the initiation of algal blooms. With few exceptions, allelopathic effects were only significant at very high cell densities typical of blooms. We conclude that there is no experimental support for allelopathy at prebloom densities, throwing doubts on allelopathy as a mechanism in bloom formation. Most studies tested allelopathy using cell-free manipulations. With simple models we show that cell-free manipulations may underestimate allelopathy at low cell densities if effects are transmitted during cell–cell interactions. However, we suggest that the evolution of allelopathy under field conditions may be unlikely even if based on cell–cell interactions. The spatial dispersion of cells in turbulent flow will make it difficult for an allelopathic cell to receive an exclusive benefit, and a dispersion model shows that dividing cells are rapidly separated constraining clone selection. Instead, we propose that reported allelopathic effects may be nonadaptive side effects of predator–prey or casual parasitic cell–cell interactions.

There is a growing awareness that harmful blooms of cyanobacteria and planktonic protists, known as harmful algal blooms (HABs), have increased globally with serious implications for human health and economy (1). The severe socioeconomic impacts of HABs call for a better understanding of the factors and mechanisms causing blooms. Harmful effects by HAB species are largely mediated through the production of highly toxic compounds (1). The adaptive significance is still unclear, but it has been suggested that toxins confer some advantage that allows HAB species to reach the very high cell densities characterizing plankton blooms (2). One possible mechanism is that toxic compounds defend a plankter against pathogens, parasites, or predators. This mechanism is supported by recent work showing that toxin-producing species can be less preferred by predators, and that a predator presence may induce toxin production (3). A second mechanism is that the active release of toxins may inhibit the growth or survival of competing species. Such chemically mediated interference competition is known as allelopathy and is common among terrestrial plants (4–5). Many laboratory experiments have also revealed allelopathic effects for limnic and marine plankton (see Results), although most studies suggest that allelopathic effects are caused by compounds other than known toxins characterizing HAB species (6–8). It has been proposed that allelopathy might explain a competitive advantage among planktonic cyanobacteria and protists and the initiation and/or continuation of plankton blooms (9–12).

Lewis (13) pointed out some problems with the evolution of allelopathy as a competitive mechanism among plankton. In the dynamic water-column, a major problem is that the benefit from the production of a costly allelopathic compound will also be shared by nonproducers. Accordingly, it is difficult to envisage the evolution of allelopathic traits among plankton that are continuously being mixed through turbulent motion and random swimming (14). A possible way out of this evolutionary dilemma could be that asexually reproducing species may form spatially structured clones that can be favored by natural selection if released allelopathic compounds control the local invasion of competitors (14).

Since the publication by Lewis (13) in 1986, a number of research papers have reported allelopathic effects for bloom-forming species. Do these papers support the significance of allelopathy as a key factor in bloom dynamics, and what is the current view on possible evolutionary mechanisms? In a metaanalysis, we first consider the published evidence for allelopathy among plankton and under what conditions effects were found. We then use simple models to analyze whether found allelopathic effects may play a significant role under field conditions, and we also assess the likelihood for the evolution of allelopathy in plankton communities. Finally, we propose that reported allelopathic effects may be nonadaptive side effects of predator–prey or casual parasitic cell–cell interactions.

Results

Metaanalysis of Allelopathic Studies.

Based on 21 published reports, there was a strong and significant overall negative effect of culture media from potentially allelopathic species on the growth or biomass of target species [d_T = −2.50, 95% CI (−3.03; −1.96), n = 95], indicating allelopathic effects of exuded metabolites. However, among the experiments investigating allelopathic effects of exuded metabolites, 98% (93 of 95 comparisons) tested media from cultures with Chl a concentrations >5 μg L⁻¹ (bloom concentrations). When the dataset was partitioned according to the Chl a content in the cultures from which the allelopathic media was prepared, significant allelopathic effects could only be detected in studies using high [d_H = −2.49, 95% CI (−3.03; −1.95), n = 93] but not low [d_L = 2.79, 95% CI (−24.86; 19.29), n = 2] Chl a content. The Chl a content did not explain the variation in the dataset (Q_B = 0.03, P = 0.88), which is not surprising considering the low number of studies testing media from cultures with low Chl a content. Our results show that allelopathic effects are found at high cell concentrations typical for well developed plankton blooms, but that very few studies have tested allelopathic effects at prebloom concentrations. Furthermore, our literature survey showed that few studies include the possibility for cell–cell interactions (these studies were not included in the metaanalysis, see SI Text).

Modeling the Local Concentration of Allelopathic Compounds.

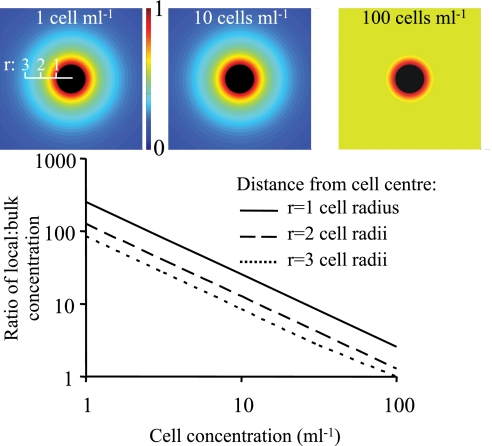
Our metaanalysis shows that very high cell densities were necessary to produce mean bulk concentrations of allelopathic compounds causing growth inhibition or cell lysis. The model in Eq. 7, however, shows that at low cell concentrations, typical of prebloom conditions, the local concentration near the allelopathic cell may be orders of magnitude higher than in the bulk (Fig. 1). As an example, the concentration 2–3 radii from an allelopathic cell (cell radius 10 μm) occurring at a density of 1 cell mL⁻¹ is 85–130 times the asymptotic bulk concentration. This high local concentration opens up the possibility for allelopathic interactions to occur during cell–cell encounters also at prebloom densities, even if the far-field bulk concentration of allelopathic compounds is below inhibitory levels.

Fig. 1.

Ratio of the local concentration of a released allelopathic compound to the far-field concentration in the bulk in the absence of flow. The ratio is modeled using Eq. 7 with a cell radius of 10 μm and results are shown for 3 distances (cell radius units) from the cell surface. The Insets give a graphical view for 3 cell densities (1, 10, and 100 cells mL⁻¹) of the relative magnitude (0–1) of an exuded compound diffusing out from the cell (in black) and out into the bulk medium (scale in cell radii).

Modeling the Encounter Rate Between Allelopathic and Susceptible Cells.

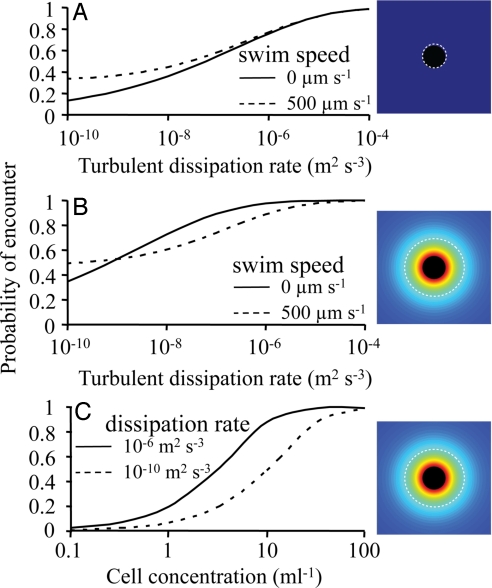
If allelopathic effects can be conveyed through cell–cell interactions, the frequency of such interactions will be critical. The rate of encounters between a susceptible cell and a population producing an allelopathic compound is modeled using Eqs. 8 and 9, and rates are transformed to the probability of at least one encounter in a cell cycle of 12 h (Eq. 10). Fig. 2A shows the encounter probability when physical contact is used as criterion for an encounter; the encounter distance is then fixed to the sum of the radii of susceptible and allelopathic cells. As expected, encounter probability increases with relative velocity caused by cell motility and when turbulence increases from stratified to well mixed conditions (dissipation rates: 10⁻¹⁰-10⁻⁴ m² s⁻³). However, when a cell releases an allelopathic compound, a susceptible cell may suffer a damage already at some threshold concentration within that chemical envelope. In this case (Fig. 2B), the encounter radius will decrease with swimming speed and turbulence (see Eq. 9), which will counteract the increase in encounter probability. This erosion of the chemical envelope due to fluid motion causes a motile cell to encounter fewer susceptible cells within a broad range of turbulent energies (Fig. 2B). Finally, encounter probability will strongly depend on the concentration of allelopathic cells. A probability of 0.5 requires a concentration of a few allelopathic cells mL⁻¹ at medium turbulent energies (Fig. 2C). During very calm conditions this encounter probability is acquired at concentrations >10 cells mL⁻¹.

Fig. 2.

The probability of encounter between a susceptible cell and a population of cells producing an allelopathic compound (Eqs. 8–10). (A) Encounter radius is equal to the physical dimension of the cells. Probability of encounter is shown for swimming (500 μm s⁻¹, typical for protists) and nonmotile cells, and for a range of turbulent dissipation rates (from calm deep to well mixed surface waters). Concentration of allelopathic cells is 10 mL⁻¹. (B) Encounter probability when encounter is a function of the radius of the chemical envelope surrounding an allelopathic cell. The radius of the allelopathic envelope under flow conditions was determined by the concentration found three cell radii from the cell surface for nonflow conditions (Eq. 9). Concentration of allelopathic cells is 10 mL⁻¹. (C) Encounter probability as a function of the concentration of allelopathic cells for two turbulent dissipation rates. In all calculations the cell radius is 10 μm and the diffusion coefficient for the allelopathic compound is 5 × 10⁻¹⁰ m² s⁻¹. The broken, white line in the graphic Insets show the position of the encounter radius. Note that in B and C, the encounter radius represents the distance from the cell centre to where the concentration of a compound elicits an allelopathic effect in the absence of flow. This distance is then a function of cell motility and turbulent energy which act to erode the chemical envelope.

Modeling the Rate of Separation Between Cells in Turbulent Flow.

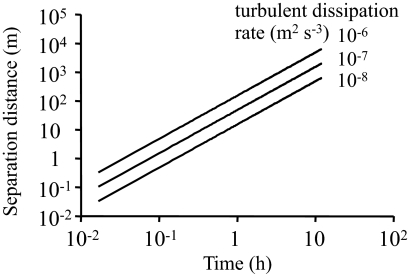
To assess the spatial and temporal scales of mixing initially close cells (e.g., after cell division or at encounter between an allelopathic and a susceptible cell), we modeled the separation distance based on the Richardson–Obukhov law (Eq. 11). The separation distance of nonmotile cells is a function of time and the intensity of turbulent mixing. There are 2 important aspects of the rate of separation. The first is the time 2 cells may interact after random encounters. Even if interactions are assumed over the very large distance of 1 cm, the separation time is expected to be <1 min, which is ≈0.1% of a 12-hour cell cycle. A second aspect is how far 2 daughter cells may separate during a cell cycle. This separation rate will determine the likelihood of clone selection for allelopathy, which will depend on the spatial correlation among related cells (see Discussion). Fig. 3 shows that for a cell cycle of 12 h, the expected separation distance is between 100 and several 1000 m.

Fig. 3.

Separation distance as a function of time for two initially close cells based on the Richardson–Obukhov law (Eq. 11). The rate of separation is shown for 3 turbulent dissipation rates representing the low-end of turbulent energy found in surface waters.

Discussion

Studies of allelopathic interactions among plankton have only found significant effects at the high cell concentrations typical for bloom densities whereas the few studies including low cell concentrations did not detect allelopathic effects. Most studies were performed using cell-free media from cultures of allelopathic species, usually to discriminate the chemically mediated effects from other kinds of interactions, e.g., predation or confounding from exploitative competition (15). This use of cell-free medium implies that most studies included in the metaanalysis are applicable only to the case where an allelopathic compound exerts its action through the mean concentration in the bulk, i.e., in the well mixed far-field at spatial scales much larger than the cells. Thus, we conclude from the metaanalysis that under totally mixed conditions the published allelopathic effects cannot explain the initiation of blooms, which must be based on mechanisms acting at low cell densities. This conclusion is further supported by modeling studies (16–17). Allelopathic interactions could still have some functional significance at high cell densities, e.g., prolonging a bloom and especially so if competitors are forced to lyse and to release assimilated nutrients. However, there are not at present any experimental data supporting allelopathy as a mechanism that can explain the formation of algal blooms when cell densities are low. Some studies may have overestimated the cell concentration required for significant allelopathic effects because of decomposing allelopathic compounds or conservative controls with low nutrient levels. However, in the metaanalysis we set the limit between low and high cell concentration rather high (5 μg Chl a L⁻¹) and this division still resulted in no significant allelopathic effects at low cell concentration.

Direct cell–cell interactions offer an alternative transmission mechanism for allelopathic compounds. A few papers reported experiments with mixtures of cells from allelopathic and a susceptible species (8, 18), although these studies were not designed to test for cell–cell interactions. In a direct test where cells were either allowed to meet or separated with a membrane, it was concluded that cell–cell interactions between 2 dinoflagellates were necessary for an allelopathic response (19). A recent study suggests that the dinoflagellate compound karlotoxin exerts its effect after cell encounters (20). The important aspect of cell–cell interactions is that the allelopathic effect depends on the local concentration of a compound during encounters between susceptible and an allelopathic cells. The concentration gradient around a cell releasing an allelopathic compound depends on molecular diffusion, cell motility, and turbulent mixing. It is clear from Fig. 1 that our simple models predict local concentrations that are orders of magnitude higher than in the bulk, especially at the low cell densities preceding a bloom. A critical question is whether cell–cell interactions will occur frequently enough to cause allelopathic effects. The model results in Fig. 2C suggest that encounter probability may exceed 0.5 when already at a few allelopathic cells mL⁻¹. An important, although poorly studied, feature of chemically mediated cell–cell interactions is that the encounter distance is a function of the size of the chemical envelope defined by the threshold concentration necessary to elicit an effect. The encounter rate is the product of the squared radius of the envelope and the relative motion between cells, and these 2 factors change in opposing directions when turbulence and cell motility increase. It is seen in Fig. 2 A and B that encounter probability with a chemical envelope increases less steeply with turbulence compared with a fixed encounter distance, and that cell motility will erode the envelope reducing the encounter probability. The dynamics of encounter probability make predictions uncertain, and the encounter with a chemical envelope deserves future empirical studies. The modeled encounter probability at densities below a few cells mL⁻¹ suggests that each encounter has to result in a significant allelopathic effect if cell–cell interactions are to play a role in prebloom competition. Alternatively, the allelopathic cell has to exert its effect at a larger distance than assumed here (3 radii = 30 μm). Although information is lacking for allelopathic effects, it has been shown that bacteria may detect chemical attractants from algal cells only at a distance of a few algal radii (21).

Lewis (13) pointed out that it is difficult to explain the evolution of allelopathic interactions in the turbulent water-column where the spatial relationships among an allelopathic producer, the released compound, and susceptible cells are highly dynamic in time. Clearly, this dynamics in space makes it difficult to explain allelopathy caused by the build-up of high mean concentrations in the bulk. In that case, it is necessary to invoke group or kin selection, i.e., species or clones that do not produce allelopathic compounds have a greater extinction risk. Importantly, this evolutionary objection also applies to allelopathic interactions based on cell–cell interactions. A mutant producing an allelopathic compound that suppresses growth of neighbor competitors must receive an exclusive benefit that is greater than the cost if it is to be favoured by natural selection. The potential problem is that during a cell cycle (typically ≈12 h) the allelopathic cell will disperse away after encounter with a susceptible cell, and its reduced growth rate will be exploited by other cells. The Richardson–Obukhov model indeed indicates that the separation distance may be very great and that only a fraction (≪1%) of a cell cycle is spent close to each encountered susceptible cell. Natural selection could also act on a clone of allelopathic cells that remains sufficiently close in space. Kàrolyi et al. (14) showed in a model of the rock-scissors-paper game that an allelopathic clone can spread in abundance but only if local mixing is low. Again, Fig. 3 shows that even under low-end turbulent conditions in the photic zone (dissipation rate: 10⁻⁸-10⁻⁶ m² s⁻³) the separation of allelopathic daughter cells on the time scale of the cell cycle is expected to be large (>100s of meters). A possible mechanism that could maintain a clone cluster in space would be a swarming behavior that counteracts turbulent diffusion in all 3 dimensions. There is yet no empirical support for clone swarming. Separation of cells may also be reduced due to vertical migration or physical mechanisms resulting in thin layers of high cell densities (22). However, turbulent mixing along the horizontal dimensions will still be present and, from geometric relations, 2-dimensional mixing would only reduce the separation distances in Fig. 3 with a factor $\sqrt{2/3}$ (assuming isotropic turbulence). Thus, it is unlikely that clusters of clonal cells are maintained under ocean turbulence. Substantial mixing of cells is supported by recent field studies where a blooming diatom showed a surprisingly high clonal diversity, and it was concluded that environmental changes, e.g., turbulent mixing, prevents individual clonal lineages to be dominant (23).

We conclude that convincing evidence is missing for allelopathy as a significant mechanism in the formation of HABs, and that the likelihood for the evolution of allelopathy as an adaptation seems weak in this system. Our simple models indicate that cell–cell interactions could work at prebloom conditions, but this does not resolve the problem of how allelopathy may have evolved. Other explanations for the production and release of allelopathic agents include defense against predators (24) and maybe parasites, where allelopathic effects may occur at high cell densities as a side effect. Moreover, we propose that reported allelopathic effects, together with recent studies of cell–cell interactions, may be interpreted as nonadaptive side effects of compounds released to aid in prey capture or in “casual parasitism” (only intermittent association between parasite and host). Key to these speculations are observations (25–26) that haptophytes of the genus Prymnesium may lyse and/or consume competing species (or predators) upon cell–cell contact and then ingest whole or part of the cell with direct benefits for the cell producing the aggressive compound. Stoecker et al. (27) and Tillmann et al. (26) also suggested that the production of toxins by harmful algae may be linked to predation where the release of toxins act to immobilize and lyse encountered cells. There is also a few reports about cell–cell interactions leading to immobilization and cell deformations and sometimes to lysis and death without observed phagotrophy (28–30). Toxins may punch holes in the cell membrane of a susceptible cell leading to increased permeability (7). Yamasaki et al. (31) also noted that cell deformations after cell–cell interactions could be reversed if the aggressive species were removed. Estep and MacIntyre (32) suggested that aggressive compounds released from the prymnesiophyte genus Chrysochromulina are used to inflict nonlethal membrane damage followed by phagocytosis/pinnocytosis of leaking nutrients (dasmotrophy). In this case, the susceptible cell may recover and the interaction is more similar to casual parasitism like haematophagy used by many insects. Clearly, additional experimental work is needed to explore the presence of chemically mediated aggressive cell–cell interactions among plankton. The challenge here is to measure the effects of encounters between aggressive and susceptible cells. Intriguing observations even suggest that motile cells may be selected to both pursue susceptible cells and to escape from aggressors (26, 33).

Materials and Methods

Metaanalysis of Allelopathic Studies.

The database was assembled by keyword searches in the ISI Web of Science covering papers published between 1986 and 2008 and from cited literature in the obtained papers and in recent reviews. Growth rate or biomass (measured either as fluorescence, cells volume⁻¹, Chl a, or C concentration) of the target algal species was used as response variable, and studies were categorized according to the Chl a content of the potentially allelopathic species. Studies were categorized into low (<5 μg L⁻¹) or high (≥5 μg L⁻¹) Chl a content (34). The criteria for including a publication in the analysis resulted in the selection of 21 published papers, and a closer description of the response and explanatory variables are presented in SI Text. Gurevitch and Hedge's (35) d was used as a measure of the effect size. All analyses were performed using the computer program MetaWin 2.0 (36). The reported results are from resampling tests generated from 4,999 iterations with 95% confidence intervals. The magnitude of the effect size was considered significant when the confidence interval did not include zero (35), and the effect of the explanatory variable was evaluated using heterogeneity statistics (Q).

Modeling the Local Concentration of Allelopathic Compounds.

The local concentration field of an allelopathic compound will affect the efficiency of cell–cell interactions. In the absence of relative water motion a water-soluble, allelopathic compound exuded from a spherical cell of radius r₀ will show molecular diffusion down a concentration gradient described by:

where c_r is the concentration at distance r from the cell centre (r ≥ r₀), Q_D is the flux out from the cell surface, D is the diffusion coefficient (here set to 5 × 10⁻¹⁰ m² s⁻¹), and c_b is the bulk water concentration (37). If the water moves relative to the plankton cell, the concentration field will be distorted and the gradient steeper. Relative water motion can be caused by swimming, sinking, or by turbulence-induced shear, and the effectiveness of the advective mass transport compared with molecular diffusion is described by the dimensionless Péclet number (Pe):

where U is swimming or sinking velocity, ε is the turbulent dissipation rate, and ν is the kinematic viscosity of water (37). We assumed turbulent dissipation rates between 10⁻¹⁰ and 10⁻⁴ m² s⁻³ representing turbulent energies in the calm deep ocean to the well mixed surface layer (38). The relative increase in the flux of a compound exuded by the cell caused by fluid motion is described by the Sherwood number:

where Q is the flux under relative fluid motion and Q_D is the flux under pure molecular diffusion. Several relationships between the Péclet and the Sherwood numbers have been suggested. We use the equation suggested by Clift et al. (39) for swimming and sinking cells:

and the equation in Karp-Boss et al. (37) for cells in linear shear with no rotation:

From the Sherwood number the change in the concentration gradient of an exuded compound due to fluid motion can be estimated as (40):

For cells swimming and sinking in turbulent shear the largest Sherwood number from Eqs. 4 and 5 is used in Eq 6. Eq. 6 takes a simplistic and symmetric view of how the concentration distribution changes under fluid motion. In reality the concentration distribution may be highly asymmetric, e.g., during swimming when water sweeps the concentration field into the rear wake. The spatial details of the concentration field requires the solving of the advective-diffusion partial differential equations and is beyond the scope of this work (41). The advantage of cell–cell chemical interactions is that the local concentration of an allelopathic compound (Eq. 1) may be many times higher compared with the concentration that builds up in the far-field bulk water. The ratio between local and bulk concentration will depend on cell concentration (n), the distance from the cell where the concentration is sufficient to inflict an allelopathic effect (r), the mixing rate, and the degradation rate of the compound. In a simplistic model we assume that mixing is fast beyond the Kolmogorov length scale [η = (ν³/ε)^1/4]. We further assume that the allelopathic compound has some half-life (T_1/2), which yields an asymptotic concentration in the bulk (c_b) of:

In the near absence of published information, we assume a half-life of 12 h, which is close to the photodegradation rate found for the algal toxin domoic acid (42). The ratio of local (c_r in Eq. 1) to bulk (c_b) concentration can then be approximated as:

Eq. 7b is only valid for cell concentrations and degradation rates where c_r ≫ c_b; at high cell concentrations the ratio between c_r and c_b asymptotically approaches unity.

Modeling the Encounter Rate Between Allelopathic and Susceptible Cells.

The probability of encounter between a susceptible cell and a population of cells producing an allelopathic compound is a function of the concentration of allelopathic cells, the encounter distance, and the relative velocity between cells. In a recent formulation (43) these components were included as:

where E is the encounter rate between a susceptible cell and a population of allelopathic cells, C_a is the concentration of allelopathic cells, R is the encounter distance, w_T is a turbulent velocity scale, and u_a and u_s are the swimming speeds of allelopathic and susceptible cells, respectively. Here, the encounter distance R is interpreted as the distance where a susceptible cell is damaged or negatively affected by the allelopathic cell. The encounter distance will depend on the steepness of the concentration gradient out from the surface of the allelopathic cell and the critical concentration where the allelopathic compound will inflict damage to a susceptible cell. This critical concentration was arbitrarily set to one third of the concentration at the cell surface when the Sherwood number is 1 (i.e., no relative water motion), and this concentration occurs at a distance 3 times the cell radius (see Eq. 6). The critical distance (R*) when an allelopathic compound exerts its effect at Sh > 1 is then:

Eq. 9 is a simplistic parameterization of how the geometry of the chemical envelope changes with Sh. It is clear that during swimming motion the chemical envelope will be swept downstream leading to fore-aft asymmetry (41). Also, under turbulent shear the envelope will differ in thickness with the thickest part along the axis of the shearing motion (37). The envelope thickness will further change if the cell is rotating either through propulsion or caused by the vorticity in turbulent shear fields. The detailed geometry of the chemical envelope requires numerical solutions of an advection-diffusion model and is outside the scope of this work. Note that the way the chemical envelope is a function of relative motion between cell and ambient water will reduce the encounter distance (R) with increasing swimming speed and turbulent dissipation rate. Encounter events were assumed to follow a Poisson process, and encounter rates were scaled as the probability (P) of encountering at least one allelopathic cell during the duration of one cell cycle (T) as:

Modeling the Separation Distance Between Cells in Turbulent Flow.

Two nonmotile cells in close proximity, e.g., after cell division or cell encounter, in turbulent flow, will on average increase their separation distance Δ_t with time t according to the Richardson–Obukhov law approximately as (44):

where C₂ is a constant (≈0.5). Strictly, Eq. 11 applies to the inertial range of turbulence. We assume that motile cells in the viscous range, taken as the Kolmogorov length scale, will rapidly separate into the inertial range where turbulence will dominate further dispersion.