The macroscopic delamination of thin films from elastic substrates

Abstract

The wrinkling and delamination of stiff thin films adhered to a polymer substrate have important applications in “flexible electronics.” The resulting periodic structures, when used for circuitry, have remarkable mechanical properties because stretching or twisting of the substrate is mostly accommodated through bending of the film, which minimizes fatigue or fracture. To date, applications in this context have used substrate patterning to create an anisotropic substrate-film adhesion energy, thereby producing a controlled array of delamination “blisters.” However, even in the absence of such patterning, blisters appear spontaneously, with a characteristic size. Here, we perform well-controlled experiments at macroscopic scales to study what sets the dimensions of these blisters in terms of the material properties and explain our results by using a combination of scaling and analytical methods. Besides pointing to a method for determining the interfacial toughness, our analysis suggests a number of design guidelines for the thin films used in flexible electronic applications. Crucially, we show that, to avoid the possibility that delamination may cause fatigue damage, the thin film thickness must be greater than a critical value, which we determine.

Thin films are adhered to substrates in a range of technological applications either to enhance the mechanical properties of bulk materials or to give the surface novel properties (1). Traditionally, the buckling and delamination of these thin coatings have been viewed as an inconvenience with research focusing on how they might be avoided. More recently, however, both the wrinkling and delamination of such films under compression have been exploited in the development of “flexible electronic” devices (2 –7). The goal for these systems is to develop electronic circuits on flexible circuit boards ultimately leading to the manufacture of, among other things, flexible displays and electronic paper (8–10). A major technological challenge limiting the development of such devices is the requirement that the substrate be able to flex without stretching and damaging the wires that make up the circuit. One way to overcome this challenge is to use a polymer substrate that is first stretched and then coated with wires according to the required pattern. On releasing the strain in the substrate, the wires are relatively stiff in compression and so buckle out of the plane to accommodate the imposed deformation. This leads first to a well-studied wrinkling instability (7, 11) and subsequently to the formation of delamination “blisters” (12): localized regions where the film and substrate are no longer bonded. Once formed, these blisters facilitate the flexion of the substrate because the wires can accommodate deformation by bending rather than stretching.

Here, we focus on the features of delamination by characterizing the relationship between the blisters' size and the material properties and their evolution. This complements the many earlier studies, which only considered the wavelength of the wrinkling instability observed prior to delamination (11, 13, 14) and the appearance of localized structures without delamination (15).

Practical applications of delamination are typically found at a microscopic scale, as for circuitry in flexible electronics (3) mentioned above. However, one unique aspect of our work is that we perform well-controlled experiments at a larger (macroscopic) scale. This enables us to readily vary and control the material properties of the system over a wider range than would have been possible at a microscopic scale. The underlying physics may nevertheless be equally applied at microscopic scales. In our experiments, a thin Bi-oriented Polypropylene film (with thicknesses h in the range 15 ≤ h ≤ 90 μm) is adhered by van der Waal's forces to a soft polymeric substrate (Vinylpolysiloxane). We use both thin substrates (which are stretched prior to adhesion) and deep substrates (which are unstretched). Relative to this initial state, the substrate is then uniaxially compressed in a linear stage. For the adhered thin film, however, compression is energetically expensive compared with bending. Therefore, above a critical value of substrate compression the thin film wrinkles with a well-defined wavelength (7, 11). Under further compression wrinkling becomes unstable: the thin film locally debonds and buckles further out of plane.

Results

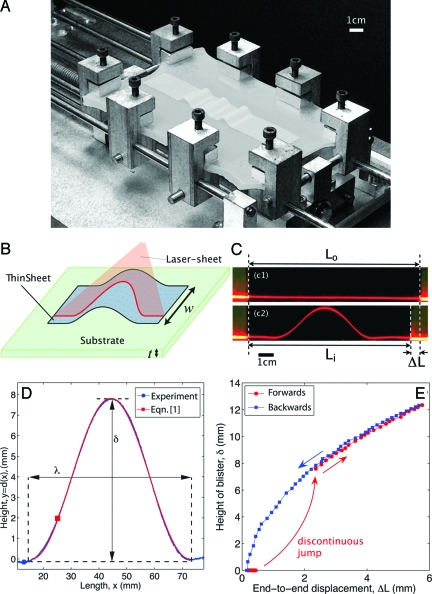
We observe that delamination occurs first with the appearance of a single blister. On further compression, a series of approximately identical blisters appear sequentially. The size of these blisters is typically much larger than the wavelength of the wrinkling instability that precedes it. A representative photograph of such an array of delamination blisters generated in our apparatus is shown in Fig. 1 A More details of the experimental procedure are given in Materials and Methods.

Fig. 1.

Macroscopic delamination blisters. (A) Macroscopic experimental setup for studying the delamination of thin films adhered to soft substrates. (B) A laser sheet is used to measure the profile of the blister(s) as the end-to-end compression ΔL is increased. (C) Plan views of the blister profile as shown by an oblique laser sheet just before (c1) and just after (c2) delamination. (D) Processing these images gives the blister profile y = d(x) (blue points), which is well fitted by the cosine form Eq. 1 (red curve). This fit gives the blister size λ and height δ. (E) Plot of the evolution of the blister height as ΔL is increased (red curve) and then decreased (blue curve). In A the film has thickness h = 50 μm, whereas for C–E, h = 90 μm.

Our investigation is twofold because we focus on understanding both the characteristic dimensions of the first blister at the onset of delamination and the evolution of multiple blisters between delamination events. Consequently, we performed two different types of experiments. First, we measured the width of the first blister at onset λ_c as a function of the material properties of the system. Second, we measured (using an inclined laser sheet) the evolution of the height profile of the blisters as the compression is increased beyond onset. A schematic diagram of this arrangement is presented in Fig. 1 B. Representative (plan view) photographs before and after the onset of delamination for a 90-μm-thick strip are shown in Fig. 1 C. From these images, we extract the height profile of the strip, a typical example of which is shown in Fig. 1 D. This profile is well approximated by a cosine form,

where δ and λ are the height and width of the blister, respectively. The form in Eq. 1 is that expected for the buckling of an Euler column for small deformations (16, 17). This allows for δ and λ to be readily determined by fitting of the experimental profiles. Our analysis is presented in terms of the end-to-end displacement ΔL = L _o − L _i, where L _o is the total uncompressed length of the flat strip and L _i is the distance from the left to the right edge of the strip once compression is applied (see Fig. 1 C). In our experiment, the total end-to-end displacement of the substrate is controlled, not ΔL itself. However, we treat ΔL as an imposed control parameter,* which is measurable directly in experiments. To illustrate the evolution of blister dimensions as ΔL increases, Fig. 1 E shows the dependence of the height of the blister δ on ΔL. Under compression of the substrate, the sheet initially remains approximately flat up to a point where both δ and ΔL change sharply. This discontinuous jump corresponds to the delamination of the strip from the substrate: a blister forms. On increasing the compression ΔL further, the height of the blister also increases. When the compression ΔL is subsequently decreased, δ decreases smoothly following the previous path. However, the blister persists beyond the compression at which it first appeared, disappearing only once ΔL ≈ 0. In what follows we do not discuss this hysteretic behavior but believe that it would be of interest to study this further in future work. Henceforth, we will focus on the onset and evolution of blisters under compression only.

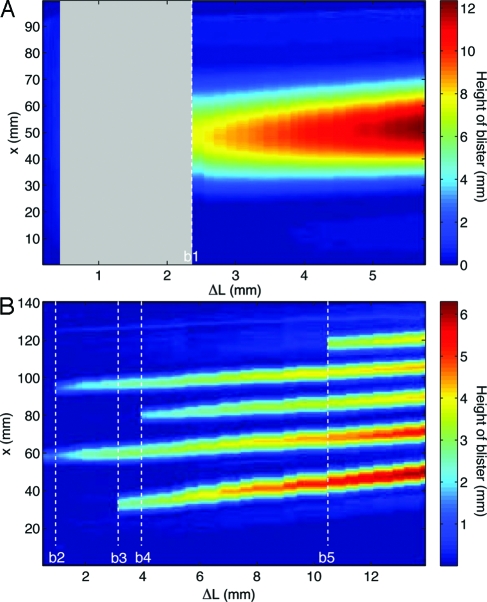
An alternative way to represent the evolution of the blister profile is to construct a space-compression diagram in which the strip height profiles d(x) of the center line of the strip are stacked as a function of ΔL. Two representative examples of such diagrams are given in Fig. 2 A and B for sheets of thickness h = 90 μm and h = 30 μm, respectively. In these diagrams, the color represents the height at each point x along the center line of the strip for a given value of ΔL. In Fig. 2 A the value of ΔL at which the single blister appears is indicated by the vertical dashed line b1. Note that there are values of ΔL through which the system does not pass (gray region). This corresponds to the discontinuity in ΔL at delamination, which can also be seen in the “forwards” curve in Fig. 1 E. If the compression is increased sufficiently, a series of approximately identical blisters are generated sequentially. A space-compression plot with successive delamination events is shown in Fig. 2 B with the appearance of four further blisters indicated by the vertical dashed lines b2, b3, b4, and b5, respectively.

Fig. 2.

Space-compression plots. Evolution of the blister profile as the end-to-end compression is increased. Color represents the blister height profile shown in the adjacent color bars. A single blister (with h = 90 μm) (A) and appearance and evolution of multiple blisters (with h = 30 μm) (B). The gray region emphasizes the discontinuity in ΔL at the first delamination event.

Blisters at Onset.

We now follow an energetical approach to develop a scaling law for the size λ_c of the blisters at onset as a function of the material properties. The elastic energy of the system is U = U_b + U_e, where U_b is the contribution due to bending of the thin film and U_e is the elastic energy of the substrate, which is localized directly underneath the blisters since this is where compression is least restricted. We neglect any compression of the relatively stiff thin film. For a strip of width w and bending stiffness B, the bending energy caused by the presence of a single blister is U_b = $1/2Bw{\int }_{-\lambda /2}^{\lambda /2}d\text{'}\text{'}{(x)}^{2}dx={\pi }^{4}Bw{\delta }^2/{\lambda }_c^3$, where d″(x) is the second derivative with respect to x of the blister profile given in Eq. 1. The elastic energy stored in the substrate U_e depends on the strain ɛ accommodated beneath each blister, the substrate elastic modulus E _s and the substrate thickness t. We estimate U_e in two relevant limiting regimes: (a) large blisters (λ ≫ w,t) and (b) small blisters (λ ≪ w,t). Intermediate regimes may be considered with similar arguments but complicate the subsequent analysis unnecessarily. In each of these limits the volume over which substrate deformation occurs (schematic presented in Figures 3 A and B, respectively) scales as the area λ², multiplied either by (a) the thickness of the substrate t or (b) the width of the strip, w. The substrate energy density in each case is E _sɛ²/2 so that the energy is U_e = αE _sɛ²λ² with α ∼ t for large blisters and α ∼ w for small blisters. The total elastic energy for n identical blisters is therefore given by

where the unknown parameters are the number of blisters n, their width λ, height δ, and the strain ɛ accommodated by each of them. Using the blister profile given in Eq. 1, we obtain the geometrical relationship

which may be used to eliminate δ from Eq. 2 in favor of ΔL. Also, the strain accommodated by each blister is ɛ = ΔL/nλ. Because ΔL is treated as a control parameter, the two unknowns are then the blister width λ and the number of blisters n. If we require that the energy release rate −∂U/∂λ = nwΔγ, where Δγ is the interfacial toughness (16, 18), we find

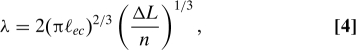where ℓ_ec ≡ (B/Δγ)^1/2 is a characteristic length that balances bending and adhesion. This length is directly analogous to the elasto-capillary length in the aggregation of wet hairs (19, 20) where surface tension replaces interfacial toughness. We note that Eq. 4 for a single blister (n = 1) was also given by Kendall (21) for a dislocation between an adhering flexible sheet and a rigid substrate. Given a fixed number of blisters, Eq. 4 governs the evolution of the blister size. However, for the apparition of the blistering pattern in the first place, the value of n is also unknown. Minimizing the elastic energy with respect to variations in n,† we find that there is a critical value of ΔL/n at onset

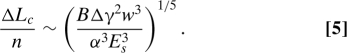Since ΔL is increasing in our (displacement-controlled) experiments, blistering first manifests itself with n = 1. Furthermore, this finite value of ΔL at onset explains the jump in ΔL observed at delamination (see Figs. 1E and 2A). The threshold blister size, λ_c, is now found by substituting the critical value of ΔL/n into Eq. 4. For large blisters (λ_c ≫ w,t) we find

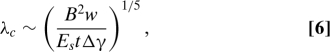whereas for small blisters (λ_c ≪ w,t) we find

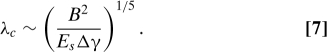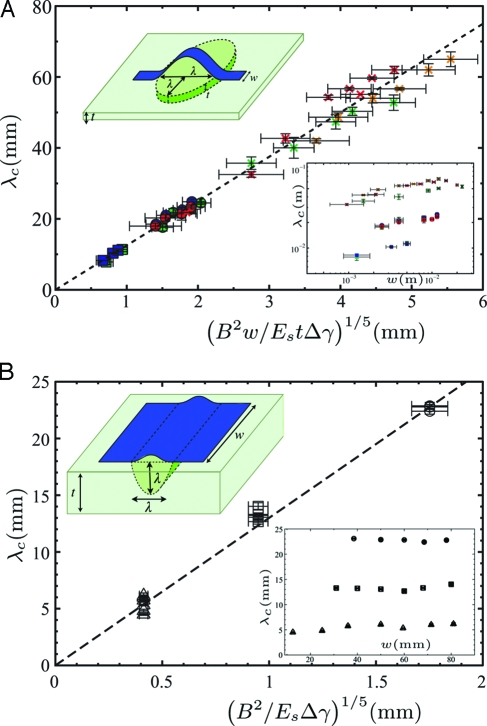
Experimental tests of the predictions Eqs. 6 and 7 are shown in Fig. 3 A and B, respectively. The raw data (for λ_c vs. w) are provided in Fig. 3 A and B Insets. The experimental results are in excellent agreement with the above scalings (dashed lines in Fig. 3). In particular, we note that large blisters, λ_c ≫ w,t, follow the λ_c ∼ w ^1/5 scaling expected, whereas for small blisters, λ_c ≪ w,t, λ_c is approximately independent of w. Furthermore, we observe that the rescalings suggested by our analysis yield a good collapse of our data onto a master curve over a wide range of material parameters. Note that our analysis is only valid if the thin film is incompressible compared with the substrate. For large blisters this requires that Eh ≫ E _s t but for small blisters the condition is Eh ≫ E _sλ. In our experiments these inequalities were satisfied by a factor of at least 20 and more typically 100.

Fig. 3.

Dimensions of blisters at onset in the two limits considered: λ ≫ w,t (A) and λ ≪ w,t (B). In each figure, Insets, Upper left, show schematic diagrams of the extent of the strained region in the substrate beneath a blister. Insets, Lower right, show raw data for λ_c as a function of w. (A) The blister size λ_c at the onset of delamination for the case of large blisters (λ ≫ w,t) as a function of the scaling prediction in Eq. 6. Data are presented for a range of substrate stretching stiffnesses E _s t and film thicknesses h. The substrate stretching stiffnesses are as follows: E _s t = 2,200 N/m (red points), E _s t = 1,200 N/m (blue points), E _s t = 800 N/m (green points), and E _s t = 220 N/m (orange points). The strip thicknesses used are as follows: h = 30 μm (■), h = 50 μm (•), and h = 90 μm (×). (B) The blister size, λ_c, at the onset of delamination for the case of small blisters (λ ≪ w,t) as a function of the scaling prediction in Eq. 7. Data are presented for three different strip thickness h: h = 15 μm (▲), h = 30 μm (■), and h = 50 μm (•). In these experiments E _s ≈ 0.22 MPa and t = 5 cm. Vertical error bars are given by the standard error of 5 repeated experiments.

Evolution of Blisters.

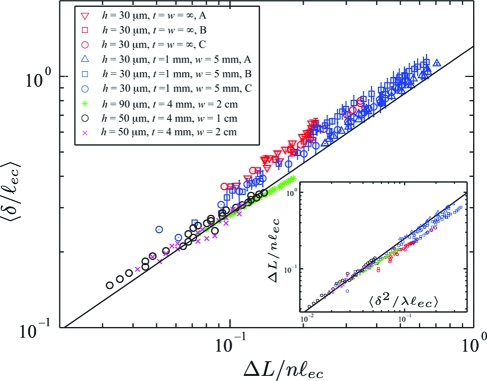
We have already observed that the blisters appear sequentially. In between each of these delamination events we see, e.g., Fig. 2, that the blister size λ and height δ evolve as the end-to-end compression, ΔL, increases. We expect that, with n fixed, λ should be governed by Eq. 4, or, after using Eq. 3,

We emphasize that Eqs. 4 and 8 depend only on the end-to-end displacement per blister, ΔL/n. Thus, these relationships are equally valid for a single blister, n = 1, and for identical multiple blisters, n > 1. Fig. 4 shows experimental measurements of the mean blister height, 〈 δ 〉, as a function of ΔL/n for a range of different material properties and with different numbers of blisters. Plotting the results in this way allows a direct comparison of the evolution of single and multiple blisters with the theoretical prediction in Eq. 8. The agreement between Eq. 8 and the experimental results is striking because there are no adjustable parameters in our model. We also note that the geometrical relationship of Eq. 3 is well satisfied for an arbitrary number of blisters (Fig. 4 Inset). However, the experimental values of δ are slightly above our predictions. We speculate that this slight discrepancy may be ascribed to the softness of the substrate: the film induces a dip in the surface of the substrate in the region of the contact between film and substrate (25).

Fig. 4.

The evolution of the mean blister height 〈δ〉 as the end-to-end displacement ΔL is increased. Experimental results (points) are shown for a variety of different film thicknesses and widths and for different values of the substrate properties. The solid line shows the theoretical prediction Eq. 8, which has no adjustable parameters. (Inset) Experimental measurements of the blister geometry (points) compare well with the theoretical prediction Eq. 3 (line). 〈·〉 denotes the average over multiple blisters (here, results are presented for up to 5 blisters) and error bars show the standard error in this average. Points with no error bars correspond to single blisters.

Discussion and Conclusions

Having validated our theoretical formalism with macroscopic experiments, we conclude by considering its application to the microscopic situations relevant for a wide range of technological applications.

Measuring the Interfacial Toughness.

We note that the interfacial toughness Δγ can be simply expressed in terms of the height and width of the blister by eliminating ΔL between Eqs. 8 and 4:

Hence, Δγ can be easily estimated if the value of the bending stiffness B is known along with the blister profile, in particular, the values of λ and δ. In the delamination of thin metal films—h = O(100 nm)—from polymeric substrates under compression B is known and the blister dimensions—λ = O(10 μm) and height δ = O(1 μm)—are typically measured by atomic force microscopy. However, the value of the interfacial toughness Δγ is much more difficult to determine (18, 26, 27). In Table 1 we provide a survey of the relevant parameters from several studies of straight-sided blisters in the literature (22–24). By substituting these values into Eq. 9 we are able to estimate the interfacial toughness for each of those cases (Table 1, last column). Our estimated values are in reasonable agreement with values determined in similar systems via alternative methods (27, 28). We note, in particular, that in the experiments of Foucher (24) only the film thickness was varied and we therefore expect that the estimates of Δγ should be mutually consistent, as is indeed the case.

Table 1.

Typical values from the literature for the properties of blisters and the associated estimate of the interfacial toughness Δγ

Reference	Thin film type	h, nm	δ, nm	λ, μm	Δγ(Jm−2)
Cleymand et al. (22)	Stainless steel	58	250	2.3	1.3
Parry et al. (23)	Nickel	50	250	3.5	0.2
Foucher (24)	Nickel	100	340	3.4	3
Foucher (24)	Nickel	200	670	8.9	2
Foucher (24)	Nickel	300	1, 000	12.8	3.7

These experiments were all performed on polycarbonate substrates.

Implications for Stretchable Electronics.

We conclude by highlighting some of the implications of our work for stretchable electronics, the technological application that motivated our study. First, we note that the film-substrate system produces blisters with an intrinsic size. This is important for experiments using predefined adhesion patterns (3) because the presence of an intrinsic length scale may lead to the appearance of defects in imposed patterns with different length scales. Indeed, Sun et al. (3) found empirically that the highly adhesive patch of their substrate patterning should be narrower than some critical width to avoid the formation of unwanted delamination blisters (see ref. 3, figure S1). Our formalism can be used to predict this critical size in terms of the mechanical properties of the system. Moreover, the microfabrication process could be simplified significantly by tuning the material properties to produce blisters of a given size, removing the need to selectively alter the substrate adhesion.

In applications of flexible electronics, it is vital that the device retains its mechanical and electrical integrity during repeated use (29). In particular, the buckled wires in these devices should not deform plastically or fracture because this would compromise their conducting characteristics. There are two possible routes to minimize such effects. One is to appropriately choose the material properties of the mechanical system so that buckling does not cause damage. Alternatively, more complex design strategies, for example, multilayer neutral mechanical plane designs (4), can be employed. We consider the former possibility here and show that a simple design criterion could be used in delamination-based devices (3) to avoid irreversible deformation. For this, we assume that irreversible deformations occur when the stress reaches a critical value, σ_∞—the yield stress. In linear elasticity theory the maximum stress in a deformed sheet is proportional to both the thickness of the sheet and its curvature (30). Requiring this maximum stress to be smaller than σ_∞ we find that

where E is the Young's modulus of the film and ν is its Poisson ratio. For a given material, this requires that the thickness be greater than a critical value

where ɛ_∞ = σ_∞/E is the yield strain of the film. This safety requirement is independent of the degree of compression and it applies equally well to multiple blisters far beyond onset as it does to a single blister just beyond the blistering threshold. For the films used in our experiments, we measured σ_∞ = 14 ± 3 MPa giving h _c = 27 ± 12 μm. This estimate is consistent with our observations that only the thinnest films (h = 15 μm) used in our experiments undergo irreversible deformations.

For thin metal films, the critical thickness in Eq. 11 is at least 100 nm and, more typically, 10 μm. These relatively large critical values explain why cracking has been observed in some microscopic experimental realisations (24, 31), while also suggesting that plastic deformation may have occurred in others. With films made from other materials, however, it may be possible to make use of significantly thinner sheets without risking irreversible deformations. For example, using typical values for silicon we find h _c ≈ 10 nm. Assuming that the strength of ultrathin graphite films is comparable with the extremely high strength of monolayer graphene sheets (32), our analysis yields h _c ≈ 0.5 nm, which corresponds to one or two atomic thicknesses [Recent experiments have shown that the deformation of ultrathin graphite films down to thicknesses of as few as 8 atomic layers are well described by continuum elasticity theory (34).] Recently, there has been significant progress in developing techniques for uniform film deposition (33) and transfer onto arbitrary substrates (35). From a mechanical point of view, these advances along with a small critical thickness h _c suggest that ultrathin and high-strength films, such as graphene sheets, may be the ideal material for applications of bendable circuitry at small scales using delamination structures. Moreover, there is potential for further improvement on the robustness of devices by combining the criterion for material properties that we have proposed with more advanced multilayer designs (4).

Materials and Methods

General.

Biaxially oriented polypropylene sheets (Innovia Films) with thicknesses h = 15,30,50, and 90 μm were used. The rectangular strips had widths in the range 1 mm ≤ w ≤ 25 mm. Experiments with strips of different length ℓ showed that the onset blister size was not significantly altered provided that the length is greater than λ_c. For all experiments reported here ℓ > 2λ_c.

Polymer substrates were made from Vinylpolysiloxane (Zhermack). Two different polymer melts were used: pink (8 Shore A) and green (22 Shore A). In general, the Young's moduli of these materials were E _s ≈ 220 kPa and E _s ≈ 800 kPa, respectively though variations were accounted for by direct measurements (see: Measurement of material properties).

For deep substrates we compress uniaxially starting from the undeformed state. For thin substrates, this would produce buckling of the substrate and so we instead first stretch the substrate (uniaxially), adhere the strip to the substrate, and then release the strain gradually. Within the theory of linear elasticity, this is equivalent to a compression relative to the stretched state.

Blister Profile Measurements.

The blister width at the onset of delamination λ_c was measured from digital photographs (taken from above) by using ImageJ. To measure the evolution of λ and δ as the compression ΔL is varied, the thin films were painted black. (Measurements of λ_c using this method were consistent with those obtained using the first method confirming that painting has little effect on the material properties of the film.) A laser sheet at an oblique angle was then used to highlight the deflection of the blister and digital photographs were taken from above. Image analysis software, based on the MATLAB image processing toolbox, was written in-house and used to extract the blister profile, d(x). The maximum of this profile gives the blister height δ. Denoting the two values of x, where d(x) = δ/2, as x ₁ and x ₂, we define the blister size by λ = 2|x ₁−x ₂| (i.e., double the width at half-maximum), which is consistent with the natural definition of λ because of the sinusoidal blister profile in Eq. 1. However, this is a more robust and reproducible method of measuring λ than measuring the point of contact of the film with the substrate from laser profiles.

Measurement of Material Properties.

The elastocapillary length, ℓ_ec, was measured by clamping one end of the film with an imposed vertical displacement and measuring the extent of de-adhered part of the film. This experiment is the dry adhesion equivalent of the capillary-induced sticking of two hairs (20). In processing our experimental data we use the value of ℓ_ec, not Δγ. However, for completeness we note that typically the corresponding interfacial toughness is Δγ ≈ 0.3 J m⁻².

The bending rigidity of films was obtained by clamping horizontally one end of each of several strips, and measuring the deflection under their own weight as a function of their length. We deduce bending rigidity by comparing these results with numerical integration of an elastic beam in a gravitational field with the same mass density (measured directly with a precision scale).

The stretching stiffness, E _s t, of thin substrates was measured by using a dynanometer to measure the force-displacement curve for stretching strains <10%. Over this range of strains, the force-displacement curve is linear, allowing the stretching stiffness E _s t to be determined from the gradient.