Influence of the coupling of interdomain and overall motions on NMR relaxation

Abstract

Most theoretical models for NMR relaxation in liquids assume that overall rotational motion can be described as rotational diffusion with a single diffusion tensor. Such models cannot handle motions (such as between “closed” and “open” states of an enzyme, or between conformers of a partially disordered system) where the shape of the molecule (and hence its rotational diffusion behavior) fluctuates. We provide here a formalism for dealing with such problems. The model involves jumps between discrete conformers with different overall diffusion tensors, and a master (rate) equation to describe the transitions between these conformers. Numerical examples are given for a two-site jump model where global and local motions are concerted, showing how the rate of conformational transitions (relative to the rate of rotational diffusion) affects the observed relaxation parameters.

The interpretation of NMR relaxation parameters in terms of molecular parameters has a long and successful history. The “classic” analysis, which is widely used, describes rotational tumbling by a diffusion equation with a single (perhaps anisotropic) diffusion tensor; superimposed on this are internal motions (of various amplitudes and timescales) that are assumed to be independent of overall rotation (1). The internal motions themselves may be modeled as diffusive motion, such as diffusion in a cone or in a more general restraining potential (2, 3), or may be treated as jumps between a set of discrete conformers, where populations and rate constants of conversion among these species are specified in a master equation (4–6).

In many interesting cases, however, the assumption that rotational tumbling can be described with a single diffusion tensor is not realistic. These include large-amplitude interdomain motions and proteins that are at least partially disordered. In both cases, there are significant populations of conformations with quite different shapes and hence diffusion tensors. The timescale of such global conformational changes can be similar to that of the overall reorientational dynamics, further complicating the problem.

At present, approaches used to analyze NMR relaxation in such systems effectively assume that the overall tumbling and interdomain motions are uncorrelated. The simplest such procedure is to use the extended model-free approach (7), as has been done by Baber et al. for calmodulin (8), where it is assumed that the overall tumbling motion can be described by the diffusion tensor of the dynamically averaged structure and the slow internal motion is identified with the interdomain motions with respect to this frame. More recently, Ryabov and Fushman introduced the ITS (interconversion between two states) model and applied it to di-ubiquitin (9). With respect to overall and interdomain motions, their model is simply a two-site jump model (6, 10) with full anisotropic (but independent) overall motion.

In this article we consider the simplest class of models where internal and overall tumbling motions are not statistically independent. In brief, we assume that the system can jump among discrete conformations with different diffusion tensors and orientations of the vector of interest. Formally, our approach is based on an equation describing the composite conformational exchange-rotational diffusion process (11–13), which provides the total correlation function characterizing laboratory frame reorientation of the vector of interest. Although some of the quantities needed to make use of the formalism (such as the diffusion tensor of each state) may be difficult to determine experimentally, theory [e.g., hydrodynamic modeling (14, 15) of putative structures of the interconverting species] may provide some of the missing input.

As an example, we apply our method to two particularly simple scenarios. The first allows interconversion between two conformations with different isotropic rotational correlation times. This leads to biexponential decays of the time correlation functions that are formally equivalent to the Lipari–Szabo model-free theory (1), but where the parameters have different physical meanings. A second scenario allows the conformations to undergo anisotropic rotational diffusion. We also examine the problems that might be encountered if one tried to force-fit such systems to a model with only a single diffusion tensor.

For the sake of simplicity, we do not treat here the ever-present and heterogeneous fast local motions. In the context of the extended model-free approach (7), we consider only motions that would be described by the slow internal correlation time and order parameter. The simplest way to adapt the formalism of this article to describe fast internal motion is to multiply the correlation functions by [$[{𝓢}_f^2+\left(1-{𝓢}_f^2\right)ext\left(-t/\tau f\right)]$

Results and Discussion

Fluctuating Isotropic Overall Diffusion Tensors.

Much of the relaxation behavior of systems with fluctuating diffusion tensors can be seen in the special case where all these tensors are isotropic. Consider an isotropically reorienting macromolecule with rotational diffusion coefficient D. Let n be a rigidly attached unit vector, pointing along an internuclear vector (for dipolar relaxation) or along a principal axis of the chemical shift tensor [for chemical shift anisotropy (CSA) relaxation]. Then, the relevant reorientational correlation function is 〈P ₂[n(t) · n(0)]〉 = exp(−6Dt), where P ₂(x) = (3x ² − 1)/2 is the second Legendre polynomial. Now imagine that because of global conformational changes the rotational diffusion coefficient depends on time. Then, if the vector n does not move at the instant the rotational diffusion coefficient changes, the reorientational function can be written as

where the angular brackets denote averaging of the fluctuations of D. The problem of evaluating such an average has been solved in a completely different NMR context. (For other physical problems that involve the same mathematics see ref. 13.) Specifically, to describe the influence of chemical exchange on NMR lineshapes, one can use Kubo–Anderson theory (16–18) to evaluate the magnetization 〈exp(i ∫ ω(τ)dτ)〉, where ω(τ) is a fluctuating resonance frequency. We can use this formalism to calculate the reorientational correlation function in Eq. 1, even though the physics of the two problems are quite different.

As the simplest example, consider a macromolecule that fluctuates between two states that have overall diffusion coefficients D ₁ and D ₂. For this model,

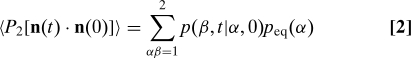The sum is over the possible initial and final states α and β, and p(β,t|α,0) ≡ p_βα can be found by solving

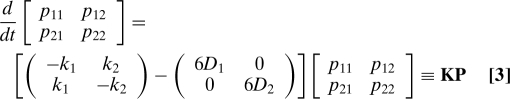subject to the initial conditions P(0) = I, where I is a 2 × 2 unit matrix. Here, k ₁(k ₂) is the rate of transition between states 1 → 2(2 → 1), and p _eq(α) is the normalized equilibrium population of state α: p _eq(1) = k ₂/(k ₁ + k ₂), p _eq(2) = k ₁/(k ₁ + k ₂). Eq. 3 has the formal solution p(β,t|α,0) = [exp(K t)]_βα. The matrix exponential can be expressed in terms of the eigenvectors and eigenvalues of K, KT = Tk, as exp(K t) = T ⁻¹exp(k t)T.

Let us now generalize this in two directions. First, suppose that there are N states with rotational diffusion coefficients D _α, i = 1,2,…N. Second, assume that when the system switches from one state to another, not only the overall motion, but also the orientation of the unit vector changes. Hence, each state is specified by both D _α and n _α, so that n _α · n _β is the cosine of the angle between unit vectors in states α and β. Let R _αβ be the rate constant for transitions from state β to α, with R _αα = −∑_β≠α R _βα. The generalization of Eq. 3 is

with initial condition p _βα(0) = δ_αβ. The generalization of Eq. 2 is

As before, p _eq(α) is the normalized equilibrium population of state α (Rp _eq = 0). Again, the solution of Eq. 4 can be written in terms of the matrix exponential. In the special case where D _α = D for all α, the above formalism gives the reorientational correlation for an N site jump for internal motions of an isotropically reorienting macromolecule in the limit that internal and overall motions are independent (1, 5, 19).

As a simple illustration of this formalism consider the kinetic scheme in Fig. 1. In this model, vertical transitions represent local motions (i.e. changes in the orientation of the vector in a body-fixed frame), whereas horizontal transitions represent global motions that change the overall diffusion coefficient, but not the body-fixed orientation of the vector. The diagonal transition involves simultaneous changes in both the rotational diffusion coefficient and local geometry. If we forbid all transitions except the diagonal one shown in Fig. 1, then global and internal motions are completely concerted. This case is the most different from the usual formalism where global and local motions are independent, so it is worthwhile to examine it in some detail.

Fig. 1.

Simple model for local (vertical) and global (horizontal) conformational changes. The size of the circles reflects the magnitude of the overall isotropic rotational correlation time. The conventional analysis, which assumes that overall and internal motions are independent, is appropriate when only an single vertical pathway is present, and the corresponding correlation function is given in Eq. 6 with parameters in Eq. 7. If only the diagonal pathway is allowed, so that the overall rotational tumbling time and the local orientation of the vector of interest change simultaneously, the correlation function is still given by Eq. 6 but now with parameters in Eq. 8.

If only one of the vertical pathways is allowed, the reorientational correlation function is that of the familiar two-site jump model for local motions and has the model-free form:

where D is the rotational diffusion constant for overall isotropic motion and

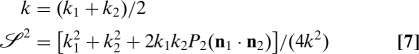This is the result that would be obtained if the formalism of Ryabov and Fushman (9) were applied to this simple problem.

Using the formalism outlined above, we can show that the correlation function for the “diagonal” model of Fig. 1 (in which global and local motions are concerted) also has the model-free form, but with parameters that have a different physical meaning. By solving Eq. 3, we find that D, k, and 𝓢 ² in the conventional theory (Eqs. 6 and 7) must be replaced by the following effective values:

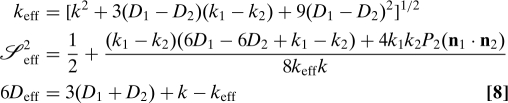As expected from the analogy with lineshapes (16, 17), the deviation from the standard theory depends on the ratio of the difference between D ₁ and D ₂ and interconversion rate k (from Eq. 7). The two models become the same as (D ₁ − D ₂)/k → 0.

The first line of Eq. 8 is half the difference between the eigenvalues of the matrix K in Eq. 3. The third line is the eigenvalue with the smaller magnitude. These results mean that, if the model-free formalism was blindly applied to fit data for this model with concerted overall and internal motions, the fit would be perfect, but the extracted parameters could not be interpreted correctly in the usual way. For example, the extracted 𝓢² would now depend not only on the amplitude of the internal motion but also on the timescales of internal and overall motions. However, if the rate of transition between the two states is faster than the difference between the rotational diffusion coefficients of the two states, then the concerted system would be closely approximated by a system with the average rotational diffusion coefficient that undergoes independent two-site internal motion. Thus, the model-free approach would give the correct amplitude for the internal motion, even though local and global transitions are concerted.

These results suggest that Baber et al.'s extended model-free analysis of interdomain motions in calmodulin (8) provides a meaningful estimate of the amplitude of such motions. In this study, the effective overall correlation time was found to be ≈10 ns, whereas the interdomain correlation time was ≈3 ns. This timescale separation is sufficient for the extracted order parameter describing the amplitude of interdomain motions to be essentially uncontaminated by contributions due to coupling of the interdomain and overall motions.

Although this model is quite simple, it does illustrate some of the key physical ideas and the structure of the mathematical formalism. It is the simplest model that treats transitions that change the rotational diffusion constant, a feature that has been omitted from the ITS model for NMR relaxation in systems undergoing large-scale conformational changes (9).

Formal Approach to Exchange Diffusion.

The above exposition was somewhat informal. Here, we give a more formal derivation, starting with the work of Berne and Pecora (11), which allows generalizations (such as to anisotropic diffusion) to be made in a straightforward manner. Let us consider a system where the diffusion tensor of each conformation is axially symmetric with rotational diffusion coefficients D _⊥ ^α and D _∥ ^α, α = 1,2,…N. Suppose that in state α the vector of interest makes a polar angle θ_α with respect to the symmetry axis of the diffusion tensor. Assume that at the moment an α → β transition occurs, the orientation of the monitored vector in the laboratory frame changes by an angle Ψ_αβ. Immediately after the transition, the vector of interest continues to move by rotational diffusion, which is now characterized by a polar angle θ_β with the (new) principal diffusion axis. Because we are considering axially symmetric diffusion tensors, the dynamics before and after the transition do not depend on the azimuthal angles ϕ_α and ϕ_β.

If the direction of the symmetry axis of the diffusion tensor is the same in all conformational states, we can assign for each state angles θ_α and ϕ_α that locate the monitored vector in the (common) diffusion tensor frame. The more general situation in which the direction of this symmetry axis changes in different states is rather complex.

As shown in Methods, the time correlation function relevant to NMR relaxation can be written as

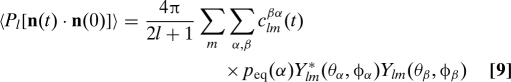where the Y _lm are spherical harmonics and the time-dependent expansion coefficients c _lm ^βα(t) are solutions of

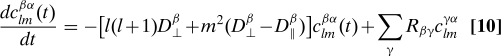which must be solved subject to the initial conditions c _lm ^βα(0) = δ_βα. Eqs. 9 and 10 are the main results of this section, and they reduce to Eqs. 5 and 4 when the diffusion tensors are isotropic. For NMR dipolar or CSA relaxation, we need only consider l = 2, and a separate set of equations can be solved for each value of |m|. The solution can again be written as a matrix exponential. For systems with isotropic overall tumbling, c _lm ^βα(t) is independent of m. This allows us to use the addition theorem for spherical harmonics to carry out the sum over m in Eq. 9, recovering Eq. 5, with the identification p(β,t|α,0) = c _2m ^βα. For axially symmetric tops and l = 2, we have

where ϕ_αβ = ϕ_α − ϕ_β.

Illustrative Calculations.

We now present numerical results for the isotropic two-state model system discussed above, whose effective model-free parameters are given in Eq. 8. We discuss how it might be possible to distinguish between conformational exchange among states with different rotational properties versus more localized internal motion superimposed on global tumbling characterized by just a single diffusion coefficient. We are particularly interested in parameters that arise from (relatively) slow exchange between two states with different rotational constants, because this is the regime that we expect to be relevant to large-amplitude conformational transitions.

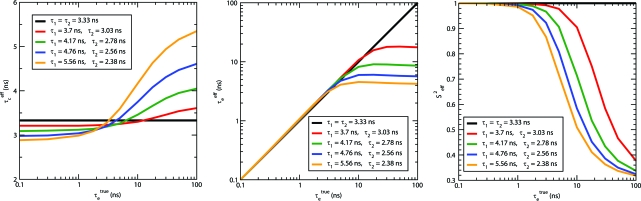
In Fig. 2, we plot the effective model-free parameters (τ_c ^eff ≡ (6D _eff)⁻¹, τ_e ^eff ≡ (2k _eff)⁻¹, and 𝓢_eff ²) against the true timescale for exchange, τ_e ^true = (k ₁ + k ₂)⁻¹. In Fig. 3 we plot the effective generalized order parameters as a function of τ_e ^true for several values of the jump angles and p _eq(1) = 0.5.

Fig. 2.

Effective model-free parameters as a function of the true timescale for conformational exchange, τ_e ^true = (k ₁ + k ₂)⁻¹. Colors correspond to pairs of states with different rotational constants. (Left) Effective global tumbling time, τ_c ^eff = 1/6D _eff. (Center) Effective internal correlation time, τ_e ^eff = 1/2k _eff. (Right) Effective order parameter, 𝓢 _eff ². In all cases, p _eq(1) = 0.3, n ₁ = n ₂.

Fig. 3.

Effective model-free parameters. (Left) Effective order parameters for different jump angles Δθ ≡cos⁻¹[n ₁ · n ₂]. τ_c ¹ = 5.56 ns, τ_c ² = 2.38 ns. (Center) ${\tau }_c^{\text{eff}}/{\tau }_c^{\text{av}}=\bar{D}/D_{\text{eff}}$ as a function of 6ΔDτ_e ^true for pairs of states with different rotational constants. (Right) Values of τ_c ^eff (solid lines) and τ_e ^eff (dashed lines), plotted against τ_e ^true = (k ₁ + k ₂)⁻¹. In all cases, p _eq(1) = p _eqx(2) = 0.5.

Fast jumps between global conformations.

The plots reveal the existence of an averaging regime in the fast-exchange limit, which is at the left-hand side of each profile. In this limit, the effective tumbling time is determined by the weighted average of the diffusion constants of the individual spheres (D _eff(fast) = D̅ ≡ p _eq(1)D₁ + p _eq(2)D ₂), the observed internal timescale is the true timescale for exchange (τ_e ^eff(fast) = τ_e ^true), and the apparent order parameter becomes what is expected for the true local internal dynamics superimposed on single tensor (isotropic) tumbling, i.e., the familiar two-state jump model in the second line of Eq. 7. Hence, in this example, the model-free approach would work even though overall and local motions are concerted as long as τ_e ^true < 2 ns.

Slow jumps between states.

The slow-exchange limit is seen at the right-hand edge of Figs. 2 and 3. Here, time-correlation functions and spectral densities are the population-weighted average of the two states. Hence, the effective tumbling time is the tumbling time for the slow sphere (sphere “1”), the apparent internal timescale is determined by the difference between the two diffusion constants (τ_e ^eff(slow) = (6ΔD)⁻¹, where ΔD ≡ D ₂ − D ₁), and the effective order parameter is the population of the slow state. Outside the slow-exchange limit, pairs of spheres with a larger ΔD depart from the averaging limit for smaller values of τ_e ^true than do those with a smaller ΔD.

This behavior can be rationalized as follows. When the random hops between the two spheres becomes fast enough, a vector rigidly attached to the protein effectively samples both of the diffusion constants (weighted by their equilibrium populations) over any small angle it traverses. Under this condition, the single diffusion tensor description of tumbling is adequate. Departure from the averaging regime should largely depend on ΔDτ_e ^true (see Eq. 8). With this in mind, in Fig. 3 we have plotted the ratio τ_c ^true/τ_c ^true(fast) = $\bar{D}$/D _eff as a function of 6ΔDτ_e ^true when p _eq(1) = 0.5. It is evident that deviation of the effective model-free parameters from their fast-exchange limits grows with 6ΔDτ_e ^true. This ratio reaches its maximum value $\bar{D}$/D ₁ (where D ₁ is the diffusion constant for the larger sphere) in the slow-exchange limit. For fixed values of 6ΔDτ_e ^true and 6$\bar{D}$ (i.e., along a vertical line in Fig. 3 Center), spheres characterized by larger 6ΔD exhibit greater deviation from 1 because, on average, larger angle displacements of the fast sphere take place before jumps to the slow form, implying that the motion of the vector is more heterogeneous. However, for fixed 6ΔDτ_e ^true and 6ΔD, increasing $\bar{D}$ also increases the ratio for the same reason.

Is it possible to distinguish slow exchange between states with different rotational properties from internal motion superimposed on single tensor tumbling? This is clearly not possible if one has access to the correlation function of only a single spin, because any set of effective model-free parameters that can be produced by our model has a plausible interpretation from within the single tensor paradigm. However, in our model, not only τ_c ^eff, but also τ_e ^eff should have the same value for any spin in the protein. Thus, a signature of global conformational changes that alter the overall diffusion tensor is the existence of a single internal correlation time. However, this effective internal time must be shorter than the global tumbling time or it will not have a significant effect on the relaxation. With this in mind, we have plotted both τ_c ^eff and τ_e ^eff against τ_e ^true in Fig. 3 to explore conditions under which τ_e ^eff is less than τ_c ^eff. As can be seen in the orange curves in Fig. 3, τ_c ^eff may be greater than τ_e ^eff for large enough values of ΔD, even for slow exchange. This is in contrast to the green curves, which correspond to a smaller value of ΔD and for which τ_e ^eff > τ_c ^eff for slow enough exchange. The orange curves thus correspond to a situation in which even slow conformational exchange leads to a fairly short effective (global) internal timescale; finding this to be nearly constant for many vectors might then be an indication of conformational exchange between states of different rotational tumbling times.

Concluding Remarks

We have developed a method for obtaining time correlation functions and spectral densities when a macromolecule undergoes exchange between conformations with different overall rotational properties. For many values of the expected input parameters, k _α and D _α (shown in Figs. 2 and 3), the resulting effective model-free parameters are not qualitatively different from those that would be extracted from a conventional model-free analysis (1) [or, in practice where fast local motions are allowed, the extended model-free analysis (7)]. The simple formulas for a two-state isotropic case, given in Eq. 8, can be used qualitatively to estimate the likely deviations from the single-diffusion-tensor limit, given estimates of diffusion constants and rates of conformational transitions. These analytical results can be applied in a qualitative way to more complex systems to assess the sensitivity of NMR relaxation parameters to the assumption of a single overall diffusion tensor.

The results presented here are limited to systems in which each conformer tumbles as a symmetric top and where the symmetry axis of the diffusion tensor is the same for all states. The physics of the situation, however, suggests that the only variables that are important are θ_α, the angle between the monitored vector and the symmetry axis of the diffusion tensor, and Ψ_αβ, the orientation change in the laboratory frame for the α → β transition. (One can also make the substitution θ_α → π − θ_α without changing the physics of the model.) If the value of Ψ_αβ is such that it is possible to define azimuthal angles ϕ_α, ϕ_β such that cosΨ_αβ = ±cosθ_αcosθ_β + sinθ_αsinθ_βcos(ϕ_α − ϕ_β), then the problem simplifies. In this case, we expect that this can be treated as though the orientation of the diffusion tensor does not change, but instead the angles of the monitored vector change from θ_α,ϕ_α to θ_β,ϕ_β (or to π − θ_β,ϕ_β). In a future study, the conserved symmetry axis constraint should be removed, and the formalism generalized to treat fully anisotropic overall motion. A key feature of this more general theory is the presence of coupling between different values of m in the analogue of Eq. 10.

It is also possible to write analogous expressions for the correlation function and equations of motion when the conformational dynamics are diffusive, instead of given by a jump model. Such a formulation extends our approach to nonactivated structural transitions. However, the challenge for such more sophisticated models is not really to write down and solve the equations of motion, or to find the corresponding spectral densities and relaxation parameters. Rather, the challenge is to find circumstances where enough is known about the number of states, and their detailed (anisotropic) rotational diffusion tensors to warrant applying such detailed models. One promising avenue exploits the significant recent improvements in the ability to compute rotational diffusion tensors from structure (14, 15). The input required to apply the theory described here would then consist of two or more structural models and the rate constants for interconversion between them. The number of fitting parameters would be similar to that required for analysis of micro- to millisecond chemical exchange data (20), and could serve to extend ideas developed there to shorter timescales.

Methods

With use of the addition theorem for spherical harmonics, the general form of the angular time correlation function is

For NMR relaxation experiments, l = 2. Here, n is a lab frame (LF) unit vector specifying the internuclear orientation or the principal axis of an axially-symmetric chemical shift tensor whose relaxation behavior is being monitored (21–23). NMR relaxation also depends on other fluctuating parameters, such as the internuclear distance (for dipolar relaxation) or the magnitude of the chemical shift anisotropy (for CSA relaxation). For simplicity, we have omitted such interaction strength factors here; as long as the fluctuations in these factors are independent of angular motion, their effects can be readily added to the formalism outlined here (6, 24).

Two operations are needed to rewrite Eq. 12 in a form amenable to treatment by the propagator method. First, we decompose the motion of n into global reorientation of a body-fixed reference frame (BF) coordinate system, and the trajectory of the vector in the body-fixed frame, n _BF. Then, the total correlation function can be decomposed into contributions from each of the species in the exchange-diffusion system (11, 25), each with its own BF coordinate system. Eq. 12 then becomes

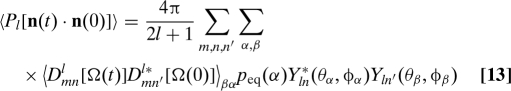Here, Ω are the Euler angles that rotate the LF axes into the BF axes, and the D _mn ^l are Wigner rotation matrices (26). Greek indices α and β label conformations or states adopted by the protein, and the subscript βα indicates that the initial state for this term is assumed to be α, and the state at time t is β; summing over all values of α and β then yields the total time-correlation function. As described above, (θ_α,ϕ_α) give the orientation of the vector of interest, n _BF (e.g., an NH bond vector) in the principal axis frame of state α.

We write the global correlation function in Eq. 13 as

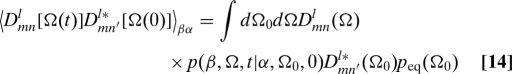Here, p(β,Ω,t|α,Ω_o,0) is the conditional probability for a molecule to be in conformation β and lab-frame orientation Ω at time t, given that it was in conformation α and orientation Ω₀ at t = 0; this is a generalization of the well-known Green's functions for pure rotational diffusion (27, 28). In an isotropic medium, the equilibrium probability of the LF orientation Ω₀ is p _eq(Ω₀) = 1/(8π²).

We employ a standard technique of expanding the propagator in Eq. 14 in terms of the eigenfunctions of the rotational diffusion operator for state β (4, 11). For an axially symmetric top, we may write

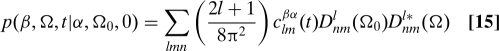D_nm ^l are Wigner matrices, which are eigenfunctions of the diffusion operator for axially symmetric tensors. (26, 29) The time-dependent expansion coefficients c_lm ^βα (t) are solved for later. We can evaluate Eq. 14 by substituting Eq. 15 into Eq. 14 and using orthogonality properties of the Wigner rotation matrices. Substituting the result into Eq. 13 yields the total correlation function given in Eq. 9 above.

When the conformational states are discrete, the time evolution of the Green's function in Eq. 15 is governed by the following equation of motion (11, 25)

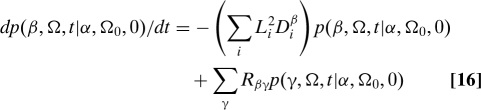Here, L _i is an angular momentum operator and R is the rate matrix for transitions, as before. We use the diagonal form of the diffusion operator, $\sum {\text{L}}_i{\text{D}}_{ij}^{\beta }{\text{L}}_j$, because the body-fixed frame diagonalizes this operator. We obtain equations of motion for the time-dependent expansion coefficients by substituting Eq. 15 into Eq. 16, using the fact that D _mn ^l is an eigenfunction of the diffusion operator for a symmetric top with eigenvalue l(l + 1)D _⊥ + m ²(D _⊥ − D _∥). The resulting equation for the time-dependent expansion coefficients is given by Eq. 10 above.