Percolation on fitness landscapes: effects of correlation, phenotype, and incompatibilities

Abstract

We study how correlations in the random fitness assignment may affect the structure of fitness landscapes, in three classes of fitness models. The first is a phenotype space in which individuals are characterized by a large number n of continuously varying traits. In a simple model of random fitness assignment, viable phenotypes are likely to form a giant connected cluster percolating throughout the phenotype space provided the viability probability is larger than 1/2ⁿ. The second model explicitly describes genotype-to-phenotype and phenotype-to-fitness maps, allows for neutrality at both phenotype and fitness levels, and results in a fitness landscape with tunable correlation length. Here, phenotypic neutrality and correlation between fitnesses can reduce the percolation threshold, and correlations at the point of phase transition between local and global are most conducive to the formation of the giant cluster. In the third class of models, particular combinations of alleles or values of phenotypic characters are “incompatible” in the sense that the resulting genotypes or phenotypes have zero fitness. This setting can be viewed as a generalization of the canonical Bateson-Dobzhansky-Muller model of speciation and is related to K- SAT problems, prominent in computer science. We analyze the conditions for the existence of viable genotypes, their number, as well as the structure and the number of connected clusters of viable genotypes. We show that analysis based on expected values can easily lead to wrong conclusions, especially when fitness correlations are strong. We focus on pairwise incompatibilities between diallelic loci, but we also address multiple alleles, complex incompatibilities, and continuous phenotype spaces. In the case of diallelic loci, the number of clusters is stochastically bounded and each cluster contains a very large sub-cube. Finally, we demonstrate that the discrete NK model shares some signature properties of models with high correlations.

1 Introduction

The notion of fitness landscapes, introduced by a theoretical evolutionary biologist Sewall Wright in 1932 (see also Kauffman 1993; Gavrilets 2004), has proved extremely useful both in biology and well outside of it. In the standard interpretation, a fitness landscape is a relationship between a set of genes (or a set of quantitative characters) and a measure of fitness (e.g. viability, fertility, or mating success). In Wright’s original formulation the set of genes (or quantitative characters) is the property of an individual. However, the notion of fitness landscapes can be generalized to the level of a mating pair, or even a population of individuals (Gavrilets, 2004).

To date, most empirical information on fitness landscapes in biological applications has come from studies of RNA (e.g., Schuster 1995; Huynen et al. 1996; Fontana and Schuster 1998), proteins (e.g., Lipman and Wilbur 1991; Martinez et al. 1996; Rost 1997), viruses (e.g., Burch and Chao 1999, 2004), bacteria (e.g., Elena and Lenski 2003; Woods et al. 2006), and artificial life (e.g., Lenski et al. 1999; Wilke et al. 2001). The three paradigmatic landscapes — rugged, single-peak, and flat — emphasizing particular features of fitness landscapes have been the focus of most of the earlier theoretical work (reviewed in Kauffman 1993; Gavrilets 2004). These landscapes have found numerous applications with regards to the dynamics of adaptation (e.g., Kauffman and Levin 1987; Kauffman 1993; Orr 2006a,b) and neutral molecular evolution (e.g., Derrida and Peliti 1991).

More recently, it was realized that the dimensionality of most biologically interesting fitness landscapes is enormous and that this huge dimensionality brings some new properties which one does not observe in low-dimensional landscapes (e.g. in two- or three-dimensional geographic landscapes). In particular, multidimensional landscapes are generically characterized by the existence of neutral and nearly neutral networks (also referred to as holey fitness landscapes) that extend throughout the landscapes and that can dramatically affect the evolutionary dynamics of the populations (Gavrilets, 1997; Gavrilets and Gravner, 1997; Reidys et al., 1997; Gavrilets, 2004; Reidys et al., 2001; Reidys and Stadler, 2001, 2002).

An important property of fitness landscapes is their correlation pattern. A common measure for the strength of dependence is the correlation function ρ measuring the correlation of fitnesses of pairs of individual at a distance (e.g., Hamming) d from each other in the genotype (or phenotype) space:

$$\rho (d)=\frac{\mathrm{cov}{[w(.),w(.)]}_d}{\mathrm{var}(w)}$$ (1)

(Eigen et al., 1989). Here, the term in the numerator is the covariance of fitnesses of two individuals at distance d, and var(w) is the variance in fitness over the whole fitness landscape. For uncorrelated landscapes, ρ(d) = 0 for d > 0. In contrast, for highly correlated landscapes, ρ(d) decreases with d very slowly.

The aim of this paper is to extend our previous work (Gavrilets and Gravner, 1997) in a number of directions paying special attention to the question of how correlations in the random fitness assignment may affect the structure of fitness landscapes. In particular, we shed some light on issues such as the existence and number of viable genotypes, as well as the number and size of the clusters of viable genotypes. To this end, we introduce a variety of models, which could be divided into two essentially different classes: those with local correlations, and those with global correlations. As we will see, techniques used to analyze these models, and answers we obtain, differ significantly. We use a mixture of analytical and computational techniques; it is perhaps necessary to point out that these models are very far from trivial, and one is quickly led to outstanding open problems in probability theory and computer science.

We start (in Section 2) by briefly reviewing some results from Gavrilets and Gravner (1997). In Section 3 we generalize these results for the case of a continuous phenotype space when individuals are characterized by a large number of continuously varying traits such as size, weight, color, or the concentrations of some gene products. The latter interpretation of the phenotype space may be particularly relevant given the rise of proteomics and the growing interest in gene regulatory networks.

The main idea behind our local correlations model studies in Section 4 is fitness assignment conformity. Namely, one randomly divides the genotype space into components which are forced to have the same phenotype; then, each different phenotype is independently assigned a random fitness. This leads to a simple two-parameter model, in which one parameter determines the density of viable genotypes, and the other the correlations between them. We argue that the probability of existence of a giant cluster (which swallows a positive proportion of all viable genotypes) is a non-monotone function of the correlation parameter and identify the critical surface at which this probability jumps almost from 0 to 1. In Appendix B we also investigate the effects of interaction between conformity structure and fitness assignment.

Section 5 introduces a class of models where genotypes are eliminated due to random incompatibilities between alleles. These models are characterized by global correlations. When there are only two alleles at each locus, the models are equivalent to random versions of the SAT problem, which is the canonical constraint satisfaction problem in computer science. In general, a SAT problem involves a set of Boolean variables and their negations that are strung together with OR symbols into clauses. The clauses are joined by AND symbols into a formula. A SAT problem asks one to decide, whether the variables can be assigned values that will make the formula true. Arguably, SAT is the most important class of problems in complexity theory. In fact, the general SAT problem was the first known NP-complete problem and was established as such by S. Cook in 1971 (Cook 1971). An important special case, K- SAT, has the length of each clause fixed at K. Even considerable simplifications, such as 3- SAT (see Section 5.4), remain NP-complete, although 2- SAT (see Section 5.1) can be solved efficiently by a simple algorithm. See e.g. Korte and Vygen (2005) for a comprehensive presentation of the theory. Difficulties in analyzing random SAT problems, in which formulas are chosen at random, in many ways mirror their complexity classes, but even random 2- SAT presents significant challenges (de la Vega, 2001; Bollobás et al., 1994). In our present interpretation, the main reason for these difficulties is that correlations are so high that the expected number of viable genotypes may be exponentially large, while at the same time the probability that even one viable genotype exists is very low. In Section 5, we show that the high correlations in the random 2- SAT model essentially force the landscape to either have no viable genotypes or else to have fairly large sub-cubes contained within any cluster of viable genotypes. Moreover, the number of such clusters will be, in a proper interpretation, finite. The theory for higher order incompatibilities is closely related and we briefly review the existing literature for 3- SAT. We also describe pairwise incompatibility models on multiallelic genotype spaces and continuous phenotype spaces where we address the question of existence of viable individuals.

In Section 6 we demonstrate that the discrete NK model shares some signature properties of models with high correlations. The proofs of our major results are relegated to Appendices A–E.

We summarize our main findings, provide their intuitive explanations, and briefly discuss their biological significance at the end of each section. Our most general results, their theoretical and biological significance, implications, and limitations are discussed in Section 7.

2 The basic case: binary hypercube and independent binary fitness

We begin with a brief review of the basic setup, from Gavrilets and Gravner (1997) and Gavrilets (2004). There are n diallelic loci with alleles 0 and 1. Each genotype is represented by a binary sequence of length n. The genotype space, i.e. the set of all possible genotypes, can be represented by an n-dimensional binary hypercube G. In this space, genotypes are linked by edges induced by bit-flips, i.e., mutations at a single locus, for example. For n = 4, a sequence of mutations might look like

$$0000\leftrightarrow 1000\leftrightarrow 1001\leftrightarrow 1101\leftrightarrow 1100.$$

The (Hamming) distance d(x, y) between genotypes x and y is the number of loci in which x and y differ or, equivalently, the least number of mutations which connect x and y.

The fitness of each genotype x is denoted by w(x). We will describe several ways to prescribe the fitness w at random, according to some probability measure P on all 2²ⁿ possible assignments. Then we say that an event A_n happens asymptotically almost surely (a. a. s.) if its probability P(A_n) → 1 as n → ∞. Typically, A_n will capture some important property of (random) clusters of genotypes.

We will commonly assume that fitness w takes only two values so that each genotype x is either viable (w(x) = 1) or inviable (w(x) = 0). As a natural starting point, Gavrilets and Gravner (1997) considered uncorrelated landscapes, in which w(x) is chosen to be 1 with probability p, for each x independently of others. Thus, p can be viewed as the probability that a random combination of genes results in a viable individual. Such binary fitness assignment is not as restrictive as one might expect. If fitness were to be a random number between 0 and 1, then p could be interpreted as the width of an acceptable “fitness band” (Gavrilets and Gravner, 1997; Gavrilets, 2004). We continue to refer to viable genotypes for the rest of this section and note that this is a well-studied problem in mathematical literature, although it presents considerable technical difficulties and some issues are still not completely resolved.

Given a particular fitness assignment, viable genotypes form a subset of G, which is divided into connected components or clusters. For example, with n = 4, if 0000 is viable, but its 4 neighbors 1000, 0100, 0010, and 0001 are not, then it is isolated in its own cluster.

Perhaps the most basic result determines the connectivity threshold (Toman, 1979): when p > 1/2, the set of all viable genotypes is connected a. a. s. By contrast, when p < 1/2, the set of viable genotypes is not connected a. a. s. This is easily understood, as the connectedness is closely linked to isolated genotypes, whose expected number is 2ⁿp(1 − p)ⁿ. This expectation makes a transition from exponentially large in n to exponentially small at p = 1/2. The events {x is isolated}, x ∈ G, are only weakly correlated, which implies that when p < 1/2 there are exponentially many isolated genotypes with high probability, while when p > 1/2, a separate argument shows that the event that the set of viable genotypes contains no isolated vertex but is not connected becomes very unlikely for large n. This is perhaps the clearest instance of the local method: a local property (no isolated genotypes) is a. a. s. equivalent to a global one (connectivity).

Connectivity is clearly too much to ask for, as p above 1/2 is not biologically realistic. Instead, one should look for a weaker property which has a chance of occurring at small p. Such a property is percolation, a. k. a. existence of the giant component. For this, we scale p = λ/n, for a constant λ. When λ > 1, the set of viable genotypes percolates, that is, it a. a. s. contains a component of at least c · n⁻¹2ⁿ genotypes, with all other components of at most polynomial (in n) size. When λ < 1, the largest component is a. a. s. of size Cn. Here and below, c and C are some constants. These are results from Bollobás et al. (1994).

The local method that correctly identifies the percolation threshold is a little more sophisticated than the one for the connectivity threshold, and uses branching processes with Poisson offspring distribution — hence we introduce notation Poisson(λ) for a Poisson distribution with mean λ. Viewed from, say, genotype 0…0, the binary hypercube locally approximates a tree with uniform degree n. Thus viable genotypes approximate a branching process in which every node has the number of successors distributed binomially with parameters n − 1 and p, hence this random number has mean about λ and is approximately Poisson(λ). When λ > 1, such a branching process survives forever with probability 1 − δ > 0, where δ depends on λ and is given by the implicit equation

$$\delta =e^{\lambda (\delta -1)}.$$ (2)

(e.g., Athreya and Ney 1971). Large trees of viable genotypes created by the branching processes which emanate from viable genotypes merge into a very large (“giant”) connected set. On the other hand, when λ < 1 the branching process dies out with probability 1.

The condition λ > 1 for the existence of the giant component can be loosely rewritten as

$$p>\frac{1}{n}.$$ (3)

This shows that the larger the dimensionality n of the genotype space, the smaller values of the probability of being viable p will result in the existence of the giant component. Biological populations can evolve along this giant cluster by mutation and random drift and can diverge dramatically without the need to cross any fitness valleys or any help from selection. See Gavrilets and Gravner (1997); Gavrilets (1997, 2004); Skipper (2004); Pigliucci and Kaplan (2006); Wilkins (2007) for discussions of biological and philosophical significance and implications of this important result.

3 Percolation in a continuous phenotype space

In this section we assume that individuals are characterized by n continuous traits, labeled 1, 2,…,n (such as size, weight, color, or concentrations of particular gene products), each of which can have value between 0 and 1. A phenotype is therefore given by n trait-values, that is, by numbers z₁,…, z_n ∈ [0, 1]. Let P = [0, 1]ⁿ be the phenotype space, i.e., the set of all possible phenotypes.

We begin with a modification of the model of independent binary fitness assignment used in the previous section. First, we choose N points x₁,…, x_N ∈ P uniformly at random where N is a Poisson(λ) random variable. (This construction is known as Poisson point location.) Points x₁,…, x_N will be interpreted as “peaks” of equal height in the fitness landscape. Note that in this section, parameter λ gives the expected number of peaks in the phenotype space. Second, we declare any phenotype within r of one of the peaks, where r is a small positive number, viable and any phenotype not within r of one of the peaks inviable. Parameter r can be interpreted as measuring how harsh the environment is. For simplicity, we will assume “within r” to mean that “every coordinate differs by at most r.” Note that this makes the set of viable phenotypes correlated, albeit the range of correlations is limited to 2r.

Our most basic question is whether a positive proportion of viable phenotypes is connected together into a giant cluster. Note that the probability p that a random point in P is viable is equal to the probability that there is a “peak” within r from this point. Therefore,

$$p=1-\exp [-\lambda {(2r)}^n]\approx \lambda {(2r)}^n.$$

This is also the expected combined volume of viable phenotypes.

We will consider peaks x_i and x_j to be neighbors if they share a viable phenotype, that is, if their r-neighborhoods overlap; and we consider them to be connected if they are linked by a chain of consecutively neighboring peaks. By the standard branching process comparison, the necessary condition for the existence of a giant cluster is that a peak x neighbors more than one other peak on the average. All peaks within 2r of the focal peak are its neighbors. Therefore, the expected number of peaks neighboring x is

$$\nu =\lambda ·{(4r)}^n,$$

and ν > 1 is necessary for percolation. As demonstrated by Penrose (1996) (for a different choice of the norm, but the proof is the same), this condition becomes sufficient when n is large.

If ν > 1 and fixed, then a. a. s. a positive proportion of all peaks (that is, cN peaks, where c = c(ν) > 0) are connected in one “giant” component, while the remaining connected components all have size of order log N. On the other hand, if ν < 1, all components a. a. s. have size of order log N.

Note that the expected number λ of peaks in P can be written as ν · (4r)⁻ⁿ. Thus, the condition ν > 1 for the existence of the giant component of viable phenotypes can be loosely rewritten as

$$p>\frac{1}{2^n}.$$ (4)

This shows that viable phenotypes are likely to form a large connected cluster even when one is very unlikely to hit one of them at random, if n is even moderately large. The same conclusion and the same threshold are valid if instead of n-cubes we use n-spheres of a constant radius.

Thus, dramatic divergence in phenotype without any loss in fitness is possible if the dimensionality of the phenotype space is sufficently large. The percolation threshold in the continuous phenotype space given by inequality (4) is much smaller than that in the discrete genotype space which is given by inequality (3). For example, the percolation threshold in the 10-dimensional continuous space P is similar to that in the genotype space G corresponding to 1024 diallelic loci. An intuitive reason for this is that continuous space offers a viable point a much greater opportunity to be connected to a large cluster. Indeed, in the discrete genotype space G there are n neighbors per each genotype. In contrast, in the continuous phenotype space P, the ratio of the volume of the space where neigboring peaks can be located (which has radius 2r) to the volume of the focal n-cube (which has radius r) is 2ⁿ.

4 Percolation in a correlated landscape with phenotypic neutrality

The standard paradigm in biology is that the relationship between genotype and fitness is mediated by phenotype (i.e., observable characteristics of individuals). Both the genotype-to-phenotype and phenotype-to-fitness maps are typically not one-to-one. Here, we formulate a simple model capturing these properties which also results in a correlated fitness landscape. Below we will call mutations that do not change phenotype conformist. These mutations represent a subset of neutral mutations that do not change fitness.

We propose the following two-step model. To begin the first step, we make each pair of genotypes x and y in a binary hypercube G independently conformist with probability q_d where d = d(x, y) is the Hamming distance between x and y. We then declare any pair x and y to belong to the same conformist cluster if they are linked by a chain of conformist pairs. This version of long-range percolation model (cf., Berger 2004; Biskup 2004) divides the set of genotypes G into conformist clusters. We postulate that all genotypes in the same conformist cluster have the same phenotype. Therefore, genetic changes represented by a change from one member of a conformist cluster to another (i.e., single or multiple mutations) are phenotypically neutral. In the second step, we make each conformist cluster independently viable with probability p = λ/n. This generates a random set of viable genotypes, and we aim to investigate when this set has a giant connected component.

To illustrate our model, we can interpret the “genotype” as a linear RNA sequence. This sequence folds into a 3-dimensional molecule which has a particular structure, and corresponds to our “phenotype.” Finally, the molecule itself has a particular function, e.g., to bind to a specific part of the cell or to another molecule. A measure of how well this can be accomplished is represented by our “fitness.”

The distribution of conformist clusters depends on the probabilities q₁, q₂, q₃,… which determine how the conformity probability varies with genetic distance. We will study the case when q₁ = q > 0, q₂ = q₃ = … = 0 (Häggström, 2001). That is, q is the probability that a pair of nearest neighbors is a conformist pair. Thus, we can talk about conformist edges or equivalently conformist mutations, and q is the probability that a mutation is conformist. (Note however that it is possible that nearest neighbors x and y are in the same conformist cluster even if the edge between them is non-conformist.) Figure 1 illustrates our 2-step procedure in a four-dimensional example.

Figure 1.

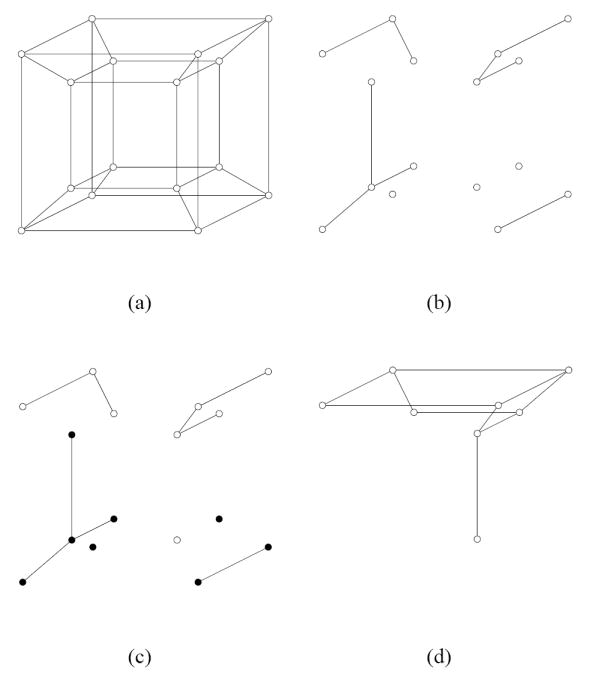
A four-dimensional example. (a) Start with the four-dimensional hypercube. (b) On the first step, create conformist clusters by randomly eliminating each edge with probability 1 − q. In the example, there are 7 conformist clusters left. (c) On the second step, remove each conformist cluster with probability 1 − p; the vertices to be removed are black. In the example, there are 3 viable conformist clusters left. (d) The remaining viable genotypes have nearest neighbors connected by edges. In the example, all remaining viable genotypes are connected in a single component.

We expect that a more general model with q_k declining fast enough with k is just a smeared version of this basic one, and its properties are not likely to differ from those of the simpler model. We conjecture that for our purposes, “fast enough” decrease should be exponential with a rate logarithmically increasing in the dimension n, e.g. for large k, q_k ≤ exp(−α(log n)k), for some α > 1. (This is expected to be so because in this case the expected number of neighbors of the focal genotype is finite.)

We observe that the first step of our procedure is an edge version of the percolation model discussed in the second section, with a similar giant component transition (Bollobás et al., 1992). Namely, let q = μ/n. Then, if μ > 1, there is a. a. s. one giant conformist cluster of size c · 2ⁿ, with all others of size at most Cn. In contrast, if μ < 1 all conformist clusters are of size at most Cn. Note that the number of conformist clusters is always on the order 2ⁿ. In fact, even the number of “non-conformist” (i.e., isolated) clusters is a. a. s. asymptotic to e^−μ2ⁿ, as the probability P(x is isolated) = (1 − μ/n)ⁿ.

Denote by x 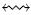y (resp. x 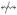y) the event that x and y are (resp. are not) in the same conformist cluster. First, we note that the probability P(x 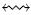y) that two genotypes belong to the same conformist cluster depends on the Hamming distance d(x, y) between them, and on q = μ/n. In particular, we show in Appendix A that, if μ < 1 and d(x, y) = k is fixed, then

(5)

The dominant contribution k!q^k is simply the expected number of conformist pathways between x and y that are of shortest possible length.

It is also important to note that, for every x ∈ G, the probability P(x is viable) = p, therefore it does not depend on q. Moreover, for x, y ∈ G,

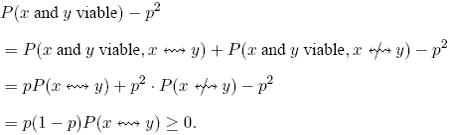Therefore, the correlation function (1) of fitness is

(6)

which clearly increases with q and, thus, with μ. The correlation function ρ(x, y) decreases exponentially with distance d(x, y) when μ < 1, and is bounded below when μ > 1. Nevertheless, as we will see below, we can effectively use local methods for all values of μ. Therefore, in this model the probability of being viable is controlled by parameter λ while the correlation structure of the landscape is controlled by parameter μ.

Proceeding by local branching process heuristics analogous to those used in Section 2, we reason that a surviving node on the branching tree can have two types of descendants: those that are connected by conformist mutations and those that are in different conformist clusters and viable independently. Therefore the number of descendants in the branching process is approximately Poisson(μ + λ).

The above argument can only work when μ < 1, as otherwise the correlations are global. If μ > 1, we need to eliminate the entire conformist giant component, which is a. a. s. inviable (because p is small). Locally, we condition on the (supercritical) branching process of the supposed descendant to die out. Such conditioned process is a subcritical branching process, with Poisson (μδ) distribution of successors (Athreya and Ney, 1971) where δ = δ(μ) < 1 is given by the equation δ = exp(μ(δ − 1)), analogous to the equation (2). This gives the conformist contribution, to which we add the independent Poisson(λδ) contribution.

To have a convenient summary of the conclusions above, assume that μ is fixed and let ζ(μ) be the smallest λ which a. a. s. ensures the giant component, i.e.,

$$\zeta (\mu )=\inf \{\lambda :{\mathrm{a\; cluster\; of\; at\; least}\mathit{cn}}^{-1}{2}^n\mathrm{viable\; genotypes\; exists}\mathrm{a}.\mathrm{a}.\mathrm{s}.\mathrm{for\; some}c>0\}.$$

One would expect that for λ < ζ(μ) all components are a. a. s. of size at most Cn. The asymptotic critical curve is given by λ = ζ(μ), where

$$\zeta (\mu )=\{\begin{array}{cc}1-\mu & \mathrm{if}\mu \in [0,1],\\ \frac{1}{\delta }-\mu & \mathrm{if}\mu \in [1,\infty ).\end{array}$$ (7)

The asymptotic critical curve ζ(μ) reaches the smallest value of 0 at μ = 1. To intuitively understand why percolation occurs the easiest with μ ≈ 1 (that is, when the probability of a conformist mutation is ≈ 1/n), it helps to think of the model as a branching process on clusters rather than on genotypes. Suppose we fix a particular set of k genotypes as a viable conformist cluster. The number of genotypes neighboring this cluster is then fixed, but the number of neighboring conformist clusters is random. For any μ < 1, it follows from equation (5) that the expected number of neighboring clusters is asymptotically the same as the number of neighboring genotypes. Consequently, we expect the overall number of descendants in the branching process to be greater if the size of the neighboring clusters is greater on average; which is exactly what happens as μ increases towards 1. If μ > 1, then there is a positive proportion of the neighboring genotypes that are in the giant cluster. This giant cluster is likely to be inviable, so the parameter λ must be greater to compensate for its loss.

In fact, one can prove rigorously (Pitman, unpub.) that 1 − μ is a lower bound on the critical surface by comparison with an edge percolation model in which each edge is retained independently with probability p + q − pq. We also remark that the number of viable clusters is on the same order as the number of all viable genotypes, that is, 2ⁿ/n. Since p = λ/n, it follows that the number of viable genotypes is on the order of 2ⁿ/n.

We have not been able to find an analytic proof that ζ(μ) (7) is also an upper bound, i.e., that the actual critical surface is given by ζ. Thus, we resort to computer simulations for confirmation. For this, we indicate global connectivity with the event A that a genotype within distance d = 2 of 0…0 is connected (through viable genotypes) to a genotype within distance d = 2 of 1…1. We make this choice because the distance 2 is the smallest that works with asymptotic certainty. Indeed, the genotypes 0…0 and 1…1 are likely to be inviable. Even the number of viable genotypes within distance one of each of these is only of constant order. It follows that, for any μ > 0, the probability of connectivity between a viable genotype within distance one of 0…0 and a viable one within distance one of 1…1 does not converge to 1 but is of a nontrivial constant order. By contrast, there are about n² vertices within distance 2 of 0…0 among which of order n are viable.

When λ > ζ(μ) the probability of the event A should therefore be (exponentially) close to 1. On the other hand, when λ < ζ(μ) the probability that a connected component within distance 2 of either 0…0 or 1…1 extends for distance of the order n is exponentially small. We further define the critical curves

$$\begin{array}{ccc}{\lambda }_m& =& \mathrm{the\; smallest}\lambda \mathrm{for\; which}P(A)>0.1,\\ {\lambda }_M& =& \mathrm{the\; largest}\lambda \mathrm{for\; which}P(A)<0.9.\end{array}$$

We approximated λ_m and λ_M for n = 10,…, 20 and μ = 0(0.1)2, with 1000 independent realizations of each choice of n, μ, and λ. We used the linear cluster algorithm described in Sedgewick (1997). Unfortunately, simulations above n ≈ 20 are not feasible. The results are depicted in Figure 2.

Figure 2.

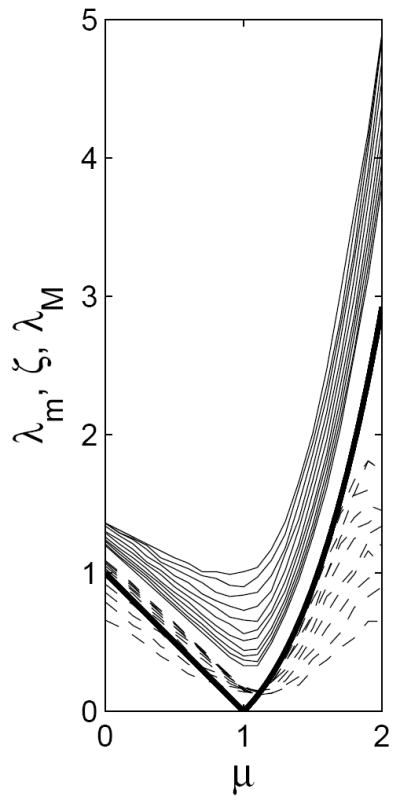
Simulated lower bounds λ_m (dashed curves) and upper bounds λ_M (solid curves), and ζ (thick curve) plotted against μ, for n = 10,…, 20. Lower bounds increase with n, and upper bounds decrease, for this range of n.

We make the following observations relating to Figure 2:

• Even for low n, both critical curves approximate well the overall shape of the theoretical limit curve ζ.

• The two curves λ_m and λ_M appear to be approaching a limiting curve away from the theoretical limiting curve ζ. However, this need not be interpreted as evidence against ζ being the actual limiting curve. Indeed, this behavior is an instance of a sharp threshold (Friedgut, 1999): if one fixes a μ, and increases λ from 0 to ∞, then the global connectivity probability P(A) rises from 0.1 to 0.9 within a very short interval (of length λ_M − λ_m) even for a relatively low n. The location of this sharp increase gets close to ζ much later; in symbols, λ_M − λ_m ≪ |ζ − λ_m| for large n.

• For μ < 1, λ_m tends to be above the limit curve. This is not surprising because the local argument always gives an upper bound on the probability P(A) of event A.

• The approximation of λ_m appears to deteriorate near μ = 2, which stems from the increased probability of survival of the giant component for larger μ.

Summarizing, we have shown that this more realistic model with phenotypic neutrality and fitness correlation shares the most important property of simpler models considered above - the existence of a percolating giant cluster of viable genotypes extending throughout the genotype space. More specifically, the number of clusters of viable genotypes is on the order of 2ⁿ/n for any λ and μ, and percolation occurs for λ larger than ζ(μ) given by equations (7). In terms of the viability probability p, the percolation threshold is thus inversely proportional to the dimensionality n of the genotype space (because p = λ/n). Conformist mutations are most advantageous at about μ = 1, which is the point of phase transition between between local and global conformist connectivity. In particular, for μ ~ 1, percolation could potentially occur for p on a scale smaller than 1/n. What is also clear from the heuristics and simulations is that conformist clustering, and thus correlations, can help or hinder connectivity in fitness landscapes. Indeed, the critical probability for global connectivity in the uncorrelated landscape is about λ = 1 (Section 2). In the correlated landscape model considered here, the critical value ζ < 1 approximately for μ < 1.5 (Figure 2). However, for large values of μ, correlations hinder connectivity.

In the model studied above, the viability probability p was independent of the size of the conformist clusters. In Appendix B, we consider a simple generalization that can be tuned to create positive or negative correlations between conformist cluster size and viability.

5 Percolation in incompatibility models

In the model considered in the previous section correlations rapidly decreased with distance. This property made local analysis possible. The models we introduce now are fundamentally different in the sense that correlations are so high that the local method gives a wrong answer.

In the previous sections, in constructing fitness landscapes we were assigning fitness to individual genotypes or phenotypes. Here, we make certain assumptions about “fitness” of particular combinations of alleles or the values of continuously varying phenotypic characters. Specifically, we will assume that some of these combinations are “incompatible” in the sense that the resulting genotypes or phenotypes under given environmental conditions have reduced (or zero) fitness (Orr, 1995; Orr and Orr, 1996; Gavrilets, 2004). The resulting models can be viewed as a generalization of the Bateson-Dobzhansky-Muller model (Cabot et al., 1994; Orr, 1995; Orr and Orr, 1996; Orr, 1997; Orr and Turelli, 2001; Gavrilets and Hastings, 1996; Gavrilets, 1997; Gavrilets and Gravner, 1997; Gavrilets, 2003, 2004; Coyne and Orr, 2004) which represents a canonical model of speciation.

5.1 Diallelic loci

We begin by considering n diallelic loci and assuming that each pair of alleles is independently incompatible with probability

$$p=\frac{c}{2n}.$$

We let a single pair of incompatible alleles make an individual inviable. Thus, the variable p characterizes the probability of being inviable rather than viable as in the previous sections.

There are $4·\left(\begin{array}{c}n\\ 2\end{array}\right)$ allele pairs in all, and we form a random list F of those that are incompatible. We denote the allele pair u at locus i and υ at locus j by (u_i, υ_j). In this nonstandard notation, (0₁, 0₂) ∈ F, for example, means that allele 0 at locus 1 and allele 0 at locus 2 are incompatible. In general, if (u_i, υ_j) ∈ F, all genotypes with u in position i and υ in position j are inviable. A genotype x is then inviable if and only if there exist i and j, with i < j, so that u and υ are, respectively, the alleles of x at loci i and j, and (u_i, υ_j) ∈ F. For example, if F₁ = {(0₁, 0₂), (1₂, 0₃), (1₁, 1₂)}, viable genotypes may have 011, 100, and 101 as their first three alleles. For F₂ = F₁ ∪ {(0₁, 1₃), (1₁, 0₂)}, no viable genotype remains.

Incompatibility (0₁, 0₂) is equivalent to two implications: 0₁ ⇒ 1₂ and 0₂ ⇒ 1₁ or to the single OR statement 1₁ OR 1₂. In this interpretation, the problem of whether, for a given list of incompatibilities F, there is a viable genotype is known as the 2 -SAT problem (Korte and Vygen, 2005). The associated digraph D_F is a graph on 2n vertices x_i, i = 1,…n, x = 0, 1, with oriented edges determined by the implications. A well-known theorem (Korte and Vygen, 2005) states that a viable genotype exists iff D_F contains no oriented cycle from 0_i to 1_i and back to 0_i for any i = 1,…n in D_F. For example, for the incompatibilities F₂ as above, one such cycle is 0₁ → 1₂ → 1₃ → 1₁ → 1₂ → 0₁.

Existence of viable genotypes

In this model, viable genotypes exist only if the probability of pairwise incompatibility p is smaller than 1/(2n). More precisely, let N be the number of viable genotypes. Then

• if c > 1, then a. a. s. N = 0.

• if c < 1, then a. a. s. N > 0.

This result first appeared in the computer science literature in the 90’s (see de la Vega 2001 for a review), and it is an extension of the celebrated Erdös-Rényi random graph results (Bollobás, 2001; Janson et al., 2000) to the oriented case.

Note that the expectation $E(N)=2^n{(1-p)}^{\left(\begin{array}{c}n\\ 2\end{array}\right)}\approx 2^n{e}^{-\mathit{cn}/4}$, which grows exponentially whenever c < 4 log 2 ≈ 2.77. Neglecting correlations would therefore suggest a wrong threshold for the existence of viable genotypes. The local method based on analysis of the averages (e.g., used in Gavrilets 2004, Chapter 6) is even farther off, as it suggests an a. a. s. giant component when p < (1 − ε) log n/n for any ε > 0.

The number of viable genotypes

Assume that c < 1. Sophisticated, but not mathematically rigorous methods based on replica symmetry (Monasson and Zecchina, 1997; Biroli et al., 2000) from statistical physics suggest that, as n → ∞, lim n⁻¹ log N varies almost linearly between log 2 ≈ 0.69 (for small c, when, as we prove below, this limit is log 2 + O(c)) and about 0.38 (for c close to 1). One can however prove that n⁻¹ log N is for large n sharply concentrated around its mean (de la Vega, 2001).

Upper and lower bounds on N can also be obtained rigorously. For example, if X is a number of incompatibilities which involve disjoint pairs of loci (i.e., those for which every locus is represented at most once among the incompatibilities), then N ≤ exp(n log 2 + X log(3/4)), as each of the X incompatibilities reduces the number of viable genotypes by the factor 3/4. If we imagine adding incompatibilities one by one at random until there are about cn of them, then after we have k incompatibilities on disjoint pairs of loci the waiting time (measured by the number of incompatibilities added) for a new disjoint one is geometric with expectation $\left(\begin{array}{c}n\\ 2\end{array}\right)/\left(\begin{array}{c}n-2k\\ 2\end{array}\right)$. Therefore, X is a. a. s. at least Kn, where K solves the approximate equation

$$\left(\begin{array}{c}n\\ 2\end{array}\right)\left(\sum _{k=0}^{\mathit{Kn}}\frac{1}{\left(\begin{array}{c}n-2k\\ 2\end{array}\right)}\right)~\mathit{cn},$$

or

$${\mathit{\int }}_0^{\mathit{Kn}}\frac{1}{{(n-2k)}^2}\mathit{dk}~\frac{c}{n},$$

which reduces to K = c/(1 + 2c). This implies that in the limit of large n the upper bound on N can be written as

$$\frac{1}{n}\log N\le \frac{1}{1+2c}\log 2+\frac{c}{1+2c}\log 3.$$ (8)

A lower bound is even easier to obtain. Namely, the probability that a fixed location (i.e., locus) i does not appear in F is (1 − p)^{4(n − 1)} → e^−2c, and then it is easy to see that the number of loci represented in F is asymptotically (1 − e^−2c)n. As the other loci are neutral (in the sense that changing their alleles does not affect fitness), n⁻¹ log N is asymptotically at least e^−2c log 2. Clearly, this gives a lower bound on the exponential size of any cluster of viable genotypes.

If this was an accurate bound, it would imply that the space of genotypes is rather simple, in that almost all its entropy would come from neutral loci. (By analogy with physical systems, entropy is a measure of the amount of choice (“number of degrees of freedom”) one has in selecting a viable genotype.) The Appendix C presents two arguments which will demonstrate that this is not the case.

The structure of clusters

The derivations in Appendix C show that every viable genotype is connected through mutation to a fairly substantial viable sub-cube. In this sub-cube, alleles on at most a proportion r_u(c) < 1 of loci are fixed (to 0 or 1) while the remaining proportion 1 − r_u(c) could be varied without effect on fitness. Note from Figure 4 in Appendix C that 1 − r_u(c) ≥ 0.3 for all c, and that such a phenomenon is extremely unlikely on uncorrelated landscapes. Namely, in the setting of Section 2, the probability that a viable subcube of size k exists anywhere is at most

Figure 4.

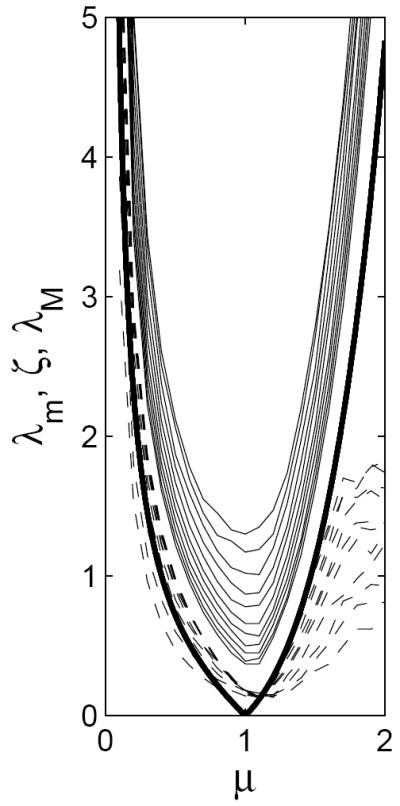
Simulated lower bounds λ_m (dashed curves) and upper bounds λ_M (solid curves), and ζ (thick curve) plotted against μ, for n = 10,…, 20 in the model from Appendix B. Lower bounds increase with n, and upper bounds decrease, for this range of n. Compare to Figure 2.

$$\left(\begin{array}{c}n\\ k\end{array}\right)·p^{2^k}\le \exp (k\log n+2^k\log p),$$

so even at the connectivity threshold p = 1/2 the size of largest viable subcube is a. a. s. of order log log n. Note also that, for c < 1, N ≥ 2^{(1 − r_u(c))n} a. a. s. and so in the limit of large n the lower bound on N can be written as

$$\frac{1}{n}\log N\ge (1-r_u(c))\log 2.$$ (9)

The number of clusters

The natural next question concerns the number of clusters R when c < 1. This again has quite a surprising answer, unparalleled in landscapes with rapidly decaying correlations. Namely, R is stochastically bounded, that is, for every ε > 0 there exists an z = z(ε) such that P(R ≤ z for all n) > 1 − ε. This follows from a result in Pitman (unpub.), which shows that the distribution of R converges in distribution to 2^X, where X is distributed Poisson(λ) for

$$\lambda =-\frac{1}{2}(\log (1-c)+c).$$

The probability that there is a unique cluster thus converges to $e^{-\lambda }=\sqrt{(1-c)e^c}$.

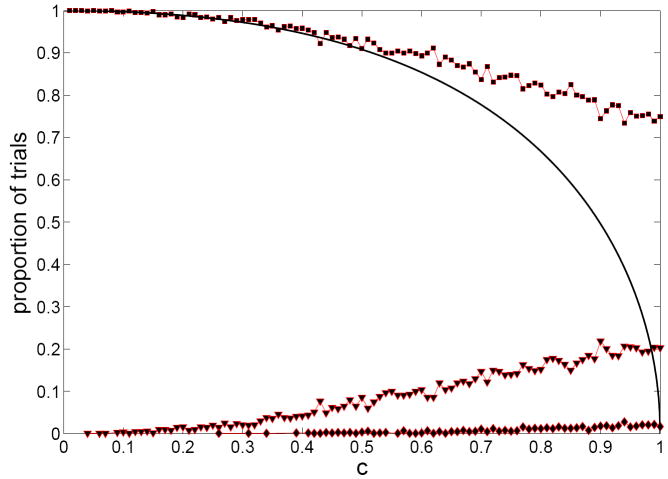
Asymptotically, a unique cluster has a better than even chance of occurring for c below about 0.9, and is very likely to occur for small c, though of course not a. a. s. so. To confirm, we have done simulations for n = 20 and c = 0.01(0.01)1 (again 1000 trials in each case) and got distribution of clusters depicted in Figure 3. The results suggest that the convergence to limiting distribution is rather slow for c close to 1, and that the likelihood of a unique cluster increases for low n.

Figure 3.

Simulated number of clusters, vs. c for n = 20, with the proportion (out of 1000) of trials with exactly one (squares), exactly two (triangles), and at least three (diamonds) clusters. The solid curve is $\sqrt{(1-c)e^c}$.

To summarize, in the presence of random pairwise incompatibilities, the set of viable genotypes is, when nonempty, divided into a stochastically bounded number of connected clusters, where a unique cluster is usually the most likely possibility. These clusters are all of exponentially large size (with bounds given by equations 8 and 9), in fact they all contain sub-cubes of dimension at least (1 − r_u(c))n. However, the proportion of viable genotypes among all 2ⁿ genotypes is exponentially small, by equation (8).

In fitness landscapes based on incompatibilities, high correlations make a significant proportion of genetic information irrelevant in the sense that genotypes can be changed by mutations at many loci without affecting fitness. This might be expected from the perspective that the model of lethal allele pairs (i.e., pairwise incompatibilities) is a natural generalization of the much simpler model of lethal alleles in which each of 2n alleles is independently lethal with probability p. In this model, the proper scale is $p=c/\sqrt{n}$. A viable genotype exists when there is no locus at which both alleles are lethal, which happens with probability (1 − p²)ⁿ ~ e^−c2. (Note that there is not a sharp threshold in this mode, i.e., taking the existence probability from 1 to 0 requires varying c from 0 to ∞.) Moreover, all the loci for which neither allele is lethal can be changed by mutation without affecting fitness. The number of such loci is about ${(1-p)}^{2}n\ge n-2c\sqrt{n}$, so nearly all loci are neutral. It is also interesting to point out that the uncorrelated model, where viability of genotypes is independently determined is at the other extreme — viability of genotypes is based on lethal combinations of all n alleles.

In the following sections, we study the conditions for the existence of viable genotypes in several related models starting with complex incompatibilities.

5.2 Complex incompatibilities

Here we assume that incompatibilities involve K (≥ 2) diallelic loci (Cabot et al., 1994; Orr and Orr, 1996; Gavrilets, 2004). Determining whether a viable combination of genes exists is then equivalent to the K -SAT problem (Korte and Vygen, 2005). Even for K = 3, this is an NP-complete problem (Korte and Vygen, 2005), so there is no known polynomial algorithm to answer this question. The random case, which we now describe, is also much harder to analyze than the 2 -SAT one. Let F be a random set to which any of the $2^K\left(\begin{array}{c}n\\ K\end{array}\right)$ incompatibilities belong independently with probability

$$p=\frac{K!}{2^K}·\frac{c}{n^{K-1}}.$$

Here c = c(K) is a constant, and the above form has been chosen to make the number of incompatibilities in F asymptotically cn. (Note also the agreement with the definition of p in Section 5.1 when K = 2.) For a fixed K, it has been proved (Friedgut, 1999) that the probability that viable genotype exists jumps sharply from 0 to 1 as c varies. However, the location of the jump has not been proved to converge as n → ∞. Instead, a lot of effort has been invested in obtaining good bounds. For example (Achlioptas and Peres, 2004), for K = 3, c < 3.42 implies a. a. s. existence of viable genotype, while c > 4.51 implies a. a. s. nonexistence (while the sharp constant is estimated to be about 4.48, see e.g. Biroli et al. 2000). For K = 4 the best current bounds are 7.91 and 10.23. For large K, the transition occurs at c = 2^K log 2 − O(K) (Achlioptas and Peres, 2004).

Techniques from statistical physics (Biroli et al., 2000) strongly suggest that, for K ≥ 3, there is another phase transition, which for K = 3 occurs at about c = 3.96. For smaller c, the viable genotypes are conjectured to be contained in a single cluster. For larger c, the space of viable genotypes (if nonempty) is divided into exponentially many connected clusters. It appears that 3 -SAT is already noticeably closer than 2 -SAT to the uncorrelated model in Section 2 where the number of clusters is on the order of the number of viable genotypes and to the weakly correlated model of Section 4.

Perhaps more relevant to genetic incompatibilities is the following mixed model (commonly known as (2 + p) -SAT), Monasson and Zecchina 1997). Assume that every 2-incompatibility is present with probability c₂/(2n), while every 3-incompatibility is present with probability 3c₃/(4n²). The normalizations are chosen so that the numbers of 2-incompatibilites and 3-incompatibilities are asymptotically c₂n and c₃n, respectively.

If c₂ (resp. c₃) is very small, then the respective incompatibility set affects a very small proportion of loci, therefore c₃ (resp. c₂) determines whether a viable genotype is likely to exist. Intuitively, one also expects that 2-incompatibilities should be more important than 3-incompatibilities as one of the former type excludes more genotypes than one of the latter type. A careful analysis confirms this. First observe that c₂ > 1 implies a. a. s. non-existence of a viable genotype. The surprise (Monasson and Zecchina, 1997; Achlioptas et al., 2001) is that if c₃ is small enough, c₂ < 1 implies a. a. s. existence of viable genotypes, so the 3-incompatibilities do not change the threshold. This is established in Monasson and Zecchina (1997) by a physics argument for c₃ < 0.703, while Achlioptas et al. (2001) gives a rigorous argument for c₃ < 2/3. Therefore, even if their numbers are on the same scale, if the more complex incompatibilities are rare enough compared to the pairwise ones, their contribution to the structure of the space of viable genotypes is not essential.

5.3 Multiallelic loci

Here we assume that at each locus there can be a (≥ 2) alleles (cf., Reidys 2006). In this case, the genotype space is the generalized hypercube G_a = {0,…, a − 1}ⁿ. For a = 3 this could be interpreted as the genotype space of diploid organisms without cis-trans effects (Gavrilets and Gravner, 1997), a = 4 corresponds to DNA sequences, and a = 20 corresponds to proteins. Much larger values of a can correspond to a number of alleles at a protein coding locus and we will see later that there is not much difference between this model and a natural continuous space model.

We will assume that each pair of alleles, out of total number of $a^2\left(\begin{array}{c}n\\ 2\end{array}\right)$ is independently incompatible with probability

$$p=\frac{c}{2n}.$$

The main question we are interested in here is for which values of c viable genotypes exist a. a. s.

Clearly, if N is the number of viable genotypes, then the expectation

$$E(N)=a^n{(1-p)}^{\left(\begin{array}{c}n\\ 2\end{array}\right)}\approx \exp (n\log a-\frac{1}{4}\mathit{cn})$$

and so there are a. a. s. no viable genotypes when c > 4 log a. On the other hand, clearly there are viable genotypes (with all positions filled by 0’s and 1’s) when c < 1. It turns out that the first of these trivial bounds is much closer to the critical value when a is large. Before we proceed, however, we state a sharp threshold result from Molloy (2003): there exists a function γ = γ(n, a) so that for every ε > 0,

• if c > γ + ε, then a. a. s. N = 0.

• if c < γ − ε, then a. a. s. N > 0.

In words, for a fixed a, the probability of the event that N ≥ 1 transitions sharply from large to small as c increases through γ. As it is not proved that lim_n→∞ γ(n, a) exists, it is in principle possible that the place of this sharp transition fluctuates as n increases (although it must of course remain within [1, 4 log a]).

Our main result in this section is

$$\gamma =4\log a-o(1),\mathrm{as}a\to \infty .$$ (10)

This somewhat surprising result in proven in Appendix D by the second moment method, as developed in Achlioptas and Moore (2004) and Achlioptas and Peres (2004).

Equation (10) implies that viable genotypes exist only if the incompatibility probability

$$p<\frac{2\log a}{n},$$ (11)

which decreases linearly with the number of the loci n but increases only logarithmically with the number of alleles a. That is, multiple alleles widen the conditions for the existence of viable genotypes but the effect is not too strong.

5.4 Continuous phenotype spaces

Here we extend the model of pair incompatibilities for the case of continuous phenotypic space P = [0, 1]ⁿ. Again, each phenotype is characterized by values z₁,…, z_n, each between 0 and 1, which specify n continuous traits. This time we also have a small r > 0 as a parameter. For each pair of traits (i, j), i < j, we independently choose a Poisson(λ) number of points П_ij uniformly at random in the unit square [0, 1] × [0, 1]. These points will be interpreted as “gorges” of equal deapth in the fitness landscapes. As in the discrete case, we assume that λ = c/(2n). Then we declare each phenotype z = (z₁,…, z_n) ∈ P inviable if it has two traits i < j so that (z_i, z_j) is within r of the “gorge” П_ij. Our procedure can be visualized as throwing a random number of (n − 2)-dimensional square tubes of inviable phenotypes into the phenotype space.

Our main result here is that the existence threshold is on the order c ≈ − log r/r². Namely, we prove in Appendix E that there exists a constant C > 0 so that for small enough r,

• if $c>4\frac{-\log r}{r^2}$, then a. a. s. N = 0.

• if $c<\frac{-\log r-C}{r^2}$, then a. a. s. N > 0.

In the basic and continuous models in Sections 2 and 3, the difference in percolation thresholds (given by equations 3 and 4) was dramatic. In contrast, the continuous and discrete cases here are a lot closer. The scaling of the critical probability is 1/n for both cases, and as explained in Appendix E, the continuous case described here is related to the discrete one (from Section 5.3) with a ≈ 1/r and the incompatibility probability p ≈ r²/n.

Overall, the results presented in Section 5 show that the structure of fitness landscapes in incompatibility models are very different from that in models considered in earlier sections. Although both types of models result in large clusters of viable genotypes, the former allow for more neutral changes on local scales (because incompatibilites are rare) but for less extensive genetic divergence on larger scales (because viable clusters are repreented by subcubes rather than trees) than the latter.

6 Notes on neutral clusters in the discrete NK model

The model considered here is a special case of the discretized NK model (Kauffman, 1993), introduced in Newman and Engelhardt (1998a). This model features n diallelic loci each of which interacts with K other loci. To have a concrete example, assume that the loci are arranged on a circle, so that n + 1 ≡ 1, n + 1 ≡ 2, etc., and let the interaction neighborhood of the i’th locus consist of itself and K loci to its right i + 1,…, i + K. For a given genotype x ∈ G = {0, 1}ⁿ, the neighborhood configuration of the i’th locus is then given by N_i(x) = (x_i, x_i+1,…,x_i+K) ∈ {0, 1}^K+1. To each locus and to each possible configuration in its neighborhood we independently assign a binary fitness contibution. To be more precise, we choose the 2^K+1n numbers υ_i(y), i = 1,…,n and y ∈ {0, 1}^K+1, to be independently 0 or 1 with equal probability, and interpret υ_i(y) as the fitness contribution of locus i when its neighborhood configuration is y. The fitness of a genotype x is then the sum of contributions from each locus:

$$w(x)=\sum _{i=1}^n{\upsilon }_i(N_i(x)).$$

In Kauffman (1993), the values υ_i were taken from a continuous distribution. In Newman and Engelhardt (1998a), these values were integers in the range [0, F − 1] so that our model is a special case F = 2. The NK model results in a correlated fitness landscape; the corresponding correlation function (1) can be found explicitly (Fontana et al., 1993; Campos et al., 2002; Gavrilets, 2004).

We define neutral clusters as connected components of same fitness. The K = 0 case, wich corresponds to an additive fitness model, is easy but nevertheless illustrative. Namely, a mutation at locus i will not change fitness iff υ_i(0) = υ_i(1); let D be the number of such loci. Since the fitnesses contributions are assigned randomly and with equal probabilities, each locus has a 50% chance to be in this category. Then D ~ n/2 a. a. s., the number of different fitnesses is n − D, each neutral cluster is a sub-cube of dimension D, and there are exactly 2^{n − D} neutral clusters.

The next simplest situation is when K = 1, so that each locus interacts with one other locus. Let D₁ be the number of loci i for which the fitness contribution υ_i is constant, i.e., does not depend on the configuration in the i’th neighborhood N_i. Then D₁ ~ n/8 a. a. s. (because out of the 2⁴ = 16 possible functions υ_i, two are constant, the 0 and the 1), and each neutral cluster contains a sub-cube of dimension D₁. Moreover, let D₂ be the number of loci i for which υ_i(00) = υ_i(01) ≠ υ_i(10) = υ₁(11). Note that there are again two functions with this property, and that any genotypes that differ at such a locus i must belong to a different neutral cluster. Consequently, the number of different neutral clusters is at least 2^D₂ and there are exponentially many of them, as again D₂ ~ n/8 a. a. s. This division of genotype space into exponentially many clusters of exponential size persists for every K, although the distribution of numbers and sizes of these clusters is not well understood (see Newman and Engelhardt 1998a for simulations for n = 20).

Overall, neutral clusters are a prominent feature of the NK model. We also mention that the question of whether a genotype with the maximal possible fitness n exists for a given K is in many way related to issues in incompatibilities models (Choi et al., 2005).

7 Discussion

In this section we summarize our major findings and provide their biological interpretation.

The previous work on neutral and nearly neutral networks in multidimensional fitness landscapes has concentrated exclusively on genotype spaces in which each individual (or a group of individuals) is characterized by a discrete set of genes. However many features of biological organisms that are actually observable and/or measurable are described by continuously varying variables such as size, weight, color, or concentration. A question of particular biological interest is whether (nearly) neutral networks are as prominent in a continuous phenotype space as they are in the discrete genotype space. Our results provide an affirmative answer to this question. Specifically, we have shown that in a simple model of random fitness assignment, viable phenotypes are likely to form a large connected cluster even if their overall frequency is very low provided the dimensionality of the phenotype space, n, is sufficiently large. In fact, the percolation threshold for the probability of being viable scales with n as 1/2ⁿ and, thus, decreases much faster than 1/n which is characteristic of the analogous discrete genotype space model.

Earlier work on nearly neutral networks has been limited to consideration of the relationship between genotype and fitness. Any phenotypic properties that usually mediate this relationship in real biological organisms have been neglected. In Section 4, we proposed a novel model in which phenotype is introduced explicitly. In our model, the relationships both between genotype and phenotype and between phenotype and fitness are of many-to-one type, so that neutrality is present at both the phenotype and fitness levels. Moreover, this model results in a correlated fitness landscape in which the correlation function can be found explicitly. We showed that phenotypic neutrality and correlation between fitnesses can reduce the percolation threshold. Our results suggest that the most conducive conditions for the formation of the giant component is when the correlations are at the point of phase transition between local and global. To explore the robustness of our conclusions, we then look at a simplistic but mathematically illuminating model in which there is a correlation between conformity (i.e., phenotypic neutrality) and fitness. The model has supported our conclusions.

In Section 5, we studied a number of models that have been recently proposed and explored within the context of studying speciation. In these models, fitness is assigned to particular gene/trait combinations and the fitness of the whole organisms depends on the presence or absence of incompatible combinations of genes or traits. In these models, the correlations of fitnesses are so high that local methods lead to wrong conclusions. First, we established the connection between these models and SAT problems, prominent in computer science. Then we analyzed the conditions for the existence of viable genotypes, their number, as well as the structure and the number of clusters of viable genotypes. These questions have not been studied previously. The majority of our results are for the case of pairwise incompatibilities between diallelic loci, but we also looked at multiple alleles and complex incompatibilities. In the case of diallelic loci we showed that the number of clusters is stochastically bounded and each cluster contains a very large sub-cube. Our results suggest (in the context of the mixed model) that more complex incompatibilities are less important than less complex incompatibilities in controlling the structure of the space of viable genotypes. However, complex incompatibilities appear to allow for exponentially many clusters of viable genotypes. Finally, we generalized some of our findings to continuous phenotype spaces.

In Section 6, we provided some additional results on the size, number and structure of neutral clusters in the discrete NK model which represent a popular tool for studying adaptation (Kauffman and Levin, 1987; Kauffman, 1993; Newman and Engelhardt, 1998b; Welch and Waxman, 2005).

In the majority of models studied here, we assumed for simplicity that fitness can take only two values: zero and one. In Section 2, we mentioned the relationship between viable genotypes and fitness bands. This concept is explored in some detail in our previous work (Gavrilets, 1997; Gavrilets and Gravner, 1997; Gavrilets, 2004) where we showed that many results on viable genotypes in uncorrelated landscapes easily generalize to the case of continuously changing fitness. The same is true of the models in Sections 3 and 4. For simplicity, our analysis has been restricted to very symmetric models. However, we expect that many conclusions of this paper can be generalized to nonsymmetric fitness assignments provided the dimensionality of fitness landscapes is very large.

Overall, our results reinforce the previous conclusion (Gavrilets, 1997; Gavrilets and Gravner, 1997; Reidys et al., 1997; Gavrilets, 2004; Reidys et al., 2001; Reidys and Stadler, 2001, 2002) that percolating networks of genotypes with approximately similar fitnesses (holey landscapes) is a general feature of multidimensional fitness landscapes (both uncorrelated and correlated and both in genotype and phenotype spaces). The evolution along such networks can readily proceed by mutation and random genetic drift (Kimura, 1983; Ohta, 1992, 1998; Lynch, 2007) and result in the accumulation of reproductive isolation between diverging lineages and in allopatric, parapatric or sympatric speciation (Cabot et al., 1994; Orr, 1995; Orr and Orr, 1996; Orr, 1997; Orr and Turelli, 2001; Gavrilets and Hastings, 1996; Gavrilets, 1997; Gavrilets and Gravner, 1997; Gavrilets, 2003, 2004; Coyne and Orr, 2004). Selection (e.g., for local adaptation or sexual) can either help or hinder these processes depending on whether its net effect is diversifying or stabilizing.

Some more general theoretical lessons of our work are that

• Correlations may help or hinder connectivity in fitness landscapes. Even when correlations are positive and tunable by a single parameter, it may be advantageous (for higher connectivity) to increase them only to a limited extent. One reason (see Section 4.2) is that high correlations may result in a loss of very large phenotypically similar clusters.

• Averages (i.e., expected values) can easily lead to wrong conclusions, especially when correlations are strong (see Section 5.1). Nevertheless, they may still be useful with a crafty choice of relevant statistics (see Achlioptas and Peres (2004) and Appendix D).

• Very high correlations may fundamentally change the structure of connected clusters. For example, clusters may look locally more like cubes (Section 5) than trees (Sections 2, 3 and 4) and their number may be reduced dramatically (Section 5).

• Necessary analytic techniques may be unexpected and quite sophisticated; for example, they may require detailed understanding of random graphs, spin-glass machinery, or decision algorithms.

Figure 5.

The upper bound r_u(c) for the number of fixed loci (non-*’s) in the implicant of shortest length included in every cluster of viable genotypes, plotted against c. As explained in the text, 1 − r_u(c) is a lower bound on the dimension of the subcube specified by the implicant.

APPENDIX

Appendix A. Proof of equation (5)

To prove equation (5), we assume that μ < 1 and show that for a fixed k (which does not grow with n), the event that x and y at distance k are in the same conformist cluster is most likely to occur because x and y are connected via the shortest possible path. Indeed, the dominant term k!q^k is the expected number of conformist pathways between x and y that are of shortest possible length k. This easily follows from the observation that on a shortest path there is no opportunity to backtrack; each mutation must be toward the other genotype. We can assume that x is the all 0’s genotype and y is the genotype with 1’s in the first k positions and 0’s elsewhere. There are k! orders in which the 1’s can be added.

To obtain the lower bound we use inclusion-exclusion on the probability that x y through a shortest path. Let I_k = I_k(x, y) be the set of all paths of length k between x and y. Then

where Aα is the event that a particular path α consists entirely of conformist edges. Notice that two distinct paths of the same length differ by at least two edges. Thus, we get the following upper bound

$$\sum _{\alpha ,\beta }P(A_{\alpha }\cap A_{\beta })<{(k!)}^2{q}^{k+2},$$

and the lower bound in (5) follows.

The upper bound is a little more difficult to obtain (it is only here that we use μ < 1) and we need some notation. Each genotype can be identified with the set of 1’s that it contains, so for any two genotypes u and υ we let u Δ υ denote the set of loci on which they differ. Notice that if u Δ υ is even (resp. odd) then every path between u and υ is of even (resp. odd) length because each mutation which alters the allele at a locus not in u Δ υ must later be compensated for.

To estimate the expected number of conformist pathways, we will need to bound the number of paths of length l between x and y. This is given by

$$k!\left(\begin{array}{c}l\\ m\end{array}\right)m!n^m\text{where}m=\frac{l-k}{2}.$$

We show this via the methods of Bollobás et al. (1992). They obtain an estimate for the number of cycles of a given length through a fixed vertex of the cube.

Given a path, say x = υ₀, υ₁,…, υ_l = y, between x and y, let us associate the sequence (ε₁i₁,…,ε_li_l) where

$${\upsilon }_j△{\upsilon }_{j-1}=\{i_j\}\mathrm{and}{\epsilon }_j=\{\begin{array}{cc}+1& \mathrm{if}{\upsilon }_j={\upsilon }_{j-1}\cup i_j\\ -1& \mathrm{if}{\upsilon }_j={\upsilon }_{j-1}\backslash \{i_j\}\end{array}$$

j = 1,…,l. Since distinct paths will have distinct sequences we can bound the number of paths by finding an upper bound for the number of sequences.

Note that there must be m + k positive entries, which occur at $\left(\begin{array}{c}l\\ m+k\end{array}\right)=\left(\begin{array}{c}l\\ m\end{array}\right)$ possible locations. The absolute values of m of these entries are chosen freely from {1,…,n}, while the remaining k must be the integers 1,…,k. There are n^mk! ways to do this. We are free to order the m negative entries and the bound follows.

We now assume that d(x, y) is even and relabel d(x, y) = 2k. We omit the similar calculation for odd distances. Define b = −3k/(2 log μ) and t = ⌊b log n⌋. Then the expected number of conformist paths between x and y can be expressed as

$$\begin{array}{lll}\sum _{l\ge k+1}\sum _{I_{2l}}{q}^{2l}& =& \sum _{k+1\le l<t}\sum _{I_{2l}}{q}^{2l}+\sum _{l\ge t}\sum _{I_{2l}}{q}^{2l}\\ & <& \sum _{k+1\le l<t}\left(\begin{array}{c}2l\\ l-k\end{array}\right)n^{l-k}(l-k)!(2k)!q^{2l}+\sum _{l\ge t}{n}^{2l}{q}^{2l}\\ & =& \sum _{k+1\le l<t}{(2l)}^{l-k}{n}^{l-k}{q}^{2(l-k)}(2k)!q^{2k}+\sum _{l\ge t}{\mu }^{2l}\\ & <& (2k)!q^{2k}{\sum _{l\ge k+1}(2\mathit{b\mu q}\log n)}^{l-k}+O({\mu }^{2b\log n})\\ & =& k(2k)!q^{2k}O(q\log n)+O(n^{2b\log \mu })\\ & =& k(2k)!q^{2k}O(n^{-1}\log n).\end{array}$$

Appendix B. Correlations between conformity and viability

Assume now that conformist clusters are formed as in Section 4 (i.e., with edges being conformist with probability q = μ/n), are still independently viable, but now the probability of their viability depends on their size. We will consider the simple case when an isolated genotype (one might call it non-conformist) is viable with probability p₀ = λ₀/n, while a conformist cluster of size larger than 1 is viable with probability p₁ = λ₁/n.

In this case, the probability that a random genotype is viable,

$$P(x\mathrm{is\; viable})={(1-q)}^n{p}_0+(1-{(1-q)}^n)p_1~\frac{1}{n}(e^{-\mu }{\lambda }_0+(1-e^{-\mu }){\lambda }_1).$$

Moreover, by a similar calculation as before,

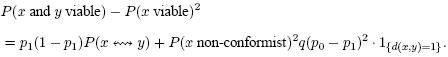Here, the last factor is the indicator of the set {(x, y), d(x, y) = 1}, which equals 1 if d(x, y) = 1 and 0 otherwise. Therefore, for d(x, y) ≥ 2, the correlation function (1) is

which is smaller than before iff λ₁ < λ₀. However, it has the same asymptotic properties unless λ₁ = 0.

Assume first that μ < 1. The local analysis now leads to a multi-type branching process (Athreya and Ney, 1971) with three types: NC (non-conformist node), CI (non-isolated node independently viable, so no conformist edge is accounted for), and CC (non-isolated node viable by conformity, so a conformist edge is accounted for). Note that while the type NC is a new feature, the difference between CI and CC was the key to our earlier local analysis in Section 4.1 — a neighbor of a viable genotype may be viable because of a conformist edge between them or because it belongs to an independently viable conformist cluster.

Note first that a genotype is non-conformist with probability about e^−μ. Hence a node of any of the three types creates a Poisson(e^−μλ₁) number of type NC descendants, and a Poisson((1 − e^−μ)λ₁) number of type CI descendants. In addition, the type CI creates a Poisson(μ), conditioned on being nonzero, number of descendants of type CC and type CC creates a Poisson(μ) number of descendants of type CC. Thus the matrix of expectations, in which the ijth entry is the expectation of the number of type j descendants from type i, is

$$M=\left[\begin{array}{ccc}{e}^{-\mu }{\lambda }_0& (1-e^{-\mu }){\lambda }_1& 0\\ e^{-\mu }{\lambda }_0& (1-e^{-\mu }){\lambda }_1& \mu /(1-e^{-\mu })\\ e^{-\mu }{\lambda }_0& (1-e^{-\mu }){\lambda }_1& \mu \end{array}\right].$$

When μ > 1, μ needs to be replaced by μδ, and λ₁ by λ₁δ, where δ = δ(μ) is given by (2).

It follows from the theory of multi-type branching processes (Athreya and Ney, 1971) that the critical surface for survival of a multi-type branching process is given by det(M − 1) = 0.

The simplest case is when only non-conformist genotypes may be viable, i.e., λ₁ = 0. In this case the critical surface is given by λ₀e^−μ = 1 (Pitman, unpub.). Not surprisingly, the critical λ₀ necessary to achieve global connectivity strictly increases with μ, which is the result of negative correlations between conformity and viability.

The other extreme is when non-conformist genotypes are inviable, i.e., λ₀ = 0. As an easy computation demonstrates, the critical curve is now given by λ₁ = ζ(μ), where

$$\zeta (\mu )=\{\begin{array}{cc}\frac{1-\mu }{\mu e^{-\mu }+1-e^{-\mu }}& \mathrm{if}\mu \in [0,1],\\ \frac{{\rho }^{-1}-\mu }{\mu e^{-\mu }+1-e^{-\mathit{\mu \rho }}}& \mathrm{if}\mu \in [1,\infty ).\end{array}$$ (12)

Note that ζ(μ) → ∞ as μ → 0. We carried out exactly the same simulations as before. These are also featured in Figure 4, and again confirm our local heuristics. We conclude that positive correlations between viability and conformity tend to lead to a V-shaped critical curve, whose sharpness at critical conformity μ = 1 increases with the size of correlations. In short, then, correlations help more if viability probability increases with size of conformist clusters.

Appendix C. Cluster structure under random pair incompatibilities

Here we show that, under random pairwise incompatibilities model introduced in Section 5.1, connected clusters include large subcubes. The basic idea comes from Boufkhad and Dubois (1999). A configuration a ∈ {0, 1, *}ⁿ is a way to specify a sub-cube of G, if *’s are thought of as places which could be filled by either a 0 or a 1. The number of non-*’s is the length of a. Call a an implicant if the entire sub-cube specified by a is viable.

We present two arguments, beginning with the one which works better for small c. Let the auxiliary random variable X be the number of pairs of loci (i, j), i < j, for which:

• (E1)There is exactly one incompatibility involving alleles on i and j.
• (E2)There is no incompatibility involving an allele on either i or j, and an allele on k ∉ {i, j}.

Assume, without loss of generality, that the incompatibility which satisfies (E1) is (1_i, 1_j). Then fitness of all genotypes which have any of the allele assignments 0_i0_j, 0_i1_j and 1_i0_j, and agree on other loci, is the same. Note also that all pairs of loci which satisfy (E1) and (E2) must be disjoint. Therefore, if x is any viable genotype, its cluster contains an implicant with the number of *’s at least X plus the number of free loci. To determine the size of X, note that the expectation

$$E(X)=\left(\begin{array}{c}n\\ 2\end{array}\right)4p{(1-p)}^3{(1-p)}^{8(n-2)}~c{e}^{-4c}n$$

and furthermore, by an equally easy computation,

$$E(X^2)-E{(X)}^2=O(n),$$

so that X ~ ce^−4cn a. a. s. It follows that every cluster contains a. a. s. at least exp((e^−2c + ce^−4c) log 2−ε)n), viable genotypes, for any ε > 0.

The second argument is a refinement of the one in Boufkhad and Dubois (1999) and only works better for larger c. Call an implicant a a prime implicant (PI) if at any locus i, replacement of either 0_i or 1_i by *_i results in a non-implicant. Moreover, we call a the least prime implicant (LPI) if it is a PI, and the following two conditions are satisfied. First, if all the *’s are changed to 0’s, then no change from 1_i to 0_i results in a viable genotype. Second, no change *_i1_j to 1_i*_j, where i < j, results in an indicator.

Now, every viable genotype must have an LPI in its cluster. To see this, assume we have a PI for which the first condition is not satisfied. Make the indicated change, then replace some 0’s and 1’s by *’s until you get a prime indicator. If the second condition is violated, make the resulting switch, then again make some replacement by *’s until you arrive at a PI. Either of these two operations moves within the same cluster, and keeps the number of 1’s nonincreasing and their positions more to the left. Therefore, the procedure must at some point end, resulting in an LPI in the same cluster.

For a sub-cube a to be an LPI, the following conditions need to be satisfied:

• (I1)Every non-* has to be compatible with every other non-*, and with both 0 and 1 on each of the *’s.
• (I2)Any of the four 0,1 combinations on any pair of *’s must be compatible.

• (LPI1)Pick an i with allele 1, that is, a 1_i. Then 0_i must be incompatible with at least one non-*, or at least one 0 on a *. Furthermore, if 0_i has an incompatibility with a 0 on a * to its left, it has to have another incompatibility, either with a non-*, or with a 0 or a 1 on a *.
• (LPI2)Pick a 0_i. Then 1_i must be incompatible with a non-*, or a 0 or a 1 on a *.

The first two conditions make a an implicant, and the last two an LPI. Note also that these conditions are independent.

Let now X be the number of LPI of length rn. We will identify a function L₄ = L₄(r, c) such that

$$\frac{1}{n}\log E(X)\le L_4.$$

Let

$$L_1=L_1(\beta ,p,z)=z(\beta \log p+(1-\beta )\log (1-p)-\beta \log \beta -(1-\beta )\log (1-\beta )).$$

This is the exponential rate for the probability that in zn Bernoulli trials with success probability p there are exactly βn successes, i.e., this probability is ≈ exp(L₁n). Further, if κ, ε, δ ∈ (0, 1) are fixed, then among sub-cubes with rn non-*’s and αn 1’s (α ≤ r), the proportion which have εn 1’s in [κn, n] and δn *’s in [1, κn] has exponential rate

$$\begin{array}{lll}{L}_2& =& L_2(r,c,\kappa ,\alpha ,\epsilon ,\delta )\\ & =& L_1((\alpha -\epsilon )/\kappa ,\alpha ,\kappa )+L_1(\epsilon /(1-\kappa ),\alpha ,1-\kappa )\\ & & +L_1(\delta /(\kappa -\alpha +\epsilon ),1-r,\kappa -\alpha +\epsilon )+L_1((1-r-\delta )/(1-\kappa -\epsilon ),1-r,1-\kappa -\epsilon ).\end{array}$$

(Here all four first arguments in L₁ are in [0, 1], or else the rate is −∞.)

The expected number of LPI, with r,κ, ε, δ given as above, has exponential rate at most (and this is only an upper bound)

$$\begin{array}{lll}{L}_3& =& L_3(r,c,\kappa ,\alpha ,\epsilon ,\delta )\\ & =& -(1-r)\log (1-r)-\alpha \log \alpha -(r-\alpha )\log (r-\alpha )\\ & & -c{(1-r/2)}^2\\ & & +(r-\alpha )\log (1-\exp (-c(1-r/2)))\\ & & +(\alpha -\epsilon )\log (1-\exp (-c/2))+\epsilon \log (1-\exp (-c/2)-\frac{1}{2}\delta c\exp (-c(1-r/2)))\\ & & +L_2(r,c,\kappa ,\alpha ,\epsilon ,\delta ).\end{array}$$

The next to last line is obtained from (LPI1), as εn 1’s must have δn *’s on their left.

It follows that L₄ can be obtained by

$$L_4(r,c)=\underset{\kappa }{\inf }\underset{\alpha ,\epsilon ,\delta }{\sup }{L}_3(r,c,\kappa ,\alpha ,\epsilon ,\delta ).$$

If L₄(r, c) < 0, all LPI (for this c) a. a. s. have length at most r. Numerical computations show that this gives a better bound than 1 − e^−2c − ce^−4c for c ≥ 0.38. Let us denote the best upper bound from the two estimates by r_u(c). This function is computed numerically and plotted in Figure 3.

Appendix D. Proof of equation (10)

In this section we assume that genotypes have multiallelic loci, which are subject to random pair incompatibilities. The model introduced in Section 5.2 is the most natural, but is not best suited for our second moment approach. Instead, we will work with the equivalent modified model with m pair incompatibilities, each chosen independently at random, and the first and the second member of each pair chosen independently from the an available alleles. We will assume that $m=\frac{1}{4}{\mathit{ca}}^{2}n$, label $c^{\prime }=\frac{1}{4}c$, and denote, as usual, the resulting set of incompatibilities by F.

To see that these two models are equivalent for our purposes, first note that the number of incompatibilities which are not legitimate, in the sense that the two alleles are chosen from the same locus, is stochastically bounded in n. (In fact, it converges in distribution to a Poisson(c′a²) random variable.) Moreover, by the Poisson approximation to the birthday problem (Barbour et al., 1992), the number of pairs of choices which result in the same incompatibility in this model is asymptotically Poisson(c′a²/2). In short, then, the procedure results in the number m − O(1) of different legitimate incompatibilities. If m in the modified model is increased to, say, m′ = m + n^2/3, then the two models could be coupled so that the incompatibilities in the original model are included in those in the modified model. As the existence of a viable phenotype becomes less likely when m is increased, this demonstrates that (10) will follow once we show the following for the modified model: for every ε > 0 there exists a large enough a so that c′ < log a − ε implies that N ≥ 1 a. a. s.

To show this, we introduce the auxiliary random variable

$$X=\sum _{\sigma \in G_a}\prod _{I\in F}(w_0{1}_{\{\mid I\cap \sigma \mid =0\}}+w_1{1}_{\{\mid I\cap \sigma \mid =1\}}),$$

where 1_A is the indicator of the set A. The size of the intersection I ∩ σ is computed by transforming both the incompatibility I and the genotype σ to sets of (indexed) alleles, and the weights w₀ and w₁ will be chosen later. To intuitively understand the statistic X, note that when w₀ = w₁ = 1, the product is exactly the indicator of the event that σ is viable and X is then the number of viable genotypes N. In general, X gives different scores to different viable genotypes — however, the crucial fact to note is that that X > 0 iff N > 0. Therefore

$$P(N>0)=P(X>0)\ge {(E(X))}^2/E(X^2),$$

which is how the second moment method is used (Achlioptas and Moore, 2004).

As

$$\begin{array}{ccc}P(\mid \sigma \cap I\mid =0)& =& {\left(\frac{a-1}{a}\right)}^2,\\ P(\mid \sigma \cap I\mid =1)& =& \frac{2(a-1)}{a^2},\end{array}$$

we have

$$E(X)=a^n{\left(w_0{\left(\frac{a-1}{a}\right)}^2+w_1\frac{2(a-1)}{a^2}\right)}^m.$$

Moreover

$$E(X^2)=\sum _{\kappa =0}^n{a}^n\left(\begin{array}{c}n\\ \kappa \end{array}\right){(a-1)}^{\kappa }(w_0^{2}P(00)+2w_0{w}_{1}P(01)+w_1^{2}P(11)),$$

where P(01) is the probability that I has intersection of size 0 with σ = 0₁…0_k0_k+1…0_n and of size 1 with τ = 1₁…1_k0_k+1…0_n, and P(00) and P(11) are defined analogously. Thus, if k = αn,

$$\begin{array}{lll}P(00)& =& {\left(1-\frac{1+\alpha }{a}\right)}^2,\\ P(01)& =& \frac{2\alpha }{a}\left(1-\frac{1+\alpha }{a}\right),\\ P(11)& =& \frac{2(1-\alpha )}{a}\left(1-\frac{1+\alpha }{a}\right)+2{\left(\frac{\alpha }{a}\right)}^2.\end{array}$$

Let Λ = Λ_a,w0,w1(α) be the n’th root of the k = (αn)’th term in the sum for E(X²), divided by E(X)². Hence

$$\begin{array}{ll}\Lambda =& \frac{{(a-1)}^{\alpha }}{a·{\alpha }^{\alpha }{(1-\alpha )}^{1-\alpha }}\\ & \times \frac{{\left(w_0^2{\left(1-\frac{1+\alpha }{a}\right)}^2+4w_0{w}_1\frac{\alpha }{a}\left(1-\frac{1+\alpha }{a}\right)+2w_1^2\left(\frac{(1-\alpha )}{a}\left(1-\frac{1+\alpha }{a}\right)+{\left(\frac{\alpha }{a}\right)}^2\right)\right)}^{c^{\prime }{a}^2}}{{\left(w_0{\left(\frac{a-1}{a}\right)}^2+w_1\frac{2(a-1)}{a^2}\right)}^{2c^{\prime }{a}^2}}.\end{array}$$

Let α* = (a − 1)/a. A short computation shows that Λ = 1 when α = α*.

If Λ > 1 for some α, then E(X²)/(E(X))² increases exponentially and the method fails (as we will see below, this always happens when w₀ = w₁ = 1, i.e., when X = N). On the other hand, if Λ < 1 for α ≠ α*, and $\frac{d^2\Lambda }{d{\alpha }^2}(\alpha \ast )<0$, then Lemma 3 from Achlioptas and Moore (2004) implies that E(X²)/(E(X))² ≤ C for some constant C, which in turn implies that P(N > 0) ≥ 1/C. The sharp threshold result then finishes off the proof of (10).

Our aim then is to show that w₀ and w₁ can be chosen so that, for c′ = log a − ε, Λ has the properties described in the above paragraph. We have thus reduced the proof of (10) to a calculus problem.

Certainly the necessary condition is that $\frac{d\Lambda }{d\alpha }(\alpha \ast )=0$, and

$$\frac{d\Lambda }{d\alpha }(\alpha \ast )=-\frac{2}{a^3}{(w_0(a-1)-w_1(a-2))}^2,$$

so we choose w₀ = a − 2 and w₁ = a − 1. (Only the quotient between w₀ and w₁ matters, so a single equation is enough.) This simplifies Λ to

$$\Lambda ={\Lambda }_{\alpha }(\alpha )=\frac{{(a-1)}^{\alpha }}{a{\alpha }^{\alpha }{(1-\alpha )}^{1-\alpha }}·\frac{{\left({\left(\alpha -\frac{a-1}{a}\right)}^2-\frac{{(a-1)}^4}{a^2}\right)}^{c^{\prime }{a}^2}}{{\left(\frac{{(a-1)}^2}{a}\right)}^{2c^{\prime }{a}^2}}.$$

Let φ = log Λ. We need to demonstrate that φ < 0 for α ∈ [0, α*) ∪ (α*, 1] and that φ″(α*) < 0. A further simplification can be obtained by using x − Cx² ≤ log(1 + x) ≤ x (valid for all nonnegative x), which enables us to transform φ (without changing the notation) to

$$\varphi (\alpha )=c^{\prime }\frac{a^4}{{(a-1)}^4}{\left(\alpha -\frac{a-1}{a}\right)}^2-\alpha \log \alpha -(1-\alpha )\log (1-\alpha )+\alpha \log (a-1)-\log a.$$

Now

$${\varphi }^{″}(\alpha )=2c^{\prime }\frac{a^4}{{(a-1)}^4}-\frac{1}{\alpha (1-\alpha )}.$$

So automatically, for c′ large but c′ = o(a), φ″(α*) < 0 for large a. Moreover, φ cannot have another local maximum when φ″ > 0. If φ(α) ≥ 0 for some α ≠ α*, then this must happen for an α in one of the two intervals [0, 1/(2c′)+O((c′)⁻²)] or [1 − 1/(2c′) − O((c′)⁻²), 1]. Now, φ has a unique maximum at α* in the second interval. In the first interval, a short computation shows that

$$\varphi (\alpha )=-\epsilon -\alpha \log a+O\left(\frac{\mathrm{log\; log}a}{\log a}\right),$$

which is negative for large a. This ends the proof.

This method yields nontrivial lower bounds for γ for all a ≥ 3, cf. Table 1.

Table 1.

The lower bounds on γ obtained by the method described in text, compared to the easy upper bounds 4 log a.

a	l. b. on γ	4 log a
3	1.679	4.395
4	2.841	5.546
5	3.848	6.438
6	4.714	7.168
7	5.467	7.784
8	6.128	8.318
9	6.715	8.789
10	7.242	9.211
20	10.672	11.983
30	12.608	13.605
40	13.944	14.756
50	14.960	15.649
100	18.017	18.421
200	20.982	21.194
300	22.663	22.816
400	23.846	23.966
500	24.759	24.859

Appendix E. Existence of viable phenotypes

In this section we describe a comparison between models from Sections 5.2 and 5.3 that will yield the result in Section 5.3. We discretize the continuous phenotype space and in the process obtain slightly dependent incompatibilities which cause a loss of precision by the factor 4.

We begin by assuming that a = 1/r is an integer, which we can do without loss of generality. Divide the i’th coordinate interval [0, 1] into a disjoint intervals I_i0,…,I_{i,a − 1} of length r. Note that in our notation, the first subscript of I specifies a particular trait while the second subscript specifies a particular interval of the trait’s values. To a phenotype x ∈ P we assign an element Δ(x) of the generalized hypercube G_a by Δ(x)_i = j iff x_i ∈ I_ij.

Note that Δ(x)_i = Δ(y)_i implies that |x_i − y_i| ≤ r. Therefore, as soon as I_i1j1 × I_i2j2 contains a point z ∈ Π_i1i2, every x with Δ(x)_i1 = j₁ and Δ(x)_i2 = j₂ has |x_i1 − z_i1| ≤ r and |x_i2 − z_i2| ≤ r and is therefore inviable by definition. Moreover, by the fundamental property of a Poisson point location (e.g., Penrose, 1996), each product I_i1j1 × I_i2j2 intersects Π_i1i2 independently with probability 1 − exp(−λr²) ~ cr²/(2n), for large n. The result from Section 5.2 implies that, when cr² > 4 log a = −4 log r, a. a. s. no Δ(x) is viable and thus there is a. a. s. no viable genotype.

On the other hand, let I^ε be the closed ε-neighborhood of the interval I in [0, 1] (the set of points within ε of I), and consider the events that the square $I_{i_1{j}_1}^{r/2}\times I_{i_2{j}_2}^{r/2}$ contains a point in Π_i1i2. These events are independent if we restrict j₁, j₂ to even integers, as these squares are then disjoint. Moreover, each event has probability 1 − exp(−4λr²) ~ 4cr²/(2n), for large n. We thus look for a viable genotype with Δ(x)_i even for all i. This reduces the number of traits a by a factor of 2, and it follows from Section 5.2 that a viable genotype x with all Δ(x)_i even a. a. s. exists as soon as 4cr² < 4(log(a/2) − o(1)) = (−4 log r − log 2 − o(1)).