Mechanisms of Base Selection by Human Single-stranded Selective Monofunctional Uracil-DNA Glycosylase

Abstract

hSMUG1 (human single-stranded selective monofunctional uracil-DNA glyscosylase) is one of three glycosylases encoded within a small region of human chromosome 12. Those three glycosylases, UNG (uracil-DNA glycosylase), TDG (thymine-DNA glyscosylase), and hSMUG1, have in common the capacity to remove uracil from DNA. However, these glycosylases also repair other lesions and have distinct substrate preferences, indicating that they have potentially redundant but not overlapping physiological roles. The mechanisms by which these glycosylases locate and selectively remove target lesions are not well understood. In addition to uracil, hSMUG1 has been shown to remove some oxidized pyrimidines, suggesting a role in the repair of DNA oxidation damage. In this paper, we describe experiments in which a series of oligonucleotides containing purine and pyrimidine analogs have been used to probe mechanisms by which hSMUG1 distinguishes potential substrates. Our results indicate that the preference of hSMUG1 for mispaired uracil over uracil paired with adenine is best explained by the reduced stability of a duplex containing a mispair, consistent with previous reports with Escherichia coli mispaired uracil-DNA glycosylase. We have also extended the substrate range of hSMUG1 to include 5-carboxyuracil, the last in the series of damage products from thymine methyl group oxidation. The properties used by hSMUG1 to select damaged pyrimidines include the size and free energy of solvation of the 5-substituent but not electronic inductive properties. The observed distinct mechanisms of base selection demonstrated for members of the uracil glycosylase family help explain how considerable diversity in chemical lesion repair can be achieved.

Three glycosylases that initiate DNA repair via the base excision repair (BER)² pathway are found on human chromosome 12. These three glycosylases are designated as UNG, TDG, and hSMUG1 (1–4). Several groups are currently investigating the structure and properties of these glycosylases in order to determine their physiological roles. A common property of these enzymes is the cleavage of uracil residues from DNA, although each of the glycosylases repairs additional lesions. Despite low sequence homology (8%), these three glycosylases share a common fold and overall architecture (5). Subtle differences in structure apparently distinguish these repair enzymes with respect to substrate and context preferences.

UNG is the most active of the glycosylases. UNG recognizes uracil residues when found in single strand, or double strand DNA paired with adenine or mispaired with guanine (6); however, only a small number of other pyrimidines are also targets. UNG is spliced into two forms, UNG1 and UNG2. UNG1 is targeted to the mitochondrion, whereas UNG2 is found primarily in the cell nucleus (7). Due to the capacity of UNG to repair uracil in many contexts, as well as its association with DNA replication machinery and cell cycle specificity, it is thought that a primary role for UNG is in the repair of uracil misincorporated opposite adenine during DNA replication (8, 9). Recent studies also suggest an important role for UNG in removing uracil residues in DNA generated by activation-induced deaminase as part of somatic hypermutation and class switch recombination in activated B-cells (10–12).

In contrast to UNG, the related glycosylases hSMUG1 and TDG appear to target uracil and uracil analogs mispaired with guanine (3, 13, 14). Although hSMUG1 was originally characterized as a single strand selective glycosylase (13), more recent studies suggest it is more active on mispaired uracil in duplex DNA (14), and it has an extended substrate range, removing several oxidized pyrimidines (15–18), including 5-hydroxymethyluracil (HmU), 5-formyluracil (FoU), and 5-hydroxyuracil (HoU). TDG appears to act exclusively on duplex substrates, with a strong preference for mispaired pyrimidines, including thymine, and a strong preference for damage located in CpG dinucleotides (19–21). The apparent sequence selectivity of TDG has led to suggestions that the primary role of TDG is the repair of deaminated 5-methylcytosine residues in CpG dinucleotides (20).

In this paper, we have investigated the enzymatic properties of recombinant human SMUG1 in single-turnover kinetic assays on a series of oligonucleotide substrates containing purine and pyrimidine analogs. In the first set of experiments, the capacity of hSMUG1 to cleave uracil opposite a series of purine analogs was measured to determine if the preference of hSMUG1 for mispairs can be attributed to reduced duplex stability or if hSMUG1 recognizes specific functional groups on the purine opposite the target uracil. In the second series of experiments, a series of 5-substituted uracil analogs was paired opposite guanine to probe the mechanisms by which hSMUG1 distinguishes potential substrates. This series includes uracil, a series of oxidatively damaged pyrimidines, and the 5-halouracils, which serve to measure both substituent size and electronic inductive properties. New to this series is 5-carboxyuracil (CaU), the last in the sequence of damage products arising from oxidation of the thymine methyl group (22–24).

Previous studies with other glycosylases described above have highlighted the importance of size and electronic inductive properties of 5-substituted pyrimidines in substrate selection. In contrast, the capacity of hSMUG1 to recognize HmU but not thymine has been attributed to the hydrophilicity and hydrogen-bonding capacity of the HmU substituent (15–18). In this paper, selected physical properties have been calculated for each pyrimidine examined, including solvent-accessible surface area (SASA) and the free energy of solvation in water. The SASA is introduced as a parameter to define the relative size of the 5-substituted pyrimidines, whereas the free energy of solvation in water is proposed to describe the capacity of the 5-substituted pyrimidine to interact with or replace water within the hSMUG1 pyrimidine binding pocket. The observed kinetic rate constants are compared with the physical properties of the modified bases and base pairs in order to explain the mechanisms by which hSMUG1 identifies and distinguishes target lesions. Our results indicate that the strategies used by hSMUG1 to select target bases and avoid normal bases contrast with those of other members of the uracil DNA-glycosylase family.

MATERIALS AND METHODS

Oligonucleotide Synthesis and Characterization

Oligonucleotides were prepared by solid phase synthesis methods as described previously (25–28). Following synthesis and deprotection, oligonucleotides were purified with Poly-Pak II cartridges and were denaturing gel-purified when necessary. The presence of modified bases was verified by gas chromatography/mass spectrometry following acid hydrolysis and conversion to the trimethylsilyl ethers.

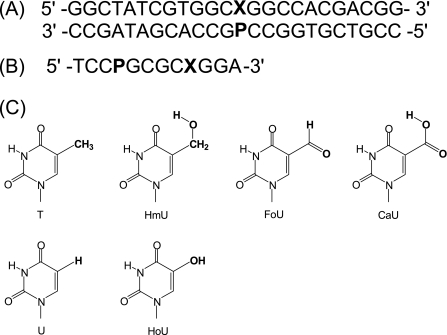
Two sets of oligonucleotides were synthesized. A set of oligonucleotide 24-mers containing uracil with different 5-substituents (X) and purine analogs (P) was synthesized for hSMUG1 activity assays (Fig. 1A). Another set of self-complementary 12-mers containing a uracil and a purine analog was synthesized for melting temperature (T_m) measurements in which the target uracil analog was placed within the same sequence context as in the 24-mer glycosylase assays (Fig. 1B). A 12-base sequence was selected for the thermodynamic studies, because the predicted T_m would be within an appropriate range for UV melting studies (29). The self-complementary 12-mers were designed by keeping the two adjacent bases on each side of the uracil and purine analog base pair constant and linking the two five-base fragments in the 5′ → 3′ orientation. MALDI-TOF mass spectrometry analysis and T_m values of the series of 12-mers examined here have been previously reported (30). Oligonucleotide duplex thermodynamics (ΔG_duplex) were measured at 100 mm NaCl, 10 mm sodium phosphate at pH 7, and T_m values are reported for 28 μm total strand concentration.

FIGURE 1.

Sequences of oligonucleotides and structures of uracil analogs used in this study. A, oligonucleotide duplex used for glycosylase assays, in which X represents thymine, uracil, or a 5-substituted uracil analog and P is a purine. B, sequence of the self-complementary oligonucleotide used for the determination of duplex stability. C, structures of uracil analogs.

Preparation and Characterization of the Ionization Properties of 5-Carboxy-2′-deoxyuridine

Commercially available trifluoromethylthymidine (Sigma) was hydrolyzed in alkaline solution to 5-carboxy-2′-deoxyuridine (31) and purified by silica gel chromatography. The identity of 5-carboxy-2′-deoxyuridine was confirmed by mass spectrometry. Ionization constants were determined by spectrophotometric titration as described previously (32).

Cloning and Isolation of hSMUG1

RNA of hSMUG1 was isolated from HeLa S3 cell line (ATCC catalog number CCL-2.2) using TRIzol reagent according to instructions provided by the manufacturer (Invitrogen). mRNA was reverse transcribed by using the SuperScript First-Strand (Invitrogen) standard protocol. First strand cDNA synthesis was performed by priming with 20 pmol of oligo(dT) in 20 μl of reaction mixture containing 10 mm each of dATP, dCTP, dGTP, and dTTP, 40 units/μl RNase Out recombinant ribonuclease inhibitor, and 50 units/μl SuperScript II reverse transcriptase. The reverse transcription reaction was stopped by cooling to 4 °C for 10 min. The resulting cDNAs were then amplified with Phusion high fidelity DNA polymerase (New England BioLabs, Beverly, MA) according to the manufacturer's instructions. Thirty-six cycles of PCR (10 s at 98 °C, 30 s at 61 °C, and 30 s at 72 °C) were performed. The sequences of oligonucleotides used for PCR were designed based on the cDNA sequence of AF125182 reported by Haushalter et al. (13). The following sequences were used: 5′-cggcggggatccatgccccaggctttcctgct-3′ (sense, carries a BamHI restriction site) and 5′-cttttccttttgcggccgctcatttcaacagcagtggcag-3′ (antisense, carries a NotI restriction site).

After resolution of the products by electrophoresis in 1% agarose gel, the expected 819-bp product was extracted using the QIAquick gel extraction kit (Qiagen, Valencia, CA) and ligated into glutathione S-transferase fusion expression vector pGEX-4T-1 (Amersham Biosciences) previously digested with BamHI and NotI. Ligated products were electroporated into Escherichia coli BL21 Star DE3 (Invitrogen). The plasmid was isolated and purified using a QIAprep Spin Miniprep kit (Qiagen), and both strands of the insert were confirmed via sequencing (Davis Sequencing, Inc., Davis, CA) using the primers 5′-TTGGTGGTGGCGACCATCCTCCAA-3′ (pGEXmcs5′) and 5′- CTGCATGTGTCAGAGGTTTTCACC-3′ (pGEXmcs3′).

Purification of Recombinant hSMUG1

To purify hSMUG1 expressed as a recombinant protein in E. coli, 2 liters of E. coli BL21 Star DE3 carrying the hSMUG1-glutathione S-transferase construct were grown in LB broth with 50 μg/ml ampicillin at 37 °C until A₆₀₀ = 0.6–0.7 and then induced with 0.2 mm isopropyl-β-d-thiogalactopyranoside overnight at 30 °C. The cells were harvested by centrifugation, resuspended in lysis buffer (50 mm Tris, pH 7.4, 150 mm NaCl, 5 mm MgCl₂, 0.01% Triton X-100), supplemented with 1 mm dithiothreitol, 1 mm phenylmethylsulfonyl fluoride, and incubated at room temperature for 30 min. Lysis was then completed by sonicating the suspension on ice using a Branson Sonifier Cell Disruptor 200 at six bursts of 10 s each, with a 90-s interval between pulses. The lysate was clarified by centrifugation (12,000 rpm for 30 min at 4 °C), and the supernatant was then mixed with swelled glutathione-agarose beads (Sigma) and incubated at 4 °C overnight with gentle agitation. The suspensions were centrifuged at 3,000 rpm for 5 min at 4 °C, and the beads were washed twice with lysis buffer, followed by twice with thrombin buffer (50 mm Tris, pH 7.4, 150 mm NaCl, 5 mm MgCl₂, 1 mm dithiothreitol).

The recombinant protein glutathione S-transferase- hSMUG1 was resuspended in 15 ml of thrombin buffer and then was cleaved with 100 units/ml thrombin (Sigma) at 37 °C for 1 h and subsequently purified by FPLC using a Superdex 75 column (GE Healthcare). The protein was concentrated using Centricon YM-10 membranes (Millipore, Billerica, MA). The protein concentration was determined using the BCA protein assay reagent kit (Pierce). The protein was analyzed on NuPAGE 4–12% BisTris gels (Invitrogen) stained with Simply Blue (Invitrogen) and confirmed by Western blots using primary hSMUG1 antibody (Santa Cruz Biotechnology, Inc., Santa Cruz, CA). Furthermore, hSMUG1 was digested with trypsin following the protocol of Matsudaira (33) and analyzed by MALDI-TOF mass spectrometry (data not shown) (Bruker Daltonics, Billerica, MA). To further verify that there was no E. coli uracil-DNA glycosylase contamination after purification, we tested the hSMUG1 recombinant activity in the presence of a uracil glycosylase inhibitor using a single-stranded uracil-containing oligonucleotide corresponding to Fig. 1 as a substrate, and as expected, there was no significant difference in the amount of excised single-stranded uracil-containing oligonucleotide with or without the addition of uracil glycosylase inhibitor (data not shown).

Determination of Single-turnover Kinetics on Oligonucleotide Substrates

Oligonucleotide Labeling and Annealing

5′-End radiolabeling was performed using adenosine [γ-³²P]ATP (MP Biomedical, Costa Mesa, CA) and T4 polynucleotide kinase (New England BioLabs, Beverly, MA) under conditions recommended by the enzyme supplier. Labeled mixtures were subsequently centrifuged through G-50 Sephadex columns (Roche Applied Science) to remove excess unincorporated nucleotide. Labeled single-stranded oligonucleotides were annealed to a 2-fold molar excess of unlabeled complementary strand in 20 mm Tris-HCl (pH 8.0), 1 mm EDTA, 1 mm dithiothreitol, 0.1 mg/ml bovine serum albumin, and 100 mm NaCl. The mixture was heated to 95 °C for 5 min and cooled slowly to room temperature.

Enzymatic Reactions under Single-turnover Conditions

The cleavage rates were determined under single-turnover conditions. DNA substrates (50 nm) were incubated with 200 nm hSMUG1 at 37 °C in the reaction buffer containing 20 mm Tris-HCl (pH 8.0), 1 mm EDTA, 1 mm dithiothreitol, 0.1 mg/ml bovine serum albumin, and 100 mm NaCl. At selected time points 10-μl samples were removed and stopped by adding 5 μl of 0.1 m NaOH and an equal volume of Maxam-Gilbert loading buffer (98% formamide, 0.01 m EDTA, 1 mg/ml xylene cyanol, and 1 mg/ml bromphenol blue) and 1 μl (50 pmol) of an unlabeled complementary oligonucleotide as a reannealing competitor. The backbone was cleaved at the apyrimidinic sites with NaOH by heating at 95 °C for 30 min. For oligonucleotides containing FoU and HoU, reactions were stopped by heating to 75 °C for 5 min and then cooled to room temperature. The abasic site was cleaved by human AP endonuclease at 37 °C for 1 h in reaction buffer provided by the manufacturer (Trevigen, Gaithersburg, MD). Reaction samples were electrophoresed on 18% denaturing polyacrylamide gels (8 m urea), and the bands corresponding to substrate and products were visualized and quantified using a PhosphorImager (GE Healthcare). The reaction rate constant, k_obs, was determined by fitting time course data to a single exponential (y = a(1 − a^−bx)) using SigmaPlot 10.0, where a represents the maximum level of product ratio, and b is the reaction rate constant, k_obs.

A rapid quenched flow apparatus (RQF-3; KinTek Corp., Austin, TX) was used for reactions requiring a short time course (53 ms to 200 s, U:G, U:Hx, and U:Pu). Rapid quench reactions were performed using the standard conditions described above, except that the reaction volume was 35.5 μl, and 100 μl of 50 mm NaOH was used to quench reactions. The quenched reactions were heated at 95 °C for 30 min to cleave abasic sites and then dried under reduced pressure. DNA was redissolved in 20 μl of Maxam-Gilbert loading buffer, and 1 μl (50 pmol) of the unlabeled complementary oligonucleotide was added as a reannealing competitor. Samples were analyzed as described above.

Computational Methods and Procedures

Free Energy of Solvation

In this work, the recently developed M06-2X (34) flavor of density functional theory (DFT) was used to determine the solvation free energy of the various substituted uracil analogs. M06-2X has been shown recently to provide good accuracy in predicting the binding energy and structure of van der Waals complexes (35), since it is a hybrid DFT functional with 54% Hartree-Fock meta-exchange in the functional. Thus, the M06 family of DFT functionals describes aromatic-aromatic interactions accurately without adding empirical corrections to account for the dispersion term, which was a limitation of previous DFT functionals, such as LDA, PW91, PBE, and B3LYP (36–40).

Following Kelly et al. (41), the solvation free energy can be written as follows,

where X represents the pyrimidine of interest and with the total solvation free energy being the difference in free energy between the gas phase electronic structure calculation and the aqueous phase calculation. These two separate calculations are performed for each substituted uracil analog (5-substituent = Br, CH₃, I, Cl, F, CHO, COOH, CH₂OH, OH, and H), as described below. At physiological pH, 5-carboxyuracil would exist predominantly as the ionized carboxylate anion. We find that the most accurate way to calculate the free energy of solvation is to first calculate the solvation free energy of the neutral molecule and then apply a correction determined by the difference between the carboxylate pK_a and the pH of the solvent (42), as discussed below.

Gas Phase Calculations

The M06-2X DFT calculations used the cc-pVTZ(-f)++ basis set and were performed with the Jaguar 7.5 quantum chemistry software. In several previous studies of nitrogen-containing heterocyclic compounds, this methodology gave results of high accuracy (43) and comparable with a higher level of theory, such as G3B3 (44). The cc-pVTZ(-f)++, which is also denoted as “aug-cc-pVTZ” (for “augmented correlation-consistent basis set with polarized valence triple-ζ”), is the cc-pVTZ++ basis set of Dunning et al. (45, 46). For 5-iodouracil, the effective core potentials were used on the iodine heavy atom, with the rest of the atoms using the cc-pVTZ(-f)++ basis set, and this basis set is denoted cc-pVTZ-PP(-f)++.

The standard Gibbs free energy of each substituted uracil analog in the gas phase (42) is given by the following,

where E_0K is the total electronic energy at 0 K, ZPE is the zero-point vibrational energy, and G_0→298 is the Gibbs free energy change from 0 to 298 K at 1 atm calculated using the rigid rotor-harmonic oscillator approximation without scaling.

Solution Phase Calculations

The free energy of solvation of aromatic compounds in water can be obtained by coupling DFT with a Poisson-Boltzmann continuum solvent (43). In this approach, the solute, described quantum mechanically, is immersed in a continuum solvent described with a self-consistent reaction field, obtained through numerical solution of the Poisson-Boltzmann equation. The solute is assigned a dielectric constant of 1 (a vacuum), whereas the solute-solvent boundary, described as the solvent-accessible surface area (SASA), uses standard atomic radii taken from Tannor et al. (47, 48). The following radii were used: 1.9 Å for sp³-hybridized carbon, 1.6 Å for nitrogen and oxygen, and 1.15 Å for hydrogen. The solvent is characterized by a probe radius (1.4 Å in the case of water) rolled along the solute boundary and having a constant dielectric (79.2 for water). The SASAs of the various analogs (relative to uracil) are used in Table 1 to include the effect of the substituent size on the measured rate.

TABLE 1.

Rate constants and physical characteristics for base pairs examined in this study

The values include measured rate constants for hSMUG1 gly co sylase cleavage reactions (k_obs), melting temperature (T_m) from Refs. (30) and (52), measured free energy of duplex formation (ΔG_duplex) determined from thermal melting studies, calculated SASA for py rim i dine bases, and calculated free energy of solvation in water for py rim i dine bases. Calculated values for SASA and ΔG_solv⁰ correspond to neutral molecules. Calculated values for FoU correspond to the anti conformer. 2AA, 2-aminoadenine; 2AP, 2-aminopurine.

	kobs	Tm	ΔGduplex	SASA	ΔGsolv0
	s−1	°C	kcal mol−1	Å2	kcal mol−1
U:G	1.34 ± 0.15 × 10−1	49.1 ± 0.1	−10.8 ± 0.4	262.69	−16.76
U:Hx	6.34 ± 0.82 × 10−1	49.0 ± 0.7	−10.4 ± 0.5
U:Pu	8.05 ± 0.55 × 10−2	52.4 ± 0.3	−12.1 ± 0.3
U:A	5.78 ± 0.14 × 10−4	64.4 ± 0.5	−15.9 ± 0.5
U:2AA	3.83 ± 0.59 × 10−4	66.3 ± 0.5	−15.3 ± 0.9
U:2AP	2.93 ± 0.12 × 10−3	61.1 ± 0.1	−14.7 ± 0.3
FU:G	4.72 ± 0.16 × 10−3	48.9 ± 0.4	−10.9 ± 0.4	273.50	−17.20
ClU:G	9.40 ± 0.60 × 10−5	50.4 ± 0.4	−11.1 ± 0.2	289.43	−16.60
BrU:G	<1.0 × 10−6	50.0 ± 0.3	−11.1 ± 0.2	298.05	−16.47
IU:G	<1.0 × 10−6	49.9 ± 0.3	−11.1 ± 0.4	308.35	−16.18
HoU:G	4.14 ± 0.25 × 10−2	49.2 ± 0.4	−10.4 ± 0.5	270.02	−23.60
T:G	<1.0 × 10−6	50.2 ± 0.1	−11.3 ± 0.3	286.95	−16.16
HmU:G	3.48 ± 0.18 × 10−2	49.5 ± 0.5	−11.1 ± 0.2	299.04	−22.54
FoU:G	1.33 ± 0.08 × 10−2	46.3 ± 0.2	−9.50 ± 0.2	293.24	−19.17
CaU:G	2.58 ± 0.19 × 10−2	49.7 ± 0.4	−11.0 ± 0.4	296.81	−18.83

The charge distribution of the solute was represented by atom-centered point charges adjusted to reproduce the electrostatic potential (ESP) derived from the quantum mechanics electron density. The cavity term (used to represent the energy required to create the solute cavity in the solvent) was calculated using the empirical relation given in Ref. 45. Calculations were carried out using both gas phase geometries and geometries optimized in the solvent reaction field.

RESULTS

Oligonucleotides containing a series of modified purines and pyrimidines were prepared and characterized as described previously (30). Sequences used in this study are shown in Fig. 1. The free energy of duplex formation for the self-complementary 12-mer oligonucleotides containing purine and pyrimidine analogs was determined from UV melting studies, and the results are presented in Table 1. Recombinant hSMUG1 was overexpressed and purified as described previously (13). Characterization of the recombinant protein included MALDI-TOF mass spectrometry analysis of tryptic peptides (data not shown).

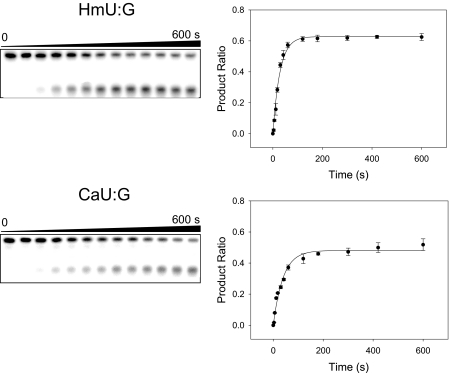
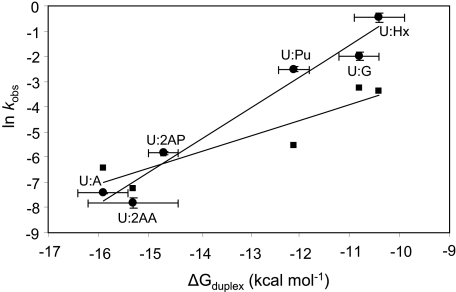
In the first series of experiments, hSMUG1 activity against uracil paired with a series of purines was investigated. An example set of kinetic data is shown in Fig. 2. The measured rate constants (k_obs), determined under single-turnover conditions, are shown in Table 1. An inverse relationship between the natural logarithm of the enzymatic rate constant and the free energy of duplex formation was observed and is shown in Fig. 3.

FIGURE 2.

Kinetic study of hSMUG1 cleavage of 5-substituted uracil analogues paired with guanine illustrating the gel electrophoretic assay (left) and time-dependent product ratios (right). Single-turnover reactions were performed at 37 °C with 50 nm substrate and 200 nm hSMUG1 in the reaction buffer, as described under “Materials and Methods.” Top, HmU:G as a substrate; bottom, CaU:G as a substrate.

FIGURE 3.

Linear relationship between the free energy of duplex formation, ΔG_duplex, and observed cleavage rate constants. MUG data from Ref. 52 is presented as squares, and hSMUG1 from this study is presented as circles. The natural logarithms of the observed rate constants (ln k_obs) for MUG and hSMUG1 are plotted versus ΔG_duplex. Straight lines are obtained for hSMUG1 with a slope of 1.26, intercept of 12.35, and r² = 0.96 and for MUG with a slope of 0.63, intercept of 3.02, and r² = 0.85.

In a second set of experiments, hSMUG1 single-turnover kinetic activity against a series of 5-substituted uracil analogs was measured (Table 1). In order to understand the mechanism of base selection for the uracil analogs tested, selected properties were either measured or calculated for each of the uracil analogs examined in the kinetic studies. Rate constants were then compared with physical parameters as described below.

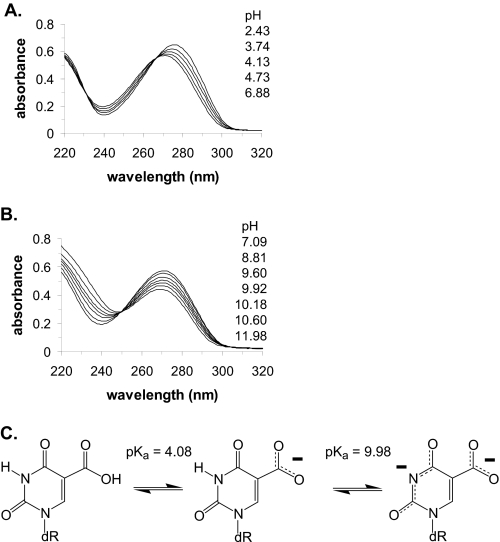
The oxidation of the thymine methyl group results in a series of damage products, including HmU, FoU, and CaU. Although hSMUG1 has been shown previously to recognize and remove HmU and FoU (15–18), it has not yet been tested with CaU. The carboxyl group of CaU would be expected to be ionized under physiological conditions. Ionization of the carboxyl group of CaU could also have a profound effect upon ionization of the N3 proton. We therefore prepared 5-carboxy-2′-deoxyuridine by an established method (31) and determined the pK_a values for the 5-carboxyl group and the N3 proton by spectrophotometric titration (32), as shown in Fig. 4.

FIGURE 4.

Ionization of 5-carboxyuracil. A, ionization of the 5-carboxyl group with a pK_a of 4.08. B, ionization of the N3 ring nitrogen with a pK_a of 9.98. C, structures of the neutral and ionized forms of CaU.

The measured pK_a values are 4.08 ± 0.1 for the 5-carboxyl group and 9.98 ± 0.1 for the N3 position. Previously, we have shown that the pK_a of the N3 proton of uracil derivatives can be estimated based upon the inductive property of the 5-substituent (49). In the case of CaU, the ionization of the 5-carboxyl group would influence the pK_a of the N3 proton. If the 5-carboxyl group were unionized, it would withdraw electron density from the pyrimidine ring (σ meta-Hammett parameter (σ_m) = 0.37) (50), predicting a pK_a for the N3 position of 7.86 ± 0.14. Alternatively, if the carboxyl group were ionized, it would donate electron density to the pyrimidine ring, predicting a pK_a for the N3 proton of 9.90 ± 0.14. Upon the basis of the experimentally determined pK_a value of the 5-carboxyl group, we would expect it to be predominantly ionized at physiological pH, resulting in an increase in the N3 pK_a relative to 2′-deoxyuridine. The measured value for the pK_a of the N3 proton of 9.98 is close to the value of 9.90 predicted from the inductive property of an ionized carboxyl group (49).

In a previous study, we demonstrated that the rate of base cleavage by MUG was inversely proportional to the size of the 5-substituent (52). In that study, we examined only spherical substituents whose size could be estimated from van der Waals radii and bond lengths. In the current study, we examined several additional pyrimidines with more complicated 5-substituents. We therefore determined the SASA of the uracil analogs with 5-substituents as an index of relative size by computational methods, and the values are presented in Table 1. The 5-formyl group of FoU can rotate around the 5-position and is found in either syn or anti conformations, as described previously (51). The anti conformation has been determined to be the preferred orientation. Therefore, the SASA value for FoU recorded in Table 1 corresponds to the anti conformer. Although SASA values have been determined previously for some pyrimidines (53), these values have not been determined for the entire series of pyrimidines examined here.

Previous studies have established that hSMUG1 can recognize and remove pyrimidine damage products with 5-substituents capable of hydrogen bonding that could potentially displace water molecules from the hSMUG1 pyrimidine binding cleft (15–18). In order to derive a molecular property that might be able to quantitatively predict the capacity of uracil analogs to bind to hSMUG1, we calculated the free energy of solvation in water for each substituent, and the corresponding values are recorded in Table 1. Although the free energy of solvation has been determined for several of the substituents examined here in other types of molecules (54), the free energy of solvation has not been previously calculated for the series of 5-substituted uracil analogs examined here.

As discussed above, the formyl group of FoU can be found in either syn or anti conformation. Since the anti conformation is preferred, the free energy of solvation for FoU in Table 1 corresponds to the anti conformer. Two of the uracil analogs, HoU and CaU, have acidic protons and can be ionized under physiological conditions. In our experience, the calculation of the free energy of solvation of ionized molecules in water is unreliable due to the inherent difficulty in obtaining reliable values for the electrostatics of the charged species. Therefore, a commonly applied solution is to accurately calculate the free energy of solvation for the neutral species and then to apply a correction factor based upon pK_a values and solution pH to account for ionization,

where

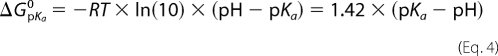The free energy of solvation of HoU in water was determined to be −24.17 kcal mol⁻¹ and would correspond to the free energy of solvation for the neutral molecule when the solvent pH was equal to the pK_a of the 5-hydroxyl proton. The measured pK_a for the 5-hydroxyl group of 5-hydroxy-2′-deoxyuridine is 7.6 (49), and the hSMUG1 experiments were performed at pH 8.0 and 37 °C. The corresponding correction factor would be −0.57 kcal mol⁻¹, so that the free energy of solvation for ionized HoU would be −24.75 and −23.60 kcal mol⁻¹ for neutral HoU at pH 8.0. The value for the neutral species is recorded in Table 1.

Similarly, the free energy of solvation for neutral CaU was calculated to be −24.39 kcal mol⁻¹. The experimentally measured value for the pK_a of the 5-carboxyl proton reported here is 4.08. Since CaU would be expected to be predominantly ionized at pH 8, a correction factor of 5.57 kcal mol⁻¹ would be required. Since the neutral form of CaU would spontaneously ionize at pH 8, the free energy of solvation of the ionized CaU would be −29.95, whereas the free energy of solvation of the neutral molecule at pH 8 would be −18.83 kcal mol⁻¹. The value for the neutral molecule is recorded in Table 1.

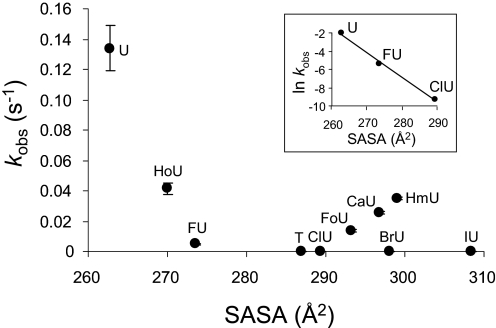
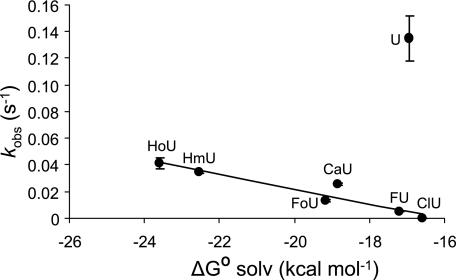
A complex relationship between the observed enzymatic rate constant (k_obs) and the SASA was observed and is presented in Fig. 5. The natural logarithm of the observed rate constant (ln k_obs) was observed to decrease linearly with increasing SASA for a subset of the analogs examined (Fig. 5, inset). The observed enzymatic rate constant (k_obs) was also observed to decrease linearly for several of the pyrimidine analogs except uracil as the magnitude of the free energy of solvation in water (ΔG_solv⁰) for the corresponding pyrimidine became less favorable (Fig. 6). Further relationships between the properties of the analogs examined and the observed cleavage rate constants were explored and are presented under “Discussion.”

FIGURE 5.

Relationship between SASA and glycosylase kinetics. The observed rate constants (k_obs) for hSMUG1 cleavage of uracil analogs paired opposite guanine are plotted against the SASA. Inset, the impact of the size alone on the apparent rate constant. In the inset, values of ln k_obs for U:G, FU:G, and ClU:G are plotted versus SASA. A straight line is obtained, with slope of −0.27, intercept of 69.19, and r² = 0.99.

FIGURE 6.

Relationship between glycosylase cleavage rates and ΔG⁰ solvation. The observed rate constants (k_obs) for hSMUG1 cleavage of uracil analogs opposite guanine are plotted against ΔG⁰ solvation. A line is drawn through all the points except uracil. The slope of this line is −5.58 × 10⁻³ with intercept of −8.96 × 10⁻², and r² is 0.90.

DISCUSSION

Human single strand selective monofunctional uracil-DNA glycosylase, hSMUG1, is one of three glycosylases encoded on human chromosome 12 that removes uracil from DNA. Like the other two glycosylases, UNG and TDG, hSMUG1 is a monofunctional glycosylase, generating an abasic site in the initiation of the base excision repair pathway essential for maintaining genomic integrity (1–4). Although UNG, TDG, and hSMUG1 share many similarities, there are significant differences in the range of damaged and modified bases acted upon by these enzymes, suggesting that they may have unique physiological roles in genome maintenance. In the experiments described here, we wished to examine more extensively the potential substrates for hSMUG1 and to determine the mechanisms by which hSMUG1 locates and interrogates potential substrates.

In order to accomplish this goal, a series of oligonucleotides (Fig. 1) containing purine and pyrimidine analogs were constructed and characterized using standard methods (30) (see Fig. 2 of Ref. 52 for structures of modified purines paired with uracil). Duplex stability was determined by measuring the temperature dependence of the oligonucleotide UV absorbance at 260 nm in aqueous solution as a function of oligonucleotide concentration (Table 1). Several properties of the potential uracil analog substrates were determined either experimentally or computationally, as presented in Table 1 and discussed further below. The human DNA repair enzyme, hSMUG1, was cloned and purified as previously reported (13) and characterized by MALDI-TOF mass spectrometry. The capacity of hSMUG1 to cleave uracil and its analogs from duplex substrates was measured in single-turnover kinetic assays as shown in Fig. 2. Catalytic rate constants are presented in Table 1. Previous studies have established that E. coli MUG and hSMUG1 bind tightly to the abasic site-containing oligonucleotide following the removal of a target base (13, 14, 52). Due to the strong product binding displayed by some glycosylases, steady-state kinetic analysis does not give an accurate reflection of relative rates with different potential substrates. Single-turnover kinetic conditions are therefore required. Our preliminary studies with hSMUG1 also indicated strong product binding, and therefore the kinetic studies performed here were conducted under single-turnover conditions.

In our previous study of a related glycosylase, E. coli MUG, three parameters were identified that are used by MUG to select a target pyrimidine (52). These factors were 1) duplex stability (pyrimidines in less stable duplex structures were repaired faster), 2) 5-substituent size (pyrimidine analogs with smaller 5-substituents were repaired faster than those with larger substituents), and 3) 5-substituent electronic inductive effects (pyrimidines with electron-withdrawing substituents in the 5-position were repaired faster than those with electron-donating substituents). Based upon the similarities in the enzymatic properties of MUG and hSMUG1, it was expected that hSMUG1 would use similar strategies for substrate selection. In this study with hSMUG1, we have used the same battery of oligonucleotide substrates to probe the mechanisms of base selection, and we have added additional analogs reported to be repaired by hSMUG1, including a series of pyrimidines oxidized in the 5-position, including HmU, FoU, CaU, and HoU.

In the first study with hSMUG1, the repair of a target uracil residue paired opposite a series of purine analogs was examined. The purines selected would allow simultaneous assessment of the potential impact of the purine on duplex stability and could probe for the importance of specific functional groups. Within this series, the target uracil could be found in a base pair configuration similar to a Watson-Crick base pair with one (U:Pu), two (U:A, U:2APu), or three (U:AA) hydrogen bonds or mispaired in a wobble geometry with two hydrogen bonds (U:G, U:Hx). The thermodynamic stability of the uracil-containing oligonucleotides within this series varies significantly, as indicated in Table 1.

The single-turnover kinetics for the repair of uracil within this series of duplex oligonucleotides was measured, and the observed rate constants (k_obs) are presented in Table 1. Inspection of the data indicates that the observed rate constants decline as the free energy of duplex formation increases. Note that a larger negative value for the free energy of duplex formation (ΔG_duplex) indicates greater duplex stability. A plot of the natural logarithm of the observed rate constant versus the free energy of duplex formation is shown in Fig. 3. The line describing the data for the six uracil-containing base pairs is indicated in Equation 5,

A predicted rate constant (k_duplex), based upon the measured helix stability (ΔG_duplex), can then be determined (Equation 6). In order to compare rate constants based upon additional parameters described below, a relative rate constant (k_rel,duplex) can be calculated (Equation 7). A predicted rate constant is converted to a predicted relative rate constant by dividing k_duplex by the rate constant for the U:G pair given by Equation 6. Because the U:G pair is common to both sets of oligonucleotides used here, the rate constant for the U:G pair is used to normalize each data set.

Enzyme cleavage data previously reported for MUG is presented with data obtained in this study with hSMUG1 (Fig. 3) using a common series of oligonucleotide substrates containing purine analogs opposite the target uracil. Linear relationships between ln k_obs and ΔG_duplex are observed for both MUG and hSMUG1; however, the slope of the line is greater for the hSMUG1 data. Within the same sequence context, MUG removes uracil mispaired with guanine 25 times faster than uracil paired with adenine (52), whereas the mispaired uracil is repaired 223 times faster by hSMUG1, indicating that hSMUG1 is more selective than MUG for mispaired structures. Within the CpG/A dinucleotide sequence examine here, TDG is reported to cleave U:G 788 times faster than U:A (19). The mechanism for TDG selectivity has not yet been reported.

The known glycosylases flip the target base from the duplex into a pyrimidine binding pocket within the enzyme prior to hydrolysis of the glycosidic bond (5). Although the energetics of base flipping by the glycosylase are not the same as duplex melting, we believe that melting differences observed within a homologous series of oligonucleotides do provide a reasonable estimate of the impact of specific base substitutions on the energy cost of removing a base from the duplex. An alternative theory is that the glycosylase can distinguish uracil mispaired with guanine from uracil paired with adenine by interrogating functional groups of the purine remaining in the duplex following extrusion of the target uracil, as suggested for MUG (55). Within the series of purines examined here, removal of the guanine 2-amino group, forming the U:Hx base pair, enhanced rather than diminished the rate of uracil cleavage. Removal of the 6-oxygen and the 2-amino group, which also changes the N1 position from a hydrogen bond donor to an acceptor (U:G to U:Pu), reduces cleavage rates only modestly. The data reported here indicate that hSMUG1 probably exploits the reduced stability of mispairs in its search for target bases. The data reported here cannot determine whether hSMUG1 scans for extruded bases or tests for reduced stability of duplex structures.

An additional and somewhat unique physiological role proposed for hSMUG1 is the repair of damaged bases arising from oxidation of the thymine methyl group. Previous studies have demonstrated that hSMUG1 can recognize and remove the oxidation damage products, HmU and FoU (15–18). In this study, we have examined for the first time the capacity of hSMUG1 to remove CaU, the last in the series of thymine methyl group oxidation products (Fig. 2 and Table 1). As demonstrated here, hSMUG1 efficiently cleaves CaU, extending its substrate range and further confirming its role in the repair of DNA oxidation damage. In order to more fully understand CaU, its ionization constants were measured as shown in Fig. 4. The capacity of hSMUG1 to select oxidized bases over thymine is remarkable and has been previously attributed to water molecules within the pyrimidine binding pocket of the glycosylase that could be displaced by uracil analogs with hydrogen bonding substituents in the 5-position but not by the thymine methyl group (14–18).

In the studies reported here, we have attempted to more fully understand the mechanism by which hSMUG1 distinguishes among 5-substituted uracil analogs. Previous studies with both MUG and TDG have demonstrated that a substituent in the 5-position of the uracil analog could have a profound impact on the glycosylase cleavage rate (52, 56). In our studies with MUG, we demonstrated that smaller and more electron-withdrawing substituents facilitated cleavage, whereas larger and more electron-donating substituents had the opposite effect. We therefore examined hSMUG1 cleavage of a series of 5-substituted uracil analogs mispaired with guanine. As shown in Table 1, hSMUG1 is observed to cleave mispaired FU:G 29 times more slowly than U:G. This was a surprising finding, since MUG cleaves FU 4.8 times faster than U (52), and TDG cleaves FU 78 times faster that U (19). The selective cleavage of FU:G over U:G by MUG was attributed to the electron-withdrawing 5-fluoro substituent that could potentially stabilize the glycosylase transition state (52). The observation reported here with hSMUG1, however, suggests that the inductive properties of the 5-substituent are not utilized by hSMUG1 for target selection, and therefore the hSMUG1 transition state could diverge significantly from MUG and TDG.

Substituent size was shown to be a significant factor for base selection by MUG, and we wished to test the importance of substituent size with hSMUG1 as well. In the previous study, however, we examined only spherical 5-substituents, the size of which could be estimated from published bond lengths and van der Waals radii. In order to include the additional oxidation products HmU, FoU, CaU, and HoU in the analysis, an alternative method was needed to estimate the size of the various 5-substituents. We therefore calculated the SASA for each of the pyrimidines examined here, as shown in Table 1. All of the pyrimidines examined here are 5-substituted uracil analogs or uracil. Differences in the calculated SASA within this series can be attributed to relative differences in the size of the 5-substituent.

The activity of hSMUG1 against uracil and each of the 5-substituted pyrimidines paired with guanine was measured, and the observed rate constants are recorded in Table 1. Observed rate constants are plotted versus SASA, as shown in Fig. 5. Inspection of the data in this figure indicates that the observed rate constant is not a simple function of the SASA. The magnitude of the rate constant declines with increasing SASA for most of the analogs. However, for the oxidation damage products derived from thymine (FoU, CaU, and HmU) rate constants increase with increasing SASA.

Measurable rate constants were obtained for U:G, FU:G, and ClU:G (Table 1). No cleavage was detected for T, BrU, or IU. Unlike the oxidation damage products, the halogen substituents would not readily form hydrogen bonds with water molecules or pyrimidine binding pocket amino acid residues and were therefore used to estimate the impact of size alone on the apparent rate constants. When the ln k_obs is plotted versus SASA for U:G, FU:G, and ClU:G, a straight line is obtained (Fig. 5, inset) with slope −0.27 and intercept 69.19. The correlation coefficient (r²) with these three data points is 0.99.

The natural logarithm of the rate constant as a function of size, based upon the data presented in Fig. 5 (inset) is expressed as Equation 8. The rate constant (k_SASA) for a uracil analog with known SASA can then be predicted by Equation 9.

Within the U, FU, and ClU series, the FU and ClU analogs have similar electron-withdrawing properties, but the U hydrogen substituent is neither electron-withdrawing nor electron-donating. With MUG, the observed rate constant dropped by a factor of 3 from FU to ClU, and this drop was attributed to the increased size of Cl relative to F. With hSMUG1, the observed rate constant drops by a factor of 52 from FU to ClU. Therefore, the pyrimidine binding pocket of hSMUG1 is much tighter with respect to the size of the substituent alone, and the rate constant drops exponentially with increasing substituent size (SASA). The observed rate constants for the series U, FU, ClU drop exponentially with increasing SASA, as shown in the inset of Fig. 5. Cleavage was undetectable for T, BrU, and IU. The exponential decline of k_obs for U, FU, and ClU with increasing SASA confirms the absence of an influence of substituent inductive effect, as discussed above.

Previous enzymatic and structural studies have discussed the capacity of hSMUG1 to recognize and cleave oxidation damage products like HmU. It is amazing that the hSMUG1 could cleave U, avoid T, and cleave the larger HmU. The pyrimidine binding pocket of SMUG1 has bound water molecules that form hydrogen bonds with amino acid residues lining the pocket. It has been proposed that the hydroxymethyl group of HmU could displace the bound water molecules and form hydrogen bonds with the pocket whereas this would not be possible with the thymine methyl group (13–18). The hydroxymethyl group of HmU is hydrophilic, whereas the thymine methyl group is hydrophobic.

In order to further understand the substituents that could form potential hydrogen bonds, we sought a parameter that could distinguish substituents that favorably interact with water from those that did not, such as the thymine methyl group. We therefore calculated the free energy of solvation in water (ΔG_solv⁰) for each of the pyrimidines examined here, the results of which are recorded in Table 1. The magnitude of the free energy of solvation is greater for hydrophilic compounds (larger, negative values are more favorable), and these values become smaller in magnitude and approach zero for more hydrophobic compounds. Within the series of uracil analogs examined here, differences in ΔG_solv⁰ can be attributed to the effect of the 5-substituent, since the remainder of the molecule remains constant.

Observed rate constants are plotted versus the free energy of solvation for each pyrimidine in Fig. 6. Rate constants decline as the free energy of solvation in water diminishes in magnitude, and rate constants approach zero when ΔG_solv⁰ declines to approximately −16 kcal mol⁻¹. The solvation free energy for the ClU analog is −16.6 kcal mol⁻¹, and the observed enzymatic rate constant is the lowest observed. The solvation free energy for the BrU, T, and IU analogs is less favorable than −16.6 kcal mol⁻¹ (Table 1), consistent with no observable enzyme cleavage. The parent pyrimidine uracil does not fall on this line. The 5-hydrogen of uracil is the smallest possible substituent; therefore, size rather than the free energy of solvation might dominate its enzymatic rate constant.

The equation for the line in Fig. 6, relating the observed rate constant with the solvation free energy for the analog is given as Equation 10.

The free energy of solvation in water reasonably accounts for the differences in the observed rate constants for several of the analogs recognized by hSMUG1. Analogs with substituents that interact well with water would more easily displace or rearrange bound water molecules, forming hydrogen bonds with amino acid residues or bound water molecules. The model presented here does not represent a significant departure from previous proposals on the selectivity of hSMUG1 (14–17). Rather, the difference between our model and previous proposals is that we do not require any specific hydrogen bonds between the substituent and the enzyme. Instead, we allow the substituent to move, replace, or displace the bound water molecules in any manner that minimizes the free energy of the system. We believe the data presented here support this model.

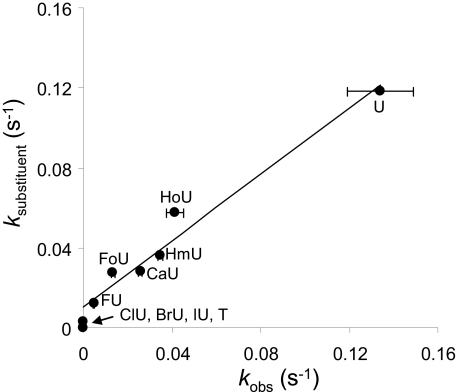
The analogs U, FU, and ClU have the most similar solvation free energy but differ significantly in size, allowing isolation of the impact of substituent size on observed cleavage rate constants (Equation 9). However, for the remaining analogs, it is not possible to isolate size and solvation free energy. We therefore constructed an equation combining both properties to provide a predicted rate constant for the 5-substituent, k_substituent, which is a function of both SASA and the free energy of solvation (Equation 11).

In this equation, rate constants fall exponentially with increasing SASA and increase linearly with increasing water solvation free energy. In order to compare this data set with the previous data set examining the free energy of duplex formation (Equation 7), the predicted rate constant, k_{rel,substituent}, relative to the U:G pair, can be calculated by normalizing to the value predicted for U:G according to Equation 11. The relative rate constant predicted based upon the combined effects of size (SASA) and free energy of solvation for the substituent, k_{rel,substituent}, can be expressed as Equation 12.

The comparison of the observed and expected rate constants, combining both size and solvation energy according to Equation 12 is shown in Fig. 7. Good agreement between the expected and observed values is obtained, indicating that Equation 11 reasonably describes the characteristics for a uracil analog that most importantly influence enzymatic rate constants.

FIGURE 7.

The comparison of observed rate constants (k_obs) and expected rate constants based upon substituent characteristics (k_substituent). The observed rate is plotted against the expected rate based upon Equation 11. A straight line is obtained, with slope of 0.83, intercept of 0.01, and r² = 0.97.

The above consideration of the impact of size and solvation free energy has not yet accounted for differences in the free energy of duplex formation. Within the series of uracil analogs paired with guanine, observed melting temperatures vary from 50.4 to 46.3 °C, and free energy of duplex formation varies from −11.1 to −9.5 kcal mol⁻¹, as shown in Table 1. Although differences in the free energy of duplex formation between paired and mispaired structures are significantly larger than differences between the uracil analogs paired with guanine, we wished to combine the parameters examined here.

In order to combine the substituent effect with the duplex stability effect, the relative rate constants, normalized to the U:G mispair present in each set, were combined to provide an equation that would predict the rate constant for each of the base pairs examined here as functions of its free energy of duplex formation (ΔG_duplex), free energy of solvation in water (ΔG_solv⁰), and SASA, as given by Equation 13.

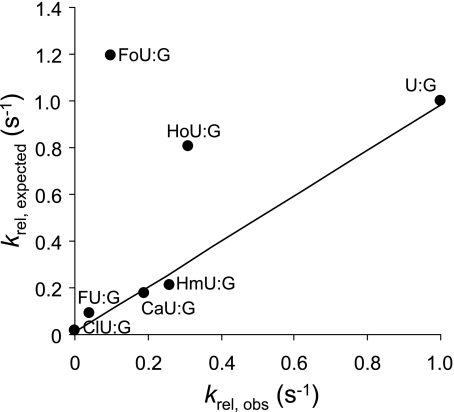
The observed relative enzyme rate constants (k_rel,observed) for the series of mispairs containing damaged bases examined in this study are as follows: U:G > HoU:G > HmU:G > CaU:G > FoU:G > FU:G > ClU:G > BrU:G, IU:G, T:G. The cleavage rates for BrU:G, IU:G, and T:G were below the limit of detection for the experimental methods used here. The expected relative rate constants (k_rel,expected) based upon the model presented here are as follows: FoU:G > U:G > HoU:G >HmU:G > CaU:G > FU:G > ClU:G > BrU:G > IU:G >T:G. With the exception of FoU:G, the model accurately predicts the relative rate constants for the series.

The expected rate constants, determined with Equation 13 and the parameters presented in Table 1, are compared with the observed relative rate constants in Fig. 8. Most of the points fall on a line; however, the expected cleavage rate constants as predicted by the model are higher than the relative observed rates for FoU:G and HoU:G. The unusual feature of both the FoU:G and HoU:G base pairs is that the free energy of duplex formation for both is lower than for the U:G base pair (Table 1). A previous study has confirmed that substitution with FoU considerably lowers oligonucleotide melting temperatures, consistent with the results reported here (57).

FIGURE 8.

Relationship between observed relative rate constants (k_rel,obs) and expected relative rate constants based on duplex formation energy of the oligonucleotide, size, and free energy of solvation of the uracil 5-substituent (k_rel,expected). The expected relative rates are calculated with respect to the rate of cleavage of the U:G base pair according to Equation 13. A straight line is obtained for several of the analogs with slope of 0.98, intercept of 9.20 × 10⁻³, and r² = 0.99. Values for the FoU:G and HoU:G pairs do not fall on this line.

We noted that when the expected and observed rates were compared, based upon the substituent effects alone (Fig. 7) and not including duplex energy, all points fell on a line. However, when duplex stability was included (Fig. 8), the points for FoU:G and HoU:G deviate from a line describing the other base pairs examined. A potential explanation for the apparent anomalous behavior of the FoU:G and HoU:G is that reduced duplex stability increases enzyme rate constants only to a point and that further reduction of duplex stability provides no additional advantage for the enzyme. If the rate of pyrimidine extrusion has reached a maximum value when duplex stability drops to that of the U:G mispair, another step along the reaction coordinate, such as the rate of glycosidic bond cleavage, might become rate-limiting. Alternatively, the energetics of duplex melting might differ from the energetics of enzymatic base extrusion with some modified base pairs due to additional chemical properties. In the study reported here, both SASA and ΔG_solv⁰ were calculated for the major conformations of the neutral species. Both FoU and HoU have pK_a values near physiological pH, and the enzyme active site might alter pK_a values, and substituents may be found in multiple conformations.

In summary, we have extended the substrate range of hSMUG1 to include CaU, the last in the series of thymine methyl group oxidation damage products. This result strengthens the suggested role for hSMUG1 in the repair of DNA oxidation damage. Our results indicate that hSMUG1 distinguishes paired from mispaired uracil primarily on the basis of reduced duplex stability for the mispair and that recognition of specific functional groups on the purine in the opposing strand contributes minimally. The most unique property of hSMUG1 is its capacity to cleave uracil but not thymine yet still cleave the larger oxidation damage products. The preference of hSMUG1 for U:G over T:G can be attributed primarily to the greater size of the T methyl group relative to the hydrogen of U. In contrast to other glycosylases, hSMUG1 does not exploit the electronic inductive property of the 5-substituent. The capacity to recognize and repair HmU and other oxidized pyrimidines probably resides in a pyrimidine-binding pocket on the enzyme. In accord with previous models, this pocket has mobile water molecules that can be displaced or rearranged to accommodate some 5-substituents. Preferred substrates carry substituents that can partially replace interactions with critical amino acid residues vacated by the displaced or rearranged water molecules. The model for selectivity toward the oxidized bases presented here does not differ conceptually from previous models, based upon structural studies (15–18). Rather, we present a parameter, the free energy of solvation in water (ΔG_solv⁰) that can be used to reasonably describe in a quantitative manner the favorable properties previously ascribed to the oxidized base targets of hSMUG1. The exploitation of distinct chemical properties of damaged and modified bases and base pairs by members of the uracil glycosylase family provides at the same time necessary discrimination between normal and damaged DNA and a broad spectrum of possible damage that can be accommodated.