Introduction
It is well established that children, adults, and nonhuman animals share a basic ability to perceive and compare nonsymbolic quantities of items, commonly referred to as “numerosity.” Symbolic numerical representations build on these basic abilities to enable human children and adults to use precise number words, symbols, and linguistic quantifiers. In the past five years, results from single-unit physiology, behavioral studies of human and monkey performance on numerosity tasks, computational modeling, and functional neuroimaging have provided profound insights into the neural mechanisms that underlie these symbolic numerical abilities, and suggest how higher-order human numerical capacities may have arisen from these evolutionarily conserved more basic mechanisms. These studies converge on two regions, the intraparietal sulcus (IPS) and the prefrontal cortex (PFC), as being critical for representing numerosity and for the acquisition of higher-order numerical abilities.
In this Mini-Symposium, we present these findings in detail, to provide a coherent picture of how various aspects of higher-order numerical understanding arise from basic mechanisms of numerosity perception in the IPS and PFC. Jessica Cantlon and Ilka Diester will present behavioral and electrophysiological evidence for basic numerical abilities in nonhuman primates, suggesting that these abilities are important phylogenetic precursors to human numerical abilities. Cantlon will describe cross-species behavioral experiments which demonstrate that humans and nonhuman primates share a basic ability to mentally manipulate numerical representations in arithmetic operations. In particular, both macaques and humans (when kept from counting) can identify the approximate sum of two arrays of dots, demonstrating a shared behavioral competency for evaluating nonsymbolic numerosity. Building on this shared ability to manipulate nonsymbolic quantities, Diester will discuss recent work demonstrating that as little as 3 months of training allows macaques to learn the correspondence between quantities and symbols. Single-unit recordings demonstrate that this mapping is mediated by prefrontal neurons, whereas neurons in the IPS have been shown to respond to numerosity, but do not link between quantities and symbols.
These numerical competencies appear early in human development and appear to depend on prefrontal mechanisms early in development, with an increasing role for parietal mechanisms later in development. Daniel Ansari will present neuroimaging studies of typical and atypical development that have examined the neural substrates of symbolic and nonsymbolic number comparison. The results of these studies are consistent with Diester's physiology results, in that frontal cortex plays a greater role in mapping between quantities and symbols early in the acquisition of numerical abilities, whereas parietal cortex plays a greater role with increasing expertise.
However, numbers do not merely represent quantities that can be manipulated to perform simple additions or to identify which of two quantities is larger. Numbers also form an ordered sequence, similar to sequences in other non-numerical domains (e.g., letters of the alphabet). Filip van Opstal will present the results of computational modeling and neuroimaging experiments that link the quantity representation described above (“cardinality”) and the representation of ordered series, (“ordinality”), or rank, and show that such links depend on interactions between the hippocampus and parietal cortex. With formal education, numbers (and other ordered sequences) are automatically represented on a spatially organized mental number line in adult humans. Edward Hubbard will describe neuroimaging studies designed to explore the parietal mechanisms of this mapping between numbers and space by identifying regions that are functionally equivalent to those identified in the macaque IPS, and measuring interactions between these regions. Finally, Vanessa Troiani will discuss neuroimaging and patient studies that explore the comprehension of quantifier terms, such as “all” and “half,” which, unlike many other semantic systems, depends on the parietal cortex, rather than the temporal regions traditionally implicated in semantic representations.
Together, these studies demonstrate that higher-order human numerical abilities, including sequencing, the mental number line, and semantic quantifiers, depend on phylogenetically conserved neural circuits which originally evolved for basic processes of estimation and manipulation of numerical quantities. Because these numerical abilities can be impaired after lesions, especially those involving the parietal cortex (Gerstmann's syndrome or corticobasal degeneration) and those caused by developmental abnormalities (Turner syndrome, Williams syndrome, fragile X or fetal alcohol syndrome), a better understanding of the neural mechanisms of numerical cognition will help to better understand what goes wrong in these clinical populations, and will hopefully lead to improved remediation and retraining strategies. Integrating across a range of findings, these studies have relevance not only for our understanding of the mechanisms of higher-order cognition, but also for development of numerical cognition itself, developmental disorders affecting numerical cognition, and the evolution and development of human semantic systems more generally.
Basic math…in monkeys
Nonhuman animal species as diverse as pigeons and primates possess a capacity for basic magnitude representation (Dehaene et al., 1998; Hauser et al., 2000; Hauser et al., 2002). For example, rats, pigeons, nonhuman primates, and several other nonhuman animal species can choose the larger or smaller numerical value from two visual arrays of elements, and the precision with which they are successful is predicted by Weber's law (for review, see Gallistel, 1990; Brannon, 2005). In addition to these basic abilities, nonhuman animal species can be trained to use symbolic representations of number in a variety of tasks (Matsuzawa, 1985; Boysen and Berntson, 1989; Harris and Washburn, 2005). Many of the signatures of semantic numerosity processing, such as the numerical distance effect (faster and more accurate responses to quantities that are more dissimilar), are present in macaque monkeys, suggesting a shared evolutionary basis for such effects (Cantlon and Brannon, 2005, 2006).
Furthermore, when adult humans are tested on the same numerical comparison task as nonhuman primates and prevented from verbally counting, the discrimination performance of the two species is similarly predicted by Weber's law and is, in fact, virtually identical (Cantlon and Brannon, 2006). These types of findings provide compelling evidence that humans are not unique in their ability to extract numerical information from discrete sets of objects or events in the world. Rather, humans share a capacity for approximate numerical discrimination with a whole host of nonhuman species. One issue left unresolved by previous research, however, has been the extent to which nonhuman animals can mentally manipulate numerical representations in an arithmetic-like operation.
Arithmetic operations, such as addition, subtraction, division, and multiplication, require mental transformations over numerical values. Addition is an arithmetic operation that involves combining two or more quantitative representations (addends) to form a new representation (the sum). Cantlon and Brannon (2007) tested whether rhesus monkeys can perform mental addition by presenting them with a nonverbal addition task. Moreover, they tested college students on the same nonverbal addition task as monkeys, with the goal of investigating parallels between their arithmetic performance. In the nonverbal addition task, monkeys and college students were presented with two sets of dots on a computer monitor, separated by a delay. After the presentation of these two “sample” sets, subjects were required to choose between two arrays: one with a number of dots equal to the numerical sum of the two sets and a second, distractor array that contained a different number of dots. The addition problems consisted of addends ranging from 1 to 17, tested in all possible combinations. Monkeys and college students successfully solved the addition problems, and the two species' accuracy and response times were similarly constrained by the numerical ratio between the choice stimuli, or Weber's law (Fig. 1a). A series of control conditions verified that monkeys' successful performance was not based on simple heuristics. Overall, these findings support the claim that mental arithmetic is a fundamental, evolutionarily widespread cognitive process.
Figure 1.
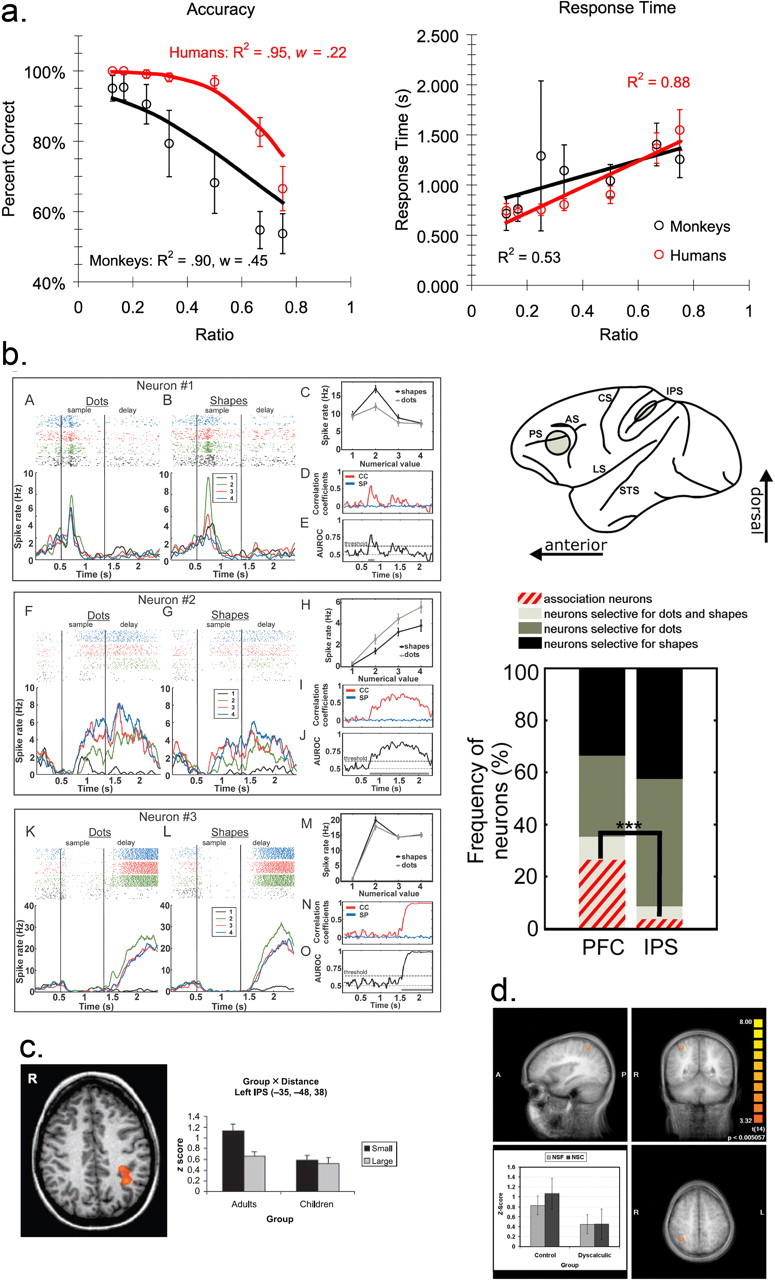
a, Accuracy (left) and response times (right) for humans and monkeys on a nonsymbolic addition task. Red circles indicate human performance, and the black circles indicate monkey performance. The similarity of the shape of the best fit lines suggests similar overall behavioral competencies, although humans tend to be more accurate overall for similar response times (from Cantlon and Brannon, 2007). b, Single-unit responses from three macaque PFC neurons showing similar tuning curves for nonsymbolic (dots) and symbolic (shapes) numerosities. The right side of the figure indicates the regions that were recorded from and the frequency of neurons that showed different patterns of stimulus tuning in the PFC and IPS (from Diester and Nieder, 2007). c, Human IPS regions become more involved in numerical tasks as people age, as shown by the presence of distance effects in the left IPS in adults, but not in children (from Ansari and Dhital, © 2006 by MIT Press). d, In contrast, the recruitment of the IPS is absent in children with developmental dyscalculia (reprinted from Price et al., 2007, with permission from Elsevier).
Semantic mapping of symbol-like signs to numerical categories in the monkey prefrontal cortex
Building on the basic understanding of magnitudes described above, humans have developed number symbols which allow for a high precision in addressing numerical values and complex mathematical calculations. A fundamental first step for the acquisition of numerical symbols is the semantic association of signs with cardinalities. To investigate the primitives of such a semantic mapping process, Diester and Nieder (2007) trained monkeys to judge analog and symbol-like numerical representations. On different trials, the monkeys either had to judge whether two successive visual displays contained the same quantity of items or to associate visual shapes with varying numbers of items. Many neurons in the lateral PFC and the fundus of the IPS were tuned for quantity, regardless of the exact physical appearance of the displays. Their tuning curves formed overlapping filters, which may explain why behavioral discrimination improves with increasing numerical distance and why discrimination of two quantities with equal numerical distance worsens as their numerical size increases (number size and distance effect) (Nieder and Miller, 2002, 2004; Diester and Nieder, 2007).
Monkeys that had learned to associate visual shapes with varying numbers of items showed these psychophysical effects also with the symbol-like shapes. By recording single-cell activity in the PFC and IPS, Diester and Nieder (2007) found that the responses of many prefrontal neurons to the visual shapes reflected the associated numerical value in a behaviorally relevant way (“association neurons”) (Fig. 1b). In contrast, such association neurons were rarely found in the parietal lobe. These findings resemble data from functional magnetic resonance imaging (fMRI) studies in preschoolers lacking proficiency with number symbols, who show elevated PFC activity when dealing with symbolic cardinalities (Ansari, 2005). Together, these studies suggest an essential role for the prefrontal cortex in establishing semantic associations between signs and abstract numerical categories, a cognitive precursor that may ultimately give rise to symbolic thinking in linguistic humans.
Symbolic and nonsymbolic numerical magnitude processing in the brain: a developmental perspective
Turning now from nonhuman primates to human studies, there is a growing body of evidence from functional neuroimaging studies with adult humans that the IPS plays a crucial role in the processing and representation of both symbolic and nonsymbolic numerical magnitude (Dehaene et al., 2003), contrary to the observation that the IPS represents only nonsymbolic magnitude in monkeys, discussed above. This apparent contradiction may be partially resolved by taking into account how these abilities and their neural substrates develop. Although even very young infants can process nonsymbolic representations of numerical magnitude (Xu and Spelke, 2000), children only gradually learn the meaning of invented, cultural symbols for the representation of numerical magnitude, such as Arabic numerals and number words.
In light of this, the study of age-related changes in neural activation during symbolic and nonsymbolic number processing can shed further light on both the commonalities and differences in the brain representation and processing of symbolic and nonsymbolic numerical magnitude. Specifically, the study of developmental changes provides a unique window into the neurocognitive mechanisms involved in the specialization of brain circuits for the processing of symbolic numerical magnitude. To explore these questions, Ansari and colleagues will present data from investigations of the neural correlates of symbolic and nonsymbolic number comparison in both children and adults using fMRI (Ansari et al., 2005; Ansari and Dhital, 2006). These studies revealed that the degree to which the IPS was recruited during both symbolic and nonsymbolic numerical magnitude processing increased with age (Fig. 1c). These findings suggest the existence of dynamic, age-related changes in the functional neuroanatomy underlying very basic numerical magnitude processing, and thereby highlight the importance of taking a developmental perspective on brain function (Johnson, 2001). Further supporting the idea of a functional relationship between this circuitry and mathematical ability, children with specific mathematical difficulties (developmental dyscalculia) fail to show the typical specialization of parietal brain circuits for the processing of numerical magnitude (Fig. 1d) (Price et al., 2007).
Against this background of evidence for age-related specialization of the parietal cortex for numerical magnitude processing, Ansari will present recent findings from adults that demonstrate that although conjunction analysis revealed common activation underlying symbolic and nonsymbolic numerical magnitude comparison in the IPS, multiple brain regions are involved in format-specific processing of numerical magnitude. Specifically, regions of the posterior parietal cortex and cuneus were found to be significantly more modulated by nonsymbolic compared with symbolic number comparison. In contrast, a region of the left temporoparietal cortex, spanning regions of the superior temporal and supramarginal gyri, was observed to be significantly more activated during symbolic than during nonsymbolic comparison. A subsequent comparison between children and adults demonstrated significant age-related increases in the left temporoparietal regions for symbolic number processing. In contrast, regions found to be specifically modulated by the nonsymbolic magnitude comparison task exhibited similar levels of activation in children and adults. Together, these data suggest the existence of differential pathways for the processing of symbolic and nonsymbolic numerical magnitude in the brain and furthermore reveal that left temporoparietal structures undergo a process of age-related specialization for the processing of symbolic representations of numerical magnitude.
Links between numerical processing and sequence processing
Although there exists a large degree of agreement on the involvement of the IPS in number processing, the specificity of the IPS to numbers is much less agreed on. The close relation between space, time, and quantity in both neuropsychological (Zorzi et al., 2002) and behavioral (Church and Meck, 1984) studies has led some to suggest the existence of a generalized magnitude system rather than a specific number system in IPS (Walsh, 2003). A recent review, however, pointed out that although there is some evidence for a common encoding mechanism for physical dimensions and numbers, both shared and distinct representations could exist (Cohen Kadosh et al., 2008). Similarly, the relationship between the representation of numerical and symbolic non-numerical ordinal information has been somewhat unclear. Although it has been suggested that the representation of numerical and symbolic non-numerical ordered sequences must be similar (Chiao et al., 2004), a recent computational and behavioral study demonstrated important differences in their representations (Van Opstal et al., 2008a). Specifically, whereas the representation of numbers in memory is marked by broad tuning curves, the tuning curves on the representation of non-numerical ordered sequences are peaked. According to a neural network model of number processing, a difference in tuning curves would be expected because of the absence of summation coding in non-numerical order processing (Verguts and Fias, 2004). Furthermore, because these neural network simulations revealed that very basic one-layered neural networks are capable of “storing” ordered sequences and generate a comparison distance effect (Verguts et al., 2005; Van Opstal et al., 2008a), there might be no need for a dedicated brain area to store or process ordered sequences with ensuing comparison distance effects. Instead, ordered sequences may be stored in many different neocortical areas depending on the stimulus type at hand [e.g., letters and numbers in IPS (Fias et al., 2007), animals in temporal cortex (Thioux et al., 2005), arbitrary symbols in angular gyrus (Van Opstal et al., 2008b)].
Links between numbers and space
Although previous neuroimaging studies in humans and single-unit physiology studies in monkeys have shown that neurons in the intraparietal sulcus are active during numerical tasks, the exact functional equivalencies between numerical processing regions in humans and macaque lateral and ventral intraparietal areas (LIP and VIP, respectively) remain unclear. To explore this question, Hubbard will present data from a study that used two physiologically inspired localizer tasks, saccadic eye movements and sensitivity to visual and tactile motion, to identify human areas (hLIP and hVIP) that are functionally equivalent to macaque LIP and VIP, respectively (E. M. Hubbard, P. Pinel, A. Jobert, D. Le Bihan, and S. Dehaene, submitted). They then examined the topographical relations between these activations and calculation-related activations and also measured voxel-by-voxel correlations between these tasks to test the hypothesis that mental arithmetic depends on shifting of attention along the “mental number line” mediated by parietal and frontal regions.
Calculation was found to overlap minimally with hVIP, with hVIP lying in the medial wall of the IPS, and calculation activating more lateral regions (Fig. 2a, lower insets), indicating a partial homology between human and macaque parietal regions. In contrast, there was substantial anatomical and functional overlap between calculation and saccadic eye movements (Fig. 2a, purple regions), demonstrating the importance of visuospatial processes for mental arithmetic. Finally, using multi-voxel correlation techniques, they found positive correlations between the activation patterns for mental calculation and eye movements, especially in frontal regions, suggesting that this overlap between calculation and eye movements results from activation of shared neural populations. These findings are consistent with the view that human numerical abilities arise from an evolutionarily conserved network of parietal and frontal regions, and provide further support to the notion of a human mental number line.
Figure 2.
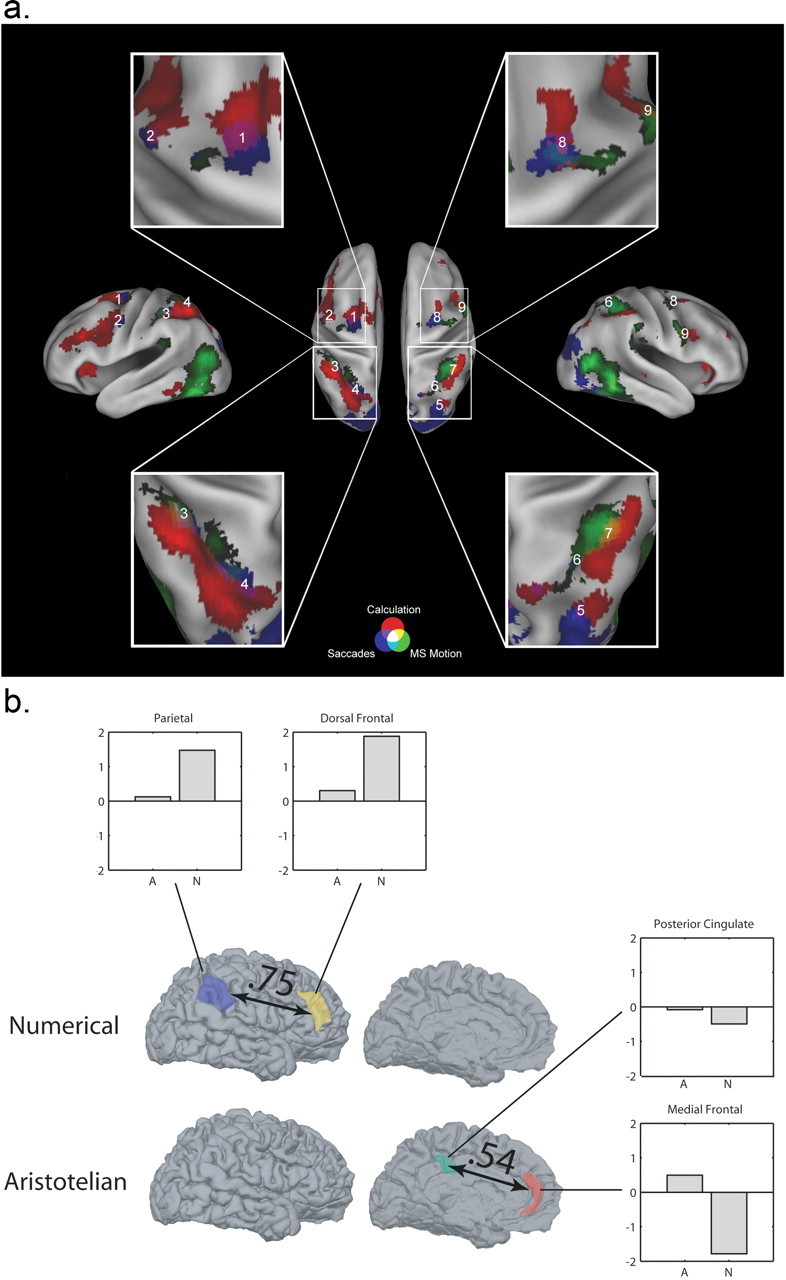
a, Calculation overlaps very little with regions that respond to visual and tactile motion (putative hVIP) but overlaps more substantially with saccade-related regions (putative hLIP and hFEF) in parietal and frontal cortex. Calculation is indicated in red, saccades in blue, and multisensory motion in green. Regions of overlap are indicated in yellow, teal, purple. and white, and are numbered for easy reference in the inset enlargements (from Hubbard et al., submitted). b, Numerical quantifier comprehension leads to increased activations and higher functional correlations between parietal and lateral frontal regions, whereas Aristotelian quantifier comprehension depends on interactions between the posterior cingulated cortex and medial frontal regions. Network correlation analysis of classes of quantifiers was performed, with significant correlation values, and parameter estimates for activations in each anatomic region for Aristotelian (A) and numerical (N) quantifiers. [From Troiani et al., copyright Elsevier (2008).]
Semantic quantifiers
Full comprehension of numerical concepts such as the word “ten,” the numeral 10, or an array of countable objects relies on regions of parietal cortex, in particular, the IPS (Piazza et al., 2007). However, the importance of number and magnitude extends beyond domains traditionally thought of as mathematics into forms that appear to be more associated with language. We use terms like “most” and “at least” in a seemingly effortless manner in everyday conversations. These words compose a category known as natural language quantifiers. Quantifier terms are well defined semantically (van Benthem, 1986), yet little is known about their neuroanatomical basis. Recent neuroimaging and patient data have begun to shed light on the importance of magnitude processing regions, such as the IPS, in comprehending these quantification terms. By elucidating the neural underpinnings of concepts such as quantifiers, we can develop a more comprehensive understanding of the semantics of numerical concepts.
Patients with focal neurodegenerative disease have provided the first evidence of a double dissociation between traditional semantic concepts, thought to be housed in the left temporal lobe, and the semantics of number, which appear to rely on parietal cortex. Semantic dementia (SD) is a progressive neurodegenerative condition causing left temporal lobe atrophy and impaired object naming. Several studies have indicated preserved numerical comprehension in cases of SD, including preserved comprehension of quantifier terms, such as “more” and “dozen,” in this patient population (Halpern et al., 2004a; Cappelletti et al., 2006). A longitudinal case study of the comprehension of various types of number knowledge in a patient with SD concluded that the preservation of parietal cortex in this patient was the potential source of preserved magnitude comprehension in several domains (Jefferies et al., 2005). This patient could no longer read or write numbers, but demonstrated preserved knowledge in estimation and even identifying linguistic opposites, such as big and small. Patients with corticobasal degeneration (CBD), a neurodegenerative condition causing posterior parietal atrophy (Murray et al., 2007), present evidence for the other side of this dissociation. This population has extreme difficulty with small number comprehension, but relatively intact object knowledge (Halpern et al., 2004b). In addition to core numerical comprehension deficits, CBD patients have difficulty understanding quantifier terms such as “more than half” (McMillan et al., 2006).
Functional imaging in healthy adults has also provided useful information in the identification of the neural substrate for numerical semantics. Right parietal cortex is activated during assessments of statements containing a quantifier term (McMillan et al., 2005). A more recent study differentiates between quantifier subtypes requiring explicit numerical processing (e.g., “>3”) and terms that are founded in logic (i.e., “some” or “all”). Healthy young adults were asked to assess quantifier statements containing either a numerically based or logic-based quantifier. Right parietal and dorsal frontal cortex was recruited for quantifier terms requiring access to magnitude, but not for logical quantifiers (Troiani et al., 2008). Activity in frontal and parietal cortex was also found to be correlated for numerical quantifiers (Fig. 2b), consistent with other research linking frontal and parietal mechanisms in support of symbolic numerical comprehension.
Together, these findings support several ideas surrounding the semantics of number. Primarily, the importance of the IPS in magnitude is broader than mere support for Arabic numerals and number words and includes maintenance of linguistic terms like quantifiers. Although a full model of the semantics of number would plausibly rely on more than magnitude processing regions, current research reinforces a distributed model of semantic storage (Martin, 2007), with the recruitment of IPS for words and concepts reliant on magnitude processing.
Conclusions
These studies thus provide compelling evidence that human numerical abilities arise from behavioral competencies and neural substrates that are shared with non human animals. Studies with nonhuman primates reveal striking similarities with humans in several magnitude processing tasks, including comparison, addition, and even in their ability to learn to map numerical symbols onto nonsymbolic quantities. Such abilities in humans depend on similar neural substrates, with decreasing recruitment of frontal cortex and increasing specialization of parietal structures with development and education. These parietal and frontal mechanisms then also form parts of circuits that are involved in ordinal sequence representation, in mappings between numbers and space, and in the comprehension of semantic quantifiers. These studies thus give us the beginnings of a comprehensive account of how some uniquely human abilities arise from phylogenetically conserved abilities. Future studies will build on these findings to further elucidate the behavioral and neural mechanisms that are important for numerical competencies across their range of manifestations.
Footnotes
E.M.H. was supported the by a Marie-Curie Numeracy and Brain Development (NUMBRA) postdoctoral fellowship. J.F.C. is supported by a National Research Service Award postdoctoral fellowship (1F32HD057758). I.D. was supported by a Junior Research Group Grant SFB 550/C11 from the German Research Foundation. F.v.O. is a Postdoctoral Fellow of the Research Foundation–Flanders (FWO-Vlaanderen). D.A. is supported by a Discovery grant from the Natural Sciences and Engineering Research Council of Canada. V.T. is supported by National Institutes of Health Grant NS044266.
References
- Ansari D, Dhital B. Age-related changes in the activation of the intraparietal sulcus during nonsymbolic magnitude processing: an event-related functional magnetic resonance imaging study. J Cogn Neurosci. 2006;18:1820–1828. doi: 10.1162/jocn.2006.18.11.1820. [DOI] [PubMed] [Google Scholar]
- Ansari D, Garcia N, Lucas E, Hamon K, Dhital B. Neural correlates of symbolic number processing in children and adults. Neuroreport. 2005;16:1769–1773. doi: 10.1097/01.wnr.0000183905.23396.f1. [DOI] [PubMed] [Google Scholar]
- Brannon EM. What animals know about number. In: Campbell JID, editor. Handbook of mathematical cognition. New York: Psychology Press; 2005. pp. 85–108. [Google Scholar]
- Cantlon JF, Brannon EM. Semantic congruity affects numerical judgments similarly in monkeys and humans. Proc Natl Acad Sci U S A. 2005;102:16507–16511. doi: 10.1073/pnas.0506463102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cantlon JF, Brannon EM. Shared system for ordering small and large numbers in monkeys and humans. Psych Sci. 2006;17:401–406. doi: 10.1111/j.1467-9280.2006.01719.x. [DOI] [PubMed] [Google Scholar]
- Cantlon JF, Brannon EM. Basic math in monkeys and college students. PLoS Biol. 2007;5:e328. doi: 10.1371/journal.pbio.0050328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cappelletti M, Butterworth B, Kopelman M. The understanding of quantifiers in semantic dementia: a single-case study. Neurocase. 2006;12:136–145. doi: 10.1080/13554790600598782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiao JY, Bordeaux AR, Ambady N. Mental representation of social status. Cognition. 2004;93:B49–B57. doi: 10.1016/j.cognition.2003.07.008. [DOI] [PubMed] [Google Scholar]
- Church RM, Meck WH. The numerical attribute of stimuli. In: Roitblat HL, Beaver TG, Terrace HS, editors. Animal cognition. Mawhah, NJ: Erlbaum; 1984. pp. 445–464. [Google Scholar]
- Clark R, Grossman M. Number sense and quantifier interpretation. Topoi. 2007;26:51–62. [Google Scholar]
- Cohen Kadosh R, Cohen Kadosh K, Kaas A, Henik A, Goebel R. Notation-dependent and independent representations of numbers in the parietal lobes. Neuron. 2007;53:307–314. doi: 10.1016/j.neuron.2006.12.025. [DOI] [PubMed] [Google Scholar]
- Cohen Kadosh R, Lammertyn J, Izard V. Are numbers special? An overview of chronometric, neuroimaging, developmental and comparative studies of magnitude representation. Prog Neurobiol. 2008;84:132–147. doi: 10.1016/j.pneurobio.2007.11.001. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Dehaene-Lambertz G, Cohen L. Abstract representations of numbers in the animal and human brain. Trends Neurosci. 1998;21:355–361. doi: 10.1016/s0166-2236(98)01263-6. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Piazza M, Pinel P, Cohen L. Three parietal circuits for number processing. Cogn Neuropsych. 2003;20:487–506. doi: 10.1080/02643290244000239. [DOI] [PubMed] [Google Scholar]
- Diester I, Nieder A. Semantic associations between signs and numerical categories in the prefrontal cortex. PLoS Biol. 2007;5:e294. doi: 10.1371/journal.pbio.0050294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fias W, Lammertyn J, Caessens B, Orban GA. Processing of abstract ordinal knowledge in the horizontal segment of the intraparietal sulcus. J Neurosci. 2007;27:8952–8956. doi: 10.1523/JNEUROSCI.2076-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallistel CR. The organization of learning. Cambridge, MA: MIT; 1990. [Google Scholar]
- Halpern C, Clark R, Moore P, Antani S, Colcher A, Grossman M. Verbal mediation of number knowledge: Evidence from semantic dementia and corticobasal degeneration. Brain Cogn. 2004a;56:107–115. doi: 10.1016/j.bandc.2004.07.001. [DOI] [PubMed] [Google Scholar]
- Halpern CH, Glosser G, Clark R, Gee J, Moore P, Dennis K, McMillan C, Colcher A, Grossman M. Dissociation of numbers and objects in corticobasal degeneration and semantic dementia. Neurology. 2004b;62:1163–1169. doi: 10.1212/01.wnl.0000118209.95423.96. [DOI] [PubMed] [Google Scholar]
- Jefferies E, Bateman D, Lambon Ralph MA. The role of the temporal lobe semantic system in number knowledge: evidence from late-stage semantic dementia. Neuropsychologia. 2005;43:887–905. doi: 10.1016/j.neuropsychologia.2004.09.009. [DOI] [PubMed] [Google Scholar]
- Johnson MH. Functional brain development in humans. Nat Rev Neurosci. 2001;2:475–483. doi: 10.1038/35081509. [DOI] [PubMed] [Google Scholar]
- Martin A. The representation of object concepts in the brain. Annu Rev Psychol. 2007;58:25–45. doi: 10.1146/annurev.psych.57.102904.190143. [DOI] [PubMed] [Google Scholar]
- McMillan CT, Clark R, Moore P, Devita C, Grossman M. Neural basis for generalized quantifier comprehension. Neuropsychologia. 2005;43:1729–1737. doi: 10.1016/j.neuropsychologia.2005.02.012. [DOI] [PubMed] [Google Scholar]
- McMillan CT, Clark R, Moore P, Grossman M. Quantifier comprehension in corticobasal degeneration. Brain Cogn. 2006;62:250–260. doi: 10.1016/j.bandc.2006.06.005. [DOI] [PubMed] [Google Scholar]
- Murray R, Neumann M, Forman MS, Farmer J, Massimo L, Rice A, Miller BL, Johnson JK, Clark CM, Hurtig HI, Gorno-Tempini ML, Lee VM, Trojanowski JQ, Grossman M. Cognitive and motor assessment in autopsy-proven corticobasal degeneration. Neurology. 2007;68:1274–1283. doi: 10.1212/01.wnl.0000259519.78480.c3. [DOI] [PubMed] [Google Scholar]
- Nieder A. Counting on neurons: the neurobiology of numerical competence. Nat Rev Neurosci. 2005;6:177–190. doi: 10.1038/nrn1626. [DOI] [PubMed] [Google Scholar]
- Nieder A, Miller EK. A parieto-frontal network for visual numerical information in the monkey. Proc Natl Acad Sci U S A. 2004;101:7457–7462. doi: 10.1073/pnas.0402239101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nieder A, Freedman DJ, Miller EK. Representation of the quantity of visual items in the primate prefrontal cortex. Science. 2002;297:1708–1711. doi: 10.1126/science.1072493. [DOI] [PubMed] [Google Scholar]
- Piazza M, Pinel P, Le Bihan D, Dehaene S. A magnitude code common to numerosities and number symbols in human intraparietal cortex. Neuron. 2007;53:293–305. doi: 10.1016/j.neuron.2006.11.022. [DOI] [PubMed] [Google Scholar]
- Price GR, Holloway I, Räsänen P, Vesterinen M, Ansari D. Impaired parietal magnitude processing in developmental dyscalculia. Curr Biol. 2007;17:R1042–R1043. doi: 10.1016/j.cub.2007.10.013. [DOI] [PubMed] [Google Scholar]
- Thioux M, Pesenti M, Costes N, De Volder A, Seron X. Task-independent semantic activation for numbers and animals. Brain Res Cogn Brain Res. 2005;24:284–290. doi: 10.1016/j.cogbrainres.2005.02.009. [DOI] [PubMed] [Google Scholar]
- Troiani V, Peelle JE, Clark R, Grossman M. Is it logical to count on quantifiers? Dissociable neural networks underlying numerical and logical quantifiers. Neuropsychologia. 2008 doi: 10.1016/j.neuropsychologia.2008.08.015. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Benthem J. Essays in logical semantics. Dordrecht, The Netherlands: D Reidel Publishing Company; 1986. [Google Scholar]
- Van Opstal F, Gevers W, De Moor W, Verguts T. Dissecting the symbolic distance effect: comparison and priming effects in numerical and non-numerical orders. Psychon Bull Rev. 2008a;15:419–425. doi: 10.3758/pbr.15.2.419. [DOI] [PubMed] [Google Scholar]
- Van Opstal F, Verguts T, Orban GA, Fias W. A hippocampal-parietal network for learning an ordered sequence. Neuroimage. 2008b;40:333–341. doi: 10.1016/j.neuroimage.2007.11.027. [DOI] [PubMed] [Google Scholar]
- Verguts T, Fias W. Representation of number in animal and humans. J Cogn Neurosci. 2004;16:1493–1504. doi: 10.1162/0898929042568497. [DOI] [PubMed] [Google Scholar]
- Verguts T, Fias W, Stevens M. A model of exact small-number representation. Psychon Bull Rev. 2005;12:66–80. doi: 10.3758/bf03196349. [DOI] [PubMed] [Google Scholar]
- Walsh V. A theory of magnitude: common cortical metrics of time, space and quantity. Trends Cogn Sci. 2003;7:483–488. doi: 10.1016/j.tics.2003.09.002. [DOI] [PubMed] [Google Scholar]
- Xu F, Spelke ES. Large number discrimination in 6-month-old infants. Cognition. 2000;74:B1–B11. doi: 10.1016/s0010-0277(99)00066-9. [DOI] [PubMed] [Google Scholar]
- Zorzi M, Priftis K, Umiltà C. Neglect disrupts the mental number line. Nature. 2002;417:138–139. doi: 10.1038/417138a. [DOI] [PubMed] [Google Scholar]


