PathMiner: predicting metabolic pathways by heuristic search

Abstract

Motivation

Automated methods for biochemical pathway inference are becoming increasingly important for understanding biological processes in living and synthetic systems. With the availability of data on complete genomes and increasing information about enzyme-catalyzed biochemistry it is becoming feasible to approach this problem computationally. In this paper we present PathMiner, a system for automatic metabolic pathway inference. PathMiner predicts metabolic routes by reasoning over transformations using chemical and biological information.

Results

We build a biochemical state-space using data from known enzyme-catalyzed transformations in Ligand, including, 2917 unique transformations between 3890 different compounds. To predict metabolic pathways we explore this state-space by developing an informed search algorithm. For this purpose we develop a chemically motivated heuristic to guide the search. Since the algorithm does not depend on predefined pathways, it can efficiently identify plausible routes using known biochemical transformations.

Contact

imran.shah@uchsc.edu

Availability

The system is available for testing at http://pathminer.uchsc.edu

1 INTRODUCTION

Even with the availability genomic blueprint for a living system and functional annotations for its putative genes, the experimental elucidation of its biochemical processes is still a daunting task. Though it is possible to organize genes by broad functional roles, piecing them together manually into consistent biochemical pathways quickly becomes intractable. In this paper we present a computational approach for automated pathway prediction that is useful for exploring plausible biochemical routes underlying metabolic processes. We have implemented this approach in Common Lisp and we are making it available as a flexible web-based interactive system, called PathMiner. There are at least two broad biological applications of this work. First, to investigate pathways in an organism using information about its functionally characterized proteins. Second, to synthesize novel pathways for engineering new metabolic capabilities.

A number of metabolic pathway reconstruction tools have been developed since the availability of the first microbial genome, Haemophilus influenza (Fleischmann et al., 1995). These include PathoLogic (Karp and Riley, 1994), MAGPIE (Gaasterland and Selkov, 1995; Gaasterland and Sensen, 1996) and WIT (Overbeek et al., 2000) and PathFinder (Goesmann et al., 2002). The goal of most pathway inference methods has generally been to match putatively identified enzymes with known, or ‘reference’, pathways. Although reconstruction is an important starting point for elucidating the metabolic capabilities of an organism based upon prior pathway knowledge, reconstructed pathways often have many missing enzymes, even in essential pathways.

The issue of redefining microbial biochemical pathways based on ‘missing’ enzymes is important since there are many examples of alternatives to standard pathways in a variety of organisms (Cordwell, 1999). Furthermore, engineering a new pathway into an organism through heterologous enzymes also requires the ability to infer new biochemical routes. Going beyond standard pathways is an important goal of PathMiner. As such, it complements existing approaches like PathoLogic, which find the best candidate reference pathways and the corresponding genes in a living system. PathMiner can be used interactively to search for metabolic routes in the context of specific organisms or to identify synthetic pathways.

Our work is also related to previous approaches on pathway synthesis including, the work of Seressiotis and Bailey (1988), and later, Mavrovouniotis’s approach for pathway generation based on the consideration of thermodynamic feasibility of reactions (Mavrovouniotis, 1993). Our approach is novel because we use chemically motivated heuristics to guide the search for pathways.

2 METHODS

We abstract metabolic processes in terms of a biochemical state-space: compounds define the states and transformations between compounds define the state-transitions. Pathway prediction is then considered as a problem of searching the biochemical state-space. In the following section we describe the state-space and our algorithm for predicting pathways through search.

2.1 The biochemical state-space

Our notion of the biochemical state-space is based on resolving enzyme-catalyzed biochemistry into two components. First, the chemical component that represents the transformations between metabolites. Second, the biocatalytic component that involves catalysis of transformation by enzymes. This logical separation between enzymes and the chemistry they catalyze is evolutionarily plausible and functionally relevant, since an enzyme can often catalyze multiple transformations. Abstracting the interaction of an enzyme with a chemical transformation has been discussed by Karp (Karp and Riley, 1994) and it is important to our notion of a biochemical state-space. By considering chemical transformations and enzymes separately we can reason with them rationally to infer plausible pathways.

2.1.1 Compounds

We define a simple representation for compounds that captures their essential chemical properties that are available from existing sources of data. We denote a compound as x in our state-space and describe it by a set of chemical descriptors, x_k. Thus, every metabolite can be placed at a point in hyperspace, which is defined by x =(x₁, x₂, x₃, …, x_N). Currently, we describe compounds based on the composition of their atoms and bonds, which includes a total of 145 unique features, shown in Figure 1.

Fig. 1.

The alphabetical list of 145 descriptors we use for representing our chemical state-space. Atoms are shown using their IUPAC symbols and bonds as atoms joined by a bond. Single, double and triple bonds are shown as the symbols −, = and #, respectively.

Based on the 145 descriptors in Figure 1, α-D-glucose (adg) is represented as the vector x^adg = (0, 0, 0, 0, 0, 6, 0, 0, 0, …). Similarly, pyruvate (pyr) is represented as the vector x^pyr = (0, 0, 0, 0, 0, 3, 0, 0, 0, …). Since the chemical descriptor space is large and the vector for any given compound is sparse, we express compound vectors succinctly using an attribute-value notation. In this notation carbon dioxide, x^CO₂, is described in equation (1).

$${\mathbf{x}}^{{\text{CO}}_2}=[(\text{C}1)(\text{O}2)(\text{C}=02)]$$ (1)

Equation (1) states that CO₂ is defined by the state-vector, x^CO₂, which contains three components: the number of carbon atoms (x_C = 1), the number of oxygen atoms (x_O = 2), and the number of C==O bonds (x_C=O = 2). The set of 145 descriptors represent most compounds uniquely but since we do not represent chirality, stereoisomers map to identical points in the state-space. For example, the representation of β-D-glucose and α-D-glucose are identical. We are exploring methods for representing chirality to overcome this issue.

2.1.2 Transformations

To represent transformations we approximate the complex bond changes that occur when one compound is converted to another. We abstract transformations as transitions between compound states and denote them by t. Consider the transformation of α-D-glucose (x^adg) into α-D-glucose-6-phosphate (x^adg6P). We define this transformation, x^adg → x^adg6P, as the vector difference, which is shown in equation (2).

$$\begin{array}{l}{\mathbf{t}}^{\text{adg},\text{adg}6\text{P}}={\mathbf{x}}^{\text{adg}6\text{P}}-{\mathbf{x}}^{\text{adg}}\\ =[(\text{C}6)(\text{H}12)(\text{O}10)(\text{P}1)\cdots ]\\ -[(\text{C}6)(\text{H}12)(\text{O}6)(\text{P}0)\cdots ]\\ =[(\text{P}1)(\text{O}4)(\text{P}-\text{O}3)]\end{array}$$ (2)

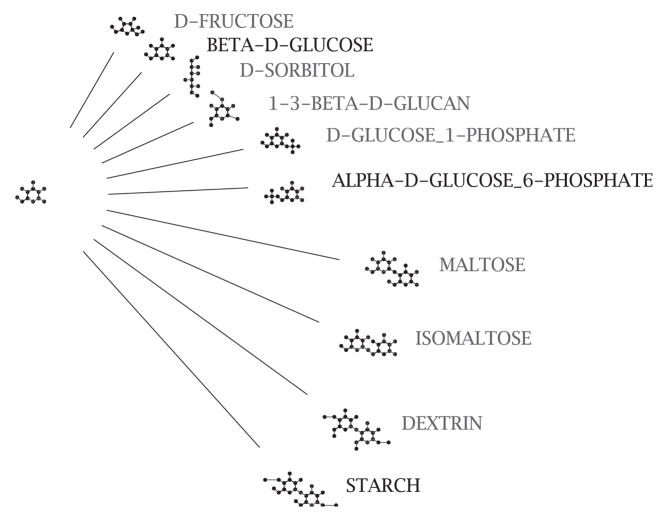
In equation (2), the term t^adg,adg6P describes the state-transition as the addition of [(P1)(O4)(P-O3)]. This set of descriptors corresponds to a known chemical moiety, which is the phosphate functional group ( ${\text{PO}}_4^{3-}$). Though it is not possible to do so in all cases, the interpretation of state-transitions is often chemically intuitive. Each compound can be chemically transformed into a number of other ‘successor’ compounds. For example, some of the chemical successors of α-D-glucose are shown in Figure 2. We denote the set of known chemical successors of x as T (this is discussed further in Section 2.3).

Fig. 2.

Known chemical successors of α-D-glucose (adg), denoted as T^adg. The figure shows the chemical structure of adg on the left and the successors on the right.

Each state-transition can be related to a known enzyme. At present we consider biochemical transformations as state-transitions, t, that approximate the complex bond changes in enzyme-catalyzed reactions. As we gather additional data on the biochemical attributes of reactions, like structural and energetic changes, we will modify this representation accordingly.

2.2 Pathway prediction as search

After defining compounds as states and transformations as state-transitions we consider pathway inference as a state-space search problem. State-space search has been well-studied in Artificial Intelligence (AI) research (Pearl, 1984). We consider the problem of predicting a metabolic pathway as searching a route from an initial compound to a destination compound through a series of state-transitions. We denote the initial compound x⁰, the destination compound x^L and the pathway between these two as P^0,L (please see equation (3)).

$${\mathbf{P}}^{0,L}={\mathbf{x}}^0\to {\mathbf{x}}^1\to {\mathbf{x}}^2\to \cdots \to {\mathbf{x}}^m\to \cdots \to {\mathbf{x}}^L$$ (3)

The simplest approach for pathway inference is uninformed search, which includes depth-first search and breadth-first search methods. In uninformed search, successive states from x⁰ are explored blindly until the goal, x^L, is reached. In real-world problems, like metabolic pathway search, blind search can lead to a combinatorially large number of possible solutions. For practical purposes it is important to prune the set of solutions to a smaller subset. To address this issue, informed search techniques can reason over the state-space to infer pathways that satisfy some optimality condition. For example, heuristic search is an informed search technique that can systematically explore a state-space by measuring the cost associated with any state-transition (Pearl, 1984). Informed searches generally take the form of best-first searches that use a heuristic evaluation function, called F, to prune the combinatorially large possibilities faced by other methods. A simplified version of best-first search is given in algorithm 1.

Algorithm 1.

Best-first search algorithm to find pathway, P^0,L, from an input compound, x⁰, to output compound, x^L, using the heuristic evaluation function, F. In each iteration the successors, T, of the best state in the list X are explored as follows. If the goal is reached then the search terminates with a path, P^0,L. Otherwise, there are two options. First, if the state x^m is not in X, then it is added to it using push(x^m, X), and a pointer from the state to its parent is created with point(x^m, x). Second, if the state is in X then its heuristic score is updated to the lower out of the current and old values. Each state in X points to its predecessors and the path from x⁰ can be traced using path(x^m). The search terminates when there are no more states to explore.

The heuristic evaluation function, F, can be calculated using different methods. For example, greedy search minimizes the cost of reaching the goal state from the current state (called H). Conversely, uniform cost search minimizes the cost of reaching the current state from the initial state (called G). We use A^* (A-star) search, which uses an evaluation function that is the sum of the estimated cost thus far (G) and the estimated cost to the goal (H). In effect, this minimizes the overall path cost (F = H + G). To infer biochemical pathways by heuristic search, however, we need a strategy for calculating the cost of a pathway.

2.2.1 Heureka

But how do we define the cost of state changes in our state-space representation? Generally, the biological factors that determine the cost of a pathway in a living system are not always known. Evolution, environment, bioenergetics, kinetics, growth, or a broader metabolic context, all may contribute to the existence of a metabolic pathway in an organism. The problem is that it is difficult to calculate the contribution of most of these factors due to the scarcity of data, or the limitations of our knowledge. We use our state-space to define the cost based on the chemical efficiency of a pathway. While this may not be always biologically correct, it is congruent with the notion that living systems tend to optimize their growth. Furthermore, it is a useful heuristic for finding synthetic pathways.

To formalize the notion of cost in our state-space we define the difference between any two compounds as Δx and the corresponding distance as |Δx|. For a state-transition this is simply t = Δx. The distance, |Δx|, can be calculated using the Manhattan metric or the Euclidean metric, which are given in equations (5) and (4), respectively. Either the Manhattan distance or the Euclidean distance are admissible as heuristics because they always represent the shortest distance between any two compounds. In this work we used the Manhattan distance (equation [5]) because we find the discrete chemical changes more intuitive and the computation is more efficient.

$$\mid \mathbf{\Delta }\mathbf{x}{\mid }_{\text{E}}=\sqrt{\sum _{k=0}^{k=N}{(\mathrm{\Delta }{x}_k)}^2}$$ (4)

$$\mid \mathbf{\Delta }\mathbf{x}{\mid }_{\text{M}}=\sum _{k=0}^{k=N}\mathrm{\Delta }{x}_k$$ (5)

Using the notion of distance between states we can evaluate the functions F, G and H that are required for heuristic search. Consider the hypothetical pathway shown in equation (3), which begins with the initial state, x⁰, ends with the final state, x^L, and has any intermediate state, x^m. The calculation of the cost functions G and H at the intermediate state, x^m, is given in equations (6) and (7), respectively.

$$G(0,m)=\sum _{i=1}^{i=m}\mid {\mathbf{x}}^i-{\mathbf{x}}^{i-1}\mid$$ (6)

$$H(m,L)=\mid {\mathbf{x}}^m-{\mathbf{x}}^L\mid$$ (7)

For A^* search the state selected for further exploration minimizes the total cost, F = G + H, which is shown in equation (8). Intuitively, G(0, m) is the actual distance due to chemical transitions from x⁰ to x^m, whereas H (m, L) is a ‘guess’ for the shortest possible distance to the goal state x^L.

$$\begin{array}{l}F(0,m,L)=G(0,m)+H(m,L)\\ =\sum _{i=1}^{i=m}(\mid {\mathbf{x}}^i-{\mathbf{x}}^{i-1}\mid )+\mid {\mathbf{x}}^m-{\mathbf{x}}^L\mid \end{array}$$ (8)

Our intuition behind heuristic search for a pathway is as follows. We want to find the series of efficient biochemical transformations that convert one compound into another. In our state-space the heuristic (H) is a guide for the chemical proximity of any intermediate state to the goal. By using the evaluation function in equation (8) in algorithm 1, we select the pathway that efficiently converts the input to the output. The efficiency of this conversion is not determined by the length of the pathway. Rather, it is defined by an optimal value for the heuristic evaluation function, F. Though we have chosen to calculate this function in terms of chemical distance, any biochemical property that can be calculated from available biochemical information could be used here.

We can also guide the search by using biological information. For example, we can search for pathways in an organism using a list of enzymes annotated in the genomic sequence. This is accomplished by modifying algorithm 1 to alter the successors for each state (at statement, T ← successors(x)). Since each state-transition is associated with an enzyme, the available state-transitions and allowed successors for each state are constrained by the available enzymes.

2.2.2 Evaluating efficiency

In order to evaluate the efficiency of different search methods for computing each pathway we calculate the effective branching factor, called b^*. The branching factor, called b, is the number of successors for a given state. The effective branching factor for a given computed pathway of length L with M nodes expanded is defined as the branching factor that a uniform tree of depth d would possess in order to contain M states. The relationship between M, d, b^* is expressed by a polynomial given in equation (9), which we solve numerically to estimate b^*.

$$M=\sum _{j=0}^{j=L}{(b^{\ast })}^j$$ (9)

2.3 Data

PathMiner can use compound, transformation and enzyme information from any source. In this work we used KEGG (Goto et al., 2003) for its accessibility and breadth of metabolic data. We developed parsers to import KEGG data into Lisp (the programming language in which PathMiner is implemented). To populate our biochemical state-space we extract compound data from KEGG. The state-transitions required some additional work because we want to use only the main substrates in transformations (or main transformations). Consider the reaction:

$$\text{Ethanol}+{\text{NAD}}^{+}\leftrightharpoons \text{Acetaldehyde}+\text{NADH}+{\text{H}}^{+}$$

We would like to map this reaction to the state-transition Ethanol ⇋ Acetaldehyde, but not to Ethanol ⇋ H⁺. While we are developing algorithmic approaches to decomposing reactions into substrate and product relations, we have decided to use the KEGG pathway maps which already contain ‘main’ reactions. This data is available from the KEGG pathway map files, which contain unordered lists of the main transformations. Finally, we also use the KEGG genomic annotations to extract the Enzyme Commission (EC) numbers for the putative enzymes in each organism. Though we used KEGG data in our initial investigation we also plan to utilize MetaCyc and other sources of functional annotation in the future. PathMiner currently has data on 3890 compounds, 2917 transformations, and 100 organisms with annotations of putative gene functions.

2.4 Implementation

PathMiner has a modular and distributed architecture. There are two modes for interacting with the system: from the graphical user interface (GUI) through a web-browser, and from an interactive Common Lisp shell. The GUI is implemented as a Java client application that communicates with a Common Lisp server through TCP/IP using a custom Lisp protocol.

The server is implemented in Allegro Common Lisp and contains modules for data management, pathway inference by heuristic search, visualization and distributed computing. The purpose of the data management and pathway inference modules have been discussed in Sections 2.3 and 2.2, respectively. The visualization module is responsible for producing a representation of the pathway suitable for rendering on the client. The distributed computing module is responsible for handling all client and server interaction, and for distributing the client requests across a Lisp Parallel Virtual Machine (McShan and Shah, 2002). A demonstration of the interactive graphical client and instructions about usage are available at http://pathminer.uchsc.edu.

3 RESULTS

We present the results of searching sample metabolic pathways using PathMiner. First, we compare the efficiency of uninformed versus heuristic search in our biochemical state-space. Then we present a brief overview of using the web-based system and a description of the pathway visualization.

We compared the efficiency of three different search algorithms in our state-space including, breadth-first search, depth-first search and heuristic search (described in Section 2.2). The results for four sample searches are summarized in Table 1. The predicted pathways include examples of biodegradation, biosynthesis and biochemical engineering. For each of the pathway searches we report on the number of states explored (M), the length of the pathway (L), the cost (F), the effective branching factor (b^*), and the computation time (t). The computation time was measured by the Common Lisp function, called ‘time’, which reports on the CPU usage of any computation. The timing was carried out by conducting the searches in the interactive Common Lisp shell. The timing reported in Table 1 was measured using Allegro Common Lisp running in the RedHat Linux 7.3 operating system on a Sony PCG-C1MW laptop, containing a Transmeta Crusoe TM5800 Processor and 384 MB of main memory.

Table 1.

The Table shows the performance of the different search algorithms in our state-space for four sample queries

Alg	M	L	F	b*	t(s)
Example (a): from α-D-Glucose to pyruvate
BFS	209	5	29	2.65	8.86
DFS	26	22	491	1.01	1.64
A*	27	6	29	1.44	1.83
Example (b): from citrate to L-tyrosine
BFS	126	3	37	4.63	6.76
DFS	4718	123	2013	2.00	69.14
A*	20	6	13	1.34	1.98
Example (c): from α-D-glucose to 1,3-propanediol
BFS	652	7	81	2.33	19.42
DFS	19	17	185	1.01	1.83
A*	112	7	31	1.74	6.90
Example (d): from citrate to L-histidine
BFS	653	6	45	2.73	16.97
DFS	—	—	—	—	>104
A*	72	7	15	1.61	4.20

Each example summarizes the results for a query from a starting compound to a goal compound. In each example, the columns contain the statistics for the computed pathways and the rows compare the results for the different search algorithms. In each example, from left to right the columns contain the algorithm (Alg); the total number of states explored in the search (M); the length of the path (L); the path cost (F), which is calculated using equation (8); the effective branching factor (b^*), which is computed using equation (9); and the time required for the computation (t). For each example, the second row shows the results for breadth-first search (BFS); the third row for depth-first search (DFS); and the fourth row for A^* search (A^*).

The pathway queries in Table 1 cover three kinds of metabolic themes including, biodegradation (example (a)), biosynthesis (examples (b) and (d)), and engineering (example (c)). We describe the efficiency of our heuristic search algorithm in example (a). The exploration of the pathway from α-D-glucose to pyruvate yields a large number of possible solutions using blind search strategies. Table 1 demonstrates the efficiency of heuristic search in our state-space over blind search strategies. Although breadth-first search finds the shortest path, it is the least efficient because it explores the largest number of states. Depth-first search is more efficient since lesser nodes are explored, but the drawback is that it produces a much longer path. The last column on the right shows the path found by heuristic search, which is the most efficient in the F -cost but not always the shortest (this path is shown visually in Figure 3). The quantitative performance measures for each of the search methods are also summarized in Table 1. We have conducted similar analysis of other pathway searches using the three methods and we find that A^* is the most efficient in F cost and in the number of states explored. Though breadth-first gives the shortest path length, L, A^* is the most efficient in exploring the state-space and in optimizing the F cost. The effective branching factor b^* is another useful metric for comparing the searches. The bread first search has the highest branching factor (2.27) because it explores all immediate successors first; the depth-first search has the lowest b^* (1.28) closely followed by A^* (1.38). Though the branching factor of depth-first search is the lowest, it produces very long pathways, which do not seem to be very plausible. The time required for each search is roughly proportional to M.

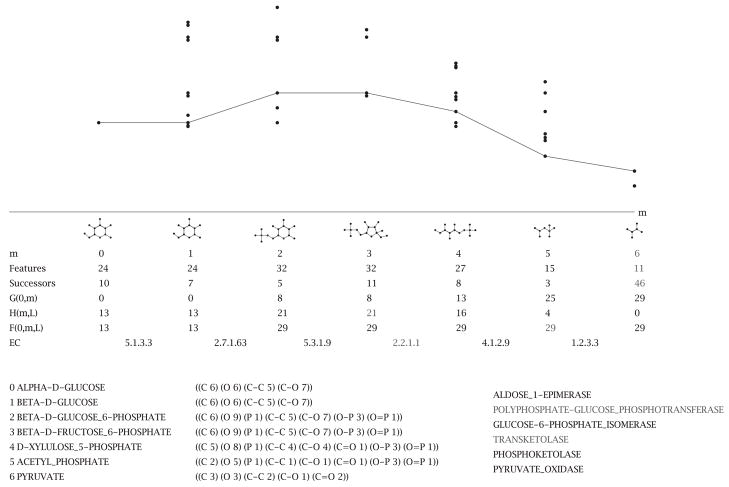
Fig. 3.

The figure shows the visualization of a linear pathway. From top to bottom the figure shows: the profile of the F -cost along the steps in the pathway; the successors of each state are shown as points; the chemical structure of the main compounds at each step; helpful statistics about each step in the pathway; and the EC number of the enzymes involved in catalyzing the transformations. The lower part of the visualization shows the compound names, their state descriptors, and the name of the enzyme.

4 DISCUSSION AND CONCLUSION

We have developed an algorithm to predict pathways based on a biochemical state-space and a heuristic search algorithm. In this work we use chemical efficiency as a heuristic for evaluating pathway cost. To calculate this heuristic we develop a biochemical state-space based on the chemical properties of compounds and transformations. We show that our heuristic search strategy always produces biochemical pathways that are optimal in terms of the heuristic. Furthermore, we show that the algorithm is more efficient than uninformed search techniques. The heuristic we have developed favors pathways that are ‘chemically parsimonious’. We also show that this notion of parsimony does not produce the shortest pathways.

One of the limitations of our approach is that it does not favor transformations that involve the addition of large functional groups to compounds. For instance, in many processes it is necessary to phosphorylate compounds. Since this involves the transfer of a large phosphate moiety to a compound, our heuristic will rarely select such a transformation. Another limitation of our approach is that we currently consider most transformations to be reversible. Defining the rules of reversibility for enzyme-catalyzed transformations are generally difficult and irreversible transformations can be reversible under different physiological conditions. We intend to address these issues in future versions of PathMiner. Finally, since all issues cannot be addressed algorithmically, we have also developed a graphical interface for PathMiner so that users can interactively guide the search based on their requirements.

We are testing PathMiner for two kinds of applications: for analyzing pathways in living systems and for engineering synthetic pathways. The system is flexible and extensible so we can modify it to improve the heuristics in the light of improving biological information. We believe PathMiner is a useful exploratory tool that complements existing microbial reconstruction approaches.

With more genomic sequencing projects underway and confident functional characterizations absent for many of the genes, automated strategies for predicting biochemical pathways can aid biologists inunraveling the complex processes in living systems. At the same time, pathway inference approaches can also help in designing synthetic processes using the repertoire biocatalysts available in nature.