Predicting the Subcellular Localization of Human Proteins Using Machine Learning and Exploratory Data Analysis

Abstract

Identifying the subcellular localization of proteins is particularly helpful in the functional annotation of gene products. In this study, we use Machine Learning and Exploratory Data Analysis (EDA) techniques to examine and characterize amino acid sequences of human proteins localized in nine cellular compartments. A dataset of 3,749 protein sequences representing human proteins was extracted from the SWISS-PROT database. Feature vectors were created to capture specific amino acid sequence characteristics. Relative to a Support Vector Machine, a Multi-layer Perceptron, and a Naïve Bayes classifier, the C4.5 Decision Tree algorithm was the most consistent performer across all nine compartments in reliably predicting the subcellular localization of proteins based on their amino acid sequences (average Precision=0.88; average Sensitivity=0.86). Furthermore, EDA graphics characterized essential features of proteins in each compartment. As examples, proteins localized to the plasma membrane had higher proportions of hydrophobic amino acids; cytoplasmic proteins had higher proportions of neutral amino acids; and mitochondrial proteins had higher proportions of neutral amino acids and lower proportions of polar amino acids. These data showed that the C4.5 classifier and EDA tools can be effective for characterizing and predicting the subcellular localization of human proteins based on their amino acid sequences.

Introduction

Intensified efforts at characterizing gene function are a natural consequence of the recent surge in high-throughput sequencing of eukaryotic genomes. Protein subcellular localization is an important characteristic of gene function since most proteins in specific activity states are typically localized within a specific cellular compartment. Localization of proteins in appropriate compartments is vital for the function and integrity of the internal structure of the cell. Thus, identifying the subcellular localization of proteins is particularly helpful in their functional annotation. Exhaustive experimental studies have been carried out to elicit the subcellular localization of the entire yeast proteome (1) and the mitochondrial proteomes of human (2), rat (3), and Arabidopsis (4); however, such large-scale experimental studies are not feasible for all genomes. Hence, experimental annotation of protein localization is unable to keep up with the pace at which new gene sequences emerge from high-throughput genome sequencing projects. As a result, the gap between the sequenced and functionally annotated genes in the genome databases is rapidly widening.

A number of computational methods have been developed over the past decade for automated prediction of the subcellular localization of eukaryotic proteins. These methods may be broadly categorized into four classes: (1) Methods based on sorting signals that rely on the presence of localization-specific protein sorting signals, which are recognized by the localization-specific transport machinery to enable their entry [for example, MitoProt (5), PSORT-II (6), and TargetP (7)]; (2) Methods based on differences in the amino acid composition or amino acid properties of proteins from different subcellular localizations [for example, Sub-Loc (8), Esub8 (9), and pSLIP (10)]. In this category, methods using neural networks and Support Vector Machines (SVMs) have been developed; (3) Methods based on lexical analysis of key words in the functional annotation of proteins [such as LOCkey (11)]; (4) Methods using phylogenetic profiles or domain projection (12), or localization-specific protein functional domains 13., 14..

In this study, we combine the use of Machine Learning (ML) with Exploratory Data Analysis (EDA) techniques to examine and characterize amino acid sequences of human proteins localized in nine cellular compartments, including the cytoplasm, nucleus, golgi apparatus, lysosome, plasma membrane, endoplasmic reticulum, peroxisome, extracellular compartment (for example, secretory proteins), and mitochondrion. ML is useful for the purpose of class prediction. It is a field of scientific study that concentrates on methods for computer programs to improve their performance by learning (that is, modifying behavior) from previous data examples. During the learning process, structural patterns in the given dataset (“training set”) are established; these patterns then constitute the basis upon which predictions are made when presented with data of unknown classification (“test set”).

Since proteins localized in particular cellular compartments have certain features in common, ML algorithms have been used previously to predict the subcellular localization of proteins (8). The ML methods used in the current studies were: J48, an implementation of the C4.5 Decision Tree algorithm (15); SVM (16); Multi-Layer Perceptron (MLP; a neural network implementation); and Naïve Bayes (NB) classifier (17). There are three classes of features of amino acid sequences used in ML (18), namely Composition, Transition, and Distribution. These features have been successfully used in ML algorithms to predict protein secondary structure (19) and subcellular localization (8).

On the other hand, EDA tools (20) seek to identify patterns within datasets by emphasizing graphics. EDA graphics do not rely on means and variances but rather on the median, ranks, depths, and outlier-insensitive spread measures (such as the fourth-spread) inherent in a distribution. They quickly lead to the identification of inherent underlying structures of datasets. In contrast to confirmatory analyses, exploratory analyses are robust and resistant to the undue influence of data outliers. In this study, the Decision Tree (J48) emerges as being the most consistent performer across all the nine human cellular compartments, relative to SVM, MLP, and NB classifier. In addition, the promise of EDA in characterizing underlying structures within data distributions is exploited to identify primary protein structure features unique to specific subcellular localizations.

Results and Discussion

The current studies have identified certain properties shared by proteins localized in specific cellular compartments, which rely on the physicochemical properties (electronic, bulk, and steric) of amino acid side chains as detailed in Table 1. The categorizations used for Hydrophobicity and Charge are non-numeric (Table 1); nonetheless, they detail the propensity of each amino acid for localization in the hydrophobic (membranes) and soluble environments of the cell. Categorizations used for Normalized van der Waals volume (NVWV), Polarity, and Polarizability were based on previously calculated values 21., 22.. These calculated biophysical parameters of amino acid side chains are orthogonal. For instance, Polarizability is related to molar refractivity while NVWVs model dispersion forces (21); whereas molar refractivity and dispersion forces are not directly related. There are, nonetheless, correlations between certain parameters. For instance, there is strong correlation between Polarizability and NVWV values (21). Since these calculated values constitute the basis upon which the amino acids were grouped in the current study (Table 1), the elements of the feature vector, though incongruent, are not completely independent of each other. Instead, they complement each other, providing a rich dataset for any given amino acid sequence. For each given amino acid side chain, the measured van der Waals volume (V) was normalized as follows:

$$\mathrm{NVWV}\left(\mathrm{side\; chain}\right)=\left[\mathrm{V}\left(\mathrm{side\; chain}\right)-\mathrm{V}\left(\mathrm{H}\right)\right]/\mathrm{V}\left({\mathrm{CH}}_2\right)$$

The side chain of alanine has NVWV=1; each additional CH₂ increases this by one unit.

Table 1.

Amino Acid Groupings

	Group 1	Group 2	Group 3
Hydrophobicity	polar R K E D Q N	neutral G A S T P H Y	hydrophobic C V L I M F W
NVWV	0–2.8 G A S C T P D	2.95–4.0 Ν V E Q I L	4.43–8.08 M H K F R Y W
Polarity	4.9–6.2 L I F W C M V Y	8.0–9.2 Ρ A T G S	10.0–13.0 H Q R K N E D
Polarizability	0–0.108 G A S D T	0.128–0.186 C P N V E Q I L	0.219–0.409 K M H F R Y W
Charge	positive H R K	negative D E	other M F Y W C P N V Q I L N

Machine Learning

To evaluate the accuracy of ML classification, two scenarios were considered: (1) using the entire data as both the training and test set, and (2) separating the dataset into disjoint training and test sets using a ten-fold cross validation technique (Table 2; ref. 23., 24.). In Table 2A, when the test option is “train set only”, all test instances were part of the training set. On the other hand, when the test option is “ten-fold cross validation”, an average value was obtained for ten different sets of the re-organized data such that in each case, 90% of the data were used for training and 10% for testing. The former case represents the most optimistic possible performance of each learning scheme (training set error). Table 3 shows that even with this most optimistic measure, SVM and MLP did not classify as accurately as J48 for the nucleus, lysosome, and peroxisome. NB recorded the highest number (57.5%) of incorrectly classified human protein instances (Table 2A).

Table 2.

Evaluation of Machine Learning Algorithms^*

Table 2A
Method	Test option	Correctly classified	Incorrectly classified
J48	Train set only	3,560 (95.0%)	189 (5.0%)
	ten-fold cross validation	2,390 (63.8%)	1,356 (36.2%)
MLP	Train set only	3,370 (89.9%)	379 (10.1%)
	ten-fold cross validation	2,892 (77.1%)	857 (22.9%)
SVM	Train set only	2,927 (78.1%)	822 (21.9%)
	ten-fold cross validation	2,842 (75.8%)	907 (24.2%)
NB	Train set only	1,634 (43.6%)	2,215 (56.4%)
	ten-fold cross validation	1,595 (42.5%)	2,154 (57.5%)
Table 2B
Method	Test option	Correctly classified	Incorrectly classified
J48	Train set (All species); Human test set	3,584 (95.6%)	165 (4.4%)
SVM	Train set (All species); Human test set	2,726 (72.7%)	1,023 (27.3%)
MLP	Train set (All species); Human test set	1,397 (37.3%)	2,352 (62.7%)
NB	Train set (All species); Human test set	1,294 (34.5%)	2,455 (65.5%)
Table 2C
Method	Test option	Correctly classified	Incorrectly classified
J48	Train set (Non-human species); Human test set	3,069 (67.4%)	1,483 (32.6%)
SVM	Train set (Non-human species); Human test set	3,032 (66.6%)	1,520 (33.4%)
MLP	Train set (Non-human species); Human test set	2,779 (61.1%)	1,773 (38.9%)
NB	Train set (Non-human species); Human test set	1,379 (30.3%)	3,173 (69.7%)

^*Evaluation of a variety of Machine Learning algorithms when applied to the methods characterizing human protein amino acid sequences. A. Training and testing were performed on human sequences only. B. Training was performed with 22,565 sequences from a variety of species available on SWISS-PROT but testing was performed on a subset of 3,749 human sequences only. C. Training was performed with 18,013 sequences from a variety of non-human species available on SWISS-PROT but testing was performed on 4,552 human sequences only.

Table 3.

Impact of Attribute Type Pool on the Performance of Machine Learning Algorithms^*

Type	Localization	J48		NB		SVM		MLP
		P	S	P	S	p	S	p	S
C, T, and D	CYT	0.919	1	0.085	0.241	1	0.025	0.653	0.405
	NUC	0.951	0.980	0.780	0.418	0.734	0.903	0.889	0.968
	GOL	0.779	0.831	0.067	0.348	0.667	0.022	0.686	0.393
	LYS	0.793	0.767	0.062	0.767	0	0	0.875	0.350
	PLA	0,971	0.982	0.920	0.536	0.813	0.948	0.929	0.987
	END	0.876	0.829	0.357	0.324	0.679	0.324	0.891	0.624
	POX	0.731	0.576	0.049	0.424	0	0	0.364	0.242
	EXC	0.959	0.936	0.593	0.367	0.786	0.669	0.893	0.900
	MIT	0.971	0.880	0.368	0.184	0.795	0.663	0.903	0.848
C and T	CYT	0.908	1	0.156	0.291	0	0	0.407	0.278
	NUC	0.943	0.968	0.749	0.570	0.690	0.878	0.842	0.883
	GOL	0.798	0.753	0.091	0.124	0	0	0.477	0.348
	LYS	0.833	0.583	0.110	0.650	0	0	0.623	0.550
	PLA	0.950	0.982	0.905	0.544	0.748	0.932	0.899	0.943
	END	0.890	0.806	0.224	0.471	0.522	0.206	0.577	0.571
	POX	0.810	0.515	0.038	0.455	0	0	0.286	0.061
	EXC	0.920	0.911	0.498	0.470	0.681	0.466	0.851	0.777
	MIT	0.924	0.832	0.395	0.291	0.738	0.492	0.733	0.754
C and D	CYT	0.878	1	0.099	0.266	1	0.025	0.563	0.456
	NUC	0.942	0.980	0.799	0.397	0.735	0.878	0.879	0.916
	GOL	0.871	0.685	0.060	0.348	1	0.022	0.692	0.404
	LYS	0.745	0.683	0.056	0.783	0	0	0.697	0.383
	PLA	0.961	0.985	0.925	0.517	0.760	0.941	0.889	0.960
	END	0.884	0.759	0.336	0.276	0.644	0.224	0.860	0.653
	POX	0.769	0.606	0.058	0.394	0	0	0.429	0.182
	EXC	0.941	0.934	0.595	0.375	0.787	0.629	0.836	0.828
	MIT	0.964	0.877	0.354	0.184	0.768	0.579	0.872	0.819
D and T	CYT	0.888	1	0.100	0.215	1	0.025	0.442	0.532
	NUC	0.942	0.965	0.729	0.307	0.664	0.815	0.841	0.852
	GOL	0.766	0.809	0.066	0.427	0	0	0.643	0.303
	LYS	0.667	0.633	0.048	0.750	0	0	0.611	0.367
	PLA	0.957	0.980	0.849	0.505	0.697	0.919	0.798	0.973
	END	0.883	0.712	0.270	0.159	1	0.006	0.720	0.424
	POX	0.682	0.455	0.054	0.303	0	0	0.500	0.091
	EXC	0.939	0.911	0.554	0.331	0.753	0.555	0.919	0.708
	MIT	0.926	0.887	0.271	0.136	0.663	0.369	0.871	0.657

^*Performed on the human protein sequences (training set). C=Composition type attributes, T=Transition type attributes, and D=Distribution type attributes. CYT=cytoplasm, NUC=nucleus, GOL=golgi complex, LYS=lysosome, PLA=plasma membrane, END=endoplasmic reticulum, POX=peroxisome, EXC=extracellular/secretory compartment, MIT=mitochondrion. P=Precision, S=Sensitivity.

The ten-fold cross validation test option was the better indicator of the learning schemes’ generalizability by calculating its performance on an independent test set; it is also a measure of each scheme’s predicted error rate (test set error). When the classification was conducted based on the training set along with ten-fold cross validation, the accuracy rates for human proteins decreased across all learners. MLP, SVM, and J48 emerged best with 2,892, 2,842, and 2,390 (out of 3,749) correctly classified human protein sequences, respectively (Table 2A).

Comparing both testing schemes in Table 2A, J48 did best (relative to MLP, SVM, and NB) when tested with sequences derived from the training set only. On the application of ten-fold cross validation (a predictor of the error rate), J48 did not perform as well as MLP. Nonetheless, J48 was the more consistent high performer across all compartments (Table 3; Figure S1). Furthermore, upon training with the data generated from 22,565 sequences from all species, and testing with a subset of human sequences, J48 outperformed the other learning schemes in correctly classifying 95.6% of instances (Table 2B). This speaks to the fact that testing with instances derived only from the training set results in the most optimistic outcomes, which makes an estimate of the model’s error rate a necessity. Indeed as shown in Table 2C, upon training with a separate dataset of sequences from a variety of non-human species available on SWISS-PROT and then testing with only a dataset of human sequences, J48 and SVM ranked highest for accuracy, correctly classifying 67.4% and 66.6% of instances, respectively (Table 2C). The lowered performance in this latter case is attributable to the fact that the training data were derived from the sequences from a diverse set of eukaryotic organisms with no representation of human sequences. Thus J48 performs creditably in terms of the ability to generalize unseen sequences.

A closer look at the data indicated that although the accuracy of classification for SVM was high for other subcellular localizations, it consistently classified cytoplasm, golgi, lysosome, and peroxisome proteins poorly (Table 3). Similarly, MLP consistently classified cytoplasm, golgi, lysosome, and peroxisome proteins poorly (Table 3). Thus J48 emerged as the most consistent accurate classifier for all the subcellular localizations considered (Figure S1).

Even with the high-performance J48 classifier, outcomes varied with subcellular localizations. Relatively speaking, proteins localized in the golgi apparatus, lysosome, and peroxisome were less likely to be correctly classified than proteins of the cytoplasm, plasma membrane, nucleus, extracellular compartment, and mitochondrion (Table 4). The contrast became stark when the ten-fold cross validation was applied: although there was a precipitous drop in the accuracy of prediction for proteins of other localizations, those of the nucleus, plasma membrane, extracellular compartment, and cytoplasm remained relatively high. This could be attributed to the relatively smaller training sets available for golgi, lysosome, and peroxisome.

Table 4.

Performance of Decision Tree (J48) Using Instances for Training

Localization	TP rate	FP rate	Precision	Sensitivity	F-measure
PLA	0.982	0.020	0.971	0.982	0.977
NUC	0.980	0.017	0.951	0.980	0.965
CYT	1	0.002	0.919	1	0.958
EXC	0.936	0.007	0.959	0.936	0.947
MIT	0.880	0.002	0.971	0.880	0.924
END	0.829	0.006	0.876	0.829	0.852
GOL	0.831	0.006	0.779	0.831	0.804
LYS	0.767	0.003	0.793	0.767	0.780
POX	0.576	0.002	0.731	0.576	0.644

The effect of using subsets of the features with the ML algorithms was examined. Precision is a measure of the positive predictive value, that is, the proportion of the claimed subcellular localizations that are indeed those specified subcellular localizations:

$$\mathrm{Precision}=\mathrm{True\; Positives}/\left(\mathrm{True\; Positives}+\mathrm{False\; positives}\right)$$

Sensitivity (or Recall) is a measure of the probability that the test would reject a false null hypothesis:

$$\mathrm{Sensitivity}=\mathrm{True\; Positives}/\left(\mathrm{True\; Positives}+\mathrm{False\; Negatives}\right)$$

As Table 3 indicates, the Precision and Sensitivity values of all the learners decreased from the highest values (when all attribute types were used) when only pairs of attribute types (from among Composition, Transition, and Distribution) were available. Models that used a combination of all attribute types performed better, in terms of Precision and Sensitivity, than those that only used any attribute type subset (or subset combinations). J48 performed better than SVM and MLP in classifying proteins of the golgi, lysosome, endoplasmic reticulum, and peroxisome (all of which present a more difficult classification problem than the other compartments).

There were high J48 True Positive rates and low False Positive rates for all compartments, with the exception of the peroxisome and lysosome (Table 4). The F-measure is the harmonic mean of Precision and Sensitivity and can be used as a single measure of a test’s performance:

$$\mathrm{F-measure}=\left(2\times \mathrm{Precision}\times \mathrm{Sensitivity}\right)/\left(\mathrm{Precision}+\mathrm{Sensitivity}\right)$$

Accordingly, the highest J48 F-measures were those for proteins of the plasma membrane and nucleus; the lowest were those for the peroxisome and lysosome proteins.

NB classifiers work best if all attributes are truly independent of each other; they classify correctly as long as the correct class is more probable than any other class. Correlations exist between certain values present in the vector, for example between Polarizability and NVWV (21); this could explain the less than impressive performance of NB. The advantage that Decision Trees have, in this regard, are their ability to choose the best attribute to split on at each node.

The J48 version of the C4.5 Decision Tree (15) is implemented as follows: the algorithm works top-down, seeking at each stage an attribute that best separates the classes. The attribute with the greatest information gain is chosen. It then recursively processes the sub-problems resulting from the split until the information is zero or reaches a maximum. The information measure (entropy) is calculated as follows:

$$Entropy\left(p_1,p_2\mathrm{,\dots },p_n\right)=-p_1\mathit{lo}{\mathit{g}}_2{p}_1-p_2\mathit{lo}{\mathit{g}}_2{p}_2\cdots -p_n\mathit{lo}{\mathit{g}}_2{p}_n$$

where p₁, p₂,…, p_n are fractions representing the data distribution at a node (attribute) and sum up to 1.

Exploratory Data Analysis

Following the application of Tukey’s Median Polish (MP) algorithm (25) to the data, a diagnostic plot of the comparison values against the residuals yielded no clear pattern (Figure S2), indicating that there was no systematic departure from the additive model assumption underlying the MP algorithm. A clear and consistent diagnostic plot would have indicated non-additivity and signaled a need to transform the data before further analyses.

The vectors derived from the human protein dataset were grouped, depending on which of the nine, compartments they are localized in. For each of the localizations, the median value for each attribute was the entry used for the table to which MP was applied (Figure 1). The MP procedure laid out the column effects (Figure 2). The lowest effects were due to the Composition of the ungrouped individual amino acids; the highest effects were due to the Distribution of grouped amino acids. These observations were consistent with the attributes used by the J48 learner for its initial splits (Figure 3). These indicate that it is the set of physicochemical properties of the individual amino acids, rather than their unique identities, that help determine the subcellular localization of the proteins of which they are a part. It has been known that the distribution of charge and hydrophobicity is crucial for targeting a protein to its intended subcellular localization (7).

Fig. 1.

A description of the table to which Tukey’s MP algorithm was applied. The vectors derived from the human protein dataset were grouped, depending on which of the nine compartments they are localized in (cytoplasm, nucleus, golgi apparatus, lysosome, plasma membrane, endoplasmic reticulum, peroxisome, extracellular compartment, and mitochondrion). For each of the localizations, the median value for each attribute was the entry used for the table.

Fig. 2.

The impact of attribute pool on relative contributions of attribute types to data. Changes in MP column effects (effects of 125 sequence amino acid characteristics) occurred with the diversity of attribute type used. A. Composition, Transition, and Distribution attributes were used. B. Only Composition and Transition attributes were used. C. Only Composition attributes were used. Column effect patterns were preserved in all cases, the lowest being the Composition of individual amino acids (A). In the absence of Distribution type (B and C) and/or Transition type (C) attributes, the effects of the remaining attribute type(s) increased.

Fig. 3.

A depiction of the root (initial splits) of the Decision Tree (J48) on the human amino acid sequence data following training with human sequences. The root includes Composition, Transition, and Distribution type attributes.

The row effects (range: −0.2 through 0.1; median: 0) were much lower than the column effects (range: −25.1 through 74.9; median: 0), indicating that the measured amino acid feature influenced the numerical response more than the cellular localization of a protein did. This indicates that the individual elements of the vector generated for a protein are less dependent on the cellular compartment to which the protein belongs than they are on the attribute of the sequence they represent. There were differences in the row effects (Figure S3): the extracellular compartment, peroxisome, cytoplasm, and lysosome had the lowest effects. This signifies that, in relative terms, these compartments presented the more difficult classification tasks. This observation is largely supported by the Precision and Sensitivity values noted in Table 2, Table 3 (where all attribute types were used). A stem-and-leaf display of the column effects (Figure S4) indicated that the extremely low and extremely high responses had to do with the Distribution of amino acids. Table 5 summarizes the observations from 50 boxplots, depicting the distribution of the data derived from Composition and Transition type attributes.

Table 5.

Notable Composition and Transition Patterns from Boxplots

Localization	Composition		Transition
	High level	Low level	High level	Low level
CYT	NVWV Group 2; Polarizability Group 2; Charge Group 2	NVWV Group 1	Hydrophobicity Groups 1 and 3; Polarity Groups 1 and 3; Charge Groups 2 and 3	NVWV Groups 1 and 3
NUC	Hydrophobicity Group 1; NVWV Group 1; Polarity Group 3; Polarizability Group 1	Hydrophobicity Group 3; NVWV Group 2; Polarity Group 1	Hydrophobicity Groups 1 and 2; Polarity Groups 2 and 3;	Hydrophobicity Groups 2 and 3 Polarity Groups 1 and 2; Polarizability Groups 2 and 3
GOL	NVWV Group 2; NVWV Group 3		NVWV Groups 2 and 3
LYS	NVWV Group 1; Polarizability Group 1	NVWV Group 2	NVWV Groups 1 and 3; Polarizability Groups 1 and 3
PLA	Hydrophobicity Group 3; NVWV Group 2; Polarity Group 1	Hydrophobicity Group 1; Polarity Group 3; Charge Group 1; Charge Group 2	Hydrophobicity Groups 2 and 3; NVWV Groups 1 and 2	Hydrophobicity Groups 1 and 3; Polarity Groups 1 and 3
END	Hydrophobicity Group 3; NVWV Group 2; NVWV Group 3; Polarizability Group 3	NVWV Group 1; Polarizability Group 1	Hydrophobicity Groups 1 and 3; NVWV Groups 2 and 3; Polarity Groups 1 and 3; Polarizability Groups 2 and 3
POX			Hydrophobicity Groups 1 and 3; NVWV Groups 2 and 3; Polarity Groups 1 and 3; Charge Groups 1 and 3
EXC	NVWV Group 1; Polarizability Group 1; Polarizability Group 2	NVWV Group 3; Polarizability Group 3	Hydrophobicity Groups 1 and 3 Polarity Groups 1 and 3 Polarizability Groups 1 and 2	NVWV Groups 2 and 3
MIT	Charge Group 1	Polarizability Group 2	Hydrophobicity Groups 1 and 3; Polarity Groups 1 and 3; Charge Groups 1 and 3

Generally, the more discriminative attributes of a Decision Tree appear closer to the root. The first three splits of the tree (Figure 3) involve both a Composition type attribute measuring percent polarity of Group 1 and a Distribution type attribute of Group 1 Polarity (Polarity_Percent_Group1 and Polarity_GP1_Distribution_25^th_Percentile_Occurrence, respectively). Notably, the Polarizability attributes were the only class of features that did not appear in the first few informative splits of the tree. This may be attributable to the fact (21) of correlations between calculated Polarizability values for amino acid side chains and those of NVWVs (Table 1).

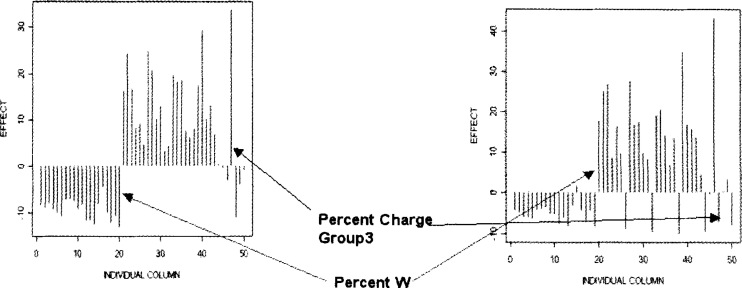
As can be seen from Figure 3, J48 was most strongly influenced by attributes characterizing Polarity Percent Group1 (polarity between 0–0.108) of the amino acid sequence. Closer examination of plots of the column effects indicates distinct differences in the patterns of effects between those human sequences with Polarity Percent Group1 ≤ 37.9 and those with Polarity Percent Group1 > 37.9 (Figure 5). For example, there are differences in the patterns of the Percent W as well as the Percent Charge Group3 column effects. In both cases, the column effect decreases dramatically between those two groups (Polarity Percent Group1 ≤ 37.9 or > 37.9). However, there was a dramatic increase in column effect for the 20^th column (Percent W) between those two groups. There were several other contrasting changes in effect between those two groups involving Composition, Transition, and Distribution type columns (Figure 5). Similar EDA examination of different groups of amino acid sequences based on the J48 tree categorizations (Figure S6) would demonstrate contrasts that confirm the underlying reason for the success of this learning scheme.

Fig. 5.

An illustration of the contrasting patterns in MP column effects between amino acid sequences on either side of a J48 split. The chart highlights two of the columns whose effects differ sharply between the two groups: Percent Charge Group3 and Percent W.

In some instances, the level of difficulty in classifying proteins of certain compartments may be attributable to a number of factors. Firstly, cellular organelles are not as homogenous (26) as most current annotations would seem to suggest. The nucleus, for instance, has a matrix, a nucleolus, and an envelope. Each sub-compartment often has a proteome with a unique set of features and functions, some of which could more closely resemble features of other localizations or organelles. Database annotations with such acids across the sequences: the low values indicated that low proportions of the specified amino acid type occurred at the beginnings of the sequences, and the high values confirmed that high proportions were stretched across entire sequences. They also showed that, next to the low response Distribution data, the directly measured proportions (Composition) of individual amino acids influenced the numerical responses least.

An investigation was implemented to find out if all the three attribute types (Composition, Transition, and Distribution) were necessary to best characterize each protein. The MP algorithm was performed in the presence of different attribute types, and the column effects were plotted (Figure 2): (1) Composition, Transition, and Distribution attributes were used; (2) Only Composition and Transition attributes were used; (3) Only Composition attributes were used. This confirmed (Figure 2A) that the highest effects were attributable to the Distribution data and that the lowest effects were attributable to the Composition of individual amino acids, as well as Distribution (the first occurrence of each amino acid clasification member along a sequence). Even in the absence of Distribution type attributes (Figure 2B and C) and/or Transition type attributes (Figure 2C), the patterns of column effects were preserved, the lowest being the Composition of individual amino acids. However, note that while the patterns were conserved, the magnitude of the effects of the remaining attribute type(s) increased in the absence of Distribution and/or Transition type attributes. Composition, Transition, and Distribution type columns together provided higher effects than any subsets in particular. The pattern of column effects changed when Composition and Transition type columns or only Composition type columns were used. This observation was borne out by the mix of attributes upon which the initial J48 splits occurred (Figure 3).

When sequence amino acids were grouped in terms of hydrophobicity, NVWV, polarity, polarizability, and charge, interesting patterns emerged. EDA graphics confirmed certain expected patterns. For example, a stem-and-leaf display of the residuals of MP showed that plasma membrane proteins have high incidences of transitions between hydrophobic and neutral amino acids (Figure S5); this observation was borne out by boxplots (Table 5; transitions between Hydrophobicity Groups 2 and 3). Similarly, boxplots in Figure 4 showed that nuclear proteins tend to have higher proportions of polar amino acids and lower proportions of hydrophobic amino acids. In contrast, proteins localized on the plasma membrane have higher proportions of hydrophobic amino acids and lower proportions of polar amino acids; cytoplasmic proteins have higher proportions of neutral amino acids; and mitochondrial proteins have higher proportions of neutral amino acids and lower proportions of polar distinctions are not yet widely available. Scott et al. (27) have sought to reduce the effects of this shortcoming by factoring in protein interaction data and specific sub-compartmental protein data in a process that improves subcellular localization prediction. Secondly, there are instances in which proteins typically associated with certain organelles have been detected in the proteome of other organelles 28., 29.. While these could be artifacts of fractionation procedures, they are sometimes biologically significant (29). Thirdly, isoforms of certain proteins occur in or shuttle between multiple localizations, such as the cytoplasm and the nucleus. These include a number of enzymes with multiple isoforms that are localized in multiple localizations depending on the spatial and temporal patterns of protein expression. As an example, the enzyme adenylate kinase [AK (EC 2.7.4.3)] has six isoforms in humans, which are distributed across the cytoplasm, mitochondrion, and nucleus (30). Since the features of these proteins are very similar, it is difficult to predict the localization of such proteins.

Fig. 4.

Boxplots depicting the distribution, based on Composition (Hydrophobicity) of human amino acids within the specific cellular localizations.

Conclusion

Previous subcellular localization predictors that use amino acid compositions have used neural networks (31), the covariant discriminant algorithm (32), and SVMs (8); each predictor has achieved a unique accuracy rate over up to four eukaryotic or prokaryotic subcellular compartments. In this study, nine human (eukaryotic) cellular compartments were examined, and the Decision Tree J48 emerged as performing consistently better at classifying across all compartments (including those that present with difficult classification tasks). This scheme is better able to handle functional annotation tasks that involve gene products localized outside of those eukaryotic cellular compartments. Furthermore, the unique features of the nine human compartments in terms of amino acid composition and transition have been outlined; this result provides a ready guide for such annotation tasks.

Materials and Methods

Data collection and filtering

We used protein sequences from the SWISS-PROT database release 45.0 (http://www.ebi.ac.uk/swissprot) for training and testing purposes in this study. To obtain high-quality datasets, we filtered the data as follows: (1) Include sequences only from the animal species that have experimentally derived annotations for “subcellular localization”. (2) Remove sequences with ambiguous and uncertain annotations, such as “by similarity”, “potential”, “probable”, “possible”, and so on. (3) Remove sequences known to exist in more than one subcellular localization, such as those that shuttle between the cytoplasm and the nucleus. Finally, we selected only those subcellular localizations with at least 100 annotated sequences. These localizations include (the number of sequences are shown in parentheses): CYT-cytoplasm (2,673), END-endoplasmic reticulmn (794), EXC-extracellular/secretory compartment (7,077), GOL-golgi complex (253), LYS-lysosome (179), MIT-mitochondrion (2,019), NUC-nucleus (4,112), PLA-plasma membrane (5,273), and POX-peroxisome (185). From these datasets, we separated a subset of 3,749 proteins belonging to human.

Machine Learning

Three classes of features of amino acid sequences were used in the current study, including Composition, Transition, and Distribution. These features are focused on physicochemical properties of the primary structure of proteins. Composition is a reference to the proportions of amino acid types contributing to the protein sequence. Transition represents the frequency with which specific amino acid types are followed or preceded by other amino acid types within the sequence. Distribution captures the dissemination of specific amino acid types within specific portions of the sequence (or the entire sequence). These feature types have been used in previous ML algorithms to characterize amino acid sequences based on hydrophobicity, NVWV, polarity, polarizability, and charge (Table 1).

Based on numerical attributes characterizing amino acid Composition, Transition, and Distribution along with the categories just outlined (Table 1), a Common Lisp algorithm (33) was used to generate a vector of size 125 for each protein. The breakdown of the elements of each vector is outlined as in Figure 6A.

Fig. 6.

Structure of the data used. A. For each amino acid sequence examined, Composition (С), Transition (Τ), and Distribution (D) data (as described in the text) were calculated and placed in a vector in the order shown. 1–20: Composition, individual natural amino acids; 21–23: Composition, Hydrophobicity (members of Groups 1, 2, and 3, respectively); 24–26: Transition, Hydrophobicity (between members of Groups 1 and 2; between members of Groups 2 and 3; and between members of Groups 1 and 3, respectively); 27–41: Distribution, Hydrophobicity (the 1^st, 25^th, 50^th, 75^th, and 100^th percentile occurrences for members of Groups 1, 2, and 3, respectively). Similarly, the rest of each vector was constituted as follows: 42–44: Composition, NVWV; 45–47: Transition, NVWV; 48–62: Distribution, NVWV; 63–65: Composition, Polarity; 66–68: Transition, Polarity; 69–83: Distribution, Polarity; 84–86: Composition, Polarizability; 87–89: Transition, Polarizability; 90–104: Distribution, Polarizability; 105–107: Composition, Charge; 108–110: Transition, Charge; 111–125: Distribution, Charge. B. from each protein’s amino acid sequence, a vector was generated as above. A matrix consisting of an aggregate of all the vectors generated was then created and used for ML and EDA.

A matrix consisting of a vector of each of the proteins (Figure 6B) was thus generated and used as a training set for ML (32). Based on the data, predictive classifications (based on instances derived from the training set alone as well as the training set in conjunction with ten-fold cross validations) were made by using J48, SVM, MLP, and NB classifier. These algorithms are all available through the Weka ML workbench (http://www.cs.waikato.ac.nz/ml/weka/).

Exploratory Data Analysis

The data was also analyzed using EDA tools. The MP algorithm (25) was used along with boxplots (35) in these studies to help establish effects. The MP procedure fits an additive model:

$$\mathrm{Response Variable}=\mathrm{Common Value}+\mathrm{Row Effect}+\mathrm{Column Effect}+\mathrm{Residual}$$

where the Common Value is constant throughout the table; the Row Effect is constant by rows; the Column Effect is constant by columns; and the Residuals or remaining effects represent departures of each data array element from the purely additive model. MP works iteratively on a data table, alternatively finding and subtracting column medians and row medians until all columns and rows have zero medians. The residuals, row effects, or column effects may then be illustrated graphically by the way of a stem-and-leaf display or boxplot. Boxplots depict the distribution’s central tendency (median), spread (fourth-spread), skewness (based on the relative positions of the median, lower fourth, and upper fourth), tail length, as well as outliers.

The R language (http://www.r-project.org/) statistical environment was used to implement the EDA aspects of the study. Furthermore, for each subcellular compartment, Boxplots (36) were generated for each amino acid category and feature. Comparisons were made within and between the data for the cell compartments.

Authors’ contributions

GKA conducted the Machine Learning and Exploratory Data Analysis experiments and co-wrote the draft manuscript. SML conceived the original idea of using this approach of protein characterization, wrote the initial code implementing it and wrote portions of the manuscript. CG collected the dataset used for the experiments, wrote the code for cleaning up the data to render them useful for the experiments, co-wrote and edited the various drafts of the manuscript. All authors read and approved the final manuscript.

Competing interests

The authors have declared that no competing interests exist.

Supporting Online Material

http://bioinformatics.albany.edu/gpb/gka/supl_figs.html

Figures S1–S6