Softness, strength and self-repair in intermediate filament networks

Abstract

One cellular function of intermediate filaments is to provide cells with compliance to small deformations while strengthening them when large stresses are applied. How IFs accomplish this mechanical role is revealed by recent studies of the elastic properties of single IF protein polymers and by viscoelastic characterization of the networks they form. IFs are unique among cytoskeletal filaments in withstanding large deformations. Single filaments can stretch to more than 3 times their initial length before breaking, and gels of IF withstand strains greater than 100% without damage. Even after mechanical disruption of gels formed by crossbridged neurofilaments, the elastic modulus of these gels rapidly recovers under conditions where gels formed by actin filaments are irreversibly ruptured. The polyelectrolyte properties of IFs may enable crossbridging by multivalent counterions, but identifying the mechanisms by which IFs link into bundles and networks in vivo remains a challenge.

Introduction

The mechanical function of intermediate filaments is evident in many biological systems. The classic examples of IFs as biomaterials are the chemically crosslinked and dehydrated IFs that form the matrix of skin, hair, hooks and nails, but the much more delicate hydrated polymers within the cytoskeleton of live cells also have essential mechanical functions. Numerous human diseases characterized by inadequate resistance to forces applied externally, for example to skin, or internally due to contractions by muscle or osmotic stresses are associated with defects in intermediate filament structure or expression [1–4]. The strutures and assembly mechanisms of IFs have been extensively studied (reviewed in [5, 6]). IFs also perform non-mechanical functions in the cell [7, 8], but the unique polymeric structure of IF allows them to form dynamic soft viscoelastic materials with non-linear elasticity well suited for their role to preserve tissue integrity. Cells rich in intermediate filaments such as neurons and unactivated astrocytes of the central nervous system are among the softest cells measured [9] and recent studies of purified IFs reveal that these polymers are exceptionally flexible but resistant to breakage, compared to other cytoskeletal polymers.

Elasticity of single semiflexible polymers

The mechanical properties of IF networks depend equally and independently on two factors, the physical properties of the individual filament, and the geometry and chemical bonds by which the filaments are held together in the network. Most studies of purified IFs have measured the viscoelastic properties of macroscopic IF networks and inferred the properties of the filaments by comparison with model networks or with the viscoelasticity of actin or other biopolymer gels [10–17]. These studies have generally shown that crosslinked IF networks are significantly softer than other cytoskeletal gels and can withstand larger deformations without breaking. More recently, single filament measurements, made possible largely by advances in methods to image and manipulate single IFs in hydrated suspensions have focused attention on the unusual elastic properties of single filaments.

Intermediate filaments, like their cytoskeletal counterpart F-actin are examples of semi-flexible polymers, a class of polymers that are too soft to be truly rodlike, but too stiff to be modeled as freely flexible chains similar to those in rubberlike networks. More precisely, a filament is said to be semiflexible when its persistence length is of the same order as its contour length. Both in vivo and in vitro, IFs can be several microns long, and when crosslinked into networks, the physically relevant length is the distance between network junction points or crosslinks, which is generally on the order of a 100 to 1000 nm. The persistence length λ is qualitatively the distance along a filament’s contour along which that filament appears straight. More precisely persistence length is defined by the expression

$$<cos\theta (\text{s})>={\text{e}}^{-\text{s}/\lambda }$$ (1)

where <cos θ(s)> is an ensemble average of the angle θ formed by two tangents drawn at distances s along the contour.

The persistence length, a geometrical quantity derived from images taken by microscopy is related to the elastic bending constant of the filament K by the expression

$$\text{K}={\lambda }_{\text{p}}/{\text{k}}_{\text{B}}\text{T}$$ (2)

where k_BT is the thermal energy. K quantifies how much force it takes to deform the filament to a given deflection. For a uniform solid, the bending modulus is simply related to the stretching modulus, also called the Young’s modulus E, by the expression K = EI where E is the Young’s modulus, a material property of the IF, and I is the area moment of inertia of the filament = πa⁴/4 where a is the filament radius.

Most estimates of IF flexibility are derived from measurements of the persistence length taken from light, electron, or atomic force microscopy. Figure 1 shows typical images of neurofilaments adhered to a surface, taken by atomic force microscopy (AFM).

Figure 1. Flexibility of neurofilaments.

Atomic force micrograph showing a typical image of hydrated, native bovine spinal cord neurofilaments deposited from solution on a mica surface to which they strongly adhere. Note the significant flexibility on a length scale less than a micron. Occasionally, stretched filaments such as that shown in the center with apparently smaller diameters are seen, possibly as the result of flow-induced forces as the filaments adhered or as the AFM cantilever moved laterally across the surface.

From images such as these, the persistence length is measured either by a direct determination of the tangent-tangent autocorrelation of function eq. 1 from digitized images [14] or by comparing the contour length and the end to end distance R of the filament:

$$<{\text{R}}^2(\text{s})>=4\lambda \text{s}(1-(2\lambda /\text{s})(1{-\text{e}}^{-\text{s}/2\lambda }))$$ (3)

This expression assumes that the filament has sufficient mobility along the surface to come to thermal equilibrium in 2-D. However, in most experimental cases, the filament deposits from a dilute solution onto the surface composed of mica, glass, plastic, aluminum oxide or other materials and it is not clear if the initial contact is irreversible or whether it can move as subsequent parts of the filament contact the surface. Unlike F-actin or microtubules, IFs are sufficiently flexible that filaments longer than a few microns cannot be clearly imaged by light microscopy in 3-D solution because their contours cross over in the field of view. Therefore a filament that gradually absorbs to the surface may trap loops and other curved structures that would rarely occur if it could come to equilibrium on the surface. As a result, the bending modulus inferred using equation 2 from persistence length calculated from equation 3 may differ significantly from the true bending modulus, depending on whether the image observed is a true 2-D equilibrium structure or a 2-D projection of the 3-D structure. In addition, more subtle effects of contour length on the value of λ obtained from images can also lead to smaller errors and an apparently length-dependent filament stiffness. These issues have been recently explored in several studies that examine how length affects persistence length measurements [18] and how different surfaces allow or prevent relaxation of an absorbed IF [19, 20].

Stiffness and durability of single IFs

A consistent result of measurements of IF stiffness is that the filaments are surprisingly flexible and highly resistant to damage by large deformations. As discussed in several recent studies, the very low value of E for IFs measured by a variety of methods may be an important mechanical feature of IFs that differentiates them from other biopolymers.

Analysis of images such as those in Figure 1 for a variety of different intermediate filament types summarized in Table 1 generally have yielded values for persistence length in the range of 300 nm to slightly over 1 μm [18, 20–22]. Variability in measurements may arise in part from the difficulty in determining whether the filaments can relax on the 2D surface. On some surfaces such has mica, IFs are so tightly bound that when an AFM tip is used to apply an upward force, the IF does not detach from the surface as other polymers do, but instead, individual IF subunits appear to peel off the surface of the filament [23]. Despite some uncertainty in relating measured persistence length to filament stiffness, these results consistently show that IFs are an order of magnitude more flexible than F-actin and thousands of times softer than microtubules. Measurements of persistence length derived not from images but from the fluctuations of filaments detected by dynamic light scattering confirmed that the persistence length of desmin filaments is in the range of a several hundred nm [24].

Table 1.

Summary of persistence lengths and resistance to deformation of cytoskeletal filaments compared to two model helical single molecules.

Filament type	Persistence length	Resistance to breakage by elongation	Recovery after network disruption
Microtubules	> 1 mm [55]	Minimal/negligible	No
F-actin	3 – 17 μm [55–59]	Limited, break when thermal fluctuations are pulled straight	No
Intermediate filaments	Desmin 500 nm [24] Vimentin 1000–1300 nm [20] Keratin (K8/K18) 200 nm [60] Neurofilaments 450 nm [18, 22]	Generally very high Networks survive shear strain >200% [12, 14] Individual filaments extend >200% by thinning [21]	Yes
Single alpha helical coiled-coil	Myosin rod 26 nm [59] Tropomyosin: smooth muscle 55 nm, skeletal muscle 150 nm[26]

A direct measurement of the force required to bend an IF is reported from a recent study that measured K by placing a short (250 nm) vimentin filament above a hole on an otherwise flat aluminum oxide surface, applying a force with an AFM cantilever tip and measuring the resulting downward deflection [25]. The value of Young’s modulus obtained by this method was in the range of 300–400 MPa, but increased to approximately 900 MPa when the filaments were fixed with gluteraldehyde. These values, which quantify the elastic properties of the material within the IF can be compared with results from similar measurements of F-actin that report Young’s moduli in the range of 2 GPa. Therefore both imaging and deformation studies of single IFs show that even though they have a larger cross-sectional area than F-actin, they are also approximately ten times more flexible.

The high flexibility of IFs is not simply related to the model for IFs as formed by multiple overlapping alpha helical coiled-coil subunits. As pointed out by Hohenadl et al. [24] the persistence length of a pure helical coiled-coil dimer like skeletal muscle tropomyosin is 150 nm [26] only slightly less than that of an IF that contains at least 16 dimers per cross section, depending on the filament type. The greater stiffness observed when IFs are chemically crosslinked suggests that part of the flexibility may be lost when protofibrils within the IF are prevented from sliding longitudinally. But even if each dimer could freely slide, the stiffness of the IF would at least increase linearly with the number of dimers per cross section, yielding a minimal value of persistence length as 16 × 150 nm = 2.4 μm, which is well below most reported values for IFs. The flexibility of IFs therefore suggests that the helics could uncoil under stress or that the interruptions in the alpha helical structure of IF subunits may be essential for their flexibility.

In addition to their flexibility, another mechanical feature of IFs that distinguishes them from other cytoskeletal filaments is their resistance to breakage. Measurements of the tensile strength of keratin-like IF bundles from hagfish slime show that the longitudinal stiffness of these IFs increases the more they are pulled, and that, consistent with an array of approximately longitudinally-oriented helical subunits, the longitudinal resistance can be greater than the bending stiffness [27]. AFM studies have also been able to stretch single surface-bound IFs bound until they break. Although such studies cannot resolve the force needed to break the IFs they reveal two remarkable structural properties, illustrated schematically in Figure 2. Desmin, keratin K5/K14, and neuronal IFs can each stretch more than 200% before they break, with some filaments stretching 320% [21]. As they stretch, the filaments also become thinner, suggesting that the subunits within the IF can slide past each other to accommodate the unusually large strains. By comparison, F-actin and MTs rupture at even a few % longitudinal strain.

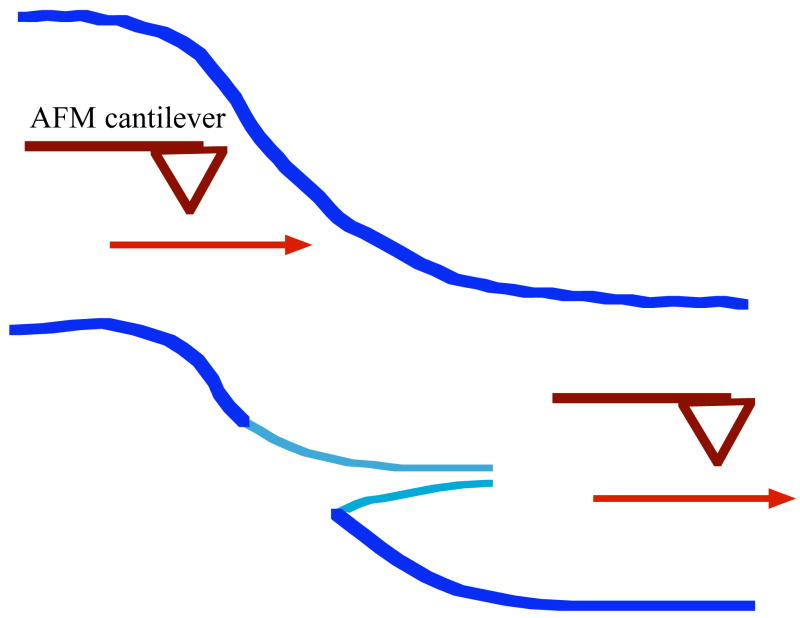
Figure 2. Schematic diagram showing the stretching of a surface bound IF.

subjected to a point force by lateral movement of a rigid silicon-nitride tip of an AFM cantilever as depicted by the arrow. At the point where the AFM contacts the filament, the diameter decreases as the contour length increases. Maximal stretching ratios of 320% were observed with an average strain of 220% reported before the filaments ruptures. Derived from Kreplak et al. [21].

Viscoelasticity of IF networks in vitro

Both the softness of IFs and their resistance to breakage are evident in viscoelastic measurements of macroscopic IF networks. Macroscopic viscoelasticity is generally measured by forming a gel between plates of a rheometer and then measuring the force per unit area (stress) required to deform the sample to a predetermined degree (strain). The ratio of stress to strain is defined as the elastic modulus and usually shear deformations are applied to measure the shear stress G, reported in Figures 3 and 4. For a simple elastic solid the shear modulus is a constant that is independent of the extent of strain or the period of time that the stress is applied. For viscoelastic materials like IF networks the time and strain dependence of G can be used to infer the nature of crosslinks between filaments and the extent of single filament deformation. A practical difficulty in measuring elastic moduli for IF gels is that unless the filaments are crosslinked, they will slide in response to the stress and so dissipate the force and underestimate the elasticity of the filaments. In general tests of IF associated proteins have not revealed sets of efficient IF crosslinkers analogous to the potent F-actin crosslinkers such as filamin or alpha-actinin, and therefore some tests of IF rheology rely on electrostatic interactions between filaments mediated by multivalent counterions to produce transiently crosslinked networks. In particular, NFs have been shown to be efficiently crosslinked after addition of 5 mM Mg²⁺ [12, 28], and measurements of these in vitro networks may be a model for other IFs.

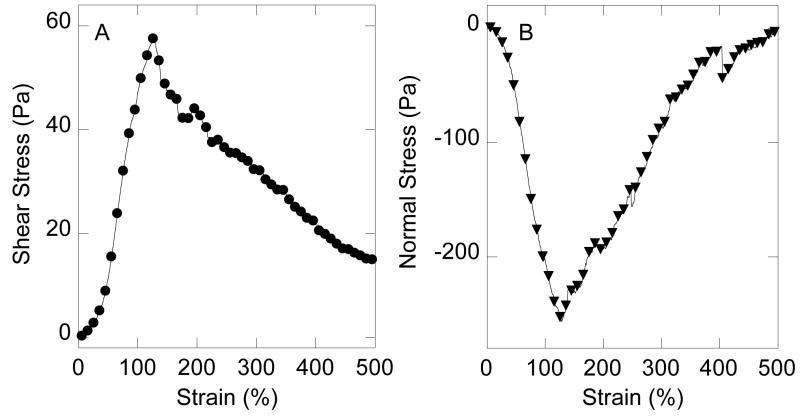
Figure 3. Non-linear elasticity of neurofilament networks.

Neurofilaments (4 mg/ml) were gelled by addition of 5 mM MgCl2 and subjected to increasing shear strain at a rate of 2.5%/s (3A). The resulting shear stress was measured at intervals as the network was deformed. 3B. Simultaneously, a downward force, perpendicular to the plane of shear was measured as the sample was initially deformed, and the resulting normal stress follows a time course similar to that of the non-linearly increasing shear stress shown in Figure 3A. Experimental details are given in [12, 14, 31].

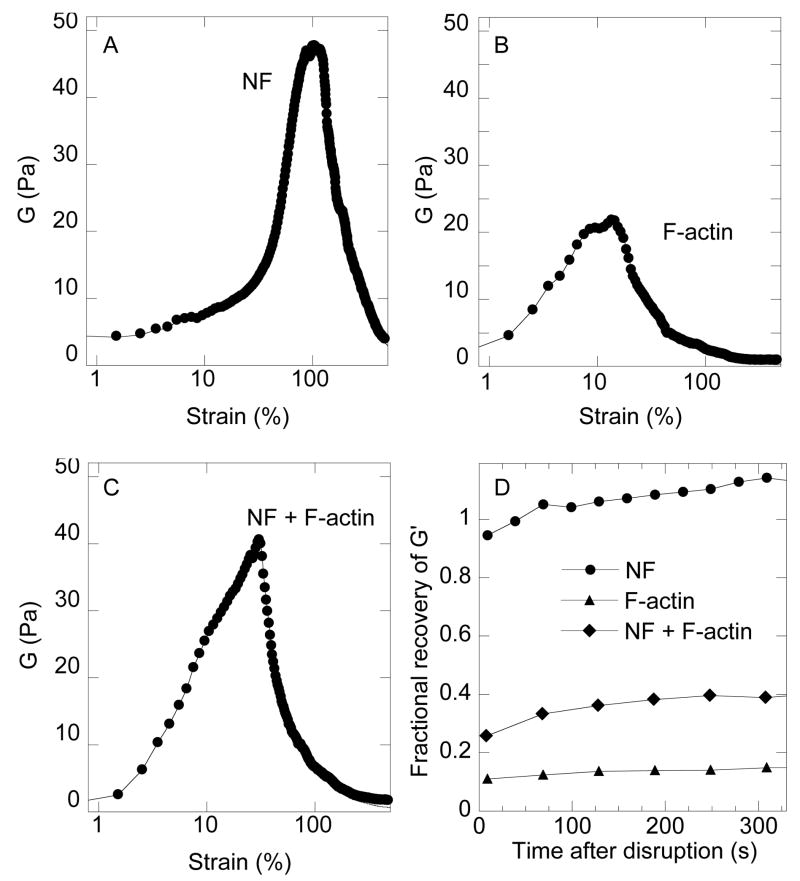
Figure 4. Strain stiffening and recovery of neurofilament networks.

The static shear modulus G is calculated from the ratio of stress to strain from Figure 3 as the sample is increasingly deformed. Similar measurements for 4 mg/ml F-actin with 5 mM MgCl₂ and a mixture of 2 mg/ml NF and 2 mg/ml F-actin (Figures 4B and 4C, respectively). The recovery of the elastic modulus after the sample was returned to its initial configuration is shown in 4D with values of elastic moduli measured at 2% strain normalized to their values before the sample was subjected to large strains.

The strong dependence of IF stiffness with increasing extent of deformation is evident in the plot of shear stress vs. shear strain for a 4 mg/ml NF gel crosslinked by 5 mM Mg²⁺ shown in Figure 3. As the strain increases up to 100% the shear stress also increases, and the upward curvature of shear stress is a signature of strain-stiffening, a generic feature of semiflexible polymer networks [14]. At these very large strains, a few filaments may be particularly highly elongated and provide disproportionately large amounts of resistance. By comparison, actin filament networks of similar concentration would rupture at strains of approximately 10% [29, 30]. Figure 3B shows that NF gels also exhibit the unusual property of negative normal stress, by which they exert a contractile force between the rheometer plates as the shear strain is increased. The normal stress remains negative over the strain range where the shear stress also increases, and returns to near zero when the NF network softens. Negative normal stress is a recently reported general effect in crosslinked semiflexible polymer gels [31], and may play a role in remodeling of NF or other IF networks in response to large deformations such as occur when organelles are transported through the cytoskeletal meshwork.

The combination of softness and durability of NF gels is seen by direct comparison with networks of F-actin and combined networks containing both filament types. Figure 4A shows the shear modulus of an NF gel over a range of strains and compares it to gels of an equal weight concentration of F-actin and a mixture containing 50% by weight of both filament types. The shear modulus of NFs measured at very small strains is similar to that of F-actin, but as the strain increases, so does the shear modulus of NFs, whereas the modulus of F-actin initially also increases but then rapidly decreases at strains above 10% as the filaments either break or buckle. Mixtures containing both filament types show a roughly intermediate property. They stiffen at smaller strains compared to NFs alone, presumably because of the presence of the stiffer F-actin, but also begin to weaken at small strains. The large strains where NFs networks remain intact, correspond to conditions where many filaments are pulled out nearly straight, as estimated by the relation between persistence length and network mesh size [14] and therefore the very large strains (300%) seen in AFM deformations before NFs rupture [21] are required to explain the ability of macroscopic NF networks to resist such large deformations.

Even after the NF networks are strained beyond their yield point by shear strains of 500%, when the sample is returned to rest and then its elasticity is measured at small strain, the values of shear modulus rapidly return to near their initial values (Figure 4D). Similar recovery was also reported for vimentin [13], and keratin [10] but in that case surface activity of the filaments at the air-water interface may also contribute to the recovery observed [10]. In contrast F-actin networks are irreversibly weakened by 500% strain and regain less than 15% of their initial stiffness. Mixtures of NFs and F-actin recover to an intermediate level of 40 % over the 300 s period of measurement. These results suggest that NFs unlike actin can rapidly recover contacts with each other, perhaps by reforming the dynamic interactions between filaments formed by the NF sidearms. The transience of the many possible sidearm interactions may be a mechanism to maintain NF-NF spacing and bonding when the network is subjected to small stresses but then release at large stresses to prevent breakage of the NF contour.

Electrostatic properties of IFs

Intermediate filaments like most biopolymers are negatively charged, and the distance between fixed charges is less than the Bjerrum length, a parameter that sets the length scale where electrostatic energies become larger than the thermal energy kT. For such highly charged filaments, polyelectrolyte effects can lead to filament bundling in the presence of multivalent counterions even in solutions of high ionic strength. The charge density of most intermediate filaments is nearly as high as that of DNA [32]. Neurofilaments in particular have unusual polyelectrolyte properties because in addition to their highly anionic core filament, the sidearms of both the neurofilament medium (NFM) and neurofilament high molecular weight (NFH) chains also have anionic charges that increase strongly as the sidearms become fully phosphorylated. The sequences of these largely unstructured polypeptides create a unique gradient of local negative charge density that is maximal near the filament core and decreases to near neutrality with some regions of net positive charge at the sidearm tip [33]. A possible consequence of polyelectrolyte effects for IF self-assembly is shown in Figure 5, where filament bundle formation, as measured by increasing light scattering intensity, occurs as submillimolar concentrations of the polycation pentalysine are added. These results show that even presumably nonspecific polyvalent cations such as Lys5 can be potent bundling agents, and that dephosphorylated NFs appear to be somewhat more susceptible to bundling by small concentrations of polyvalent cations. The polyelectrolyte effects of IFs are relatively unexplored, but may be relevant to the robust bundle formation in cells that is difficult to reproduce in vivo with purified systems in simple buffers.

Figure 5. Neurofilament bundling by polyvalent cations.

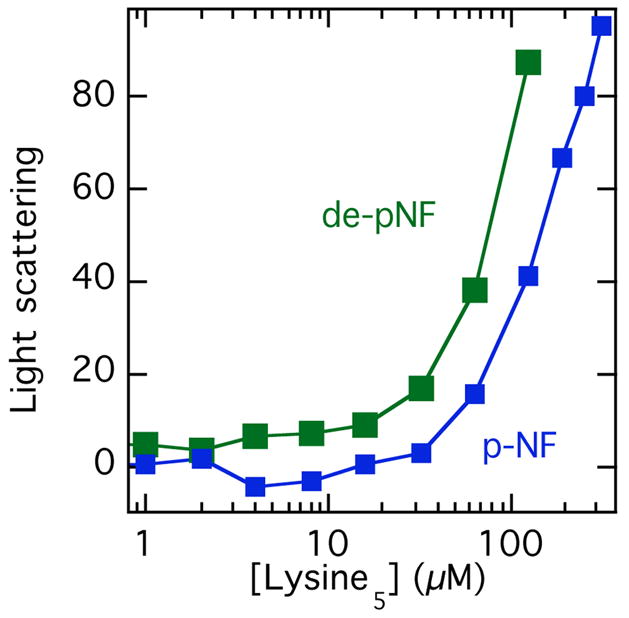
NF bundling, as measured by increased light scattering intensity after adding pentameric lysine oligomers to phospho- or dephospho NF solutions in isotonic salt solutions. Dephospho NFs were prepared by treating native NFs purified from bovine spinal cord with phosphatase, as described in [33].

IF crosslinkers, with emphasis on neurofilaments

As demonstrated by the relative simplicity of preparing samples of IFs for single filament analysis, IF polymers, like F-actin and microtubules do not bind strongly to each other unless filament-filament crosslinks are stabilized electrostatically by multivalent counterions or more specifically by the actions of crosslinking proteins. Neurofilaments and other IFs bearing long C-terminal extensions, sidearms, that extend away from the alpha helical polypeptides forming the IF polymer core have the potential for more complex associations between filaments because they interact with each other to bridge two filaments.

IFs can form mechanically relevant links to each other, to other cytoskeletal filaments, to membrane complexes, and to internal organelles. These links are mediated by specific proteins connecting the two structures at constant distances determined by their length and the occurrence of binding sites at opposite ends of the crossbridging molecule. Such crossbridges include microtubule-associated proteins (MAPs) [34], molecular motors [35–40], and a class of large proteins related to spectrin and plakins such as plectin and BPAG 1 [41] [42]. In situ, an extensive crossbridging between IFs occurs in the large gliofilament bundles of astrocytes [43], in keratins of hair follicles [44, 45] and in neurofilaments (NFs) within neurons [46]. The large extent of crossbridges per unit length of NF polymers depends on the molecular composition of NFs in which lateral projections from the NFH and NFM carboxyterminal tail domains provide both attractive [28] and repulsive [47] interactions between NFs. The mechanisms of direct interactions between the NF tail domains and other NFs or other cytoplasmic structures may constitute a model for the presumed functions of several other members of the IF family such as nestin and synemin that also have long carboxyterminal tail domains.

Since the first evidence of extensive NF crossbridging in situ [46, 48], the role of the NF sidearm has been difficult to characterize. Some studies suggest that the high phosphorylation level of NF tail domains may induce an electrostatic repulsion between adjacent polymers, their spacing being regulated by the phosphorylation level of the NF projections [49]. On the other hand, in vitro experiments using purified native NFs suggest specific although weak interactions between single polymers, an effect that is essential to the purification procedure for native NFs from spinal cord extracts [28]. In vitro NFs can form very long birefringent arrays in which individual NFs run parallel to each others, similar to the NF bundles in situ [28]. Since NFs are very flexible polymers like all other types of IFs [20], such an organization is highly suggestive of a large number of binding sites between NFs over long distances. In addition, synthetic peptides containing one (inhibition) or two (activation) Lys-Ser-Pro hexaaminoacid repetitive sequences of the NFH tail domain affect NF gelation in opposite manners [50]. These data suggesting that antiparallel NF projections may overlap their repetitive Lys-Ser-Pro central domains are in agreement with the observation that NF interactions are strongly regulated by the phosphorylation of these sites both in vitro and in situ [12, 51].

The two effects, long-range repulsion due to steric and electrostatic forces and short-range attraction due to multiple but dynamic interactions between specific sites within the NF sidearms both appear to be important in defining the interactions of NFs and potentially other IFs with each other. As a result, the NF sidearms may both set the distance between NFs and other filaments as well as organize and stabilize these interactions [52]. An interplay between attractive and repulsive interactions may be required in vivo for the renewing of NFs along the axon by their active MT-dependent transport and for the dynamic incorporation of single NFs within bundles [53, 54]. The multiple dynamic interactions between NFs may also account for the unusual ability in vitro to rapidly reform elastic networks after extensive fluidization and deformation of the network structure as seen in Figure 4.

Conclusions and future directions

The mechanical properties of intermediate filaments may be essential to some of their biological functions because they are so different from those of other cytoskeletal polymers. IFs of all kinds are much more flexible than either actin filaments or microtubules and they are much more resistant to breaking as they are bent or elongated. Both of these properties relate to the unique structure of extensively overlapping alpha helical coiled-coil subunits interrupted by more flexible polypeptide linking sequences. Several recent studies, largely guided by use of atomic force microscopes to image and manipulate IFs have led to quantitative description of IF elasticity. A challenge for future studies is to define how IFs are linked to each other and to other structures within the cells to produce the networks seen in vivo that provide cells with their ability to accommodate deformations without damage.

Abbreviations

AFM

atomic force microscopy

IF

intermediate filament

NF

neurofilament

NFH

neurofilament high molecular weight chain

NFM

neurofilament medium molecular weight chain