Signal Propagation in Drosophila Central Neurons

Abstract

Drosophila is an important model organism for investigating neural development, neural morphology, neurophysiology, and neural correlates of behaviors. However, almost nothing is known about how electrical signals propagate in Drosophila neurons. Here, we address these issues in antennal lobe projection neurons, one of the most well studied classes of Drosophila neurons. We use morphological and electrophysiological data to deduce the passive membrane properties of these neurons and to build a compartmental model of their electrotonic structure. We find that these neurons are electrotonically extensive and that a somatic recording electrode can only imperfectly control the voltage in the rest of the cell. Simulations predict that action potentials initiate at a location distant from the soma, in the proximal portion of the axon. Simulated synaptic input to a single dendritic branch propagates poorly to the rest of the cell and cannot match the size of real unitary synaptic events, but we can obtain a good fit to data when we model unitary input synapses as dozens of release sites distributed across many dendritic branches. We also show that the true resting potential of these neurons is more hyperpolarized than previously thought, attributable to the experimental error introduced by the electrode seal conductance. A leak sodium conductance also contributes to the resting potential. Together, these findings have fundamental implications for how these neurons integrate their synaptic inputs. Our results also have important consequences for the design and interpretation of experiments aimed at understanding Drosophila neurons and neural circuits.

Introduction

The fruit fly Drosophila melanogaster is an increasingly important model organism for studying neural circuits, but we lack a clear idea of how electrical signals propagate in Drosophila central neurons. Like most insect central neurons, they generally have a unipolar morphology with the soma separated from the rest of the cell by a long neck of membrane (see Fig. 1A). Therefore, synaptic potentials traveling to the spike initiation zone (SIZ) bypass the soma. Studies of neurons in locusts, moths, and blowflies have found that signals often propagate poorly from the dendrites (Borst and Haag, 1996; Christensen et al., 2001; Peron et al., 2007). This is relevant because most recordings of Drosophila central neurons are made at the soma. However, fruit flies are 100-fold smaller than blowflies and >1000-fold smaller than locusts. One might reasonably ask whether action potentials are necessary for synaptic inputs to propagate to the axon terminal.

Figure 1.

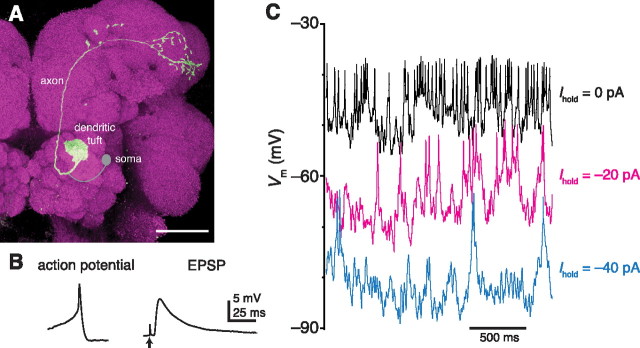
Characteristic features of Drosophila antennal lobe projection neurons. A, Morphology of an antennal lobe PN. Cell fill (biocytin) is in green, neuropil marker (nc82) is in magenta (maximum z-projection of a confocal stack). The soma and primary neurite were removed when the recording pipette was retracted so they are shown schematically in gray. Scale bar, 50 μm. B, Comparison of an action potential and a unitary EPSP recorded from a Drosophila PN. The PN was depolarized to −40 mV to elicit the action potential, and the EPSP was recorded at −65 mV. The EPSP is an average of 10 sweeps. The stimulus artifact is indicated by an arrow. C, Recordings of spontaneous activity in current-clamp mode with different levels of holding current. Note that action potentials persist even when the soma is hyperpolarized.

A related question is the true resting potential of Drosophila central neurons. The resting potential sets the driving force for synaptic currents and controls the activation of voltage-gated conductances. Recent studies of Drosophila neurons in situ report resting potentials between −50 and −60 mV (Rohrbough and Broadie, 2002; Choi et al., 2004; Jiang et al., 2005; Gu and O'Dowd, 2006; Park and Griffith, 2006; Sheeba et al., 2008a,b). These values are more depolarized than the potassium reversal potential (generally the major determinant of the resting potential), but the reasons for this are unknown. Accurately measuring the true resting potential is fundamental for understanding electrical signaling in these neurons and discriminating between physiological and pathological recording conditions.

To address these issues, we focused on projection neurons (PNs) of the Drosophila antennal lobe. Many studies have investigated the development, morphology, synaptic inputs, and sensory responses of antennal lobe PNs (for review, see Jefferis and Hummel, 2006; Hallem et al., 2006; Fiala, 2007; Olsen and Wilson, 2008a). They have stereotyped morphologies (Jefferis et al., 2001; Marin et al., 2002; Wong et al., 2002) and physiological responses (Ng et al., 2002; Wang et al., 2003; Wilson et al., 2004). Recordings can be made from functionally equivalent PNs in different experiments by labeling them with green fluorescent protein (GFP) (Olsen et al., 2007; Schlief and Wilson, 2007; Datta et al., 2008; Kazama and Wilson, 2008; Murthy et al., 2008; Olsen and Wilson, 2008b).

In the first part of this study, we investigate how electrical signals propagate in PNs. We use morphological and electrophysiological data to model a PN as a series of passive electrical compartments. This model allows us to predict membrane voltages at experimentally inaccessible locations based on experimental measurements at accessible locations. We use this model to investigate three questions. First, how effectively can a somatic electrode control the voltage throughout the cell? Second, where in the cell do spikes initiate? Third, how well do synaptic events propagate from the dendrite? In the second part, we investigate what influences the apparently depolarized resting potential in Drosophila antennal lobe PNs.

Materials and Methods

Fly stocks.

Flies were raised on standard cornmeal agar medium. Recordings from DM1 PNs were made from NP5221-Gal4,UAS-CD8GFP flies (Tanaka et al., 2004), and all other recordings were made from either GH146-Gal4,UAS-CD8GFP (Stocker et al., 1997) or NP3062-Gal4,UAS-CD8GFP (Kazama and Wilson, 2008). The NP fly lines are available from the Drosophila Genetic Resource Center (Kyoto Institute of Technology, Kyoto, Japan). All experiments were performed with adult female flies that were 2–10 d after eclosion.

Electrophysiology.

Whole-cell patch-clamp recordings from antennal lobe PNs were made as described previously (Wilson and Laurent, 2005). The antennae were acutely removed for all experiments except those in Figures 1C and 7. The brain was perfused with a saline solution containing (in mm): 103 NaCl, 3 KCl, 5 N-Tris(hydroxymethyl)methyl-2-aminoethane-sulfonic acid, 8 trehalose, 10 glucose, 26 NaHCO₃, 1 NaH₂PO₄, 1.5 CaCl₂, and 4 MgCl₂ (osmolarity adjusted to 270–275 mOsm). The saline was bubbled with 95% O₂/5% CO₂ gas for a final pH of 7.3. For the sodium exchange experiments, NaCl was replaced by 103 mm N-methyl-d-glucamine and 103 mm HCl. For the chloride exchange experiments, NaCl and KCl were replaced with sodium gluconate and potassium gluconate, respectively; the ground electrode in these experiments was placed inside a large patch pipette containing 3 m KCl under positive pressure (see below). Tetrodotoxin (TTX; EMD Biosciences) was added from a stock solution in citrate buffer for a final concentration of 1 μm in the saline reservoir. A stock solution of digoxin (Sigma) in water was made immediately before the experiment and diluted in the saline reservoir to a final concentration of 100 μm.

Figure 7.

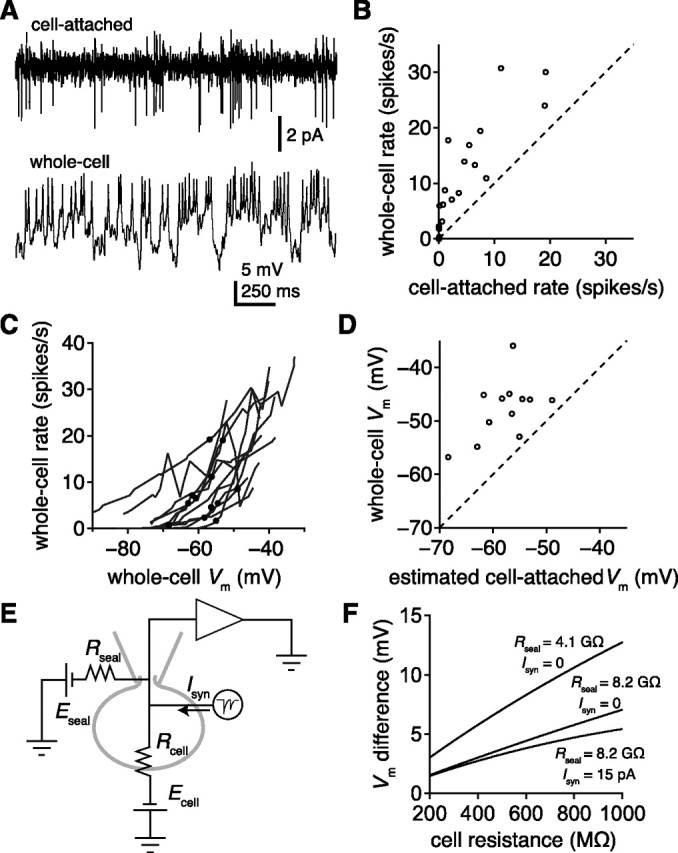
The seal conductance can explain why cells are depolarized in whole-cell mode. A, Cell-attached (top) and whole-cell (bottom) recordings of spontaneous activity from the same PN. Subthreshold fluctuations (bottom) reflect spontaneous synaptic input from ORNs. B, Comparison of spontaneous PN firing rates in whole-cell mode versus cell-attached mode (n = 27 cells). C, Relationship between firing rate and V_m measured in whole-cell mode. V_m was varied by injecting different amounts of holding current. Each gray line represents a different cell. Black dots indicate where the whole-cell rate matched the cell-attached rate of that cell (n = 12 cells). D, Comparison of estimated V_m in cell-attached mode (black dots from C) and the whole-cell V_m recorded in the same cells with no injected current. E, Equivalent circuit model of the cell in the whole-cell configuration (see Materials and Methods). F, Predicted difference in V_m after the switch from cell-attached to whole-cell mode. The difference decreases with a higher seal resistance (R_seal), here modeled as the median of our measurements or else half that value, and also decreases in the presence of synaptic input current (I_syn).

Patch-clamp electrodes were filled with an internal solution consisting of the following (in mm): 140 potassium aspartate, 10 HEPES, 1 EGTA, 4 MgATP, 0.5 Na₃GTP, 1 KCl, and 13 biocytin hydrazide (adjusted to 265 mOsm and pH 7.3). For the current-clamp recordings in Figure 3, data were gathered with an AxoClamp 2B amplifier (Axon Instruments), low-pass filtered at 5 kHz with an external 4-pole Bessel filter (Warner Instrument), and sampled at either 20 kHz (current pulse experiments) or 10 kHz (white-noise experiments). The capacitance compensation and bridge balance were used and adjusted optimally. For the white-noise experiments, a time-varying current stimulus (3.2 s duration) was injected into the cells. The stimulus had a time step of 0.1 ms and was constructed by setting its amplitude at each step to a value randomly selected from a Gaussian distribution centered at 0 pA with a SD of 17 pA. This stimulus had an approximately flat power spectrum up to 5 kHz (or half the sampling frequency), after which the power fell off at higher frequencies. For all other experiments, data were collected with an Axopatch 200B amplifier (Axon Instruments), low-pass filtered at 1 kHz, and sampled at 5 kHz or 10 kHz. In cell-attached experiments, action currents were recorded in voltage-clamp mode with a holding potential of 0 mV and filtered at 0.5 kHz. Data were acquired with custom software written in Igor Pro (Wavemetrics).

Figure 3.

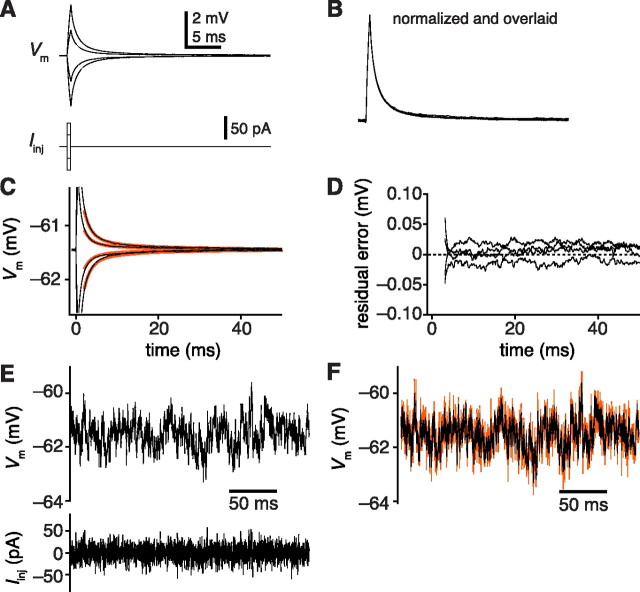
Fitting the electrophysiological properties of the model. A, Membrane potential responses (top, averages of 507 sweeps) to brief current pulses (bottom). B, The same average traces normalized to their peaks. C, Data from A overlaid with the responses of the best fit model (orange). Note that the fit begins 1.5 ms after the end of the current injection pulse. D, Residual error between the data and the model responses shown in C. E, Membrane potential response (top, average of 506 sweeps) to white-noise current injection (bottom). F, Data from E overlaid with the prediction of the model (orange).

All traces are corrected for the liquid junction potential (Neher, 1992). To measure this potential, a ground electrode was made by placing a silver/silver chloride wire inside a large patch-type pipette filled with 3 m KCl. Positive pressure was applied so that KCl solution flowed continuously from the pipette. A recording pipette filled with potassium aspartate internal solution was placed in the bath, which was also filled with a simplified internal solution (omitting MgATP, Na₃GTP, and biocytin hydrazide). The potential difference between these pipettes was set to zero, then the bath fluid was exchanged for the regular external saline solution. The measured potential was observed to increase to +13 mV. Therefore, this potential was subtracted from all our measured intracellular membrane potentials.

In Figure 7, the holding current was set to different levels during different sweeps, and the membrane potential and firing rate were measured for each sweep. To measure the membrane potential, recordings were low-pass filtered with a cutoff frequency of 20 Hz to remove spikes and then averaged over the 4 s sweep. In general, we collected 40–70 sweeps per cell, corresponding to 4–7 holding current levels. We interpolated between these measurements to generate the gray lines in Figure 7C. We estimated the true cell-attached membrane potential by finding the x-value of the point on the gray trace that corresponded to the cell-attached firing rate.

The seal conductance was estimated by clamping the patch to different potentials and measuring the holding current. The relationship between the current and the voltage was fit with a straight line, and the slope of this line was taken as the estimate of the seal conductance.

For the voltage ramp experiments of Figure 8, the ramp command proceeded at 25 mV/s from −93 mV to +7 mV. The resting potential was estimated by fitting the current–voltage relationship with a straight line in a range below the activation of the large inward currents and escaping action potentials, then determining where this line crossed zero.

Figure 8.

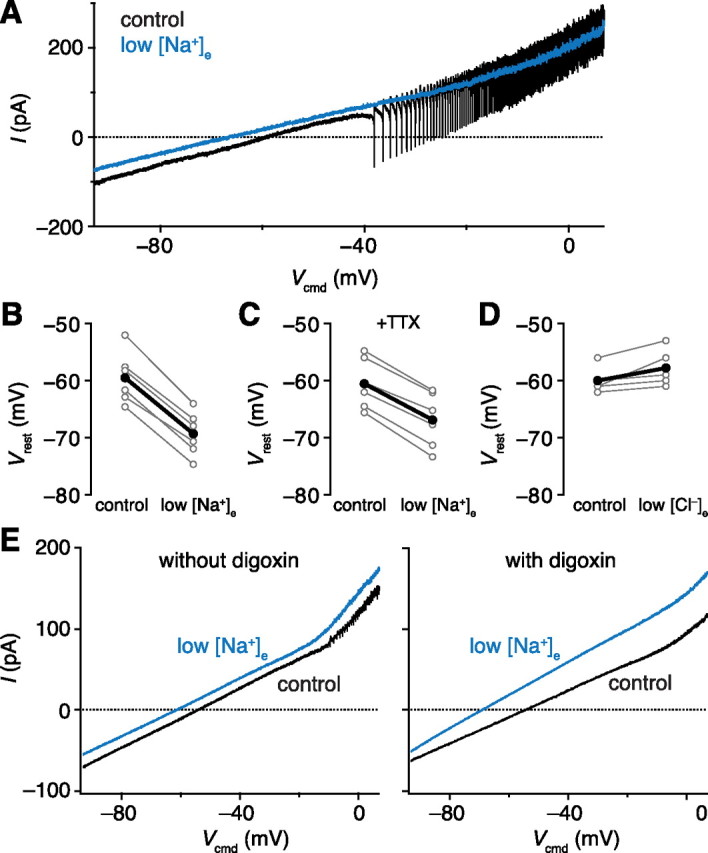
A sodium conductance depolarizes the resting membrane potential of projection neurons. A, Current–voltage relationships measured by a slow voltage ramp command. Single sweeps are shown. B, Resting potentials in control and low [Na⁺]_e (p = 1.25 × 10⁻⁵, paired t test). Individual cells are in gray and averages are in black for B–D. C, Resting potentials in control and low [Na⁺]_e in the presence of TTX (p = 2.13 × 10⁻⁵, paired t test). The hyperpolarization caused by low [Na⁺]_e is significantly smaller in TTX [p = 8.21 × 10⁻⁴, difference = (−5.07, −1.87) mV, unpaired t test]. D, Resting potentials in control and low [Cl⁻]_e (p = 0.0514, paired t test). E, Average current–voltage relationships (n = 6 sweeps) recorded from a representative PN in control and low [Na⁺]_e with and without digoxin. Low [Na⁺]_e caused a statistically significant hyperpolarization in digoxin (n = 5, p = 8.82 × 10⁻⁴, paired t test).

Imaging and morphological reconstruction.

For experiments using identified PNs, cells were filled with biocytin during the recording, and the morphology of the recorded cell was visualized post hoc with biocytin after incubation with 1:1000 streptavidin:Alexa Fluor 568 (Invitrogen) as described previously (Wilson and Laurent, 2005). In addition, the neuropil was visualized with a primary incubation of 1:10 mouse anti-nc82 antibody (Developmental Studies Hybridoma Bank, University of Iowa, Iowa City, IA) and a secondary incubation of 1:250 anti-mouse:Alexa Fluor 488 (Invitrogen). Images were taken on a Zeiss LSM 510 confocal microscope with a 40× or 63× oil-immersion objective. Other images were obtained from Jefferis et al. (2007) at the website FlyBrain@Stanford (http://flybrain.stanford.edu). Images were reconstructed using Imaris (Bitplane), and the morphologies were exported in NEURON format (Hines and Carnevale, 1997). Other reconstructions of the axon endings were taken from Jefferis et al. (2007). All reconstructions were converted to the NeuroML format (Crook et al., 2007).

Synthetic dendritic tufts were generated with a custom program that generated NeuroML files specifying a dichotomously branching structure. Based on our confocal images of actual DM1 tufts, the diameters of the initial branches in the synthetic tufts decreased in size over four levels from 3 to 0.3 μm. All branches beyond the fourth level had diameters of 0.3 μm. The total cytoplasmic volume of each of these tufts was of the same order of magnitude as the cytoplasmic volume in an actual tuft, as estimated by summing the number of pixels whose fluorescence exceeded the background level in confocal images of biocytin-filled PNs (data not shown). The finest branch diameter was chosen to approximately match the diameter of the finest branches in electron microscopic images of the cockroach antennal lobe (Distler and Boeckh, 1997).

A custom program combined the NeuroML files into full DM1 PN morphologies. The combined morphologies were imported into neuroConstruct 1.1.2 (Gleeson et al., 2007) for simulation management.

Modeling the electrotonic structure.

Models were fit in NEURON 6.2 by varying the membrane resistance (R_m), membrane capacitance (C_m), and intracellular resistivity (R_i) to produce the best fit to the data. The membrane parameters were assumed to be uniform across the cell. Morphologies were divided into segments that were each no longer than an electrotonic distance of 0.1, assuming a membrane resistance value of 1 kΩ cm². This value was ∼10-fold smaller than the lowest values produced by the fitting procedure, so the electrotonic lengths of the segments were still shorter in the final models. The model we use for most of the study (Fig. 4B, morphology 2) had 3693 segments. Models were calculated with a fixed time step of 0.01 ms.

Figure 4.

Voltage changes are attenuated as they propagate from the soma. A, The model was used to simulate a voltage step from V_rest in voltage-clamp mode with an electrode at the soma. Steady-state voltage attenuation from the soma is shown for three models having the same morphology (dendrite 2 from B), each independently fit to data recorded from different DM1 PNs. B, Steady-state voltage attenuation from the soma is shown for three models having different dendritic tufts. In other respects, all three models had the same morphology, and all were fit to the same physiological data set (cell 3 from A). For illustrative clarity, we show here (and in Figs. 5, 6) a z-projection of the three-dimensional morphology (Fig. 2).

The recording pipette was modeled as two resistors in series with a capacitor connected from the point between the resistors to ground. The value of each resistor was half the series resistance of the pipette, and the value of the capacitor represented the stray capacitance of the pipette. The series resistance was set to 30 MΩ, and the pipette capacitance was set to 1 pF. Varying these pipette parameters over a wide range produced only small changes in the parameters returned after fitting the model (data not shown). The responses of the model were convolved with a Gaussian filter kernel to recapitulate the external low-pass filtering in the experimental setup.

Fitting the model of the electrotonic structure.

The membrane parameters of the model were determined using the built-in PRAXIS (principal axis) optimization method of NEURON. This algorithm sought a point in the three-dimensional space defined by the free parameters (R_m, C_m, and R_i) that minimized an error function defined as the square difference between the model responses and the averaged experimental responses to current pulses. The procedure ended when the algorithm determined that a particular point represented a minimum. For a given morphology and data set, multiple initial guesses all converged to the same values of the free parameters. The responses to current pulses (0.5 ms duration) of four different amplitudes were fit simultaneously (Roth and Häusser, 2001). The fit interval began 1.5 ms after the end of the current pulse to avoid pipette artifacts (Major et al., 1994) and lasted until 75 ms after the end of the pulse.

Because the conductance of an isolated PN soma is low (data not shown), some fits were performed in which the R_m of the soma and primary neurite was set to a fixed, high value (50 kΩ cm²). In these cases, the values of R_m for the rest of the cell returned by the fitting algorithm were correspondingly lower; however, the overall electrotonic structures were similar. Therefore, all simulations in the Results section use uniform membrane parameters. We also built models of PNs that innervate the glomerulus VM2 and found they appeared to have electrotonic structures that were approximately similar to the DM1 electrotonic structures. However, the VM2 fits converged to values of R_i (>800 Ω cm) that were substantially higher than those reported from a variety of preparations in the literature [30–400 Ω cm, summarized by Borst and Haag (1996)], so we did not pursue further investigations with those models.

We have submitted the DM1 PN model to the publicly accessible ModelDB repository (http://senselab.med.yale.edu/modeldb).

Modeling action potential propagation.

In Figure 5, we voltage-clamped different sites in the model cell with an action potential waveform command. This waveform was obtained from an antennal lobe local neuron (LN). This recorded LN action potential was wider than real DM1 PN action potentials recorded at the soma (which in turn are presumably wider than the action potential waveform at the spike initiation zone because of cable filtering). Therefore, the height and width of the action potential waveform command were scaled so that after the spike propagated to the soma, it matched the height and width of real action potentials recorded from DM1 PNs. The recorded LN action potential was sped up 16-fold and doubled in height to produce the waveform used in Figure 5.

Figure 5.

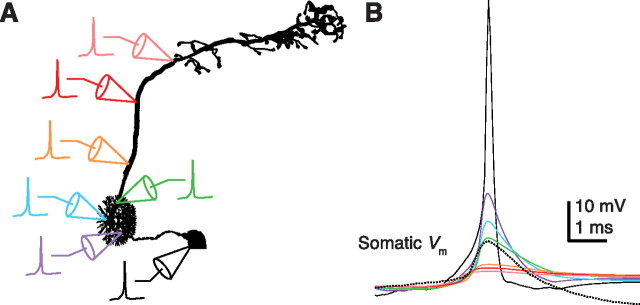
Action potentials likely originate in the proximal axon. A, Locations in the model where the membrane was voltage-clamped with an action potential waveform. Note that all locations are on the soma, primary neurite or axon; the purple, blue, and green electrodes are not in the dendritic tuft. B, Simulated somatic membrane potential resulting from the passive propagation of the action potential waveform from the locations illustrated in A (colored traces). A real action potential recorded from the soma of a DM1 PN is shown for comparison (dotted line). The action potential waveform used for the voltage clamp (black trace) was recorded from the soma of an antennal lobe local neuron; its amplitude was increased and its kinetics were made faster until the somatic potential fit the size and shape of action potentials recorded in PNs (see Materials and Methods).

Modeling synaptic inputs.

Simulated EPSPs were generated with synaptic conductances located at the terminal branches of the dendritic tuft. The reversal potential for the synaptic conductances was set to −10 mV. The time course of the synaptic conductances was determined by the sum of two exponentials. When the synaptic conductance was only at a single site, the time constant of the rise was 0.01 ms, the time constant of decay was 0.6 ms, and the maximum synaptic conductance was 0.1 nS. When the synaptic conductances were on 25 randomly chosen branches, the rise time constant was 0.2 ms, the decay time constant was 1.1 ms, and the maximum synaptic conductance was 2.7 × 10⁻⁴ nS.

Modeling the seal conductance.

The equivalent circuit model shown in Figure 7E is composed of the input resistance of the cell (R_cell), the resting potential (E_cell), the seal conductance (R_seal), the seal reversal potential (E_seal), and incoming synaptic current (I_syn). R_cell was varied, and the change in the membrane potential resulting from the seal conductance was calculated over a range of R_cell values and three values of R_seal. In all calculations, E_cell was set to −65 mV, E_seal to 0 mV, and spontaneous synaptic input was represented by a constant −15 pA current when incorporated. The equation describing the lines in Figure 7F is as follows:

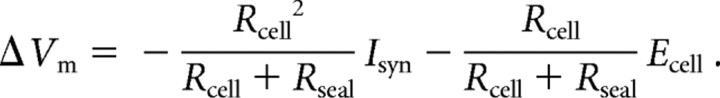Data analysis.

Analyses of electrophysiological data were performed in Igor Pro. Statistical tests were performed using R (Ihaka and Gentleman, 1996). Data are reported as mean ± SEM, and 95% confidence intervals are reported in parentheses.

Results

The soma of a PN connects to a primary neurite that divides into a dendritic branch and an axonal branch (Fig. 1A). Consequently, the soma (which is the only location on the cell accessible to whole-cell patch-clamp electrodes) is distant from the parts of the cell that receive and transmit electrical signals. Action potentials recorded at the soma in current-clamp mode are only 5 to 15 mV in amplitude (Fig. 1B). Assuming that action potentials are >40 mV at the spike initiation zone, this observation suggests that spikes are not initiated near the soma (Hoyle and Burrows, 1973).

In vivo, the dendritic tuft of a PN is bombarded by spontaneous excitatory synaptic input from olfactory receptor neurons (ORNs) (Kazama and Wilson, 2008), and this drives spontaneous action potentials in PNs (Fig. 1C). Hyperpolarizing the soma below −70 mV typically does not completely suppress spontaneous firing (Fig. 1C). This, too, suggests that the soma is distant from the site of spike initiation, and it argues that a somatic electrode can only imperfectly control the voltage at other locations in the cell.

Nevertheless, some signals appear to propagate effectively to the soma. Unitary synaptic potentials and even miniature synaptic potentials can be observed in somatic recordings (Kazama and Wilson, 2008). Indeed, action potentials are so small and unitary synaptic potentials are so large that their amplitudes at the soma are approximately comparable (Fig. 1B). Together, these observations imply that the relationship between the soma and the other compartments of the cell is different from the arrangement in most vertebrate neurons.

Some of these features are common to many insect neurons. However, models of other invertebrate neurons (Edwards and Mulloney, 1984; Borst and Haag, 1996; Christensen et al., 2001; Tobin et al., 2006; Peron et al., 2007) may not completely generalize to Drosophila neurons. For example, unitary synaptic events are visible in somatic recordings from Drosophila antennal lobe PNs, whereas somatic recordings from neurons in larger insects generally do not reveal unitary synaptic events (but see Crossman et al., 1971). Therefore, we sought to develop a model of the electrotonic structure of a Drosophila antennal lobe PN.

Modeling the morphology

As a first step, we modeled the morphology of Drosophila antennal lobe PNs. We focused on an identified class of PN, defined as having a dendritic tuft innervating glomerulus DM1. We could not collect morphological and electrophysiological data from the same DM1 PN because retracting the whole-cell patch pipette after a recording distorts the cell (stretching the primary neurite and typically detaching the soma). Instead, we took advantage of the stereotypy of these cells and collected morphological data from multiple DM1 PNs in different preparations. These data are available at http://flybrain.stanford.edu and in supplemental Images 1–4, available at www.jneurosci.org as supplemental material. The final model (Fig. 2A) was constructed by selecting a typical exemplar for each subcellular compartment and joining these compartments together using custom software (see Materials and Methods) (supplemental Fig. 1, available at www.jneurosci.org as supplemental material).

Figure 2.

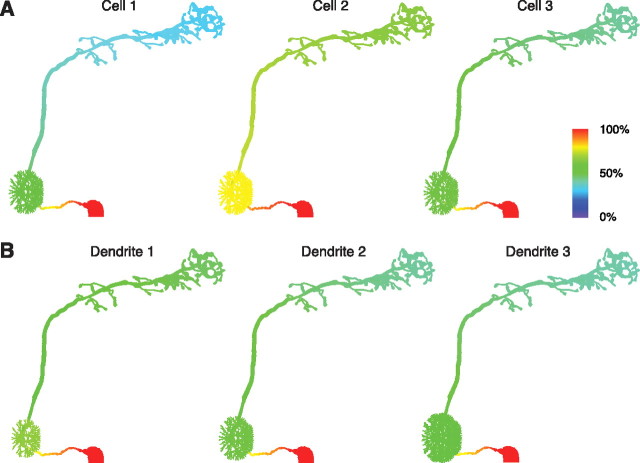
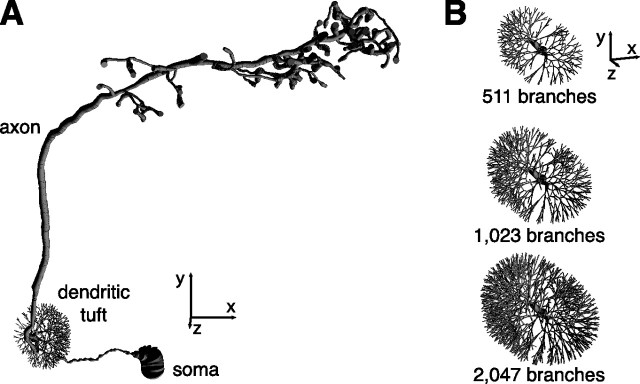
Modeling projection neuron morphology. A, Model of a DM1 PN. All axes are 20 μm. B, Synthetic dendritic tufts used in PN models. All axes are 10 μm.

The dendritic tuft of a PN contains many fine branches, numbering in the hundreds or possibly more (see supplemental Images 1–4, available at www.jneurosci.org as supplemental material). The structure of this tuft is too fine to visualize with conventional light microscopy. Therefore, we instead constructed synthetic dendritic tufts and incorporated them into our model. Although the coarse structure of the tuft is constrained by data, the fine structure is necessarily arbitrary. We, therefore, varied the fine morphology of the dendritic tuft systematically (Fig. 2B) (see also Materials and Methods) and measured how this affects the electrotonic structure of the cell. The impact of fine dendritic morphology on our model is described below.

We divided the model cell into several thousand segments (see Materials and Methods), each with its own length (l), surface area (a), and cross-sectional area (A). Each segment contains a pathway for intracellular current flow, modeled as a resistor (r_i) and a pathway for current flow across the membrane, modeled as a resistor (r_m) and a capacitor (c_m) in parallel. The electrical behavior of each segment depends only on its geometry (l, a, and A) and on properties that are independent of the geometry of the cell and are assumed to be passive and uniform throughout the cell (R_i, the specific intracellular resistivity; R_m, the specific membrane resistance; and C_m, the specific membrane capacitance):

• r_i = R_i · l/A

• r_m = R_m /a

• c_m = C_m · a.

These three geometry-independent properties (R_i, R_m, C_m) are the free variables in our model.

Fitting the membrane parameters of the model

We next determined the properties (R_i, R_m, C_m) that best matched the electrophysiological responses of the cell. We gathered electrophysiological data to constrain these properties by recording from GFP-labeled DM1 PNs in current-clamp mode, injecting brief (0.5 ms) square pulses of current, and recording the membrane potential responses (Fig. 3A). To ensure that the membrane was responding passively, we used only small current injections. Normalized and overlaid, the responses evoked by four different current pulse amplitudes are indistinguishable (Fig. 3B), confirming that responses were purely passive.

Next, we varied R_i, R_m, and C_m to find the best fit to our electrophysiological data. All three properties were varied simultaneously using the NEURON modeling environment (see Materials and Methods). The fitting algorithm converged to values that produced good fits to the data (Fig. 3C). The difference between the model prediction and the mean membrane potential response was small (Fig. 3D) and much less than the SEM of the data.

In the same cells, we also injected an approximate white-noise current which fluctuated at many frequencies (Fig. 3E). The data we recorded in response to this stimulus served as an independent check on the ability of our model to predict how the cell would respond to many frequencies of current injection. Because the white-noise stimulus has a mean value of zero, it also ensures that the membrane potential does not deviate from rest for more than a few milliseconds and thereby helps prevent activation of voltage-dependent conductances (Wright et al., 1996). The models produced from fitting to square current pulses also accurately predicted the responses to white-noise current injection (Fig. 3F). This strengthens the conclusion that our model is a good description of the behavior of these cells in their linear (passive) regime.

Finally, we asked whether other models could explain our data equally well. We varied R_i, R_m, and C_m around the values returned by the fitting procedure to generate an array of alternative models. For each model, we generated a predicted response to step current injections and compared the error between our data and the model prediction (supplemental Fig. 2, available at www.jneurosci.org as supplemental material). The error function had a distinct minimum at the original best fit values and was sensitive to changes in all three parameters. Therefore, our model is a unique solution within the parameter space we have explored. This model allows us to ask how electrical signals propagate throughout the cell.

Attenuation of somatic voltage changes

How effectively can an electrode at a PN soma control the voltage in other cellular compartments? This is an important question for the design of electrophysiological experiments because the soma is the only location in these cells that is accessible to a patch-clamp electrode. To address this question, we introduced a voltage change at the soma of our model and examined the steady-state attenuation of this signal throughout the cell. We found that the somatic voltage change can propagate to the dendritic tuft and the axonal arbor. However, it is substantially attenuated in the dendrite and severely attenuated in the axon (Fig. 4A). Much of this attenuation occurs along the primary neurite that links the soma with the rest of the cell. If spikes are initiated at some distance from the soma along the primary neurite or in another location even more distant from the soma, this result would help explain why hyperpolarizing the soma to −70 mV sometimes fails to block spike initiation (Fig. 1C).

To explore how variability among cells may affect these conclusions, we recorded from three DM1 PNs and fit models with the same morphology to each of their responses. The fits of these three data sets converged to somewhat different values (Table 1) and so produced somewhat different electrotonic structures with different degrees of steady-state attenuation from the soma (Fig. 4A). This variability could arise from either biological or experimental factors. However, all fitted membrane parameters were in a physiologically realistic range (Table 1), and the same overall pattern of attenuation was observed for all three data sets. Cell 3 produced a model that showed a level of steady-state attenuation across the cell that was intermediate to the other two models, so we used this model in the rest of the study.

Table 1.

Best fits of three different DM1 electrophysiological recordings

	Rm (kΩ cm2)	Cm (μF cm−2)	Ri (Ω cm)
Cell 1	8.3	2.6	163.9
Cell 2	20.4	1.5	102.5
Cell 3	20.8	0.8	266.1

We next investigated how the geometry of the dendritic tuft affects the electrotonic structure of the model. We fit three morphological models having different tufts to the same electrophysiological data set (Fig. 4A, cell 3). Changing the size of the tuft caused systematic shifts in the parameters generated by the fitting procedure (Table 2). For example, increasing the size of the tuft produced somewhat larger values of R_m to compensate for the decreased overall membrane resistance caused by larger surface area. However, these changes had little impact on the overall electrotonic structure of the cell (Fig. 4B). Therefore, we focused on a single geometry (Fig. 4B, dendrite 2) in the rest of our investigations with the model.

Table 2.

Modeling different dendritic tufts

	Dendrite 1	Dendrite 2	Dendrite 3
Number of tuft branches	511	1023	2047
Total length (μm)	2157	3181	5229
Total surface area (μm2)	7343	8308	10,238
Rm (kΩ cm2)	19.2	20.8	26.4
Cm (μF cm−2)	0.80	0.79	0.61
Ri (Ω cm)	224	266	311

Attenuation of action potentials

What is the location of the SIZ in these cells? We assume that spikes are large at the SIZ (although we cannot directly test this assumption); if so, the SIZ must be somewhat distant from the soma. It should be noted that somatic recordings from some types of Drosophila neurons (e.g., antennal lobe local neurons) reveal action potentials >40 mV in amplitude; these cells presumably differ from antennal lobe PNs in having a shorter electrotonic distance between the SIZ and the soma. We used an action potential recorded from an antennal lobe local neuron as the basis for modeling the spike waveform at the SIZ of a PN (see Materials and Methods). We voltage-clamped the model cell with this waveform at different locations along the axon and measured the resulting potentials at the soma (Edwards and Mulloney, 1984). Clamping the membrane potential at different sites (Fig. 5A) produced varying degrees of attenuation in the soma (Fig. 5B). Placing the clamp in the soma or primary neurite produced an action potential in the soma that was larger and faster than those observed experimentally. Placing it more distally produced smaller, slower spikes and was in better agreement with the data. The best fit was obtained when the spike initiated near the start of the axon, just distal to the location where the primary neurite bifurcates into the axonal and dendritic branches. This suggests that the SIZ lies near this site. Because all spikes recorded in the same PN have a similar size, it seems probable that spikes initiate from only one location, unlike in some other insect neurons (Heitler and Goodman, 1978).

Attenuation of synaptic potentials

The dendritic tuft of a PN receives excitatory synaptic input from ORNs. Unitary ORN–PN synaptic events in the PN dendrite produce relatively large EPSPs at the soma. ORN synaptic inputs are the only source of large, fast EPSPs in PNs (Olsen et al., 2007; Kazama and Wilson, 2008). How well do these EPSPs propagate from the dendritic tuft to other locations in the cell? In other words, how large must these EPSPs be in the dendrite to produce the large EPSPs we record in the soma? To address this question, we simulated synaptic input to the dendritic tuft of our model PN. We varied the amplitude and kinetics of synaptic conductances in the dendrite and tried to produce simulated EPSPs that, after propagation to the soma, matched the properties of real unitary EPSPs recorded with a somatic electrode.

We initially modeled an ORN–PN synapse as a conductance placed on a single terminal branch in the PN dendritic tuft. The resulting unitary EPSP decayed to 10% of its original amplitude when it reached the soma (Fig. 6A,B). As a consequence, this model could not generate unitary somatic EPSPs resembling those we recorded in response to single-axon stimulation. Even when the membrane potential of the dendritic branch reached an extreme value equal to the reversal potential of the synaptic conductance, the amplitude of the EPSP in the soma was only half that observed experimentally (Fig. 6A). This suggests that a unitary ORN–PN synapse is unlikely to be confined to a single PN dendritic branch.

Figure 6.

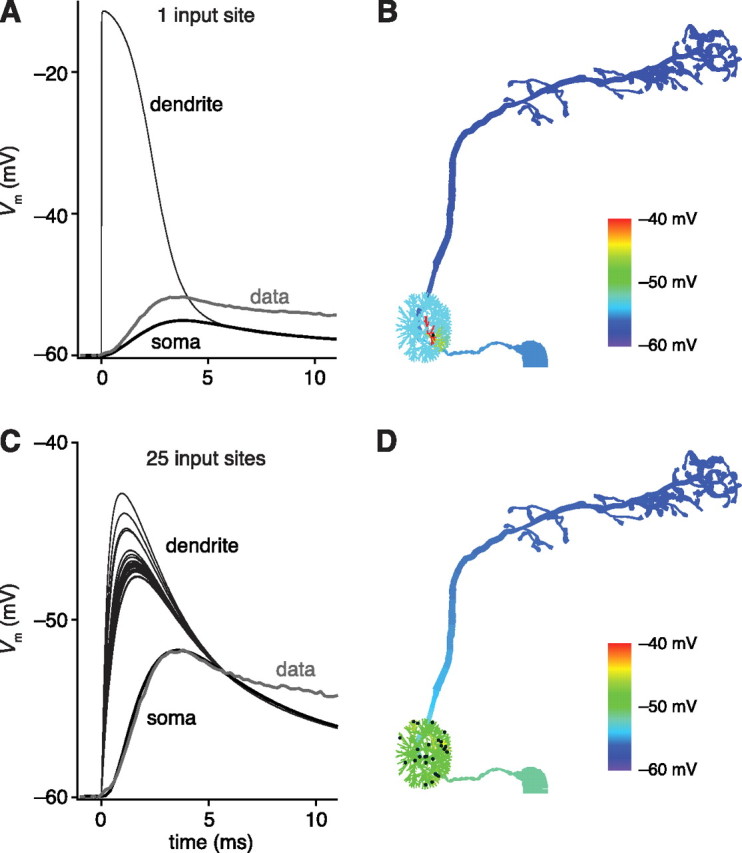
Spatially distributed synaptic contacts can account for large somatic EPSPs. A, When synaptic current is generated at only one dendritic site, a simulated EPSP propagates poorly to the soma. Even when the dendritic EPSP is as large as possible (nearing the reversal potential for the synaptic conductance), the resulting somatic EPSP is much smaller than an experimentally measured unitary EPSP. B, Peak membrane potential at each location in the cell resulting from synaptic current is generated at only one dendritic site (as in A). The black dots indicate the branches with synapses in B and D. C, When synaptic conductances are distributed randomly among 25 terminal branches, the simulated dendritic EPSPs sum effectively to produce a large somatic EPSP. Dendritic EPSPs can be reasonably small and can be tuned to produce a somatic event that fits the data. D, Peak membrane potential at each location in the cell resulting from activation of synaptic conductances on 25 branches across the dendritic tuft. In tuning all these simulations, we did not attempt to fit the late phase of the EPSP, because it is contaminated by lateral excitation (Olsen et al., 2007; Kazama and Wilson, 2008).

Next, we asked what happens when the unitary synaptic conductance is distributed across many terminal branches. Each ORN-to-PN synapse corresponds to many presynaptic vesicular release sites (10 to 50, depending on the glomerulus and the method of estimation) (Kazama and Wilson, 2008), and it is reasonable to imagine that these release sites could be divided among multiple dendritic branches. In an extreme case, each release site could be situated on a different branch. Therefore, we tried modeling the synapse as 25 identical synaptic conductances distributed across 25 dendritic branches. With this model, we were able to tune the amplitudes and kinetics of these 25 conductances to generate a somatic EPSP that matched the kinetics and amplitude of an experimentally measured EPSP (Fig. 6C,D). This result argues that a single ORN axon distributes release sites onto multiple dendritic branches of each postsynaptic PN. This distributed model would explain why EPSPs propagate so well to the soma. In this model, EPSPs also propagate more effectively into the initial part of the axon (Fig. 6D) as compared with the single-site model. Nevertheless, EPSPs still did not cause substantial voltage changes at the axon terminals, implying that action potentials are indeed necessary for synaptic output in PNs.

Finally, as a check on our model, we asked if it could accurately predict the appearance of miniature EPSCs (mEPSCs) recorded at the soma. Based on the fit to unitary EPSPs measured at the soma, the model makes a prediction about the amplitude and kinetics of the underlying quantal conductances, assuming that each of the 25 dendritic sites corresponds to a single presynaptic release site. We simulated a voltage-clamp experiment in the model cell (V_hold = −65 mV) and asked what currents measured at the soma would result from a single quantal conductance in the dendrite. The model predicted that mEPSCs should have an amplitude of ∼1.5 pA and a rise time of ∼1 ms. This prediction is an excellent match to mEPSCs measured in PNs in the presence of TTX, as well as estimates of quantal amplitude based on multiple-probability fluctuation analysis (Kazama and Wilson, 2008). Note that our model does not generate a strong prediction about the precise number of release sites per ORN axon, nor does it imply that every release site is necessarily situated on a different branch; rather, it simply argues that release sites are likely to be distributed among many branches.

Determining the resting membrane potential

Because a passive electrical model by definition has no voltage-dependent components, it can only generate predictions about the relative differences in the membrane potential across the cell. The absolute membrane potential determines the size of voltage-gated and synaptic currents and the probability of action potential initiation. Therefore, it is important to measure accurately the absolute resting membrane potential of Drosophila neurons. Reported values for the resting potential of Drosophila neurons vary widely, from −25 mV (Wu et al., 1983) to −70 mV (Byerly and Leung, 1988).

To estimate the resting potential in intact PNs, we took advantage of the fact that these neurons typically fire spontaneously in vivo when ORN inputs are intact, reflecting ongoing synaptic input from receptor neurons. Spike rates can be monitored in PNs extracellularly, in cell-attached mode (Fig. 7A). Because the spontaneous firing rate depends on the resting membrane potential, we can use the firing rate in cell-attached mode as a way to estimate the true resting potential of these neurons. PN firing rates generally increased immediately after rupturing the membrane patch beneath the pipette (Fig. 7A,B), implying that the resting potential measured in whole-cell mode is somewhat more depolarized than the resting potential in intact neurons. We varied the holding current in whole-cell mode to alter the firing rate of the cell to find the somatic potential where the whole-cell firing rate matched the cell-attached rate (Fig. 7C). On average, we had to hyperpolarize the membrane from −47.8 ± 1.6 mV to −57.8 ± 1.5 mV to recapitulate the cell-attached firing rate (n = 12) (Fig. 7C,D). Thus, the true value of the resting potential (the estimated cell-attached membrane potential, based on the cell-attached firing rate) is likely to be ∼10 mV less depolarized than what we measure at the soma in whole-cell mode. Because somatic voltage changes are attenuated in the rest of the cell, the SIZ and dendrite are likely to sit closer to their true resting potential during a whole-cell recording than the soma does.

Why does the cell depolarize upon whole-cell break-in? The change in the firing rate occurs as fast as we can measure it, so it is unlikely to result from intracellular dialysis with the pipette solution. A more likely scenario is that breaking into the cell introduces current flow through the cell membrane adjacent to the pipette (the seal). The resistance of the seal is generally high compared with the resistance of the cell, so current flow through the seal has little impact on the resting potential in most neurons. However, Drosophila neurons are extremely small and have high input resistances (598.0 ± 69.3 MΩ, n = 14, measured with antennae removed). As the input resistance approaches the seal resistance, the current flow through the seal resistance has a proportionately larger effect. We, therefore, considered how the seal resistance would affect the measured resting potential using a simple equivalent circuit model (Fig. 7E). Taking values for the seal resistance (10.1 ± 1.6 GΩ, n = 13) and cell resistance from experimental measurements, this model predicts that the transition to a whole-cell configuration will depolarize a PN by several millivolts, with the exact magnitude of this effect depending on the input resistance and the level of ongoing synaptic input to the cell (Fig. 7F). Thus, the seal conductance can explain the discrepancy between the cell-attached and whole-cell firing rates. This partially accounts for why depolarized resting potentials are consistently reported in Drosophila literature.

Ionic mechanisms underlying the resting potential

Even after correcting for the seal conductance, PNs rest substantially depolarized to the potassium reversal potential (E_K, equal to −97 mV for our solutions). Therefore, we hypothesized that other currents contribute to the resting potential. We recorded from PNs in voltage clamp and used slow voltage ramp commands to estimate the resting potential by determining the potential at which zero net current flows (Fig. 8A). We then altered the ionic composition of the external saline and measured how this affected the resting potential.

When we lowered the external sodium concentration ([Na⁺]_e), the resting potential was hyperpolarized by ∼10 mV (Fig. 8B). This suggests that a resting sodium current contributes to the depolarized resting potential of PNs. The effect of lowering [Na⁺]_e was partially blocked by TTX (Fig. 8C). This implies that TTX-sensitive and TTX-insensitive channels both contribute to the resting sodium conductance. Lowering [Cl⁻]_e did not significantly change the resting membrane potential (Fig. 8D), so we conclude that there is little chloride current flowing at rest in PNs.

We also considered an alternative explanation for the effects of lowering [Na⁺]_e—namely that we might be affecting the sodium/potassium pump rather than a sodium-permeable channel. Each cycle of this pump exchanges three sodium ions from inside the cell with two potassium ions from outside the cell and so generates an outward current (Thomas, 1972); when [Na⁺]_e is lowered, the driving force on the pump would increase. To test this possibility, we measured the effect of low [Na⁺]_e in the presence of digoxin, a blocker of the sodium/potassium pump. Lowering [Na⁺]_e still hyperpolarized the membrane potential (Fig. 8E), suggesting that the effect is unlikely to result from a change in the pump current.

Discussion

Here, we show that many characteristic physiological features of Drosophila antennal lobe PNs follow straightforwardly from the morphologies of these neurons, given physiologically plausible passive membrane properties. These results better define the context for designing and interpreting electrophysiological experiments in these neurons. They also have important implications for how these neurons integrate their synaptic inputs. Our results are likely to generalize to other Drosophila neurons that have the same approximate size and overall morphology as antennal lobe PNs.

Implications of the electrotonic model

Drosophila neurons are much smaller than the well studied neurons of larger invertebrates. Nevertheless, our results argue that the electrotonic size of Drosophila antennal lobe PNs is comparable with the electrotonic size of those larger neurons (Edwards and Mulloney, 1984; Borst and Haag, 1996; Christensen et al., 2001; Tobin et al., 2006; Peron et al., 2007). The large electrotonic size of PNs has important implications for the design of physiological experiments in these neurons. Because a voltage step at the soma declines to ∼40–70% of its original amplitude at the predicted spike initiation zone, we can easily explain the observation that action potentials persist when the soma is substantially hyperpolarized. Also, since the dendritic tuft only experiences a voltage change 50–80% of that imposed at the soma, techniques like voltage clamping to the reversal potentials of synaptic currents may be impracticable. Replacing potassium with cesium in the internal patch pipette solution should improve voltage control in these cells, although voltage-clamp experiments will still be imperfect (Williams and Mitchell, 2008).

If PNs are electrotonically extensive, why do synaptic events propagate so well to the soma? One reason is that synaptic events are slower than action potentials and thus are less attenuated by cable filtering. We do find that simulated EPSPs arising at only a single site in the dendritic tuft attenuate substantially, to an extent comparable with the reported attenuation of dendritic signals in other insect neurons (Borst and Haag, 1996; Peron et al., 2007). However, when the conductances underlying a unitary synaptic event are distributed across many dendritic branches, these conductances can sum more effectively and can produce large unitary EPSPs at the soma. Antennal lobe PNs are somewhat unusual neurons in that they receive feed-forward input exclusively from a population of neurons (i.e., ORNs) whose receptive fields are virtually identical to each other. Therefore, unlike many other cells, they probably do not perform dendritic computations that rely on the specific spatial locations of synaptic inputs. The absence of this restriction may allow synapses to be distributed across the dendritic tuft to produce a strong connection.

Our model also predicts that the SIZ lies near the axon initial segment. This allows us to model how unitary EPSPs decay as they propagate to the SIZ. If we estimate that each unitary EPSP is the sum of 25 distributed dendritic events, each ∼15 mV in amplitude (as in Fig. 6C), then the summed unitary EPSP will decay to ∼6 mV by the time it reaches the SIZ. Given that the true resting potential of these neurons is approximately −60 mV, and assuming a spike threshold at the SIZ near −40 mV, this implies that three nearly synchronous ORN spikes should be sufficient to drive a PN spike if unitary EPSPs summed linearly. Because EPSPs are extremely attenuated by the time they reach the axon terminals, it is almost certain that action potentials are necessary for signaling to higher brain regions and consequently are a good measure of PN output.

Model assumptions and caveats

It is useful to distinguish between what we can term raw properties of the model (R_m, C_m, and R_i) and core properties (like the membrane time constant and electrotonic distances) that are derived from combinations of the raw properties (Major et al., 1994). We showed that the raw properties of our model were a uniquely good fit to the morphological and electrophysiological data used to constrain the model (supplemental Fig. 2, available at www.jneurosci.org as supplemental material), and thus the core properties of the model are also a uniquely good fit. Nevertheless, even a model with a good fit will only be correct if the data used to constrain the model is itself free of errors. In particular, raw properties are susceptible to systematic errors in the morphological reconstruction or recording conditions. However, because raw properties can trade-off with each other to generate the same core properties, the core properties tend to be more resilient (Major et al., 1994; Roth and Häusser, 2001). We observed this type of trade-off when exploring the parameter space of our models (supplemental Fig. 2, available at www.jneurosci.org as supplemental material). Because our major conclusions rely on the core properties of our models, they are likely to be more robust than statements about the raw properties.

One important source of error is the morphology of our model. We ideally would have liked to collect physiological and morphological data from the same individual cells, but this was not possible because the soma and primary neurite are distorted by the removal of the patch pipette at the end of a recording. Therefore, to model the morphology, we combined reconstructions of different components of the DM1 PN from different preparations. This technique is made possible because the morphologies of these neurons are stereotyped within and across preparations. However, we found that models based on physiological data from different cells had somewhat different core properties (Fig. 4A), and this may in part reflect a mismatch between that cell's actual morphology and that of the model. Specifically, Drosophila antennal lobe PNs (and indeed entire Drosophila brains) vary slightly in their overall size depending on the density of the culture in which the fly was reared. Variability in the morphologies of the cells in our data set is probably the largest source of uncertainty in the model.

The PN dendritic tuft is difficult to model accurately because its fine processes are below the resolution of conventional light microscopy. However, varying the size of the tuft had little overall effect on the core properties of the model. Therefore, it is unlikely that our uncertainty about its exact morphology introduces additional uncertainty about our conclusions.

Aside from error in the morphology in the model, another source of error is introduced by the electrophysiological recording procedure. We attempted to limit artifacts introduced by recording conditions in several ways. To reduce the influence of the pipette resistance and capacitance, we fit the model with data acquired only after the current injection pulse had ended. We also created a model of the pipette and confirmed that varying the parameters of the model pipette had little effect on model fits (data not shown). Thus, errors arising from the pipette resistance and capacitance are likely to be minor. Nevertheless, it is likely that the effective value of the seal resistance varied across recordings, and this may be one reason why data from different electrophysiological recordings yielded somewhat different best-fit models. Other investigators have improved their modeling accuracy further by simultaneously recording from two locations in the same neuron (Roth and Häusser, 2001), which allows for better estimates of R_i (Stuart and Spruston, 1998). However, this is not feasible for most Drosophila neurons.

Finally, in constructing the model, we must assume spatially homogeneous and purely passive membrane parameters; otherwise, the proliferation of degrees of freedom in the model would make it impossible to select a single model out of the many that would fit the data equally well. For example, our model assumes that synaptic potentials are not amplified by voltage-gated conductances as they propagate to the soma and to the SIZ. We are still able to explain the fast, large EPSPs observed in the soma assuming purely passive propagation. However, we cannot rule out the possibility that EPSPs are actively amplified. In that case, synaptic conductances might not be as distributed across the tuft as we predict; alternatively, the initial amplitudes of unitary quantal EPSPs might be smaller than our estimates. Similarly, action potentials arising in the axon might not propagate into the soma entirely passively. If action potentials were boosted by voltage-gated conductances as they propagated to the soma, we would underestimate the distance from the SIZ to the soma.

Resting membrane potential

Our compartmental model generates predictions about the relative differences in the membrane potential across space and time. However, we also wanted to determine the range of true absolute membrane potentials in these cells. Therefore, we sought to accurately measure the resting membrane potential and to understand its determinants.

We found that the conductance around the membrane-glass interface is likely the major source of systematic experimental error in measuring the resting potential in these neurons. This conductance has a larger impact in Drosophila neurons than in many neurons in vertebrates and larger insects because Drosophila neurons have a relatively high input resistance. As the input resistance approaches the seal resistance, this error becomes larger. The error introduced by the seal conductance can be counteracted in PNs by injecting a small, constant amount of hyperpolarizing current so that V_rest is hyperpolarized by ∼10 mV. The magnitude of the requisite correction will vary somewhat in other types of Drosophila neurons, based on the input resistance and the level of ongoing synaptic current in these cell types.

After correcting for systematic experimental error (i.e., the seal conductance), we estimate that the true resting potential of these neurons is approximately −55 to −60 mV when spontaneous synaptic input from ORNs is intact and approximately −65 mV when input from ORNs is removed. This is still well above E_K. Accordingly, we find that there is a substantial resting sodium conductance in these cells. Using the Goldman–Hodgkin–Katz voltage equation and assuming that sodium and potassium are the only permeant ions, we estimate the sodium-to-potassium permeability ratio to be 0.080. Some of the sodium current is carried by TTX-sensitive channels; however, unlike in some other insect neurons (Lapied et al., 1989), they are not responsible for the majority of the resting sodium current. A possible candidate channel is the Drosophila homolog of NALCN, which is a sodium-permeable leak channel in mammalian neurons (Lear et al., 2005; Lu et al., 2007).

Interactions between theory and experiment

This model rests upon a solid foundation of experimental data. In particular, we have more experimental information about the physiological properties of unitary feed-forward synapses in Drosophila antennal lobe PNs than we do about most central synapses in insects (Kazama and Wilson, 2008). Direct experimental knowledge of unitary EPSP amplitudes in PNs and the number of release sites per ORN axon were essential constraints in modeling how synaptic potentials propagate from the dendrite into the rest of the cell. Similarly, experimental measurements of mEPSC amplitude and rise time allowed us to validate this aspect of the model.

Conversely, a useful model will make new experimental predictions and suggest avenues of experimental investigation that might not have otherwise seemed interesting. One prediction of our model is that a single ORN axon makes synaptic contacts that are distributed across many dendritic branches within the dendritic tuft of an individual PN. In our model, this geometry was crucial for the effective summation of quantal EPSPs to produce a large unitary EPSP at the soma and the site of spike initiation. Based on experimental measurements, we know that each ORN connects to every one of the approximately four PNs in its target glomerulus (H. Kazama and R. I. Wilson, unpublished observations). Moreover, all the vesicles released by an ORN spike onto a single PN must produce a summed unitary EPSP with a specific and well regulated amplitude (Kazama and Wilson, 2008). The challenge of forming these precise but distributed synaptic contacts may represent an interesting wiring problem for the developing circuit.