Oscillations in shoal cohesion in zebrafish (Danio rerio)

Abstract

In many species, group cohesion may be the result of a compromise between opposing forces (e.g. predator avoidance and competition for food). However, little empirical data exists on the dynamics of group cohesion. We present moment-to-moment positional data on zebrafish shoals and analyze temporal changes in inter-individual distances. We demonstrate that the distance between shoal members does not settle at any given value, as has previously been assumed, but oscillates with a period between 5 and 15 s.

Many species, from ants to humans, live in groups and interact with each other [13,14]. Members of groups often face opposing forces: some factors may favor tighter groups and others favor more dispersed groups. For example, numerous group-forming species must balance the requirements of efficient foraging with protection from predation: foraging efficiency increases with decreasing group density [10,12] but protection from predation decreases [4,6]. Many researchers have argued that as a result of such opposing forces, group density should settle at a species-specific optimal value.

Whilst several models have been developed to take such opposing forces into account and to explain how an optimal group density or size are achieved (e.g. Refs. [16,7]), the temporal dynamics of group density changes, if they occur at all, have been ignored. Most previous experimental studies of group behavior have averaged the distances between group members over several observation periods, or considered only the nearest neighbors of each individual (e.g. Ref. [8]). Thus, the data to validate or disprove the existence of an optimal group density or its temporal stability do not exist.

Here, using custom software [5], we examined high temporal resolution data on the positions of free-swimming zebrafish (Daniorerio). We focused on the distances between individuals within a group (AvD) and examined how they change over time. Our initial examination of the data suggested that there may be regular oscillations in shoal density, as measured by the average distance between fish, and we investigated whether these oscillations were robust and whether they had a characteristic frequency. We show that zebrafish do not settle on an average distance from conspecifics in the shoal, but that shoal density fluctuates with a characteristic frequency.

Video files were recoded for the current analysis as described elsewhere [5]. Detailed methods of the experiment are available in [5]. All analyses were run in Mathematica (Version 4.0 for Windows, Wolfram Technologies). The code used to perform the analysis is available from the corresponding author on request. Kolmogorov–Smirnov tests (K–S) were performed using SPSS (version 15.0 for Windows). For all statistical analyses, alpha was set at 0.05.

To examine shoaling preferences, 3 groups of 16 zebrafish each were placed in a 91-cm diameter circular tank and filmed from above for 30min per session for 6 sessions. Using custom software described in detail elsewhere [5], we extracted from the videos of the experiments the average distance in cm between any two fish (AvD). AvD is the average of the inter-individual distances (IIDs), which are the average distance of a given fish from all the other fish in the enclosure.

Five 1-min long sections of the sessions (at 5, 10, 15, 20, and 25 min from the start of the session) were coded at 1 s intervals (one frame per second). Thus, each dataset consisted of 60 points, representing the average distance between any two fish over the course of a minute.

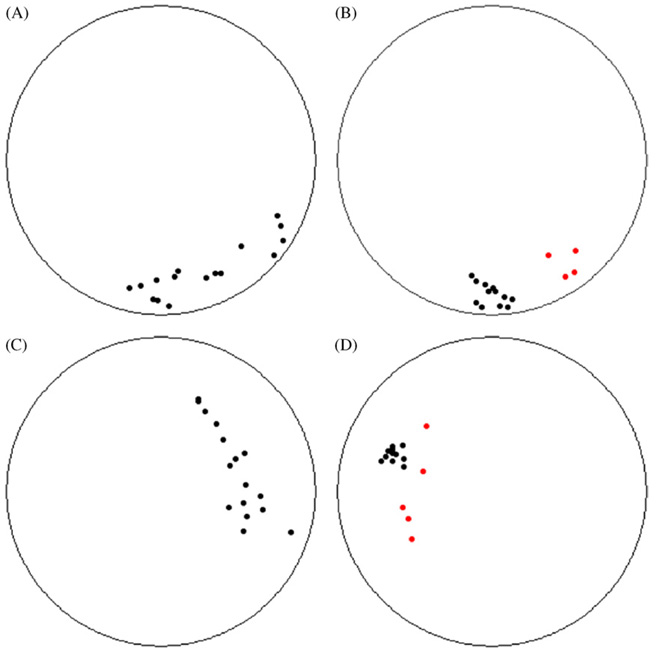
Before an analysis of changes in the distance between shoal members can be attempted, it is necessary to determine, for each frame, which fish are part of the shoal (or whether there is more than one shoal). We frequently observed one or more fish swimming far away from the rest of the group. Including these fish in the analysis of distance would artificially inflate the AvD. Previous authors have either assumed that all the fish in an experimental tank are members of a shoal (e.g. Ref. [11]), or have used a simple heuristic to determine shoal membership, most commonly regarding any fish within four or five body lengths of each other as members of the same group (e.g. Refs. [2,10]). Here we attempt to provide a more objective criterion that takes into account the distribution of all the fish in the tank as follows: for each frame we calculated AvD and the IIDs for each fish (as defined above). The IIDs were ranked by size, such that the fish closest to the others was first and the fish farthest from all others was last. We examined the change in this value from one fish to the next (i.e. ΔIID). If a large leap was identified in the ranked list of distances, this implied that fish ranked beyond the leap were not members of the shoal (although they may have been members of a separate shoal). We used a threshold criterion such that if ΔIID exceeded √AvD, all fish beyond that point (i.e. with greater IIDs) were considered not part of the shoal, and were removed from all further analysis (the square-root threshold was arbitrarily determined, based on comparisons of different thresholds to group membership decisions made by an experienced coder). The AvD for each frame was then recalculated using only those fish remaining. Fig. 1 shows data for four sample frames and indicates the fish that were removed by our criterion in each frame.

Fig. 1.

Sample plots of fish distributions in the tank, demonstrating the shoal-membership criterion. Each plot shows the positions of all 16 fish within the tank at one time point. Each dot represents one fish. Red dots are fish that were removed from the analysis by our group membership criterion. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)

The above selection criterion has an advantage over using an absolute distance, such as a certain number of body lengths (BLs) as a threshold for group membership as it takes into account the overall cohesion of the shoal. Intuitively, a fish that is 2 BL away from a group that are all, on average, 0.5 BL from each other should not be considered part of the group (e.g. Fig. 1D). However, a fish that is 2 BL away from a group that are, on average, 2.5 BL from each other should be considered part of the group (Fig. 1C). In addition, traditional measures of shoal membership often only take into account the nearest neighbor of each fish [10]. However, if a small group of fish splits off from the main shoal, their nearest neighbor distances would remain small, despite no longer being part of the shoal (Fig. 1B). Our criterion can detect and exclude such subgroups with a high degree of accuracy. By taking into account all IIDs and the AvD, the current measure more closely reflects our intuitions about shoal membership. How many neighbors fish take into consideration when making shoaling decisions is still subject to debate [1,15].

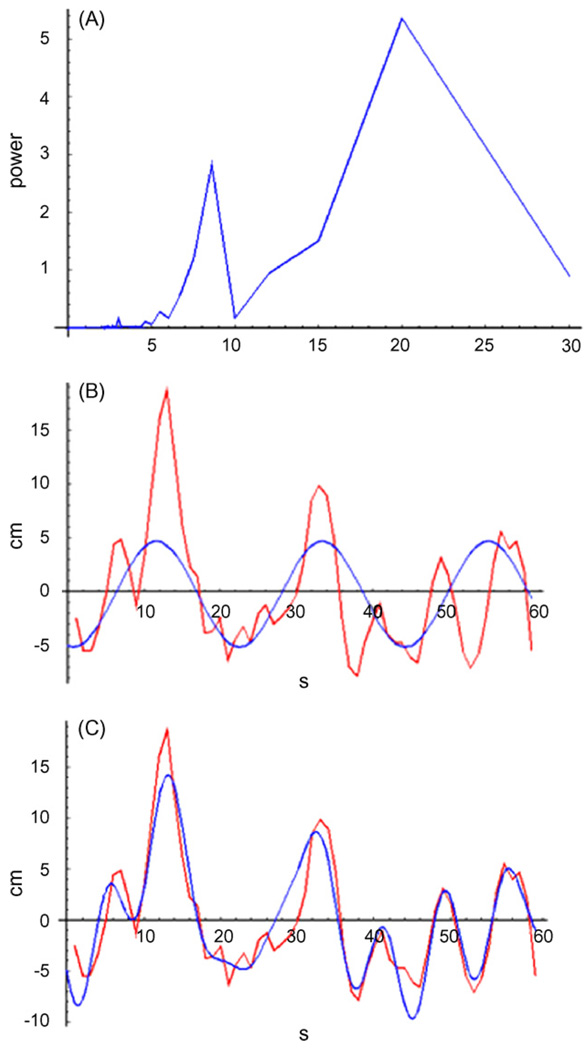
Initial observations of the data suggested that AvD may vary periodically and this was examined by fitting a periodic model to each dataset. The model used consisted of five superimposed sine-wave terms, each of the form: α sin(βt + γ) + ε, where α is the amplitude of the sine-wave, β the frequency, γ the horizontal offset (necessary since the data could begin at any phase of the sine-wave), and ε a random error series. The coefficient we focused our analysis on was the frequency (or period) of the model, β. The regression was first run with just one term (Fig. 2B); the values of the coefficients (except the error series, ε) determined from this regression were then fixed and a second term was added in a stepwise manner until all five terms were present in the model (Fig. 2C).

Fig. 2.

A sample dataset, demonstrating the steps of the regression analysis. (A) Power plot of the fast Fourier transform (FFT) for this dataset, showing the relative power of periodic components at different periods. Note the strong peak at a period of about 20 s and a smaller peak around 8 s. (B) Plot of the average distance between shoal-mates (AvD, in red) and the best-fit single term model fit to it (in blue). Note that the period of the model is close to 20 s, as predicted by the peak in the FFT. (C) Plot of the AvD (in red) and the best-fit full (5-term) model. Note that a term with a period around 8 s, corresponding to the secondary peak in the FFT, has been added to the 20-s term. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)

Initial values for the regression coefficients were selected using the fast Fourier transform (FFT) of the data (Fig. 2A). For the first term, the frequency of the highest peak of the FFT was used as the starting value of β (the frequency), and the power of that peak in the FFT as the starting value for α (the amplitude). The next highest point was used for the second term, and so on. The initial values of γ (the offset) and ε were set at 1 and 0, respectively. Before starting the regression analysis, the mean of the data was subtracted from all data points.

To determine whether a five-term model was best (and not more or less), we calculated the Bayesian Information Criterion (BIC) for each term. The BIC is a measure used for multivariate model selection (lower BIC scores characterize models that fit the data better). We examined the decrease in BIC as a function of adding more terms to the model (this was possible because we used a stepwise method for generating our regression; thus, we could test the BIC after the addition of each term separately). On average, adding the second term to the model decreased the BIC by 12.9 (±1.96 S.E.M.), adding the third term decreased it further by 10.1 (±1.44), the fourth term by 9.06 (±1.58), and the fifth term by 4.55 (±0.91). Note the drop in the value for the fifth term. We determined that adding a sixth term to the regression would not significantly improve the fit of the model to the data. We also excluded from our analysis any terms for which the BIC increased relative to the model without that term (i.e. additional terms that degraded the fit of the model). Only 13 such terms were found (out of 365) and, in all but one case, this was the fifth term, further supporting our notion that additional regression terms would not add much to the power of the model.

To identify whether the data were significantly periodic we calculated the R² of each model term in each dataset.

To identify the characteristic frequency of the oscillation, we first eliminated all model elements that were deemed to be spurious. We used four different criteria to judge the reliability of each sine-wave term: (1) any terms with an oscillation period greater than the length of the dataset (1 min, i.e. terms where β < 2Π/60) were discarded, as these represent long-term trends in the data (which we have examined elsewhere; [5]); (2) any terms for which the 95% confidence intervals for β encompassed 0 were also discarded; (3) any terms for which the R² was non-significant (i.e. F(2,58) < 3.15) were discarded; and finally; (4) terms for which α was smaller than 1 were also discarded (terms with a small amplitude contribute little to the overall shape of the model). The remaining terms of the regression were compared across groups and sessions using a two-sample K–S test. Finally, we pooled all the retained sine-wave terms from all datasets (a total of 302 of 365 terms were retained) and sorted them by the value of β.

If the fluctuations we observed in the data are random (or noise), they should occur with equal probability throughout the range of frequencies we examined. Conversely, if the oscillations are a characteristic feature of shoaling behavior, we would expect the frequencies of the terms in our model (the values of β) to cluster around a particular value. Thus we compared the distribution of frequencies of the retained terms to a uniform distribution using a one-sample K–S test.

We first examined the number of terms rejected as spurious by each of our significance criteria. Five terms overall were rejected due to having periods longer than 60 s; seven terms were rejected due to the 95% confidence interval of β encompassing 0; three terms had a non-significant R²; 55 terms were rejected for having amplitude coefficients (α) smaller than 1. Some terms failed to pass more than one criterion. Overall, 63 of 365 terms were rejected.

As only 3 of the 365 sine-wave terms had non-significant correlation coefficients, this implies that there is a periodic oscillation in the average distance between freely shoaling zebrafish that is not the result of random fluctuations or noise. For obvious reasons, the R² of later terms in the model were higher. Excluding the three rejected terms, the average R² of the first term of the model for each dataset was 0.22 (±0.12), for the second term 0.36 (±0.16), for the third term 0.45 (±0.16), for the fourth term 0.51 (±0.16), and for the final term 0.56 (±0.15).

We selected a cut-off criterion of 1 for α, i.e. we rejected any term that did not result in a maximal change in AvD of at least 2cm (an amplitude of 1 gives a sine-wave that ranges from −1 to 1). The α values of all terms (rejected and retained) ranged from 0.04 to 19.1, with a mean of 3.34 (±2.46). Thus, on average, the oscillations in the distance between the fish caused, at their maxima, a change in AvD of about 6.7cm (which, for zebrafish, is about 1.5 body lengths).

Fig. 3 presents the histograms for the regression results. Each column of the histogram measures the number of regression terms that had a frequency (β) coefficient in a particular range. The columns are arranged by the period of the term, which is the reciprocal of the frequency. As can be seen, the period of the oscillations in AvD are distributed around an average value between 5 and 15 s (53.8% of the terms had periods in this range). This holds true for only the retained terms or for all terms. A one-sample K–S test confirmed that the distribution is significantly different from uniform (D* = .468, p < .001). This was also true for the distributions of individual groups or individual sessions within the data (D* values from .275 to .529, all p < .002). There were no significant differences between the three groups (two-sample K–S test: group 1 vs. 2, D* = .127, n1 = 130, n2 = 102, p = .319; group 1 vs. 3, D* = .178, n1 = 130, n2 = 71, p = .108; group 2 vs. 3, D = .083*, n1 = 102, n2 = 71, p = .933) or across days of exposure to the tank (n values from 43 to 61, D* values from .082 to .211, p values from .995 to .231).

Fig. 3.

Histogram of the results of the regression analysis for all data. The bars represent the number of regression terms found with a given period. Black bars show all terms; white bars show only those terms that passed all four significance criteria. Note the distinct peak around a period of 5–15 s, implying that the fluctuations in shoal cohesion are regular and periodic.

The above results on the precise, moment-to-moment, locations of freely swimming zebrafish strongly imply that the distances between individuals within a shoal (a measure of shoal cohesion) oscillate with a period between 5 and 15 s. To the best of our knowledge, this is the first time that such an analysis has been reported and such oscillation has been conclusively demonstrated for members of a group of any vertebrate species.

One possible explanation of these oscillations relates to the opposing forces that shoaling fish have been theorized to be exposed to. Our data suggest that zebrafish do not achieve a balance between protection from predation and foraging by compromising on a particular density of shoaling, as previous authors have assumed, but by the cohesion of a shoal fluctuating periodically, with fish moving closer and farther away from their neighbors. If the oscillations reported here are indeed driven, as we suggest, by the need to balance safety and foraging efficiency, then they may be affected by environmental manipulations such as the appearance of a predator or presentation of food [5].

Some models of shoaling behavior, with appropriate parameter values, have implied the types of oscillations we report here (e.g. Refs. [16,7]). But, surprisingly, most models have ignored their own predictions and assumed that the oscillations do not occur in reality arguing that such behavior would be energetically counter-productive (e.g. Ref. [16], p. 485). However, our empirical data conclusively show, for the first time, that such oscillations do occur.

There are many possible mechanisms that could generate the type of behavior we report. The oscillations may arise from the biological properties of the organisms forming the group. Alternatively, periodic changes in the inclination of a fish to match the orientation of its neighbors might be responsible (e.g. Refs. [8,9]). Further study of these possibilities may help elucidate the underlying mechanisms of shoaling.

A possible biological mechanism that may explain oscillations in group density of zebrafish is the processing of and responding to perceptual signals: a slight delay in the response of a fish to changes in the speed or orientation of its neighbors could, in principle, lead to the observed oscillation. Alternatively, characteristics of motor function such as the maximal speed or turning rate achievable by the fish may in principle generate oscillations. However, the timescale on which the oscillations we report occur is longer than would be expected if the behavior were being driven by perceptual or response limitations of the fish (as some models have assumed, e.g. Ref. [16]). Though no data on response latencies for zebrafish exist, Hunter [3] has reported response latencies in shoals of Mackerel in a range of 0.05–0.5 s, an order of magnitude faster than the oscillations we report. Thus, it is unlikely that response limitations of the zebrafish are responsible for the observed oscillations.

The data presented here raise the intriguing possibility that oscillations like those we report could be a central feature of the behavioral responses of animal groups, independent of the particular species studied. Finding a set distance from others may not be the optimal strategy in a temporally or spatially heterogeneous environment. Instead, testing the optimum by moving away from and closer to its value with some regularity may be the appropriate strategy.