Optimization of nanoparticle core size for magnetic particle imaging

Abstract

Magnetic particle imaging (MPI) is a powerful new research and diagnostic imaging platform that is designed to image the amount and location of superparamagnetic nanoparticles in biological tissue. Here, we present mathematical modeling results that show how MPI sensitivity and spatial resolution both depend on the size of the nanoparticle core and its other physical properties, and how imaging performance can be effectively optimized through rational core design. Modeling is performed using the properties of magnetite cores, since these are readily produced with a controllable size that facilitates quantitative imaging. Results show that very low detection thresholds (of a few nanograms Fe₃O₄) and sub-millimeter spatial resolution are possible with MPI.

Magnetic particle imaging (MPI) is a powerful new tomographic imaging platform for visualizing magnetic nanoparticles in a variety of applications, including diagnostic imaging, hyperthermia treatment and drug delivery [1]. Using MPI's unique detection scheme, which has been demonstrated in proof-of-principle experiments by its inventors [2,3], nanoscale magnetic molecular probes (NMPs) are imaged directly with high sensitivity and spatial resolution. MPI technology is scalable, and potentially capable of full-body imaging in animals and humans. With direct NMP detection, MPI should achieve greater sensitivity than magnetic resonance imaging (MRI), the current standard technique for imaging NMPs in biomedicine. MPI is also quantitative because, unlike MRI, image intensity is directly related to local NMP concentration. Moreover, MPI is relatively inexpensive since it does not require a costly superconducting magnet (like MRI), or SQUID detectors to achieve high sensitivity (like magnetorelaxometry imaging).

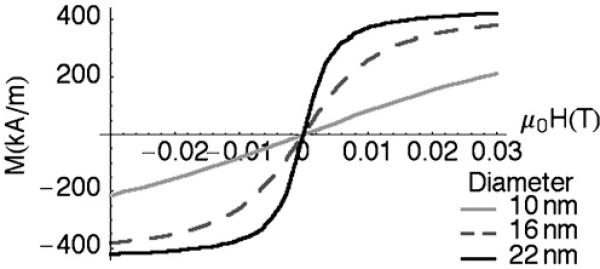
During an MPI scan, NMPs are magnetized by a radiofrequency (RF) magnetic field and their time-varying magnetization induces a time-dependent voltage across an inductively coupled receiver coil [2,3]. Because the magnetization curve for superparamagnetic nanoparticles is nonlinear (Fig. 1), induced signal contains higher-order harmonics that can be detected and distinguished from applied RF by a simple Fourier transform. Since the third harmonic is the largest it is commonly exploited for signal detection. Generally, signal localization can be understood by considering how harmonic response varies when a static magnetic field is superimposed with applied RF. If the static field is strong, Fig. 1 shows that particle magnetization saturates. In this case, no MPI signal is detected because particle magnetization is constant and no harmonics are generated in the receiver coil. Conversely, in the absence of a static field, particle magnetization is free to respond to the applied RF and harmonic generation is maximized. To localize the MPI signal these differences are exploited by generating a strong static field gradient. Particles far away from the origin then contribute nothing to the detected signal, since they experience strong static fields that saturate their magnetization. Particles at the center of the applied gradient, however, produce maximum signal because the static field is zero. Images are formed by moving the sample within the localizing field gradient, or conversely, moving the point of zero-field through the sample volume [2,3].

Fig. 1.

M vs. H for a steady (static) applied field.

The above discussion highlights how MPI signal strength and spatial resolution are both determined by the magnitude of harmonics in NMP magnetization under RF field, and by the static field required to saturate these harmonics. In turn, harmonic production is set by the NMP magnetization curve, a material property of the NMPs. In this paper, we present modeling results discussing AC magnetization for superparamagnetic NMPs. We show that choosing NMPs with monodisperse magnetic cores of a particular size, such as those we synthesize in our lab [4,5], will optimize a fixed-frequency MPI system's performance. We also identify optimal NMP-core properties for a prototype MPI device built in our laboratory. While MPI is compatible with NMPs made from a variety of materials, we have chosen to consider magnetite (Fe₃O₄) due to its biocompatibility and frequent use in magnetic imaging [6].

Superparamagnetism occurs in ferromagnetic particles smaller than a critical diameter D_sp, when the magnetocrystalline energy barrier is less than thermal energy at room temperature. In the superparamagnetic state, the magnetic moment is un-blocked and the average value for a single particle, or system of particles, will be zero in the absence of an applied field. In this case, the material exhibits no remnant magnetization or coercive field.

In the presence of an applied magnetic field, superparamagnetic NMP cores are magnetized and their magnetic moments tend to align along the applied field direction. However, thermal agitation will compete with magnetic ordering. Assuming that particles do not interact, the magnetic response for a system of NMPs will obey the Langevin function [7]

$$\frac{M}{M_s}=\text{Coth}\left[\frac{v{M}_s{\mu }_{0}H}{k_{b}T}\right]-\frac{k_{b}T}{v{M}_s{\mu }_{0}H},$$ (1)

where ν is the volume of the magnetic core, M_s is the saturation magnetization of the particle in kA/m (446 kA/m for magnetite), T is the sample temperature in Kelvin (taken to be 300 throughout), μ₀ is 4π × 10⁻⁷ H/m, μ₀H is the applied field (in Tesla) and k_b is the Boltzmann constant, 1.38 × 10⁻²³ J/K.

When NMPs are placed in an oscillating field (B) defined by some fixed angular frequency (ω), it becomes necessary to consider the relaxation time (τ) for their magnetic moment to change direction. Magnetic relaxation occurs in two distinct modes. Small particles relax by the Neél mechanism when their individual atomic moments can rotate freely. Neél relaxation is described by [8]

$${\tau }_N=\frac{\sqrt{\pi }}{2}{\tau }_0\frac{\text{exp}\left[\rho \right]}{{\rho }^{1∕2}},$$ (2)

where ρ = Kv/k_bT, K is the magnetocrystalline anisotropy constant in J/m³, and τ₀ is taken to be 10⁻¹⁰ s consistent with theoretical calculations and experimental measurements of magnetite [9].

Generally, the energy barrier (Kν) for magnetic moment rotation increases with particle volume. Correspondingly, τ_N increases with size until the magnetocrystalline energy exceeds the particle's thermal energy and its magnetic moment becomes blocked. When Neel relaxation is slow and no longer effective, blocked crystals will relax by the Brown mechanism that involves the physical rotation of the particle to re-align its moment with the applied field. The characteristic time for Brownian relaxation is given by [8]

$${\tau }_B=\frac{3V\eta }{k_{b}T},$$ (3)

where V is the hydrodynamic volume of the particle including any surfactant, and η is the viscosity of the suspending solvent in Pa s. Here, Brownian relaxation times are calculated for particles suspended in water (η = 0.89 mPa s) when they are coated with a 23 nm thick layer of oleic acid and pluronic F127 to promote biocompatibility [5].

In practice, NMPs will relax by the faster of the two modes according to their size and anisotropy. For intermediate sizes, the effective relaxation time is given by [9]

$$\tau =\frac{{\tau }_B{\tau }_N}{{\tau }_B+{\tau }_N}.$$ (4)

To account for this finite relaxation time when particles are subject to an alternating applied field, we modify Eq. (1) by including the complex susceptibility, so that [10]

$$\frac{M}{M_s}=({\chi }^{\prime }+i{\chi }^{\prime \prime })\left(\text{Coth}\left[\frac{v{M}_s{\mu }_{0}H}{k_{b}T}\right]-\frac{k_{b}T}{v{M}_s{\mu }_{0}H}\right),$$ (5)

where χ′ = 1/(1+(ωτ)²), χ″ = ωτ/(1+(ωτ)²), and τ is the effective relaxation time. When ωτ << 1, χ′ dominates. Near ωτ = 1, χ″ is significant and represents a phase shift between the crystalline magnetic moment and the applied field, resulting in a decrease in measured magnetization.

For many ferrofluids there is a range of particle diameters (d) that can be described by a log-normal distribution function g(d), such that [11]

$$g\left(d\right)=\frac{1}{\sigma d\sqrt{2\pi }}\text{exp}\frac{-{\left(\ln (d∕d_0)\right)}^2}{2{\sigma }^2}.$$ (6)

Here, d₀ is the median particle diameter and σ is the standard deviation of ln(d). Including this distribution function, the magnetization for a NMP sample is given by

$$\frac{M\left(d\right)}{M_s}={\int }_0^{\infty }\chi \left(\text{Coth}\left[\frac{v{M}_s{\mu }_{0}H}{k_{b}T}\right]-\frac{k_{b}T}{v{M}_s{\mu }_{0}H}\right)g\left(d\right)dd,$$ (7)

where χ = χ′+iχ″. To evaluate Eq. (7) we have implemented the Simpson method in Mathematica version 5.2. Generally, calculation time can be reduced by integrating the distribution function over a physically realistic range of d values from 0 to 200 nm. The effective relaxation time (τ) is independently calculated for each size in the distribution.

To illustrate the relationship between NMP harmonic response and MPI signal strength, we consider an RF field of 10 mT at 50 kHz (f₀), and a simple solenoidal receiving coil tuned to resonate at 150 kHz (3f₀). The test coil consists of 40 turns of wire wound around a NMR tube with a 10 mm diameter. In this case, signal is the emf induced at (3f₀) by a liquid suspension of NMPs. Neglecting sample losses, which are relatively small, the signal-to-noise ratio per unit volume of NMPs (SNR_ν) in a solenoidal MPI receiver can be expressed as the ratio of induced emf to Johnson noise [12,13]

$$SN{R}_v=\frac{6\pi f_0{M}_3{B}_{axial}}{\sqrt{4k_{B}T{R}_{coil}\Delta f}},$$ (8)

where M₃ is the magnitude of the third harmonic in NMP magnetization in A/m, B_axial is the axial field produced by unit current in the receiving coil (2.25 mT/A), T is the coil temperature in Kelvin, R_coil is the AC coil resistance (0.238 Ω), and Δf is the bandwidth of the receiver (1 kHz).

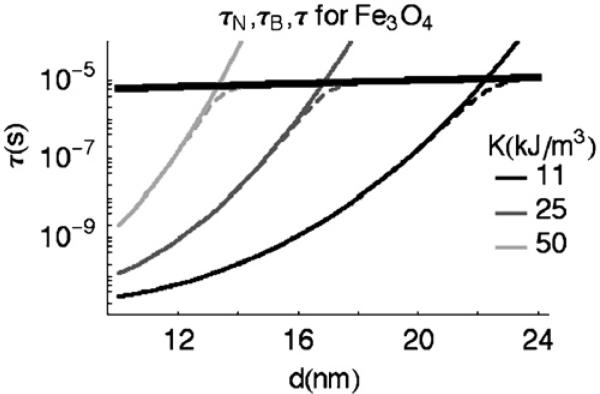
Relaxation times in Fig. 2 are calculated for individual magnetite NMPs and are plotted as a function of magnetic-core diameter. Neél relaxation times (τ_N) are calculated for several values of the anisotropy constant K, since theoretical calculations for magnetite predict K to be 11 kJ/m³ [14], while measured values can be slightly higher, up to about 50 kJ/m³ [10]. Real NMP samples will likely have a range of K values, depending on synthesis and processing techniques. Furthermore, τ will also be affected by any functional groups attached to the surfactant layer that alter the hydrodynamic volume (V) in Eq. (3).

Fig. 2.

The characteristic relaxation times for magnetite, plotted as a function of NMP core diameter for several K values: τ_N (narrow solid curves), τ_B (thick solid curve), and τ (dotted curves). τ₀ is 1 × 10⁻¹⁰.

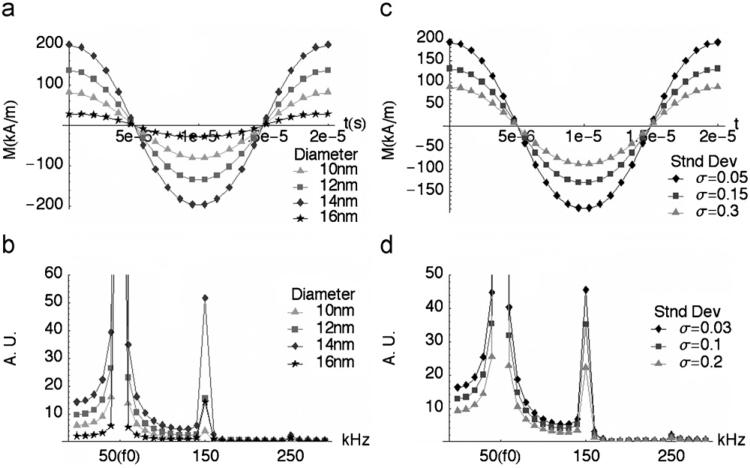
In Fig. 3, both magnetization and third-harmonic amplitude are shown to increase with NMP diameter before decreasing sharply due to rapidly increasing relaxation time. For these calculations, K is 25 kJ/m³. For monodisperse particles, M and M₃ are both maximum for NMPs that are approximately 15 nm in diameter, given a 50 kHz RF field. Optimal size is determined by the relaxation time τ and will therefore vary with RF field frequency. Fig. 3 also shows that magnetization for a given NMP concentration will be reduced when there is a distribution of particle sizes about the optimal. Put another way, the observed MPI signal will be dominated by NMP cores that are near the optimal size. While off-sized NMPs contribute to the total volume, or dose, of material, they do not contribute significantly to the harmonic signal, thereby reducing sensitivity for a given concentration.

Fig. 3.

Magnetization and harmonic response for magnetite nanoparticles subject to an applied field of 10 mT, at 50 kHz. The effective relaxation time is calculated for each size using K = 25 kJ/m³ and a surfactant layer thickness of 23 nm. (a) M(t) vs. particle size, (b) Fourier spectrum of M(t) vs. particle size, (c) M(t) for increasingly broad particle size-distributions, where the median diameter is 14 nm, and (d) Fourier transform of M(t) including size-distribution.

To optimize NMPs experimentally, it will also be important to consider NMP dynamics. For example, magnetic relaxation will differ from Eq. (4) for samples with strong inter-particle interactions or agglomeration. Generally, such behavior should be minimized where possible to ensure that samples perform consistently over time and to avoid in vivo complications from large agglomerates.

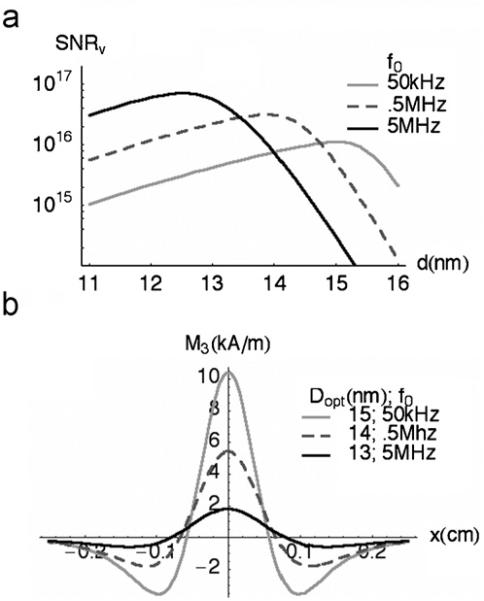
For an MPI system operating at fixed frequency, Fig. 3 shows that maximum harmonic generation occurs for monodisperse NMP samples of a particular size. Fig. 4a shows how SNR performance predicted by Eq. (8) varies with particle size and frequency for the same test coil. Additional AC losses are included at higher frequencies to account for the skin effect, such that R_coil is 0.836 Ω at 1.5 MHz (3f₀), and 2.7 Ω at 15 MHz (3f₀) [15]. Projected performance indicates that the highest achievable sensitivity will occur for an MPI system operating at high frequency with relatively small NMP cores. However, for a system operating at an arbitrary fixed frequency, the optimum NMP size will be the largest permitted by the relaxation-time constraint. For our test coil, Fig. 3 shows that the optimum NMP diameter is approximately 15 nm if K is 25 kJ/m³ and the RF field is 10 mT. In this case, Eq. (8) predicts the SNR per unit particle volume to be ∼1.1 × 10¹⁶. Consequently, an SNR of 5 only requires 4.5 × 10⁻¹⁶ m³ of material, or 2.4 ng of magnetite, since the density of magnetite is 5.25 × 10⁶ g/m³. Remarkably, this sensitivity is achieved with a single scan of 1 ms. Since the volume enclosed by the receiving coil is ∼6.2 mL the concentration sensitivity is 4.9 × 10⁻⁹ mol Fe/L, better by a factor of two than the maximum performance estimates of MPI's inventors [2].

Fig. 4.

MPI performance for magnetite NMPs. K is fixed at 25 kJ/m³: (a) SNR per volume of magnetite, plotted as a function of diameter at several drive frequencies (f₀), and (b) spatial resolution for optimally sized NMPs in a uniform field gradient of 0.15 T/cm, aligned with the RF field.

Unlike sensitivity, spatial resolution has no direct frequency-dependence. Rather, it is determined by NMP size and the strength of applied field gradients [2]. In Fig. 4b, the third-harmonic magnitude has been calculated for optimally sized NMPs inside a field gradient of 0.15 T/cm. The observed negative lobes are caused by blurring from the RF field, which is oriented along the applied gradient. Here, spatial resolution is defined as the distance between points where the lobes cross the x-axis. Maximum resolution, observed for 15 nm NMPs (at 50 kHz RF), is approximately 1.2 mm. Generally, resolution can be improved by using larger NMPs or by reducing the RF field magnitude [3].

Table 1 lists the optimal particle diameters and anticipated resolution for experimental conditions considered in this study. It also lists projected detection limits assuming a minimum SNR of 5. While actual MPI performance will certainly depend on device engineering, this study shows that proper selection of NMP cores can provide a significant enhancement. For example, in Fig. 4, the observed SNR increases are due solely to NMP properties, since device parameters are held constant. Using NMPs several nanometers larger or smaller than the optimum value can reduce SNR per volume by an order of magnitude. These results emphasize the importance of careful nanoparticle characterization, as well as the need to produce highly uniform and monodisperse magnetic cores [4].

Table 1.

MPI performance for optimally sized NMPs.

K (kJ/m3)	dopt (nm)	Sensitivity, SNR = 5		Resolution (mm)
		Mass (nanograms Fe3O4)	Concentration (nanomol Fe/L)
11	19	0.5	1.1	0.8
25	15	2.4	4.9	1.2
40	13	8	16.7	1.6

40 turn, 1 cm solenoid receiving coil at 50 kHz, 10 mT RF, 0.15 T/cm field gradient.

Though we have discussed a specific model MPI device in presenting our method for optimizing NMPs, the same approach could be used to optimize NMPs for a variety of different experimental coil designs, such as larger coils capable of imaging animals or humans, or smaller coils with ultra-high high resolution and sensitivity. In principle, while sensitivity and resolution will vary between coils, optimal NMPs exist for any device. In future work, we plan to experimentally measure the change in SNR as a function of NMP properties for samples of varying size and dispersity.