Methods for Estimating and Interpreting Provider-Specific Standardized Mortality Ratios

Abstract

Standardized Mortality Ratios (SMRs) are widely used as a measurement of quality of care for profiling and otherwise comparing medical care providers. Invalid estimation or inappropriate interpretation may have serious local and national consequences. Estimating an SMR entails producing provider-specific expected deaths via a statistical model and then computing the “observed/expected” ratio. Appropriate comparison of estimated SMRs requires considering both estimated values and statistical uncertainty. With statistical uncertainty that varies over providers, hypothesis testing to identify poor performers unfairly penalizes large providers; use of direct estimates unfairly penalizes small providers. Since neither approach suffices, we report on a suite of comparisons, each addressing an important aspect of the comparison. Our approach is based on a hierarchical statistical model. Goals include estimating and ranking (percentiling) provider-specific SMRs and calculating the probability that a provider's true SMR percentile falls within a specified percentile range. We present the issues and related statistical models for comparing SMRs and apply our approaches to the 1998 United States Renal Data System (USRDS) dialysis provider data.

1. Introduction

Use of performance assessments in the health and social sciences has increased substantially. For example, goals for health services research and evaluation at the clinic, physician, and other health service provider levels (e.g., “dialysis centers” for End-Stage Renal Disease [ESRD] patients) include valid and efficient estimation of population parameters (such as average performance over providers), estimation of between-provider variation (variance components), and inferences focused on provider-specific performance. These latter include estimating provider-specific Standardized Mortality Ratios (SMRs), estimating their percentiles to be used in profiling/league tables, identifying excellent and poor performers, and determining “exceedences” (how many and which true, underlying, provider-specific SMRs exceed a threshold).

Estimated SMRs [1] are used to evaluate performance relative to dataset-specific or national norms; financial and reputational consequences are associated with good and poor performance. Therefore, invalid estimation or inappropriate interpretation can have serious local and national consequences. For a fair comparison, mortality must be adjusted for case mix and both an estimated SMR for each provider and the considerable range of the associated variability must be taken into account. The current method of calculating ESRD dialysis provider-specific SMRs [18] is reasonably straightforward: produce provider-specific expected deaths based on a statistical model, and then compute the “observed/expected” ratio. Complications arise from the need to specify a reference population (providers included, the time period covered, attribution of events), the validity of the model used to adjust for important patient attributes (age, gender, race, diabetes, type of dialysis, severity of disease, vintage [the time from the first ESRD service date to the starting time of follow-up], etc.), the need to adjust for potential biases induced when attributing deaths to providers, and the need to account for informative censoring.

A valid comparison of providers requires simultaneous consideration of estimated values and their statistical uncertainty. The large variation in dialysis provider sizes produces large differences in the variances of the estimated SMRs. With this differential statistical stability, using hypothesis tests to identify poor performance can unfairly penalize large providers with relatively stable estimated SMRs (the test has relatively high power to detect small differences), while direct use of estimates can unfairly penalize small providers (unstable estimates are likely to be extreme). Gelman and Price [6] and Shen and Louis [14] formalized this competition and have shown that no single set of estimates or assessments can effectively address them all. Therefore, a “suite” of goal-specific robust summaries and inferences is needed. Tracking, reporting, and analyzing the consequences of uncertainty are key because in many contexts available information is insufficient to support definitive comparisons and conclusions.

Producing valid SMR estimates is challenging and a key initial step, but policy goals also include identifying providers who perform substantially above or below average (outlier detection), estimating the number of providers whose SMR exceeds some intervention standard (exceedences), and percentiling providers. Analyses must be tuned to these goals, be robust, and communicate uncertainty. Importantly, even “optimal” procedures may have poor performance because available information may be insufficient to produce procedures with acceptable operating characteristics. Therefore, risk performance and relevant uncertainties must be communicated [11, 12].

Bayesian hierarchical models coupled with a relevant loss function are very effective in structuring ranking and related inferential goals. Such models retain a provider-specific focus while improving statistical stability. They properly structure addressing nonstandard goals and allow all relevant uncertainties to be reflected in statistical inferences. Examples of the power of the Bayesian approach in structuring goals are presented in Appendix B of Carlin and Louis [2]. Properly specified, hierarchical models account for the sample design and provide the necessary structure for developing scientific and policy-relevant inferences. Hierarchical models explicitly identify population parameters (e.g., typical performance), between-provider variation (variance components) and provider-specific parameters represented as random effects. The latter are the “underlying truths” to be estimated, displayed in a histogram, and percentiled. Hierarchical models properly structure statistical analyses directed to assessments and substantial progress has been made in tuning such models to these goals, such as performance evaluations of health service providers [3, 7, 10, 12, 13], assessment of post-marketing drug side-effects [5], analyzing spatially structured health information [4], and percentiling teachers and school burgeoning [11].

Developing valid, provider-specific expected deaths is essential in producing valid estimated SMRs; however, in this report we focus on using observed and expected deaths to produce information on SMRs and using this information to compare providers. We use the death rate model currently employed by the United States Renal Data System (USRDS, see [17]), which is evaluated by the USRDS and displayed explicitly in Section 3. We compare dialysis provider adjusted SMRs with each other for 1998 using information from the USRDS [8, 9, 17]. The USRDS database contains information on more than 3500 dialysis providers in 1998. Providers have a wide variety of patient populations and range from quite small (less than 10 patients per year) to quite large (more than 700 patients per year). The large range of statistical variability in estimated SMRs challenges standard methods.

Sections 2 and 3 present the data set and the USRDS death rate model; Sections 4 and 5 present methods used for estimating and percentiling SMRs and computing percentile-range probabilities; Section 6 compares results from candidate methods using the 1998 ESRD provider data; and Section 7 summarizes, discusses issues, and identifies areas requiring additional research.

2. Data

We constructed a provider-specific profile from 1998 ESRD Facility Survey data, patient-level data, and ESRD Medicare claims. ESRD Facility Survey data are collected annually by the Centers for Medicare and Medicaid Services (CMS, formerly HCFA: Health Care Financing Administration). The data set includes provider identification, provider type, types of dialysis, and numbers of patients at the beginning and the end of the survey year (taken from CMS Facility Survey form 2744). For comparing dialysis provider performance, only providers rendering dialysis services are considered. Such providers include dialysis centers, dialysis facility hospitals, independent dialysis facilities, and mixed facilities that provide both transplant and dialysis services.

The patient-level data set contains basic information including demographics (e.g., birth date, race, gender, date of ESRD onset), primary cause of kidney failure, and transplant and death dates. The USRDS database contains information on Medicare claims for ESRD patients since 1991. It includes the service period, treatment modality, clinical diagnoses and procedure codes, and provider identification. To ensure a stable treatment modality, we ignored a new modality or provider switches that occurred within 60 days from the last switch [17].

By cross-referencing ESRD service provider survey data, patient-level data, and ESRD Medicare claims, we constructed a patient-modality-provider file that traces when, where, and what kinds of services each patient received. Comparison of SMRs is performed on yearly period prevalent cohorts consisting of patients who were alive and on dialysis at the beginning of each year, or new patients starting dialysis during that year. A patient would experience the event if he/she died during that year, or his/her follow-up is censored at the earliest date of renal transplantation, provider change, and/or the end of the year. Patients who died of AIDS are excluded from the analysis and patients are censored if they died of street drug use or an accident unrelated to ESRD treatment.

3. Expected deaths

A Poisson mixed effects model was used to produce national category-specific death rates [17], where the categories are defined by age, race, gender, ESRD primary diagnosis, vintage, and year. Based on the national category-specific death rates, the provider-specific expected deaths were calculated. The specific death model is as follows,

$$\begin{array}{cc}\hfill c_i\mid & \gamma ~\text{Poisson}\left(t_i{e}^{X_i\beta +Z_i\gamma }\right),\hfill \\ \hfill & \gamma ~N(0,{\sigma }^{2}I),\hfill \end{array}$$

where c_i is the number of deaths in category i, t_i is the total follow-up time of patients in category i, β is the vector of fixed effects, and γ is the vector of random effects. Fixed effects regressors included age, race, gender, ESRD primary diagnosis, vintage, year, and all two-way interactions among age, race, gender, and ESRD primary diagnosis. Random effects are the four-way interactions of age, race, gender, and ESRD primary diagnosis. Age was used as a continuous variable in the two-way interactions and a categorical variable (a category for each five years) in the main effect and four-way interactions. To stabilize the estimates for 1998, three years of data (1996, 1997, and 1998) were used with weights ⅓, ½ and 1, respectively.

4. The MLE

Assume there are K providers and provider k has death count Y_k,expected death μ_k (from the mixed Poisson model in Section 3), true SMRs ρ_k, and a Poisson model

$$Y_k\mid {\mu }_k,{\rho }_k~\text{Poisson}\left({\mu }_k{\rho }_k\right).$$

Then, the MLE of ρ_k and its estimated variance are

$$\begin{array}{cc}\hfill {\widehat{\rho }}_k^{ml}& =\frac{Y_k}{{\mu }_k}\hfill \\ \hfill \widehat{Var}\left({\widehat{\rho }}_k^{ml}\right)& =\frac{Y_k}{{\mu }_k^2}=\frac{{\widehat{\rho }}_k^{ml}}{{\mu }_k}.\hfill \end{array}$$ (1)

5. Bayesian inferences

The MLE is the traditional estimate and when the numbers of observed and expected deaths are sufficiently large, it performs well. However, for providers with a relatively small number of expected deaths, the MLE is very unstable and estimates for these providers will tend to be at the extremes. To stabilize estimates and structure subsequent inferences, we use a Bayesian hierarchical model:

$$\begin{array}{cc}\hfill Y_k\mid {\mu }_k,{\rho }_k& ~\text{Poisson}\left({\mu }_k{\rho }_k\right)\hfill \\ \hfill {\theta }_k& =\log \left({\rho }_k\right)\hfill \\ \hfill {\theta }_k\mid \zeta ,\lambda & ~N(\zeta ,{\lambda }^{-1})\hfill \\ \hfill \zeta & ~N(0,{\sigma }^2)\hfill \\ \hfill \lambda & ~\text{Gamma}(a,a^{-1}),\hfill \end{array}$$ (2)

where σ² and a are fixed, E(λ) = a · a^-1 = 1, var(λ) = a (a^-1)² a^-1

For model (2), the joint posterior distribution of (θ₁,...,θK, ζ λ) is

$$\begin{array}{cc}\hfill P& ({\theta }_1,\dots ,{\theta }_K,\zeta ,\lambda \mid Y)\hfill \\ \hfill & \propto \text{exp}\left\{\sum _{k=1}^K({\theta }_k{y}_k-{\mu }_k{e}^{{\theta }_k})-\frac{\lambda }{2}\left[\sum _{k=1}^K{({\theta }_k-\zeta )}^2+2a\right]-\frac{{\zeta }^2}{2{\sigma }^2}\right\}{\lambda }^{\frac{K}{2}+a-1}.\hfill \end{array}$$ (3)

5.1. The posterior mean (PM)

In the Bayesian approach, the posterior structures all inferences. For example, under squared-error loss $\mathrm{SEL}={({\rho }_k^{\mathrm{est}}-{\rho }_k)}^2$ on SMR, the posterior mean ${\tilde{\rho }}_k^{\mathrm{pm}}=E[\rho \mid \mathrm{data}]$ is the optimal estimate.¹ It shrinks the MLE toward a common value, striking an effective trade-off of bias and variance to produce a lower MSE than for the MLE. For example, when Y_k = 0 both the posterior mean and the posterior variance will be greater than 0, moving the estimate and its standard error away from the overly optimistic MLE = 0. For an almost uninformative prior on λ (a very small a), a large value of μ_k and most Y - values, this estimate will be close to the MLE.

5.2. Ranks and percentiles

Though the posterior means are optimal SMR estimates under squared-error loss, their histogram is underdispersed relative to the true, underlying SMR distribution. Furthermore, ranks or percentiles based on them are not optimal. The histogram based on the MLEs is overdispersed and percentiles based on them are far from optimal. Percentiles computed from the MLE can be particularly problematic because the high-variance estimates tend to be at the extremes. And percentiles based on p-values or Z-scores from testing the hypothesis that ρ_k = 1 create the opposite problem; low-variance estimates tend to be flagged as deviant. To see this, consider the Z-score,² $Z_k=\log \left({\tilde{\rho }}_k^{ml}\right)\sqrt{{\mu }_k}$. From (1), a large μ_k produces a small variance and so low variance providers tend to produce large |Z_k|.

To strike an appropriate signal-to-noise balance, we use the posterior distribution (3) and a loss function to optimize ranking or percentiling. Following Shen and Louis [15], p. 2297, for optimal ranks, let R_k be the true rank of provider k, then $R_k={\Sigma }_{j=1}^{K}I({\rho }_k\ge {\rho }_j)$. Without ties, the smallest ρ_k has rank 1 and so on. With T_k the estimated rank of ρ_k, for mean squared-error loss on the ranks $\mathrm{SELR}={(R_k^{\mathrm{est}}-R_k)}^2$, the posterior expected ranks ${\stackrel{‒}{R}}_k=E[R_k\mid Y]={\Sigma }_{j=1}^K\mathrm{Pr}({\rho }_k\ge {\rho }_j\mid Y)$ are optimal. These ${\stackrel{‒}{R}}_k$ are shrunken toward the mid-rank (K + 1)/2, thus compressing “percentiles” toward the 50th. The ${\stackrel{‒}{R}}_k$ are usually not integers, which can be attractive, since integer ranks can overstate distance and understate uncertainty. For example, $\left({\stackrel{‒}{R}}_k\right)$ of 1.0, 1.1, 3.9 indicate similarity between the first two providers, and a larger difference between the first two and the third. If integer ranks are required, rank the ${\stackrel{‒}{R}}_k$ to produce SEL optimal, integer ranks ${\widehat{R}}_k$.

In the sequel, we use percentiles rather than ranks. Percentiles are more directly interpretable and their statistical properties are almost independent of the number of providers K. We have:

$$\begin{array}{cc}\hfill P_k^{\mathrm{true}}& =100\frac{R_k}{K+1}\hfill \\ \hfill {\widehat{P}}_k& =100\frac{{\widehat{R}}_k}{K+1}\hfill \\ \hfill {\stackrel{‒}{P}}_k& =100\frac{{\stackrel{‒}{R}}_k}{K+1}.\hfill \end{array}$$ (4)

5.3. Percentile range probabilities

Even optimal percentiles will not perform well if there is insufficient statistical information. An empirical evaluation of percentile accuracy is available by computing the posterior probability that a provider's SMR is truly in a target percentile region (e.g., below the 20th, above the 80th). The computation is straightforward, though numerically challenging:

$$pr[P_k^{\mathrm{true}}\in [80,100]\mid \text{all data}]=\sum _{\ell =\left[.80K\right]}^K{\pi }_{k\ell },$$ (5)

where

$${\pi }_{k\ell }=pr\left[P_k^{\mathrm{true}}=\frac{\ell }{K+1}\mid \text{all data}\right].$$

Note that by conditioning on all data, we are also conditioning on the values of ${\stackrel{‒}{P}}_k$ and ${\widehat{P}}_k$. Therefore (5) produces a plot of these probabilities versus the optimal percentile.

Similarly, we can calculate the posterior probability that a provider's true SMR exceeds a threshold. For example, let ρ* be a cut-point defining poor performance (e.g., ρ* = 2.0). Then, the posterior probability that provider k exceeds the threshold is, pr[ρk > ρ* | all data].

5.4. Computation

Computing the MLE is straightforward. For the hierarchical model we use Markov Chain Monte Carlo (MCMC, see [2]). For Model (2), the joint posterior is (3) and the full conditional distributions of θ₁,...,θ_K, ζ, and λ are

$$P({\theta }_k\mid \text{all others})\propto \text{exp}\left\{{\theta }_k{y}_k-{\mu }_k{e}^{{\theta }_k}-\frac{\lambda }{2}{({\theta }_k-\zeta )}^2\right\},k=1,2,\dots ,K$$

$$P(\zeta \mid \text{all others})\propto \text{exp}\left\{-\frac{\lambda }{2}\sum _{k=1}^K{({\theta }_k-\zeta )}^2-\frac{{\zeta }^2}{2{\sigma }^2}\right\}$$

$$\lambda \mid \text{all others}~\text{Gamma}\left(\frac{K}{2}+a,{\left[\frac{1}{2}\sum _{k=1}^K{({\theta }_k-\zeta )}^2+a\right]}^{-1}\right).$$

To make the hyperprior “non-informative,” we chose a = 10^-4 and σ² = 10⁶. The Gibbs sampler was used to generate the λs. To generate the ζ s and all θ_ks, the Metropolis-Hastings method with symmetric Normal proposal densities was used. We ran the MCMC algorithm for 20,000 iterations with a burn-in period of 15,000. Trace plots show that the algorithm converged after 10,000 runs.

Posterior means, posterior credible intervals, ranks, percentiles, the percentile-range probabilities, and the threshold-crossing probabilities can be computed from the MCMC output [4, 11].

Sensitivity of results to the prior were checked by using a variety of values for σ² and different means and variances in the Gamma prior for λ. So long as σ² and the variance of the Gamma prior are sufficiently large, results are virtually identical to those presented. Importantly, the burn-in period can depend quite strongly on these variations. Serial dependence exists in the MCMC samples. Assuming the draws of θs are normally distributed and using AIC as the criterion, most of the series have lag 1 with autocorrelation (r) 0.61 - 0.66. This dependence affects the results slightly. Based on the lag 1 autocorrelation and the sample size (5000) used for inference, the effective size is approximately n(1 - r²) ≥ 5000(1 - 0.66²) = 2822, which is large enough to make inference. To remove the dependence, we also calculated the estimates using some subsets by taking every kth draw from the original series with k = 3, 5, 10, 20. Comparing to the estimates from all draws (the last 5,000 draws of the 20,000 iterations), the average of the four changes distributes from 1% to 10%; 70% of the changes are less than 5%.

6. Results

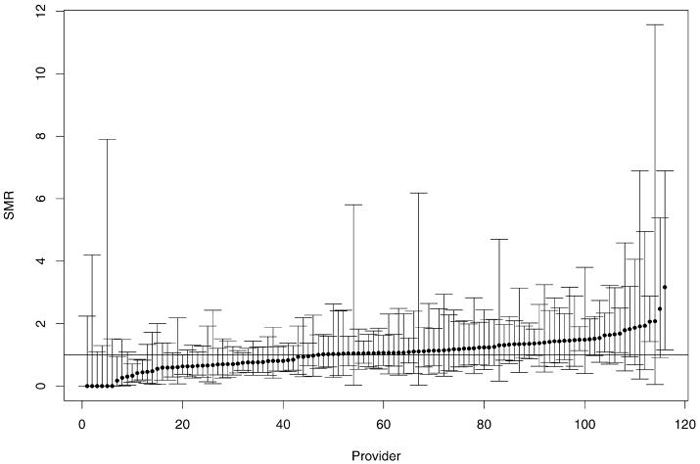
For a representative sample of providers in 1998, figure 1 displays the “caterpillar plot” of the MLE estimates and exact 95% confidence intervals (the 2.5th percentile to the 97.5th percentile of $\frac{Y}{\mu }$, Y ~ Poisson(μ)). Note that variances of the MLEs are quite large and have a broad range of values.

Figure 1.

MLE SMRs (dots) with their 95% exact confidence intervals. The horizontal line indicates SMR = 1 and the providers are sorted by their MLE SMRs.

Performance of MLE-based percentiles depends on the ratio of their variances to the spread of the prior distribution of SMRs and on the pattern of their relative variances. Table 1 shows this dependency as a function of patient-years by reporting the percentage of providers in patient-year categories with MLE-estimated percentiles in the bottom 25% (small SMRs), middle 50% (moderate SMRs), and upper 25% (large SMRs). If the MLEs had equal variability, each stratum would have approximately 25% of the providers with small estimated SMRs, 50% with moderate, and 25% with large. However, Table 1 shows that small providers usually had extreme (very large or very small) SMRs and that large providers usually had moderate SMRs. For example, in the <10 patient-years stratum, about 60% of providers had small SMRs, 30% had large SMRs, and only 10% had moderate SMRs. However, in the ≥250 patient-years stratum, no providers were in the small SMR category and approximately 87% were in the moderate SMR category.

Table 1.

Percentages of providers in small MLE SMR category (the bottom 25%), moderate MLE SMR category (the middle 50%), and large MLE SMR category (the upper 25%) for each provider stratum with strata defined by total follow-up patient-years.

Provider size	Upper 25%	Middle 50%	Upper 25%	No. of providers
>10	60	10	30	429
10-20	30	32	38	367
20-30	25	43	31	417
30-40	19	54	28	340
40-50	28	57	19	350
50-60	19	62	19	290
60-70	17	60	23	254
70-80	17	59	24	204
80-90	15	66	20	151
90-100	15	68	17	139
100-130	11	74	15	235
130-170	12	66	21	161
170-250	12	74	14	73
≥250	0	87	13	15

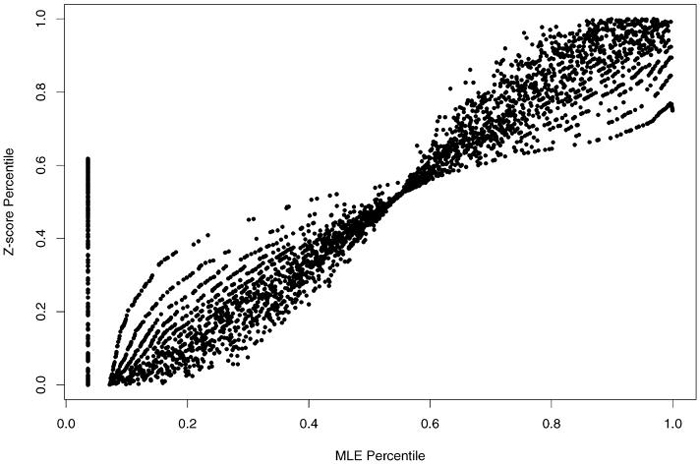
Hypothesis test Z-scores assessing whether an SMR significantly differs from 1 produced the ranks (percentiles) used to create Table 2. This table is identical in format to Table 1. In contrast to the distribution of SMRs in Table 1, here we see that small providers tend to generate Z-scores of moderate magnitude. Of small providers (<10 patient-years), 68% had moderate Z-scores (close to 0), 19% had large Z-scores (positive with large values), and only 13% had small Z-scores (negative with large values). Figure 2 displays the relation between MLE-based and Z-score based percentiles, further documenting these discrepancies. In figure 2, the points on the vertical line at the left of the figure correspond to the zero MLEs. They all have the same tie rank, 127. Each curve in the figure represents providers who have the same number of deaths. For example, the highest curve at the left half of the figure and the lowest curve at the right half of the figure represent the providers with 1 as the number of deaths. The relation between the MLE percentile and Z-score percentile is brought by ${\widehat{\rho }}^{ml}=\frac{y}{\mu }\mathrm{and}z=\log \left(\frac{y}{\mu }\right)\sqrt{\mu }$.

Table 2.

Percentages of providers in small Z-score category (the bottom 25%), moderate Z-score category (the middle 50%), and large Z-score category (the upper 25%) for each provider stratum with strata defined by total follow-up patient-years.

Provider size	Upper 25%	Middle 50%	Upper 25%
<10	13	68	19
10-20	22	50	29
20-30	26	47	27
30-40	21	52	27
40-50	31	49	20
50-60	25	53	22
60-70	27	47	26
70-80	28	46	26
80-90	26	50	25
90-100	29	47	23
100-130	33	37	29
130-170	34	33	33
170-250	26	48	26
≥250	13	47	40

Figure 2.

Z-Score percentile vs MLE percentile.

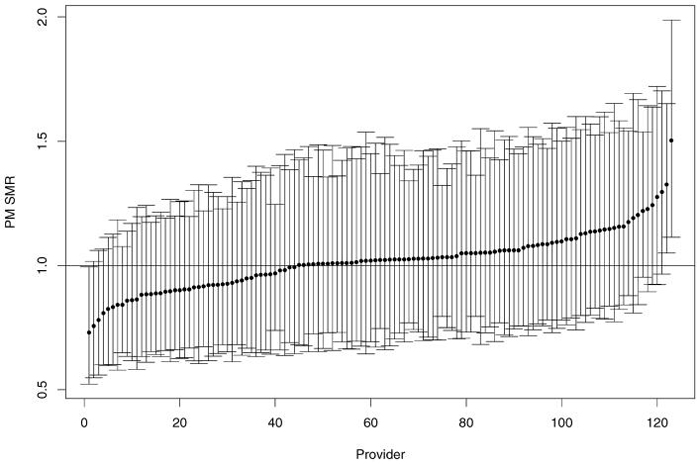
Figure 3 displays the PM estimates and their 95% posterior credible intervals (2.5% quantile to 97.5% quantile) for the random sample of providers in figure 1. The PMs are shrunken toward 1.0 relative to the MLEs; variability (as evidenced by posterior credible length) is substantially reduced, and the provider-specific posterior variance relation is substantially “flatter.”

Figure 3.

Posterior mean SMRs (dots) with their 95% posterior credible intervals sorted by PM SMRs.

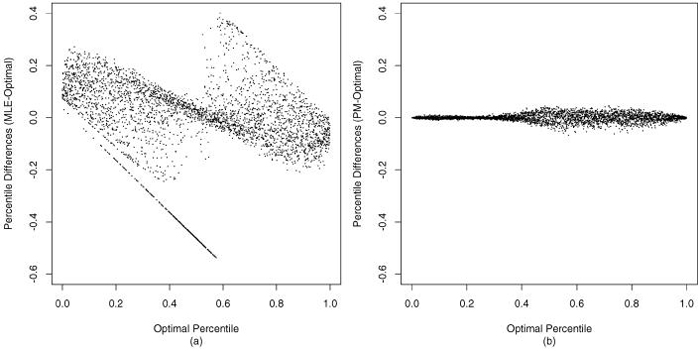
Comparing the optimal percentiles with MLE-based percentiles and the PM-based percentiles, we find that the PM-based are very close to the optimal values, but the MLE-based can be quite far from optimal. (See figure 4. The diagonal line of dots in figure 4(a) corresponds to zero MLEs.)

Figure 4.

The differences of (a) MLE percentile and (b) posterior mean percentile with optimal percentile, sorted by optimal percentile estimates.

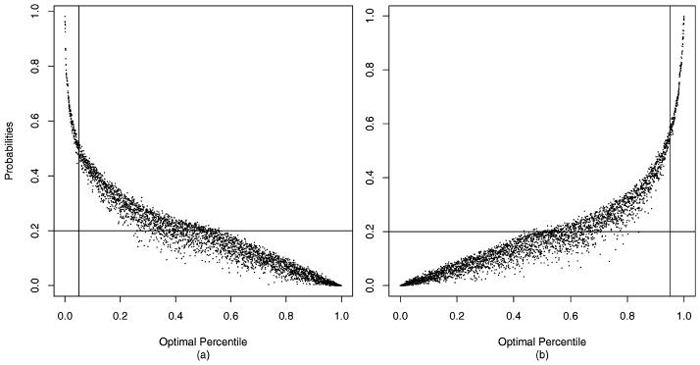
Figure 5 displays the percentile range (bottom and top quintile) probabilities computed in (5). Generally, the larger the optimally estimated percentile, the greater the probability of the true percentile being in the top quintile and the smaller the probability of being in the bottom quintile (and conversely). However, due to the differential variability of the estimates, these relations are not monotone. The relation is steeper for the relatively accurately estimated percentiles. If there were no information on providers or all were “stochastically equivalent,” the plot would be a horizontal line at 0.20; if information were infinite, the plot for dots below the 20th percentile would be 1.00 and 0 thereafter.

Figure 5.

(a) Pr($P_k^{\mathrm{true}}$ ≤ 20 | data) and (b) Pr($P_k^{\mathrm{true}}$ ≥ 80 data) sorted by optimal percentile estimates $\left({\widehat{P}}_k\right)$. The horizontal line is at 20; the two vertical lines are at the 5th and 95th percentiles, respectively.

Figure 5 shows that the “signal” in the data is relatively low. Note that providers with optimal percentiles below 5 have posterior probabilities of being in the bottom 20% greater than 0.44, but that providers with optimal percentiles at or near 20 have a probability of only about 0.3, showing that there is considerable uncertainty in which providers are truly in the bottom 20%. Probability of membership in the top quintile gives a similar message.

7. Discussion

Hierarchical models with optimal estimation of SMRs and percentiles are very effective in striking a trade-off between direct use of MLEs and use of Z-scores to identify the worst and the best performers. However, even the optimal procedure may perform poorly. Even if all aspects of the model are correct, our case study (see figure 5) and the evaluations of Lockwood et al. [11] show that the ratio of the prior variance to the variance of the MLEs (the signal-to-noise ratio) needs to be extremely large for optimal percentiles to perform well. Some improvement can be made by using a loss function for percentiles tuned to penalize more for errors in estimating extremes [16], but percentile estimates, even optimal estimates, must be used and used with caution and always accompanied by plots such as figure 5. The interprovider reliability is implicit in figure 5 in that predictive accuracy increases with increased reliability (the left-hand curve moves toward an “L” shape). Additional figures for cutpoints other than (0.20, 0.80) show performance for other definitions of “extreme.” Reliability can be investigated by computing pair-wise test statistics (differences of posterior means divided by the appropriate posterior standard errors); however, for the ranking goal displays like figure 5 are far more informative in that they consolidate performance over all providers.

Also, though the PMs, ${\widehat{P}}_k$ and ${\stackrel{‒}{P}}_k$ are optimal under squared-error loss and close to optimal for other loss functions, their operation may be unacceptable to some evaluators and providers. For example, PM-based SMRs for providers with a small number of patient-years will be close to 1 even when the MLE is far from 1, producing what may be viewed as unfair upgrading or downgrading. The model assumes a priori that after case mix adjustment provider-specific SMRs are stochastically identical. Shrinkage toward 1 is consistent with this exchangeability assumption and sends a message about uncertainty that is consistent with that delivered by confidence intervals.

Validity of statistical assessments depends on model validity. A correct case mix adjustment model is required to produce valid MLE-estimated SMRs and associated sampling distributions. A valid hierarchical model and relevant loss function are required for valid Bayesian assessments; increasing the demands on appropriate modeling. Percentile estimates are particularly sensitive to model features and research is needed to robustify the approach. Other issues have high leverage irrespective of the analytic approach. For example, rules for attributing deaths to providers for patients who switched providers must be developed and evaluated.

Provider characteristics are usually important predictors of provider performance. Including them in the model or not may also affect the validity of the model. The provider characteristics that are available in the data and that may affect death rate are “for profit” or “not for profit,” “hospital based” or “freestanding,” “reuse” or “non-reuse” of dialyzer, provider size, and water treatment methods. None of them were found significant with respect to death in analyses: This may be due to the efforts of the CMS to enhance consistency of care in the dialysis providers and the Clinic Guidelines published by the National Kidney Foundation and introduced in 1977.

Importantly, dialysis providers directly control certain aspects of care such as the amount of dialysis therapy, the treatment of anemia, and intervention to assist patients in management of dietary limitation. Other factors, such as reasons for hospitalization or the events in proximity of the death event, may be outside the direct control of dialysis units. These events associated with deaths may be attributable more directly to hospital care, physicians, and health plan policies and practices. These policies and practices may impact referrals for care and indications for hospitalization. To the extent that dialysis providers can influence care that is associated with mortality, SMR comparisons are relevant; however SMRs can overestimate the attributable risk. They are but one of many quality of care measures and others, such as hospitalization rates, should be considered.