Simple Formulas for Improved Point-Charge Electrostatics in Classical Force Fields and Hybrid Quantum Mechanical/Molecular Mechanical Embedding

Abstract

We present a simple damping scheme for point-charge electrostatics that could be used directly in classical force fields. The approach acts at the charge (or monopole) level only and allows the inclusion of short-range electrostatic penetration effects at a very low cost. Results are compared with density functional theory Coulomb intermolecular interaction energies and with several other methods such as distributed multipoles, damped distributed multipoles, and transferable Hermite-Gaussian densities. Realistic trends in the interactions are observed for atom-centered Mertz-Kollman corrected point-charge distributions. The approach allows increasing the selectivity of parameters in the case of metal complexes. In addition, two QM/MM calculations are presented where the damping function is employed to include the MM atoms located at the QM/MM boundary. The first calculation corresponds to the gas-phase proton transfer of aspartic acid through water and the second is the first step of the reaction catalyzed by the 4-oxalocrotonate tautomerase (4OT) enzyme. First, improved agreement is observed when using the damping approach compared with the conventional excluded charge method or when including all charges in the calculation. Second, in the case of 4OT, the damped charge approach is in agreement with previous calculations, whereas including all charges gives a significantly higher energy barrier. In both cases, no reparameterization of the van der Waals part of the force field was performed.

Introduction

For over 30 years, most of force fields such as AMBER [1], CHARMM [2], or GROMOS [3] have chosen a classical point-charge representation of electrostatics. Such representation has been refined over the last decade because of a direct fit of ab initio electrostatic potentials (ESP) [4, 5]. Coupled to efficient periodic boundary conditions techniques [6, 7], they have enabled long molecular dynamics simulations and have been convenient to the implementation of hybrid Quantum Mechanical/Molecular Mechanical (QM/MM) approach [8, 9]. More elaborate distributed multipole representations of the charge distribution [10–13] are also available and have been successfully used in the framework of new generation polarizable force fields [14–20]. Nevertheless, despite these sophistications, all approaches only approximate the longrange “multipolar” part of the ab initio intermolecular Coulomb interaction energy and neglect the so-called “penetration energy”, an overlap term arising in the ab initio reference calculations. In that context, several strategies have been explored in order to include such effects. Some approaches such as Sum of Interaction Between Fragment Ab initio (SIBFA; the updated version for the SIBFA program can be obtained from the authors) [14, 15] or the Effective Fragment Potential (EFP) [19] use damping functions [14, 20–22] coupled to distributed multipoles whereas others employ a simplified charge density treatment [23–25]. Among these latter methods, the Gaussian Electrostatic Model (GEM) [12, 15, 26–28], a new generation force field based on density fitting, uses a quasi-exact representation of electrostatics based on Hermite-Gaussian functions. This force field allows including long-range and short-range effects and has demonstrated the central importance of electrostatic penetration effects in the reproduction of quantum chemistry results within the framework of QM/MM embedding [27].

Relying on that work, we chose in this article to explore “simple” improvements of the electrostatic interaction energy treatments in classical nonpolarizable force fields and QM/MM using ESP-fitted point charges. To do so, we first detail a new damped charge approach and test the methodology on several complexes, including 10 stationary points on the water dimer energy [29] surface, two water clusters, and several water–metal complexes.

Subsequently, we explore the role of damped charges at the QM/MM boundary for two model reactions. An issue in QM/MM calculations is the boundary between the subsystems. In general the point charges associated with the MM atoms bonded to the QM/MM boundary atoms are zeroed out in order to avoid overpolarization of the QM wave function. However, it has been shown that this can have an impact on the results [30]. One way to overcome this problem is to “blur” the charges with a Gaussian function [31]. Here we explore the possibility of using damped charges instead, to improve the QM/MM boundary description. Note that other effects such as long-range electrostatics and polarization also play an important role [32, 33]. These effects are not considered in this work.

The investigated reactions are the gas phase proton transfer of aspartic acid through water and the first step of the reaction catalyzed by 4-oxalocrotonate tautomerase (4OT). In these two cases, we compare the damped charge results to conventional excluded charge results, as well as to results where all charges have been included for the QM/MM calculation (for the aspartic acid reaction).

Computational Details

REFERENCE CALCULATIONS

Constrained space orbital variations (CSOV) [34, 35] density functional theory reference electrostatic interaction energies have been computed using an in-house [36a] version of HONDO 95.3 [36b]. We have used the B3LYP [37, 38] functional coupled to the aug-cc-pVTZ basis set [39a] for all atoms except for metals [Mg(II), Zn(II), and Cu(I) cations] which the 6-31G** [39b] basis set was used. Mertz-Koll-man point charges [4] have been derived at the same level of theory using Gaussian 03 [40]. Damped and undamped multipole interactions have been performed using the SIBFA package [15a,b].

DAMPING SCHEMES

The classical formula for point-charge electrostatics is given below in a.u.:

$$E=(q_i{q}_j)/r_{\mathit{\text{ij}}}$$ (1)

where r_ij is the distance between atoms i and j bearing the charges.

It can be simply modified by replacing the charges by their damped value following:

$$E=(q_i*q_j*)/r_{\mathit{\text{ij}}}$$ (2)

where

$$q_i*=2q_i-(Z_i-(Z_i-q_i)(1-\text{exp}({\mathrm{\Omega }}_{\mathit{\text{ij}}})))$$ (3)

Here Z_i is the number of valence electrons of atom i, Ω_ij is a factor depending on the distance between atoms i and j and q_i denotes the charge of atom i. Several simple expressions can be derived for Ω_ij, we will here explore two of them:

$${\mathbf{\Omega }}_{\mathit{\text{ij}}}=\frac{{\mathit{\lambda }}_{\text{AB}}{r}_{\mathit{\text{ij}}}}{\frac{(Z_i-q_i)}{Z_i}}$$ (4)

where λ_AB is an adjustable parameter depending on the nature of the two interacting molecules A and B, Z_i is the number of valence electron of atom i, and q_i is its charge.

$${\mathbf{\Omega }}_{\mathit{\text{ij}}}=\frac{{\mathit{\lambda }}_{\text{AB}}{r}_{\mathit{\text{ij}}}}{R_{\text{vdw}}(i)+R_{\text{vdw}}(j)}$$ (5)

λ_AB is a transferable parameter, adjusted on water–water interactions and kept constant for all calculations. λ_AB is modulated by the R_vdw parameters which are effective van der Waals radius parameters (Å) specific for a given atom i or j. The values of the λ_AB and R_vdw parameters are given in the text.

QM/MM DETAILS

All QM/MM calculations were performed using a modified version of Gaussian 03 [40] interfaced to a modified version of TINKER [41]. The AMBER95 all-atom force field parameter set [42] and the TIP3P model for water [43] were used. In both cases we have used the pseudobond approach to model the QM/MM boundary [44, 45]. All geometry optimizations were performed at the HF/3–21G level following the iterative minimization procedure described by Zhang et al. [46]. All path optimization calculations were performed with the quadratic string method (QSM) as proposed by Burger and Yang [47]. The steepest descent results were obtained with the quadratic synchronous transit (QST3) algorithm of Gonzalez and Schlegel [48]. In all cases, the reactant and product (or intermediate for 4OT) of each path calculation were fully optimized using the default convergence in Gaussian 03 for the QM subsystem and a 0.2 kcal mol⁻¹ Å⁻¹ threshold for the MM gradient convergence. In the case of the optimizations that included the damped charges, the MM atoms with damped charges were frozen during the optimization procedure. After obtaining the end points, the paths were optimized using the iterative QSM scheme [47] until the MM environment converged to the same criteria as above for all points along the path. The QM/MM boundary was modeled using pseudobonds [44, 45] and damped charges were included in calculations as explained later.

Results and Discussion

INTERACTION ENERGIES: FROM WATER TO METALS

Both expressions of Ω_ij have been tested and appear to be quite equivalent for a given complex.

Expression 4 is very simple as it embodies a single parameter only. Nevertheless, it requires a parameterization of the sole parameter λ_AB which is specific for a given pair of interacting molecules. On the other hand, expression 5 should be transferable as λ_AB is found once and for all after fitting on a set of water dimers and can be extended to any system by parameterizing additional effective radii in the same spirit of the multipole damping function. For all calculations presented in this section, λ_AB will be fixed to −3.34, a value adjusted on water dimers.

Dimers and Clusters of Water Molecules

Van der Waals radii were chosen to be 1.56 and 1.2 Å for oxygen and hydrogen atoms, respectively, following Ref. [20].

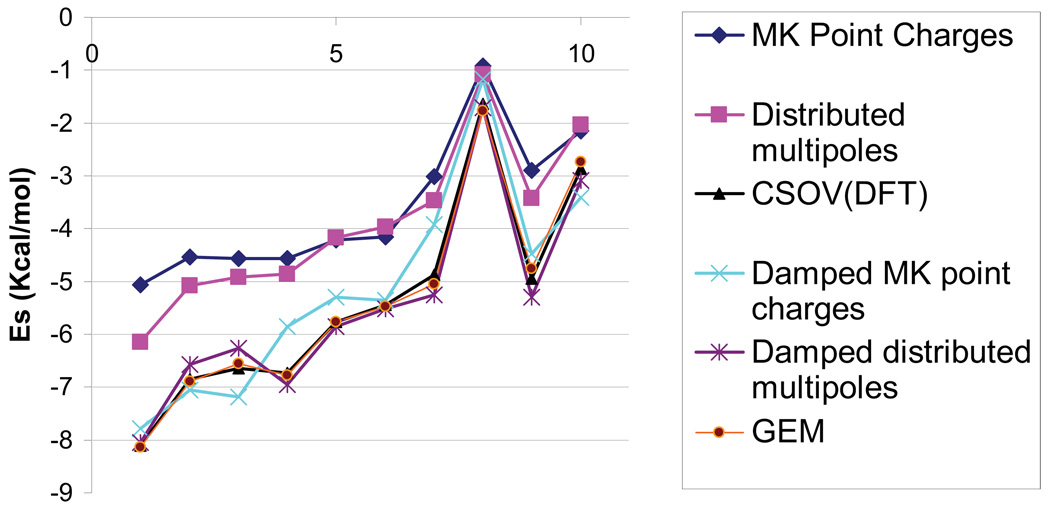
Figure 1 displays a comparison of different approaches including CSOV/B3LYP reference computations for intermolecular electrostatics in 10 stationary points on the water dimer potential-energy surface [29]. The damped approach [Eq. (5)] considerably reduces the error of the point-charge approach compared with references CSOV/B3LYP computations. Indeed, an average error of 0.48kcal/mol is observed on the 10 dimers which reduce the average error by a factor of 4, i.e., 1.88kcal/mol with respect to naked point charges. In fact, we can rank the damped and undamped point-charges approaches compared with existing methodologies such as GEM’s Hermite densities, Vigné-Maeder-Claverie distributed multipoles, damped distributed multipoles by computing electrostatics as follows:

$$\begin{array}{c}\text{DFT}>\text{GEM}>\text{Damped}\text{multipoles}\hfill \\ >\text{Damped}\text{point}\text{charges}>\text{Multipoles}\\ \hfill >\text{Point}\text{charges}\end{array}$$ (6)

This ranking clearly shows that the Hermite densities and damped multipoles are in better agreement with CSOV than the damped charges. However, the damped atom-centered point charges perform surprisingly better than distributed multipoles. This is due to the fact that naked distributed multipoles do not include the penetration energy which appears clearly nonnegligible compared with the ab initio results.

FIGURE 1.

Coulomb interaction for the 10 water dimers using different methods. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

We have also tested our damped point-charges approach on the two water clusters for which ab initio electrostatics were available at the same level [26]. We obtain a satisfactory transferability as damped point-charge electrostatics was found to be about −192.08 kcal/mol (compared with −186.84 kcal/mol for CSOV) and about −313.3 kcal/mol (compared with −309.38 kcal/mol for CSOV) for the 16 and 20 water molecule clusters, respectively.

Water–Metal Complexes

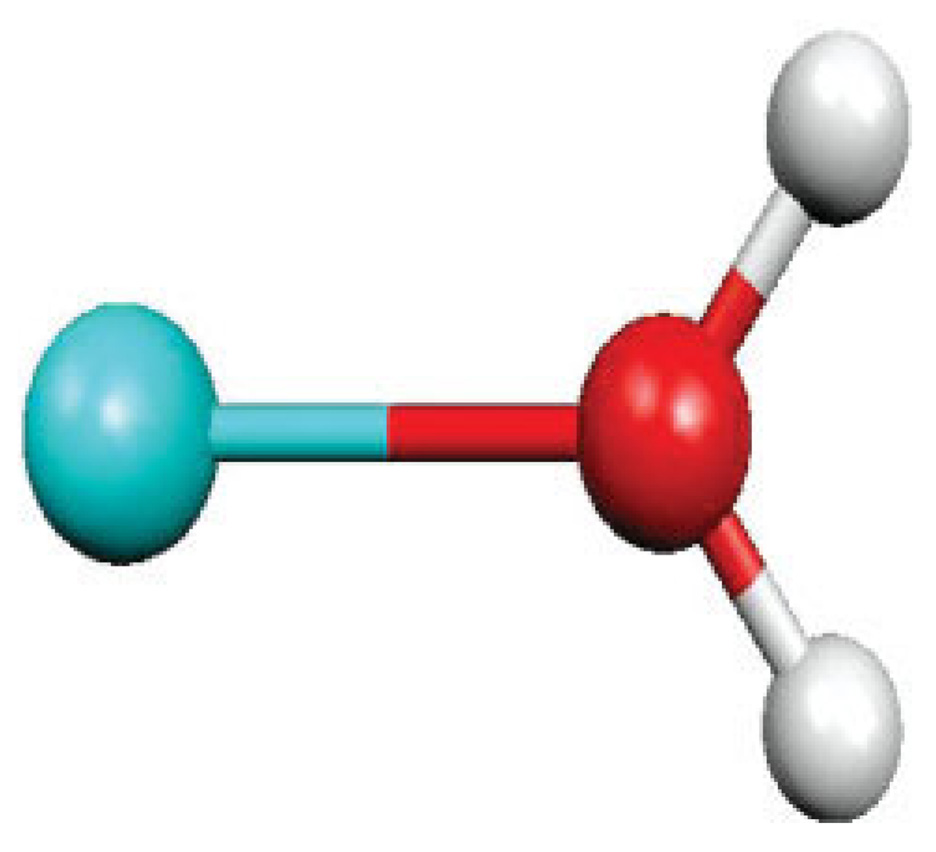
Scans of the metal cation-water oxygen distance have been performed in several C_2v metal(II)–water complexes (see Fig. 2). As seen in Table I, the approach is also performing well for metals as the damping allows including a specific parameterization of the +2 charge. Ca(II), Mg(II), and Zn(II) electrostatic interactions with water appear clearly different at a given O-Metal distance amounting to 1.9 Å, in agreement with ab initio computations. Conversely, simple point charges cannot discriminate the cations, thus giving in all cases an identical electrostatic energy of −46.53 kcal/mol. It is important to point out that such treatment could allow including relativistic effects in electrostatic by means of scalar relativistic pseudopotentials [36c,d] if aiming at considering heavy metals. As for the multipole damping function, the approach converges to the classical point-charge approximation at long range, in close agreement with ab initio benchmarks as penetration effects vanish.

FIGURE 2.

Water-M²⁺ complex orientation (M = Ca, Mg, Zn). [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

TABLE I.

Comparison of CSOV electrostatics to damped charge results for a water molecule interacting with a metal cation at a distance of 1.9 Å (Fig. 1)

Method	Ca(II)	Mg(II)	Zn(II)
CSOV	−83.81	−64.54	−76.39
Damped charge	−82.7	−65.71	−75.36
vdw	1.4	1.62	1.5

QM/MM

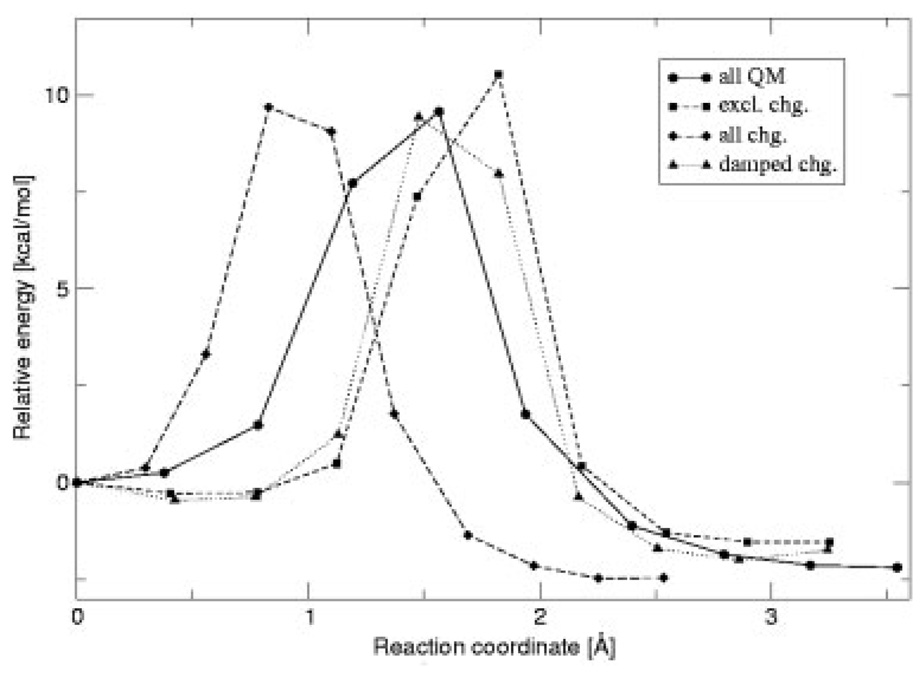
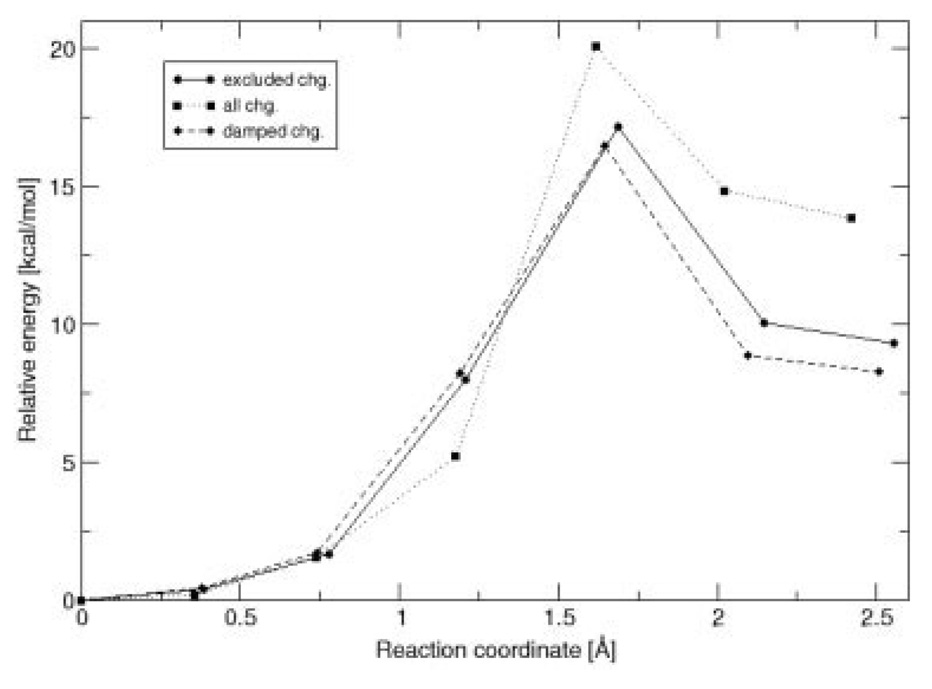
Two reactions were considered in order to test how the charges obtained with the damping function perform in QM/MM calculations. The additional effective radii (different from O and H) were taken from Ref. [20]. No reparameterization of the force field’s van der Waals parameters was made. The first reaction tested is the gas phase proton transfer of aspartic acid to water. In this case, five calculations were performed: in the first two, all atoms are treated quantum mechanically, while for the remaining three only the side-chain of Asp and the water molecule are included in the QM region. The reactions were treated as follows: (1) a QST3 calculation with all atoms treated at the QM level to determine the correct energy barrier; (2) a QSM path optimization with all atoms treated at the QM level; (3) a QM/MM QSM path optimization with excluded charges [46]; (4) QM/MM QSM path optimization including all charges in the MM subsystem; and (5) a QM/MM QSM path optimization including all charges with damped charges on the atoms directly bonded to the pseudoatom. In this case, the used λ_AB for the damping function [Eq. (5)] was −7.0. Indeed, λ_AB needs to be reparameterized in order to also include damping for the in-tramolecular charge interactions (only intermolecular interactions were considered previously) and to overcome the lack of explicit force-field polarization treatment at the boundary. An energy barrier of 10 kcal/mol is obtained with QST3 for the Asp proton transfer, compared with 9.6 kcal/mol obtained from QSM computations for path 2 (all QM atoms). This small difference is due to the fact that QSM does not have an explicit transition state (TS) optimizer [47]. Nevertheless, the agreement for the structures and the barriers are sufficient for the purpose of comparison. Furthermore, in this case, we are interested in comparing between the different paths calculated with QSM. As shown in Figure 3, the path including all charges gives TS that is too early along the reaction coordinate. For the excluded charge path, the shape is similar to the all QM atom path; however, the barrier is overestimated. On the other hand, the use of damped charges gives the correct energy, and the correct position for the TS. In all cases the calculated critical points (namely the structures of the reactants, TS, and products) are very similar for all paths, with deviations less than 0.05 Å (see Fig. 4).

FIGURE 3.

Calculated paths for the Asp reaction.

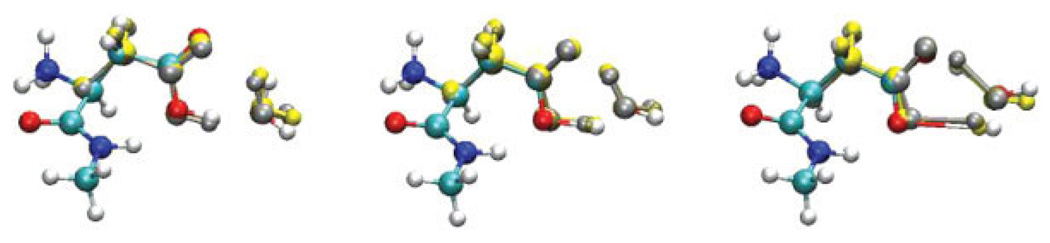
FIGURE 4.

Superposition of the calculated critical points along the calculated paths: reactant (left), transition state (middle), and product (right), for the Asp proton transfer reaction. Color code: CPK = all QM atoms; orange = excluded charge; brown = all charges included; silver = damped charges. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

The second test corresponds to the first step of the reaction catalyzed by 4OT. 4OT is a bacterial enzyme that catalyzes the isomerization of 2-oxo-4-hexenedioate to 2-oxo-3-hexenedioate [49] and is part of a metabolic pathway that enables the Pseudomonas putida bacteria to use aromatic hydrocarbons as its sole source of energy.

We have performed extensive QM/MM studies on this system previously [50–52]. In this case, the setup of the QM and MM subsystems is the same as in our previous studies for the calculations for all three paths. The three paths correspond to: (1) QM/MM QSM path optimization with excluded charges (similar to our previous studies [52]); (2) QM/MM QSM path optimization including all charges in the MM subsystem; and (3) QM/MM QSM path optimization including all charges, with damped charges [λ_AB = −5.0 in Eq. (5)] on the atoms directly bonded to the pseudobond atoms.

Figure 5 shows the three paths calculated for the 4OT reaction. As expected a large increase in the barrier is observed for path 2, for which all charges are included. This is due to the incorrect polarization of the QM wavefunction by the charges that are in close proximity to the QM/MM boundary. In comparison, the path calculated with damped charges is in good agreement with the conventional QM/MM path. This shows that the damped charges indeed provide the correct polarization environment for the QM subsystem, which allows a proper mechanistic description of the reaction.

FIGURE 5.

Calculated paths for the first step of the 4OT reaction.

Conclusion

Other effects, such as polarization (see Ref. [15a] together with references therein, and Ref. [33]), occurring in intermolecular interactions are implemented in advanced force fields, but here we have shown that a damped charge approach could be of interest for the future development of improved classical force fields. Indeed, we noticed an improvement of the agreement with ab initio calculations, as electrostatics damping allows including part of the penetration energy. The resulting point-charge energies are better than those obtained using naked “undamped” distributed multipoles. The approach offers increased accuracy and is interesting for the specific case of metal cations. Indeed, limited implementation of damped charges could be easily included in AMBER or CHARMM to improve the cation specificity which is usually completely dependent on the Lennard-Jones parametrization, because, from the sole electrostatic point of view, it is impossible to discriminate between different ions bearing the same charge. Consequently, such simple framework could be the basis for the development of simple and accurate polarizable force fields. Preliminary QM/MM tests have shown that the approach can be in principle employed to include the charges at the boundary, which are usually neglected in QM/MM calculations, by damping the charges close to the boundary without any reparameterization of the van der Waals component of the force field. These results show that the reaction paths computed using damped charges are in good agreement with reference QM paths. This last point opens the possibility of a specific parameterization of charges close to QM/MM boundary that could be automatically damped to perform more accurate QM/MM embeddings.