Folding simulations of a three-stranded antiparallel β-sheet peptide

Abstract

Protein folding is a grand challenge of the postgenomic era. In this paper, 58 folding events sampled during 47 molecular dynamics trajectories for a total simulation time of more than 4 μs provide an atomic detail picture of the folding of a 20-residue synthetic peptide with a stable three-stranded antiparallel β-sheet fold. The simulations successfully reproduce the NMR solution conformation, irrespective of the starting structure. The sampling of the conformational space is sufficient to determine the free energy surface and localize the minima and transition states. The statistically predominant folding pathway involves the formation of contacts between strands 2 and 3, starting with the side chains close to the turn, followed by association of the N-terminal strand onto the preformed 2–3 β-hairpin. The folding mechanism presented here, formation of a β-hairpin followed by consolidation, is in agreement with a computational study of the free energy surface of another synthetic three-stranded antiparallel β-sheet by Bursulaya and Brooks [(1999) J. Am. Chem. Soc. 121, 9947–9951]. Hence, it might hold in general for antiparallel β-sheets with short turns.

Theoretical and experimental studies have provided insights into the protein folding process (1). Yet, a more detailed understanding is required not only to predict the structure of a given amino acid sequence but also for protein engineering purposes, e.g., to design a sequence for a given fold. For the latter, applications relevant to biomedicine are possible. Most proteins contain regular elements of secondary structure, α-helices, and/or β-sheets. Therefore, it generally is thought that elucidating the formation of regular secondary structure elements will improve the understanding of the protein folding reaction (2–4). As it is currently not yet feasible to simulate the folding of a protein by using molecular dynamics (MD) simulations with an all-atom model (5), the common approach taken in the past is to unfold starting from the native state (6, 7). Reversible folding simulations have been limited to non-natural oligopeptides in methanol (8) or peptides with an implicit solvation model and adaptive umbrella sampling (9).

Beta3s is a designed amino acid sequence (Thr₁-Trp₂-Ile₃-Gln₄-Asn₅-Gly₆-Ser₇-Thr₈-Lys₉-Trp₁₀-Tyr₁₁-Gln₁₂-Asn₁₃-Gly₁₄-Ser₁₅-Thr₁₆-Lys₁₇-Ile₁₈-Tyr₁₉-Thr₂₀), and its solution conformation has been studied by NMR (10). Nuclear Overhauser enhancement (NOE) and chemical shift data indicate that at 10°C Beta3s populates a single structured form, the expected three-stranded antiparallel β-sheet conformation with turns at Gly-6–Ser-7 and Gly-14–Ser-15, in equilibrium with the random coil. The β-sheet population was 13–31% based on NOE intensities and 30–55% based on the chemical shift data (10). Furthermore, Beta3s was shown to be monomeric in aqueous solution by equilibrium sedimentation and NMR dilution experiments (10). In this report, the folding behavior and energy surface of Beta3s are investigated by MD simulations with an implicit model for the solvent. This approximation is justified by recent explicit water MD studies, which have shown that the solvent does not play a detailed role in the folding of Betanova, a synthetic three-stranded antiparallel β-sheet peptide with Asn-Gly as turn residues (11). The reversible folding to the correct NMR conformation is demonstrated by 58 folding events (1, 7, and 50 folding events at 300, 330, and 360 K, respectively) occurred during 47 MD trajectories, each lasting between 50 and 250 ns, with an average of about 1.4 folding events every 100 ns.

Methods

Model.

Beta3s was modeled by explicitly considering all heavy atoms and the hydrogen atoms bound to nitrogen or oxygen atoms (12). The aqueous solvent was approximated by an implicit model based on the solvent-accessible surface (13). In this approximation, the mean solvation term is given by:

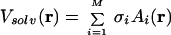1

for a molecule having M heavy atoms with Cartesian coordinates r = (r₁,… ,r_M). A_i(r) is the solvent-accessible surface area of heavy atom i, computed by an approximate analytical expression (14) and using a 1.4-Å probe radius. Furthermore, ionic side chains were neutralized (15) and a linear distance-dependent dielectric function [ɛ(r) = 2r] was used for the electrostatic interactions. The charmm param19 default cutoffs for long-range interactions were used, i.e., a shift function (12) was used with a cutoff at 7.5 Å for both the electrostatic and van der Waals terms. This cutoff length was chosen to be consistent with the parametrization of the force field. The model contains only two σ parameters: one for carbon and sulfur atoms (σ_C,S = 0.012 kcal/molŲ), and one for nitrogen and oxygen atoms (σ_N,O = −0.060 kcal/molŲ) (16). There is no bias in the model toward any particular secondary structure type. In fact, exactly the same force field and implicit solvation model have been used recently to reversibly fold to the correct conformation by standard MD three α-helical peptides (of 15, 21, and 31 residues), a β-hairpin of 12 residues, and another triple-stranded antiparallel β-sheet whose sequence identity with the one of the present manuscript is only 15% (ref. 17 and unpublished data). Furthermore, the same force field and solvation energy were used to demonstrate with an atomistic model the non-Arrhenius behavior of the temperature dependence of the folding rate (17).

Simulations.

All simulations and part of the analysis of the trajectories were performed with the charmm program (12). Constant temperature MD simulations were performed by weak coupling to an external bath with a coupling constant of 5 ps (18). The shake algorithm (19) was used to fix the length of the covalent bonds involving hydrogen atoms, which allows an integration time step of 2 fs. The nonbonded interactions were updated every 10 dynamics steps, and coordinate frames were saved every 10 ps. Table 1 contains a list of the simulations.

Table 1.

Simulations performed

Starting conformation	Temperature, K	No. of simulations	Length,* ns	No. of folding events
Extended	300	1	100	1
Folded	300	1	200	0
Extended	330	1	120	1
Folded	330	3†	200–250 (650)	6
Folded	360	1	200	4
Random	360	40‡	50–150 (2800)	46

^*The total simulation time is in parentheses. 

^†Different initial assignments of the velocities. 

^‡ Five-thousand structures were generated by randomizing the dihedral angles of the rotatable bonds, followed by 1,000 steps of energy minimization. Structures with one or more native contacts were discarded. The 40 structures with the most favorable energies were retained as starting conformations. Their average C_α rms deviation from the mean NMR model is 7.4 Å. 

Results and Discussion

Reversible Folding.

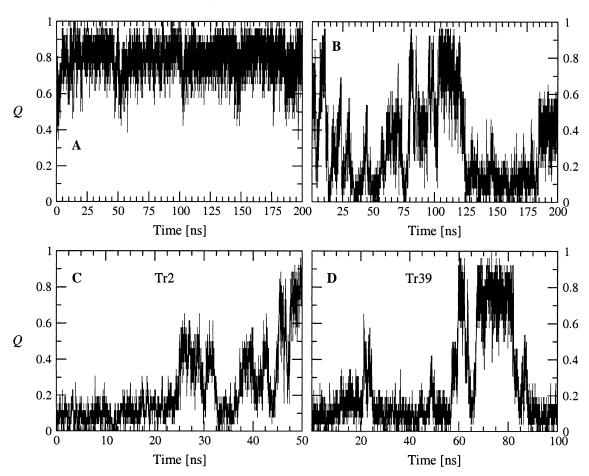
Because of the small number of NOEs the NMR conformations are not well defined. Hence, to obtain a starting conformation, a 100-ns simulation at 300 K was initiated from a completely extended conformation. It folded into an antiparallel three-stranded β-sheet at about 75 ns. This structure was the starting point of a 200-ns simulation at 300 K. The Cα rms deviation between the average structure over the whole 200-ns simulation and the average NMR conformation is 1.9 Å. Average interproton distance violations were derived from the 200-ns run as d_viol = <r(t)⁻⁶>^−1/6 − r_exp, where r(t) is the interproton distance at simulation time t, r_exp is the NOE upper distance limit (10), and <> represents a time average. It is striking that the 26 NOE restraints are satisfied (d_viol < 0.0 Å for 16 distances and d_viol < 1.0 Å for seven distances), except for three distances between C_ɛ3H Trp-2−C_β'H Asn-13, C_ɛH Tyr-11−C_γH₃ Ile-18, and C_αH Thr-1−C_δH₃ Ile-3, with d_viol values of 3.9 Å, 2.7 Å, and 3.3 Å, respectively. The four NOEs with strong and medium-strong intensity concerning C_αH−C_αH distances are satisfied with d_viol < 0.0 Å (Trp-2–Tyr-11, Gln-4–Lys-9, Trp-10–Tyr-19, and Gln-12–Lys-17). Only type II′ turns were observed at 300 K. This result is consistent with the high statistical probability of Gly and Ser at type II′ turn positions i+1 and i+2, respectively (20). The conformations sampled at 300 K were used to define a list of 26 native contacts (Table 2). Q is a progress variable defined as the fraction of native contacts that are formed, and its time dependence is plotted to monitor the change in structure during folding (Fig. 1). At 300 K, there are few unfolding events during which the system reaches conformations with Q < 0.4 but only transiently (Fig. 1A). These take place in the first 5 ns, and at about 57 ns and 197 ns. At 360 K, four folding and five unfolding events are sampled in a 200-ns simulation started from the three-stranded β-sheet (Fig. 1B). Most of these happen in the first 100 ns, whereas in the second half of the simulation the folded state is present from about 105 to 120 ns and Beta3s is denaturated from about 125 ns to 200 ns.

Table 2.

List of native contacts in Beta3s

1st residue	2nd residue	Strands	Location with respect to turn
Hydrogen bonds
Thr-1 O	H Gln-12	1-2	Distal
Ile-3 H	O Trp-10	1-2	Distal
Ile-3 O	H Trp-10	1-2
Asn-5 H	O Thr-8	1-2	Proximal
Asn-5 O	H Thr-8	1-2	Proximal
Lys-9 O	H Thr-20	2-3	Distal
Tyr-11 H	O Ile-18	2-3	Distal
Tyr-11 O	H Ile-18	2-3
Asn-13 H	O Thr-16	2-3	Proximal
Asn-13 O	H Thr-16	2-3	Proximal
Side-chain contacts
Thr-1	Gln-12	1-2	Distal
Trp-2	Tyr-11	1-2	Distal
Ile-3	Gln-12	1-2	Distal
Ile-3	Trp-10	1-2	Distal
Gln-4	Lys-9	1-2	Proximal
Asn-5	Thr-8	1-2	Proximal
Thr-8	Trp-10	2-2
Trp-10	Lys-17	2-3	Distal
Trp-10	Tyr-19	2-3	Distal
Tyr-11	Asn-13	2-2
Tyr-11	Ile-18	2-3	Distal
Gln-12	Lys-17	2-3	Proximal
Asn-13	Thr-16	2-3	Proximal
Asn-13	Ile-18	2-3
Thr-16	Ile-18	3-3
Ile-18	Thr-20	3-3

A hydrogen bond is defined as native contact if the O ⋯ H distance is smaller than 2.6 Å for more than 50% of the conformations saved during the first 100 ns of the 300-K simulation started from the folded state (Fig. 1A). An interaction between side chains of residues not adjacent in sequence is defined as a native contact if the average distance between geometrical centers is smaller than 6.7 Å. 

Figure 1.

Time dependence of the fraction of native contacts Q. (A) 300-K simulation started from the folded conformation. (B) 360-K simulation started from the folded conformation. (C and D) 360-K simulations started from random conformations 2 and 39.

To evaluate the effect of the solvation term, a 200-ns test simulation was performed at 360 K from the extended conformation without the solvent-accessible surface term. No folding event was observed. Therefore, although at 360 K the solvent-accessible surface solvation energy (Eq. 1) varies between the fully unfolded and folded states on average by only 3 kcal/mol, which is caused by the relatively small size of the system, it has a non-negligible effect on the free energy surface.

Folding Mechanism.

Sampling a statistically significant number of folding events at 300 K and 330 K is too time consuming. Therefore, the thermodynamics and kinetics of folding were investigated at 360 K, with 40 simulations started from random conformations having Q = 0. The 13 simulations that did not reach the folded state (defined by a rather stringent criterion of Q > 0.85 to neglect transient formation of the folded structure) in 50 ns were restarted and run for an additional 50 ns or 100 ns. After 150 ns, only two of 40 simulations did not reach a Q value of at least 0.85. Hence, the folded state is reached irrespective of the starting conformation within a reasonable amount of time (150 ns require approximately 10 days on a 500-MHz Pentium III processor). A typical folding event took place in the first 10 ns of trajectory 1 (Tr1, Figs. 2 and 3). The first contacts occurred close to the Gly-14–Ser-15 turn followed by the formation of the β-hairpin. Finally, the first strand consolidated on the preformed β-hairpin. At values of Q < 0.3, some small elements of non-native secondary structure are formed transiently, as illustrated by the helical turn at 5.56 ns of Tr1 (Fig. 2 Top). This also happened in other trajectories and provides further evidence that the force field and solvation model do not have a bias toward the β-sheet conformation. In Tr1, nearly 25% of the unfolded conformations have their backbone dihedral angles in the α-helical region, with (ϕ,ψ) average values of (−86.9, −50.4) ± (7.1, 6.5). The remaining 75% of the unfolded structures populate mainly the β-sheet region, with (ϕ,ψ) average values of (−103.9, 113.9) ± (12.4, 13.0). Similar results were obtained for the simulation at 330 K shown in Fig. 4. Folding is completed at about 8 ns in Tr1 (Fig. 3A), 46 ns in Tr2 (Fig. 1C), and 60 ns in Tr39 (Fig. 1D). Intermediates with Q values of about 0.4–0.6 often are observed before folding. They are essentially β-hairpins, i.e., most of the native contacts between two strands are formed (Fig. 2 Middle). In Tr2, most of the contacts between the first and second strands are formed between 25 and 30 ns, whereas most of the interactions between the second and third strands are present between 37 and 41 ns (Fig. 1C).

Figure 2.

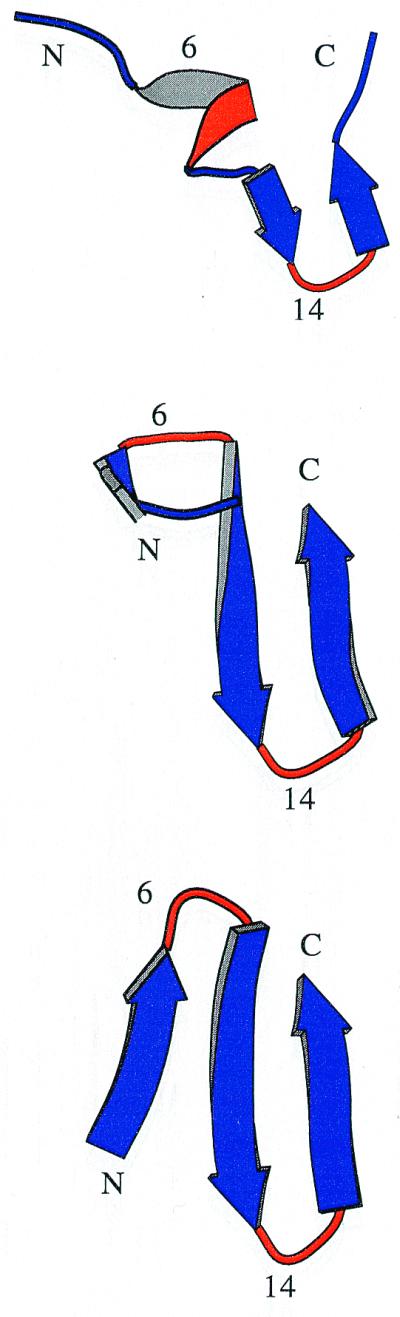
Ribbon representation of three snapshots from a 360-K trajectory started from random conformation 1 (Tr1) at (Top) 5.56 ns (Q = 0.19, rms deviation from the average NMR conformation of 6.2 Å), (Middle) 5.84 ns (Q = 0.38, rms deviation = 3.7 Å), and (Bottom) 9.71 ns (Q = 0.96, rms deviation = 2.0 Å). The secondary structure was assigned with the dssp program (28) and plotted with molscript (29). The regions of the sequence corresponding to the turns (Gly-6–Ser-7 and Gly-14-Ser-15) are colored in red.

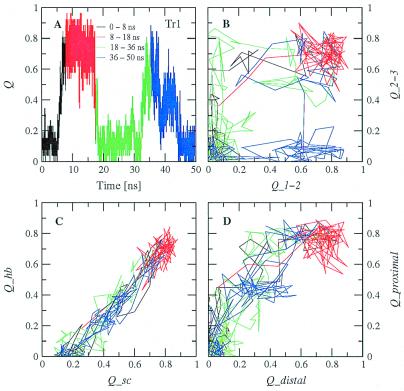
Figure 3.

(A) Time dependence of the fraction of native contacts Q for Tr1. (B) Projection into the Q₁₋₂Q₂₋₃ plane, (C) the Q_scQ_hb plane, and (D) the Q_distalQ_proximal plane for the same trajectory. The two folding events are shown with the black and green curves, and the two unfolding events are shown with the red and blue curves. (B–D) Each point corresponds to the average over 100 ps (10 conformations).

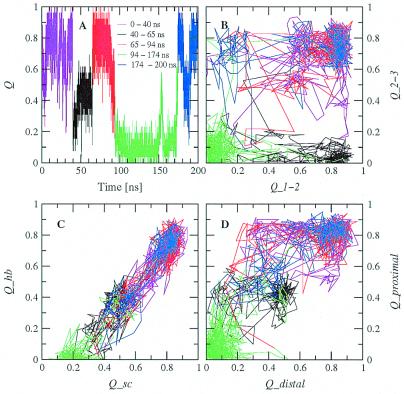
Figure 4.

Same as in Fig. 3 for a 330-K trajectory started from the folded state.

Because of its complexity, more than one progress variable is required to monitor the folding process (21). The following subsets of native contacts are particularly appropriate for a clear description of the folding pathways. Q₁₋₂ is defined as the fraction of the 11 contacts (five hydrogen bonds and six side-chain interactions) formed between strands 1 and 2, whereas Q₂₋₃ as the fraction of the 11 contacts between strands 2 and 3 (Table 2). Q_sc and Q_hb are the fraction of the 16 side-chain contacts and 10 hydrogen bonds, respectively. Q_distal and Q_proximal are the fraction of the 11 contacts far away from the turns (four hydrogen bonds and seven side-chain interactions) and the eight contacts close to the turns (four hydrogen bonds and four side-chain interactions), respectively. Two-dimensional projections into these progress variables are useful to illustrate the folding mechanism. There are two folding and two unfolding events in Tr1 (Fig. 3). The projection into the Q₁₋₂Q₂₋₃ plane indicates that in both folding events there is first the formation of most of the contacts between strands 2 and 3, followed by the association of the N-terminal strand onto the preformed 2–3 β-hairpin (Fig. 3B). Of the two unfolding events, the first is essentially the reverse of folding, whereas in the second the loss of the contacts between strands 2 and 3 precedes the rupture of 1–2 interstrand contacts. The projection into the Q_scQ_hb plane yields an almost straight line, which intersects the Q_sc axis at Q_sc ≈0.2 (Fig. 3C). This is mainly because of the presence of intrastrand side-chain contacts that precede the formation of interstrand side-chain contacts and hydrogen bonds. In general, contacts propagate from the turn as can be seen in the projection into the Q_distalQ_proximal plane (Fig. 3D). For all types of projections, a very similar behavior emerges from the trajectories at 330 K (Fig. 4). Although the exact order of events might depend on the amino acid sequence, the early formation of the turn contacts is in accord with recent implicit solvent MD simulations of Beta3s and two other β-sheet-forming synthetic peptides (22), as well as a statistical mechanical model developed to explain laser temperature-jump experiments of the folding of the β-hairpin fragment (residues 41–56) of protein G B1 (23). On the other hand, recent computational studies on the same fragment of protein G B1 have shown different behavior (24, 25).

Energy Surface at 360 K.

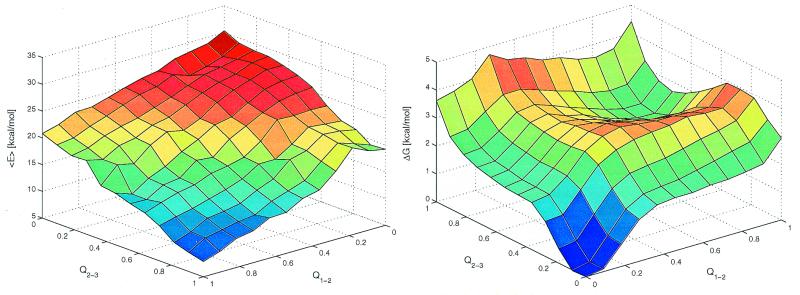
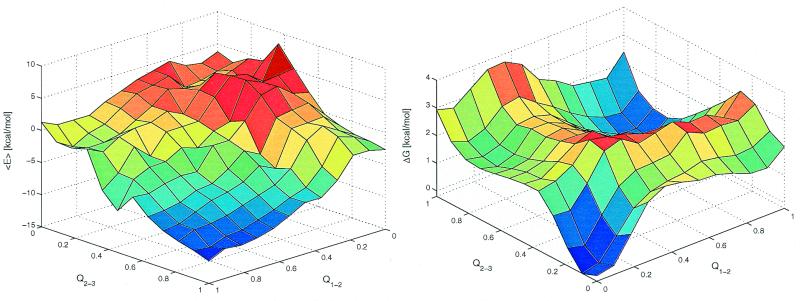
The average effective energy <E> (intramolecular plus solvation) as a function of Q₁₋₂ and Q₂₋₃ has the global minimum corresponding to the fully folded conformation (Fig. 5 Left). The free energy surface shows the global minimum corresponding to the denaturated state and a local minimum in the proximity of the folded state at (Q₁₋₂ ≈0.9, Q₂₋₃ ≈0.7) separated by relatively low free energy barriers of about 4 k_BT to 5 k_BT (Fig. 5 Right). The free energy difference between the folded (Q > 0.7) and denaturated (Q < 0.3) states is 1.7 kcal/mol and therefore 360 K is above the melting temperature of Beta3s. In addition, there are two ensembles of conformations with free energy comparable to the one of the folded state. These are β-hairpins with either Q₁₋₂ ≈0 and Q₂₋₃ ≈0.6 or Q₁₋₂ ≈0.6 and Q₂₋₃ ≈0. The free energy surface shows a relatively high degree of symmetry with respect to the diagonal of the Q₁₋₂Q₂₋₃ plane, which is caused by the partial symmetry in the sequence and structure of Beta3s and the choice of progress variables. The smoothness of the free energy surface indicates that the statistical error is small (see also Fig. 5 legend). Two transition state regions are located at TS1 (Q₁₋₂ ≈0.4, 0.5 < Q₂₋₃ < 0.8) and TS2 (0.5 < Q₁₋₂ < 0.8, Q₂₋₃ ≈0.4), i.e., after formation of a β-hairpin. They are defined by thermodynamic rather than kinetic criteria because the calculation of the transmission coefficient (21) is computationally very expensive. Because the effective energy has an almost downhill surface, the barriers arise from the loss of conformational entropy associated with fixing about two-thirds of the chain into a β-hairpin. On the triple-stranded β-sheet side of the barriers the slope is more gentle than on the coil side because the entropy loss is smaller because only one strand has to be fixed instead of two in the β-hairpin. Furthermore, the consolidation of the unstructured strand on the preformed β-hairpin is enthalpically more favorable because of the formation of a larger number of nonbonding interactions than in the β-hairpin formation. The lower barrier in TS1 (free energy difference between TS1 and denaturated state of about 3 kcal/mol) corresponds to the predominant folding pathway, which is observed 33 times, whereas 17 folding events go through the TS2 transition state (barrier of about 3.5 kcal/mol). For unfolding, 24 trajectories follow the route over the TS1 and 17 over the TS2 transition state. The main transition states are not an expanded β-sheet; rather they contain an almost fully formed β-hairpin with unstructured N-terminal strand (in TS1) or C-terminal strand (in TS2) in agreement with the explicit water MD studies of Betanova (11). On average, 2.9 side-chain contacts and 1.1 hydrogen bonds are formed between strands 1 and 2 in the conformations with Q₁₋₂ = 0.4 and Q₂₋₃ = 0.6. Similarly, 2.8 side-chain contacts and 1.2 hydrogen bonds are formed between strands 2 and 3 in the conformations with Q₁₋₂ = 0.6 and Q₂₋₃ = 0.4. This indicates that native interactions between side chains are more important than hydrogen bonds to drive the folding of Beta3s as found previously in simulations of a β-hairpin (24, 25) and Betanova (11). In the unstructured hairpin, the most frequent contacts in the transition state are close to the turn. They are Asn-13–Thr-16 (87%) and Gln-12–Lys-17 (67%) in TS2 and Asn-5–Thr-8 (79%) and Gln-4–Lys-9 (64%) in TS1. That the interactions between Asn and Thr (at turn positions i and i+3, respectively) promote β-hairpin folding is consistent with NMR data (37). The residues Gln-4 and Lys-9 are involved in the only NOE with strong intensity and residues Gln-12 and Lys-17 in one of the three NOEs with intensity intermediate between strong and medium.

Figure 5.

Average effective energy (<E>, Left) and free energy surface (ΔG, Right) at 360 K as a function of the fraction of native contacts between residues in strands 1 and 2 (Q₁₋₂), and between residues in strands 2 and 3 (Q₂₋₃). A total of 3.0 × 10⁵ conformations sampled during the 41 simulations at 360 K were used. To make it more clear, the plot of ΔG is rotated with respect to the one of <E> by 180° around an axis going through the center of the horizontal plane. <E> was evaluated by averaging the effective energy values of the conformations within a bin without minimizing them. ΔG was computed as −k_BTln(N_n,m/N_0,0), where N_n,m denotes the number of conformations with n contacts formed between strands 1 and 2 and m contacts between strands 2 and 3. The minimum and maximum values of N_n,m are 42 and 31,987, respectively. The error in ΔG is estimated by separating the 40 simulations started from random conformations into two sets of 20 simulations each. The average and maximal errors of <E> are 0.8 and 3.7 kcal/mol (bin with n = 8 and m = 4), respectively. The average and maximal errors of ΔG are 0.2 and 0.6 kcal/mol (n = 11, m = 11), respectively.

Energy Surface at 330 K.

The four simulations at 330 K were used to plot the energy surface at this temperature (Fig. 6). The average effective energy is not downhill for conformations having less than about 40% of the folded state contacts formed. Furthermore, it has a more rugged profile than at 360 K. This may be a consequence of insufficient statistics. The values of <E> range from about −15 to 5 kcal/mol (Fig. 6 Left) which is much lower than at 360 K (from 5 to 30 kcal/mol, Fig. 5 Left). The free energy surface at 330 K is very similar to the one at 360 K. The folded (Q > 0.7) and unfolded (Q < 0.3) states have comparable free energy, which indicates that 330 K is close to the melting point in the present model. The two β-hairpins, which at 360 K have a free energy comparable to the one of the folded state, have a free energy of nearly 1.2 kcal/mol above the folded state at 330 K. This may be caused by an entropic destabilization of the folded state at higher temperature values because the difference in effective energy is approximately the same at both temperatures. The main folding pathway involves first the formation of the interactions between strands 2 and 3, followed by the 1–2 contacts (Fig. 4). The most frequent contacts in TS1 and TS2 are the same as at 360 K. The fully unfolded state is slightly less stable than the conformations with only one contact formed between strands 2 and 3. The most frequent contacts present in the latter are not only proximal contacts [Asn-13–Thr-16 (20%) and Gln-12–Lys-17 (19%)], but also distal contacts [Trp-10–Lys-17 (27%) and Trp-10–Tyr-19 (24%)]. These last two contacts might be at the origin of the preferential folding pathway over the TS1 transition state.

Figure 6.

Same as in Fig. 5 for the four simulations at 330 K. A total of 0.77 × 10⁵ conformations were used. The minimum and maximum values of N_n,m are 19 and 4531, respectively. The average and maximal error of <E> are 1.9 and 7.5 kcal/mol (bin with n = 11 and m = 2), respectively. The average and maximal errors of ΔG are 0.6 and 1.8 kcal/mol (n = 0, m = 5), respectively.

Kinetic Parameters.

The folding time varies among different trajectories from 1.5 ns to 134.8 ns with an average of 31.8 ns, whereas the mean unfolding time is 7.2 ns. The fraction of unfolded conformations at time t is the percentage of runs that have not reached the folded (Q > 0.85) state at time t. At 360 K, a monoexponential fit to the fraction of conformations yields characteristic times of the decay of 30.3 ns for folding and 7.6 ns for unfolding and correlation factors of 0.99 (folding) and 0.95 (unfolding). Thus, the decay of the unfolded and folded population is very well represented by a single exponential, which is consistent with the shape of the free energy surface. Using the nonoverlapping signals of the one-dimensional ¹H-NMR spectra of Beta3s, De Alba et al. (10) estimated an upper limit for the folding time of 16–45 μs at 5°C and 4–14 μs at 10°C. The use of an implicit solvation model accelerates conformational transitions in two ways. First, because it provides a mean solvation force, the effective energy may be more smooth than the actual surface and therefore transitions are facilitated. Second, the friction exerted by the water molecules is missing. A comparison between implicit solvent and explicit water simulations of the same time length indicates that the amount of conformational space sampled in the former is larger (15). Therefore, the folding time derived from the simulations at 360 K should be a lower bound.

Conclusions

The present study shows that it is possible to simulate the reversible folding of a three-stranded antiparallel β-sheet of a designed 20-residue sequence, with an all atom description and an implicit solvent model. The 58 folding events provide a statistically significant sampling of the conformational space. Minima and transition states are localized on the projection of the folding free energy on appropriate progress variables, which are the native side-chain contacts and hydrogen bonds in the 1–2 and 2–3 β-hairpins. The simulations show that there are two folding pathways, a statistically preferred and a less frequent one. The pathway diversity and statistical predominance of a single pathway, defined by using native contacts as progress variable, were found previously by an implicit solvent MD simulation study of the unfolding of chymotrypsin inhibitor 2 (27). The main folding pathway of Beta3s starts with the formation of most of the side-chain contacts and hydrogen bonds between strands 2 and 3, followed by the 1–2 interstrand contacts. The inverse sequence of events, i.e., first formation of 1–2 and then 2–3 contacts is also possible, but less frequent. In general, contacts form first at the turns. The main unfolding pathway is the reverse of the statistically preferred folding pathway.

Abbreviations

MD

molecular dynamics

NOE

nuclear Overhauser enhancement