Physicochemical Effects Enhance Surfactant Transport in Pulsatile Motion of a Semi-Infinite Bubble

Abstract

In this study, we investigate the sorption of pulmonary surfactant (Infasurf, Ony, Buffalo, NY) occurring at the air-liquid interface of a semi-infinite finger of air as it oscillates and progresses along a small rigid tube ($1\text{mm}\text{inner diameter}$) occluded with a surfactant-doped solution of concentrations $C=0.1,0.05,\text{or}0.01\text{mg/mL}$. This simple experimental model of pulmonary airway reopening is designed to examine how altering the fluid flow field may lower reopening pressures and lead to a reduction in airway wall damage that is associated with the mechanical ventilation of an obstructed pulmonary system in airways of the deep lung with depleted endogenous and little exogenous surfactant. We analyzed a range of pulsatile flow scenarios by varying the oscillation frequency ($0\le f\le 1\text{Hz}$), the oscillation flow waveform, and the steady flow rate ($Q_{\text{steady}}=0.1\text{or}0.01\text{mL}/\text{min}$). These experimental studies indicate that a high frequency (1 Hz, amplitude = 5 mm), fast-forward oscillation waveform superimposed onto a fast steady flow ($0.1\text{mL}/\text{min}$) substantially reduces mean reopening pressures (31%) as a consequence of the modified flow field and the commensurate increase in surfactant transport and adsorption. This result suggests that imposing high frequency, low amplitude oscillations during airway reopening will help to diminish ventilator-induced lung injury.

Introduction

Diseases such as acute respiratory distress syndrome (ARDS) and respiratory distress syndrome (RDS) result in ventilation insufficiency due to airway closure (1,2). ARDS, normally affecting adults, is characterized by decreased pulmonary compliance and increased pulmonary edema, and is likely to result in surfactant insufficiency from competitive adsorption of plasma proteins to the air-liquid interface (1). RDS, affecting premature infants born with immature surfactant pulmonary systems, results in increased surface tension of the airway lining fluid and a decrease in lung compliance (2).

ARDS and RDS, by promoting airway closure and/or occlusion, frequently result in the need for mechanical ventilation. Unfortunately, mechanical ventilation, although necessary for maintaining adequate gas exchange, has been shown to damage the delicate airways of the lungs. Such damage is especially prevalent in cases where the pulmonary surfactant system, which allows the dynamic modification and stabilization of the liquid lining of the lung, is deficient (1,3,4). Ventilator-induced lung injury (VILI) can arise either from overdistension of the lung or from low-volume repetitive airway closure and reopening (4,5). Low volume VILI may be caused during airway reopening as a result of a finger of air that propagates through the liquid occlusion, which provides the basis for the model studied herein (Fig. 1). When surfactant concentrations are low, a damaging normal-stress gradient is introduced that sweeps across the epithelial cell layer as the finger of air progresses (6–8). Recent studies by Huh et al. (9) used a microfabricated airway model system to investigate epithelial cell damage resulting from the rupture of liquid plugs.

Figure 1.

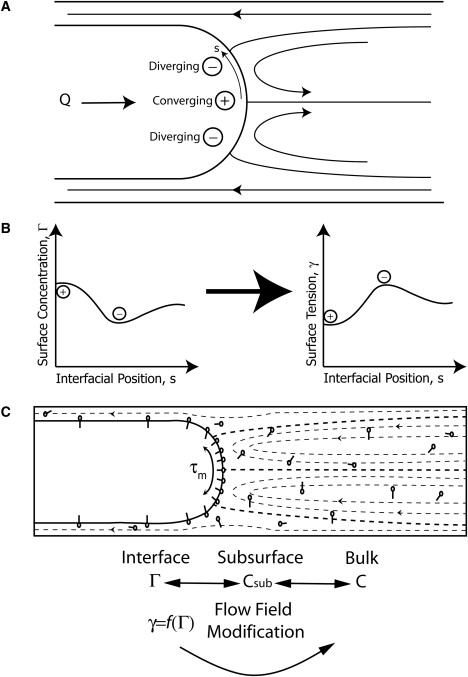
(A) Fluid flow field in which (+) is a converging stagnation point where surfactant accumulates and (−) is a diverging stagnation point where surfactant is undergoing convective depletion. (B) Depiction of the relationship between Γ (interfacial surfactant concentration), γ (interfacial surface tension), and the interfacial position coordinate s. Concentration gradients on the interface result in shear stresses called Marangoni stresses that act in the direction of high to low Γ to restore a uniform surface concentration and surface tension gradient. (C) Depiction of an air bubble propagating steadily into a tube occluded with fluid. Note that the streamlines correspond to the flow induced by a bubble moving with only a constant flow. The molecules depicted on the bubble interface and in the bulk fluid represent surfactants. In the frame of the moving bubble, the Marangoni stress, τ_m, exists due to a nonuniform surfactant concentration on the interface.

Surfactant replacement therapy (SRT) is aimed at replenishing surfactant-deficient systems with either synthetic surfactants or bovine and porcine cultivated extracts (such as Infasurf, Ony, Buffalo, NY) with the intent of reducing airway damage during mechanical ventilation (10). SRT has been successfully utilized for the treatment of RDS; in fact, the use of SRT is credited with a 60% drop in the infant mortality rate associated with RDS since 1989 and has also been proposed for patients with ARDS (1,11). Even with the benefits of SRT, however, RDS remains a leading cause of infant death (12). To better understand the dynamics that govern SRT, theoretical models have been developed (13–16).

SRT may have reduced efficacy due to inadequate surfactant transport and adsorption to the reopening interface and liquid lining of the lung. Previous work completed by Ghadiali and Gaver (17) investigated surfactant uptake by a finger of air progressed at a constant rate. Their study revealed that the pulmonary surfactant replacement Infasurf exhibited interfacial adsorption that was insufficient to maintain reopening pressures at equilibrium values (Fig. 2). Nevertheless, Infasurf at concentrations of 1 mg/mL radically reduced the damage seen in in vitro models of airway reopening (6).

Figure 2.

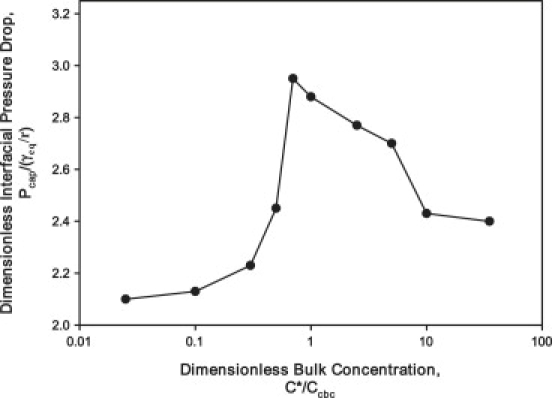
The data presented in this figure is from work completed by Ghadiali et al. (17), who investigated surfactant uptake during the steady propagation of a finger of air. In this instance, interfacial adsorption of the pulmonary surfactant replacement Infasurf was inadequate and resulted in elevated reopening pressures and interfacial rigidification. The experiments were performed at a velocity of 0.22 cm/s. $P_{\text{cap}}/({\gamma }_{\text{eq}}/R)$ represents the equilibrium pressure that would exist if surfactant adsorbed rapidly enough for surfactant to achieve the equilibrium surface tension and $C^{\ast }/C_{\text{cbc}}$ is the dimensionless bulk surfactant concentration where $C_{\text{cbc}}$ is the critical bulk concentration. The interface is saturated with surfactant when $C>C_{\text{cbc}}$.

Pulmonary surfactant acts to dynamically decrease the surface tension of the air-liquid interface. This occurs as surfactant adsorbs to the interface from the liquid bulk region (C) through convection (fluid flow) and diffusion. It is the surface concentration of surfactant (Γ) that directly modifies the interfacial surface tension (γ), as described by the equation of state $\gamma =f(\Gamma )$. When the interface is static and the bulk concentration C is large, an equilibrium surface tension, ${\gamma }_{\text{stat}}$, exists at the interface. Under dynamic conditions, surfactant convects and diffuses in the bulk, absorbs onto the interface from the subsurface (a region of the bulk that contacts the interface), and convects and diffuses along the interface. The surrounding fluid flow field affects the concentrations of surfactant available for adsorption onto the interface (Fig. 1 C). Taeusch et al. (18) experimentally investigated serum-induced barriers of surfactant adsorption to the interface and confirmed that adsorption from the subsurface to the interface is the main mechanism of transport of surfactants to the interface.

In this study, we investigate the propagation of a finger of air as it progresses through an airway obstructed by a viscous fluid occlusion doped with surfactant. This model of airway reopening is related to the classical fluid mechanics studies of semi-infinite bubble progression in a rigid capillary tube by Fairbrother and Stubbs (19), Bretherton (20), and Taylor (21). Recent theoretical investigations have included airway flexibility and demonstrated modifications of the flow fields (22–24). Our experimental model focuses on extensive closure of airways (not alveoli) ∼1 mm in diameter, where the liquid occlusion fills an entire airway, blocking air flow. Reopening the airway involves a semi-infinite finger of air infiltrating the fluid occlusion and separating the airway walls, potentially damaging the epithelial cell layer lining the airway. Airway closure of this type would occur, for example, before a newborn's first breath or in atelectasis that arises in ARDS. Systems such as the pulsating bubble surfactometer (PBS) and the captive bubble surfactometer (CBS) measure dynamic surface tension by the pure oscillation of a small air bubble in a reservoir of surfactant-doped fluid (17,25,26). These volumetric oscillations are useful in the study of alveolar dynamics but do not accurately model airway reopening. In airway reopening, the interface is continuously expanding and not simply oscillating (though a superposition of oscillation and steady flow may exist, which we term “pulsatile flow”).

In the rigid tube model shown in Fig. 1 C, convection patterns (denoted by streamlines) lead to nonuniform distributions of surfactant that result in variation of the tangential (Marangoni) stress at an air-liquid interface. Marangoni stress is a tangential component of stress acting in the direction from low to high surface tension with a magnitude proportional to the surface tension gradient. For example, Marangoni stress provides the driving mechanism for a drop of soap to spread on the surface of a liquid (27–29). In the experiment presented here, surfactant convects toward the bubble tip (from diverging (−) to converging (+) stagnation points) as shown in Fig. 1 A. This results in the surface concentration (Γ) and surface tension distribution (γ) shown in Fig. 1 B. Therefore, the resulting Marangoni stress (τ_M) acts in opposition to this flow field, “rigidifying the interface” and raising the reopening pressure. Note that the Marangoni stress modifies the flow field, which in turn influences the distribution of surfactant; these interactions are referred to as physicochemical hydrodynamics and have been studied by numerous investigators including Stebe et al. (30), Grotberg (31), Ghadiali and Gaver (17,32), Yap and Gaver (33), and Ratulowski and Chang (34). The Marangoni stress is just one of two mechanisms by which variations in γ can affect reopening pressures. The second, related to the law of Laplace, is the nonequilibrium stress that arises when slow surfactant adsorption leads to a dynamic surface tension that exceeds the equilibrium value of a static interface. Thus, there are two mechanisms by which nonuniform surfactant concentration resulting from slow adsorption can lead to a substantial increase in the pressure necessary to reopen airways over equilibrium values.

The fundamental physicochemical issue related to this study is that of dynamic surfactant transport between the bulk fluid and the air-liquid interface. Prior studies of surfactant transport to migrating bubbles (17,22,30,32,34) have shown that two processes are necessary for surfactant transport to the air-liquid interface: 1) diffusion between the bulk fluid and subsurface near the interface, and 2) kinetic adsorption/desorption between the subsurface and interface. If either of these two processes is inhibited, the surface will not be capable of maintaining a low surface tension. Below we discuss each of these barriers.

Diffusive barrier

For the interface to maintain a sufficiently low surface tension, the length over which surfactant must be transported through diffusive mechanisms is approximately equal to the adsorption depth, $\Lambda ={\Gamma }_{\text{sat}}/C$, defined as the distance into the bulk that contains the number of surfactant molecules necessary to bring the interface to the maximum equilibrium surface concentration, ${\Gamma }_{\text{sat}}$. For diffusion to be rapid enough to maintain adequate surfactant at the interface, its rate must exceed the rate of interfacial expansion. As such, in this system the Péclet number, $\text{Pe}=U{\Lambda }^2/RD$, is defined as the ratio of the diffusive timescale (${\Lambda }^2/D$) to the convective timescale ($R/U$), where the interface is expanded by a length R. Here U is the velocity of the bubble, R is the radius of the tube (a relevant geometric length scale), and D is the molecular diffusivity. If $\text{Pe}<<1$, then diffusion dominates convection, and diffusive barriers are eliminated. Increasing C leads to a reduction of Λ, thereby decreasing the diffusion barrier. Studies by Stebe and Malderelli (30) have shown that this process can be used to maintain a low surface tension interface of migrating closed bubbles, thereby “remobilizing” the interface. Experimental investigations by Ghadiali and Gaver (17) indicate that the remobilization of a semi-infinite finger of air can occur with the ionic surfactant sodium dodecyl sulfate (SDS).

Adsorptive barrier

The rate of adsorption to the air-liquid interface is equally important in maintaining a low surface tension. The ratio of the adsorption timescale to the interfacial expansion timescale in this system is approximated by the Stanton number, $\text{St}=\left(k_{a}C\right)\left(R/U\right)$, where $k_{a}C$ is the timescale of adsorption and $k_a$ is an adsorption rate constant. If $\text{St}>>1$, adsorption dominates convection and the adsorption barrier can be eliminated.

In a quasistatic system (i.e., $U<<1$ such that $\text{Pe}<<1$ and $\text{St}>>1$), Γ approaches equilibrium and the interface is now mobile. At the other extreme (i.e., $U>>1$ such that $\text{Pe}>>1$ and/or $\text{St}<<1$), the rate of interfacial creation exceeds the rate of diffusive transport and/or surfactant adsorption. Here the surface tension will be large and the interface will be immobile because of diffusive and/or adsorptive limitations. Steady-flow studies by Ghadiali and Gaver (17), which used a similar experimental apparatus as used in this study, showed that the pulmonary surfactant Infasurf has moderate adsorption properties (i.e., better than pure dipalmitoylphosphatidylcholine (DPPC)). However, even at very high bulk concentrations ($C=4.0\text{mg}/\text{ml}$) and low reopening velocities ($U=0.22\text{cm}/\text{s}$), the interface exhibited a large pressure drop (Fig. 2) and significant Marangoni stress. Using appropriate values for $k_a$, D, R, and ${\Gamma }_{\text{sat}}$ from Ghadiali and Gaver (17) and Krueger and Gaver (25), this corresponds to $\text{Pe}=2.5$ and $\text{St}=0.6$. As detailed below, this study examines the hypothesis that dynamic oscillation of the air-liquid interface can be used to overcome these transport limitations.

This study is concerned with providing insight into the development of flow fields that can be used to enhance surfactant transport and sorption during airway reopening. We hypothesized that this enhancement is possible because high levels of interfacial compression lead to surfactant being squeezed to levels in excess of the collapse concentration—the concentration at which surfactant forms a secondary layer of surfactant, as depicted in Fig. 3 (25). The formation of this secondary layer of surfactant from the primary layer may act as a reservoir (35,36), which promotes faster adsorption by providing a constant supply available for adsorption to the interface. It has been hypothesized that the reservoir consists of surfactant multilayer structures (Fig. 3). Evidence for the existence of surfactant multilayers has been documented by several researchers (25,35–37), and a number of studies have focused on the mechanisms of monolayer collapse (38–40). Walters et al. (41) concentrated on the mechanisms of surfactant adsorption to the interface. In our experimental model, we will elucidate the effects of a pulsatile flow on the transport and adsorption of surfactants to the interface by examining the dynamic changes in the ensuing reopening pressures.

Figure 3.

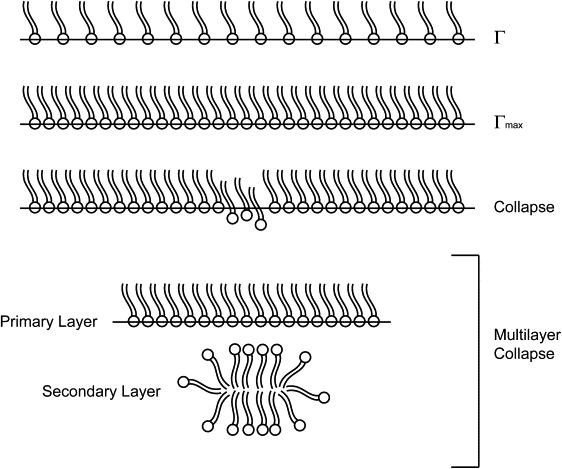
Multilayer formation. Under static conditions, the interfacial concentration of surfactant reaches an equilibrium value, Γ, that can only be increased with compression of the surface. There is a maximum interfacial concentration, Γ_max, after which the surfactant molecules start to collapse off of the surface, resulting in multilayer formation.

As such, we experimentally investigate the hypothesis that oscillating the interface using positive ($Q>0$) and negative ($Q<0$) flows as shown in Figs. 1 and 4 causes stagnation points that accumulate (+) or deplete (−) the surfactant that “sweeps” across the interface, which may result in enhanced surfactant transport. This hypothesis is consistent with theoretical predictions by Zimmer et al. (42) and Smith and Gaver (43) but has not been validated experimentally. To complete this investigation, we propagate a finger of air with a pulsatile motion within a rigid tube to determine whether selective expansion and compression of the interface can enhance surfactant transport during airway reopening. Specifically, we investigate how altering the frequency f, the steady flow $Q_{\text{steady}}$, and the oscillation waveform (symmetric (Sym), fast-forward (FF), or fast-reverse (FR)) of an air-liquid interface under airway reopening conditions changes the interfacial pressure drop as a measure of surfactant sorption kinetics. As discussed above, optimizing surfactant sorption has direct implications and applications in the current treatments of RDS and ARDS.

Figure 4.

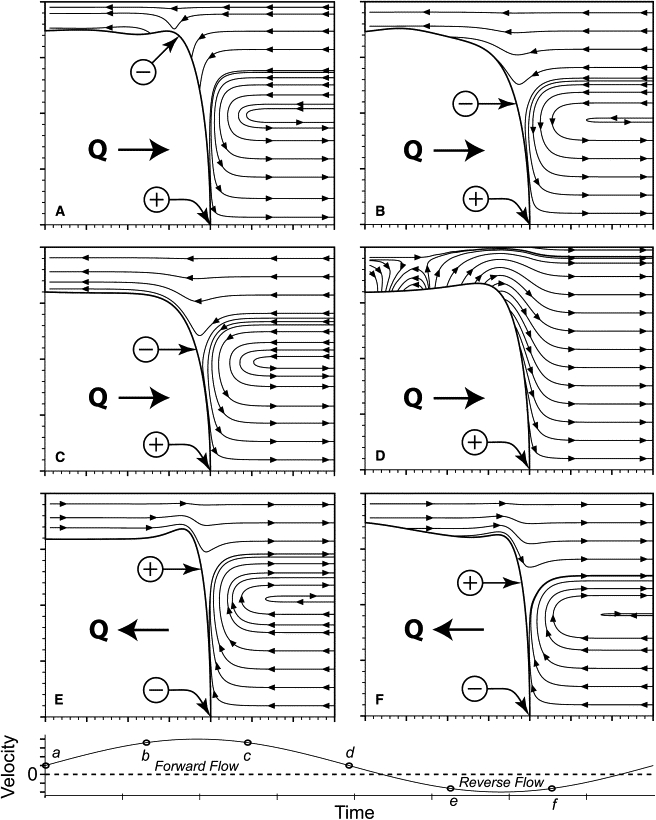
Calculated flow field that exists during the pulsatile motion of a semi-infinite bubble in a tube, demonstrating the flow field characteristics that can modify surfactant distribution (adapted from Smith and Gaver (43)).

It should be noted that the surfactant concentrations used in this study are far below physiologically normal levels. Our intent is to model disease states such as RDS and ARDS wherein surfactant deficiency and large regions of atelectesis exist. Using mechanical ventilation alone to reopen airways has been shown to damage the pulmonary airways due to extreme pressure gradients that are created in the reopening region (5). SRT has been used in conjunction with mechanical ventilation to ease this damage; however, the efficacy of SRT hinges on adequate transport and adsorption to the reopening interface and liquid lining deep within the lung (far from the sites of instillation) (13). Although exogenous surfactant is typically administered at concentrations of 20–30 mg/mL, this will be diluted substantially by existing liquid in the lung. Most importantly, exogenous surfactant is unlikely to reach the deep lung due to the many circuitous pathways that it must first traverse.

Additionally, the initial success of SRT in treating RDS is often not sustained, prompting the use of multiple doses (44,45). One of the mechanisms affecting the sustainability and efficacy of SRT is the clearance rate and deactivation of introduced surfactant. Though the clearance of introduced surfactant is known to affect surfactant transport, the mechanism underlying surfactant clearance are not well understood (13). For instance, alveolar type II cells, alveolar macrophages, and bronchial Clara cells have all been implicated in the clearing of exogenous surfactant (46–49). Regardless of the exact clearance mechanisms, the pulmonary system is once again in a state of surfactant deficiency and vulnerable to mechanical stresses. Our model of airway reopening would best be described as mimicking either this state of surfactant deficiency or a lack of adequate delivery. This study seeks to reveal how the fluid flow field affects surfactant transport and adsorption in a region of the lung with little endogenous or exogenous surfactant.

Experimental Methods

By modeling airway reopening as a semi-infinite finger of air oscillating and progressing in a rigid tube, we hope to elucidate the effects of fluid motion on surfactant adsorption. Our goal is to obtain the interfacial pressure drop at the bubble tip, thus providing the key information related to surfactant adsorption and hence to airway damage.

Experimental model

An idealized model of airway reopening is utilized to investigate the effects of three oscillation modalities on reopening pressures as an air-liquid interface migrates into a surfactant-doped bulk solution. Fig. 1 C depicts the fluid flow streamlines for a finger of air undergoing a steady flow into the fluid obstruction. With the addition of oscillation, the fluid streamlines will be significantly modified (Fig. 4). The experimental system consists of a narrow-bore (1 mm inner diameter and 90 cm in length) borosilicate glass tube maintained at 37°C with one end open to air and the other end connected to a reservoir of liquid (Fig. 5). The air-liquid interface behavior is measured at a distance >15 cm from the end of the tube in the section that is continuously warmed with a heating and circulating water bath maintained at 37°C. Due to the low thermal conductivity of air and the very low flow rate into the tube, the heat loss from the end of the tube that is open to air is insignificant, and the liquid surrounding the finger of air in that region is ∼37°C. A steady flow ($Q_{\text{steady}}$) and an oscillatory flow ($Q_{\text{osc}}\left(t\right)$) create a pulsatile waveform that is simultaneously applied to the bubble while pressure measurements, from which the interfacial pressure drop is identified (50) (see pressure calculation below), are taken far ahead of the bubble tip.

Figure 5.

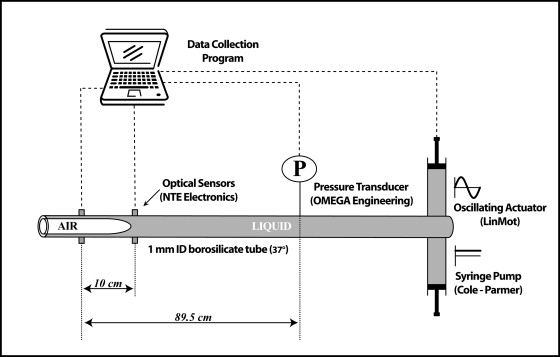
Experimental design. The finger of air is progressed steadily into the liquid obstruction by the syringe pump and oscillated by the oscillating actuator. A pressure transducer ahead of the bubble tip measures the total pressure drop.

A constant flow syringe pump (Cole-Palmer, Niles, IL) controls the magnitudes of $Q_{\text{steady}}$, whereas a linear actuator (P01-23x80/140, LinMot, Zurich, Switzerland) applies a predetermined waveform to the system, creating $Q_{\text{osc}}\left(t\right)$. The specified waveform determines the frequency of oscillation, the amplitude, and the oscillation modality. The actuator position is recorded using a linear potentiometer (RE00423; MCM Electronics, Centerville, OH). A pressure transducer (PX163 Omega Engineering, Stamford, CT) ahead of the bubble tip measures the total pressure at a fixed location, which is recorded at a rate of 100 Hz using a Labview data acquisition system (National Instruments, Austin, TX). The pressure transducer is calibrated to an accuracy of ±0.033 cm H₂0. Infrared (IR) optical sensors (NTE 3033 and 3029A, NTE Electronics, Bloomfield, NJ) located downstream from the pressure transducer sense the presence of the interface and serve as the starting location and time for data collection. In this way, a known length from the interface to the pressure transducer is established for use in the pressure calculations.

Experimental parameters

Experiments were completed as listed in Table 1 with three surfactant concentrations, three frequencies, two steady flows, and a bubble oscillation amplitude corresponding to five times the diameter of the tube. Three oscillation modalities were investigated—a Sym, an FF, and an FR waveform. FF and FR asymmetries mirror each other in their degree of asymmetry, whereas Sym is simply a sinusoid (Fig. 6). A more detailed explanation of waveform construction can be found in the Appendix under Waveform/flow construction. Each experiment was repeated three times in both purified water and in a bulk surfactant solution. Ultrapure H₂0 (18 MΩ cm and degassed for ∼45 min) was used in this system (Alpha-Q, Millipore, Bedford, MA). For the surfactant-doped experiments, surfactant solutions were prepared using Infasurf, a surfactant replacement derived from bovine surfactant. The surfactant solution was diluted from 35 mg/mL to 0.1, 0.05, and 0.01 mg/mL with a 200 mL saline solution consisting of 1.75 g NaCl and 111 mg CaCl₂. An example of the parameters describing a typical experiment can be seen in Table 1.

Table 1.

Listing of experimental parameter values

Experimental parameter	Values
Surfactant concentration	0.1 mg/mL (High)
	0.05 mg/mL (Medium)
	0.01 mg/mL (Low)
Frequency	1 Hz (High)
	0.5 Hz (Medium)
	0.1 Hz (Low)
Steady flow	0.1 mL/min (Fast)
	0.01 mL/min (Slow)
Amplitude	5

Figure 6.

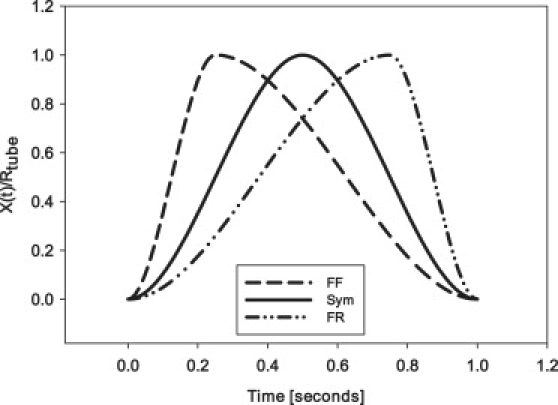
Examples of oscillation waveforms that are constructed for use in FF, Sym, and FR experiments with a frequency f = 1 Hz. As indicated by the shape of the FF waveform, there is a portion of the cycle with rapid velocity followed by a slow reverse motion. The opposite behavior is illustrated in the FR waveform example, whereas the Sym waveform is simply a sinusoid.

In the next sections, we describe the pressures in the system and the framework of our calculations for identifying the pressure drop at the tip of the migrating finger of air. Our goal is to determine the pulsatile flow characteristics that decrease the magnitude of the dynamic interfacial pressure drop to reduce airway reopening pressures.

Pressure calculations

As described above, we measure the total pressure $\Delta P_{\text{total}}\left(t\right)$ at a fixed point ahead of the bubble tip. As shown in Fig. 7, $\Delta P_{\text{total}}\left(t\right)$ consists of two components:

$$\mathrm{\Delta }{P}_{\text{total}}\left(t\right)=\mathrm{\Delta }{P}_{\text{int}}\left(t\right)+\mathrm{\Delta }{P}_{\text{vis}}\left(t\right),$$ (1)

where $\Delta P_{\text{int}}\left(t\right)$ is the interfacial pressure drop, and $\Delta P_{\text{vis}}\left(t\right)$ is the viscous pressure drop due to bulk flow between the bubble tip and the measurement point. In steady flow, $\Delta P_{\text{vis}}\left(t\right)$ is the Poiseuille pressure drop; however, in oscillating flow the pressure drop is more complex and varies with time as described below. Note that the time dependence of $\Delta P_{\text{int}}\left(t\right)$ and $\Delta P_{\text{vis}}\left(t\right)$ arises from the dynamic forcing that changes the shape of the air-liquid interface, induces pulsatile flow in the column of liquid, and varies the length between the measuring point and the bubble tip, $\Delta L\left(t\right)$.

Figure 7.

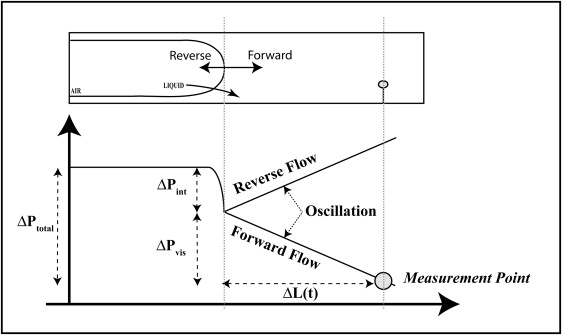
Diagram of system pressures. $\Delta L\left(t\right)$ decreases as the bubble progresses.

To identify $\Delta P_{\text{int}}\left(t\right)$, we must first compute $\Delta P_{\text{vis}}\left(t\right)$, which requires the calculation of the flow field and $\Delta L\left(t\right)$. In our theoretical model of this system, we follow the Womersley solution for $\Delta P_{\text{vis}}\left(t\right)$ for an oscillating column of fluid and assume that the tube is rigid, that the pressure gradient in the viscous flow region is only a function of time, and that there is no radial component of velocity (50). Following the Womersley solution, we decompose the forcing using a Fourier series representation to account for temporal asymmetry of the flow field. This is a nontrivial calculation due to the specific amplitude and phase associated with each term in the Fourier series and is described in the following section and in the Appendix.

Waveform/flow construction

We define the interface moving into the liquid phase as forward, whereas the interface moving back into the air is referred to as reverse. In a Sym oscillatory flow, the pulsatile component is purely sinusoidal. During FF and FR flow, there is an asymmetric bias either in the forward or reverse motion (Fig. 6). An FF oscillation moves forward for one-quarter of the time and reverse for three-quarters of the time. The FR motion mirrors this asymmetry.

For analysis, the waveform, or forcing, is decomposed into a Fourier series representation. The established waveform corresponding to the interface undergoing total oscillatory flow is described by

$$Q{\left(t\right)}_{\text{osc}}=\sum _{n=-N}^N-i2{\pi }^{2}nf{L}_p{R}_{\text{tube}}^{\text{2}}{C}_n{e}^{i2\pi nf(t+\Delta t)},$$ (2)

where n indicates the number of Fourier terms in the representation, f is the frequency of oscillation, $L_p$ is the total distance traveled by the interface in the piston, $R_{\text{tube}}$ is the tube radius (0.5 mm), $C_n$ are the Fourier coefficients (defined in the Appendix), and $\Delta t$ is the time delay associated with the phase difference between the position of the interface as it crosses the IR optical sensor and the position of the piston.

The interface position, $\Delta L\left(t\right)$, with respect to the pressure transducer (Fig. 7) is described in terms of the total flow by

$$\mathrm{\Delta }L\left(t\right)=L_{\text{o}}+\left[{\int }_0^t\frac{-(Q_{\text{steady}}+Q{\left(t\right)}_{\text{osc}})}{\pi R_{\text{tube}}^2}dt\right],$$ (3)

where $L_{\text{o}}$ is the fixed distance between the IR optical sensor and the measurement point.

The calculation of $\Delta P_{\text{vis}}\left(t\right)$, described in the next section, necessitates the use of the total flow field representation and the interface position detailed above.

Viscous pressure calculations

The viscous component from Eq. 1 of the total pressure drop is

$$\Delta P_{\text{vis}}\left(t\right)=\left\{{\left(\frac{\partial P}{\partial x}\right)}_{\text{steady}}+\sum _n^N{\left({\left(\frac{\partial P\left(t\right)}{\partial x}\right)}_n\right)}_{\text{osc}}\right\}\Delta L\left(t\right),$$ (4)

where the steady term is defined in terms of the steady flow and the oscillatory term is a summation of pressure gradients from the Fourier series representation of the oscillatory flow field. The Poiseuille flow describes the relationship for the steady component:

$${\left(\frac{\partial P}{\partial x}\right)}_{\text{steady}}=\frac{-8\mu Q_{\text{steady}}}{\pi R_{\text{tube}}^4},$$ (5)

where μ is the fluid viscosity. The oscillatory component is

$${\left({\left(\frac{\partial P\left(t\right)}{\partial x}\right)}_{\text{oscillatory}}\right)}_n=\frac{2\pi nf\mu C_n}{R_{\text{tube}}\left|Z_n\right|}{e}^{i\left(2\pi nft+\Delta {\varphi }_n-\Delta {\varphi }_{z_n}\right)},$$ (6)

where $C_n$ describe the Fourier coefficients and $\left|Z_n\right|$ originate from the flow derivation. This result is due to a calculation involving phase lags and a Fourier series expansion of the flow. A detailed explanation of this calculation can be found in the Appendix (50).

With both components of $\Delta P_{\text{vis}}\left(t\right)$ defined (Eqs. 5 and 6), $\Delta P_{\text{int}}\left(t\right)$ can now be determined from Eq. 1. $\Delta P_{\text{int}}\left(t\right)$ is the pressure drop that informs us of the interfacial surface tension, which is directly related to the surface concentration of surfactant. Thus, evaluation of $\Delta P_{\text{int}}\left(t\right)$ over a range of experimental parameters elucidates how modifications of the flow field affects surfactant transport and how these modifications may be optimized to decrease damage to the airways.

Results

We examine the effect of three oscillation modalities (Sym, FF, FR) on the interfacial pressure drop, $\Delta P_{\text{int}}\left(t\right)$, of a semi-infinite finger of air migrating into a fluid doped with surfactant. By varying f (frequency in Hz), $Q_{\text{steady}}$ (steady flow in mL/min), and C (concentration in mg/mL) for each oscillation condition, this analysis elucidates how modifications to the flow field alter surfactant adsorption and transport in our simple model of airway reopening.

As described in Experimental Methods, the total pressure, $\Delta P_{\text{total}}\left(t\right)$, consists of a viscous, $\Delta P_{\text{vis}}\left(t\right)$, and interfacial, $\Delta P_{\text{int}}\left(t\right)$, component. We isolate $\Delta P_{\text{int}}\left(t\right)$ through its direct relationship to γ and hence to the concentration of surfactant at the migrating interface. We hypothesize that a reduction in $\Delta P_{\text{int}}\left(t\right)$ will minimize airway damage.

Before investigating the effects of oscillation on $\Delta P_{\text{int}}\left(t\right)$, we consider the average pressure drop, $\overline{\Delta P_{\text{int}}\left(t\right)}$, under zero-flow (static equilibrium) and constant flow (dynamic equilibrium) conditions, where the average pressure is computed over one oscillation cycle. These initial studies set the baseline for which our oscillation flow studies are compared.

Although our primary method of evaluating surfactant transport is through the measurement of $\Delta P\left(t\right)$ across the bubble tip, a secondary (more approximate) evaluation of surfactant transport is by the calculation of an “effective surface tension”, ${\gamma }_{\text{eff}}\left(t\right)=\Delta P\left(t\right)\ast R/2$, which is based on the law of Laplace. The calculation of ${\Gamma }_{\text{eff}}$ is important for comparison to results of surfactant transport using other oscillating bubble surfactometers, such as the CBS and PBS, which also estimate the surface tension based upon the law of Laplace. However, these estimates are not exact, as discussed in the Limitations section.

Fig. 8 indicates that under both static and dynamic conditions $\overline{\Delta P_{\text{int}}\left(t\right)}$ decreases with increasing C. However, the $\overline{\Delta P_{\text{int}}\left(t\right)}$ vs. C (or ${\gamma }_{\text{eff}}$ vs. C, right axis) relationship progressively shifts upward with increasing $Q_{\text{steady}}$ due to the rarefaction of surfactant as the finger of air progresses into the liquid occlusion, creating new interfacial area. It is evident that interfacial expansion occurs more rapidly than surfactant adsorption, leading to the difference between static and dynamic $\overline{\Delta P_{\text{int}}\left(t\right)}$. These results are consistent with Ghadiali et al. (17). As described above, we seek to determine whether the addition of oscillatory motion (creating a pulsatile flow) will enhance interfacial surfactant adsorption, resulting in lower reopening pressures.

Figure 8.

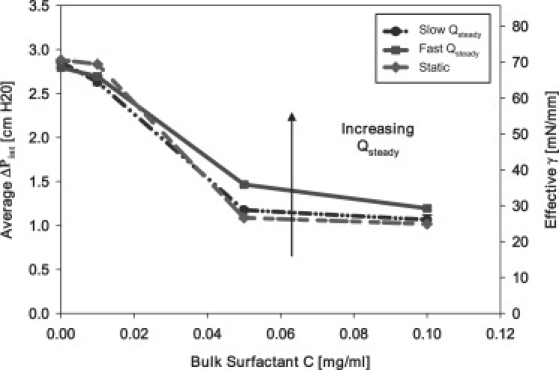
Dynamic equilibrium behavior: contrasting static bubble behavior with steady bubble progression at slow (0.01 mL/min) and fast (0.1 mL/min) flow.

Fig. 9 demonstrates general characteristics of $\Delta P_{\text{int}}\left(t\right)$ vs. $Q\left(t\right)$ for pulsatile flow with fixed f, $Q_{\text{steady}}$, and C. This figure reveals the existence of hysteresis, a result of nonlinear sorption kinetics and interfacial flows. Furthermore, these figures demonstrate that sorption rates are inadequate to maintain the system at static equilibrium ${\gamma }_{\text{stat}}$. Under Sym oscillation, the loop orientation is in the counterclockwise direction. As the bubble begins to retract ($Q_{\text{steady}}$ < 0 on the top portion of the loop), the interfacial pressure drop decreases markedly to very small values, indicating the existence of a compressed primary layer. This low plateau pressure persists after the initiation of reexpansion ($Q_{\text{steady}}$ > 0 on the bottom portion of the loop), which is consistent with the respreading of a compressed surfactant layer. This figure is thus reminiscent of measurements taken from spherical bubbles using either a PBS or CBS and provides evidence in agreement with the model of Krueger and Gaver (25).

Figure 9.

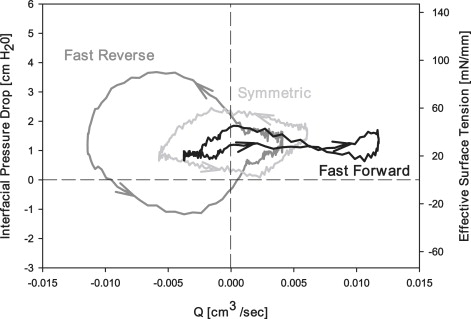
Comparison of pressure flow loops for each oscillation modality. Loops represent data from a slow Q_steady (0.01 mL/min), a medium f (0.5 Hz), and a medium C (0.05 mg/mL). The following values are the range of standard errors of each loop: FR: $0.015\le {\sigma }_m\le 0.13{\text{cm}\text{H}}_{2}0$, SYM: $0.019\le {\sigma }_m\le 0.11{\text{cm}\text{H}}_{2}0$, and FF: $0.018\le {\sigma }_m\le 0.11{\text{cm}\text{H}}_{\text{2}}0$. These standard errors were calculated by comparing the values from each individual experiment.

In comparison to FF and Sym oscillation conditions, the FR modality in Fig. 9 exhibits the largest area of hysteresis. Surprisingly, $\Delta P_{\text{int}}\left(t\right)$ increases initially upon retraction, suggesting a decrease in surfactant concentration at this stage of the oscillation. Subsequently, during and after the most rapid stage of retraction ($Q_{\text{steady}}$ < 0 at the bottom of the loop), $\Delta P_{\text{int}}\left(t\right)$ < 0. This result indicates that the interface develops a negative tip curvature, which has been shown to occur in two-dimensional planar computational systems (42) and, more recently, in two-dimensional axisymmetric computational systems (43).

In Fig. 9, the smallest hysteresis area is found under FF conditions. As with the Sym case, $Q_{\text{steady}}$ < 0 indicates the creation of a collapsed monolayer with a low plateau $\Delta P_{\text{int}}\left(t\right)$ during the retraction phase. This leftmost portion of the FF loop demonstrates that the surfactant monolayer on the interface is in the process of collapsing. This occurs near the maximum negative value of $Q_{\text{steady}}$, where the interface is at its highest rate of compression. The absence of hysteresis as the interface continues to compress provides additional evidence of a low constant interfacial surface tension that can be maintained under slow compression. As retraction slows ($dQ/dt>0$ with $Q<0$), the rate of interfacial compression appears to be insufficient to maintain a high surface concentration at the primary layer, resulting in an increase in $\Delta P_{\text{int}}\left(t\right)$. A new plateau exists near ${\gamma }_{\text{eff}}$ ∼ 24 mN/mm, indicating that surfactant in the neighborhood of the interface is adsorbing quickly as the bubble expands rapidly in this FF modality. Thus, compression of the interface may be providing a reservoir of surfactant that is available on reexpansion.

To further delineate the differences of each oscillation modality (Sym, FR, FF) on surfactant transport and adsorption, we investigate the average interfacial pressure drop $\overline{\Delta P_{\text{int}}}$ that exists during each oscillation. Fig. 10 presents $\overline{\Delta P_{\text{int}}}$ vs. f for both slow and fast $Q_{\text{steady}}$ (left and right columns, respectively) at high, medium, and low C (top, middle, and bottom rows, respectively). For orientation, the leftmost point on each graph (f = 0) represents dynamic equilibrium surface tension during steady flow (${\gamma }_{\text{dyn}}$). The horizontal line indicates the static equilibrium surface tension (${\gamma }_{\text{stat}}$). The observation that ${\gamma }_{\text{dyn}}$ > ${\gamma }_{\text{stat}}$ demonstrates the transport limitations discussed above and observed by Ghadiali and Gaver (17). Each data point represents the mean ± SE of 12 trials.

Figure 10.

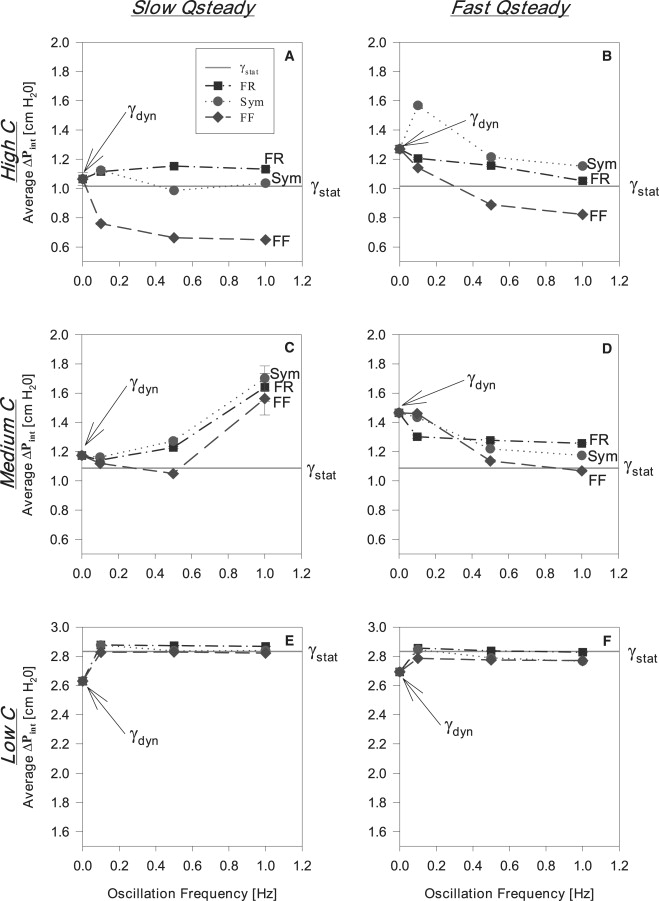
(A, C, and E) The relationship between $\overline{\Delta P_{\text{int}}}$ and oscillation frequency during slow flow (0.01 mL/min) for high (0.1 mg/mL), medium (0.05 mg/mL), and low (0.01 mg/mL) surfactant concentrations, respectively. (B, D, and F) The relationship between $\overline{\Delta P_{\text{int}}}$ and oscillation frequency during fast flow (0.1 mL/min) for high (0.1 mg/mL), medium (0.05 mg/mL), and low (0.01 mg/mL) surfactant concentrations, respectively. ${\gamma }_{\text{stat}}$ and ${\gamma }_{\text{dyn}}$ here indicate the pressures corresponding to the surface tensions established during static and dynamic equilibrium conditions, respectively.

Fig. 10, A and B, shows that at high C (0.1 mg/mL), Sym and FR modalities effect a modest change in $\overline{\Delta P_{\text{int}}}$, with higher frequencies resulting in $\overline{\Delta P_{\text{int}}}$ that is slightly less than the dynamic equilibrium pressure for steady flow. However, an FF oscillation combined with high C reduces $\overline{\Delta P_{\text{int}}}$ and hence lowers ${\gamma }_{\text{eff}}$. Most importantly, as f increases, $\overline{\Delta P_{\text{int}}}$ is reduced to values significantly below pressures corresponding to ${\gamma }_{\text{stat}}$ and ${\gamma }_{\text{dyn}}$.

Similarly, under medium C (0.05 mg/mL) conditions (Fig. 10, C and D), FF continues to exhibit lower $\overline{\Delta P_{\text{int}}}$ in comparison with a Sym and FR waveform as f increases. During slow $Q_{\text{steady}}$ (Fig. 10 C), average values tend to increase as f increases and are generally higher than their corresponding ${\gamma }_{\text{stat}}$ and ${\gamma }_{\text{dyn}}$ values. Conversely, the FF modality is approximately equal to the value at ${\gamma }_{\text{stat}}$ except at the highest frequency, where $\overline{\Delta P_{\text{int}}}$ rapidly increases. In contrast, under fast $Q_{\text{steady}}$ conditions, $\overline{\Delta P_{\text{int}}}$ decreases for all oscillation modalities with increasing f to values that are substantially lower than ${\gamma }_{\text{dyn}}$ (Fig. 10 D). However, only the FF oscillation at the highest f reaches a value less than the ${\gamma }_{\text{stat}}$ pressure.

Results for experiments with a low C (0.01 mg/mL) are presented in Fig. 10, E and F. Average pressures at this concentration are approximately those of ultrapure H₂0. All $\overline{\Delta P_{\text{int}}}$ at both $Q_{\text{steady}}$ are approximately equal to the ${\gamma }_{\text{stat}}$ pressures and slightly larger than the ${\gamma }_{\text{dyn}}$ pressures.

The data of Fig. 10, B, D, and F, are alternately presented in Fig. 11 as $\overline{\Delta P_{\text{int}}}$ vs. C at high, medium, and low f for fast $Q_{\text{steady}}$. In general, $\overline{\Delta P_{\text{int}}}$ decreases with increasing C. Fig. 11, A and B, illustrates that an FF oscillation consistently lowers reopening pressures, especially as C increases. Fig. 11 C exhibits a modest change in $\overline{\Delta P_{\text{int}}}$ at low frequencies.

Figure 11.

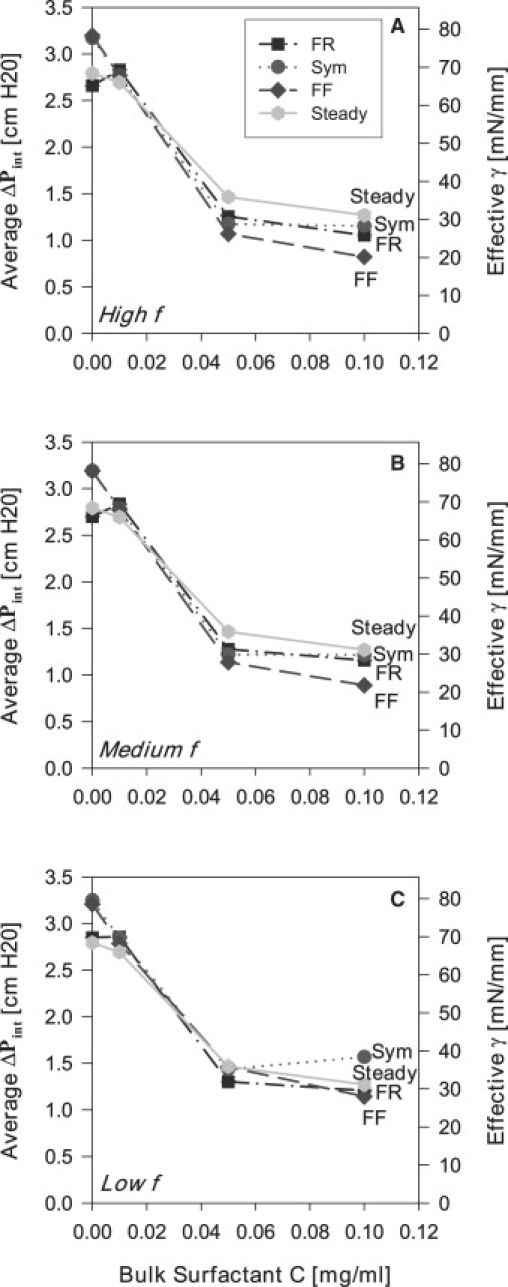
Average reopening pressure versus bulk surfactant concentration with fast flow (0.1 mL/min) at high f (1 Hz), medium f (0.5 Hz), and low f (0.1 Hz).

In summary, the results from the studies clearly demonstrate that an FF oscillation significantly reduces $\overline{\Delta P_{\text{int}}}$. This indicates that an improvement of surfactant transport and adsorption occurs through modification of the fluid flow field by an asymmetric oscillation such that the propagating finger of air moves quickly into the liquid occlusion and then retracts slowly. Therefore, an FF oscillation waveform lowers the average surface tensions and hence reopening pressures. This result may be important in the development of novel modes of mechanical ventilation that could protect the lung from VILI.

Discussion

An FF oscillation waveform combined with a fast constant flow lowers reopening pressures in an idealized model of pulmonary airway reopening and demonstrates the potential for asymmetric oscillations to protect surfactant deficient pulmonary airways during mechanical ventilation. This behavior is linked to dynamic surface tension and is supported in Fig. 12, where the percentage improvement of a 1 Hz FF oscillation over both the steady flow case and all other oscillation schemes is presented. At the highest concentration (0.1 mg/mL) investigated in this study, the average interfacial pressure is decreased by 31% over the average pressure established during steady flow. Note that this improvement exists at concentrations that are far below physiological levels. Therefore, it is hypothesized that these predictions may have relevance to the treatment of pulmonary diseases related to surfactant deficiency such as RDS and ARDS (10,51) in the deep lung with little endogenous or exogenous surfactant present.

Figure 12.

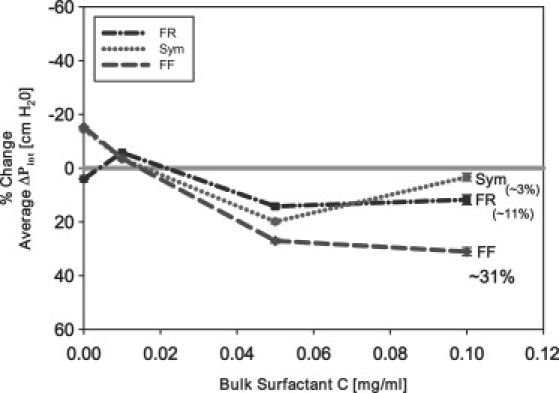
Percentage change in $\overline{\Delta P_{\text{int}}}$ as a function of C in relation to steady flow. All experiments were completed at a high frequency (1 Hz) and a fast flow (0.1 mL/min). Note that in all oscillation modalities (Sym, FR, FF), $\overline{\Delta P_{\text{int}}}$ is significantly reduced at very low C, with FF eliciting a far greater reduction in the reopening pressures.

Although an FF oscillation modality exhibits the largest decrease in reopening pressures, Fig. 12 indicates that all oscillation modalities (Sym, FR, FF) decrease reopening pressures in comparison to steady flow even at relatively low bulk surfactant concentrations. Thus, in general, imposing any oscillatory motion may help to reduce interfacial surface tensions during dynamic reopening of airways.

The lower pressures resulting from an FF oscillation suggest that the flow field established by this asymmetry facilitates enhanced net surfactant adsorption and transport to the interface. The exact mechanisms promoting faster and/or increased surfactant transport to the air-liquid interface are beyond the scope of this investigation. However, it is evident from studies by Zimmer et al. (42) and Smith and Gaver (43) that the velocity field is significantly modified throughout the oscillation cycle, which results in convective patterns that selectively deposit and cyclically compress and expand the interfacially bound surfactant during bubble propagation (Fig. 4). Even though their studies do not incorporate surfactant transport and adsorption, the streamlines determined from the movement of the bubble tip give an indication of the type of flow field that may exist were surfactants present while the interface is oscillated and progressed. The flow field provides a useful qualitative baseline that increases our understanding of the fluid flow field's effects on surfactant transport. Of most importance is the swapping of converging and diverging stagnation points along the air-liquid interface, which is likely to be responsible for the enhanced transport to the bubble tip region.

Even though streamline visualization is beyond the scope of the current project, it is clear that an FF oscillation in particular enhances surfactant transport and adsorption to the air-liquid interface, lowering pressures and surface tensions. We hypothesize that the flow field modification from oscillation builds a reservoir of surfactant molecules during the slow retraction of the FF oscillatory motion, which subsequently are redistributed during rapid bubble expansion.

An important aspect of our model is the “leakage” of surfactant from the bubble tip to the tube wall that relates to the deposition of surfactant onto the thin film created as the long finger of air progresses down the tube. Unlike the PBS, this “leakage” is a feature of our design because it provides a means for identifying the physiologically significant effects of surfactant dynamic adsorption in a continually reopening airway. In this condition, as the bubble tip progresses into the liquid occlusion, surfactant adsorbed on the interface deposits into the thin film behind the bubble tip through convection (effected by Marangoni stress) and diffusion (which is very weak). Since we observe stationary-state responses with our hysteresis loops, this deposition of surfactant to the film does not result in a cycle-to-cycle depletion of surfactant from the tip region, because the expanding bubble tip is continuously taking up surfactant from the bulk. Thus, the reduction of surface concentration due to elongation of the interface (“leakage”) as it propagates through the liquid occlusion is compensated for by the adsorption of bulk surfactant to the bubble tip. It is precisely this dynamic adsorption process that we are investigating, and our results clearly demonstrate that flow field modification can be used to enhance surfactant adsorption. It should be noted that this enhanced adsorption results in an increased surfactant concentration in the thin film, which is an added benefit during unsteady airway reopening.

This study investigates the relationship between the dynamic surface tension and changes in interfacial area. In purely oscillatory systems, this relationship defines the dilatational modulus, $E^{\ast }\equiv d\gamma /d\left(\text{ln}\delta A\right)\equiv E^{\prime }+i{E}^{″}\text{.}$ Here,$E^{\prime }$ is the in-phase component and is termed the “dilatational elasticity”, and the out-of-phase component $E^{″}$ relates to the relaxational effect of surfactant adsorption/desorption. Since this study incorporates an interface that grows with both steady and oscillatory components (i.e., pulsatile flow), the relationship between γand the instantaneous Q is not entirely represented by $E^{\ast }$. Nevertheless, the average slope of the hysteresis loops shown in Fig. 9 is associated with $E^{\prime }$, whereas the hysteresis area is correlated to $E^{″}$. From this figure it is evident that $E^{\prime }$ is relatively insensitive to pulsatile flow characteristics. In contrast, $E^{″}$ depends greatly on the nature of the asymmetry of the oscillation. This result is consistent with the hypothesis that sorption behavior is strongly related to the mode of interfacial expansion due to physicochemical hydrodynamic interactions near the bubble surface.

Limitations

Our model of airway reopening has several limitations that reduce its direct applicability to the physiological system. We have studied the process of airway reopening using a single rigid tube of fixed diameter, which is an idealized representation of the highly branched and elastic pulmonary system. Additionally, our liquid occlusion was composed of a surfactant replacement, Infasurf, diluted in a NaCl/CaCl₂ solution, whereas the actual composition of naturally occurring pulmonary fluid is unknown, especially in disease states such as ARDS where protein leakage from the vascular system can deactivate surfactant by competitive adsorption to the air-liquid interface. Although this model is clearly idealized from the physiological system, these limitations serve to focus the study on the events occurring at the air-liquid interface, specifically indicating how modifications to the flow field alter surfactant transport and adsorption.

The calculation of effective surface tension, ${\gamma }_{\text{eff}}$, although limited as an approximation, is valuable for estimating the effect of the imposed flow field on surfactant transport. To estimate the validity of this approximation, we utilize the studies of Ghadiali and Gaver (17), which show that

$$\frac{\Delta P_{\text{int}}}{\left(\frac{{\gamma }_{\text{eq}}}{R}\right)}\sim 2+\beta {\left(Ca\right)}_{\text{eq}}^{2/3}$$ (7)

for a steadily migrating finger of air in a surfactant-doped solution. In Eq. 7, $\beta {\left(Ca\right)}_{\text{eq}}^{2/3}$ is a correction to the law of Laplace. Using flow rates from the system presented here, we find that ${\left(C{a}_{\text{eq}}\right)}_{\text{max}}<{10}^{-3}$, and data from Ghadiali and Gaver (17) show $10<\beta <20$ over the range of concentrations investigated in this study. Therefore, the correction to the law of Laplace is $\beta {\left(C{a}_{\text{eq}}\right)}_{\text{max}}^{2/3}<0.18$, or ∼10% of the estimated value provided solely by the law of Laplace. Thus, ${\gamma }_{\text{eff}}$, although not the exact surface tension, provides a measure of the system's transport dynamics that is insensitive to the size of the tube.

Furthermore, the assumption of negligible hydrodynamic effects and hence uniform surface tension in regard to the validity of the law of Laplace equation has also been examined by Liao et al. (26). The finite element method was used to model the oscillation of a supported bubble in the presence of surfactant to determine the limits for measuring accurate dynamic surface tension through dynamic pressure differences. At low frequency the surface concentration is nearly uniform; however, at high frequency the oscillation deforms the bubble interface and creates a nonuniform surface concentration of surfactant. These results suggest that calculations of ${\gamma }_{\text{eff}}$ are most accurate at low frequency. Nevertheless, our estimates of ${\gamma }_{e\text{ff}}$ provide a meaningful measure of surfactant transport in this dynamic system, especially in comparison to other tools that are used to determine dynamic surface tension such as the CBS and PBS.

This analysis provides insight into mechanisms that could decrease the damage inflicted upon the pulmonary airways during mechanical ventilation. We anticipate that follow-up experiments and computational investigations will be useful in identifying specific waveforms and frequencies that would optimize surfactant transport.

Conclusion

In this rigid tube model of airway reopening, we have investigated the effects of modifying the fluid flow field on the pressures required to clear a surfactant-doped liquid occlusion. Our goal was to lower reopening pressures by enhancing surfactant transport and adsorption to the air-liquid interface through modifications to the fluid flow field.

We modified the fluid flow field by driving a finger of air using a combination of steady and oscillatory flows. Specifically, we imposed one of three oscillation waveforms (Sym, FR, FF) onto the steadily progressing finger of air and examined the resulting time-dependent reopening pressure. At medium and high frequencies, all imposed oscillations were found to lower reopening pressures from that of the steadily progressing interface. An FF oscillation in particular significantly lowered pressures and surface tensions in comparison to steady flow.

We hypothesize that the potential benefits of an FF oscillation are a consequence of the buildup of a reservoir of surfactant in the vicinity of the interface during the slow retraction phase that allows rapid readsorption during the fast expansion phase. The streamlines established by an FF oscillation waveform allow enhanced surfactant transport and adsorption to the interface, thereby maintaining lower reopening pressures. This investigation provides insight into developing improved treatments for RDS and potentially ARDS that would diminish damage to the pulmonary airways during mechanical ventilation. Future computational studies will further elucidate the mechanisms that govern the observed behavior.

Appendix

Note: ^∗Indicates a dimensional variable.

Expanded waveform construction

To facilitate the viscous pressure calculations, the asymmetrically oscillating waveform, $f^{\ast }\left(t^{\ast }\right)$, described over a period T using two polynomials, is approximated as a complex Fourier series. The Fourier coefficients are represented by

$$C_n=\frac{1}{T}\underset{-T}{\overset{T}{\int }}{f}^{\ast }\left(t^{\ast }\right)e^{-i\frac{2\pi n}{T}{t}^{\ast }}d{t}^{\ast },$$ (8)

where $f^{\ast }\left(t^{\ast }\right)$ is the function of two polynomials to be approximated, T is the period of oscillation, and n is the index of summation. The Fourier coefficients ($C_n$) are then used to approximate the piston waveform as a summation of sinusoids:

$$X_{\text{piston}}^{\ast }\left(t^{\ast }\right)=L_{\text{piston}}\sum _{n=-N}^{n=N}{C}_n{e}^{i2\pi nf(t^{\ast }+\Delta t^{\ast })}\text{.}$$ (9)

The variable $L_{\text{piston}}$ is the total distance the piston travels, N represents the number of terms in the approximation (N is set so that the largest possible frequency in the series is 5 Hz), and $\Delta t^{\ast }$ is the time delay, in seconds, associated with the position of the waveform as it crosses the triggering sensor. This piston phase is calculated by determining the location of the piston in its oscillatory cycle at the time the meniscus crosses the sensor. The phase of meniscus location is then set accordingly to correct for this discrepancy.

The following volume conservation relationship connects the piston waveform to the displacement of the air-liquid interface in the tube:

$$X_{\text{tube}}^{\ast }\left(t^{\ast }\right)={\left(\frac{R_{\text{piston}}}{R_{\text{tube}}}\right)}^2{X}_{\text{piston}}^{\ast }\left(t^{\ast }\right)+X_{\text{tube}}^{\ast }\left(0\right),$$ (10)

where $R_{\text{piston}}$ and $R_{\text{tube}}$ are the radii of the piston and tube, respectively ($R_{\text{piston}}=0.23\text{mm}$ and $R_{\text{tube}}=0.5\text{mm}$).

To determine the interfacial drop at the interface, it is necessary to first calculate the imposed flow, which is composed of both an oscillatory and a steady component. The oscillatory component,

$$Q^{\ast }{\left(t^{\ast }\right)}_{\text{osc}}=-\pi R_{\text{tube}}^2\frac{d{X}_{\text{tube}}^{\ast }\left(t^{\ast }\right)}{d{t}^{\ast }},$$ (11)

is decomposed into the contribution given by each Fourier series term and then summed to determine the total oscillatory flow. A general representation of the flow contribution broken down into each individual term is

$${\left(Q^{\ast }{\left(t^{\ast }\right)}_{\text{osc}}\right)}_n={\left[Q\text{amp}\right]}_n{e}^{i\frac{2\pi n}{T}(t^{\ast }+\Delta t^{\ast })},$$ (12)

where

$${\left[Q\text{amp}\right]}_n=-i2{\pi }^{2}nf{L}_{\text{piston}}{R}_{\text{tube}}^2{C}_n\text{.}$$ (13)

The summation of ${\left(Q^{\ast }{\left(t^{\ast }\right)}_{\text{osc}}\right)}_n$ equals the total oscillatory flow, $Q^{\ast }{\left(t^{\ast }\right)}_{\text{osc}}$.

Derivation of the viscous pressure drop: oscillatory component

In our derivation of the viscous pressure drop, we follow the Womersley solution for an oscillating column of fluid in a rigid tube (50). We assume that the pressure gradient in the viscous flow region is only a function of time and that there is no radial component of velocity. Since the walls are parallel, convective acceleration is negligible and unsteady Stokes flow provides an appropriate model. Therefore, the linearity of these equations permits the superposition of solutions.

The unsteady Stokes flow equation for an incompressible fluid is solved for each individual frequency term of the Fourier series. The following is a simplified representation of the Stokes equation in polar coordinates with corresponding boundary conditions. The axial component simplifies to

$$\begin{array}{c}\rho \frac{\partial u_n^{\ast }}{\partial t^{\ast }}=-\frac{\partial P_n^{\ast }}{\partial x^{\ast }}+\mu \left(\frac{1}{r^{\ast }}\frac{\partial }{\partial r^{\ast }}\left(r^{\ast }\frac{\partial u_n^{\ast }}{\partial r^{\ast }}\right)\right)\\ u_n^{\ast }\left(r^{\ast }=R_{\text{tube}}\right)=0\\ \frac{\partial u_n^{\ast }}{\partial r^{\ast }}\left(r^{\ast }=0\right)=0\end{array},$$ (14)

where ρ is the density and μ is the viscosity. Let $u^{\ast }=\sum _n{u}_n^{\ast }$ where $u_n^{\ast }$ satisfies Eq. 14. And, individual contributions to the pressure gradient are represented as

$${\left(\frac{\partial P^{\ast }}{\partial x^{\ast }}\right)}_n={\tilde{P}}_n{e}^{i\left(2\pi nf{t}^{\ast }+{\varphi }_n+\Delta {\varphi }_n\right)},$$ (15)

where ${\tilde{P}}_n$ is the magnitude of the pressure gradient, ${\varphi }_n$ represents the phase between the flow field and the pressure gradient, or pressure phase, and $\Delta {\varphi }_n$ is the phase originating from the placement of the waveform as it crosses the triggering sensor, or piston phase. The summation of ${\left(\partial P^{\ast }/\partial x^{\ast }\right)}_n$ approximates the total pressure gradient in the axial direction. The following variables and equations are nondimensionalized for ease of calculation:

$$u_n=\frac{\mu }{{\tilde{P}}_n{R}_{\text{tube}}^2}{u}_n^{\ast },P_n=\frac{1}{{\tilde{P}}_n{R}_{\text{tube}}}{P}_n^{\ast },t=2\pi nf{t}^{\ast },r=\frac{1}{R_{\text{tube}}}{r}^{\ast },x=\frac{1}{R_{\text{tube}}}{x}^{\ast }$$ (16)

$$\begin{array}{c}{\alpha }_n^2\frac{\partial u_n}{\partial t}=-e^{i\left(t+{\varphi }_n+\Delta {\varphi }_n\right)}+\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial u_n}{\partial r}\right)\\ u_n\left(r=1\right)=0\\ \frac{\partial u_n}{\partial r}\left(r=0\right)=0\end{array}$$ (17)

$${\alpha }_n^2=\frac{\rho R_{\text{tube}}^{2}2\pi nf}{\mu }\text{.}$$ (18)

The solution, in the form of Bessel functions, of Eq. 17 is

$$u_n\left(r,t\right)=\frac{-i}{{\alpha }_n^2}\left[\frac{J_o\left(i^{3/2}{\alpha }_{n}r\right)}{J_o\left(i^{3/2}{\alpha }_n\right)}-1\right]e^{i\left(t+{\varphi }_n+\Delta {\varphi }_n\right)},$$ (19)

where ${\alpha }_n$ is the Womersley parameter defined above in Eq. 18.

The velocities contributed from each of the Fourier series terms are then integrated over the tube area to obtain the individual flow quantities:

$$Q_n\left(t\right)=\underset{0}{\overset{1}{\int }}{u}_n\left(r,t\right)\left(2\pi r\right)dr$$ (20)

and

$$Q_n^{\ast }\left(t^{\ast }\right)=\frac{-2\pi i}{{\alpha }_n^2}\left(\frac{\tilde{P}{R}^4}{\mu }\right)\left[\frac{J_1\left(i^{3/2}{\alpha }_n\right)}{i^{3/2}{\alpha }_n{J}_0\left(i^{3/2}{\alpha }_n\right)}-1/2\right]e^{i\left(2\pi nf{t}^{\ast }+{\varphi }_n+\Delta {\varphi }_n\right)}\text{.}$$ (21)

These derived flows are simplified by

$$Z_n=\frac{-2\pi i}{{\alpha }_n^2}\left(\frac{J_1\left(i^{3/2}{\alpha }_n\right)}{i^{3/2}{\alpha }_n{J}_0\left(i^{3/2}{\alpha }_n\right)}-1/2\right),$$ (22)

which makes

$$Q_n^{\ast }\left(t^{\ast }\right)=\frac{{\tilde{P}}_n{R}^4}{\mu }\left|Z_n\right|e^{i\left(2\pi fn{t}^{\ast }+{\varphi }_n+\Delta {\varphi }_n+{\varphi }_{Z_n}\right)},$$ (23)

where $\left|Z_n\right|$ is the magnitude and ${\varphi }_{Z_n}$ is the phase contribution from $Z_n$.

Each derived flow term is then matched with the appropriate term from the differentiated Fourier series approximation of the actual waveform Eq. 9:

$${\left(Q^{\ast }{\left(t^{\ast }\right)}_{\text{osc}}\right)}_n={\left[Qamp\right]}_n{e}^{i(2\pi nf{t}^{\ast }+{\varphi }_n)}$$ (24)

$$Q_n^{\ast }\left(t^{\ast }\right)={\left(Q^{\ast }{\left(t^{\ast }\right)}_{\text{osc}}\right)}_n$$ (25)

$${\tilde{P}}_n=\frac{{\pi }^2{R}_{\text{piston}}^2{L}_{\text{piston}}\mu }{T\left(R_{\text{tube}}^4\left|Z_n\right|\right)}$$ (26)

$${\varphi }_{z_n}=-\Delta {\varphi }_n\text{.}$$ (27)

In this way, the pressure contribution from each term,

$${\left({\left(\frac{d{P}^{\ast }}{d{x}^{\ast }}\right)}_n\right)}_{\text{osc}}={\tilde{P}}_n\mathrm{Re}\left[e^{i\left(2\pi nf{t}^{\ast }+{\varphi }_n-{\varphi }_{Z_n}\right)}\right],$$ (28)

is calculated and summed to determine the total pressure contribution from oscillatory flow,${\left(d{P}^{\ast }/d{x}^{\ast }\right)}_{\text{osc}}$.