Abstract
The formation of receptor ligand bonds at the interface between different cells and between cells and substrates is a widespread phenomenon in biological systems. Physical measurements of bond formation rates between cells and substrates have been exploited to increase our understanding of the biophysical mechanisms that regulate bond formation at interfaces. Heretofore, these measurements have been interpreted in terms of simple bimolecular reaction kinetics. Discrepancies between this simple framework and the behavior of neutrophils adhering to surfaces expressing vascular cell adhesion molecule 1 (VCAM-1) motivated the development of a new kinetic framework in which the explicit formation of active bond formation sites (reaction zones) are a prerequisite for bond formation to occur. Measurements of cells interacting with surfaces having a wide range of VCAM-1 concentrations, and for different durations of contact, enabled the determination of novel kinetic rate constants for the formation of reaction zones and for the intrinsic bond kinetics. Comparison of these rates with rates determined previously for other receptor-ligand pairs points to a predominant role of extrinsic factors such as surface topography and accessibility of active molecules to regions of close contact in determining forward rates of bond formation at cell interfaces.
Introduction
Mathematical descriptions of the dynamics of cell adhesion provide an analytical framework for developing an understanding of the principal physical mechanisms that determine rates of cell bonding. A number of groups have developed such descriptions for bond formation and breakage where membranes with adhesive receptors come into contact. The seminal work on this subject is an article by Bell (1) in which basic descriptions of molecular reactions in two dimensions were developed. Bell concluded that bond formation rates between biological membranes were likely to be limited by the rate of lateral diffusion of the adhesion receptors in the cell membrane, and he proposed a simple model for how applied forces might affect bond breakage. Most subsequent work in this area has focused on bond breakage under force and understanding how loading affects the detachment of bonded surfaces from each other. This subject has benefited from a body of experimental work applying either atomic force microscopy or the bioforce probe technique to measure the breakage of single bonds under different loading conditions (2–5). A key theoretical breakthrough came with the recognition that the stochastic nature of bond breakage leads to a dependence of the most probable force at which a bond breaks on the rate at which force is applied to the bond (6). This has led to a well-developed understanding of the physical mechanisms of bond breakage and how rapid loading can actually lead to an increase in apparent bond strength.
Theoretical descriptions of bond formation have proved less amenable to experimental testing. This is largely because it is much harder to control the myriad factors that might affect bond formation than it is to control the load on a bond that has already formed. Two principal approaches for testing bond formation during cell adhesion are the flow channel and micromanipulation. Of these, the flow channel involves much higher complexity because of the mutual dependence of bond formation rates, cell deformation, fluid forces, and cell kinematics. Nevertheless, detailed dynamic computer simulations have been developed that provide good fidelity with experimental observations and the estimation of kinetic coefficients in some systems (7–9). Even so, the development of ever more realistic descriptions of cell motion and adhesion under flow remain a work in progress. In contrast, micromanipulation of cells into contact with other cells or chemically defined substrates is a relatively simple approach in which many of the key factors affecting adhesion can be controlled. The analytical framework for understanding the results of these experiments was developed by Chesla and colleagues (10), who proposed a simple bimolecular kinetic framework for interpreting cell adhesion measurements. This framework has also provided predictions that appear to be consistent with the majority of published experimental observations, and “effective” kinetic rates of bond formation have been calculated for a number of cell-substrate combinations (11–14).
The analysis here is motivated by recent observations in our laboratory of adhesion of neutrophils to surfaces coated with vascular cell adhesion molecule 1 (VCAM-1). That human neutrophils adhere at all to VCAM-1 is something of a surprise because VCAM-1 is not a ligand for the β2 integrins LFA-1 and Mac-1 that are the principal integrins on the neutrophil surface in humans. Flow cytometry measurements reveal, however, that several β1 integrins that bind to VCAM-1 are present on the neutrophil surface, albeit at 10-fold lower surface concentrations than their β2 counterparts (15–17). It is likely that this small number of molecules is a key factor underlying our observations that revealed inadequacies of the simple kinetic theories that have been used successfully in the past to describe bond formation rates. The inconsistencies between first-order kinetic descriptions and measurements of neutrophil adhesion to VCAM-1 motivated the following analysis.
Experimental Methods
Complete details of the experiments are given in the companion article in this issue (18) Briefly, adhesion probabilities were measured by repeatedly contacting neutrophils with beads (tosylactivated paramagnetic M-450 Dynabeads, Dynal, Lake Success, NY) coated with covalently attached recombinant extracellular domain of VCAM-1 (R&D Systems, Minneapolis, MN). The concentration of VCAM-1 on the bead surface was measured by labeling the beads with fluorescent antibody to VCAM-1 (R&D Systems) and measuring the intensity in flow cytometry. The fluorescence signal was calibrated using Quantum Simply Cellular beads (Flow Cytometry Standards, Fishers, IN) to determine the number of sites on the bead surface. Appropriate controls for nonspecific labeling were performed. Neutrophils were obtained from a drop of blood suspended in sterile buffer and placed in a fluid-filled chamber on the stage of an inverted microscope. The operator selected neutrophils based on their multilobular nuclei, picked them up with a micropipette, and brought them into contact with a VCAM-1 coated bead held in a second pipette (see Fig. 1 in the companion article (18)). Cell and bead were brought into contact for a predetermined duration (1 s, 2 s, 5 s, 10 s, 20 s, or 60 s) and then separated.
Figure 1.
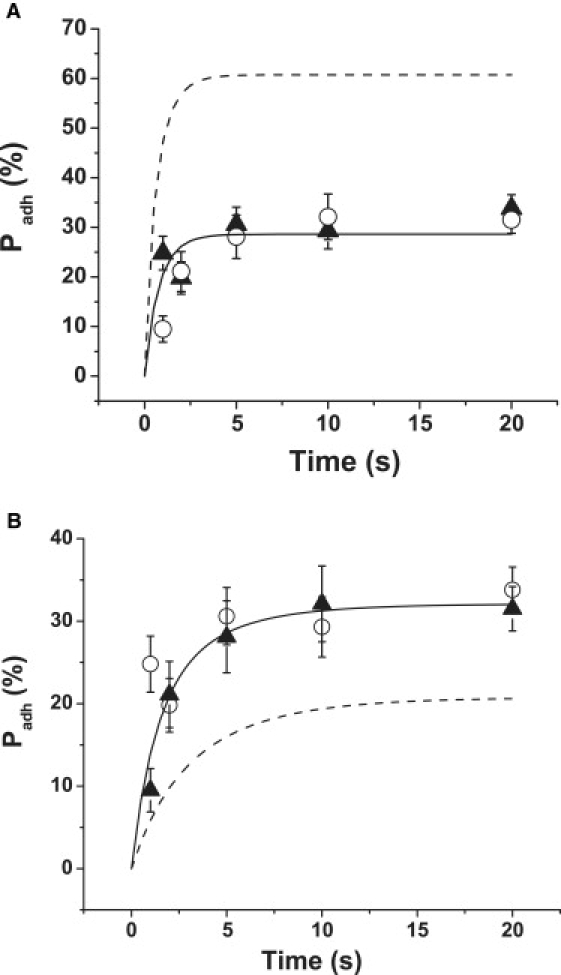
Adhesion probability of human neutrophils to VCAM-1 coated bead as a function of time. (A) Solid curve is based on a nonlinear least-squares regression of first-order kinetic theory (Eq. 1) to expected bond number 〈n〉 obtained from measurements of adhesion probability as a function of contact time for beads with a surface density of VCAM-1 (ρ1) of 310 sites/μm2. Data for these beads are shown as solid triangles. The dashed curve shows the theoretical prediction based on Eq. 1 and the kinetic parameters obtained for the solid curve but with ρ1 set to 860 sites/μm2. Measured values for adhesion to the 860 sites/μm2 beads are shown as the open circles. The discrepancy between measurement and simple first-order theory is evident. Bars represent standard error of the mean. Between 20 and 40 cell-bead pairs were tested for each data point. Probability values have been corrected for nonspecific adhesion (Eq. 14) and adjusted to account for differences in contact area. (See companion report for details (18).) (B) Predictions based on the assumption that the measured adhesion probability is the product of a constant probability that an RZ exists (PRZ = 0.35) and a first-order P〈n〉, consistent with Eq. 1. The solid curve corresponds to the fit to data obtained using beads with VCAM density of 860 sites/μm2 (solid triangles), and the dashed curve is generated from the fitted parameters but with a lower VCAM density (310 sites/μm2). Discrepancies between the predictions and measurements for the lower density beads (open circles) are evident. Probability values have been corrected for nonspecific adhesion before the calculations.
Approximately 25 contacts were performed for each cell-bead pair, except for 60 s contacts, where a new pair was selected for each test. Upon separation, adhesion was noted as a slight deflection of the cell surface as it was withdrawn. The adhesion probability was calculated as the number of contacts for which adhesion occurred divided by the total number of contacts. The macroscopic area of contact between the cell and the bead was controlled by the positioning of the bead and cell with the micropipettes and kept constant throughout the duration of contact. We attempted to impose similar areas of contact for all measurements, but some variability is inevitable. The formation of a bond is expected to increase linearly with the area of contact. Therefore, to avoid differences between measurements because of differences in contact area, adhesion probability was corrected to a standard area of contact (7.5 μm2), the mean contact area for all cells tested in the study. Nonspecific adhesion was determined from measurements of cells contacting VCAM-coated beads in the presence of an adhesion blocking antibody to β1 integrins (antibody 4B4 at a concentration of 0.1 mg/ml, Beckman Coulter, Miami, FL). Although not shown, results using blocking antibody agreed well with background levels measured by substitution of NCAM for VCAM-1 on the substrate or removal of divalent ions with EGTA.
Analysis
Inconsistencies between data and theory
Bimolecular kinetic theories have provided a reliable framework for interpreting cell adhesion measurements. These theories are based on application of simple chemical kinetics in two dimensions. The number of bonds expected to be formed when two surfaces come in contact <n> is related to forward and reverse rate constants kf and kr (10):
| (1) |
where the association constant, Ka = kf/kr, Ac is the area of contact between the two surfaces where molecules can interact, ρ1 and ρ2 are the surface concentrations of molecules on the two surfaces, and t is the length of time the two surfaces are in contact. The expected bond number is also related to the probability that adhesion will occur (Padh) between the two surfaces:
| (2) |
Theoretically, Eq. 2 is valid for Poisson processes only when the expected number of bonds is small, although in practice the predicted relationships agree well with experimental observation even when adhesion probabilities approach 1.0 (14).
A critical prediction of these theories is that when the density of either ligand becomes large, or if the contact time becomes very long, the adhesion probability should approach 1.0. This is not observed for neutrophils adhering to VCAM-1 when Mg2+ is used to induce integrin high affinity state. For surface concentrations of VCAM-1 above 200 sites/μm2, the probability of adhesion becomes independent of VCAM-1 surface concentration, but the probability of adhesion does not approach 1.0. This is illustrated in Fig. 1 A. Using Eq. 2, measurements of adhesion probability as a function of contact time were used to obtain expected bond number 〈n〉 as a function of time for beads with a surface density of VCAM-1 between 250 and 370 sites/μm2 (solid triangles). The bimolecular kinetic theory (Eq. 1) was fit to these data by nonlinear least-squares regression. The coefficients obtained from the regression were used in Eq. 1 to predict the adhesion probability as a function of contact time for beads with a higher surface density of VCAM-1 (860 sites/μm2). This is shown as the dashed curve in Fig. 1 A, predicting much higher adhesion rates for this surface concentration of VCAM-1. Measurements of adhesion probability for these beads (open circles), however, produced results that were indistinguishable from the data obtained with the lower surface concentration beads.
This disparity between theory and experiment is not resolved by postulating more complex reaction schemes in a simple two-dimensional reaction space. Even with additional reaction steps and kinetic coefficients to produce a bond, when the reaction time and the density of ligand become large, the probability of adhesion invariably approaches 1.0. To account for the observed behavior, we take into account the fact that when a cell contacts a substrate, it does not form large, uniform regions of close contact. Rather, the cell contacts the surface only at discrete locations corresponding to the tips of microvilli or the tops of membrane folds. In keeping with this, we postulate the existence of localized “reaction zones” (RZs) within the macroscopic area of contact. For these RZs to be active there are two requirements: first, there must be close physical contact between the opposing surfaces; and second, there must be adhesion molecules in the region of contact in an active (or high affinity) conformation. “Potential” RZs are regions of the surface that are not in close contact with the substrate (but which could move or deform to come in close contact) or a region of close contact that contains no adhesion molecules or no molecules in the active (high affinity) conformation.
We first considered a simple approach to account for the possible limiting effects that the absence or existence of RZs might have on bond formation. We postulated that the probability of adhesion is the product of the probability that an RZ exists, Prz, times the probability that bonds will form within the zone, P〈n〉:
| (3) |
We further assumed that the probability that an RZ exists was a constant proportional to the macroscopic area of contact, and P<n> could follow first-order kinetic behavior as described in Eqs. 1 and 2. This scheme satisfies the condition that the adhesion probability would not exceed a certain maximum value, but, unfortunately, it does not account for other aspects of observed behavior. This is illustrated in Fig. 1 B. In this case the maximum probability of adhesion PRZ is 0.35 (Fig. 1 B). The solid curve is based on a least-squares regression to the data for a surface density of 860 sites/μm2, and the dashed curve is the predicted curve for the same kinetic parameters and a density of 310 sites/μm2. The agreement between theory for the lower density (dashed curve) and measurement (open circles) is poor. These results indicate that the existence of an RZ is not a stationary, time-independent probability but, rather, must evolve over a time frame comparable to the contact times tested in the experiments. These results motivate the following analysis.
Time dependence of RZ formation
Consider a model in which the number of RZs in existence within a macroscopic area of contact evolves over time (See Fig. 2 A). We consider an RZ to be a region where the cell membrane is in proximity to the opposing substrate and to contain an unbound integrin in its high affinity state. When the integrin binds to its receptor on the substrate, a bonded zone (ZB) is formed. Potential reaction zones (PRZ) cannot form bonds but can become RZs by one or a combination of three mechanisms. These are illustrated in Fig. 2, B–D. A region containing a high affinity integrin that is not in close contact can move into close contact (Fig. 2 B), an integrin in close contact that is in a low affinity state can undergo a conformational change to a high affinity state (Fig. 2 C), or an integrin in the high affinity state may diffuse into a region of close contact that does not initially contain one (Fig. 2 D). The model does not distinguish between these different mechanisms but treats the transition from PRZ to RZ as a single kinetic step with forward and reverse rate constants k+ and k−. The general scheme takes the form shown in Fig. 2 E.
Figure 2.
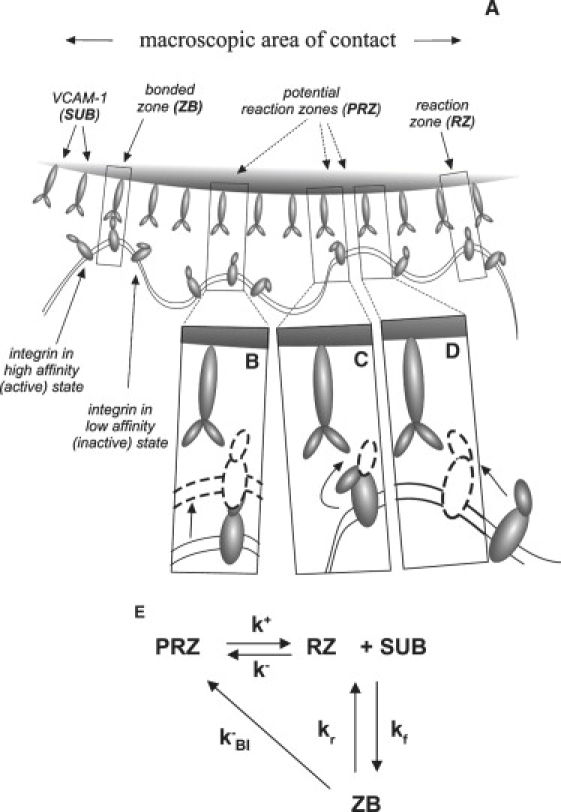
Cartoon (A) and schematic (E) of reaction scheme that allows the formation and disappearance of RZs. In panel E, PRZ and RZ represent the surface concentration of potential and active RZs in the macroscopic contact zone, ZB is the surface concentration of bonds, SUB represents the concentration of ligand on the substrate. PRZs may become (active) RZs by multiple mechanisms illustrated in B (displacement of the membrane into close contact), C (conformational change of the adhesion molecule from a low to a high affinity state), and D (diffusion of a high affinity adhesion molecule into a region of close contact). The amalgamation of these mechanisms is captured in the rate constants k+ and k− (E). Formation of a bond with an RZ is governed by kinetic constants kf and kr, and breakage of bonds to form a potential (inactive) RZ is characterized by kBI (E).
Once an RZ forms, bond formation proceeds with forward and reverse rate constants kf and kr. In the case where bonds are rare relative to the number of ligands on the substrate, the substrate concentration can be considered constant and the forward rate constant for this second-order reaction kf may be replaced by the pseudo-first-order rate k′f:
| (4) |
Finally, we note that bonds may also break directly to an inactive form of the RZ, a process governed by the rate constant k−BI.
A more general model might include the diffusion of PRZs into and out of the macroscopic region of contact. This step takes on major significance in situations where a large number of bonds form between the cell and substrate such that the supply of unbound sites in the interface becomes depleted and delivery of molecules to the contact zone becomes limiting. This case has been thoroughly treated in a recent report (19). In the analysis here, where bond formation is a relatively rare event, we can assume that this process is at steady state, with PRZs diffusing in and out of the macroscopic contact region at equal rates. Thus, the total concentration of PRZs within this region (TRZ) can be considered constant.
The governing equations for the system shown in Fig. 2 E are as follows:
| (5) |
| (6) |
| (7) |
where ZB is the concentration of ZBs in the interface. We can now eliminate PRZ by using our condition that the total concentration of RZs in the interface is constant, and obtain
| (8) |
| (9) |
An important limiting case occurs when the concentration of molecules on the substrate becomes very high, such that the forward rate k′f is much greater than kr, and we can approximate the reaction as , which leads to
| (10) |
This results in the following expression for the time evolution of bonds in the interface when substrate ligand concentrations are high:
| (11) |
where τRZ = 1/(k+ + k−BI) and KDRZ = k−BI/k+. The quantity ZBo is the zero time concentration of RZs and corresponds to the finite probability that an RZ exists upon initial contact. Note from the first term on the right-hand side of Eq. 11 that these initial bonds decay with time, whereas from the second term, new bonds evolve over time. If we suppose that the system is in steady state before contact and that contact itself does not alter the equilibrium between active and inactive zones, then the initial concentration of bonds is related to the kinetic coefficients, k+ and k−, by
| (12) |
For assessing adhesion probability, it is convenient to express this in terms of the expected number of bonds in the interface, 〈n〉. This is obtained by taking the product of the concentration ZB times the area of contact Ac:
| (13) |
Results
There are five unknown kinetic coefficients in the reaction scheme shown in Fig. 2 E. Three of the five coefficients can be determined by considering cases in which the concentration of VCAM-1 on the surface is sufficiently high that the dependence of bond formation on VCAM-1 concentration becomes negligible. In this case, we collect data obtained for all VCAM-1 concentrations above 200 sites/μm2 and fit the time dependence of adhesion probability to these data based on Eq. 13, which is valid when the substrate surface concentration becomes very large. This case is depicted in Fig. 3.
Figure 3.
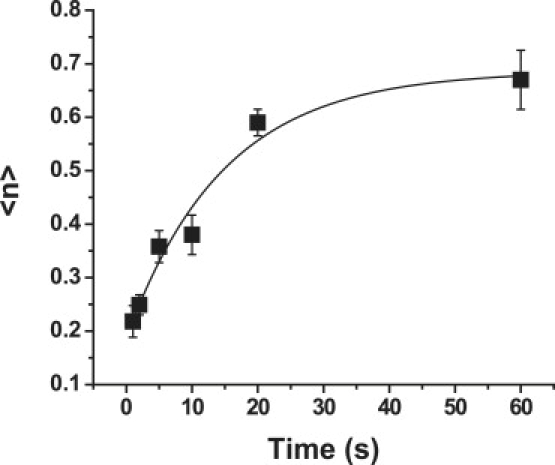
Time-dependent behavior of the system when the ligand concentration of the substrate is very large. The solid curve shows the least-squares regression of Eq. 13 for all data obtained for beads with VCAM concentration >200 sites/μm2. Error bars represent the mean ± standard error. (Note: Mean ± SE was calculated for the primary experimental measurement (Padh) then the range (Padh ± (mean ± SE)) was converted to 〈n〉 via Eq. 2. The resulting range for 〈n〉 was asymmetric, but in the figures the mean of the plus and minus errors is shown.) Each point represents between 35 and 60 cell-bead pairs, except for the 2 s and 20 s points for which there were over 140 cell-bead pairs. Values of the fitted coefficients are given in the text.
We assume a value for TRZ (5/μm2) based on the total number of VLA-4 molecules on the cell surface and normalize the data to a contact area of 7.5 μm2 (the mean contact area for all the experiments performed in the study). Nonspecific adhesion (Pbkg) was measured in the presence of blocking antibody to β1 integrins. The specific adhesion probability Padh is obtained from the probability measured in the absence of blocking antibody Pmeas according to
| (14) |
Least-squares regression results in values for the fitted coefficients of τRZ = 14.8 ± 4.09 s, and KDRZ = 53.7 ± 3.67, which corresponds to k+ = 1.2 × 10−3 s−1 and k−BI = 0.066 s−1. The initial number of RZs 〈n〉o is 0.19 ± 0.03 μm−2. Applying Eq. 12, we obtain k− = 0.25 s−1. (Fits were obtained using Origin (Microcal Software, Northampton, MA, and ± values are the standard errors of the fitted parameters.)
The ability of the model to match the dependence of adhesion on substrate concentration is illustrated in Fig. 4. In this case, we consider data obtained for contact durations of 5 s and at six different VCAM-1 concentrations ranging from 28 to 860 sites/μm2, and we obtain our theoretical curve by numerical integration of Eqs. 8 and 9. Unfortunately, the precision of the data are not sufficient to determine the remaining two parameters, kf and kr, unambiguously. Moy and colleagues (20) used atomic force microscopy to evaluate the force dependence of breakage of the VCAM-1-VLA-4 bond at different loading rates. For slow loading rates, the value for the off-rate of VLA-4 from VCAM-1 (kr) at zero force was determined to be 0.13 s−1. Using this value for kr, and the values for k+, k−BI, and <n>o obtained from the fit to the high density data, we determined kf by weighted least-squares regression with one free parameter to be 0.0051 μm2s−1, with a 90% confidence interval: (0.0010–0.091) μm2s−1.
Figure 4.
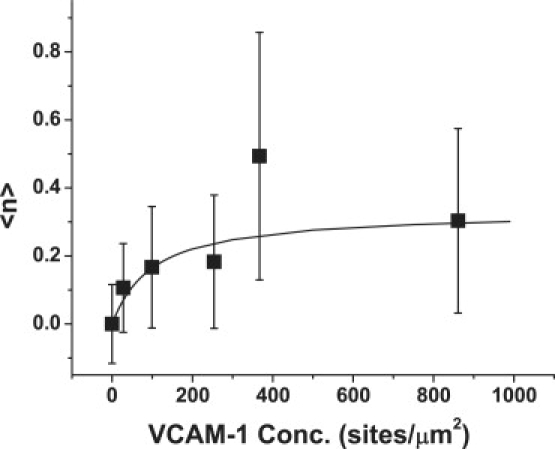
The dependence of the expected bond number on substrate concentration. The data represent measurements taken for a 5 s contact duration. The solid curve shows a weighted nonlinear least-squares regression with one free parameter (kf) between the data and the numerical integration of Eqs. 8 and 9. Values for k+, k−BI, and k− were obtained from the time dependence of the data at high density (see Fig. 3). The value for kr was fixed at 0.13 s−1 (19). The value for kf determined from the regression was 0.0051 s−1 with a 90% confidence interval (0.0010–0.091) μm2s−1.
As a check for consistency, the time courses for different surface concentrations of VCAM-1 were determined by numerical integration of Eqs. 8 and 9 using the best fit values for all the parameters given in the paragraphs above (Fig. 5 A). As expected, curves for VCAM-1 concentrations >200 sites/μm2 were similar and were well matched to the data shown in Fig. 3. In addition, curves for lower concentrations (100 and 30 sites/μm2) agreed well with measurements obtained for 5 s contacts at those concentrations. In Fig. 5 B, a three-dimensional plot of expected bond number as a function of VCAM-1 concentration and contact time for the best fit parameters is shown. Note that at VCAM-1 concentrations above 200 sites/μm2, the expected number of bonds becomes relatively insensitive to VCAM concentration, in agreement with experiment.
Figure 5.
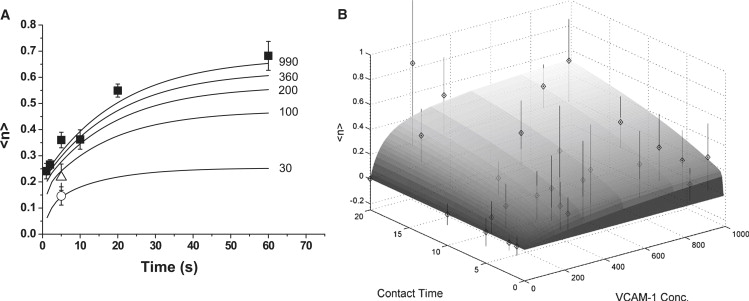
(A) Expected bond number 〈n〉 as a function of contact time at different VCAM-1 concentrations. Solid symbols are the data shown in Fig. 3, averaged for all VCAM concentrations >200 sites/μm2. Open triangle is the 5 s contact data for [VCAM-1] = 100 sites/μm2, and the open circle is the 5 s time point for [VCAM-1] = 30 sites/μm2. Curves were generated by numerical integration of Eqs. 8 and 9. The VCAM-1 concentrations used to generate the curves are given to the right of each curve (in sites/μm2). Parameter values were fixed at the values obtained in Figs. 3 and 4. (B) Three-dimensional view of the model prediction of 〈n〉 as a function of contact time (in seconds) and VCAM-1 concentration (in sites/μm2). Individual data points for all different concentrations and contact times tested are shown as diamonds. Note that lighter gray symbols fall below the surface as viewed. Error bars represent standard deviations.
Discussion
Controlled adhesion of cells to a substrate involves bond formation between adhesion molecules on the cell surface and counterreceptors on the substrate. Part of this process is limited by simple chemical kinetics of bond formation; but for molecules attached to surfaces, it is also a requirement that they be positioned in close contact so that the chemistry of bond formation can proceed. Thus, forward rates of adhesion may be limited not only by the intrinsic reactivity of the adhesive molecules involved but also by physical barriers to close contact between the surfaces and the availability of reactive molecules in those regions (21,22). In the analysis here, we extend the simpler bimolecular reaction theory developed by Chesla and colleagues (10) and explicitly address the requirement that molecules be in close physical contact before bonds can form. We postulate that RZ formation is a kinetic process that precedes bond formation. We imagine that, in general, RZ formation could involve multiple physical processes, including dynamic modulation of surface topography in the interface causing regions of the membrane to contact and separate from the substrate, lateral diffusion of adhesive molecules into and out of the regions of close contact, and/or changes in the conformation and affinity of molecules in close contact with substrate, enabling them to form bonds.
The ability to distinguish between these two aspects of cell-substrate adhesion in this study is in large part because of the relatively low number of β1 species on the cell surface. In a companion report, we provide evidence that neutrophil adhesion to VCAM-1 is mediated by β1 integrins, which are present on the cell surface at ∼8000 copies per cell, and more precisely, the integrin α4β1 (VLA-4), which is present on human neutrophils at ∼2500 copies per cell (18). These numbers are substantially less than the more common β2 forms, which are present at several tens of thousands of copies per cell (15). The mean spherical area of a neutrophil is 240 μm2, but the surface area of the membrane bilayer is approximately two times that (24), making the concentration of all β1 species on the cell surface <20 copies/μm2 and the concentration of VLA-4 on the cell surface ∼5.0/μm2. Thus, for a contact area of 7.5 μm2, the mean value for this study, there should typically be between 35 and 40 molecules in the contact zone, assuming a uniform distribution over the surface.
However, the fraction of surface area within the macroscopic contact zone that is in molecularly close contact with the substrate is substantially less than the total because of the irregularity of the surface topography. Williams and colleagues (22) estimate this fraction to be on the order of 3%, making the expected number of molecules in close contact of order 1.0. In this case, it is not surprising that the existence of a molecule in close contact with substrate would be rate limiting for bond formation. This also explains why disagreement with the bimolecular framework has not been observed in previous studies in either neutrophils (14) or other cell types (10,11,22) where the density of active molecules on the cell surface was substantially higher. In previous studies of neutrophil adhesion to ICAM-1, we surmised that physical factors contributed to the apparent kinetic constants that were determined from measurements of adhesion probability (14). Based on our findings here, it appears likely that the step of RZ formation is part of the kinetic process when other molecules mediate cell adhesion to substrates, but in situations where the density of molecules on the cell surface is so high, the existence of an RZ in the interface may not become rate limiting.
Although the number of adjustable parameters in the proposed kinetic scheme is larger than the number found in previous formulations, simpler models (as described in the Introduction) failed to provide predictions consistent with the behavior of the system. The forward rate for RZ formation and the dissociation rate of bonds to inactive forms are well determined by fits to the time course of bond formation for high VCAM-1 substrates. These are novel parameters and do not correspond to other published coefficients for VLA-4/VCAM-1 interactions. Although the physical events that correspond to these coefficients are not precisely known, the fact that the coefficients are sensitive to divalent cations in the extracellular medium (see companion report) suggests that fluctuations in the molecular affinity of VLA-4 play a significant role in the formation of these zones. Indeed, numerous reports of VLA-4-VCAM-1 interactions or interactions between VLA-4 and small peptides indicate that VLA-4 exists in different affinity states that are modulated by divalent ions in the suspending medium (25–27). These considerations favor an interpretation that it is the occurrence of a VLA-4 molecule in its high affinity state within a region of close contact that is the limiting factor for bond formation in these experiments. From a physiological perspective, this is quite satisfying because the activation state of integrins can be regulated by intracellular signaling pathways in response to chemical stimulus (28).
The values reported for the coefficients here are the best estimates we believe are possible, given the substantial variability in the data. In the limit of high VCAM-1 concentration, the fitted parameters 〈n〉o, KDRZ, and τRZ are reasonably well determined, with uncertainty <10% for KDRZ, ∼15% for 〈n〉o, and ∼35% for τRZ. If instead of using these parameters in the fit, we write Eq. 13 in terms of k+, k−, and kBI−, we find uncertainties of ∼25%, 35%, and 30%, respectively, and with substantial codependency among the coefficients. (This reflects the point that the sums and ratios of these coefficients are known with greater precision than their actual values.) The value for kr is obtained from the literature, but uncertainty in the fitted value for kf (even keeping the rest of the parameters fixed) is large: the 90% confidence interval corresponds to ±80% of the best fit value. These uncertainties result from the complexity of the model, measurement uncertainty, and the impracticality of doing thousands of experiments to account for statistical variability in the measurements.
Comparison to other measurements
A number of studies have been performed to examine binding between VCAM-1 in solution and VLA-4 on membrane surfaces. The kinetic coefficients depend critically on the divalent cation composition of the medium, and Mn2+ is frequently used to bring about an activated conformation of VLA-4. Under these conditions, the KD is on the order of 50 μM (29), and the off rate is ∼0.014 s−1 (30), making the forward rate ∼3 × 105 M−1s−1. These values are comparable to those measured for LFA-1-ICAM-1 interactions when one of the molecules is in solution and one is surface bound: kf = 2 × 105 M−1s−1 and kr = 0.03 s−1 (31,32). Although these values are not directly comparable to kinetic coefficients for surface-confined molecules, they indicate that the molecular events of bond formation for these two different molecular pairs are similar, as might be expected.
Comparison of measurements of on and off rates for surface bound molecules for these molecular pairs reveals important differences, reflecting contributions of extrinsic factors to bond formation between surfaces. The forward rate of 0.005 μm2s−1 obtained in this study is substantially faster than effective forward rates that have been estimated for LFA-1-ICAM-1 interactions, 2.5 × 10−6 μm2/s (14). Part of these differences is certainly due to the fact that the latter value encompasses not only the forward rates of molecular interaction but also the physical constraints on forming molecularly close contacts containing reactive molecules (RZ formation). Thus, both membrane topography and molecular accessibility are likely contributors to the slower forward rates reported previously for LFA-1-ICAM-1. Williams and co-workers examined the role of surface topography in cell adhesion (22) and concluded that <3% of the macroscopic contact area may actually be in close contact with substrate. Using this factor, an effective forward rate for LFA-1-ICAM-1 binding in areas of close contact would be ∼10−4 μm2/s, still substantially slower than the rate we obtain for VLA-4-VCAM-1. Part of this additional difference may be due to the possibility that not all LFA-1 molecules assume the high affinity conformation in the presence of Mg2+/EGTA. However, solution studies suggest that the conditions under which those measurements were made should be saturating for LFA-1 activation (14,33).
Other mechanisms may limit adhesion between surfaces, particularly if one is a cell surface. An important factor that may have a substantial influence on effective rates of reaction is the distribution of molecules over the cell surface. The effective coefficients are calculated on the basis of a uniform distribution of molecules on the membrane. If the distribution is nonuniform, the actual molecular concentration in the contact zone may be higher (or lower) than the mean surface concentration, causing the effective rates to be faster (or slower) than they would be if the distributions were uniform. Abitorabi (34) reports that β1 integrins tend to be clustered on the tips of the microvilli on resting neutrophils. This should lead to higher than average concentrations in the contact zone and higher effective rates than one should observe if the molecules were randomly distributed. In contrast, it is thought that β2 integrins, in particular Mac-1, tend to be found in the valleys between microvilli (See also Erlandsen et al. (35)). If LFA-1 is similarly distributed, one would expect lower effective forward rates for adhesion to ICAM-1 because the concentration of integrin in the contact zone would be lower than the mean for LFA-1.
Another potential mechanism involves the presence of the glycocalyx on the cell surface and the possibility that it may act as a steric barrier to close approach between the two surfaces (21,36). Of relevance to this is the fact that VCAM-1 is a longer molecule than ICAM-1, possessing an additional immunoglobulin G repeat that extends the binding site farther from the surface. This could mitigate effects of steric hindrance by the glyocalyx and decrease the apparent dissociation constant for bond formation. Whatever the underlying mechanism, the contrast between the similarity of binding rates measured for LFA-1-ICAM-1 and VLA-4-VCAM-1 in solution compared to the differences between rates measured for surface adhesion emphasizes the dominant role that molecular availability at the interface plays in limiting adhesion between cells and other surfaces.
Uncited References
(23)
Acknowledgments
The authors thank James McGrath, Al Clark, and Bill Simon for discussions during the development of this model and others that proved unsuitable. Martin Wegman assisted with the preparation of Fig. 5 B.
This work was supported by the U.S. Public Health Service via the National Institutes of Health under grant number PO1 HL18208.
References
- 1.Bell G.I. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 2.Evans E., Ritchie K., Merkel R. Sensitive force technique to probe molecular adhesion and structural linkages at biological interfaces. Biophys. J. 1995;68:2580–2587. doi: 10.1016/S0006-3495(95)80441-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Evans E., Leung A., Hammer D.A., Simon S.I. Chemically distinct transition states govern rapid dissociation of single L-selectin bonds under force. Proc. Natl. Acad. Sci. USA. 2001;98:3784–3789. doi: 10.1073/pnas.061324998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Evans E., Heinrich V., Leung A., Kinoshita K. Nano- to microscale dynamics of P-selectin detachment from leukocyte interfaces. I. Membrane separation from the cytoskeleton. Biophys. J. 2005;88:2288–2298. doi: 10.1529/biophysj.104.051698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Moy V.T., Florin E.L., Gaub H.E. Intermolecular forces and energies between ligands and receptors. Science. 1994;266:257–259. doi: 10.1126/science.7939660. [DOI] [PubMed] [Google Scholar]
- 6.Evans, E., and K. Ritchie. 1994. Probing molecular attachments to cell surface receptors: image of stochastic bonding and rupture processes. Proc. of the NATO Advanced Research Workshop: Scanning Probe Microscopies and Molecular Materials. Schloss Ringberg, Tegernsee, Germany. 29.5.–3.6. 1–10.
- 7.Chang K.-C., Hammer D.A. Adhesive dynamics simulations of sialyl-Lewisx/E-selectin-mediated rolling in a cell-free system. Biophys. J. 2000;79:1891–1902. doi: 10.1016/S0006-3495(00)76439-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Alon R., Hammer D.A., Springer T.A. Lifetime of the p-selectin-carbohydrate bond and its response to tensile force in hydrodynamic flow. Nature. 1995;374:539–542. doi: 10.1038/374539a0. [DOI] [PubMed] [Google Scholar]
- 9.Hammer D.A., Apte S.M. Simulation of cell rolling and adhesion on surfaces in shear flow—general results and analysis of selectin-mediated neutrophil adhesion. Biophys. J. 1992;63:35–57. doi: 10.1016/S0006-3495(92)81577-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chesla S.E., Selvaraj P., Zhu C. Measuring two-dimensional receptor-ligand binding kinetics by micropipette. Biophys. J. 1998;75:1553–1572. doi: 10.1016/S0006-3495(98)74074-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Long M., Zhao H., Huang K.S., Zhu C. Kinetic measurements of cell surface E-selectin/carbohydrate ligand interactions. Ann. Biomed. Eng. 2001;29:935–946. doi: 10.1114/1.1415529. [DOI] [PubMed] [Google Scholar]
- 12.Williams T.E., Nagarajan S., Selvaraj P., Zhu C. Concurrent and independent binding of Fcγ receptors IIa and IIIb to surface-bound IgG. Biophys. J. 2000;79:1867–1875. doi: 10.1016/S0006-3495(00)76436-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhu C. Kinetics and mechanics of cell adhesion. J. Biomech. 2000;33:23–33. doi: 10.1016/s0021-9290(99)00163-3. [DOI] [PubMed] [Google Scholar]
- 14.Lomakina E.B., Waugh R.E. Micromechanical tests of adhesion dynamics between neutrophils and immobilized ICAM-1. Biophys. J. 2004;86:1223–1233. doi: 10.1016/S0006-3495(04)74196-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bikoue A., George F., Poncelet P., Mutin M., Janossy G. Quantitative analysis of leukocyte membrane antigen expression: normal adult values. Cytometry. 1996;26:137–147. doi: 10.1002/(SICI)1097-0320(19960615)26:2<137::AID-CYTO7>3.0.CO;2-D. [DOI] [PubMed] [Google Scholar]
- 16.Reinhardt P.H., Elliott J.F., Kubes P. Neutrophils can adhere via α4β1-integrin under flow conditions. Blood. 1997;89:3837–3846. [PubMed] [Google Scholar]
- 17.van den Berg J.M., Mul F.P., Schippers E., Weening J.J., Roos D. β1 integrin activation on human neutrophils promotes β2 integrin-mediated adhesion to fibronectin. Eur. J. Immunol. 2001;31:276–284. doi: 10.1002/1521-4141(200101)31:1<276::AID-IMMU276>3.0.CO;2-D. [DOI] [PubMed] [Google Scholar]
- 18.Lomakina E.B., Waugh R.E. Adhesion between human neutrophils and immobilized endothelial ligand VCAM-1: divalent ion effects. Biophys. J. 2009;96:276–284. doi: 10.1016/j.bpj.2008.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zhu D.M., Dustin M.L., Cairo C.W., Golan D.E. Analysis of two-dimensional dissociation constant of laterally mobile cell adhesion molecules. Biophys. J. 2007;92:1022–1034. doi: 10.1529/biophysj.106.089649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zhang X., Craig S.E., Kirby H., Humphries M.J., Moy V.T. Molecular basis for the dynamic strength of the integrin α4β1/VCAM-1 interaction. Biophys. J. 2004;87:3470–3478. doi: 10.1529/biophysj.104.045690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lomakina E.B., Waugh R.E. Bond formation during cell compression. In: King M.R., editor. Cellular Engineering. Elsevier; Burlington, MA: 2006. pp. 105–122. [Google Scholar]
- 22.Williams T.E., Nagarajan S., Selvaraj P., Zhu C. Quantifying the impact of membrane microtopology on effective two-dimensional affinity. J. Biol. Chem. 2001;276:13283–13288. doi: 10.1074/jbc.M010427200. [DOI] [PubMed] [Google Scholar]
- 23.Reference deleted in proof.
- 24.Ting-Beall H.P., Needham D., Hochmuth R.M. Volume and osmotic properties of human neutrophils. Blood. 1993;81:2774–2780. [PubMed] [Google Scholar]
- 25.Chen L.L., Whitty A., Lobb R.R., Adams S.P., Pepinsky R.B. Multiple activation states of integrin α4β1 detected through their different affinities for a small molecule ligand. J. Biol. Chem. 1999;274:13167–13175. doi: 10.1074/jbc.274.19.13167. [DOI] [PubMed] [Google Scholar]
- 26.Chen L.L., Whitty A., Scott D., Lee W.C., Cornebise M. Evidence that ligand and metal ion binding to integrin α4β1 are regulated through a coupled equilibrium. J. Biol. Chem. 2001;276:36520–36529. doi: 10.1074/jbc.M106216200. [DOI] [PubMed] [Google Scholar]
- 27.Lobb R.R., Antognetti G., Pepinsky R.B., Burkly L.C., Leone D.R. A direct binding assay for the vascular cell adhesion molecule-1 (VCAM1) interaction with α4 integrins. Cell Adhes. Commun. 1995;3:385–397. doi: 10.3109/15419069509081293. [DOI] [PubMed] [Google Scholar]
- 28.Chigaev A., Blenc A.M., Braaten J.V., Kumaraswamy N., Kepley C.L. Real time analysis of the affinity regulation of α4-integrin. The physiologically activated receptor is intermediate in affinity between resting and Mn2+ or antibody activation. J. Biol. Chem. 2001;276:48670–48678. doi: 10.1074/jbc.M103194200. [DOI] [PubMed] [Google Scholar]
- 29.Jakubowski A., Rosa M.D., Bixler S., Lobb R., Burkly L.C. Vascular cell adhesion molecule (VCAM)-Ig fusion protein defines distinct affinity states of the very late antigen-4 (VLA-4) receptor. Cell Adhes. Commun. 1995;3:131–142. doi: 10.3109/15419069509081282. [DOI] [PubMed] [Google Scholar]
- 30.Zwartz G., Chigaev A., Foutz T., Larson R.S., Posner R. Relationship between molecular and cellular dissociation rates for VLA-4/VCAM-1 interaction in the absence of shear stress. Biophys. J. 2004;86:1243–1252. doi: 10.1016/S0006-3495(04)74198-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Woska J.R., Morelock M.M., Jeanfavre D.D., Bormann B.J. Characterization of molecular interactions between intercellular adhesion molecule-1 and leukocyte function-associated antigen-1. J. Immunol. 1996;156:4680–4685. [PubMed] [Google Scholar]
- 32.Labadia M.E., Jeanfavre D.D., Caviness G.O., Morelock M.M. Molecular regulation of the interaction between leukocyte function-associated antigen-1 and soluble ICAM-1 by divalent metal cations. J. Immunol. 1998;161:836–842. [PubMed] [Google Scholar]
- 33.Dransfield I., Cabanas C., Craig A., Hogg N. Divalent cation regulation of the function of the leukocyte integrin LFA-1. J. Cell Biol. 1992;116:219–226. doi: 10.1083/jcb.116.1.219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Abitorabi M.A., Pachynski R.K., Ferrando R.E., Tidswell M., Erle D.J. Presentation of integrins on leukocyte microvilli: a role for the extracellular domain in determining membrane localization. J. Cell Biol. 1997;139:563–571. doi: 10.1083/jcb.139.2.563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Erlandsen S.L., Hasslen S.R., Nelson R.D. Detection and spatial distribution of the β2 integrin (Mac-1) and l-selectin (LECAM-1) adherence receptors on human neutrophils by high-resolution field emission SEM. J. Histochem. Cytochem. 1993;41:327–333. doi: 10.1177/41.3.7679125. [DOI] [PubMed] [Google Scholar]
- 36.Bell G.I., Dembo M., Bongrand P. Cell adhesion. Competition between nonspecific repulsion and specific bonding. Biophys. J. 1984;45:1051–1064. doi: 10.1016/S0006-3495(84)84252-6. [DOI] [PMC free article] [PubMed] [Google Scholar]


