Abstract
The binding of carbohydrate substrates to concanavalin A (Canavalia ensiformis agglutinin (ConA)) is essential for its interaction with various glycoproteins. Even though metal ions are known to control the sugar binding ability of legume lectins, the interplay between sugar and metal ion binding to ConA has not been elucidated in a detailed manner at the atomic level. We have carried out long, explicit solvent molecular dynamics simulations for tetrameric, dimeric, and monomeric forms of ConA in both the presence and absence of trimannoside and metal ions. Detailed analyses of these trajectories for various oligomeric forms under different environmental conditions have revealed dynamic conformational changes associated with the demetalization of ConA. We found that demetalization of ConA leads to large conformational changes in the ion binding loop, with some of the loop residues moving as far as 17 Å with respect to their positions in the native trimannoside and metal ion-bound crystal structure. However, the β-sheet core of the protein remains relatively unperturbed. In addition, the high mobility of the ion binding loop results in drifting of the substrates in the absence of bound metal ions. These simulations provide a theoretical rationale for previous experimental observations regarding the abolition of the sugar binding ability upon demetalization. We also found that the amino acid stretches of ConA, having high B-factor values in the crystal structure, show relatively greater mobility in the simulations. The overall agreement of the results of our simulations with various experimental studies suggests that the force field parameters and length of simulations used in our study are adequate to mimic the dynamic structural changes in the ConA protein.
Introduction
Lectins are a class of proteins that interact with various glycoproteins and control a variety of processes such as defense against pathogens; legume nodulation; mitogenesis of lymphocytes, possibly through the formation of “micropatches”; fertilization; and tumor metastasis and development, among others (1–5). Concanavalin A (Canavalia ensiformis agglutinin (ConA)) is the prototype of legume lectins (6), and it was the first lectin to have its crystal structure solved (7). ConA is a homotetrameric lectin, with each monomer composed of 237 amino acid residues (8,9). ConA monomers adopt the jelly-roll fold that is conserved in the legume lectin family and several other members of the lectin family (10). The fold consists of three β-sheets, referred to as “back”, “front”, and “top” β-sheets (Fig. 1), with six, seven, and five antiparallel β-strands, respectively (6,7,11).
Figure 1.
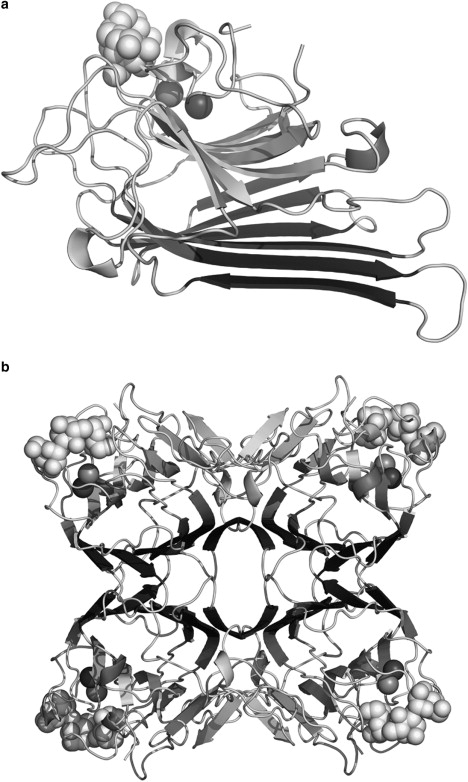
The diagram depicts monomeric (a) and tetrameric (b) ConA (1CVN). The light-colored spheres depict the trimannoside molecule, and the adjacent dark spheres represent the calcium and manganese ions.
Each monomer of ConA has only one substrate binding site, and so ConA is tetravalent. ConA has its isoelectric point at pH 7.1 (12) and exists as a dimer below pH 6 and as a tetramer near pH 7 (13,14). It has been proposed recently that the stability and pH dependence of the tetramer is influenced by two His residues (His-51 and His-131) (15). Legume lectins typically exist as dimers or as tetramers (6), with several intramolecular orientations of the monomers with respect to each other to gain increased avidity and specificity for their respective substrates (16,17).
Substrates for ConA include both mannose and glucose, although thermodynamic studies indicate that mannose binds strongly to ConA compared to glucose (18). The sugar binding pocket in legume lectins is conserved; in ConA, it consists of residues Tyr-12, Pro-13, Asn-14, Thr-15, Asp-16, Leu-99, Asp-208, and Arg-228. The interactions between lectins and substrate sugars include hydrogen bonds (19,20), ring stacking, burial of hydrophobic surface area (21), and a few water-mediated interactions (18,22).
The importance of metal ion binding in the folding of ConA to its native structure has been established in recent biophysical studies focused on folding and oligomerization (23). Previous studies have also suggested that the removal of the divalent ions from lectin abolishes its sugar binding ability (24), although the divalent ions do not interact directly with the saccharide as they do in calcium-dependent animal lectins (25). Despite the importance of metal ions in controlling the structural stability and the substrate binding ability of ConA, no atomically detailed picture is available for the conformational dynamics of these folding and binding events. Several crystallographic studies have attempted to explain the structural basis of demetalization and the consequent abolition of the sugar binding abilities of lectins (26–28). However, due to the difficulty in interpreting the electron density for the ion binding loop in demetalized ConA (28), it has not been possible to elucidate the conformational changes associated with the demetalization process.
Computational approaches are increasingly being used to explore the structure and interactions of various biological macromolecules. One such computational approach is molecular dynamics (MD), which enables the exploration of biological systems at an atomic level and can potentially provide valuable insights about these systems' dynamic properties. These functions make MD a powerful technique for understanding the intricacies of the interactions that govern the folding and binding processes of biological macromolecules. MD simulations have been used in a number of studies; for example, this technique was used to explore the thermal unfolding of peanut (Arachis hypogaea) agglutinin (PNA) and the role of metal ions in its structure and stability (29). MD simulations have also been successfully used to investigate the differential affinity of ConA for glucoside and mannoside (18). These simulations revealed some additional interactions that were not observed in the static crystal structures. In other computer simulations, the protein-ligand interactions of PNA with T-antigen and lactose were studied (22). These studies have demonstrated that MD can be complementary to crystallographic and other experimental methods and, together, these methods provide greater insight than would be possible if any were used independently.
In this work, we carried out extensive, explicit solvent MD simulation studies for ConA in the presence and absence of metal ions and trimannoside substrate. The objective of this study was to understand the role of metal ions in substrate binding and the structural stability of ConA. The crystal structure of the ConA-trimannoside complex (Protein Data Bank (PDB) entry 1CVN) (30) was simulated in aqueous environment for 3 ns with modifications such as removal of the ions and/or the trimannoside sugar. Simulations were also carried out for the monomeric and dimeric forms of ConA to explore the role of metal ions in the oligomerization process.
Methods
The MD simulations were carried out using the parallel version of AMBER9 (31) and were based on the NVT ensemble at a temperature of 300 K. This temperature was chosen because our primary objective was to study the dynamics of the metal ions and substrate binding at physiologically relevant conditions. Moreover, substrate and ion binding does not involve large-scale conformational changes in the protein, and so there was no need for volume fluctuations; we proceeded with the NVT simulations. We believe NPT simulations would also provide similar results. The starting coordinates of the ConA complex were from the PDB entry 1CVN (30), which is a complex of ConA and the N-linked glycan core trimannoside (Manα1–6(Manα1–3)Man) (30). The simulations were carried out using an explicit solvent environment. The solvated system for the ConA molecule was prepared using an explicit water box consisting of TIP3P (32) water molecules. The water box extended to 7 Å beyond the outermost atom of ConA or the ConA-sugar complex on both sides of the x, y, and z axes. The simulations were carried out both in the presence and absence of bound metal ions and trimannoside substrate. Because we chose a relatively small solvent box around the protein, no free counterions were added to the system for charge neutralization. Addition of free counterions in the solvent might have interfered with protein-bound metal ions.
The solvated system was minimized to get rid of any unfavorable contacts and then equilibrated for 20 ps to bring the temperature from ∼0 K to 300 K, after which production dynamics were run for 3 ns. A time step of 1 fs and a cutoff radius of 8 Å were used in all the simulations. The periodic boundary conditions were used to negate the surface effects at the box boundaries. The particle mesh Ewald summation method (33) was used to calculate the electrostatic potential. The bonds containing hydrogen atoms were constrained using SHAKE (34), and so bond interactions involving hydrogen atoms were not calculated concomitantly. The coordinates were saved every picosecond; thus, the trajectory from a 3 ns simulation consisted of 3000 frames.
The AMBER force fields used for the simulations were ff03 (35) for protein parameters and glycam04 (36) for sugar parameters. The force field parameters for the ions Mn2+ and Ca2+ (18) were obtained from the AMBER contributed parameters database at http://www.pharmacy.manchester.ac.uk/bryce/amber. The ptraj module of AMBER9 was used to calculate the root mean-square deviations (RMSDs), atomic positional fluctuations (APFs), B-factor (BF) values, hydrogen bonds, and the radius of gyration (Rg) values of the protein. NACCESS v2.1.1 (37) was used for the surface area calculations.
Results
The various different environmental conditions and oligomeric states under which MD simulations were carried out for ConA are summarized in Table 1. The first simulation consisted of the native tetrameric crystal structure of ConA in complex with trimannoside sugar and bound Ca2+ and Mn2+ ions in an aqueous environment. To mimic the aqueous environment, the water molecules from the crystal were removed, and the solvent molecules were introduced from the solvent box. In the subsequent simulations, the ions and the sugar molecule were removed one by one to observe the effects of these constituents on the behavior of the ConA molecule. This process resulted in four environmental conditions, viz., presence of both ions and the trimannoside sugar molecule (E1), presence of the ions in absence of the sugar (E2), presence of the sugar in the absence of the ions (E3), and the absence of both ions and the sugar (E4). Under each of these environmental conditions, a simulation of 3 ns duration was carried out for the ConA tetramer. The ConA monomer and dimer were also simulated for a duration of 3 ns each under four similar environmental conditions. Thus, trajectories were collected for a total of 12 simulations. These 12 MD trajectories were analyzed to explore the effects of different environmental conditions on the structure of ConA and its substrate recognition.
Table 1.
The summary of various simulations carried for monomeric, dimeric, and tetrameric structures of ConA
| Simulation | Concanavalin A (ConA) | Ions (Mn2+ and Ca2+) | Trimannoside sugar | Duration of simulation | |
|---|---|---|---|---|---|
| E1 | Monomer | + | + | + | 3 ns |
| AB Dimer | + | + | + | 3 ns | |
| Tetramer | + | + | + | 3 ns | |
| E2 | Monomer | + | + | − | 3 ns |
| AB Dimer | + | + | − | 3 ns | |
| Tetramer | + | + | − | 3 ns | |
| E3 | Monomer | + | − | + | 7 ns |
| AB Dimer | + | − | + | 3 ns | |
| Tetramer | + | − | + | 3 ns | |
| E4 | Monomer | + | − | − | 7 ns |
| AB Dimer | + | − | − | 3 ns | |
| Tetramer | + | − | − | 3 ns | |
The “+” and “−” symbols indicate the presence and absence, respectively, of the trimannoside substrate or ions in the simulation.
The effects of metal ions and trimannoside on the structure of ConA
The ConA tetramer in complex with sugar and metal ions (E1)
Fig. 2 shows the RMSDs for the structures sampled during various MD simulations from their respective starting structures. The 3 ns trajectory for the ConA tetramer (Fig. 2, bottom panel) showed that, in the presence of bound metal ions, the equilibrated structure deviated by only ∼1.5 Å from the starting structure. The major structural changes occurred during the initial 10 to 20 ps, with a sudden change in the RMSD to ∼1 Å. The structural deviation then continued rather slowly for the rest of the simulation to a final value of ∼1.5 Å. The structural deviations with respect to the original crystal structure were also calculated using ProFit 2.5.3 (37). They varied in the range of 1 to 1.5 Å (see Fig. S1 in the Supplementary Material) for the native ConA tetrameric sugar complex in the presence of bound metal ions. We also computed the Rg as a function of time, because any destabilization of the protein structure would result in large increase of Rg values. The Rg plots (Fig. S2) for the protein showed only a small increase of ∼0.3 Å, which would translate into a change of ∼5% in the volume.
Figure 2.
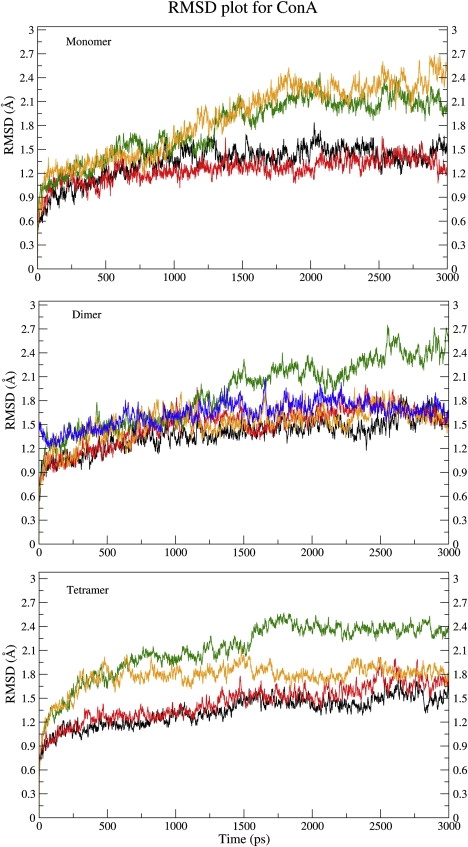
Plot showing the RMSD values between the starting structure and the structures sampled during the 3 ns simulations. The top, middle, and bottom panels show the RMSD plots for the monomer, AB dimer, and tetramer, respectively. The results from different simulations are shown: E1 (black lines), E2 (red lines), E3 (green lines), and E4 (orange lines). The RMSD plot of the dimer E2 simulation with respect to the crystal structure 1GKB is also shown (blue lines).
We also wanted to investigate whether the structural deviation described above was confined to a few local regions or over the whole protein. Using the positional fluctuations observed over the MD trajectory, we computed the theoretical BF plots for the protein over the simulation time and compared them to the experimental BF values observed in the crystal structure 1CVN. Fig. 3 shows a detailed comparison of the experimental and theoretical BF values for chain A of the ConA tetramer. The experimental BF values are also depicted in the Cα trace of ConA shown in the inset of Fig. 3. As can be seen, the regions with high experimental BF values correspond to the peaks in the computed BF curve, and they are mostly confined to the loop regions of ConA. This finding suggests that there is good agreement between experimental and theoretical BF values. In fact, the average BF value of the tetramer computed from the E1 simulation was 17.85 Å2 (Table 2) over all the backbone atoms (CA, C, and N). It is interesting to note that the average experimental BF value observed in the crystal structure of ConA (30) is 16.85 Å2, which is very close to the theoretical value observed in our simulation. However, a few relevant issues must be kept in mind when comparing the theoretical and experimental BF values. Experimental BF values or atomic temperature factors are typically used to quantitate the dynamic disorder in the position of the atoms caused by the temperature-dependent motion. Apart from the thermal motions, BF values also have contributions from other sources of experimental errors. Secondly, the MD simulations were carried out at 300 K, whereas the crystal structure was solved at 150 K. Therefore, a comparison between the theoretical and experimental BF values can only be qualitative. The apparent agreement between the two is solely because loop regions have relatively higher mobility compared to the tightly packed core of the protein. Fig. S3 a shows the computed BF values for all four chains of the tetramer from four different environmental conditions. If the BF value of a region is high, the region is expected to have high temperature-dependent vibrations; consequently, it can undergo structural changes easily and frequently. Therefore, we explored the regions with high experimental BF values. Only one region of the loop (residues 160–164) demonstrated a consistently high BF value (>40Å2) in all of the tetramer chains. In addition, the regions of the loop containing residues 183–187 and 201–205 showed high BF values, but these values were not uniformly high in all of the chains. Region 183–187 was more flexible only in chain C, whereas the 201–205 region had a high BF value only in chain B; in the remainder of the chains, these regions had normal (approximately ≤40Å2) BF values. All of the regions mentioned above correspond to loop regions of the molecule or amino acid stretches involved in ligand binding.
Figure 3.
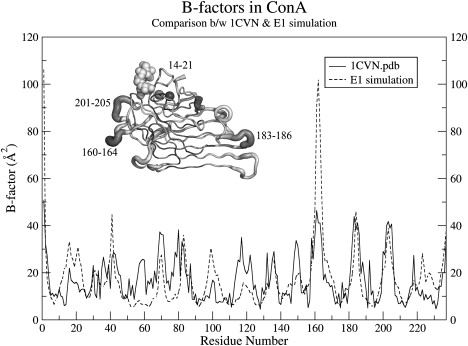
Comparison between the theoretical and experimental BF values. The plot shows the computed (dashed line) and the experimental (solid line) BF values for chain A of the ConA tetramer. The theoretical BF values have been computed using the trajectory of the simulations for the substrate-bound tetramer in the presence of metal ions (E1). The inset shows the C-alpha trace for the crystal structure of the substrate-bound ConA monomer with the thickness of the chain reflecting the experimental BF values of the constituent residues.
Table 2.
The converged values for various structural parameters (RMSD from the starting structure, Rg, and percentage of NSASA) extracted from the last 500 ps of the 3 ns simulations
| Oligomeric status | Simulation | RMSD (Å) | Rg (Å) | NSASA (%) | Average BF (Å2) |
|---|---|---|---|---|---|
| Monomer | E1 | 1.41 ± 0.09 | 17.57 ± 0.03 | 54.15 ± 0.70 | 14 ± 18 |
| E2 | 1.38 ± 0.09 | 17.27 ± 0.77 | 55.30 ± 0.56 | 12 ± 15 | |
| E3 | 2.13 ± 0.10 | 17.74 ± 0.04 | 53.01 ± 0.50 | 24 ± 47 | |
| E4 | 2.38 ± 0.13 | 17.65 ± 0.79 | 54.64 ± 0.65 | 22 ± 49 | |
| Dimer | E1 | 1.61 ± 0.11 | 25.22 ± 0.06 | 53.85 ± 0.30 | 17 ± 16 |
| E2 | 1.65 ± 0.08 | 25.11 ± 1.13 | 54.31 ± 0.29 | 20 ± 21 | |
| E3 | 2.43 ± 0.12 | 25.61 ± 0.08 | 54.41 ± 0.33 | 29 ± 91 | |
| E4 | 1.65 ± 0.09 | 25.23 ± 1.13 | 54.65 ± 0.21 | 22 ± 29 | |
| Tetramer | E1 | 1.54 ± 0.08 | 29.07 ± 0.03 | 52.17 ± 0.25 | 18 ± 17 |
| E2 | 1.72 ± 0.09 | 28.69 ± 1.28 | 52.59 ± 0.26 | 19 ± 20 | |
| E3 | 2.37 ± 0.05 | 29.48 ± 0.04 | 52.79 ± 0.28 | 31 ± 75 | |
| E4 | 1.83 ± 0.08 | 28.78 ± 1.29 | 53.68 ± 0.38 | 21 ± 30 |
Standard deviations (SD) are provided for each of the parameters. Also depicted are the computed BF values averaged over all the residues of the protein. The large SD values for computed average BF values are a result of the presence of specific loop regions with very high BF values.
Thus, the analysis of structurally flexible regions in ConA suggests that the 1.5 Å RMSD between the starting structure and the final structure derived from the MD simulation may indeed arise from structural deviations in the loop regions only, whereas the core of the ConA tetramer remains intact and relatively rigid. This inference is also supported by the observation that there is only ∼2% change in the nonpolar solvent-accessible surface area (NSASA) for the trimannoside-bound tetramer (Fig. S4). This finding means that the ConA-trimannoside complex is already in its best, folded, and stable state, so that only a slight alteration is observed in its packing after the 3 ns simulation (as a decrease in exposed NSASA). Next, we examined whether there were any changes at the secondary structure level during the simulation. To this end, we identified the hydrogen bonds present in the structures sampled during the MD simulation, and we analyzed separately the hydrogen bonds involving main-chain to main-chain (M-M) interactions and those bonds involving side chain (S-M/S) interactions. The M-M hydrogen bonds, which can be considered a measure of the secondary structure, indicated a slow drop in numbers (∼8% over the course of the 3 ns simulation (Fig. S5 a)). In contrast to the M-M hydrogen bonds, the hydrogen bonds involving side chains showed a comparatively fast decline in number (∼20%) over the 3 ns simulation (Fig. S5 b). This slow decline in the number of M-M hydrogen bonds and the relatively faster decline in the number of S-M/S hydrogen bonds suggest that there is only a minor change in the secondary structure elements but that there is a significant rearrangement of the conformations of the side chains during the simulation. Based on these results, it can be concluded that, during the MD simulation, the core of the ConA tetramer remains relatively rigid and that dynamic structural changes in the core essentially correspond to a relaxation of side-chain orientations. These observations demonstrate that the conditions needed for a simulation of native ConA were met in a manner sufficient enough to ensure that no anomalous behavior was observed during the 3 ns simulation.
ConA tetramer in the absence of trimannoside (E2)
The trajectory from the simulation in the absence of bound trimannoside (E2) was analyzed to understand the effects of substrate binding on the dynamic fluctuations in the ConA tetramer. However, the structural deviations were negligibly different compared to the simulation involving substrate-bound ConA. The final RMSD with respect to the starting structure of the simulation was ∼1.5Å at the end of the 3 ns simulation (Fig. 2). The RMSD with respect to the crystal structure was also ∼1.5 Å (Fig. S1). In addition, the change in the Rg value was similar to that observed in E1, i.e., a change in Rg of ∼0.4 Å (Fig. S2). Similarly, no appreciable changes were observed in the NSASA (Fig. S4) or the M-M and S-M/S hydrogen bonds (Fig. S5) compared to the E1 simulation. However, significant differences were observed in the thermal flexibility of the amino acid stretch 201–205 and the region 160–164 (Fig. S3). The 201–205 loop region, which is involved in substrate binding, had increased BF values (>60Å2) in all the chains except chain A. The dynamic fluctuations of the loop corresponding to the 160–164 region appeared to be correlated to the movements of the 201–205 region, even though this stretch is not directly involved in substrate binding.
ConA tetramer in the absence of metal ions (Mn2+ and Ca2+) but in complex with sugar (E3)
The E3 simulation was run for ConA in the absence of metal ions (Mn2+ and Ca2+) but in complex with the trimannoside sugar. As can be seen in Fig. 2, the RMSD increased continuously in this simulation to > 2 Å by the end of 1.5 ns; at ∼1.8 ns, the RMSD reached the maximum deviation of ∼2.5 Å. The Rg for ConA increased by ∼0.7 Å (Fig. S2), with a corresponding ∼8% increase in the volume. Analysis of the local structural fluctuations indicated that the large RMSD of the overall structure resulted from high, local mobility of certain specific amino acid stretches of the ConA protein. In the absence of metal ions, the segment demonstrating the highest thermal motion was the region corresponding to the amino acid residue stretch 14–21 (Fig. S3 a). The minimum computed BF value for this region was > 600Å2 for chain A (Fig. S3 a), whereas the other chains displayed even higher BF values for this stretch. The 68–71 region had the highest BF value in chain C (BF >180 Å2), whereas the remainder of the chains in this region were comparatively less mobile (BF < 50 Å2). Similarly, the 98–101 region had a high BF value (∼100 Å2) for chain D compared with other chains (BF < 40Å2). The 160–164 region had BF values ∼80 Å2 for all the chains, and the 201–205 region had BF values ∼60 Å2.
The NSASA of the tetramer remained ∼52.5% throughout the simulation, with the exception of transient time periods during which there were ∼1% observable increases (Fig. S4). The M-M hydrogen bonds dropped ∼7.6% within 400 ps of the simulation (Fig. S5 a), but there was no further drop. In addition, similar to the previous simulations, there was ∼20% drop in S-M/S hydrogen bonds (Fig. S5 b). These results further confirm that the absence of bound metal ions has only a minor effect on the overall core of the tetrameric structure of ConA, whereas the metal ions seem to predominantly alter the mobility of the specific loop regions. Fig. 4 shows the residue-wise RMSD with respect to the crystal structure 1CVN for the final structures obtained from the E1 and E3 simulations. As can be seen, the results essentially agree with those obtained from the analysis of computed BF values, i.e., the structural deviations are mostly restricted to the loop regions, and the maximum deviations in the absence of metal ions are confined only to the ion binding loop region. Some of the residues in the ion binding loop region had moved as far as 17 Å with respect to their position in the starting structure (Fig. 4). To further confirm the observation that the absence of metal ions does not lead to any major change in the core of the protein, we also analyzed the RMSD of the core (β-sheet) and loop regions separately over the entire 3 ns trajectory (Fig. 5). The β-sheet core region showed an RMSD of only 0.75 Å (Fig. 5) over the entire 3 ns trajectory, both in the presence and absence of bound metal ions; this finding suggests that the core region is highly stable even upon demetalization. In contrast to the core of the tetramer, the RMSD values for the loop region were different in the E1 and E3 simulations. In the presence of bound metal ions, the loop regions of all four chains in the tetramer had RMSDs between 1.0 to 1.5 Å during the 3 ns simulation; in the absence of metal ions, however, the average RMSD of the loop regions increased ≥ 3.5 Å (Fig. 5). Thus, the loop region was found to have maximum structural deviations from its native conformation upon demetalization in all four chains of ConA. We also analyzed the hydrogen bonds within the protein and plotted them according to their time of occupancy (Fig. S6). The total number of hydrogen bonds within the protein and those with occupancy > 95% were found to be comparable in the E1 and E3 simulations of the tetramer (Fig. S6). This finding also reinforced the conclusion that the structure of the core of ConA remains unaffected even in the absence of metal ions and that demetalization only changes the conformation of the loop regions.
Figure 4.
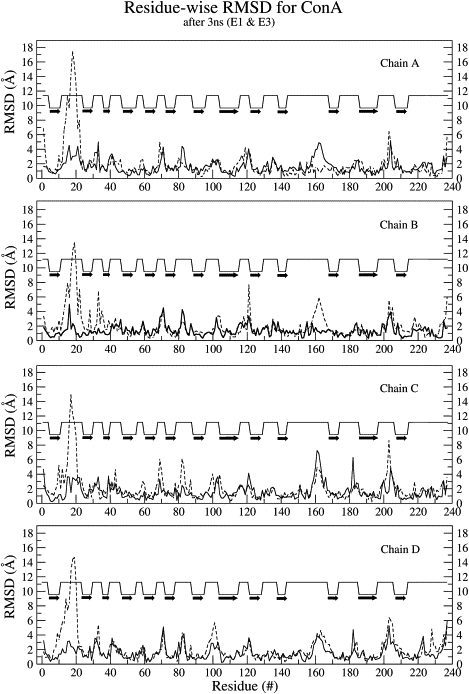
Residue-wise RMSD plot for the final structures obtained from E1 (solid line) and E3 (dashed line) simulations with respect to the crystal structure. The respective chain name is labeled in the panels, and the secondary structural states for various residues are annotated (the solid black arrows indicate β-sheets, and the lines indicate loop regions).
Figure 5.
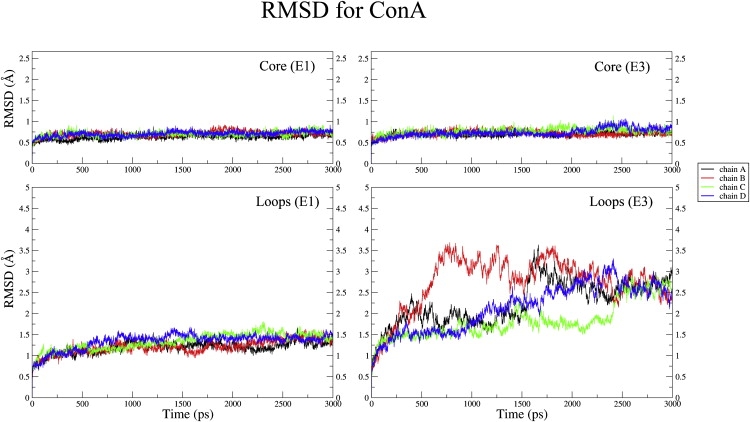
RMSD values for the core and the loop regions of the four chains of tetrameric ConA for the E1 and E3 trajectories.
ConA tetramer in the absence of trimannoside and metal ions (E4)
During the E4 simulation, in which neither the ions nor the sugar were included, the RMSD increased to ∼1.8 Å as early as 500 ps and remained stable at that value during the remainder of the simulation (Fig. 2). The Rg increased by only 0.4 Å (Fig. S2). The tetrameric core of the protein remained essentially unperturbed, as shown in an analysis of the NSASA (Fig. S4) and the M-M and S-M/S hydrogen bonds (Fig. S5). Similar to the E3 simulation, the BF values were highest for the 14–21 region (Fig. S3). The other regions with high BF values in all the chains were 160–164 and 201–205, in which all chains showed BF values >60 Å2. In the 160–164 region, chain D showed a BF value >160 Å2, whereas in the 201–205 region, chain A showed a BF value < 40 Å2. Thus, the behavior of the protein during the E4 simulation was very similar to that demonstrated during the E3 simulation.
Effects of metal ions on the binding of trimannoside
The trajectories obtained from simulations E1 and E3 were analyzed to investigate the effects of bound metal ions (Mn2+ and Ca2+) on substrate recognition by ConA. Fig. 6 shows the orientation of the trimannoside molecule with respect to ConA during the simulation in the presence (E1) and the absence (E3) of metal ions. The coordinates of substrate-bound ConA have been extracted at an interval of 100 ps from the E1 and E3 simulations, and only the final protein structure is shown for clarity. During the simulation in the presence of metal ions, the trimannoside molecule remained bound to ConA throughout the 3 ns trajectory; however, different degrees of the molecule's mobility within the binding site were observed among different chains. The different degrees of mobility were also evident within the trimannoside molecule, as demonstrated by the APF values of the trimannoside molecule bound to chain A (triA). The α(1–6)-mannose (MAN 240 in 1CVN) had an APF value of ∼1.25Å, whereas α(1–3)-mannose (MAN 242) had an APF value > 2.5Å. The overall APF value of triA was ∼1.9 Å. The trimannoside molecule bound to chain B (triB) in E1 was the least mobile compared to the others, with an overall APF value of only ∼1.3Å. The trimannoside bound to chain C (triC) and to chain D (triD) were ∼2× more mobile compared to triA and triB, with their overall APF values being ∼3.5 Å and ∼3.7 Å, respectively.
Figure 6.
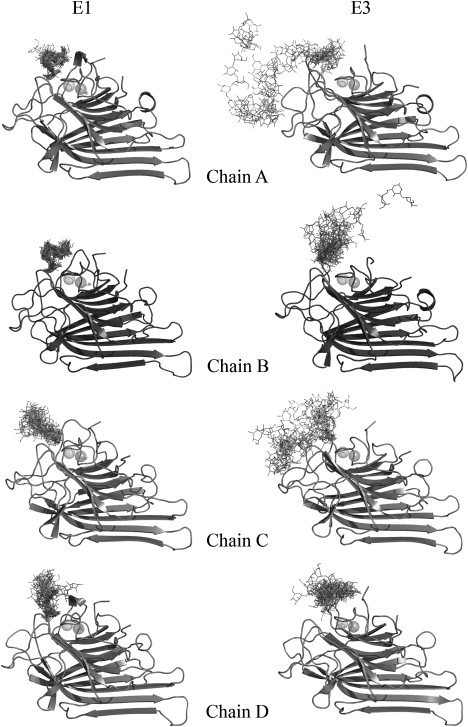
The orientations of the trimannoside sugar in the substrate binding site during the simulations for the substrate-bound ConA tetramer in the presence (E1; left panel) and the absence of the ions (E3; right panel). The frames extracted from E1 and E3 trajectories at an interval of 100 ps were superposed on the starting structure. It is clearly visible that the trimannoside substrate remains bound to ConA to a large extent during the simulation in the presence of the ions (E1), whereas it drifts away during the simulation in the absence of the ions (E3).
During the E3 simulation, the sugar molecule drifted away from its binding site (Fig. 6). The dissociation of the trimannoside molecule from its binding site occurred at different times for different chains. triA was the most mobile molecule after demetalization, so much so that it quickly moved out of its binding pocket. Its APF value in the E3 simulation was ∼13.6 Å (compared to ∼1.9 Å during E1). triB and triC were almost equally mobile, with overall APF values of ∼6.8 Å and 9 Å, respectively. Therefore, as could be expected with such high mobility, the triA, triB, and triC molecules moved out into the solution by the end of the 3 ns simulation. Strangely, triD had an APF value of ∼4.3 Å and remained almost bound to chain D.
Fig. 7 shows the occupancy of the hydrogen bonds between ConA and the trimannoside molecule during the E1 and E3 simulations. The total number of hydrogen bonds between ConA and trimannoside remained almost constant in the simulation performed in the presence of the ions. However, in the absence of divalent ions, the number of hydrogen bonds decreased dramatically. On average, both simulations showed that the number of probable hydrogen bonds between the lectin and the sugar were ∼15 per monomer/chain at the start of the simulation. This number gradually stabilized at ∼11 for the E1 simulation, but continuously decreased from ∼15 to ∼2 for the E3 simulation due to the drift of the ligand from the binding site.
Figure 7.
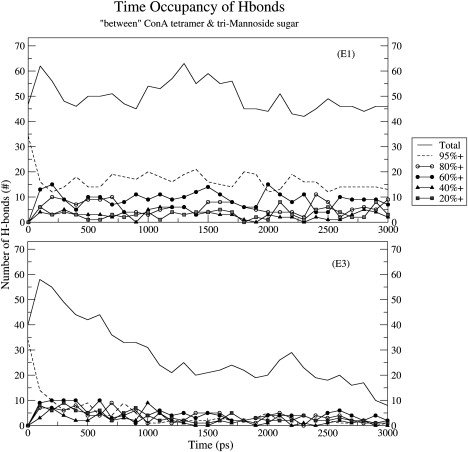
The percentage occupancy of various hydrogen bonds between trimannoside and ConA in structures sampled at an interval of 100 ps during the 3 ns simulations of substrate-bound ConA tetramer in the presence of the ions (top panel) and the absence of the ions (bottom panel).
We also calculated the residency time of all the possible hydrogen bonds between the protein and the trimannoside during the 3 ns E1 and E3 simulations. During the E1 simulation for the tetramer, there were a total of 130 different hydrogen bonds between ConA and trimannoside that were present at various points on the simulation timescale. However, 65% of those hydrogen bonds were transient; they were present for only 10 to 25% of the simulation time. Only a single set of the 29 hydrogen bonds persisted > 50% of the simulation time; thus, they can be called dynamically stable hydrogen bonds. Interestingly, the demetalization of the lectin led to an increase in the total number of different hydrogen bonds that existed during the 3 ns simulation to 179; however, only 5 of those hydrogen bonds were persistent for a period > 50% of the simulation time. Therefore, the number of dynamically stable hydrogen bonds between the trimannoside and ConA decreased dramatically upon demetalization. Table 3 lists the total number of hydrogen bonds between ConA and the sugar during the final 100 ps of the 3 ns simulation.
Table 3.
The total number of hydrogen bonds between each trimannoside and various monomers of ConA obtained from last 100 ps of the 3 ns MD simulations in the presence and absence of bound metal ions
| Oligomeric status | Simulation name | Chain A | Chain B | Chain C | Chain D |
|---|---|---|---|---|---|
| Tetramer | E1 | 11 | 15 | 5 | 15 |
| E3 | 0 | 0 | 3 | 5 |
Therefore, the results of our simulations are in agreement with the experimental observation that metal ions are essential for substrate recognition by ConA. As discussed earlier, however, the overall structure of the ConA tetramer in the absence of metal ions essentially remained intact, and structural deviations were essentially confined to the loop regions. Therefore, we analyzed the conformations of the substrate and ion binding loops in detail to understand the structural basis of the interplay between the metal ion binding and substrate recognition.
The effect of metal ions on the conformation of the ion binding loop
To demonstrate the effect of bound metal ions on the conformation of the ion binding loop, the frames were extracted from the E1 and E3 simulations at an interval of 500 ps. Fig. 8 shows the structural deviations in the ion binding loop upon optimal superposition of the protein core. The conformation of the ion binding loop of the four chains during the E1 simulation, i.e., in the presence of the ions and the sugar, is depicted in the left panel of Fig. 8, whereas the right panel depicts the conformation of this loop during the E3 simulation. The loop region was highly ordered during the simulation in the presence of the metal ions; hence, this region from different frames aligned very well (Fig. 8). The ion binding loop region obtained from the final structure of chain A in the E1 simulation also superposed very well with the corresponding region of chain A in the crystal structure 1CVN (Fig. 9 a). This finding illustrates that, in the presence of metal ions, the ion binding loop retains its native conformation throughout the 3 ns simulation. In contrast, in the absence of the ions (the E3 simulation), the ion binding loop region appears highly disordered for all four chains (Fig. 8). The superposition of the final structure of the E3 simulation on the crystal structure of metal ion-bound ConA (Fig. 9 b) demonstrates that Asn-19 of chain A moves as far as ∼15 Å with respect to its native position in the crystal structure and that Gly-18 moves even farther, to a distance of ∼17 Å. In the native conformation, the metal ions are tightly coordinated by a cluster of negatively charged residues. In the absence of metal ions, strong electrostatic repulsion makes such a conformation for this loop region energetically unfavorable, leading to a large conformational change in the ion binding loop. This large movement of the ion binding loop obstructs the substrate binding site, resulting in a drift of the trimannoside molecule from the binding site.
Figure 8.
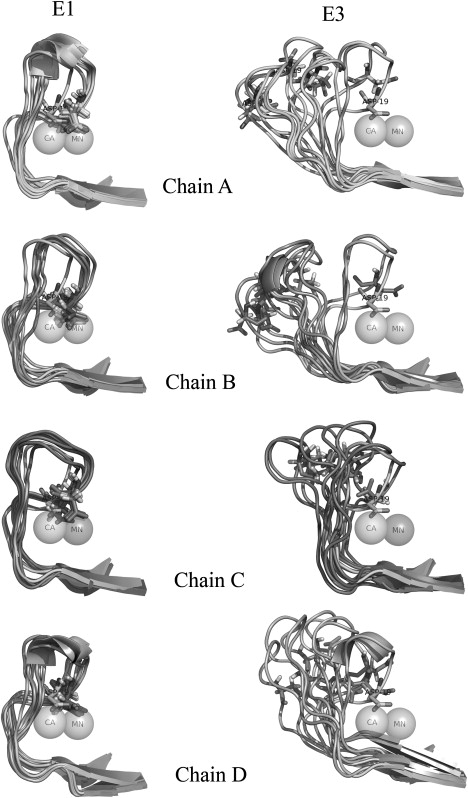
The diagram depicts the movement of the ion binding loop (the 7–25 region) for all four chains of the substrate-bound ConA tetramer during the simulations in the presence of the ions (E1) and the absence of the ions (E3). The frames extracted from E1 (left) and E3 (right) trajectories at an interval of 500 ps were superposed on the crystal structure. The large structural rearrangements of this region are clearly visible. Asp-9 is represented with sticks to depict the disruption of the Mn2+ binding site. The transparent spheres represent the Ca2+ and Mn2+ ions.
Figure 9.
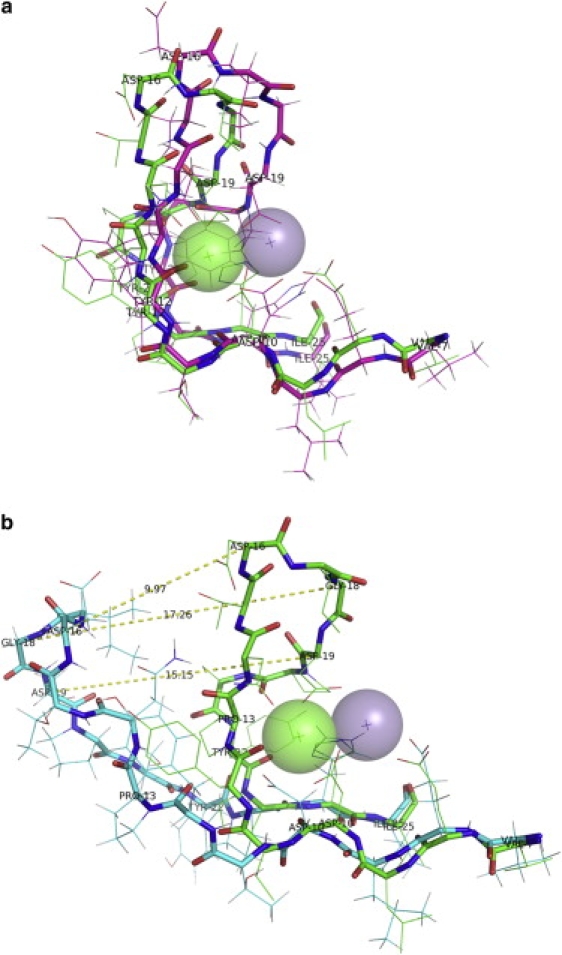
The conformation of the fragment containing the ion binding loop (the 7–25 region) in the final structure obtained from the 3 ns simulations for substrate-bound ConA tetramer in the presence of the ions (simulation E1; a) and the absence of the ions (simulation E3; b). The final structures (Cα atoms shown in cyan) obtained from E1 and E3 have been superposed on the crystal structure (Cα atoms shown in green). The dashed lines depict the distances between equivalent Cα atoms of the superposed structures. The transparent spheres depict Ca2+ ions (light green) and Mn2+ ions (purple).
Our MD simulations, therefore, provide an atomically detailed picture of the conformational changes associated with the demetalization process and the consequent destruction of the saccharide binding site on ConA. Table 2 summarizes the converged values for various structural parameters extracted from the final 500 ps of the 3 ns simulations.
The monomeric and dimeric ConA simulations
Detailed analysis of the results from the simulations of the monomer and dimer of ConA indicate that the monomer and the dimer do not behave in a manner that is dramatically different from the tetramer. The various structures sampled by the monomer and the dimer show a maximum RMSD of ∼2.5 Å, which is similar to the maximum RMSD of the tetrameric state of ConA. The only simulation in which the monomer simultaneously differed from the dimer and the tetramer was E4 where, in the absence of both ions and the trimannoside sugar, the monomer showed an RMSD value of ∼2.5 Å, whereas the dimer and tetramer systems exhibited an RMSD value of ∼1.5 to 2 Å (Fig. 2). It is possible that the structural destabilization of the monomer in the absence of metal ions as reflected by the RMSD value of 2.5 Å (Fig. 2) could have been a part of the unfolding event of ConA due to demetalization. Therefore, we lengthened the duration of the simulations to observe whether the core also unfolded in longer simulations. Because the monomer and the tetramer showed similar conformational features during the 3 ns simulations and because simulations on the monomer required less computational resources, only the demetalized monomer simulations were extended up to 7 ns. We observed that the monomer did not show any further structural destabilization. There was only a small increase in the backbone RMSD for the monomer (Fig. S7). The core and loop regions also did not show any dramatic changes in their RMSD values (Fig. S7). However, the fluctuations in RMSD values were relatively larger compared to the simulations that involved the presence of the metal ions, thus indicating reduced structural stability. The RMSD data from the 7 ns simulations of the demetalized ConA monomer also suggested that the demetalization only affected the loop conformations, whereas the core of the protein remained intact. This finding is in agreement with crystal structure data. These data show that the core structure of the demetalized ConA is very similar to the metal ion-bound form but that the loop regions have large conformational disorder. However, in view of the orders of magnitude difference in the experimental timescale of the folding process and the timescale of our simulations, our comparisons with experimental observations are only qualitative.
These findings also indicated that, even though oligomerization resulted in increased stability of the ConA tetramer, the monomer and dimer could also be stable in isolation. The stability of the monomeric and dimeric forms of ConA can be rationalized by the observation that a change in the NSASA for the monomer and dimer is comparable to that of the tetramer (Fig. S4). Thus, dissociation of the ConA tetramer does not lead to a significant increase in the NSASA. The monomer and dimer simulations also showed higher mobility in the loop region (Fig. S3 b). However, the dimer showed exceptionally increased BF values for the ion binding loop in the absence of the metal ions. The BF value for the ion binding loop of the dimer was >1000 Å2, which is about double the BF value (∼600–700 Å2) of this region in the tetramer and more than double the BF value (∼400 Å2) for the monomer in the E3 simulation. The dimer structure used in our simulations comprised the A and B chains of the ConA tetramer. However, the crystal structure of an uncomplexed dimeric ConA (1GKB) with both metal ions bound was also available in the PDB (38). Hence, we compared the results from the AB dimer simulations with 1GKB and discovered that, in terms of RMSD values, the structure sampled during the simulation showed similar deviations from 1CVN and 1GKB. This finding suggests that using an AB-dimer from 1CVN is almost as good as simulating 1GKB. Fig. S8 shows the residue-wise RMSD between 1GKB and the final structure obtained from the E2 simulation of the ConA dimer. Most of the regions in both chains show an RMSD of approximately ≤1.5 Å, with the exception of some regions — most notably the 116–121 region, which is a loop region at the interdimer interface.
Discussion
The MD simulations reported in this work provide further insights into the process of demetalization and its consequences on the substrate binding ability of a legume lectin. To the best of our knowledge, these simulations are the longest explicit water MD simulations ever carried out on this protein. Simulations have also been carried out for the monomeric and dimeric form of ConA under similar environmental conditions. It is encouraging to note that, for the substrate- and metal ion-bound native ConA tetramer, the computed BF values obtained from our MD simulations are in close agreement with the experimentally determined BF values. Comparative analysis of the twelve 3 ns MD trajectories has provided novel insights into the dynamic aspects of the structural stability and substrate recognition of ConA. The results from our simulations indicate that the core of the ConA tetramer has a tightly packed structure and that it remains intact even upon demetalization. The effect of the demetalization, however, appears to be concentrated in the loop regions. This observation is based on analyses of the RMSD, residue-wise RMSD, secondary structure content, and NSASA values for the structures sampled during various simulations. However, metal ions play a major role in stabilizing the conformation of the key loop regions of this protein, which are important for the binding of metal ions and the trimannoside substrate. The native conformation of this loop is stabilized by the coordination of the two metal ions with a cluster of negatively charged amino acids. However, in the absence of metal ions, this conformation of the ion binding loop becomes energetically unfavorable, which is probably due to strong electrostatic repulsion. Therefore, upon demetalization, this loop is characterized by high mobility; in fact, some of the amino acids in this loop moved as far as 17 Å with respect to the loop's position in the native crystal structure. This large movement of the ion binding loop obstructs the binding of the substrate, resulting in drifting of the trimannoside from ConA during simulations in the absence of metal ions. The results of these simulations thus support the long-known experimental fact that ion binding is essential for sugar binding (24,39).
Our studies have provided additional insights into the dynamics of the interplay between metal and sugar binding to ConA. The metal ions interact with the side chains on the ion binding loop, and these interactions keep the loop in a fixed conformation. In turn, this fixed conformation provides a scaffold necessary for the sugar molecule to bind to lectin both by decreasing the thermal motion of this region and, possibly, by properly orienting the side chains for a better and more optimal presentation to the sugar atoms. In contrast to the role of metal ions, substrate binding does not seem to appreciably affect the structure of the loop regions. Similarly, the simulations carried out for the monomer and the dimer suggest that the monomeric and dimeric forms of ConA also have stable structures and substrate binding ability. The comparison of dimeric simulations with 1GKB demonstrated that the choice of 1CVN, a tetrameric crystal, for obtaining coordinates for the dimeric form was as good as using the dimeric crystal structure 1GKB.
Conclusions
We carried out explicit solvent MD simulations for ConA under different environmental conditions to understand the effect of bound metal ions on its structure and substrate binding ability. These simulations revealed dynamic conformational changes associated with the demetalization of ConA. We found that demetalization leads to large conformational changes in the ion binding loop, whereas the β-sheet core of the protein remains relatively unperturbed. The increased flexibility and structural destabilization of the ion binding loop results in drifting of the substrate sugars in the absence of the bound metal ions. These results are in agreement with experimental observations about the elimination of the sugar binding ability upon demetalization. We also found that the amino acid stretches of ConA having high BF values in the crystal structure show relatively higher mobility in the simulations. These results on the dynamic aspects of the metal ion binding to legume lectins and their mode of substrate recognition add to our appreciation of the design of their combining sites (40).
Supplementary Material
Eight figures are available at www.biophys.org/biophysj/supplemental/S0006-3495(08)00017-9.
Supplementary Material
Acknowledgments
This work was supported by core grants to the National Institute of Immunology. D. M. was supported by project grants from the Department of Biotechnology, Government of India; S. K. was supported by a Junior Research Fellowship from the Council of Scientific and Industrial Research, India. Computational resources were provided under the Biotechnology Information System project of Department of Biotechnology.
Contributor Information
Debasisa Mohanty, Email: deb@nii.res.in.
Avadhesha Surolia, Email: surolia@nii.res.in.
References
- 1.Goldstein I.J., Hayes C.E. The lectins: carbohydrate-binding proteins of plants and animals. Adv. Carbohydr. Chem. Biochem. 1978;35:127–340. doi: 10.1016/s0065-2318(08)60220-6. [DOI] [PubMed] [Google Scholar]
- 2.Peumans W.J., Van Damme E.J. Lectins as plant defense proteins. Plant Physiol. 1995;109:347–352. doi: 10.1104/pp.109.2.347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hirsch A.M. Role of lectins (and rhizobial exopolysaccharides) in legume nodulation. Curr. Opin. Plant Biol. 1999;2:320–326. doi: 10.1016/S1369-5266(99)80056-9. [DOI] [PubMed] [Google Scholar]
- 4.Shur B.D., Hall N.G. Sperm surface galactosyltransferase activities during in vitro capacitation. J. Cell Biol. 1982;95:567–573. doi: 10.1083/jcb.95.2.567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Nangia-Makker P., Conklin J., Hoganand V., Raz A. Carbohydrate-binding proteins in cancer, and their ligands as therapeutic agents. Trends Mol. Med. 2002;8:187–192. doi: 10.1016/s1471-4914(02)02295-5. [DOI] [PubMed] [Google Scholar]
- 6.Ambrosi M., Cameronand N.R., Davis B.G. Lectins: tools for the molecular understanding of the glycocode. Org. Biomol. Chem. 2005;3:1593–1608. doi: 10.1039/b414350g. [DOI] [PubMed] [Google Scholar]
- 7.Edelman G.M., Cunningham B.A., Reeke G.N., Becker J.W., Waxdaland M.J. The covalent and three-dimensional structure of concanavalin A. Proc. Natl. Acad. Sci. USA. 1972;69:2580–2584. doi: 10.1073/pnas.69.9.2580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Greer J., Kaufmanand H.W., Kalb A.J. An x-ray crystallographic study of concanavalin A. J. Mol. Biol. 1970;48:365–366. doi: 10.1016/0022-2836(70)90169-5. [DOI] [PubMed] [Google Scholar]
- 9.Cunningham B.A., Wang J.L., Waxdaland M.J., Edelman G.M. The covalent and three-dimensional structure of concanavalin A. II. Amino acid sequence of cyanogen bromide fragment F3. J. Biol. Chem. 1975;250:1503–1512. [PubMed] [Google Scholar]
- 10.Bouckaert J., Hamelryck T., Wynsand L., Loris R. Novel structures of plant lectins and their complexes with carbohydrates. Curr. Opin. Struct. Biol. 1999;9:572–577. doi: 10.1016/s0959-440x(99)00007-x. [DOI] [PubMed] [Google Scholar]
- 11.Reeke G.N., Beckerand J.W., Edelman G.M. The covalent and three-dimensional structure of concanavalin A. IV. Atomic coordinates, hydrogen bonding, and quaternary structure. J. Biol. Chem. 1975;250:1525–1547. [PubMed] [Google Scholar]
- 12.Agrawal B.B., Goldstein I.J. Protein-carbohydrate interaction. VI. Isolation of concanavalin A by specific adsorption on cross-linked dextran gels. Biochim. Biophys. Acta. 1967;147:262–271. [PubMed] [Google Scholar]
- 13.Hardman K.D., Wood M.K., Schiffer M., Edmundsonand A.B., Ainsworth C.F. Structure of concanavalin A at 4.25-angstrom resolution. Proc. Natl. Acad. Sci. USA. 1971;68:1393–1397. doi: 10.1073/pnas.68.7.1393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.McKenzie G.H., Sawyerand W.H., Nichol L.W. The molecular weight and stability of concanavalin A. Biochim. Biophys. Acta. 1972;263:283–293. doi: 10.1016/0005-2795(72)90081-5. [DOI] [PubMed] [Google Scholar]
- 15.Del Sol F.G., Cavadaand B.S., Calvete J.J. Crystal structures of Cratylia floribunda seed lectin at acidic and basic pHs. Insights into the structural basis of the pH-dependent dimer-tetramer transition. J. Struct. Biol. 2007;158:1–9. doi: 10.1016/j.jsb.2006.08.014. [DOI] [PubMed] [Google Scholar]
- 16.Rini J.M. Lectin structure. Annu. Rev. Biophys. Biomol. Struct. 1995;24:551–577. doi: 10.1146/annurev.bb.24.060195.003003. [DOI] [PubMed] [Google Scholar]
- 17.Drickamer K. Multiplicity of lectin-carbohydrate interactions. Nat. Struct. Biol. 1995;2:437–439. doi: 10.1038/nsb0695-437. [DOI] [PubMed] [Google Scholar]
- 18.Bradbrook G.M., Gleichmann T., Harrop S.J., Habash J., Raftery J. X-Ray and molecular dynamics studies of concanavalin-A glucoside and mannoside complexes: relating structure to thermodynamics of binding. J. Chem. Soc., Faraday Trans. 1998;94:1603–1611. [Google Scholar]
- 19.So L.L., Goldstein I.J. Protein-carbohydrate interaction. IV. Application of the quantitative precipitin method to polysaccharide-concanavalin A interaction. J. Biol. Chem. 1967;242:1617–1622. [PubMed] [Google Scholar]
- 20.So L.L., Goldstein I.J. Protein-carbohydrate interaction. IX. Application of the quantitative hapten inhibition technique to polysaccharide-concanavalin a interaction. Some comments on the forces involved in concanavalin a-polysaccharide interaction. J. Immunol. 1967;99:158–163. [PubMed] [Google Scholar]
- 21.Elgavish S., Shaanan B. Lectin-carbohydrate interactions: different folds, common recognition principles. Trends Biochem. Sci. 1997;22:462–467. doi: 10.1016/s0968-0004(97)01146-8. [DOI] [PubMed] [Google Scholar]
- 22.Pratap J.V., Bradbrook G.M., Reddy G.B., Surolia A., Raftery J. The combination of molecular dynamics with crystallography for elucidating protein-ligand interactions: a case study involving peanut lectin complexes with T-antigen and lactose. Acta Crystallogr. D Biol. Crystallogr. 2001;57:1584–1594. doi: 10.1107/s0907444901011957. [DOI] [PubMed] [Google Scholar]
- 23.Sinha S., Mitra N., Kumar G., Bajajand K., Surolia A. Unfolding studies on soybean agglutinin and concanavalin a tetramers: a comparative account. Biophys. J. 2005;88:1300–1310. doi: 10.1529/biophysj.104.051052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Yariv J., Kalband A.J., Levitzki A. The interaction of concanavalin A with methyl alpha-D-glucopyranoside. Biochim. Biophys. Acta. 1968;165:303–305. doi: 10.1016/0304-4165(68)90063-9. [DOI] [PubMed] [Google Scholar]
- 25.Drickamer K. Increasing diversity of animal lectin structures. Curr. Opin. Struct. Biol. 1995;5:612–616. doi: 10.1016/0959-440x(95)80052-2. [DOI] [PubMed] [Google Scholar]
- 26.Bouckaert J., Loris R., Poortmansand F., Wyns L. Crystallographic structure of metal-free concanavalin A at 2.5 Å resolution. Proteins. 1995;23:510–524. doi: 10.1002/prot.340230406. [DOI] [PubMed] [Google Scholar]
- 27.Shoham M., Sussman J.L., Yonath A., Moult J., Trauband W. The effect of binding of metal ions on the three-dimensional structure of demetallized concanavalin A. FEBS Lett. 1978;95:54–56. doi: 10.1016/0014-5793(78)80050-7. [DOI] [PubMed] [Google Scholar]
- 28.Reeke G.N., Beckerand J.W., Edelman G.M. Changes in the three-dimensional structure of concanavalin A upon demetallization. Proc. Natl. Acad. Sci. USA. 1978;75:2286–2290. doi: 10.1073/pnas.75.5.2286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hansia P., Dev S., Suroliaand A., Vishveshwara S. Insight into the early stages of thermal unfolding of peanut agglutinin by molecular dynamics simulations. Proteins. 2007;69:32–42. doi: 10.1002/prot.21512. [DOI] [PubMed] [Google Scholar]
- 30.Naismith J.H., Field R.A. Structural basis of trimannoside recognition by concanavalin A. J. Biol. Chem. 1996;271:972–976. doi: 10.1074/jbc.271.2.972. [DOI] [PubMed] [Google Scholar]
- 31.Case D.A., Darden T.A., Cheatham T.E., Simmerling C.L., Wang J. University of California; San Francisco: 2006. AMBER 9. [Google Scholar]
- 32.Jorgensen W.L., Chandrasekhar J., Madura J.D., Impeyand R.W., Klein M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 33.Darden T., Yorkand D., Pedersen L. Particle mesh Ewald: an N ·log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- 34.van Gunsteren W.F., Berendsen H.J.C. Computer simulation of molecular dynamics: methodology, applications, and perspectives in chemistry. Angew. Chem. Int. Ed. Engl. 1990;29:992–1023. [Google Scholar]
- 35.Duan Y., Wu C., Chowdhury S., Lee M.C., Xiong G. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J. Comput. Chem. 2003;24:1999–2012. doi: 10.1002/jcc.10349. [DOI] [PubMed] [Google Scholar]
- 36.Woods R.J., Dwek R.A., Edgeand C.J., Fraser-Reid B. Molecular mechanical and molecular dynamic simulations of glycoproteins and oligosaccharides. 1. GLYCAM_93 parameter development. J. Phys. Chem. 1995;99:3832–3846. [Google Scholar]
- 37.Hubbard S.J., Thornton J.M. 2.1.1 ed. Department of Biochemistry and Molecular Biology, University College; London: 1993. NACCESS. Computer Program. [Google Scholar]
- 38.Kantardjieff K.A., Hochtl P., Segelke B.W., Taoand F.M., Rupp B. Concanavalin A in a dimeric crystal form: revisiting structural accuracy and molecular flexibility. Acta Crystallogr. D Biol. Crystallogr. 2002;58:735–743. doi: 10.1107/s0907444901019588. [DOI] [PubMed] [Google Scholar]
- 39.Kalb A.J., Levitzki A. Metal-binding sites of concanavalin A and their role in the binding of alpha-methyl d-glucopyranoside. Biochem. J. 1968;109:669–672. doi: 10.1042/bj1090669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Sharma V., Surolia A. Analyses of carbohydrate recognition by legume lectins: size of the combining site loops and their primary specificity. J. Mol. Biol. 1997;267:433–445. doi: 10.1006/jmbi.1996.0863. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


