Magainin 2 Revisited: A Test of the Quantitative Model for the All-or-None Permeabilization of Phospholipid Vesicles

Abstract

The all-or-none kinetic model that we recently proposed for the antimicrobial peptide cecropin A is tested here for magainin 2. In mixtures of phosphatidylcholine (PC)/phosphatidylglycerol (PG) 50:50 and 70:30, release of contents from lipid vesicles occurs in an all-or-none fashion and the differences between PC/PG 50:50 and 70:30 can be ascribed mainly to differences in binding, which was determined independently and is ∼20 times greater to PC/PG 50:50 than to 70:30. Only one variable parameter, β, corresponding to the ratio of the rates of pore opening to pore closing, is used to fit dye release kinetics from these two mixtures, for several peptide/lipid ratios ranging from 1:25 to 1:200. However, unlike for cecropin A where it stays almost constant, β increases five times as the PG content of the vesicles increases from 30 to 50%. Thus, magainin 2 is more sensitive to anionic lipid content than cecropin A. But overall, magainin follows the same all-or-none kinetic model as cecropin A in these lipid mixtures, with slightly different parameter values. When the PG content is reduced to 20 mol %, dye release becomes very low; the mechanism appears to change, and is consistent with a graded kinetic model. We suggest that the peptide may be inducing formation of PG domains. In either mechanism, no peptide oligomerization occurs and magainin catalyzes dye release in proportion to its concentration on the membrane in a peptide state that we call a pore. We envision this structure as a chaotic or stochastic type of pore, involving both lipids and peptides, not a well-defined, peptide-lined channel.

Introduction

We have recently proposed a very simple model for the mechanism of cecropin A (1), which quantitatively explains the experimental efflux kinetics data and is consistent with the all-or-none release of vesicle contents induced by that antimicrobial peptide. Essentially, the peptides bind to the membrane and reside on its surface until a membrane break point is reached. Then, the vesicle yields, releasing all its contents at once, in what may be called a chaotic pore event (2). The simplicity of the model is manifest by the need to vary only one fit parameter, in addition to including the independently measured binding and dissociation rate constants, to reproduce experimental efflux data obtained in a variety of lipid mixtures and concentrations.

In his comment, Axelsen (2) laid a challenge: how generally applicable is this model? Here we take up the challenge in an important case. We test the validity of the model to describe the mechanism of magainin 2, which is perhaps the most studied of all antimicrobial peptides. The discovery of magainins by Zasloff (3) had a profound impact on the antimicrobial peptide field. Most researchers believe that magainin functions through a toroidal pore model (4–6), but much contradictory data exists. Part of the confusion arises because different lipid model systems have been used by different authors, and transfer of conclusions from one system to another is not always warranted. To avoid this problem, we will be specific about experimental conditions when referring to the literature.

Magainin decreases or dissipates the membrane potential of several energy-transducing membranes (7,8). It stimulates respiration at low concentration, but inhibits it at high concentration, and the effects are reversible (8). All-D-magainin behaves identically to normal, all-L-magainin in terms of secondary structure, antimicrobial activity, and hemolysis, indicating that no stereochemically sensitive protein receptors are involved in peptide recognition (9,10). Antimicrobial activity is altered, significantly in some cases, by small changes in the primary sequence of magainin 2, such as deletion or substitution of a few residues, or C-terminal amidation (11,12). Using cell fixation, magainin 2 was shown to cross the bacterial cytoplasmic membrane (13).

Magainins also cause dye release from phospholipid vesicles (14,15). Pore formation by magainin 2 appears to occur concomitantly with lipid flip-flop (5), although it is not clear whether dithionite entering the vesicle is not actually responsible for what appears to be lipid flip-flop. A continuous measurement using the excimer/monomer ratio of a pyrene lipid probe incorporated in the bilayer indicates that flip-flop occurs in ∼5 min at a peptide/lipid ratio (P/L) of 1:50 (16). Matsuzaki et al. (5) argued for a lipid/peptide pore on the basis of a comparison between the rates of lipid flip-flop and lipid diffusion across a curved region of the pore. The effect of peptide charge on leakage of calcein from egg phosphatidylcholine (PC)/phosphatidylglycerol (PG) large unilamellar vesicles (LUVs) was examined (17) and it was found that the analog F12W-magainin 2 (+4 charge), which behaves very similarly to magainin 2 (18), is more efficient than one with a +2 charge, which is in turn more efficient that an analog with a +6 charge. This indicates that the activity of magainin 2 is not a monotonic function of the peptide net charge. The effect of the nature of the charged lipid species was also examined by comparing release from egg PG and bovine brain phosphatidylserine (PS) vesicles (19). Dye release from the PG vesicles was ∼10-fold faster, but it should be noted that the concentrations of the two lipids differed by a factor of 10 in those experiments. The activity of magainin, measured by calcein release from LUVs, increases from 1-palmitoyl-2-oleoylphosphatidylcholine (POPC) to POPC/1-palmitoyl-2-oleoylphosphatidylglycerol (POPG) 1:1, even more so for POPC/POPG 3:1, and >100-fold for pure POPG (20). However, the selectivity of magainin analogs toward anionic LUVs decreases as peptide hydrophobicity increases.

An interesting observation is that magainin 2a and PGLa, another antimicrobial peptide, act synergistically in inducing dye efflux from vesicles, especially in equimolar mixtures of the two peptides (21,22) and, even more potently, as cross-linked, fixed dimers (23,24). Furthermore, association of PGLa and magainin drives insertion of PGLa into the membrane (25).

The secondary structure of magainin is well established by several different methods, including two-dimensional ¹H-nuclear magnetic resonance (NMR) (26,27), Raman spectroscopy (21), ¹⁵N-chemical-shift solid-state NMR (28), and circular dichroism (CD) (17,20,29). Magainin 2 is unstructured and monomeric in aqueous solution but forms an amphipathic α-helix (Fig. 1) in trifluoroethanol (TFE)/water mixtures (26,27,29), bound to lipid membranes (21), or in micelles of dodecylphosphocholine or sodium dodecylsulfate (27). The C-terminal amidated version, magainin 2a, is also α-helical (28). The degree of helicity depends on the medium (21), but it is usually close to 50% in TFE/buffer (29) and zwitterionic, PC membranes (20,21), increasing to nearly 80% on POPC/POPG mixtures (20). However, the apparent lower helical content in zwitterionic bilayers probably reflects the lower degree of binding and not an intrinsic difference in structure relative to anionic membranes. In TFE/buffer, variants of magainin 2a decrease in helicity as the charge increases (0 > + 2 > + 4 > + 6), while remaining monomeric (17).

Figure 1.

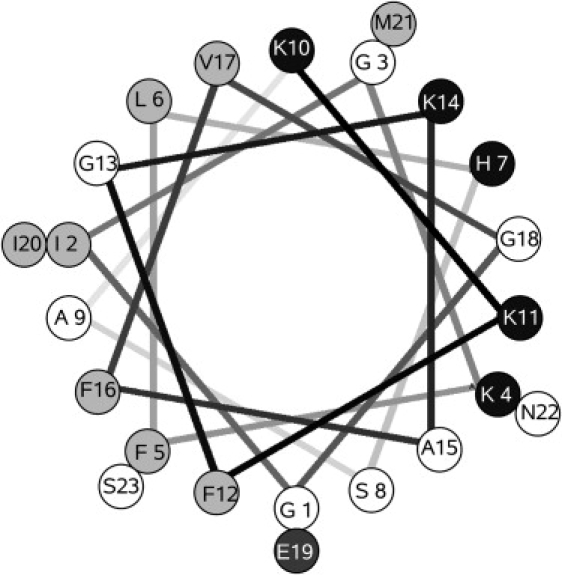
Helical wheel projection of magainin 2. Solid symbols represent basic residues; dark shading, acidic residues; light shading, hydrophobic residues; and open symbols, hydrophilic residues, according to the water/octanol transfer scale (81).

The orientation of magainin relative to the membrane has been much debated, a question closely related to the possible formation of a toroidal pore. Magainin 2a was shown to be oriented parallel to the membrane surface by ¹⁵N-chemical-shift solid-state NMR at P/L ≈ 1:30 (26,28,30). Using oriented CD (OCD) in membranes of dimyristoylphosphatidylcholine (DMPC)/dimyristoylphosphatidylglycerol (DMPG) 3:1, Ludtke (31) found that at P/L ≤ 1:60, the peptide lies parallel to the membrane, but the orientation changes to perpendicular at P/L > 1:30. However, this is not a sharp transition and the two orientations coexist over a broad range of P/L. Moreover, the threshold for change from parallel to perpendicular orientation relative to the membrane surface depends on the lipid. In POPC, even at P/L 1:20, OCD shows that magainin lies parallel to the membrane and no pore peak is observed in neutron scattering (4). In PC/phosphatidylserine (PS) mixed membranes, binding of magainin 2a causes membrane thinning by ∼1 Å from pure lipid to P/L 1:100 (32). Neutron in-plane scattering in DMPC/DMPG 3:1, which measures scatter due to D₂O in the membrane plane, shows a peak consistent with pores of ∼20 Å, which could include 4–7 magainins, at P/L 1:20 (4). It has been shown by ³¹P-solid-state-NMR (33) that the effect of magainin 2a on PC vesicles depends on the lipid acyl chain (POPC or DMPC), the lipid state, and the way lipid and peptide are mixed. Nevertheless, Bechinger (33) has argued that the results are consistent with peptide surface association, parallel to the membrane. Note that, in the work of Ludtke et al. (4), in DMPC/DMPG 3:1, at P/L 1:20 only ∼30–50% peptide insertion occurs, which is consistent with NMR showing mainly a parallel orientation (28,34). Synthetic magainin 2 mutants (F5W, F12W, and F16W) were shown to reside close to the membrane/water interface by fluorescence quenching (18). Photolabeling studies seem to indicate that magainin 2 inserts in vesicles with 20% PG at P/L 1:30 (35), although some potential drawbacks inherent to the method should be kept in mind. A parallel orientation of magainin 2, even at P/L 1:30, was also inferred from the dichroism of the amide I band in Fourier transform infrared spectroscopy (36).

A structure for a magainin toroidal pore was proposed based on a regular hexagonal arrangement of pores observed by x-ray diffraction (37). However, Münster et al. (38) found no evidence for pore formation, as their x-ray diffraction failed to indicate any lateral correlations between possible pores. On the other hand, a study by differential scanning calorimetry (39) demonstrated that the magainin analog MSI-78 increases the liquid crystalline-to-hexagonal (L_α–H_II) transition temperature of dipalmitoylphosphatidylethanolamine, as does magainin 2 (19). MSI-78 also inhibits the L_α–H_II transition of 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphatidylethanolamine (POPE) (by ³¹P-NMR), suggesting that it induces positive curvature strain, but no H_I phase is induced even at 10–15% peptide. In POPC, the peptide induced changes in bilayer structure even at 1–5%, and H_I phase appeared at 10–15% peptide. Hallock et al. (39) interpreted these results as lending support to the toroidal pore model. However, the sinking raft model is also consistent with those data (40).

The questions of oligomerization of magainin 2 and, in particular, its possible dimerization have also been addressed by many researchers. Early work (8) suggested that an oligomeric pore is the active form, while most peptide remains monomeric. This was based on a logarithmic plot of the peptide concentration required for half-maximal stimulation of cell respiration, which indicated a cooperativity parameter of n = 5. Matsuzaki et al. (18) argued for dimerization of magainin 2 based on binding isotherms, which were, however, obtained in an indirect way. But Schümann et al. (41) observed no dimerization or oligomerization on the membrane surface, using fluorescence resonance energy transfer (FRET) from F16W-magainin 2a to n-dansyl-magainin 2a. Moreover, binding isotherms obtained with isothermal titration calorimetry (ITC) do not indicate cooperativity, arguing against peptide oligomerization (42). A magainin 2 analog (F5Y,F16W) forms an antiparallel dimer, mostly helical, when bound to dilauroylphosphatidylcholine (DLPC) small unilamellar vesicles (SUVs), as determined by transferred nuclear Overhauser enhancement NMR, at 5 mM peptide and 0.5 mM lipid (43). Since the equilibrium dissociation constant, K_D, for binding to POPC SUVs is ∼200 μM (42), the vesicles should be almost covered with peptide. The dimer seems to be stabilized by an aromatic lock or zipper. However, the peptide hydrophobic surface left exposed is small and it is not clear how the dimer would bind to a membrane. The dimer position relative to the membrane surface was not determined. A phenylalanine zipper was also found by NMR for a dimer of MSI-78, a peptide similar to magainin (44). With 3 mol % peptide in POPC and POPC/POPG 3:1 bilayers, the MSI-78 peptides are helical. However, another analog, MSI-594, which contains the breaker sequence GIG, is less compact. MSI-78 forms a dimer in dodecylphosphocholine micelles, but MSI-594 is monomeric. These observations underscore the importance of detailed sequence in fine-tuning the peptide conformation and indicate that even conservative mutations do not necessarily produce peptides with similar behavior.

Thus, contradictions remain regarding the mechanism of magainin. Perhaps the most important concerns oligomerization, because whether it occurs is essential for the mechanism of pore formation. If a toroidal pore forms, is its structure determined by intermolecular interactions between the peptides? Or do several peptides simply migrate to a pore that is already forming in the membrane? In the former case, peptide oligomerization is a required step for pore formation. In the latter, this is not necessary and magainin could follow the same model as cecropin A (1). The mechanism of magainin 2 is investigated here in a model membrane system consisting of LUVs of POPC/POPG mixtures. These mixtures have been widely used to mimic bacterial lipids and do in fact resemble the lipid composition of some bacterial membranes (45,46). However, model membranes are not bacterial cells and additional factors play a role in the biological function of antimicrobial peptides. For example, in Gram-negative bacteria, the presence of lipopolysaccharide, a major component in the outer membrane (45), has important implications for peptide function (47). Nevertheless, there is no alternative to using model membranes in quantitative kinetic analyses, and we have concentrated on phospholipid mixtures whose behavior is well understood. To rigorously test the model proposed (1), it was necessary to measure the kinetics of magainin 2 binding, dissociation, and induced dye release, as well as to conclusively establish the mechanism of dye release (graded or all-or-none). In the end, we arrive at important conclusions regarding the mechanism of magainin, which we hope will contribute to resolving some of the apparent contradictions in the field. Recognizing possible mechanisms in well-characterized membrane systems through the use of quantitative models of peptide function that are simple enough to be useful is a first step—though not the final—to understand their function in bacterial membranes.

Methods

Chemicals

Magainin 2 (GIGKFLHSAKKFGKAFVGEIMNS) was purchased from American Peptide (Sunnyvale, CA). A stock solution was prepared by dissolving lyophilized peptide in deionized water/ethyl alcohol 1:1 (v/v) (AAPER Alcohol and Chemical, Shelbyville, KY). Stock peptide solutions were stored at −20°C, and kept on ice during experiments. 1-Palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC), 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphatidylethanolamine (POPE), and 1-palmitoyl-2-oleoyl-sn-glycero-3-[phospho-rac-(1-glycerol)] (POPG), in chloroform solution, were purchased from Avanti Polar Lipids (Alabaster, AL). 7-Methoxycoumarin-3-carboxylic acid (7MC), 1-[[(6,8-difluoro-7-hydroxy-4-methyl-2-oxo-2H-1-benzopyran-3-yl)acetyl]oxy] (Marina Blue (trademark), MB) succinimidyl ester, 4-chloro-7-nitrobenz-2-oxa-1,3-diasole (NBD) chloride, 8-aminonaphtalene-1,3,6-trisulfonic acid (ANTS) disodium salt, and p-xylene-bis-pyridinium bromide (DPX) were purchased from Molecular Probes/Invitrogen (Carlsbad, CA). Carboxyfluorescein (CF, 99% pure, lot No. A015252901) was purchased from ACROS (Morris Plains, NJ). Organic solvents (High Performance Liquid Chromatography/American Chemical Society grade) were purchased from Burdick & Jackson (Muskegon, MI). Lipids and fluorophores were tested by thin layer chromatography and used without further purification.

Synthesis of fluorescent probes

The syntheses of fluorescent probes, using POPE and a fluorophore attached through an amide bond to the amino group of the ethanolamine headgroup, were performed as previously described in detail for NBD-POPE and MB-POPE (48), and for 7MC-POPE (1), following the method of Vaz and Hallmann (49).

Preparation of large unilamellar vesicles

Large unilamellar vesicles (LUVs) were prepared by mixing the lipids in chloroform in a round-bottom flask, followed by rapid evaporation of the solvent in a rotary evaporator (model No. R-3000; Büchi Labortechnik, Flawil, Switzerland) at 60–70°C. The lipid film was then placed under vacuum for 4 h and hydrated by the addition of buffer containing 20 mM 3-(N-morpholino) propanesulfonic acid (MOPS), pH 7.5, 0.1 mM EGTA, 0.02% NaN₃, and 100 mM KCl or appropriately modified as indicated below. In the modified buffers, containing CF or ANTS/DPX, the KCl concentration was adjusted to yield the same measured osmolarity as in this buffer. The suspension of multilamellar vesicles that form was subjected to five freeze-thaw cycles and extruded 10× through two stacked polycarbonate filters of 0.1 μm pore size (Nuclepore; Whatman, Florham, NJ) using a water-jacketed high pressure extruder (Lipex Biomembranes, Vancouver, Canada) at room temperature. For membranes containing MB-POPE, NBD-POPE, or 7MC-POPE, the probes were added in chloroform solutions together with the lipids. Lipid concentrations were assayed by the Bartlett phosphate method (50), modified as previously described (51).

Membrane association and dissociation kinetics

To measure association of magainin 2 with membranes by FRET, F12W-magainin 2 was used. This analog, in which Phe-12 is replaced by Trp, behaves very similarly to the original magainin 2 (17,18). The kinetics of association of F12W-magainin 2 with LUVs were recorded on a stopped-flow fluorimeter (model No. SX.18MV; Applied Photophysics, Leatherhead, Surrey, UK). FRET between the Trp residue of the peptide and the lipid fluorophore 7MC-POPE incorporated in lipid membrane was used to monitor peptide binding and dissociation from LUVs as previously done for cecropin A (1). Trp excitation was at 280 nm and the emission of 7MC (maximum at 396 nm) was measured using a cutoff filter (model No. GG-385; Edmund Industrial Optics, Barrington, NJ). After mixing, the concentration of peptide was 1 μM and the lipid varied between 25 and 400 μM.

ANTS/DPX assay

Steady-state fluorescence measurements were performed in a spectrofluorimeter (model No. 8100; SLM-Aminco, Urbana, IL) upgraded by ISS (Champaign, IL). In the ANTS/DPX assay (52–54), excitation was at 365 nm (8 nm slit-width) and emission at 515 nm (16 nm slit-width). The solution encapsulated in the LUVs contained 5 mM ANTS, 8 mM DPX, 20 mM MOPS, pH 7.5, 0.1 mM EGTA, 0.02% NaN₃, and 70 mM KCl. The titrating solution contained 45 mM DPX, 20 mM MOPS, pH 7.5, 0.1 mM EGTA, 0.02% NaN₃, and 30 mM KCl. After extrusion, the LUVs with encapsulated ANTS and DPX were passed through a Sephadex-G25 column to separate the dye in the external buffer from the vesicles. Typical concentrations were ∼0.1–2 μM peptide and 500 μM lipid.

CF efflux experiments

Carboxyfluorescein (CF) efflux kinetics were measured as described before (1,40,55). Briefly, LUVs were prepared by hydration of the lipid film in 20 mM MOPS buffer, pH 7.5, containing 0.1 mM EGTA, 0.02% NaN₃, and 50 mM CF, to give a final lipid concentration of 10 mM. After extrusion, CF-containing LUVs were passed through a Sephadex-G25 column to separate the dye in the external buffer from the vesicles. For fluorescence measurements, the suspension was diluted to the desired lipid concentration in buffer containing 20 mM MOPS, pH 7.5, 100 mM KCl, 0.1 mM EGTA, and 0.02% NaN₃. The kinetics of CF efflux, measured by the relief of self-quenching of CF fluorescence, were recorded in a spectrofluorimeter (model No. 8100, SLM-Aminco) upgraded by ISS, with excitation at 470 nm and emission at 520 nm. The fastest curves were recorded using a stopped-flow fluorimeter (model No. SX.18MV, Applied Photophysics), with excitation at 470 nm and emission recorded through a long-pass filter (model No. OG 530; Edmund Industrial Optics). The peptide concentration was 1 μM after mixing, in all experiments. The fraction of CF released was determined by comparison of the fluorescence with that obtained upon addition of Triton X-100, which releases all the dye.

Analysis of binding kinetics

The kinetics of magainin binding to membranes was analyzed as previously described in detail for cecropin A (1). Briefly, reversible binding of peptides to lipid vesicles is described by

$$\begin{array}{c}{k}_{\text{on}}\left[\text{L}\right]\\ P_{\text{w}}\rightleftharpoons P_{\text{L}},\\ k_{\text{off}}\end{array}$$ (1)

where P_w represents peptide in water; L, lipid vesicles; P_L, peptide bound to the membrane; and k_on and k_off are the on- and off-rate constants. The time courses of binding and dissociation are then described by

$$P_{\text{L}}\left(t\right)=A_0\left(1-e^{-k_{\text{app}}t}\right)+A_1,$$ (2)

$$P_{\text{w}}\left(t\right)=B_0{e}^{-k_{\text{app}}t}+B_1,$$ (3)

where the apparent rate constant is given by

$$k_{\text{app}}=k_{\text{on}}\left[\text{L}\right]+k_{\text{off}}$$ (4)

and A₀, A₁, B₀,and B₁ are constants. In these equations, [L] is the vesicle concentration (related to the lipid concentration by 1 LUV ≃ 10⁵ lipids), which is considered constant because the number of peptides bound per vesicle is always small, and vesicles do not disappear when peptides bind. The binding kinetics were analyzed using Eq. 2. The apparent rate constants, obtained from single-exponential fits to the experimental binding kinetic curves, were plotted against the lipid concentration, yielding a linear plot with slope k_on and y intercept k_off (Eq. 4).

Analysis of dissociation kinetics

The dissociation kinetics experiment (1) is represented by

$$\begin{array}{ccccc}& k_{\text{off}}& & k_{\text{on}}^{\prime }\left[L^{\prime }\right]& \\ P_{\text{L}}& \rightleftharpoons & P_{\text{w}}& \to & P_{{\text{L}}^{\prime }},\\ & k_{\text{on}}\left[L\right]& & & \end{array}$$ (5)

where peptide (P_L) initially bound to donor vesicles (L) dissociates and irreversibly binds to acceptor vesicles (L′). In the experiment, the donors are mixed vesicles of POPC/POPG, whereas the acceptors are pure POPG. Since the affinity of magainin for pure POPG is much greater than for POPC/POPG mixtures and the acceptors are in excess, irreversible peptide binding to the acceptors is assumed. As previously shown (1), the kinetics corresponding to this process follow a decay function with a main apparent rate constant (k′_app) that is a function of k_on, k_off, k′_on, and the concentrations of vesicles. If the concentration of donors is decreased keeping the concentration of acceptors constant, a set of values of k′_app is obtained that closely approach the real k_off (1). A plot of k′_app against the donor lipid concentration, [L], yields a y intercept that is a good estimate of k_off.

When F12W-magainin 2 dissociates from the donor vesicles, energy transfer from its Trp to 7MC-POPE on the membrane decreases, resulting in a decay of the fluorescence emission of 7MC-POPE as a function of time, F(t). Given the values of the rate constants and lipid concentrations, the expected behavior from the simple description provided by Eq. 5 is a single-exponential decay function of the form of Eq. 3 (1). In some cases, however, a double-exponential decay was necessary to obtain a good fit. This must correspond to deviations from the simple behavior represented by Eq. 5. Rather than using a more complicated analysis in those cases, k′_app was obtained from the apparent mean lifetime (τ) defined by (56,57)

$$\tau =\int \frac{dF\left(t\right)}{dt}tdt\int \frac{dF\left(t\right)}{dt}dt,$$ (6)

$$k_{\text{app}}^{\prime }=1/\tau ,$$ (7)

which is equivalent to an amplitude-weighted average of the time constants in a multiexponential decay. All curves could be reasonably well fit with, at most, a double-exponential decay with amplitudes α and (1 − α), corresponding to a mean lifetime τ = ατ₁ + (1 − α)τ₂.

Analysis of CF efflux kinetics

Two models were used to analyze the CF efflux data. The first was the model we previously proposed for the mechanism of all-or-none dye release induced by cecropin A (1). This model, illustrated in Fig. 2 (left), was tested for magainin 2 through analysis of CF efflux kinetics. A detailed account of the model, including its expression as a set of differential equations, its constraints, and assumptions, was given in detail in our previous article (1). Briefly, there are four states in this model:

• 1.Peptide as an unstructured monomer in water.
• 2.Peptide bound, as an α-helix, to the membrane surface of full vesicles.
• 3.Peptide in the pore state of the vesicles.
• 4.Peptide bound to empty vesicles.

Figure 2.

Models proposed for the mechanisms of peptides that cause all-or-none release (left) and peptides that cause graded release (right). The peptide is represented as unstructured in aqueous solution, in accordance with experiment. When bound to the membrane, it forms an α-helix, which is shown in cross section as a cylinder, where the darker half-circles represent the hydrophobic faces and the lighter represent the hydrophilic faces. All-or-none model (1): (A) peptide in solution; (B) peptide bound to the membrane surface of dye-loaded vesicles; (C) peptide associated with vesicles in the pore state, which causes efflux in an all-or-none manner; and (D) peptide bound to an empty vesicle, from which it dissociates back into solution. The on- and off-rate constants are fixed from the independently measured binding and dissociation kinetics. (Reproduced, with modifications, from Gregory et al. (1) with permission from Biophys. J.) Graded model (40,55): Binding of peptides creates a mass imbalance across the lipid bilayer, which perturbs the membrane thus enhancing the probability of a peptide transiently inserting into the hydrophobic core and eventually crossing the bilayer. In the bilayer-inserted state, the peptide catalyzes dye efflux from the vesicle lumen; this state constitutes the apparent pore. As peptide translocation is completed, the mass balance across the bilayer is restored and the rate of efflux becomes very slow or eventually stops. (Reproduced, with modifications, from Yandek et al. (55) with permission from Biophys. J.)

The rate constants k_on and k_off describe binding to, and dissociation from vesicles (full or empty). Then, there is a certain probability, proportional to a rate constant k₁, that a vesicle with surface-associated peptides will enter a pore state; at this point, the membrane yields and all dye is released. The pore state is unstable and relaxes to an empty vesicle state with a rate constant k₂. The peptide can dissociate from the membrane and bind to another vesicle, continuing the cycle of vesicle permeabilization. Efflux occurs from the pore state (P^∗) and is described by another rate constant, k_eflx. The efflux rate observed macroscopically, expressed as the increase in the fraction of CF outside, is the product of three factors: k_eflx; the concentration of peptides in the pore state of the vesicle per unit of lipid membrane P^∗/[L]; and the fraction of vesicles still full of CF (1).

In the analysis of CF efflux, k_on and k_off were fixed at the values obtained from the binding and dissociation kinetics. Furthermore, to stringently test this model, the rate constants for formation of the pore state (k₁) and the efflux rate constant (k_eflx) were fixed at the same values used for cecropin A (1). Thus, k₂ was the only parameter allowed to vary. This is equivalent to varying the ratio k₁/k₂, which we call β. The rate constant for pore relaxation, k₂, was adjusted by requiring that one value globally fit the CF efflux kinetics for all lipid concentrations pertaining to each lipid composition. Then, a slight variation of k₂ was allowed within each lipid composition to better fit the curves for the different lipid concentrations individually, and to obtain an estimate of the error. The mean values of β obtained from those fits and their corresponding standard deviations are listed in Table 1. In addition, an amplitude factor (0.8–1.1) was allowed for each curve, which corrects for experimental error in the determination of the maximum dye release.

Table 1.

Magainin 2 on- and off-rate constants, equilibrium dissociation constants, and pore formation/relaxation ratio (β) for POPC/POPG vesicles

Vesicle composition	Binding kinetics		Dissociation kinetics	Dissociation constant∗	Pore state
POPC/POPG	kon (M−1 s−1)	koff (s−1)	koff (s−1)	KD (μM)	β = k1/k2
50:50	(9.1 ± 0.4) × 105	20 ± 9	1.65 ± 0.12	1.8	β = (9.8 ± 1.4) × 10−4
70:30	(8.5 ± 0.7) × 105	77 ± 14	30 ± 4	35	β = (2.2 ± 0.9) × 10−4
80:20	(7.8 ± 0.7) × 105	160 ± 15	88 ± 3	110	kdins = 50 ± 20 s−1
90:10	(5.5 ± 0.9) × 105	350 ± 20	200 ± 8	370	—
100:0†	9.7 × 104	600	500	5000	—

The rate constants were obtained from the fits of experimental kinetics to the model. The error is estimated from the fits using the linear regression (k_on and k_off) or the variance in fitting the individual curves (β). The two other rate constants in the model were held fixed (k_eflx = 100 M⁻¹ s⁻¹ and k₁ = 0.01 s⁻¹).

^∗Calculated using k_on from binding and k_off from dissociation kinetics.

^†Estimated by extrapolation (Fig. 5).

The second model (Fig. 2, right) was previously proposed for transportan 10 (tp10), which is a cell-penetrating peptide that causes graded dye release (55). The detailed mathematical description of this model was presented by Yandek et al. (55) and is not repeated here. We note only that the apparent rate constant for insertion k_ins depends on the difference between the concentrations ([P]) of peptide bound to the outer and inner leaflets of the lipid bilayer, $k_{\text{ins}}=k_{\text{ins}}^{\ast }\times \left|{\left[\text{P}\right]}_{\text{outer}}-{\left[\text{P}\right]}_{\text{inner}}\right|$, where k^∗_ins is a true rate constant. Thus, efflux stops when the bound peptide concentration is the same on both sides of the bilayer. The analysis was subject to similar constraints as used for the all-or-none model.

The differential equations were solved by numerical integration with a fifth-order Runge-Kutta method with constant step size (58), and the numerical solutions were fit directly to the experimental data with a simplex algorithm (58) on a Linux workstation with in-house FORTRAN code programs, using the f95 compiler (Numerical Algorithms Groups, Oxford, UK).

For the CF efflux reverse experiment, where donor (empty) vesicles were preequilibrated with magainin, the initial conditions were calculated from the integrated equations in the forward reaction, for a period equal to the preincubation time of magainin with empty vesicles, as before (1,40,55).

Results

Binding and dissociation kinetics

The kinetics of magainin 2 binding to lipid vesicles were measured by stopped-flow fluorescence, using the variant peptide F12W-magainin 2, which behaves similarly to magainin (18). Upon F12W-magainin 2 binding to the membrane, FRET occurs from the Trp residue to a lipid fluorophore incorporated in the bilayer, 7MC-POPE, and the resulting increase in fluorescence emission intensity of 7MC-POPE was used to monitor the binding kinetics (Fig. 3, left). The curves obtained were well fit by a single-exponential function (Eq. 2), yielding the value of the apparent rate constant (k_app). Tucker et al. (59) obtained kinetic association curves using a different magainin analog, which they fit with a double exponential. However, in most cases, ∼90% of the amplitude in their fits corresponded to one of the two exponentials, essentially agreeing with our results. A plot of k_app against lipid concentration yields a linear fit (Fig. 3, right) in which the y intercept is k_off and the slope is k_on (Eq. 4). The rate constants for F12W-magainin 2 binding to, and dissociation from membranes of POPC/POPG 50:50, 70:30, 80:20, and 90:10 were obtained from those fits; they are listed in Table 1 and plotted later in Fig. 5 A.

Figure 3.

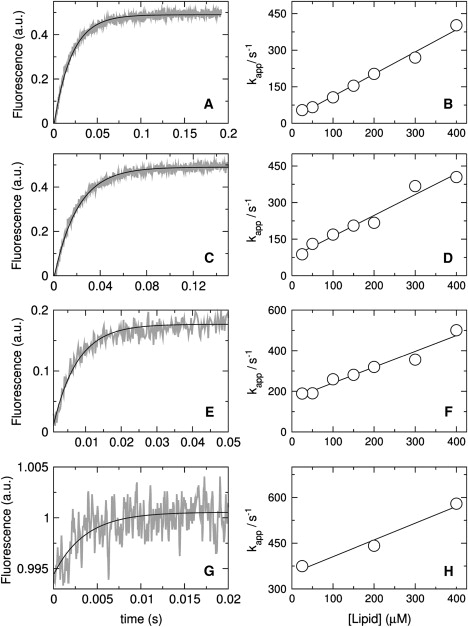
Kinetics of magainin 2 binding to vesicles of POPC/POPG 50:50 (A and B), 70:30 (C and D), 80:20 (E and F), and 90:10 (G and H). The signal recorded as a function of time is the FRET from Trp on the peptide to the lipid probe 7MC-POPE incorporated in the bilayer. On the left, the shaded curves are experimental traces recorded with 25 μM lipid and 1 μM F12W-magainin 2 (∼10 traces were averaged to improve the signal/noise ratio); the solid line is a single-exponential fit to the data (Eq. 2). On the right, the apparent rate constant (k_app) is plotted against lipid concentrations to obtain k_on from the slope and k_off from the y intercept (Eq. 4).

Figure 5.

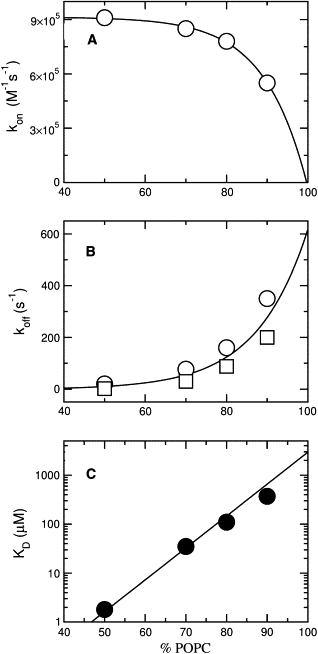
(A) On- and (B) off-rate constants, and (C) equilibrium dissociation constant for F12W-magainin 2 as a function of the POPC content in POPC/POPG mixtures. The open circles are from binding kinetics (Fig. 3) and the squares are from dissociation kinetics experiments (Fig. 4).

The value of k_off obtained from the binding kinetics can have a considerable error if the y intercept occurs close to the origin. To better determine k_off, a dissociation kinetics experiment was also performed. F12W-magainin 2 was preincubated with vesicles of POPC/POPG 50:50, 70:30, 80:20, and 90:10 containing 1 mol % 7MC-POPE (donors), which were then mixed in the stopped-flow system with pure POPG vesicles containing no probe (acceptors). Because binding of magainin is much stronger to pure POPG, once dissociation from the donors occurs, the peptide binds mainly to the acceptors. To render the process quasiirreversible, the concentration of acceptors (500 μM) was always larger than that of donors (50–300 μM). Fig. 4 shows representative kinetic curves for the various lipid compositions examined (left), and plots of the apparent off-rate constants (k′_app) against donor lipid concentration (right). These plots exhibit the expected lipid concentration dependence and, as the donor concentration approaches zero, k′_app approaches k_off (1). The off-rate constants thus obtained are also listed in Table 1. The kinetic curves in the dissociation experiment deviate more noticeably from a single exponential and the k′_app reported is a weighted average (Eq. 7). These values are similar to those obtained for k_off in the binding kinetics, though generally smaller by a factor of ∼2, a slight discrepancy also observed for cecropin A (1). As then, we used the values obtained from the dissociation experiment to calculate K_D because this measurement is more direct. However, a factor-of-2 difference in k_off has no effect on the analysis of efflux data and the values obtained from both methods have the same PG concentration dependence (Fig. 5 B). Clearly, as the POPG content of the vesicles increases, k_off decreases sharply from ∼500 s⁻¹ for pure POPC to ∼1 s⁻¹ for POPC/POPG 50:50.

Figure 4.

Kinetics of F12W-magainin 2 dissociation from vesicles of POPC/POPG 50:50 (A and B), 70:30 (C and D), 80:20 (E and F), and 90:10 (G and H). The signal recorded as a function of time is the FRET from Trp on the peptide to the lipid probe 7MC-POPE incorporated in the bilayer. Peptide, at a concentration of 2 μM, was incubated with 100–600 μM of POPC/POPG 50:50, 70:30, and 80:20, for 30, 40, and 60 min, respectively, and then mixed in the stopped flow with 1 mM POPG LUVs. The concentrations after mixing are half of those values. On the left, the shaded curves represent dissociation kinetics recorded with 50 μM donor lipid and 1 μM F12W-magainin 2 (∼10 traces were averaged to improve the signal/noise ratio); the solid line is a one- or two-exponential fit to the data. On the right, the k′_app obtained from those fits is plotted against the concentration of donor lipid to obtain k_off from the y intercept (limit of zero donors).

Binding of magainin to pure POPC was known to be weak (29) and, indeed, k_on and k_off could not be determined from the binding kinetics. Therefore, those rate constants were estimated by extrapolating to pure POPC the values of k_on and k_off obtained for POPC/POPG mixtures as a function of POPC content (Fig. 5), and are also listed in Table 1. The equilibrium dissociation constant, K_D = k_off/k_on ≈ 5 mM, confirms the very weak binding to pure POPC vesicles. K_D increases exponentially with the POPC content of the membrane (Fig. 5 C).

Mechanism of dye release

Two mechanisms are possible for peptide-induced dye release from lipid vesicles: all-or-none, in which some vesicles lose all of their contents while others are not affected; or graded, in which all vesicles lose part of their contents. The mechanism of dye release by magainin 2 was determined using the ANTS/DPX assay (52–54). A fluorophore, ANTS, is encapsulated in the vesicles together with a quencher, DPX. The fluorescence from ANTS released by the peptide to the external solution is titrated by additional DPX and subtracted out. As ANTS and DPX leak out at comparable rates, the fluorescence from ANTS remaining inside the vesicles increases. This is because quenching of ANTS fluorescence by DPX is a bimolecular process and therefore strongly dependent on quencher concentration. In all-or-none release, the degree of quenching inside the vesicles is independent of the amount of ANTS and DPX released because only the intact vesicles contribute to the inside signal. In graded release, the fluorescence of ANTS in the vesicles increases because the quencher concentration inside decreases. The assay was performed for magainin 2 with vesicles of POPC/POPG 50:50, 70:30, and 80:20. The experimental data for POPC/POPG 50:50 and 70:30 are indistinguishable and clearly show that magainin 2 induces all-or-none release (Fig. 6, solid circles). As the fraction of fluorescence outside (f_out) of the vesicles increases, the fluorescence from within the vesicles remains the same (Q_in), resulting in a horizontal line. The dependence on f_out that would correspond to graded release is given qualitatively by the dashed line in Fig. 6. For POPC/POPG 80:20 (open circles) a conclusion cannot be reached because dye release is very limited, even at long times.

Figure 6.

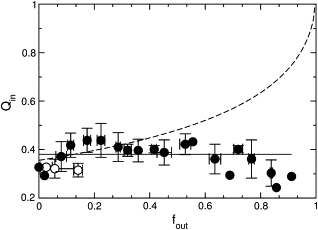
ANTS/DPX assay to determine the mechanism of release by magainin 2. The quenching function inside, Q_in = F_i/F_i^max, which is the ratio of ANTS fluorescence inside the vesicle in the presence (F_i) and absence (F_i^max) of quencher (DPX), is plotted against the ANTS fraction outside the vesicles, f_out, corrected for incomplete entrapment as described by Ladokhin et al. (54). The horizontal solid line is the result expected for all-or-none release and the dashed line is for graded release. The data points correspond to experiments on five independent vesicle preparations. Solid symbols correspond to mixtures of POPC/POPG 50:50 and 70:30; open symbols, to 80:20. Because there are slight variations in the degree of encapsulation in different preparations, the Q_in data were first normalized to the average initial fluorescence (in the absence of peptide), to bring all data sets to a common origin. The standard deviations for Q_in and f_out were calculated for each group of data points and are shown as error bars.

To ensure that the all-or-none dye release observed for POPC/POPG 50:50 and 70:30 was not an artifact of vesicle fusion, the ANTS/DPX assay was repeated with 10-fold lower concentrations of both lipid and peptide because fusion is less likely at lower lipid concentrations. The data had more scatter because of the small concentrations, but the plot still indicated all-or-none release (not shown). In addition, we directly tested for peptide-induced vesicle fusion using the assay previously described for cecropin A (1). Briefly, two suspensions of vesicles labeled either with a FRET donor (MB-POPE) or an acceptor (NBD-POPE), were mixed in equal amounts. If fusion occurred upon addition of magainin to this suspension, energy transfer would be expected, but none was observed. As a control, peptide was added to vesicles labeled with both donor and acceptor probes at half the concentration, in which case energy transfer was observed. The results (not shown) closely parallel those obtained with cecropin A (1). Thus, as also shown by others (15,19), magainin 2 does not cause significant vesicle fusion. In conclusion, our results demonstrate that magainin 2 induces all-or-none release from vesicles of POPC/POPG 50:50 and 70:30, in agreement with data from other researchers (15,17,60,61).

CF efflux kinetics

Addition of magainin 2 to phospholipid vesicles with encapsulated CF causes dye efflux. Since CF was encapsulated at high, self-quenching concentrations, its release from the vesicle lumen is accompanied by an increase in fluorescence, which was used to monitor the efflux kinetics. Magainin 2 (1 μM) was mixed with LUVs, varying the lipid concentration from 25 to 200 μM, and the kinetics of dye efflux were monitored. This experiment was performed for pure POPC and POPG (Fig. 7), and for mixtures of POPC/POPG 50:50, 70:30, and 80:20 (Fig. 8, top panels). Very little efflux occurs from pure POPC (Fig. 7, solid line), while efflux from POPG is fast (Fig. 7, dashed line). If the POPG content in a POPC matrix is increased, the efflux rate also increases (Fig. 8, top, shaded curves). Furthermore, as the lipid concentration increases, the efflux rate decreases, because the number of peptides bound per vesicle decreases.

Figure 7.

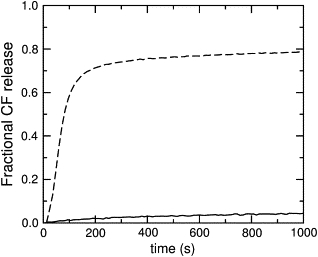
Carboxyfluorescein efflux induced by magainin 2 from vesicles of pure POPC, (solid line) and pure POPG (dashed line). In both cases the peptide concentration is 1 μM and the lipid concentration is 25 μM. The maximum possible fluorescence levels were determined by adding 1% Triton X-100 to the vesicles.

Figure 8.

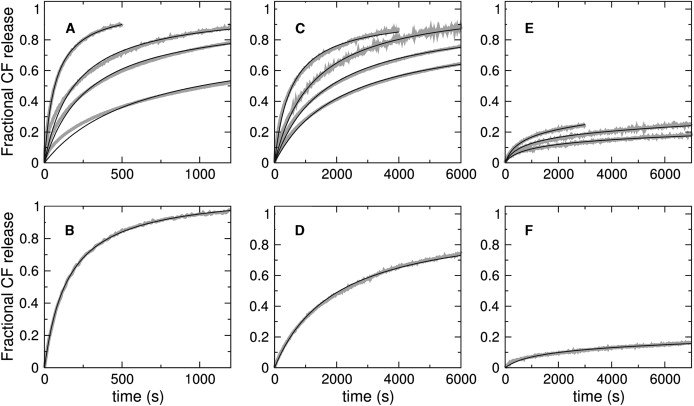
Carboxyfluorescein efflux from POPC/POPG mixtures induced by direct addition of magainin (top panels) to POPC/POPG 50:50 (A), 70:30 (C), and 80:20 (E). In each top panel, the shaded curves correspond to lipid concentrations of 25, 50, 100, and 200 μM lipid (200 μM absent in E). The fastest curve is always that for 25 μM lipid and the slowest is that for 200 μM lipid; the peptide concentration is always 1 μM. The bottom panels show the CF efflux reverse experiments for the same vesicle compositions (shaded curves): POPC/POPG 50:50 (B), 70:30 (D), and 80:20 (F). Here, 60 μM donor vesicles containing no CF were incubated with 2 μM peptide for 45, 60, and 90 min for POPC/POPG 50:50, 70:30, and 80:20, respectively. After incubation, the (empty) donor vesicles were mixed with an equal volume of 40 μM, CF-containing acceptor vesicles in the stopped-flow system, resulting in final 50 μM lipid and 1 μM peptide concentration. The maximum possible fluorescence levels were determined by adding 1% Triton X-100 to the vesicle suspension. In all panels, the curves shown are averages of approximately four independent traces recorded on the same vesicle preparation. In addition, the data was reproduced at least twice in independent vesicle preparations. The solid lines in panels A–D are the fits of the all-or-none model (Fig. 2, left); the solid lines in panels E and F are fits of the graded model (Fig. 2, right). For the all-or-none model, only one parameter was allowed to vary, β = k₁/k₂, which is given in Table 1. The fits also used the values of k_on and k_off independently obtained from the binding and dissociation kinetics.

To further constrain the analysis of the CF efflux data, a reverse experiment was carried out: the efflux kinetics were measured after magainin 2 was preincubated for ∼1 h with empty vesicles (donors), which were then mixed with vesicles containing CF (acceptors). Now, magainin must dissociate from the donor vesicles, back into solution, before it can bind to the acceptors and induce CF release. This experiment was performed for POPC/POPG 50:50, 70:30, and 80:20, the lipid composition of donor and acceptor vesicles being identical in each case (Fig. 8, bottom panels, shaded curves). The CF efflux kinetics in the reverse experiments are very similar to those in the direct addition experiments for the same lipid and peptide concentrations (compare bottom panels with the 50 μM lipid curves in top panels). Thus, after incubation with empty vesicles, magainin causes CF release from the acceptors almost as if it were directly added to the full vesicles. Using the dissociation constants determined here (Table 1), we calculated that only ∼38% of the peptide is bound after the preincubation in POPC/POPG 80:20, but ∼97% of the magainin is bound in POPC/POPG 50:50. This indicates that the peptides can readily desorb from the donors and bind to the acceptors. This experiment provides an important constraint in the analysis below.

Analysis of CF efflux kinetics

The major goal of this work was to test whether magainin conforms to the same model for all-or-none efflux as cecropin A (1). To do this, we sought to independently fix as many parameters in the model as possible. The on- and off-rate constants for binding of magainin to vesicles were independently determined and kept fixed in the fits to the CF efflux kinetics. In addition, the rate constants for efflux (k_eflx = 100 M⁻¹ s⁻¹) and formation of the pore state (k₁ = 0.01 s⁻¹) were also fixed, at the same values used for cecropin A (1). Thus, as before, only the value of k₂ was adjusted by fitting to the experimental efflux kinetics for a series of different lipid concentrations and three vesicle compositions, POPC/POPG 50:50, 70:30, and 80:20. As shown by the solid lines in Fig. 8, the model was able to describe very well the efflux curves for POPC/POPG 50:50 Fig. 8, A and B) and 70:30 (Fig. 8, C and D), in a global manner, for all lipid concentrations in the direct addition experiments and the reverse experiment. A slight deviation of the fit from the experimental trace occurs at the beginning of some curves, suggesting that perhaps a detail is missing from the model, but overall this simple model captures the essence of the mechanism of magainin. The fits can be characterized by the parameter β = k₁/k₂, which gives the ratio of the rates of pore formation to relaxation. It should be noted, however, that β is not an absolute measure but depends on k_eflx, which we kept at the same value used for cecropin A (1). Unlike for cecropin, where it stays almost constant, β increases ∼5× as the PG content of the vesicles increases from 30 to 50 mol %. Thus, magainin 2 is more sensitive to anionic lipid content than cecropin A. The values of β obtained are listed in Table 1. A variant of this model in which a magainin dimer forms as a necessary step to causing efflux was also tried, but produced very poor fits. Thus, magainin dimerization is inconsistent with the dye efflux kinetics.

For POPC/POPG 80:20, however, it was impossible to fit the curves, even relaxing all parameters in the model. The shape of the curves is simply incompatible with the model. The very small amount of dye released implies a halt in the permeabilization process that this all-or-none model cannot describe. A number of different all-or-none models were then tried, introducing variations that could, in principle, allow us to fit the data. Among these variations, two performed best. In the first, the peptide forms a nonproductive state, for example an aggregate, which does not lead to efflux and competes with the productive, pore-forming state, leading in time to a stop of the efflux. In the second, the peptide has an additional, silent mode of crossing the bilayer, that is, one that does not induce efflux. This variation follows a suggestion from Rathinakumar and Wimley (62). These two models, which contain two additional free parameters each, could fit the data in the direct reaction very well but could not fit the reverse experiment at all. Note that the reverse experiment (Fig. 8 F) shows efflux kinetics that are almost identical to those obtained by direct addition of the peptide to lipid with the same concentration (50 μM, Fig. 8 E, middle curve). In POPC/POPG 80:20, after the preincubation period, ∼60% of magainin is in solution but the remaining 40% must desorb so quickly from the donors that they behave as if added from solution to the new, CF-loaded, acceptors. Many other all-or-none models were tried, all without success. It is perhaps worthwhile to mention two of these unsuccessful models, one in which the active state was a dimer, and another in which the apparent on- or off-rate constants depended on the bound peptide concentration, which could conceivably hide some of the PG and hinder peptide binding at the later stages.

Since the all-or-none models failed for POPC/POPG 80:20, we tested the model proposed for the graded release induced by the peptide tp10 (55). In this model, the peptide causes dye efflux concomitantly with crossing the bilayer, as a response to the mass imbalance across the membrane, which is produced by the binding of the peptide itself. When the peptide concentrations bound on both sides of the membrane are approximately equal, efflux stops, which explains the small fractions of dye release. The model was described in detail before (55), and it is illustrated in Fig. 2 (right). Not to give this model any advantage, we also restricted all fit parameters in the same manner as for the all-or-none model, leaving only the rate constants k^∗_ins and k_dins, which characterize the process of crossing the membrane, to be fitted. After preliminary fits, we further fixed k^∗_ins = 0.6 M⁻¹ s⁻¹ for all concentrations and allowed only k_dins to vary; thus, the number of variable parameters was the same as for the all-or-none model. The graded model was able to fit the efflux curves for all lipid concentrations of POPC/POPG 80:20 with the same k_dins, both for the direct and reverse experiments, as shown by the solid lines in Fig. 8, E and F. These results demonstrate the importance of the reverse experiment in discriminating between models.

In conclusion, the all-or-none kinetic model is valid for magainin when the membrane contains at least 30 mol % PG. When only a small amount of PG exists in the membrane (≤20 mol %), magainin seems to follow a graded kinetic model. The possible reason for this different behavior is discussed below.

Discussion

Magainin binding to membranes

We found that magainin binds to POPC/POPG LUVs in a completely reversible manner. This is in agreement with one of the earliest experiments, in which Grant et al. (15) added unloaded to loaded PS SUVs where magainin 2a had been allowed to act. They wrote: “leakage stopped almost instantly after injection of unloaded vesicles.” In our experiments, the on-rate constants for POPC/POPG (Table 1) are essentially at the diffusion limit, which is ∼10⁶ M⁻¹ s⁻¹, expressed in terms of lipid concentration, or ∼10¹¹ M⁻¹ s⁻¹ in terms of vesicles (LUVs). The k_on increases 10-fold from pure POPC to POPC/POPG 50:50, but from POPC/POPG 80:20 to 50:50 k_on increases only slightly with anionic lipid content (Fig. 5 A). On the other hand, k_off decreases exponentially with POPG content, by more than two orders of magnitude from pure POPC to POPC/POPG 50:50 (Fig. 5 B). The equilibrium binding affinity increases by three orders of magnitude from pure POPC to POPC/POPG 50:50. Clearly, the anionic lipid content of the vesicles plays a major role in magainin binding. Does anionic lipid also matter for its activity and mechanism? Interaction of magainin-2 with PG and PC membranes has been shown to be different (63), but it could all be a matter of binding differences.

The binding affinity of magainin to lipid membranes has been examined by various authors and varies significantly with the lipid system used. A summary of dissociation constants from the literature is presented in Table 2. Binding of magainin 2a variants to POPC/POPG 3:1, measured by SUV titration, increases with peptide hydrophobicity, whereas selectivity for charged membranes decreases with increasing peptide hydrophobicity (20). Wenk and Seelig (64) determined, by ITC, that magainin 2a binds to POPC/POPG 3:1 SUVs with ΔH = −17 kcal/mol-peptide and ΔG = −8 kcal/mol at 25°C. Subtraction of the electrostatic component yielded an estimate for the bare binding to neutral vesicles of K_D ≈ 20 mM, corresponding to ΔG = −4.8 kcal/mol. Direct measurement of binding of magainin 2a by ITC to POPC SUVs yielded ΔH = −17 kcal/mol and ΔG = −7 kcal/mol at 25°C (42). Most important, the isotherms are hyperbolic in both POPC (20) and POPC/POPG 3:1 (at <7 μM magainin) (64), with no trace of cooperativity, arguing against magainin oligomerization.

Table 2.

Summary of literature data for binding of magainin peptides to lipid vesicles

Peptide	KD	Lipid membrane	Ref.	Footnotes
Magainin-1	2.5 μM	PS (bovine brain) SUV	(14)	∗
Magainin 2a	5 μM	POPG LUV	(29)	†
F12W-magainin 2	30 μM	PS/PC 2:1 (brain/egg) LUV	(19)	‡
F12W-magainin 2	30 μM	PG/PC 2:1 (egg) LUV	(19)	§
Magainin 2a	50 μM	POPC/POPG 3:1 LUV	(29)	¶
Magainin 2a	100 μM	POPC/POPG 3:1 SUV	(64)	‖
Magainin 2a	200 μM	POPC SUV	(42)	∗∗
Magainin 2a	20 mM	“Bare” neutral SUV	(64)	††
Magainin 2a	2.5 mM	POPC LUV	(29)	‡‡
F12W-magainin 2	10 mM	Egg PC LUV	(82)	§§

^∗From initial rates of calcein leakage.

^†From initial rates of calcein leakage.

^‡From Trp fluorescence.

^§From Trp fluorescence.

^¶From dye release kinetics; similar for SUVs.

^‖From ITC.

^∗∗From ITC; the value is for 22°C, interpolated from the temperature-dependent data in Wieprecht et al. (42).

^††From ITC, after subtraction of the electrostatic component.

^‡‡From dye release kinetics.

^§§From Trp fluorescence.

Mechanism of dye release: graded or all-or-none?

The nature of dye release induced by magainin was addressed by Grant et al. (15), who found all-or-none release from PS SUVs. Matsuzaki et al. (18) initially reported that magainin 2 (+4 charge) causes graded release from PG LUVs, but later (17) that F12W-magainin 2, which behaves similarly to magainin, causes all-or-none release from PC/PG 1:1 (egg) LUVs. Further, two magainin variants, with charges of +2 and +6, appear to function in all-or-none and graded manners, respectively (17). All-or-none release from PC/PG 1:1 LUVs was also observed by Dempsey et al. (61) and more recently by Tamba and Yamazaki (60), who showed that magainin 2 causes all-or-none calcein release from GUVs of DOPC/DOPG 1:1. In that study, the onset of release from each GUV was stochastic but, once started, proceeded rapidly to completion. There were no apparent changes in the vesicle, nor any micellization or disintegration. At low magainin concentration (3–5 μM) some vesicles were observed to release all their contents, whereas others released none. At >7 μM peptide, all vesicles released all contents, but at <1–2 μM, all resisted (60).

Thus, although most published results indicated all-or-none release by magainin, some uncertainty persisted, particularly if lipid or magainin version varied. Since the mechanism of dye release is an intrinsic component of the model for the quantitative analysis of efflux kinetics, it was critical to be absolutely sure about it. We found that magainin 2 causes all-or-none release from vesicles of POPC/POPG 50:50 and 70:30 (Fig. 6), but for POPC/POPG 80:20, the situation is not clear.

Finally, in the cases of cecropin A (1) and magainin 2 (this work), the average number of peptides bound per vesicle is very large, of ∼1000. Therefore, all-or-none release cannot be explained in the same manner as for cases where the average number of peptides bound per vesicle is very small, of approximately the number of peptides necessary to form a pore (65,66). In that case, vesicles that have fewer than the average number of peptides bound cannot form a pore and release nothing, while vesicles that have more release all contents. This explanation is not valid here because all vesicles have a much larger number of peptides bound than is necessary to form a pore; the all-or-none character of the release is, instead, a consequence of the stochastic nature of pore formation.

Test of models for dye release kinetics

We tested whether the all-or-none kinetic model previously proposed for cecropin A (1) (Fig. 2, left) could describe the kinetics of dye efflux induced by magainin 2. Earlier attempts at quantitatively modeling magainin-induced efflux kinetics were made, although they were not as rigorous as this one. In a very interesting article, Grant et al. (15) observed that the kinetics of dye efflux induced by magainin 2 were not simple first-order; a fast initial phase (∼100 s) was followed by a slower one. Several models were proposed (15), some quite complicated, but not analyzed in detail. Matsuzaki et al. (18) suggested that a pore-deactivating process may be responsible for the efflux kinetics not being first-order, and that a transient pore could relax the peptide concentration imbalance across the bilayer. Magainin 2 efflux data very similar to ours was published (67); however, the models used to describe the efflux kinetics included neither an explicit binding step nor an explicit pore formation step (18,67). That is, the vesicles were treated as if they began at time zero with an equilibrium concentration of bound peptides and an equilibrium density of pores, as if both the establishment of binding equilibrium and pore formation were instantaneous on the timescale of the efflux kinetics. This assumption is reasonable for binding because the corresponding equilibrium is established in ∼0.1 s (Fig. 3). However, the assumption of instantaneous pore formation is not acceptable; to compensate for the missing pore formation step, those models yielded peptide oligomerization.

In our experiments the rate of CF efflux increases with the P/L ratio (Fig. 8), in agreement with the results of Matsuzaki et al. (18). The most important conclusion we reach here is that the same model (Fig. 2, left) originally proposed for cecropin A (1) quantitatively describes efflux kinetics induced by magainin 2 from vesicles of POPC/POPG 50:50 and 70:30 (Fig. 8). Except for one, all parameters were either fixed at the same values used for cecropin A (rate constants for efflux and pore formation) or determined in independent experiments (on- and off-rate constants). Only the parameter β needs to be varied, which gives the ratio of the rate constants for pore formation and relaxation. The values of β for magainin 2 are ∼0.2–0.4 of those for cecropin A, indicating that the magainin-2 pore state is less efficient. (This could be because the pore is smaller, forms slower or closes faster, or a combination of the three.) However, magainin 2 is more sensitive to anionic lipid, as β increases ∼5× from POPC/POPG 70:30 to 50:50. A quantitative fit of the efflux kinetics was obtained for both peptides, suggesting a common mechanism. That such a simple model fits almost all data for cecropin A and magainin 2 suggests, furthermore, that their mechanisms are not that complicated. The model does not include peptide dimerization, and alternatives that included this step performed much worse in quantitatively fitting the data. Dimerization of a magainin analog (F5Y,F16W double mutant) has been observed by NMR (43). However, this was obtained under very special conditions—very high peptide (5 mM) and lipid (0.5 mM) concentration on DLPC SUVs, which are strained, and not very stable, phospholipid bilayers. The relevance of that dimer structure to the biological function of magainin remains to be demonstrated.

In POPC/POPG 80:20, the mechanism appears to be graded based on the efflux kinetics analysis, though a conclusive answer could not be obtained from the ANTS/DPX assay. The situation in this lipid mixture is probably special and not very representative of the general mechanism because the peptide on the surface nearly saturates the POPG lipid. We conjecture that this may lead to the agglutination of those lipids and formation of domains with a very high peptide density, where the perturbation of the membrane is localized. Membrane disruption may occur locally, concomitant with peptide translocation to the vesicle interior. This results in graded and limited efflux, in accordance with the same model proposed for tp10 (55) (Fig. 2, right). It is possible that domain formation also occurs, albeit to a lesser extent, upon addition of magainin to membranes of POPC/POPG 50:50 and 70:30, which could change the efflux kinetics. This could be the reason for the slight discrepancy between the initial portion of some fits and the data for those two mixtures (Fig. 8, A and C). However, the effect must be smaller than for POPC/POPG 80:20. This assertion is corroborated by a previous study of domain formation in POPC/POPS induced by a PS-binding protein, the C2 motif of synaptotagmin I, which shows that induction of PS domains goes through a maximum (68). The reason is that at high PS/C2, there is plenty of PS to satisfy all the C2 proteins, whereas at low PS/C2, the same protein binds more than one PS and agglutinates it. However, we would like to caution against a definitive interpretation of the results for POPC/POPG 80:20 because, as the percent release is small in this case, the dynamical range of the CF efflux experiment and its discriminatory power are also smaller.

The mechanism of magainin

The all-or-none kinetic model (1) is entirely consistent with what is known about the mechanism of magainin. With reference to Fig. 2 (left), at low peptide concentration on the membrane (state B), magainin is oriented parallel to the membrane surface (4,26,28,34,36) and the vesicles remain tight (60). The peptides cause bilayer thinning (6,32,69,70) and positive curvature strain (19,39). Eventually, as more peptides bind, a point of rupture is reached where the bilayer yields, allowing the contents to leak out all at once (state C). The pores seem to form and reseal stochastically and independently, without a concerted transition from a surface-associated to an inserted peptide state. A concerted transition would result in the appearance of cooperativity, which is completely absent from the dye release kinetics. Consistent with this, measurement of magainin 2a binding to POPC and POPC/POPG SUVs by ITC yielded hyperbolic isotherms (below 7μM magainin) with no indication of cooperativity (42,64). Rather, as specifically incorporated in our model (1), the peptides in a pore state catalyze efflux from lipid vesicles in proportion to the concentration of that state on the membrane.

Our results do not lead to a structural description of these pores, but provide constraints that molecular models proposed as mechanisms for these peptides must satisfy. First, the formation of stable pores can be ruled out. The fraction of peptides in the pore state must be small because they readily desorb from the vesicles. One set of values of k_on and k_off is sufficient to quantitatively describe all the data for binding (Fig. 3), dissociation (Fig. 4), and CF efflux kinetics (Fig. 8). When magainin was prebound to empty vesicles and then mixed with CF-loaded vesicles (reverse experiment, Fig. 8, bottom panels) the CF efflux rates were almost identical to those obtained by direct mixing with the loaded vesicles. If stable pores were to form, desorption must be slow because it would be limited by the rate of pore disassembly. The fraction of magainin in pores, estimated by OCD, is <50% in DMPC/DMPG 3:1 even at P/L as high as 1:20 (4), which is also in agreement with NMR and infrared data (26,28,33,34,36). Furthermore, our results indicate that no oligomerization or dimerization occurs, which would be required for any channel-type pore.

Second, formation of very transient pores is also inconsistent with the data. That would lead to graded efflux because the pore would close before all contents of the vesicle leak out, leaving some dye still inside. Thus, the sinking raft model or very short-lived perturbations can be excluded. If peptides formed a pore that then disassembled, there should be approximately equal probabilities for the peptides to translocate to the inner monolayer or to return to the outer monolayer of the membrane. Then, the amount of peptide dissociation after preincubation with donor vesicles in the reverse experiment, as well as its rate, should significantly decrease, but this is not observed in POPC/POPG 50:50 and 70:30 (Fig. 8, B and D). Dissociation from vesicles should also be slower, but to a first approximation the k_off determined from binding and dissociation kinetics (Table 1) are essentially identical, indicating little translocation. However, we do notice that the values of k_off are systematically smaller in the dissociation experiments, though only by a factor of ∼2. More important, the dissociation kinetics are somewhat biphasic (Fig. 4), requiring double-exponential fits, whereas single exponentials are sufficient for the association kinetics. This may reflect limited translocation of the peptide upon pore formation, but it must be significantly <50% because the all-or-none kinetic model quantitatively fits the CF efflux data for POPC/POPG 50:50 and 70:30, and translocation is not incorporated in the model. Evidence for translocation of magainin 2 was obtained using vesicles asymmetrically labeled with lipid fluorophores (71), but the experimental results that appear to indicate peptide translocation could also be caused by lipid flip-flop. Matsuzaki et al. (71) argued that vesicle leakage occurs simultaneously with translocation, but only ∼20% of the peptides appear to have translocated in the timeframe of those experiments. This level of translocation would be consistent with our results.

The carpet model (72,73), in its most general form, postulates that peptides bind to the membrane and lie parallel to the surface until a threshold concentration is reached. This is consistent with our results. Membrane perturbation of an unspecified kind, which includes formation of transient pores, can then occur. If the peptide concentration increases to high values (not reached in this investigation), severe membrane disruption may occur. But at no stage do stable pores exist. Unfortunately, many pictures of the carpet model show extensive membrane coverage culminating in micellization. This gives the impression that surface coverage is required, which is clearly not the case for magainin 2 and also not essential for the carpet model.

What, then, is the molecular conformation of the membrane in this pore state that leads to all-or-none dye release? It could be a bilayer with one or more large toroidal pores (69,70,74–76). The stochastic nature of the all-or-none kinetic model lies in the random formation of pores in the membrane. In the absence of peptide, formation of a lipid-lined pore is associated with a high free energy (77) and is therefore a very rare event. The presence of the peptides makes those events more frequent. In this sense, the peptide acts as a catalyst, lowering the activation free energy for efflux. We envision this happens through the effect of the peptides on the elastic properties of the bilayer and, possibly, by direct stabilization of the pores, as proposed by Lee et al. (69) and Huang (70) for antimicrobial peptides and specifically for magainin, following the ideas formulated by Brochard-Wyart et al. (74), Karatekin et al (75), and Puech et al. (76) for other systems. Our model is basically in agreement with these ideas, but the orientation and localization of the peptides when the vesicles reach the chaotic pore state are probably much less well defined than usually proposed for a toroidal pore (6).

Formation and relaxation of toroidal pores in a bilayer under mechanical stress has been observed in molecular dynamics simulations (78,79). Molecular dynamics simulations of a magainin analog interacting with a PC membrane indicate a disorganized structure of the pore and the peptides associated with it (80). We view these simulations as qualitative models and, as such, they provide interesting ideas for plausible mechanisms. The analysis presented here, on the other hand, demonstrates that the agreement of the all-or-none kinetic model with the experimental data is not only qualitative but quantitative. Furthermore, the model is the same as for cecropin A, and, because it is quantitative, it constitutes a predictive tool for other cases. More tests are in progress in our laboratory. The pore structure that corresponds to this model may apply to a variety of antimicrobial peptides. Thus, determination of the structure of these pores, at a detailed molecular level, which has not been achieved so far for any peptide, remains a major challenge in structural biophysics.