The Passive Cable Properties of Hair Cell Stereocilia and Their Contribution to Somatic Capacitance Measurements

Abstract

Somatic measurements of whole-cell capacitance are routinely used to understand physiologic events occurring in remote portions of cells. These studies often assume the intracellular space is voltage-clamped. We questioned this assumption in auditory and vestibular hair cells with respect to their stereocilia based on earlier studies showing that neurons, with radial dimensions similar to stereocilia, are not always isopotential under voltage-clamp. To explore this, we modeled the stereocilia as passive cables with transduction channels located at their tips. We found that the input capacitance measured at the soma changes when the transduction channels at the tips of the stereocilia are open compared to when the channels are closed. The maximum capacitance is felt with the transducer closed but will decrease as the transducer opens due to a length-dependent voltage drop along the stereocilium length. This potential drop is proportional to the intracellular resistance and stereocilium tip conductance and can produce a maximum capacitance error on the order of fF for single stereocilia and pF for the bundle.

Introduction

Whole-cell capacitance measurements are routinely used to study cellular events such as synapse vesicular binding and release, membrane reuptake and recycling, and membrane motor function. Assuming a constant membrane dielectric and thickness, it has been assumed that changes in capacitance strictly reflect changes in membrane surface area. Studies on the measurement of remote conductances using recordings in the soma, however, have revealed “space-clamp” errors resultant from the cable properties of the long and slender dendritic structures (1–3). If a neuron is electrotonically small and the length of its cable exceeds the membrane space constant, conductance measurements made with an electrode in the soma may be inaccurate. Additionally, somatic current estimates were shown to be less accurate as the synaptic conductance increased. Similar mechanisms might be expected to affect capacitance measurements. Using somatic electrical measurements, it is not possible to decouple voltage change due to capacitive loss from a load-dependent potential drop at some position along the length. Under the assumption that the whole cell is clamped, any change in the measured capacitance between stimulus conditions will be interpreted as being due to capacitor function. Thus somatic measurements of whole-cell capacitance may be underestimated for cells with conductive cable structures.

Hair cells of the inner ear have bundles of cable-like stereocilia located on the apex of their soma. Functionally, the hair bundle serves as a mechanoreceptor where, upon deflection, the mechanoelectric transducer (MET) located at the stereocilia tip opens. This causes calcium and potassium ions, primarily, to flow down their electrochemical gradient, resulting in depolarization of the cell and, finally, release of neurochemicals to stimulate afferent fibers of the eighth cranial nerve. As measurement techniques have improved, the number of studies relying on somatic capacitance measurements to elucidate information on synaptic events (4–6) and somatic electromotility (7,8) has increased, making recognition of potential errors resultant from “space-clamp” issues all the more important. Here, we show the effect of changes in MET conductance and interrogation frequency on passive hair bundle electrical properties and somatic capacitance measurements and demonstrate how misinterpretation of these changes as corresponding to somatic events can lead to erroneous conclusions.

Methods

A model was formulated based on Lord Kelvin's theory describing leaky transatlantic cables. The physical basis of the model is shown in Fig. 1. We assume the only current sources are at the tip and/or the insertion to the soma, so the homogeneous version of the cable equation is appropriate:

$${\lambda }_{DC}^2\frac{{\partial }^{2}v(x,t)}{\partial x^2}-\tau \frac{\partial v(x,t)}{\partial t}-v(x,t)=0,$$ (1)

where λ_DC is the direct current (DC) space constant, τ is the membrane time constant, g is the conductance, x is the distance from the tip, t is time, and v(x,t) is the spatiotemporal distribution of voltage.

Figure 1.

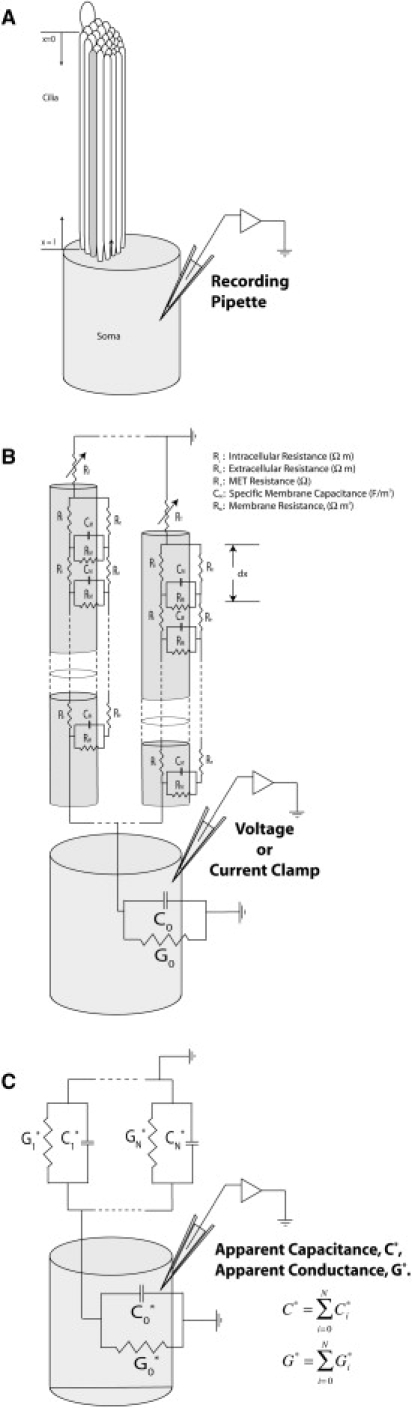
The physical basis for the model. (A) A schematic showing the stereocilia bundle extending from the apical portion of the hair cell. (B) Each stereocilium was modeled as a cable dividing its length into discrete sections, dx, accounting for the intracellular and extracellular resistances, R_i and R_e, and the lipid membrane resistance and capacitance, R_M and C_M. (C) The complex-valued impedance of each stereocilium found at the soma was determined numerically, and the result was represented as an apparent capacitance and conductance, C^∗_N, G^∗_N. The total somatic capacitance and conductance was determined as the sum of the individual stereocilia and the cell body.

The voltage considered here is the perturbation from the resting potential, so the total membrane potential is v + v_rest. The extracellular voltage was set to zero, and the current at the stereocilia tip was assumed to be equal to the transmembrane potential divided by the tip resistance. The apparent capacitance and conductance were determined by solving for the complex impedance felt at the cell soma. At the tip of the stereocilia, x = 0, the boundary condition is

$$v(0,t)=i(0,t)R_t,$$ (2)

where R_t is the MET resistance and i(0,t) is the current entering via the MET channel. At the soma, we consider voltage-clamp in the frequency domain:

$$v(l,t)=V_l{e}^{i\omega t}\text{.}$$ (3)

The DC space constant, λ_DC, is

$${\lambda }_{\text{DC}}=\frac{1}{2\pi a{G}_{\mathrm{M}}{R}_{\mathrm{i}}},$$ (4)

where a is the radius, G_m is the membrane conductance, and R_i is the intracellular resistance. The membrane time constant, τ, is

$$\tau =\frac{{\varepsilon }_{\mathrm{M}}}{G_{\mathrm{M}}h},$$ (5)

where ɛ_M is the effective membrane dielectric constant (permittivity) and h is the membrane thickness. The DC space constant, λ_DC, describes the exponential spatial decay of the voltage along the length of an infinitely long stereocilium. This DC voltage drop is due to conduction current lost to the intracellular axial resistance and through the membrane wall via its conductance. For a finite length stereocilium, the voltage drops even more rapidly due to the MET conductance leaking current at the tip. The alternating current (AC) space constant for a long stereocilium, ${\lambda }_{\text{AC}}$, is defined by the exponential spatial envelope under which the sinusoidally oscillating voltage decays. It is found from Eq. 1 using the dispersion relation $v(x,t)=V{e}^{i(\kappa x-\omega t)}$ and solving for the imaginary part of κ to obtain

$${\lambda }_{\text{AC}}=\frac{{\lambda }_{\text{DC}}}{\mathrm{Im}\left(\sqrt{(-1+i\omega \tau )}\right)},$$ (6)

where ω is the radial frequency. As the frequency is increased above the membrane time constant, the capacitance of the membrane dominates the conductance and the spatial decay of the voltage along the stereocilium is determined by the AC space constant (9).

Table 1 shows the parameter space investigated using the model. Unless otherwise noted, all figures were composed using these nominal values. The intracellular conductance upper limit is just above that for saline, and the low value was calculated based on the planar density of core actin filaments (10) assuming actin is an insulator. The tip conductance (G_T) range was based on estimates of 1–2 mechanotransducer (MET) channels per stereocilia using single-channel conductance values from 50 pS to 150 pS (11–16). The MET open probability curves were composed using the two-state model describing channel kinetics (17).

Table 1.

Model parameter space

Parameter	Units	Low value	Nominal value	High value	Reference
Stereocilia radius, a	nm	100	250	500	(18,29,30)
Stereocilia length, l	μm	1	5	50	(18, 30–32)
Intracellular conductance, $\frac{1}{R_{\mathrm{i}}}$	S/m	0.15	1	1.5	(29)
Extracellular conductance, $\frac{1}{R_{\mathrm{e}}}$	S/m	1.73	1.73	1.73	(33)
Specific membrane capacitance, CM	F/m2	0.017	0.017	0.017	(34)
Specific membrane conductance,$G_{\mathrm{M}}=\frac{1}{R_{\mathrm{M}}}$	S/m2	0.1	1	10	(29,34,35)
Tip conductance, $\frac{1}{R_{\mathrm{T}}}$	pS	100	300	300	(11,12)
Frequency, $f=\frac{2\pi }{\omega }$	Hz	0.01	0.01	18,293	(22)

To quantify the extent of capacitance underestimation using somatic voltage-clamp, the absolute error and percentage error with respect to the truly space-clamped capacitance value were calculated. The absolute error was determined as the difference between the clamped (G_T = 0) input capacitance and the value with the tip conductance greater than zero (G_T ≠ 0). The percentage capacitance error was determined as the ratio of the capacitance error to the space-clamped capacitance value.

Results

The DC space constant (Fig. 2) was calculated as a function of intracellular resistance, R_i, membrane conductance, G_m, and radius, a. For stereocilia with small radii, low intracellular conductance, and high membrane conductance values, it is conceivable that the space constant can approach magnitudes near those of stereocilia height. For our simulations, however, we were always at dimensions less than this value (λ = 353 μm). The normalized AC space constant is shown in Fig. 3 for different values of G_M. This plot shows that the cutoff frequency varies proportionally with the membrane conductance and ranges from 10 to 1000 Hz.

Figure 2.

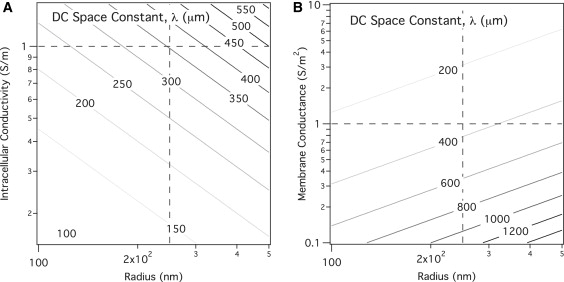
DC space constant. The DC space constant was calculated as a function of membrane conductance (A) and intracellular conductance (B). The dotted lines show the nominal parameter value for each axis, and the intersection highlights a DC space constant of 353 μm.

Figure 3.

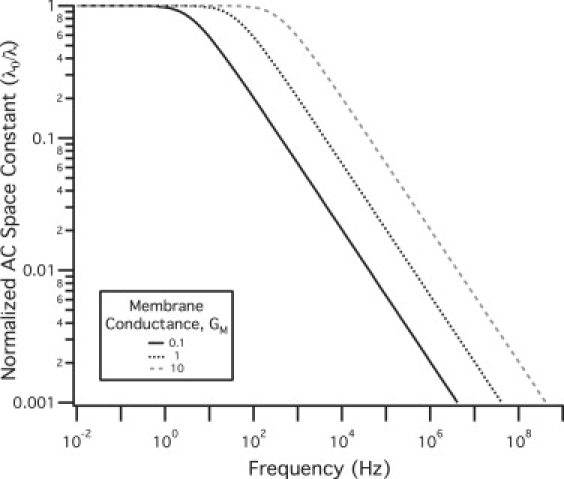
Normalized AC space constant. The AC space constant was normalized to the DC value and displayed for three membrane conductance values.

The change in membrane potential as a function of stereocilia length is shown in Fig. 4 A. With the mechanotransducer closed (G_T = 0), the structure is essentially isopotential (V/V_Soma = 0.99). As the tip conductance increases, however, current flows out of the stereocilium leading to a condition in which the structure is not space-clamped. Applying Kirchoff's current law to the circuit in Fig. 1 B, the current at the stereocilium tip will be a sum of the current through the transducer, the membrane wall, and the intracellular resistance. Since we are below the cutoff frequency, current through the membrane will be low. Under this condition, the current through the tip and the intracellular space will function as a current divider. The total change in potential between the soma (ΔV_Soma) and the grounded extracellular space will be equal to the sum of the tip potential drop (ΔV_T) and the length-dependent potential drop (ΔV_L) along the cilium. When the tip conductance is infinite, the current through the tip will be very large and ΔV_L will equal the somatic holding potential. Therefore, this plot displays the full range of membrane potential modulation resultant from a change in the tip conductance.

Figure 4.

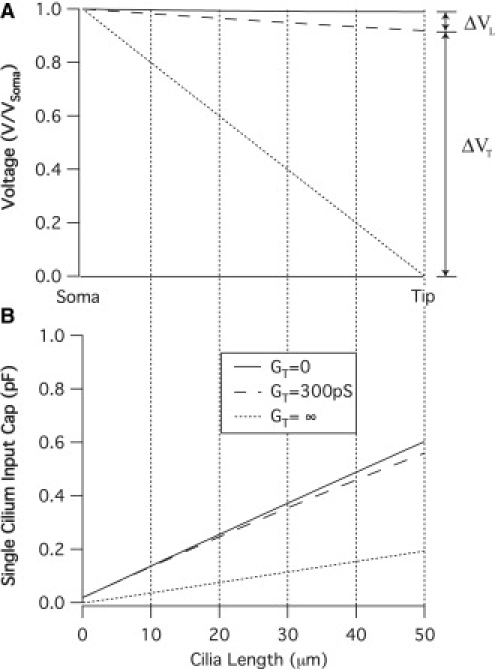
MET conductance-dependent voltage distribution and stereocilia input capacitance. (A) The normalized tip potential (V/V_Soma) changes as a function of stereocilia length for three values of tip conductance. The length-dependent, ΔV_L, and tip conductance dependent, ΔV_T, potential drops are labeled for G_T = 300 pS. The voltage drop along the stereocilia causes a reduction in the capacitance felt at the soma (B). The capacitance measured with the METs closed (G_T = 0) represents the space-clamped value. As ΔV_L increases, the input capacitance decreases, resulting in a larger error in measurement.

Space-clamp errors can result in a change in the apparent capacitance. Fig. 4 B shows the single stereocilia input capacitance corresponding to the membrane potential curves shown in Fig. 4 A. The input capacitance when the MET is closed (G_T = 0) is equal to the stereocilia surface area multiplied by the specific membrane capacitance and represents the condition in which the cilium is space-clamped. The somatic capacitive current will be a sum of all capacitive currents along the length of the stereocilia, each of which will be proportional to the derivative of voltage with respect to time. When ΔV_L is greater than zero, the magnitude of the potential along the length decreases, resulting in a reduction of the capacitive currents contributing to the somatic measurement. This will be detected as a reduction in the input capacitance and represents an error with respect to the space-clamped condition. Under the assumption that the stereocilia are voltage-clamped, therefore, this mechanism will result in an underestimation of the surface-area-dependent capacitance.

The error in single stereocilium input capacitance as a function of the tip conductance and the corresponding percentage capacitance error can be seen in Fig. 5. The magnitude of the capacitance change when the tip is short circuited (G_T = ∞) represents the largest space-clamping error. Under this condition, ΔV_L will always equal the somatic holding potential and the percentage error will be constant. When ΔV_L is less than the somatic holding potential, on the other hand, this value will increase proportionally to the stereocilia length, resulting in an increase in the percentage capacitance error (Fig. 5 B). In sum, the magnitude of capacitance underestimation will increase as the stereocilium length increases until the length-dependent voltage drop is equal to the somatic holding potential, at which point the error becomes constant.

Figure 5.

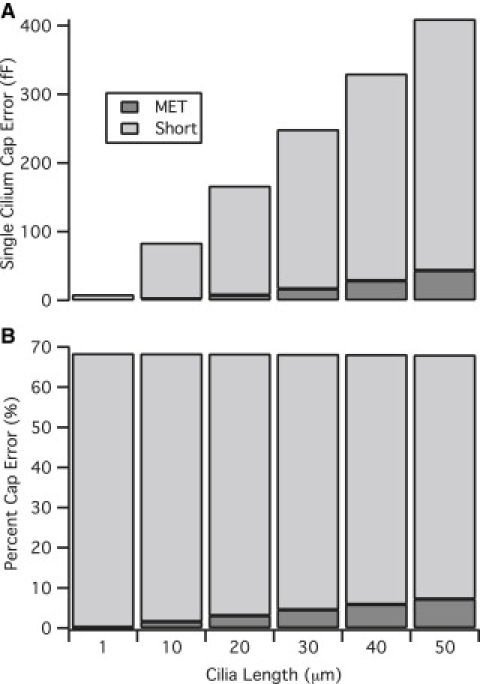
Space-clamp error. The single stereocilium capacitance difference (A) with respect to the space-clamped value is displayed for the MET open (G_T = 300 pS) and the tip short-circuited to the extracellular space (G_T = ∞). The percentage capacitance error (B), as expected, increases with length until the length-dependent potential drop is equal to the somatic holding potential (ΔV_L = V_Soma) and then plateaus at 67% (2/3).

As the stereocilium tip is deflected, the MET open probability has been shown to have an asymmetric, sigmoidal-like relationship to tip displacement (17). The kinetics of channel opening will cause the voltage, current, and capacitance modulation to exhibit a similar trend. The magnitude of voltage modulation is directly proportional to the tip conductance and, for values representing a cilium with one (G_T = 150 pS) or two (G_T = 300 pS) METs, can change by as much as 3.5%–7%, respectively. The ratio of the tip current to the current leaving the soma will also increase proportionally to the conductance at the tip and will be larger for shorter stereocilium. This is because the length-dependent voltage drop will be less, leading to a larger tip potential and, it follows, a larger tip current. Finally, the input capacitance error can be seen to reach a magnitude of 40 fF for a cilium modeled with two channels.

The capacitance magnitude for single stereocilium of typical dimensions is shown in Fig. 6 A. The capacitance from a single stereocilium can approach 1 pF for larger structures, as may be found in the vestibular canals, though for complete utricular and cochlear hair cell bundles (length <10 μm), the value is predicted to be <0.4 pF. The capacitance error is shown to increase as the radius decreases. This occurs because the intracellular resistance, which is inversely proportional to the radius, will increase, resulting in a larger length-dependent potential drop. The capacitance error for a single cochlear or utricular stereocilium will be <5 fF, though for bundle sizes of 75–125 stereocilium/hair cell can reach magnitudes of 0.375–0.75 pF.

Figure 6.

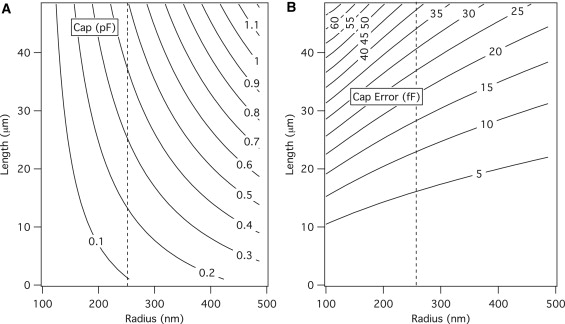
Single stereocilium DC capacitance magnitude and capacitance error for typical hair cell stereocilia dimensions. The dotted lines show the nominal parameter value for each axis. The intracellular resistance is inversely proportional to the radius leading to an increase in the capacitance error as the cilium width decreases.

The taper region present at the base of stereocilia in most hair cells was not explicitly included in the simulations of the stereocilia itself, but can easily be treated as a lumped series resistance between the soma and the stereocilia. Presence of the series resistance does not have any significant effect on the capacitance measured in the soma when the MET is closed due to the fact that the stereocilia are nearly isopotential with the soma in this case. If the tip of the stereocilia were short circuited, the series resistance would drop the voltage in the stereocilia and thereby further reduce the capacitance measured in the soma relative to the closed MET case. This effect would accentuate the effect described here and cause the capacitance to modulate even more than predicted by the simulations (5%–15% depending upon specific morphological and MET conductance values).

Implications for the bundle

Morphometric data compiled by Silber et al. for the red-eared slider turtle was used to estimate the space-clamped input capacitance of the bundle for six typical cell types (Table 2) (18). The bundle surface area was calculated assuming single-stereocilium cylindrical geometry using published values for the height range and diameter of the kinocilium and stereocilia specific to each cell type. The surface area was multiplied by the specific membrane capacitance to find the contribution from each stereocilium, and these were added in parallel to determine the magnitude of the bundle capacitance. Superimposed upon a whole-cell capacitance range from 8 to 18 pF (19), utricular bundle modulation may account for 25%–45% of the overall modulation of the capacitance measured in the soma.

Table 2.

Utricular bundle capacitance contribution

Cell type	No. SC	Diameter (μm)	Height (μm)	Total capacitance (pF)
1	50	0.265	1.2–3.9	2.09
2	35	0.269	1.3–3.8	2.44
3	62	0.250	1.2–7.8	2.57
4	86	0.325	1.6–8.0	7.62
5	78	0.325	1.1–8.2	6.72
6	54	0.265	1.1–5.5	2.73

Cochlear morphometric data on inner (IHC) and outer (OHC) hair cells compiled by Lim et al. were used to compute the overall capacitance and the load-dependent input capacitance error for the chinchilla (20,21). Raw data showing the height of the tallest stereocilia and the number of stereocilia per row per cell was fit with a third- to fifth-order polynomial (Fig. 7). A graphic illustration showing the gradient in height of the bundle rows along the basilar membrane was used to curve-fit the tonotopic variation in bundle row height. Together, these fits were used to compose maps of stereocilia dimension as a function of the distance from the apex for the long, medium, and short stereocilia rows of each cell type (Fig. 7). The tonotopic variation in cell best frequency (22) was used to calculate the AC capacitance as a function of frequency (Fig. 8). The audible range of the chinchilla cochlea is ∼100–20,000 Hz. At frequencies above the corner frequency (340 Hz), the capacitance current will be a sum of the tip-load-dependent current and current through the membrane capacitor. For the chinchilla, the stereocilia bundle can be seen to contribute between 1.5 and <4 pF to the overall capacitance measured at the soma with maximum capacitance errors occurring in cells in the low frequency apical turn of the cochlea.

Figure 7.

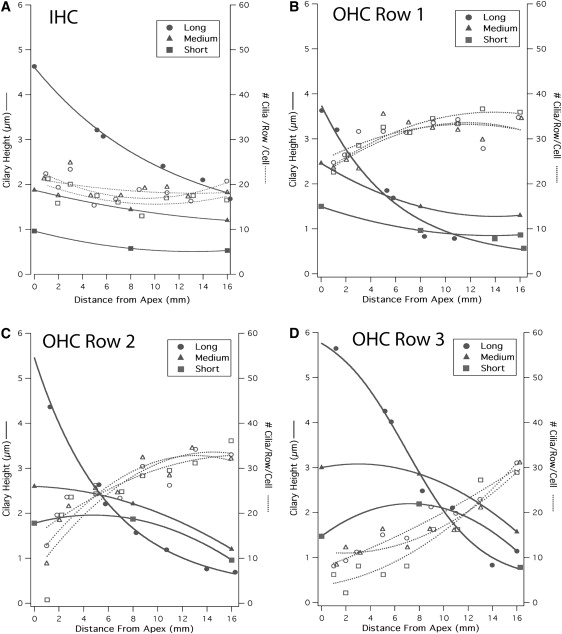
Morphometric data for the chinchilla cochlea reproduced from Lim et al. (20,21) was digitized and fit with polynomial curves. The stereocilia height and number of stereocilia per row per cell are shown for the long, medium, and short rows, respectively, within the hair cell bundle for IHCs (A) and OHCs rows 1 (B), 2 (C), and 3 (D). These data were used in the analysis to estimate capacitance errors as displayed in Fig. 8.

Figure 8.

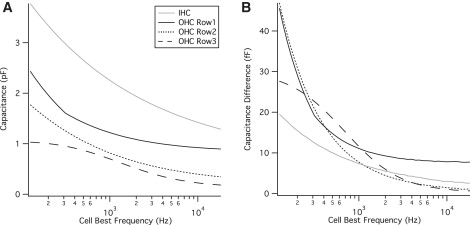
Chinchilla cochlear hair cell stereocilia bundle capacitance and associated capacitance error. The tonotopic variation in cell best frequency was used to convert the position along the basilar membrane into cell best frequency, and the AC capacitance under the space-clamped condition (G_T = 0) was calculated (A). The associated bundle capacitance error was calculated as the difference between the space-clamped conditions and the measured capacitance calculated with two METs per cilium tip (G_T = 300 pS).

Discussion

Load-dependent space-clamping errors are known to influence the measurement of synaptic events in neurons (1–3). Such findings, however, have not been extended to include the effect on somatic capacitance estimates. As shown here, capacitance errors in hair cells can be as large as 20–65 fF for a single long stereocilium, and for shorter structures can reach magnitudes of 375–750 fF when calculated for the bundle (75–125 stereocilia/bundle). In comparison with cochlear hair cell exocytosis magnitudes of 50–150 fF (23), this error represents a significant contribution to the overall capacitance modulation and, if unrecognized, might lead to considerable errors in interpretation. Compounding this is the fact that the capacitance measurement error is not static and changes in magnitude depending upon the open probability of the MET channels. Hence, dynamic changes in capacitance measured in the soma may be due to changes in the status of the MET channels, even in the complete absence of synaptic transmission or membrane area changes. These results motivate blockage of MET channels during studies of synaptic-related capacitance modulation in hair cells. Furthermore, studies designed to look at frequency selectivity of ribbon synapses (4) have compared capacitance values at different frequencies of interrogation (5–200 Hz). If the AC cutoff frequency of the stereocilia is below the range of interrogation frequencies, these capacitance magnitudes may correspond to different bundle capacitance values because the stereocilia will not be “space-clamped” and results may not be indicative of vesicular fusion. In summary, capacitance measurements made in the soma will be compromised by any loss of “space-clamp” and can occur due to a tip conductance-dependent voltage drop or to current loss through the membrane wall at frequencies above the AC cutoff frequency.

Results demonstrate a somatic capacitance change that occurs in the hair cell soma as MET channels at the tips of the stereocilia open and close which could lead to a potential artifact in some experimental settings. This mechanism may also have physiologic relevance, and it is of interest to ask how this might contribute to the tuning performed by the stereocilia bundle. Previous theories have suggested that the tonotopic gradation in stereocilia height can be understood by analysis of free-standing stereocilia from lizard as mechanical (24,25) resonators. For stereocilia with a membrane over the top, this analysis is inadequate. In the turtle, an additional mechanism was proposed relating the height to the magnitude of tip displacement as a function of angular displacement for different stereocilia lengths (26). We have shown that the length of the stereocilium determines a proportional voltage drop, thus influencing the current transfer between the tip and the soma. This input/output cascade will further be influenced by the magnitude of the conductance change at the cilium tip. Inward current through the MET will also be reduced when it gets to the soma as the frequency of stimulation exceeds the AC cutoff frequency. These findings suggest that the electrical filtration performed by the stereocilia may provide an upper limit to the stereocilia height. Furthermore, this mechanism may explain why vestibular hair cells, sensitive to lower frequencies, have longer bundles than do shorter bundle length, high-frequency cochlear hair cells; and this mechanism could be useful in experimental comparisons of these two populations.

Simulations in this study were performed with the stereocilia under zero-displacement conditions while modulating the tip conductance in a manner consistent with displacement-induced MET conductance changes. Recent work has suggested that flexoelectric-induced radius changes may cause conversion of input electrical current into mechanical work, thus generating a piezoelectric-like force in stereocilia bundles (28,36). Under this condition, during excitatory bundle deflections the membrane dielectric is expected to increase and may augment the current lost to force production, thereby further amplifying errors resultant from the compromise in “space-clamp”.

Uncited references

27.