Diffusion, Exclusion, and Specific Binding in a Large Channel: A Study of OmpF Selectivity Inversion

Abstract

We find that moderate cationic selectivity of the general bacterial porin OmpF in sodium and potassium chloride solutions is inversed to anionic selectivity in concentrated solutions of barium, calcium, nickel, and magnesium chlorides. To understand the origin of this phenomenon, we consider several factors, which include the binding of divalent cations, electrostatic and steric exclusion of differently charged and differently sized ions, size-dependent hydrodynamic hindrance, electrokinetic effects, and significant “anionic” diffusion potential for bulk solutions of chlorides of divalent cations. Though all these factors contribute to the measured selectivity of this large channel, the observed selectivity inversion is mostly due to the following two. First, binding divalent cations compensates, or even slightly overcompensates, for the negative charge of the OmpF protein, which is known to be the main cause of cationic selectivity in sodium and potassium chloride solutions. Second, the higher anionic (versus cationic) transport rate expected for bulk solutions of chloride salts of divalent cations is the leading cause of the measured anionic selectivity of the channel. Interestingly, at high concentrations the binding of cations does not show any pronounced specificity within the divalent series because the reversal potentials measured in the series correlate well with the corresponding bulk diffusion potentials. Thus our study shows that, in contrast to the highly selective channels of neurophysiology that employ mostly the exclusion mechanism, quite different factors account for the selectivity of large channels. The elucidation of these factors is essential for understanding large channel selectivity and its regulation in vivo.

Introduction

Ion selectivity is a critical property of the channels of excitable membranes (1,2). It is essential for the cell function that each ionic species (typically “small ions” such as Na⁺, K⁺, Ca²⁺, or Cl⁻) permeates across membranes at different regulated rates, and this regulatory mission is often accomplished by selective ion channels. In the case of large channels represented by bacterial porins (3–5), toxins (6–9), voltage-dependent anionic channels of outer mitochondrial membrane (10), and others, the conduction of small ions has not been necessarily attributed to their major functions. Most of these channels were designed by nature to facilitate the exchange of metabolites and other larger molecules between cells and between organelles within cells. However, the exploration of large channel selectivity to small ions is appealing as it tests our understanding of physical principles underlying transport through these nanoscale objects.

The functional aspects of small-ion conduction by large channels are still debated (5,10). A recent study of a bacterial porin, OmpF, demonstrated that this channel develops a nearly ideal cationic selectivity when salt concentration is reduced to a subdecimolar range (11). A plausible functionally important consequence of this finding is that under special but physiologically relevant conditions bacteria can develop a significant transient potential across the outer membrane. This potential may serve as an important physiological signal.

The ability of channels to discriminate between ions depends on their intrinsic properties (size, hydration, etc.) as well as on the interaction of permeant ions with the channel and among themselves. In other words, ion selectivity is a property of the system that necessarily includes both the channel and the electrolyte. In this sense, two factors have been cited as the main contributors to the large channel selectivity: the differences in ion mobilities and the electrostatic exclusion due to the interaction between permeating ions and channel ionizable residues. The latter is usually considered to be the leading reason for the high selectivity. However, other factors—such as entropic effects related to the preferential rejection of ions because of their size, short range nonelectrostatic interactions, and osmotic effects—may play a role in certain specific cases. As many of these factors are closely interconnected, experiments designed to separate their roles are necessary.

Several experimental protocols provide the means of different quantitative estimations for ion selectivity. To this end, mole fraction, conductance ratio, and reversal potential measurements define operational quantities accounting for this property (12). As may be expected, these protocols provide similar but not identical results. Mole fraction experiments give a quantification of ion partitioning between the channel and the surrounding solution, i.e., the excess chemical potential of ions inside the channel. Conductance ratio measurements yield information about both partitioning and relative diffusivities of the ions in the channel, but require comparison of different sets of measurements and certain model assumptions to deduce selectivity. Reversal potential measurement is the method of choice to quantify selectivity because it provides a joint measure of partition and diffusion, and the sign of the measured potential provides a quick estimate of the channel selectivity via the anion-cation permeability ratios given by the Goldman-Hodgkin-Katz (GHK) equation (1). For a large channel, cation selectivity is explained as a consequence of a negative effective charge of the channel, whereas an anionic selectivity is immediately connected to a positive effective charge. This method is so popular that in practice it is considered almost a universal indicator of ion selectivity, irrespective of the experimental conditions used (13).

We would like to note that this procedure was originally proposed for experiments performed at moderate gradients of KCl solutions buffered at neutral pH and with salts of divalent cations present in micromolar or millimolar concentrations. At such conditions, the specific binding of ions is usually irrelevant, and diffusion potentials are also negligible because K⁺ and Cl⁻ have almost equal bulk mobilities and, therefore, hydrated sizes. This allows one to reduce the description to electrostatic exclusion only and to interpret selectivity exclusively in terms of the effective channel charge. However, in experiments with concentrated solutions used at large gradient ratios (50 ∼100) and electrolytes such as NaCl or LiCl and, indeed, chloride salts of divalent cations such as CaCl₂ or MgCl₂, the description of selectivity in terms of ion accumulation/depletion can only be an oversimplification of the problem since the contributions of specific binding and diffusion potentials can be quite significant. As often happens, popular approaches far from the conditions where they have proved to be successful can lead to a poor description of the system and, therefore, must be carefully inspected.

There is abundant but scattered information on the selectivity of large channels. The main message of the existing literature can be summarized by saying that ion selectivity is not just a number, a universal property of the channel itself but, on the contrary, a strong function of several factors including salt concentration, solution pH, channel orientation, lipid membrane composition, and type of electrolyte (e.g., 11,14–17).

In this work we study OmpF, a general diffusion bacterial porin that forms large channels in the outer membrane of Escherichia coli (5,18). Each monomer assembles into a 16-stranded β-barrel, leaving an hourglass-shaped aqueous pore with a diameter in the range of 1–4 nm (19). In planar lipid bilayers OmpF homotrimeric channels allow multiionic transport and exhibit moderate cationic selectivity in solutions of monovalent salts at neutral pH (11). This selectivity has been reported to be highly sensitive to the charge state of the ionizable residues of the channel (16), particularly of those lying at the channel constriction (20). Here we show that, depending on the experimental conditions, selectivity of the channel may be dominated by different sources. In particular, we report an unusual inversion of normally cationic selectivity of OmpF in solutions of divalent cations such as Ca²⁺ and Mg²⁺.

Materials and Methods

Wild-type (WT) OmpF, mutants D113A and E117A, were a generous gift of Drs. Prashant Phale, Anne Delcour, and Mathias Winterhalter. Mutant D113C/E117C was kindly provided by Dr. Henk Miedema. Bilayer membranes were formed from two monolayers prepared from a 1% solution of diphytanoylphosphatidylcholine (DPhPC) (Avanti Polar Lipids, Alabaster, AL) in pentane (Burdick and Jackson, Muskegon, MI) on 70–80-μm-diameter orifices in the 15-μm-thick Teflon partition that separated two chambers (21,22). The orifices were pretreated with a 1% solution of hexadecane in pentane. The total capacitance depended on the actual location of the orifice in the film (and thus the area of the film exposed to salt solution), but membrane capacitance was always ∼100–150 pF. Aqueous solutions of KCl were buffered by 5 mM MES (2-(N-morpholino)-ethanesulphonic acid) at pH values below pH 6, by 5 mM HEPES (4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid) at pH values (6–8), by 5 mM CHES (2-(cyclohexylamino)ethanesulfonic acid) at pH 9, and by 10 mM CAPS (3-(cyclohexylamino)propanesulfonic acid) at pH values above 9. All measurements were performed on single OmpF channels at room temperature (23.0°C ± 1.5°C). Single-channel insertion was achieved by adding 0.1–0.3 μl of a 1 μg/ml solution of OmpF in the buffer that contained 1 M KCl and 1% (v/v) octyl polyoxyethylene (Alexis, Switzerland) to 1 ml aqueous phase at the cis side of the membrane only while stirring.

If not stated otherwise, the membrane potential was applied using Ag/AgCl electrodes in 2 M KCl, 1.5% agarose bridges assembled within standard 200 μl pipette tips (21). Potential is defined as positive when it is greater at the side of protein addition (the cis side of the membrane cell). An Axopatch 200B amplifier (Molecular Devices, Sunnyvale, CA) in the voltage-clamp mode was used for measuring the current and applying potential. Data were filtered by a low-pass eight-pole Butterworth filter (Model 9002, Frequency Devices, Haverhill, MA) at 15 kHz and directly saved into the computer memory with a sampling frequency of 50 kHz. The membrane chamber and the head stage were isolated from external noise sources with a double μ-metal screen (Amuneal Manufacturing, Philadelphia, PA).

The reversal potential was obtained as follows. First, a lipid membrane was formed at a given salt concentration gradient. Second, a single OmpF channel was inserted at zero potential and the channel conductance was checked by applying +50 mV (−50 mV in divalent salts) and then switching potential polarity (Fig. 1). Third, the ionic current through the channel was manually set to zero by adjusting the applied potential. The potential needed to achieve zero current, V_0Exp, was then corrected by the liquid junction potential (LJP) calculated from Henderson's equation (see Appendix) to obtain reversal potential. Each point was measured for at least three different channels in three different experiments to ensure reproducibility and to estimate the standard deviation. In some experiments, negative potentials of ∼100 mV were applied to speed up channel insertion.

Figure 1.

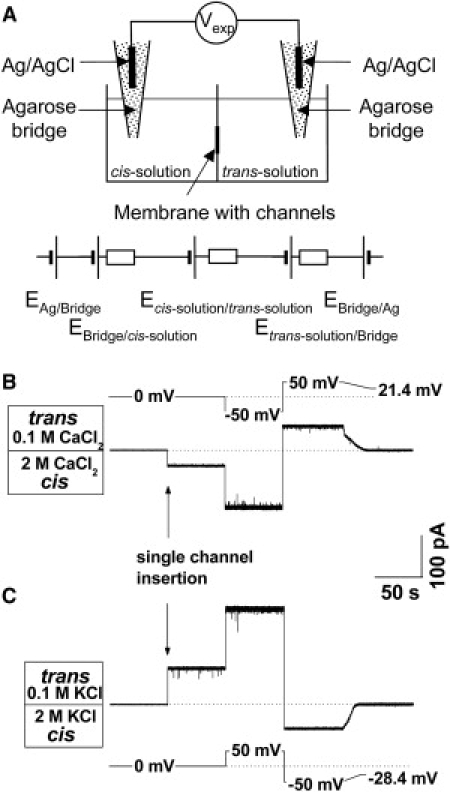
(A) Schematic illustration of the electric elements contributing to the measured potential V_exp (after Finkelstein and Mauro (25)). The goal is to measure zero-current potential between the cis and trans solutions of the cell. At equal concentrations and same salt types in the bridges, the electrochemical potentials E_Ag/Bridge and E_Bridge/Ag compensate each other because they are equal in modulus and opposite in sign. These are equilibrium silver/silver chloride electrode potentials. Potentials between the agarose bridges are nonequilibrium and stem from the differences in diffusion coefficients of the involved ionic species and can be estimated from Henderson's equation (50). Depending on experimental conditions, they can be either of the same or opposite sign (see Appendix). The internal resistances of the elements representing contacts between silver/silver chloride electrodes and solutions in bridges are not shown, as they are much smaller than all other resistances in the system. Current traces of spontaneous channel insertion at 20-fold gradients of CaCl₂ (B) and KCl (C). The potentials that should be applied to zero currents in the two cases are of opposite signs.

Results and Discussion

Measuring OmpF selectivity inversion

One of the unexpected results of this study is OmpF selectivity inversion in concentrated solutions of salts of divalent cations. Fig. 1 demonstrates typical current traces of spontaneous channel insertion at 20-fold gradients of a divalent salt (2.0 M CaCl₂ from the cis side and 0.1 M CaCl₂ from the trans side, Fig. 1 B) and a monovalent salt (2.0 M KCl from the cis side and 0.1 M KCl from the trans side, Fig. 1 C). It is seen that channel insertion results in a finite current jump even at zero applied potential and that the directions of the currents for these two salts are opposite. Correspondingly, potentials that are necessary to apply to zero currents in the two cases are of opposite signs, namely V_0Exp = −28.4 mV for KCl and V_0Exp = +21.4 mV for CaCl₂.

These experimentally found potentials contain significant corrections arising from liquid junctions between the agarose-filled parts of the electrodes (see Materials and Methods) and the electrolyte solutions they are in contact with (Fig. 1 A). The origin of LJPs is related to the difference in cation and anion concentrations and mobilities both in solutions of the membrane cell and in solutions in the agarose-filled parts of the electrodes (23–25). Because concentrations of the solutions in the opposite halves of the cell are not the same, these potentials are not equal to each other. Indeed, as Table 3 demonstrates, these potentials depend not only on salt concentrations in the cell but also on salt concentration in the agarose-filled parts of the electrodes. For this reason, in the case of an asymmetric system LJPs do not compensate for each other. To obtain a true reversal potential which relates to the physical parameters of the system under study, but not to the details of the measuring procedure (such as type and concentration of salts in the bridges), LJPs should be accounted for. Because the direct measurement of these potentials is problematic (23,26), we use Henderson's equation for their calculation (Appendix).

Table 3.

Measurements of reversal potential in OmpF channel using Ag/AgCl electrodes with different KCl concentrations in salt bridges

	KCl salt concentration in bridges (M)	V0Exp (mV)	LJPcis (mV)	LJPtrans (mV)	LJP (mV)	RP (mV)
3.0/0.1 M KCl	2.0	−26.9 ± 2.3	−0.18	−1.34	−1.52	−25.4 ± 2.3
	0.1	−26.5 ± 2.1	−1.52	0	−1.52	−25.0 ± 2.1
	0.01	−26.0 ± 1.6	−2.55	1.03	−1.52	−24.5 ± 1.6
3.0/0.1 M NaCl	2.0	−22.6 ± 0.7	−5.56	−0.74	−6.30	−16.3 ± 0.7
	0.1	−28.7 ± 0.5	−17.82	4.39	−13.43	−15.3 ± 0.5
	0.01	−32.2 ± 0.9	−29.52	12.73	−16.79	−15.4 ± 0.9
2.0/0.1 M NaCl	2.0	−22.1 ± 0.4	−4.39	−0.74	−5.13	−17.0 ± 0.4
	0.1	−27.0 ± 0.1	−15.88	4.39	−11.50	−15.5 ± 0.1
	0.01	−30.8 ± 0.3	−27.41	12.73	−14.68	−16.1 ± 0.3
1.0/0.1 M NaCl	2.0	−23.7 ± 0.2	−2.68	−0.74	−3.42	−20.3 ± 0.2
	0.1	−28.1 ± 0.4	−12.73	4.39	−8.34	−19.8 ± 0.4
	0.01	−31.1 ± 0.8	−23.83	12.73	−11.10	−20.0 ± 0.8
2.0/0.1 M CaCl2	2.0	21.4 ± 0.8	−11.29	0.91	−10.38	31.8 ± 0.8
	0.1	8.0 ± 0.4	−32.31	11.29	−21.01	29.0 ± 0.4
	0.01	4.6 ± 1.5	−51.78	26.79	−24.99	29.6 ± 1.5
2.0/0.1 M MgCl2	2.0	21.8 ± 1.0	−12.35	1.06	−11.28	33.1 ± 1.0
	0.1	12.3 ± 0.7	−35.58	12.35	−23.24	35.5 ± 0.7
	0.01	7.0 ± 0.2	−57.24	29.46	−27.78	34.8 ± 0.2

V_0Exp is the potential V_Exp corresponding to zero current through the circuit shown in Fig. 1A. Liquid junction potential LJP^cis is a potential between the agarose bridge of the cis electrode and the solution in cis compartment. LJP^trans is defined as a potential between the solution in the trans compartment and the agarose bridge of the trans electrode, so that it should be added to its cis counterpart to obtain the total correction. The total correction then should be subtracted from V_0Exp to calculate the reversal potential.

Reversal potentials are calculated from the experimentally found potentials V_0Exp, corresponding to zero current in the circuit shown in Fig. 1 A. The results of the measurements, examples of which are given in Fig. 1, B and C, and Table 3, are presented in Fig. 2. The data for KCl are in good agreement with all data reported earlier in the literature at the same conditions (11,15,16,27–29). However, this is not the case for the reversal potentials in NaCl or CaCl₂ solutions where one can find a great dispersion in the reported values and corresponding interpretations (11,27–31). This dispersion is sometimes attributed to the variability in the parameters of the OmpF channels used in the reconstitution experiments, but such a conjecture is barely convincing. Indeed, channels do show persistent variability of their properties (32). However, it is not clear why the same reasons would not affect KCl data to a similar extend as for the other electrolytes. Thus, we can conclude that something not present in KCl experiments is probably misleading in experiments with other salts. This motivated us to closely inspect the measuring procedure of reversal potential (Appendix).

Figure 2.

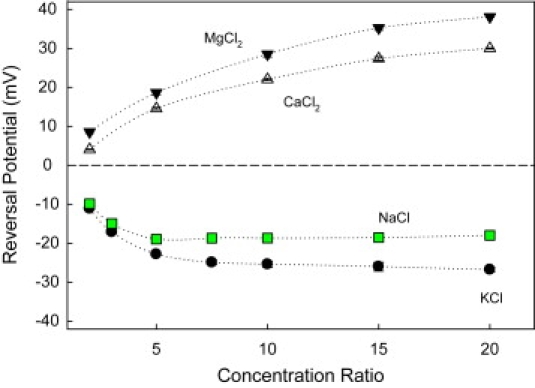
OmpF channel reversal potential measured in monovalent (KCl, NaCl) and divalent salts (CaCl₂, MgCl₂) at pH 6. Salt concentration is 0.1 M on the trans side, and concentration on the cis side varies up to a 20-fold concentration ratio. Error bars are smaller than the symbol size. Each point was measured for at least three different channels in three different experiments.

The reversal potentials in Fig. 2 are measured at pH 6. It is seen that in 1-1 salts, the channel favors the passage of cations (negative reversal potentials), whereas in 2-1 salts it is more permeable to anions (positive reversal potentials). Indeed, standard calculations of permeability ratios according to the GHK equation indicate that OmpF is moderately cation selective for KCl ($P_{{\mathrm{K}}^{+}}/P_{\text{Cl}-}=2.9$ at C_cis = 2 M and C_trans = 0.1 M) but displays an anionic selectivity of divalent cations ($P_{{\text{Mg}}^{2+}}/P_{\text{Cl}-}=0.1$ at C_cis = 2 M and C_trans = 0.1 M). Therefore, if the electrostatic exclusion due to the charges on the OmpF molecule is considered the only possible source of ion selectivity, this would lead to the conclusion that the effective negative channel charge acting on monovalent cations (11,16) is transformed into a positive charge acting now on divalent cations. Clearly, additional effects contributing to the overall selectivity must be present.

Different sources of ion selectivity

To clarify the many sources of ion selectivity and the role of diffusion, we can consider Planck's expression for the potential difference across a constrained liquid junction for a z₊:z₋ binary electrolyte, so that diffusion potential scales with the logarithm of the concentration ratio:

$$\Delta {\varphi }_{\text{diff}}\equiv {\varphi }_{\mathit{cis}}-{\varphi }_{\mathit{trans}}=\left(\frac{k_{\mathrm{B}}T}{e}\right)\frac{D_{-}-D_{+}}{z_{+}{D}_{+}-z_{-}{D}_{-}}\ln \frac{C_{\mathit{cis}}}{C_{\mathit{trans}}},$$ (1)

where k_B and T have their usual meaning of the Boltzmann constant and absolute temperature, respectively, and e is the elementary charge. D_i denote the ionic diffusion coefficients. By means of Eq. 1, we can calculate the bulk diffusion potential for any electrolyte involved in our study at every concentration ratio. This provides an alternative representation of Fig. 2 by plotting reversal potential data against their respective bulk diffusion potentials. The plots for 2-1 salts shown in Fig. 3 display a clear correlation between measured reversal potential and calculated bulk diffusion potential. This agreement, not found in the case of 1-1 salts, suggests that the measured potential for salts of divalent cations is mostly due to the different mobilities of anions and cations.

Figure 3.

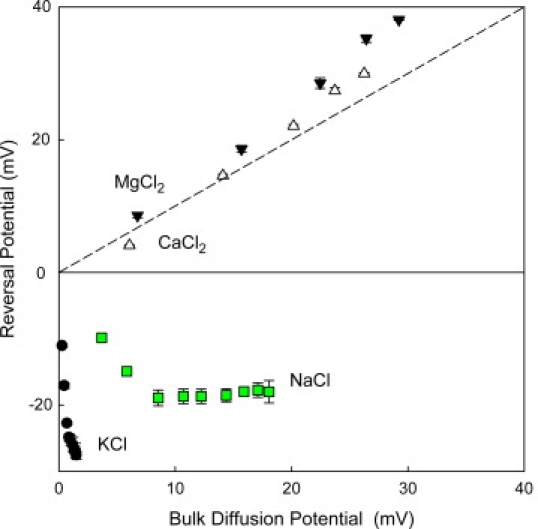
Reversal potential as a function of bulk diffusion potential expected for different salts at their concentration gradients varied up to a 20-fold ratio (Fig. 2). Bulk diffusion potential is calculated for each pair of concentrations of every salt according to Planck's equation (see main text).

To understand why 1-1 salts and 2-1 salts behave differently, we will concentrate now on two alkaline chlorides (KCl and NaCl), where electrostatic exclusion must be identical and only diffusional effects are expected to be different. In cation-selective channels like OmpF, the contribution of electrostatic exclusion to reversal potential is a potential that is more negative on the high concentration side. However, for salts of anions with higher mobility than the cation, the diffusion potential is more positive on the highly concentrated side. Thus, in KCl, NaCl, LiCl, and other chloride salts of cations with larger hydrated radii, the two contributions (electrostatic exclusion and diffusion) have opposite signs. In KCl, the diffusion potential is very small, but in other salts like NaCl it may be significant. Fig. 4 shows the reversal potential measured in OmpF at pH 6 for an increasing concentration ratio of KCl (solid circles) and NaCl (solid squares). From the reversal potential in Fig. 4, one could think that the channel prefers potassium ions over sodium ions. However, the difference between the reversal potentials in KCl and NaCl scales rather well with the logarithm of the concentration ratio. This fact suggests that if it were not for the differences in the diffusivities of potassium and sodium, the channel would be equally selective to both salts. In other words, the difference in the reversal potentials would be just the difference in the diffusion potential of NaCl and KCl, which can be calculated as follows:

$$\Delta {\varphi }_{\text{diff}}^{\text{NaCl}}-\Delta {\varphi }_{\text{diff}}^{\text{KCl}}=\left(\frac{k_{\mathrm{B}}T}{e}\right)\left[\frac{D_{\text{Cl}}-D_{\text{Na}}}{D_{\text{Na}}+D_{\text{Cl}}}-\frac{D_{\text{Cl}}-D_{\mathrm{K}}}{D_{\mathrm{K}}+D_{\text{Cl}}}\right]\ln \frac{C_{\mathit{cis}}}{C_{\mathit{trans}}}\text{.}$$ (2)

Figure 4.

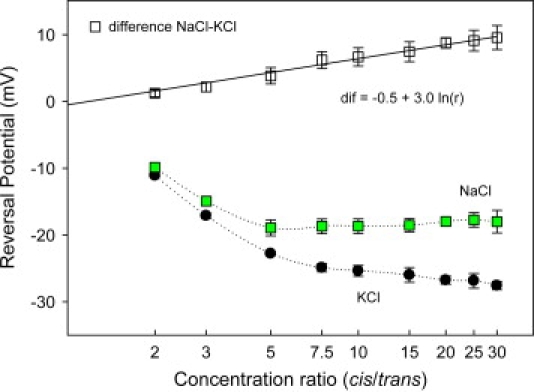
Reversal potential as a function of the cis/trans concentration ratio for KCl (circles) and NaCl (solid squares) at pH 6. Solution concentration on the trans side was fixed at 0.1 M, whereas the concentration on the cis side was increased from 0.1 M to 3 M. Membranes were formed from DPhPC. The difference between the values of reversal potential in NaCl and KCl solutions (open squares) scales with the natural logarithm of the concentration ratio (r = 0.99).

The slope of the regression line in Fig. 4 is 3.0, the value that indeed differs from 4.8, which is the slope predicted by Eq. 2 using infinite dilution bulk diffusion coefficients. This difference is expected because of the several factors (such as hydrodynamic hindrance, ion-residue interactions, and ion-ion correlations) that surely change diffusion coefficients in the pore and also because in the general case diffusion potentials are not additive components of reversal potentials (11). Nevertheless, this result illustrates the importance of different bulk diffusivities of ions in OmpF selectivity.

Specific binding of divalent cations

Previous studies demonstrated that the OmpF charge is largely regulated by the solution pH (11,16). Continuum electrostatic calculations show that lowering pH decreases the overall negative charge of the channel and eventually changes its sign (11,29). To check how reversal potential depends on the magnitude of the channel negative charge, we performed measurements over a broad range of pH in 10-fold concentration gradient (0.1 M cis | 1 M trans). From Fig. 5 we see that the reversal potential in 2-1 salts is less sensitive to channel residue ionization than it is in KCl, implying that the overall charge felt by permeating ions in the presence of high concentrations of CaCl₂ and MgCl₂ is virtually the same within the pH 4–10 range.

Figure 5.

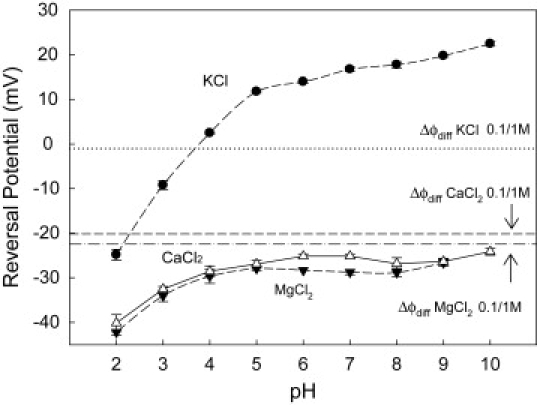
Reversal potential measured in salts of monovalent and divalent cations at the inverted (0.1 M cis | 1 M trans) gradient at different pH. The corresponding bulk diffusion potentials for this gradient are also shown. Over a broad range of pH, the reversal potential in 2-1 salts is only weakly sensitive to channel residue ionization. This contrasts with the known titration behavior of OmpF in monovalent salts where increasing proton concentration beyond pH 4 results in the inversion of both reversal potential and the channel effective charge (11,16,29).

Fig. 5 also compares the results for 1-1 and 2-1 salts with their bulk diffusion potentials calculated using Eq. 1 and shown by the horizontal dashed lines. This comparison clearly demonstrates that in the case of KCl, diffusional effects are not relevant and the electrostatic exclusion dominates the channel cation selectivity. Conversely, both 2-1 salts display anionic selectivities that are comparable but larger than their respective bulk diffusion potentials. This points to a binding of divalent cations to channel residues, which screens and might even overcharge the “initial” negative charge of the channel. Binding divalent cations also interfere with the proton titration of the channel acidic residues, explaining why the reversal potential in 2-1 salts is only weakly sensitive to pH. This conjecture has been supported by the crystallographic structure of OmpF in MgCl₂ presented recently by Cramer and collaborators (33), who found a binding site for magnesium cations located in the narrow constriction of the channel.

Similar selectivity inversion was also found for high concentrations of other divalent salts with the results shown on the right-hand side of Fig. 6. Again, it is interesting to note that the reversal potential measured in these solutions correlates well with their bulk diffusion potentials calculated using Eq. 1. This indicates that under the conditions studied, all four divalent cations screen the channel negative charges in a very similar way, so that the differences in the reversal potentials are coming from the differences in their mobilities.

Figure 6.

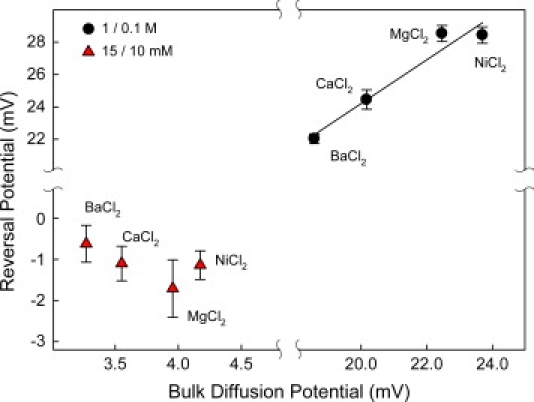
(Right) Reversal potential measured in salts of divalent cations at high concentrations (1.0 M cis | 0.1 M trans) displays correlation between the reversal potential and the corresponding bulk diffusion potentials for the 1.0|0.1 gradient. Although binding properties of these four divalent cations are very different in other systems (neutral lipid bilayers, for instance), here the reversal potential seems to be sensitive only to cation diffusivity. (Left) At small concentrations of divalent cations (15 mM cis | 10 mM trans), the channel regains its cationic selectivity. Correlation between reversal potential and bulk diffusion potential is lost. Both sets of measurements are performed at pH 6.

Remarkably, at small concentrations of divalent salts, the channel regains its cationic selectivity and the correlation with the diffusion potential is lost (left-hand side of Fig. 6). This is exactly what one would expect for the charge-screening mechanism. Concentrations of divalent cations that are too small do not lead to efficient screening, so that the overall charge of the channel stays at its net-negative value as in the presence of 1-1 salts. This leads to the expected cationic selectivity and probably restores the specificity in the binding of divalent cations.

Fig. 7 A shows the reversal potential at a 10-fold cis/trans concentration ratio but different absolute concentrations of KCl (circles) and CaCl₂ (triangles). In both electrolytes, reversal potential depends not only on the concentration ratio but also on absolute concentration following, apparently, a similar trend. Note, however, that cationic selectivity found for KCl increases as concentration decreases, whereas anionic selectivity found in CaCl₂ follows the opposite behavior. This is more clearly seen in Fig. 7 B, where reversal potential data are presented in terms of permeability ratios. The data for KCl can be easily understood in terms of electrostatic exclusion. As the concentration increases, the screening of channel fixed charges is more effective and selectivity decreases. CaCl₂ data are clearly incompatible with such a mechanism. Increasing concentration produces a gain of anionic selectivity, pointing again to the proposed binding of divalent cations that screen the negative charge of the channel. In such a picture, when concentration decreases, the binding becomes less probable so that in the low concentration limit we find values of reversal potential below the calculated diffusion potential for a concentration ratio r = 10.

Figure 7.

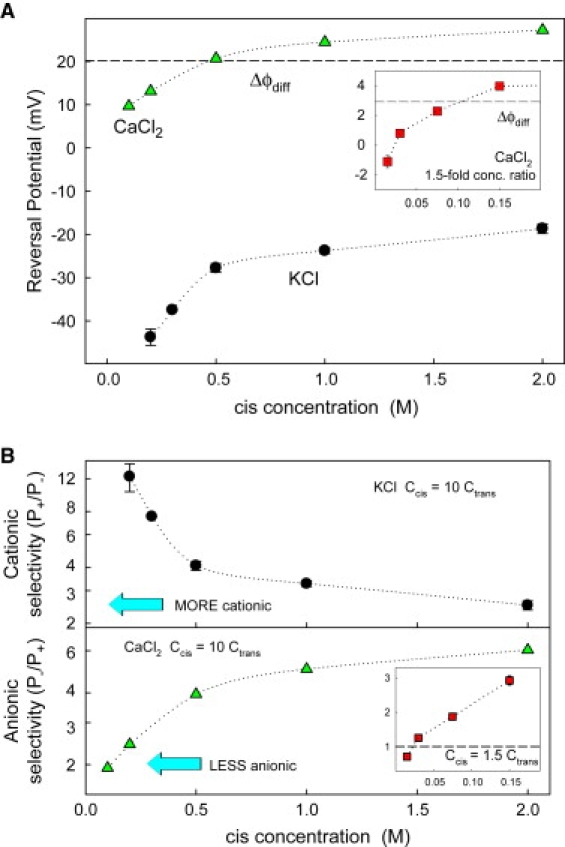
(A) Reversal potential measured at a 10-fold cis/trans concentration ratio but different absolute concentrations of KCl (circles) and CaCl₂ (triangles) at pH 6. In KCl the channel shows cationic selectivity that is enhanced at low concentrations. In CaCl₂ the channel does not increase its anionic selectivity at low concentrations but becomes less selective to anions. At low enough CaCl₂ concentrations (see insets that show measurements at 1.5-fold cis/trans concentration ratio), OmpF seems to recover its “normal” negative fixed charge since the reversal potential is lower in magnitude than the free solution diffusion potential and, for the smallest concentrations, the selectivity gets cationic again. (B) Selectivity of the channel, calculated from data in (A).

This means that the concentration is not high enough to ensure the binding of divalent cations and the consequent screening of the channel negative charges. This is especially true in the less concentrated compartment, where we can speculate that the channel charge is not completely neutralized and some negative groups are still active. If this is true, a reversal potential below the diffusion potential is expected as exclusion effects appear. This point becomes clearer when the concentration ratio is kept small, r = 1.5, and both sides can be at a relatively low concentration (Fig. 7, A and B, inset). Then, negative values of reversal potential are found, showing that there is no binding, and the channel restores its original cation selectivity. Note that this situation is never realized in Figs. 2 and 5, as the “diluted” side is always kept at 0.1 M. The inset in Fig. 7 B also demonstrates that possible electrokinetic effects (34) are not among the major causes of selectivity inversion. It is seen that decreasing the salt gradient by a factor of 7 does not lead to any qualitative changes in channel selectivity.

The elucidation of the residues that are responsible for the binding of divalent cations and consequent selectivity inversion is not straightforward in light of electrophysiological measurements. Mutagenesis involves conformational changes that further modify the total net charge of the protein. Thus, the rationalization of selectivity experiments with mutants is far from being trivial. Table 1 is a good example of this. Reversal potential measurements in a 10-fold concentration gradient of CaCl₂ (1 M cis | 0.1 M trans) are presented for WT OmpF and three of its mutants: Two single-site mutants, D113A and E117A, and a double-site mutant, D113C/E117C. The substitution of negatively charged acids of the channel constriction by neutral residues like alanine and cysteine (where divalent cations do not bind) yields a gain of anionic selectivity. This could be roughly explained by invoking the change in the net charge of the protein produced by mutagenesis: Compared to WT OmpF, the mutants D113A and E117A have an extra positive charge and the D113C/E117C mutant has two extra positive charges. However, in such a scenario, the role of the divalent binding is unclear. A much more detailed study involving up to 34 OmpF mutants in salts of divalent cations reached similar conclusions (31): Charge is not the sole determinant of the ion selectivity of OmpF mutants: Other parameters also contribute to this property. Thus, mutations in this system involve simultaneous changes of too many physical quantities (net charge, spatial distribution of residues, the possibility of binding, the available volume for permeating ions, etc.) to give a quantitative interpretation of measured data.

Table 1.

Measurements of reversal potential at pH 6 in 1 M cis | 0.1 M trans CaCl₂ using WT and several OmpF mutants

	WT	D113A	E117A	D113C/E117C
RP (mV)	24.5 ± 0.6	33.2 ± 2.2	30.8 ± 1.5	30.1 ± 0.7

In this context, a recent publication of W. Cramer's group is highly relevant. A 1.6 Å OmpF structure in 1 M MgCl₂ showed that one Mg²⁺ is bound in the selectivity filter between Asp-113 and Glu-117 of loop 3 (33). In light of this study, we decided to investigate, at least qualitatively, the source of observed anionic selectivity of the D113C/E117C mutant, where the specific binding of the divalent cations should be absent. To this end, reversal potential experiments at a 10-fold cis/trans concentration ratio but different absolute concentrations of CaCl₂ were performed for both the WT OmpF and D113C/E117C mutant (data shown in Table 2).

Table 2.

Reversal potential (mV) measured at pH 6 and 10-fold cis/trans concentration ratio but different absolute concentrations of CaCl₂ using WT and the double OmpF mutant D113C/E117C

cis/trans concentration (M)	WT	D113C/E117C
0.2/0.02	13.1 ± 1.5	37.9 ± 2.2
0.5/0.05	20.7 ± 0.9	30.7 ± 2.2
1.0/0.1	24.5 ± 0.6	30.1 ± 0.7
2.0/0.2	27.3 ± 1.2	25.1 ± 0.5

The anionic selectivity found for the D113C/E117C mutant increases as concentration decreases, whereas the anionic selectivity of WT OmpF follows the opposite behavior, as shown in Fig. 7, A and B. As may be expected after the analysis of the 1.6 Å OmpF structure, this indicates that Ca²⁺-specific binding is not present in the case of the D113C/E117C mutant, since the increase of CaCl₂ concentration leads to a loss of anionic selectivity. Then the source of anionic selectivity in the D113C/E117C mutant may be the excess of positive charge in the channel constriction after the neutralization of both Asp-113 and Glu-117 acids. Consequently, the trend found for the D113C/E117C mutant qualitatively resembles the trend found for WT OmpF in KCl, which easily rationalizes invoking electrostatic screening. As concentration increases, the screening of channel fixed charges is more effective and selectivity decreases.

Interestingly, Fig. 7 also demonstrates that steric (or entropic) effects are not dominant in selectivity inversion. Indeed, one of the possible alternative explanations of anionic selectivity of OmpF in CaCl₂ may be preferential exclusion of cation simply because the size of the Ca²⁺-hydrated ion is larger than that of Cl⁻. For KCl, diluting the salt only increases channel cationic selectivity. For CaCl₂, the channel anionic selectivity is decreased as the concentration is lowered. Furthermore, at very low salt concentration, the channel becomes cation selective. As noted before, it is natural to expect this result within the proposed binding of divalent cations: Less CaCl₂ means less Ca²⁺ binding, smaller screening, and, therefore, lower anionic selectivity.

With steric exclusion stemming from the larger ion size of Ca²⁺, one would expect an opposite behavior. Indeed, if anionic selectivity was due not to electrostatic—as we hypothesized above—but to steric exclusion, then the selectivity should be more pronounced at smaller salt concentrations. This is clear from the following argument. Let us calculate the electrical energy of a concentration fluctuation as a function of its size assuming that cations and anions confined by a cube with sides l behave as independent particles with switched-off Coulombic interactions. Then the expected root mean-square fluctuation of the particle number is simply ${\left(n{l}^3\right)}^{1/2}$, where n is particle concentration. The resulting potential can be roughly estimated as$\varphi \sim e{\left(n{l}^3\right)}^{1/2}/\varepsilon l$, where ɛ is the dielectric constant of the medium. Therefore, the energy of such fluctuation is$E\sim \varphi e{\left(n{l}^3\right)}^{1/2}\sim e^{2}n{l}^2/\varepsilon$. The characteristic energy E is proportional to the square of the linear dimension and is commeasurable with k_BT at room temperature for dimensions close to the Debye screening length. This simple estimate demonstrates that on length scales larger than the screening length, any deviations in cationic concentration and anionic concentrations should be strongly correlated by obeying the electroneutrality principle. Therefore, because the Debye screening length increases with the decreasing salt concentration, the compensation of steric exclusion of Ca²⁺ ions by the forces maintaining electroneutrality should be smaller. This would lead to higher anionic selectivity at smaller CaCl₂ concentration.

From Figs. 3 and 5, it follows that anionic selectivity of the OmpF channel in the presence of high concentrations of calcium and magnesium chlorides exceeds the selectivity expected from the difference in bulk solution diffusion coefficients for the cations and anion. One of the possible interpretations of this observation would be that divalent ions actually overscreen the negative charge of the channel introducing charge inversion. As evidenced by a recent stream of publications in the leading physics journals (e.g., (35–44)), inversion of the charge of charged surfaces by multivalent counterions is quite a general phenomenon attracting the attention of many researchers from different fields. Among the objects studied are nanochannels (37,43,45), amine-terminated silicon dioxide surfaces (36), anionic monolayers (42), DNA coils (46), actin filaments (47), protein complexes (41), asymmetric lipid bilayers (48), and charged colloidal particles (39). Charge inversion has been observed by studying electrokinetic phenomena (electrophoresis or streaming current), colloid stability, phase separation, or resonant x-ray scattering, or by measuring the attraction force between like-charged surfaces.

Several origins are proposed for the charge inversion in electrolyte solutions (40). Apart from the specific interaction between divalent cations and particular surfaces, alternative theories considering counterion correlations are available (35,44). However, the applicability of such physical theories of charge inversion near charged interfaces in electrolytic solutions to the findings reported here is problematic for several reasons. First, the interface in the case of the OmpF channel is an amphoteric surface, with a discrete, highly inhomogeneous distribution of positive and negative charges. Second, and most important, the effective surface charge density in the pore is only ∼0.1 e/nm² (29). This low charge density poses an immediate problem for the explanation based on a two-dimensional strongly correlated liquid of counterions (35,49) because the inverse dimensionless temperature of such a liquid for the divalent counterions can be estimated as 1.1.

Conclusions

Though most of the experimental conditions of this study diverge significantly from typical physiological conditions, investigations of ion channels in the wide range of salt concentrations and large gradients and in the presence of diverse electrolytes advance our understanding of the physics of ion transport. The obtained results show that several physicochemical phenomena are crucially involved in the mechanism of ion selectivity of large channels. An immediate consequence is that the interpretation of the measured reversal potential—the most popular parameter used to evaluate selectivity—in the framework of models that are too simplistic can lead to a distorted picture. We can also conclude that the selectivity mechanisms of the mesoscopic systems, which in this study are represented by the OmpF channel, are qualitatively different from those of the highly selective channels of neurophysiology (1).

We summarize our main findings as follows:

• 1.Contrary to the cationic selectivity for the monovalent salts at neutral pH, the OmpF channel at high concentrations of salts of divalent cations exhibits an anionic selectivity. Specifically, the sign of reversal potential for chloride salts of Ca²⁺, Mg²⁺, Ba²⁺, and Ni²⁺ is opposite to that found for monovalent salts.
• 2.Two major factors contribute to the selectivity inversion in this large channel in salts of divalent cations: 1), the binding of permeant ions to the channel, which compensates, or slightly overcompensates, for the negative charge of the OmpF molecule and 2), the anionic selectivity coming from the differences in ion mobilities.
• 3.Other possible factors such as steric depletion of ions, occurring when their size is comparable to the size of the pore, channel-specific changes in hydrodynamic hindrance for cations and anions, and electrokinetic effects induced by the salt gradient appear to play only a minor role in the studied cases.
• 4.At sufficiently small concentrations of chloride salts of divalent cations, the channel regains its “original” cationic selectivity.
• 5.Selectivity measurements in the D113/E117C OmpF mutant are consistent with the existence of a binding site for divalent cations at the channel constriction, as recently evidenced by the high resolution OmpF crystal structure in MgCl₂ solution.

Appendix: Correction of the Measured Zero Current Potential by Liquid Junction Potentials

Though the LJP corrections are routinely used in modern electrophysiology, they are ignored often enough to deserve a revision of the current situation in this short Appendix. Electrophysiological measurements are mostly done with reversible Ag/AgCl electrodes, which in many cases are immersed in salt bridges of a certain concentration. When measuring electric potential differences between two solutions of different concentration (as is the case of reversal potential), one cannot ignore that each bridge is in contact with a different solution. The potential difference generated across each bridge/solution interface, known as LJP, is different, so that the total contribution of both LJP to the total measured potential is different from zero. Seminal studies by Barry and Neher (24,26) indicate that LJP is small (∼1 mV) in the reversal potential experiments done with KCl involving KCl bridges. That is why these corrections are usually bypassed when measurements are performed at physiological conditions (moderate gradients of KCl solutions at decimolar concentrations buffered at neutral pH, occasionally also containing salts of divalent cations in micromolar or millimolar concentrations). However, in experiments with other salts (NaCl, LiCl, CaCl₂, MgCl₂, etc.) LJP contribution becomes significant and may be comparable to the actual reversal potential. The situation is aggravated when electrode salt bridges are diluted, sometimes to prevent contamination of the measuring solutions. LJP can then be several times larger than the actual RP. This fact has long been noted (23) but repeatedly ignored, thus leading to some inconsistencies in the selectivity data.

Direct measurements of LJP are difficult (23,26), so that, to determine the actual reversal potential, it is necessary to rely on LJP theoretical estimates. LJP between two solutions—left (L) and right (R)—is defined as

$$\text{LJP}\equiv {\varphi }_{\mathrm{L}}-{\varphi }_{\mathrm{R}}=-\frac{k_{\mathrm{B}}T}{e}\sum _i\underset{R}{\overset{L}{\int }}\frac{t_i}{z_i}d\ln a_i,$$ (A1)

where t_i, z_i, and a_i denote the transport number (or fractional conductance), valence, and activity of the ith ion, correspondingly. The above definition is not very practical and has been replaced by an approximation due to Henderson (50,51), which makes LJP computation straightforward. Henderson simplified the problem in two ways. First, he treated the electrolyte solutions as ideal (i.e., constant mobilities are assigned and activities are replaced by concentrations). Second, he assumed that the junction may be represented by a continuous series of mixtures of the two end solutions (i.e., linear ion concentration profiles). Thus, Eq. A1 reduces to

$$\text{LJP}=-\left(\frac{k_{\mathrm{B}}T}{e}\right)\frac{\sum _i{z}_i{D}_i\left[C_{i,\mathrm{L}}-C_{i,\mathrm{R}}\right]}{\sum _i{z}_i^2{D}_i\left[C_{i,\mathrm{L}}-C_{i,\mathrm{R}}\right]}\ln \frac{\sum _i{z}_i^2{D}_i{C}_{i,\mathrm{L}}}{\sum _i{z}_i^2{D}_i{C}_{i,\mathrm{R}}}\text{.}$$ (A2)

Most authors resort to the calculation of LJP using Henderson's equation. As for the assumption of linear concentration profiles, it has been shown recently that calculation of LJP from numerical solutions of Nernst-Planck and Poisson equations yields identical results as Henderson's equation in the vast majority of cases of interest (52). However, when solutions cannot be regarded as ideal or the ionic strength of the two solutions in contact is very different, Henderson's equation becomes a poor approximation, and then LJP calculations demand a proper estimation of ionic activity coefficients and ion mobilities as a function of concentration (53,54).

An indirect way of checking the validity of the LJP calculation from Henderson's equation is to measure the reversal potential of a channel in a given pair of solutions but using a different salt bridge concentration in each series of experiments. If the LJP estimation is good, the channel reversal potential, once corrected, should be the same irrespective of the salt concentration in the bridge. Table 3 shows the zero current potential measured in OmpF in different salt solutions. Cis and trans bridges contained equal KCl concentrations varying from 2 M to 0.01 M. One can see that LJP contribution may be significant, particularly when salts of divalent cations are used, and it changes with the KCl bridge concentration. However, in all cases the actual reversal potential is the same within experimental error no matter what salt bridge concentration is used.

Interestingly, when the same species of electrolyte is used in the solutions and in the electrode salt bridge and the salt concentrations in the trans and cis bridges are equal, according to Henderson's equation, the total LJP should be the same irrespective of the salt concentration in the bridge. A simple inspection of Eq. A2 applied to each interface shows that if the ratios of the anion/cation diffusivities are the same in the solutions and in the bridges, the salt concentrations in both bridges enter only as their ratio:

$$\text{LJP}={\text{LJP}}_{\mathit{cis}}+{\text{LJP}}_{\mathit{trans}}=\left(\frac{k_{\mathrm{B}}T}{e}\right)\frac{D_{-}-D_{+}}{z_{+}{D}_{+}-z_{-}{D}_{-}}\ln \frac{C_{\mathit{trans}}{C}_{\mathit{cis}}^{\text{bridge}}}{C_{\mathit{cis}}{C}_{\mathit{trans}}^{\text{bridge}}}\text{.}$$ (A3)

Data in Table 3 for 3.0/0.1 M KCl solutions and Table 4 for 3.0/0.1 M NaCl solutions are compatible with this statement. This result is perhaps the origin of most mistakes concerning LJP corrections to the measured reversal potential. Following the pioneer studies (24,26) performed under physiological conditions and with KCl bridges, the protocol is sometimes erroneously extended to altogether different conditions. Data in Table 4 also show that in different pairs of NaCl solutions and NaCl bridges, the LJP is not dependent on the salt bridge concentration. In this case, the LJP correction is much bigger than for KCl. Finally, one can compare the corrected RP for 3.0/0.1 M NaCl solutions when using KCl bridges (rows 4–6 in Table 3) and using NaCl bridges (Table 4). The agreement shows that for the salt gradients explored here, Henderson's equation is a good approximation for estimating LJP contribution.

Table 4.

Measurements of reversal potential in the OmpF channel using Ag/AgCl electrodes with different NaCl concentrations in salt bridges

	NaCl salt concentration in bridges (M)	V0Exp (mV)	LJPcis (mV)	LJPtrans (mV)	LJP (mV)	RP (mV)
3.0/0.1 M NaCl	2.0	−32.5 ± 1.0	−2.16	−15.93	−18.08	−14.4 ± 1.0
	0.1	−33.4 ± 1.5	−18.08	0	−18.08	−15.3 ± 1.5
	0.01	−32.8 ± 1.4	−30.33	12.24	−18.08	−14.7 ± 1.4