Equilibrium Unfolding Thermodynamics of β₂-Microglobulin Analyzed through Native-State H/D Exchange

Abstract

The exchange rates for the amide hydrogens of β₂-microglobulin, the protein responsible for dialysis-related amyloidosis, were measured under native conditions at different temperatures ranging from 301 to 315 K. The pattern of protection factors within different regions of the protein correlates well with the hydrogen-bonding pattern of the deposited structures. Analysis of the exchange rates indicates the presence of mixed EX1- and EX2-limit mechanisms. The measured parameters are consistent with a two-process model in which two competing pathways, i.e., global unfolding in the core region and partial openings of the native state, determine the observed exchange rates. These findings are analyzed with respect to the amyloidogenic properties of the protein.

Introduction

Amide hydrogen exchange is to date one of the most powerful techniques used to gain insight into macromolecule dynamics and thermodynamics (1–3). In general, under the so-called EX2 limit, exchange experiments carried out under native conditions permit the measurement of the equilibrium concentrations of protein conformations with the lowest free-energy levels. These conformations include not only the native state, but also partially or substantially unfolded forms that exist at very low concentrations. Thus, the definition of the protein energetic landscape is even more essential for those proteins whose unfolded forms have a functional or a dysfunctional role. This may be the case with amyloidogenic proteins, whose fibril-competent species are usually other than the native state. According to the simplest reasonable mechanism, unfolding of amyloidogenic proteins leads to the exposure of sticky assembly-prone regions that result in fibril extension even under mild conditions. One of these proteins is β₂-microglobulin (β₂m), whose deposition in amyloid plaques is responsible for dialysis-related amyloidosis (DRA), which occurs in patients subjected to long-term hemodialysis (4). Its native fold consists of seven β-strands organized into two β-sheets linked by a single disulphide bridge between positions 25 and 80 to form the classical β-sandwich motif (Fig. 1).

Figure 1.

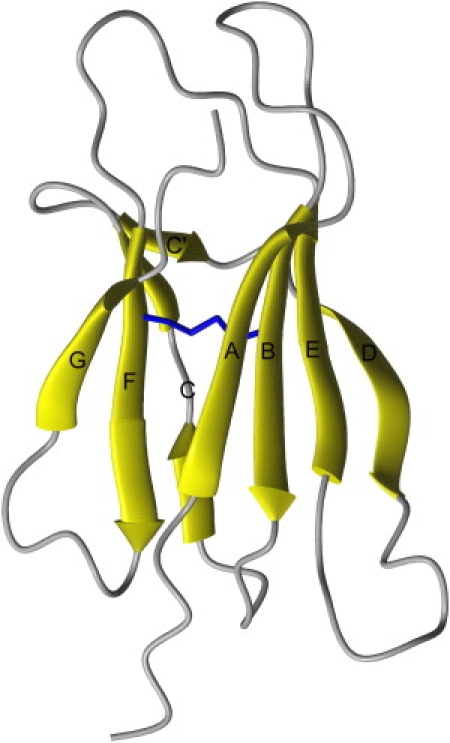
MOLMOL (49) ribbon representation of β₂m solution structure (first model of PDB 1JNJ (42)). The two residues involved in the disulphide bridge are shown as sticks.

The basic theory of hydrogen exchange chemistry in proteins was developed in Linderstrom-Lang's laboratory (5). The general pathway of the chemical reactions governing amide hydrogen exchange is

$$\mathrm{N}\leftrightarrows \mathrm{O}\to {\mathrm{O}}^{\ast },$$ (1)

where N is the exchange-incompetent native state, O stands for a whatever exchange-competent open state, and the asterisk indicates that deuterium has been incorporated into the exchanging position. For each amide hydrogen, the observed rate of isotope exchange is given by

$$k_{\text{obs}}=\frac{k_{\text{op}}\times k_{\text{rc}}}{k_{\text{op}}+k_{\text{cl}}+k_{\text{rc}}},$$ (2)

where k_op and k_cl are the rates for the opening and closure reactions governing the equilibrium between the N and O species, and k_rc is the corresponding intrinsic (random coil) hydrogen exchange rate that applies to the exchange-competent state O. The values of k_rc are known, since they have been accurately redetermined in short unstructured peptides (6).

Depending on the value of the different rate constants, two limiting regimes can be achieved, either with a double (EX2) or with a single (EX1) rate-determining step (5), whereby Eq. 2 becomes

$$k_{\text{obs}}^{\text{EX}2}=\frac{k_{\text{op}}\times k_{\text{rc}}}{k_{\text{cl}}}\text{for}{k}_{\text{op}},k_{\text{rc}}<<k_{\text{cl}},$$ (3)

or

$$k_{\text{obs}}^{EX1}=k_{\text{op}}\text{for}{k}_{\text{op}},k_{\text{cl}}<<k_{\text{rc}}.$$ (4)

Most commonly, exchange in proteins occurs through an EX2 limit, although EX1 has been observed also (7–9). The EX1 limit generally holds under conditions in which the denatured state is the most populated exchange-competent state and the rate of refolding is much lower than the rate of exchange from the denatured state. In this case, the exchange rates of different hydrogens are correlated, since the limiting step is the unfolding reaction. However, we cannot exclude the possibility that uncorrelated EX1 exchange, arising from local opening reactions, occurs above pH 9 toward alkaline denaturation (7).

We present here the results obtained for β₂m. Through native-state H/D exchange, we determined the contributions of EX1 and EX2 regimes to the observed exchange rates. In addition, we found 1), a significantly limited occurrence of local opening processes in the inner core of the protein, especially in proximity to the disulphide bridge; 2), a fast exchange in the edge strand, D, that undergoes local opening processes; and 3), residual structure in the unfolded state close to the disulphide bridge.

Materials and Methods

Proteins

Expression and purification of β₂m was carried out as previously reported (10) by ASLA Biotech (Riga, Latvia), with additional ¹⁵N uniform labeling. A methionine residue was always present at the N-terminal position of all recombinant products. All the recombinant proteins gave a single species when assayed by electrospray-ionization mass spectrometry.

H/D exchange measured by NMR

Hydrogen-deuterium exchange experiments were acquired at various temperatures, ranging from 301 to 315 K. At each temperature, the time dependence of the amide hydrogen signals was followed by monitoring the volume changes in a time series of ¹⁵N-¹H single quantum correlation experiments (11). Samples were prepared with the lyophilized protein dissolved in D₂O buffer containing 70 mM phosphate and 100 mM NaCl, to reach protein concentrations of ∼0.5 mM. The apparent pH measured after dissolving the protein was 6.6. Data acquisition started ∼10 min after dissolution and kept going for 30–96 h, depending on the temperature used. For each heteronuclear single quantum correlation experiment, 50 increments were acquired in the indirect dimension and 2048 points in the direct dimension; nitrogen decoupling was achieved by the use of a GARP train (12), whereas the echo-antiecho scheme was employed for sign discrimination with respect to the nitrogen carrier frequency (13). For some temperatures, we used an ERETIC signal (14,15) that was set to occur at the carrier frequency in F1 and at 11 ppm in F2. The ERETIC signal was to ensure an internal amplitude reference against possible scaling artifacts introduced by the processing and/or analysis softwares. The experiments were acquired and processed with Topspin (Bruker BioSpin, Karlsruhe, Germany). In F1, the original data set was extended by linear prediction (50 points) and zero-filled to 256 points; then a Lorentz-to-Gauss function was employed, with exponential and Gaussian broadening factors of 1 and 0.2 Hz, respectively. In F2, a squared sinebell function with a shift of π/2.2 was employed, before zero-filling to 2048 points. Following 2D Fourier transform, a fifth-order polynomial baseline correction was applied. Processed spectra were imported in Felix2K (Accelrys, San Diego, CA) for subsequent analysis to evaluate peak integrals.

Data analysis

Residue-specific values of k_rc were calculated using the spreadsheet available on the Web (6,16). Fitting the time dependence of the integrals gave exponential decays, in which the constant of decay is the observed exchange rate, k_obs (Table S1 in Supplementary Material). In general, no peaks with >20% overlap were considered, except that from Phe-70. The Phe-70 HN-N resonance overlap with the corresponding Lys-91 connectivity was ignored, because the fast exchange of the latter leaves the Phe-70 signal free of extra contribution and suitable for the fit after the initial phase of the decay.

The values of observed exchange rates obtained at 10 different temperatures within the range 310–315 K were converted into −[ln$(k_{\text{obs}}^i/T)$ and $\left[R\times T\times \text{ln}\left(k_{\text{rc}}^i/k_{\text{obs}}^i\right)\right]$. A subset of 17 amide hydrogens without any significant peak overlap, whose exchange could be measured at more than six temperatures, and for which the $\left[R\times T\times \text{ln}\left(k_{\text{rc}}^i/k_{\text{obs}}^i\right)\right]$ values versus temperature exhibit a square correlation coefficient >0.9 is referred to as the “most precise subset” of data. All the details concerning statistical analysis and errors are reported in the Supplementary Material.

Results and Discussion

Partial openings and global unfolding: EX1 and EX2 contributions

Equation 2, in the Introduction, is derived for a hypothetical system with a single opening process. However, in protein exchange, several different opening reactions are possible, ranging from local single-residue or multiple-residue-correlated fluctuations to cooperative global or subglobal unfolding processes. According to one of the simplest models, the two-process model (17), the following structural openings can occur from the native state:

• 1.Global unfolding, which is expected to promote the exchange of all hydrogens and has a marked thermal dependence.
• 2.Partial openings, ranging from local fluctuations to subglobal unfoldings. Under typical experimental conditions, the rates for the closure reactions are fast enough to achieve the EX2 limit regime. Local fluctuations are noncooperative openings leading to the exposure of individual amide hydrogens, with little entropy variation; different models of the structural nature of local fluctuations have been proposed, such as diffusion of water molecules in the protein matrix (17) or distortional motions leading to NH exposure (18). Subglobal openings are cooperative events leading to the exposure of a group of amide hydrogens simultaneously, with a significant entropy variation (19).

All amide protons that are significantly exposed and exchange rapidly without the need of any structural opening are not considered here.

The possible opening pathways are summarized in the following scheme:

$$N\iff \left[\begin{array}{c}P\to P\ast \\ D\to D\ast \end{array}\right],$$ (5)

where P and D are, respectively, the partially opened and globally unfolded exchange-competent species.

In principle, if only one opening reaction were present, it would be possible to determine whether a set of amide hydrogens exchanges under the EX1 or EX2 mechanism. In fact, Eqs. 3 and 4 show how a plot of k_obs against k_rc would be linear for hydrogens exchanging in the EX2 limit but would show no correlation in the EX1 limit. However, in our case, more than one opening reaction is involved, and the behavior of k_obs versus k_rc depends also on the specific probability of each opening reaction. According to the two-process model (17,20–22), the observed rate of exchange for a residue i can be written as

$$k_{obs}^i=\frac{k_{\text{ND}}\times k_{\text{rc}}^i}{k_{\text{DN}}+k_{\text{rc}}^i}+\frac{k_{\text{NP}}\times k_{\text{rc}}^i}{k_{\text{PN}}},$$ (6)

assuming that $k_{\text{NP}}^i$ << $k_{\text{PN}}^i$, $k_{\text{ND}}$ << $k_{\text{DN}}$, and $k_{\text{PN}}^i$ >> $k_{\text{rc}}^i$. The first two assumptions are implied by the higher stability of the native state in comparison to the open states. The rationale behind the third assumption is that relaxation to the native state from a partially open conformation should be very fast, because only a single residue or at most small regions of the protein are involved. The first and second terms of Eq. 6 represent the contributions to the exchange process of global unfolding and partial opening, respectively.

Introducing the term Aⁱ as the ratio $(k_{\text{NP}}^i\times k_{\text{DN}})/(k_{\text{PN}}^i\times k_{\text{ND}}),$ Eq. 6 becomes

$$k_{\text{obs}}^i=\frac{k_{\text{ND}}\times k_{\text{rc}}^i}{k_{\text{DN}}+k_{\text{rc}}^i}+\frac{A^i\times k_{\text{ND}}\times k_{\text{rc}}^i}{k_{\text{DN}}}.$$ (7)

The Aⁱ parameters encode the contribution of partial openings to the exchange, i.e., the relative concentration of each partially open conformation with respect to the globally unfolded species. The partial opening events, represented by the second term in the equation, contribute to the exchange only if Aⁱ is not zero. This condition is broken, in fact, in the presence of a global unfolding process that overrides local fluctuations and subglobal processes, and highlights an established hierarchical distance between classes of local and global opening events (21). Since for β₂m (23)—and for proteins with similar unfolding ΔG—the rate of relaxation to the native state from the globally unfolded state is on the order of the experimental $k_{\text{rc}}^i$ values, we expect that at high values of the intrinsic constant, the contribution of global unfolding to the exchange process will approach the EX1 limit. This means that beyond a threshold value of the intrinsic exchange rate, the contribution of the first term on the right-hand side of Eq. 7 should become almost constant, and should be dominant when Aⁱ ∼ 0 at the same time. Indeed, Fig. 2 a shows that among the most precise data subsets (see Materials and Methods), the amide hydrogens of Cys-25, Arg-81, Tyr-26, Asn-24, Asn-83, and Ser-28 (pink squares), characterized by the highest $k_{\text{rc}}^i$ values, exhibit almost constant values of $k_{\text{obs}}^i$, independent of $k_{\text{rc}}^i$. This group of amides will be henceforth referred to as EX1-like hydrogens. These residues belong to the disulphide-linked strands, in the most stable region of the protein, and therefore partial opening processes should be irrelevant. Thus, $k_{\text{obs}}^i$ is determined only by the first term of Eq. 7, because the opening event hierarchy imposes a globally driven process, i.e., Aⁱ ∼ 0. The lower points in the $k_{\text{obs}}^i$ versus $k_{\text{rc}}^i$ plot describe the theoretical curve in the absence of partial-opening contributions (Fig. 2 a, inset). A rough fit of these data (Leu-40, Asp-38, Val-82, Arg-81, and Cys-25) with the theoretical curve would give $k_{\text{DN}}$ = 2.9 s⁻¹ and $k_{\text{ND}}$ = 4.9 × 10⁻⁴ s⁻¹, i.e., a value of 5.4 kcal/mol for the ΔG of unfolding, in reasonable agreement with previously reported experimental values (23,24).

Figure 2.

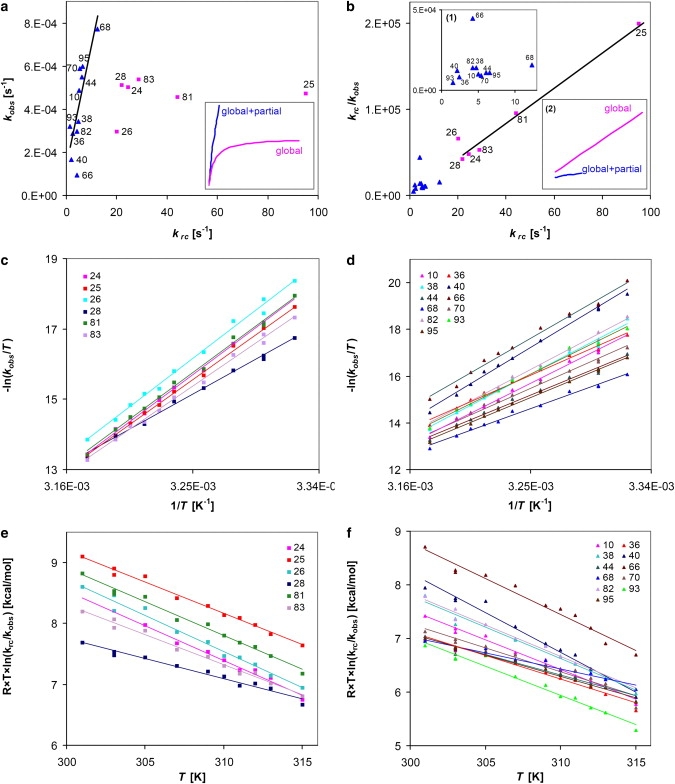
EX1- and EX2-limit contributions to the measured parameters. (a) Plot of the observed versus the unstructured values of exchange rates at 315 K; data for EX2-like hydrogens have a Pearson product-moment correlation coefficient of 0.80 and a Spearman rank order correlation of 0.86. (Inset) Expected trends for globally-driven and two-process-driven exchange. Analogous patterns were observed using lower-temperature data. (b) Plot of k_rc/k_obs versus k_rc at 315 K. (Inset 1) Magnification of EX2-like hydrogen dat., (Inset 2) Expected trends for globally-driven and two-process-driven exchange. (c and d) Plot of −ln(k_obs/T) values versus 1/T for EX1- and EX2-like hydrogens, respectively. (e and f) Plots of $\left[R\times T\times \text{ln}\left(k_{\text{rc}}^i/k_{\text{obs}}^i\right)\right]$ values versus T for EX1- and EX2-like hydrogens, respectively.

Conversely, the other data points in Fig. 2 a (blue triangles) show a linear correlation between $k_{\text{obs}}^i$ and $k_{\text{rc}}^i$. A linear behavior is well explained by Eq. 7 only if the set of exchanging protons has similar values of Aⁱ in the partial-opening term and $k_{\text{rc}}^i$ linearity in the global-unfolding term. This is expected to be the case when, besides a global opening process, much larger or comparable contributions from partial openings exist that depend on the same opening event, or on a few events with similar kinetic or thermodynamic parameters. Since the linearity in $k_{\text{rc}}^i$ is the hallmark of the EX2 regime (Eq. 3), by analogy to the two-process-driven exchange described by Eq. 7, the group of amides exhibiting a linear $k_{\text{obs}}^i$ versus $k_{\text{rc}}^i$ plot will be referred to as EX2-like hydrogens.

From the above considerations, we conclude that partial openings appear to be less effective for those amide hydrogens close to the disulphide bridge, most of which are in fact EX1-like hydrogens.

Similar insights come also from recasting Eq. 7 as

$$\frac{k_{\text{rc}}^i}{k_{\text{obs}}^i}=\frac{k_{\text{DN}}\times \left(k_{\text{DN}}+k_{\text{rc}}^i\right)}{\left(1+A^i\right)\times k_{\text{DN}}\times k_{\text{ND}}+A^i\times k_{\text{ND}}\times k_{\text{rc}}^i}.$$ (8)

The quantity described by Eq. 8 is the familiar protection factor commonly used to compare the so normalized exchange rates when the EX2 limit is dominant. Only when exchange proceeds under a pure EX2 limit with respect to any process involved, i.e., when $k_{\text{rc}}^i$ << $k_{\text{DN}}$, and

$$\frac{k_{\text{rc}}^i}{k_{\text{obs}}^i}=\frac{k_{\text{DN}}}{\left(1+A^i\right)\times k_{\text{ND}}},$$ (9)

will there be no correlation between $k_{\text{rc}}^i/k_{\text{obs}}^i$ and $k_{\text{rc}}^i$.

Under a pure EX1 limit for exchange under global unfolding $(k_{\text{rc}}^i>>k_{\text{DN}}),$ Eq. 8 becomes

$$\frac{k_{\text{rc}}^i}{k_{\text{obs}}^i}=\frac{k_{\text{DN}}\times k_{\text{rc}}^i}{k_{\text{DN}}\times k_{\text{ND}}+A^i\times k_{\text{ND}}\times k_{\text{rc}}^i}.$$ (10)

If Aⁱ ∼ 0, i.e., there is no contribution from partial-opening processes, a linear correlation will be observed with slope equal to the reciprocal of the opening rate and zero intercept. Instead, if partial openings contribute to the observed exchange rates, the values of $k_{\text{rc}}^i/k_{\text{obs}}^i$ will reach an asymptotic value of k_DN/(Aⁱ × k_ND) as $k_{\text{rc}}^i$ increases. The result of this analysis (Fig. 2 b) highlights the high values of $k_{\text{rc}}^i/k_{\text{obs}}^i$ for the amide hydrogen of residues Tyr-66 and Tyr-26 that reflect a persistent protection in exchange-competent states. Thus, a nucleus of residual structure involves the two β-strands B and E paired in proximity to the cysteine at position 25.

The distinction within our data between EX1- and EX2-like hydrogens is confirmed by the examination of the thermal behavior expressed by −$\left[\text{ln}\left(k_{\text{obs}}^i/T\right)\right]$ and $\left[R\times T\times \text{ln}\left(k_{\text{rc}}^i/k_{\text{obs}}^i\right)\right]$ values (Fig. 2, c–f). The former quantity, under a pure EX1 limit and no contribution from partial openings, gives indications about the activation parameters for the global unfolding reaction, since Eq. 4 can be combined with reaction-rate theories (25–27) to give

$$-\text{ln}\left(\frac{k_{\text{obs}}^i}{T}\right)=-\text{ln}\left(\frac{k_{\text{ND}}}{T}\right)=-\text{ln}\left(\frac{\nu }{T}\right)-\frac{\Delta S_{\text{ND}}^{‡}}{R}+\frac{\Delta H_{\text{ND}}^{‡}}{R\times T},$$ (11)

where $\Delta H_{\text{ND}}^{‡}$ and $\Delta S_{\text{ND}}^{‡}$ are the activation enthalpy and entropy for the unfolding process, and ν is a prefactor that could be alternatively expressed according to gas-phase transition-state theory (25,26) or condensed-phase Kramers' theory (27). Fig. 2 c shows that EX1-like hydrogens converge toward similar values at 315 K, with the exception of Tyr-26 because of the presence of the above-mentioned residual structure in the unfolded state. The convergence observed in Fig. 2 c as the temperature is raised suggests a progressive thermal approach to general EX1 limit conditions, i.e., correlated exchange. Instead, as expected, EX2-like amides conserve a relative dispersion of $k_{\text{obs}}^i$ values in the whole thermal range (Fig. 2 d), reflecting a lack of correlation in partial opening processes.

Also, the trends of the $\left[R\times T\times \text{ln}\left(k_{\text{rc}}^i/k_{\text{obs}}^i\right)\right]$ values can provide suggestive insights. Equation 9 applies under EX2-limiting conditions, and thus,

$$R\times T\times \text{ln}\left(\frac{k_{\text{rc}}^i}{k_{\text{obs}}^i}\right)=R\times T\times \text{ln}\left[\frac{k_{\text{DN}}}{(1+A^i)\times k_{\text{ND}}}\right]=-R\times T\times \text{ln}\left(e^{(G_D-G_N)/R\times T}+e^{(G_P-G_N)/R\times T}\right)=\Delta G_{EX2}.$$ (12)

Equation 12 is the basis for two-process models (17) and the so-called thermodynamic hierarchy (21). In fact, since partial openings and global unfolding have different entropies, the driving process for the chemical exchange of a hydrogen depends on temperature. As a general rule, the wider the opening reaction, the higher the thermal dependence of its free-energy change for commonly observed protein thermodynamic parameters. It is possible to define, for each hydrogen i, a value $T_c^i$ corresponding to the temperature of convergence between ΔG for a partial opening process and ΔG for the observed global unfolding, i.e., when Aⁱ = 1. According to temperature conditions, we make the following observations.

• 1.
  When T << $T_c^i$, partial opening is most likely achieved and the exchange is locally driven:

  $$\Delta G_{\text{EX}2}=G_P-G_N=\Delta G_{\text{op}}^{\text{partial}}.$$ (13)
• 2.
  For T ≈ $T_c^i$, both partial and global unfolding pathways drive the exchange reactions, because the free energy losses upon partial opening or global unfolding are comparable. In particular, when T = $T_c^i$:

  $$\Delta G_{\text{EX}2}=G_D-G_N-R\times T\times \text{ln}2.$$ (14)
• 3.
  At T >> $T_c^i$, global unfolding has the lowest free-energy change:

  $$\Delta G_{\text{EX}2}=G_D-G_N=\Delta G_{\text{op}}^{\text{global}}.$$ (15)

Taking Eqs. 13–15 into consideration, it is interesting to note the converging trend of the $\left[R\times T\times \text{ln}\left(k_{\text{rc}}^i/k_{\text{obs}}^i\right)\right]$ values at 312–315 K (Fig. 2 f). This convergence leads to almost equal values of $\left[R\times T\times \text{ln}\left(k_{\text{rc}}^i/k_{\text{obs}}^i\right)\right]$ at high temperatures, in agreement with a transition from partial-opening- to global-unfolding-driven exchange that occurs close to the range of the experimental temperatures. A rough fit of the $\left[R\times T\times \text{ln}\left(k_{\text{rc}}^i/k_{\text{obs}}^i\right)\right]$ values at 312–315 K for the converging amide hydrogens of Tyr-10, Glu-36, Asp-38, Leu-40, Glu-44, Thr-68, Phe-70, Val-82, and Trp-95 gives enthalpy and entropy values of ∼49 kcal/mol and ∼140 cal/(K × mol), in agreement with reported thermodynamic values for global unfolding (28).

It is also interesting to note the almost coincident values of $\left[R\times T\times \text{ln}\left(k_{\text{rc}}^i/k_{\text{obs}}^i\right)\right]$ over the whole thermal range for the three amides of Glu-36, Glu-44, and Trp-95 and the two amides of Asp-38 and Val-82, which could point out the occurrence of correlated subglobal opening events before reaching the convergence in correspondence of the globally-driven unfolding.

Exceptions to the general converging trend in Fig. 2 f are the Tyr-66 and Val-93 amide protons. Although the $\left[R\times T\times \text{ln}\left(k_{\text{rc}}^i/k_{\text{obs}}^i\right)\right]$ values for these two residues are very different, it is intriguing that the two protons are both involved in hydrogen bonds to the cysteine residue joining positions 25 and 80. In agreement with the previous considerations made in Fig. 2 b, the high values of $\left[R\times T\times \text{ln}\left(k_{\text{rc}}^i/k_{\text{obs}}^i\right)\right]$ for Tyr-66 are consistent with the presence of residual structure in the globally unfolded state. The low values of $\left[R\times T\times \text{ln}\left(k_{\text{rc}}^i/k_{\text{obs}}^i\right)\right]$ for Val-93 are probably due to its having a higher occurrence of partial opening processes compared to the other core protons considered in Fig. 2 f. In the graph in Fig. 2 f, we also note the slight divergence of Thr-68 $\left[R\times T\times \text{ln}\left(k_{\text{rc}}^i/k_{\text{obs}}^i\right)\right]$ values, which at high temperatures overcome the $\left[R\times T\times \text{ln}\left(k_{\text{rc}}^i/k_{\text{obs}}^i\right)\right]$ values of all the other converging amides. This is consistent with Thr-68 exhibiting the highest $k_{\text{rc}}^i$ values among the set of converging residues, i.e., higher deviations from the ideal EX2 limits for the global process.

Lack of convergence of exchange data appears to be the rule in Fig. 2 e, where nearly parallel curves are observed for the $\left[R\times T\times \text{ln}\left(k_{\text{rc}}^i/k_{\text{obs}}^i\right)\right]$ values of EX1-like hydrogens. This trend appears to be in contrast with the pattern that the same hydrogens exhibit in Fig. 2 c, but it is just the effect of the function actually plotted that, according to Eq. 12, highlights the EX2 process, by definition simply missing in EX1-like hydrogens.

Enthalpy-entropy compensation for exchange free energies

Since possible errors arise because of deviations from the EX2 limit, the $\left[R\times T\times \text{ln}\left(k_{\text{rc}}^i/k_{\text{obs}}^i\right)\right]$ values of EX2-like hydrogens will be referred to as $\Delta G_{\text{obs}}^i$. These quantities, formally corresponding to protection-factor-related ΔG values, do not necessarily represent real free-energy differences between distinct states of the system, but rather indicative parameters from the exchange observables.

For all EX2-like hydrogens, the plot of $\Delta H_{\text{obs}}^i$ against $\Delta S_{\text{obs}}^i$ values gives a nearly perfect correlation (data not shown). This kind of enthalpy-entropy compensation in protein exchange thermodynamics has been previously reported by other groups (29,30). In theory, in the EX2 limit, a perfect linear correlation between $\Delta H_{\text{obs}}^i$ and $\Delta S_{\text{obs}}^i$ would mean that $\Delta G_{\text{obs}}^i$ curves of each residue are concurrent lines to the common point of coordinates (m,q):

$$\Delta H_{\text{obs}}^i=m\times \Delta S_{\text{obs}}^i+q,$$ (16)

$$\Delta G_{\text{obs}}^i\left(T\right)=\Delta H_{\text{obs}}^i-T\times \Delta S_{\text{obs}}^i=\left(m-T\right)\times \Delta S_{\text{obs}}^i+q,$$ (17)

$$\Delta G_{\text{obs}}^i(T=m)=q.$$ (18)

Thus, the enthalpy-entropy correlation suggests that the opening free energies converge at a single common temperature. The limiting values of the convergence temperature and free-energy difference are equal, respectively, to the slope and the intercept of the $\Delta H_{\text{obs}}^i$ versus $\Delta S_{\text{obs}}^i$ regression equations.

There is debate in the literature as to whether enthalpy-entropy compensation is just an experimental artifact, due to the restricted accessible ΔG(T) windows, or a characteristic signature of the thermodynamics of macromolecules in water solutions (31–40). There is no doubt that a kind of compensation for the folding/unfolding processes is consistent with the view that the transition from the unfolded state to the native state is accompanied by a large restriction in the conformational freedom, i.e., by a large unfavorable $-T\times \Delta S$ term. Since denaturation ΔG values are small, to accommodate the unique functional flexibility of proteins, the $-T\times \Delta S$ term must be almost completely (up to the resulting ΔG) compensated for by a favorable ΔH. This ensures the convergence of denaturation free energies of proteins to the typical small values within the limited interval of biologically relevant temperatures.

However, the compensation presented here goes beyond the trivial compensation depicted above and does not regard a single unfolding process but the $\Delta G_{\text{obs}}^i$ values that, according to Eq. 12, are the combinations of two opening processes. Indeed, a compensation of this kind—if any—could hide possible clues about the enthalpy-entropy relationships in partial and global opening processes. Given this possibility, it is important to assess the statistical validity of the enthalpy-entropy compensation and to exclude the possibility that the observed correlation is fully artifactual. By retaining only the most precise data subset showing EX2-like behavior (see Materials and Methods), the best linear regression of $\Delta H_{\text{obs}}^i$ and $\Delta S_{\text{obs}}^i$ gives (Fig. 3)

$$\Delta H_{\text{obs}}^i=\left(317\pm 4\text{K}\right)\times \Delta S_{\text{obs}}^i+\left(5.8\pm 0.4\text{kcal}/\text{mol}\right).$$ (19)

According to Krug et al. (33), the robustness of the enthalpy-entropy compensation can be proved by the regression analysis of enthalpy versus free energy evaluated at the harmonic mean of the experimental temperatures (307 K). A plot of this kind for our data shows that the ΔG_obs values at 307 K for EX2-like hydrogens have a satisfactory linear correlation with the corresponding ΔH_obs values (Fig. 3, inset 1), excluding the outliers Tyr-66 and Val-93 (Supplementary Material).

Figure 3.

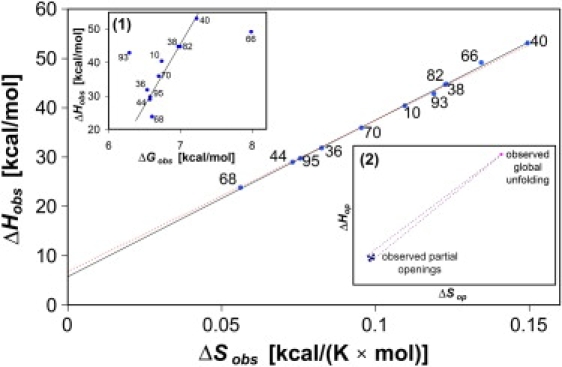
Plot of the observed enthalpy of opening against the observed entropy of opening; (solid line) linear fit of experimental values; (dashed line) expected random linear fit. (Inset 1) Plot of the observed enthalpy of opening against the observed free energy of opening at 307 K; (solid line) linear fit of experimental values, except outlier data of Val-93 and Tyr-66, with a Pearson product-moment correlation coefficient of 0.94 and a Spearman rank order correlation of 0.83. The slope of the solid line is significantly different from the random value of 1 (P = 2.3 × 10⁻⁴, according to Student's t-test) (33). (Inset 2) Hypothetical distribution of enthalpy and entropy values for different kinds of opening reactions.

Parametric and nonparametric statistical tests were performed on these data, and the relative outcomes are reported in the Supplementary Material. The accurate statistical analysis does not challenge the occurrence of an enthalpy-entropy compensation in the data for EX2-like hydrogens, which is also evident in the observed convergence of the $\left[R\times T\times \text{ln}\left(k_{\text{rc}}^i/k_{\text{obs}}^i\right)\right]$ values within similar temperatures (Fig. 2 f). This inference is quite valuable, since it points out that the transition from partial-opening-driven exchange to global-unfolding-driven exchange (Eqs. 13–15 and Appendix) occurs within a limited range of temperatures for the considered residues. In other words, the coordinated convergence of observed free energies takes place because the $T_c^i$ values are similar. This is especially true for all the considered EX2-like hydrogens, except Tyr-66 and Val-93. In fact, Tyr-66 and Val-93 are not converging at all and were considered as outliers in the above analysis.

As defined above, the $T_c^i$ value for the proton i represents the temperature of convergence between the ΔG values of two opening processes, a partial opening involving proton i and the global unfolding. Using the reverse of the procedure adopted for Eqs. 16–18, we can write

$$\Delta G_{\text{op}}^{\text{global}}(T=T_c^i)=\Delta G_{\text{op}}^{\text{partial}}(T=T_c^i);$$ (20)

$$\Delta H_{\text{op}}^{\text{global}}-T_c^i\times \Delta S_{\text{op}}^{\text{global}}=\Delta H_{\text{op}}^{\text{partial}}-T_c^i\times \Delta S_{\text{op}}^{\text{partial}};$$ (21)

$$T_c^i=\frac{\Delta H_{\text{op}}^{\text{global}}-\Delta H_{\text{op}}^{\text{partial}}}{\Delta S_{\text{op}}^{\text{global}}-\Delta S_{\text{op}}^{\text{partial}}}.$$ (22)

The last equation shows that $T_c^i$ can also be defined as the slope of the straight line connecting the coordinates of the partial opening with those of the global unfolding in an enthalpy-entropy plot for the opening processes (Fig. 3, inset 2). This kind of plot regards the opening processes, and so should not be confused with the entropy-enthalpy plot for the exchange process, reported in the body of Fig. 3. In the entropy-enthalpy plot for opening processes, the limiting values of the convergence temperature and free-energy difference for the two opening processes are equal to the slope and the intercept of ΔH_op versus ΔS_op regression, respectively. It follows that the similarity of the $T_c^i$ values for some protons of the core could be explained by a model in which the opening enthalpy and entropy values are very similar for the partial openings (Fig. 3, inset 2). The coordinates of the points $[\Delta S_{\text{op}}^{\text{partial}},\Delta H_{\text{op}}^{\text{partial}}]$, for partial openings around these hydrogens should cluster in a limited region of the whole ΔH_op(ΔS_op) plot; thus, the slopes of the lines connecting global- to partial-opening points, i.e., $T_c^i$ values, would be very similar (Fig. 3, inset 2).

A related interesting observation is that the values of global unfolding free energy are not zero at $T_c^i$ (Fig. 3). A convergence value of zero would be found if, on a per-residue basis, enthalpy and entropy values for opening were equally balanced between global unfolding and partial openings. Evidently, partial openings are characterized by a reduced entropic gain over enthalpic penalty when compared with global unfolding, and so are more difficult to achieve on a per-residue basis.

H/D exchange compared to structural properties of β₂m

On the basis of previous results that showed a temperature-dependent formation of fibrils on poly-L-lysine-coated mica, it could be proposed that a structural transition of β₂-microglobulin, occurring in the presence of temperature alterations in the physiological range, is correlated with enhanced amyloidogenic potential (41). The data presented here do not show any thermal discontinuity in the exchange rates or free energies, which suggests that the effect of temperature on amyloid, if any, is to increase the concentration of unfolded species, which can exploit the enhanced diffusion and the decrease in kinetic barriers to trigger nucleation.

For all β₂m slow-exchanging amide protons, we can find the H-bonded partner in the NMR structure (42) or in the x-ray structure (43–45) of the isolated protein. The protection pattern is shown in Fig. 4, and the hydrogen bonds involved are listed in Table 1. Two slow-exchanging amide hydrogens, namely those of His-84 and Leu-39, form hydrogen bonds with water molecules in the x-ray structure (Fig. 5). In particular, the water bound to the amide proton of His-84 is also held by the hydrogen bonds to the carbonyl oxygens of His-84 and Leu-87, and to the side chain of Asn-83. The water bound to the amide proton of Leu-39 is held even more tightly by the hydrogen bonds to the carbonyl oxygen of Ile-46, the carboxylic oxygen of Asp-38, and the hydroxyl group of Tyr-66. In solution, the Leu-39 amide hydrogen is detectable even at 315 K, whereas the His-84 amide hydrogen is visible only below 303 K.

Figure 4.

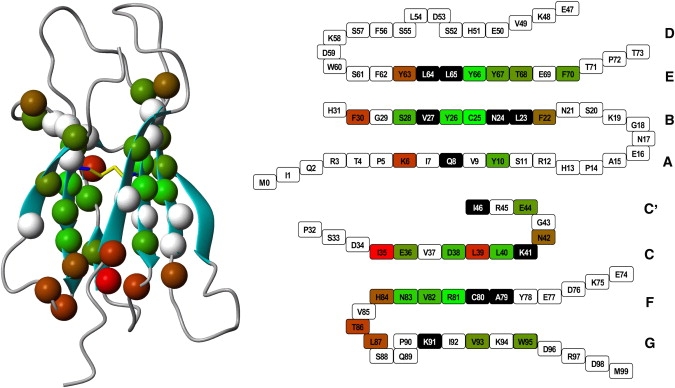
Amide hydrogens observed in this study in the MOLMOL (49) ribbon representation of β₂m (first model of PDB 1JNJ (42)) (left) and in a schematic representation of the secondary structure (right). The color scale is related to log₁₀(k_rc/k_obs) values at 301 K, where red and green indicate fast and slow exchangers, respectively. Residues in white on the left picture and in black on the right picture have an overlap of >20% with other peaks.

Table 1.

H-bonds involving the observed hydrogens in x-ray and NMR structures

Donor	Acceptor		Donor	Acceptor		Donor	Acceptor
	X-ray	NMR		X-ray	NMR		X-ray	NMR
6	28	28 (20)	38	81	38sc (2)	70	21	68 (10)
8	26	26 (20)	39	water	—	79	40	40 (18)
10	24	24 (20)	40	79	79 (20)	80	93	93 (19)
22	12	21sc (12)	41	44	44 (20) 41sc (1)	81	38	38 (20)
23	68	68 (20)	42	77	42sc (9)	82	91	91 (16) 80 (1)
24	10	10 (20)	44	41	—	83	36	36 (20)
25	66	66 (18)	46	39	39 (19)	84	water	—
26	8	8 (7) 24 (10)	63	55	55 (1)	86	84Nsc	84Nsc (19) 84 (1)
27	64	64 (3)	64	27	27 (8)	87	84	84 (20)
28	6	6 (20)	65	53	52 (8)	91	82	82 (20)
30	62	28 (9) 62 (1)	66	25	25 (11)	93	80	80 (12) 91 (8)
35	—	33 (10)	67	51	50 (14)	95	78	78 (16)
36	83	83 (20)	68	23	23 (20)

The x-ray structure is from PDB file 1LDS (43), and the NMR structure is from PDB file 1JNJ (42). A hydrogen bond is considered to be formed when the distance between the proton on the donor atom and the heavy atom acceptor is <2.5 Å; in addition, the angle formed by the proton-donor atom vector with the proton-acceptor atom vector must be >120°. Where not specified, the acceptor atom is the backbone carboxylic oxygen of the residue indicated by the number; the superscript “sc” indicates that the acceptor atom belongs to the side chain of the residue. For NMR structures, the number shown in parentheses indicates the occurrences of hydrogen bonds over the 20 structures.

Figure 5.

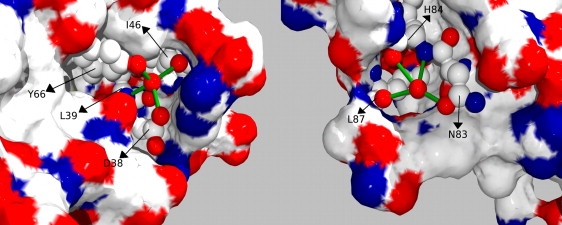
Localization of the two water molecules, bound to the amide hydrogens of Leu-39 (left) and His-84 (right). The images have been made using the PDB file 1LDS (43).

There are some exchangeable amide hydrogens, H-bonded in the NMR and/or the x-ray structure, whose exchange is not slow enough to be measured. In particular, Arg-12, Gly-18, Lys-19, Asn-21, Val-49, Glu-50, Ser-52, Ser-55, Thr-73, Asp-76, and Val-85 backbone amides donate hydrogen bonds in >60% of the conformers within the NMR structure ensemble, but do not show exchange protection. Among those hydrogen-bonded amide protons, it is not possible to decide whether Arg-12 NH has some low degree of protection because of overlap with the corresponding Asp-38 resonance. The fast exchange of these protons means that the local dynamics around those locations permit frequent contacts between the amide hydrogens and the catalyst OD⁻. This observation is rather consistent, because the majority of these amide hydrogens belong to loop regions (Gly-18, Lys-19, Asn-21, Thr-73, and Asp-76), two are located at the terminal of a strand (Arg-12 and Val-85), while the others reside on strand D (Val-49, Glu-50, Ser-52, and Ser-55).

The highly dynamic character of strand D is consistent with the poor ordering of this strand, evident by visual inspection of the NMR ensemble of structures (42). Actually, a regular strand D occurs only in the isolated β₂m crystal structure (43–45), whereas in MHC-I crystal, strand D is bisected by a bulge at residues 53 and 54 (46). The higher solvent accessibility of the isolated β₂m in comparison with the HLA complex could explain the weaker packing forces within strands D and E and the intervening DE loop (42). The dynamicity of strand D is also evident from the apparent local correlation times (45), which point out the occurrence of microsecond-to-millisecond conformational exchange phenomena.

In apparent contrast with the absence of the sheet-partner D strand in solution, the amide hydrogens of strand E, Tyr-63, Leu-65, and Tyr-67, are instead exchanging slowly enough to be measured in our experimental conditions. A possible explanation for the discrepancy between strand D and strand E exchange rates is that the amide hydrogens of strand E are efficiently buried, even though they are poorly H-bonded, and hence, their direct contacts with the solvent are less frequent. This would hold true especially for Tyr-63 and Leu-65, which show low protection factors. An alternative is that the occurrence of even a poor β-sheet H-bonding pattern for strand E may be invoked in support of a transient β-sheet conformation in solution, as proposed earlier (43). Indeed, a mechanism of transient β-strand sliding for strand D would explain the asymmetric exchange behavior for strands D and E, but also the NMR relaxation assessments that appear consistent with conformational exchange processes along fragment 53–65 of β₂m (45).

The mathematical analysis of the exchange rates and free energies for the most accurate set of data, reported in the previous paragraphs, revealed the presence of four subsets of hydrogens:

• 1.amide hydrogens with no or very few contributions from partial opening events;
• 2.amide hydrogens with significant contributions from both partial and global opening events;
• 3.amide hydrogens with very high contributions from partial opening events;
• 4.amide hydrogens with residual structure in the globally unfolded state.

The above analysis can be extended to include those hydrogens that do not belong to the most accurate set, though still discarding data with significant peak overlap. Some of these amide hydrogens have $\left[R\times T\times \text{ln}\left(k_{\text{rc}}^i/k_{\text{obs}}^i\right)\right]$ values that prove low and quite independent of temperature, suggesting the presence of very local fluctuations. The location of these additional amides in the protein structure is consistent with the last inference, since they are found at terminals of strands (Lys-6, Phe-22, Phe-30, and Ile-35), in strand E facing the labile strand D (Tyr-63 and Leu-65), and in the FG loop (Thr-86, Leu-87), or they form hydrogen bonds with water molecules in the x-ray structure (Leu-39). Another low value (5.5 kcal/mol) for $\left[R\times T\times \text{ln}\left(k_{\text{rc}}^i/k_{\text{obs}}^i\right)\right]$ is observed for Lys-91 at 315 K, the only temperature at which this cross-peak is free from overlaps. However, the exchange free energy of Lys-91 is more likely correlated, through a cooperative subglobal unfolding, with that of the neighboring Val-93, which shows a thermal dependence too high to be accounted for by only small local fluctuations. Furthermore, three hydrogens—from Leu-23, Val-27, and Ile-46—are affected by peak overlap at the same temperatures, whereas at the other temperatures they show $\left[R\times T\times \text{ln}\left(k_{\text{rc}}^i/k_{\text{obs}}^i\right)\right]$ values very similar to the set of converging hydrogens.

Additional analysis suggests that in addition to their presence near Tyr-26 and Tyr-66, residual structured regions could still be present in the observed globally unfolded state near Tyr-67 and Cys-80, not surprising for residues that are in proximity to the disulphide bridge and the aromatic cluster of strand E. Residual structure in unfolded states has also been found previously in acid-denatured β₂m, especially around the aromatic residues of the native strand E, and its presence is highly dependent upon the presence of a disulphide bridge between Cys-25 and Cys-80 (47). The presence of residual structure in unfolded states could be relevant to fibrillogenesis, since reduced β₂m, in which the intrachain disulfide bond is reduced, loses the ability to form rigid fibrils at pH 2.5 (48).

Appendix

The statistical validity of enthalpy-entropy compensation for the exchange process (Fig. 3 and Supplementary Material) is quite valuable despite possible deviations affecting the data due to simultaneous non-EX2-limit processes. To rationalize this issue, we can define Bⁱ as $k_{\text{rc}}^i/k_{\text{DN}}$ and consider how Aⁱ and Bⁱ values—parameters that express the occurrence of partial openings and the deviations from the EX2 limit for global unfolding, respectively—affect the observed exchange free energy changes. Starting from Eq. 8, the observed values of $\left[R\times T\times \text{ln}\left(k_{\text{rc}}^i/k_{\text{obs}}^i\right)\right]$ are given by

$$R\times T\times \text{ln}\left(\frac{k_{\text{rc}}^i}{k_{\text{obs}}^i}\right)=R\times T\times \left[\text{ln}\left(\frac{k_{\text{DN}}}{k_{\text{ND}}}\right)+\text{ln}\left(1+B^i\right)-\text{ln}\left(1+A^i+A^i\times B^i\right)\right].$$ (23)

The ΔG_obs values calculated for different hydrogens would be similar if the quantity

$${\Delta }^i=R\times T\times [\text{ln}(1+B^i)-\text{ln}(1+A^i+A^i\times B^i)],$$ (24)

corresponding to the differences between the observed and global unfolding ΔG values, is small or similar for all considered hydrogens. Let us first consider the case of a pure global-unfolding EX2 limit, i.e., Bⁱ = 0. Since Aⁱ values, given by

$$A^i=e^{\frac{G_D-G_P^i}{R\times T}},$$ (25)

range between 0 and 1 when the temperatures are > $T_c^i$, the corresponding Δⁱ values range between 0 and −0.4 kcal/mol. Thus, in the EX2 limit for global unfolding and at temperatures higher than any $T_c^i$ values, all observed free energy values would be similar. It follows that below the EX2 limit, the coordinated convergence of observed free energies toward globally-driven exchange would take place if the $T_c^i$ values of the involved partial openings are similar.

When the EX2 limit for global unfolding does not hold, at temperatures higher than $T_c^i$, Δⁱ falls between [ln(1 + Bⁱ) − ln(2 + Bⁱ)], for Aⁱ = 1, and [ln(1 + Bⁱ)] for Aⁱ = 0; this interval may not be sufficiently small, depending on the range of Bⁱ values. However, Δⁱ values are less sensitive to Bⁱ values when Aⁱ is around unity: the significant presence of partial openings must be invoked to explain the similarity of observed free energies. Similar to the pure EX2 limit for global unfolding, a correlated convergence between observed free energy differences can be reached provided that the involved partial openings have similar $T_c^i$ values.

Supplementary Material

Six tables are available at www.biophys.org/biophysj/supplemental/S0006-3495(08)00037-4.