Backbone Structure of Transmembrane Domain IX of the Na⁺/Proline Transporter PutP of Escherichia coli

Abstract

The backbone structure is determined by site-directed spin labeling, double electron electron resonance measurements of distances, and modeling in terms of a helix-loop-helix construct for a transmembrane domain that is supposed to line the translocation pathway in the 54.3 kDa Na⁺/proline symporter PutP of Escherichia coli. The conformational distribution of the spin labels is accounted for by a rotamer library. An ensemble of backbone models with a root mean-square deviation of less than 2 Å is obtained. These models exhibit a pronounced kink near residue T341, which is involved in substrate binding. The kink may be associated with a hinge that allows the protein to open and close an inwardly oriented cavity.

Introduction

Despite recent advances (1–3), the process of determining the three-dimensional structures of membrane proteins is still highly challenging and progress is rather slow (4). This applies in particular to integral α-helical membrane proteins with more than a few transmembrane (TM) domains that are too large for current NMR approaches and are often very difficult to crystallize. Many transporters, which are potential pharmaceutical targets, belong to this category of proteins. New techniques for their structural characterization are thus required. Site-directed spin labeling (SDSL) can complement crystallographic techniques because membrane proteins can be studied in liposomes or detergent micelles, and NMR because there is no significant limitation to the size of the protein (5). For instance, a structural model of the KcsA channel in its open state has been derived from the crystal structure of the closed state and continuous-wave electron paramagnetic resonance (EPR) measurements on spin-labeled mutants (6). By combining SDSL with pulsed EPR techniques, longer-range distances can be measured and distance distributions derived (7,8). Thus, a detailed picture of large-amplitude conformational motion in the ATP-binding cassette transporter MsbA can be obtained (9). In the lactose permease LacY, sugar-triggered conformational rearrangements on both sides of the molecule have been observed, strongly supporting the alternative access mechanism of transport (10). Furthermore, the structures of the soluble protein complex of histidine kinase CheA and its coupling protein CheW (11), and of the dimer of the Na⁺/H⁺ antiporter NhaA of Escherichia coli (12) have been determined by rigid-body refinement based on structures of the component proteins. The latter study demonstrated that the use of labels with the size of a few Ångstroms does not pose a resolution limit if the conformational distribution of the label is modeled (7,13) so that distance distributions can be fitted to the experimental data.

In this work we extend this approach to ab initio structure determination. Specifically, we work out the backbone structure of TM domain IX of the Na⁺/proline transporter PutP of E. coli by obtaining distance distribution measurements for 16 spin-labeled double mutants using the four-pulse double electron electron resonance (DEER) technique (14). PutP belongs to the sodium/solute symporter family (SSSF, TC 2.A.21, SLC5), which contains several hundred members of prokaryotic and eukaryotic origin (15). Proteins of this family utilize a sodium motive force to drive uphill transport of substrates such as sugars, amino acids, vitamins, ions, myo-inositol, phenyl acetate, and urea. Some transporters are implicated in human disease (e.g., Na⁺/glucose transporter (SGLT1), Na⁺/iodide symporter (NIS)) or play an important role in medical therapy (e.g., NIS) (16,17). Furthermore, bacterial transporters such as the Na⁺/proline transporter PutP of Staphylococcus aureus contribute to virulence (18). Until very recently, no high-resolution structure was available for any member of the protein family. The first x-ray structure in this protein family, for the sodium/galactose transporter vSGLT of Vibrio parahaemolyticus (19), is surprisingly analogous to the structure of the leucine transporter LeuT_Aa of Aquifex aeolicus from the neurotransmitter/sodium symporter (NSS) family (20), although proteins from both families are dissimilar on the sequence level.

Recent kinetic and protein chemical analyses suggest that amino acids of TM domain IX (e.g., Ser³⁴⁰ and Thr³⁴¹) form part of the ion and/or substrate translocation pathway of PutP (21). The number of residues conserved within the SSS family, together with the previously shown functional significance of TM IX of NIS (22), suggests that the domain may fulfill similar functions in the transport cycle of the other members of the family. Therefore, we set out to determine the structure of TM IX of PutP.

Such TM domains are often discontinuous helices in related transporters whose x-ray structures have been determined (23). Therefore, we describe the backbone structure of TM domain IX in terms of a helix-loop-helix model. This model consists of two sections with an ideal α-helical secondary structure that are joined by an intervening loop. The length l of this loop and its position p in the sequence are fit parameters. Furthermore, the dihedral angles ϕ_i and ψ_i (i = p… p + l − 1) for the residues in the loop section are fitted, whereas the dihedral angles in the helical sections are fixed. Thus, altogether 2l + 1 parameters have to be determined. This is achieved by acquiring experimental data on distance distributions for 16 pairs of spin labels that scan the shape of the TM domain, and by fitting the 12 best primary experimental data sets by distance distributions simulated for different helix-loop-helix models. The remaining four data sets are used to derive lower bounds for distances and to reject structures that violate these lower bounds. This procedure provides an ensemble of structural models with low root mean-square deviation (RMSD) between simulated and experimental data. The backbone RMSD of <2 Å of this ensemble indicates that structural models of membrane proteins can be derived from SDSL EPR data with a resolution that allows discussion of the structure-function relations.

Materials and Methods

Sample preparation

The putP alleles encoding double Cys PutP molecules used in this study were generated by site-directed mutagenesis using plasmid pT7-5/putP(ΔCys) as a template and synthetic mutagenic oligonucleotides in one- or two-step PCR reactions using Taq-DNA polymerase. Plasmid pT7-5/putP(ΔCys) is a derivative of pT7-5 (24) and contains the lac promoter/operator for expression of the putP gene and an engineered cassette version of this gene that is devoid of all five native Cys residues. PCR fragments were digested with PstI and SpeI or AflII and ligated with similarly treated plasmid pT7-5/putP(ΔCys). For overexpression, the putP alleles were cloned into plasmid pTrc99a (25) using restriction endonucleases NcoI and HindIII. The resulting plasmids were transformed into E. coli WG170 (F⁻ trp lacZ rpsL thi Δ(putPA)101 proP219) (26). Cells were grown, membranes were prepared, and PutP was solubilized and purified by Ni-nitrilotriacetic acid affinity chromatography as previously described (27). The double Cys PutP was labeled with (1-oxyl-2,2,5,5-tetramethylpyrroline-3-methyl)-methanethiosulfonate (MTSSL; Toronto Research Chemicals, Toronto, Canada) on the column. For this purpose, 1 mM MTSSL in buffer W (50 mM KP_i, pH 8.0, 300 mM KCl, 10 mM imidazole, 10% glycerol (v/v), 0.04% β-D-dodecylmaltoside (w/v)) was applied to the column and incubated at 4°C for 3 h. The unbound label was removed by washing the column with buffer W, and the labeled protein was eluted with 200 mM imidazole in buffer W. After elution, the protein was reconstituted under nonreducing conditions into liposomes composed of E. coli lipids (67% phosphatidylethanolamine, 23.2% phosphatidylglycerol, and 9.8% cardiolipin; Avanti Polar Lipids, Alabaster, AL) at a lipid/protein ratio of 20:1 (w/w) as previously described (27). Finally, the proteoliposomes were washed twice with 50 mM KP_i, pH 7.5, and resuspended in the same buffer to yield a PutP concentration of 100–250 μM. The proteoliposomes were frozen and stored in liquid nitrogen until use.

Unless the native Cys residues C344 and C349 were used for labeling, they were mutated to Ser residues. The following spin-labeled double mutants were prepared: W325R1 combined with C344R1 and C349R1, and G328R1 combined with L330R1, S332R1, A336R1, M339R1, S340R1, T341R1, L342R1, S343R1, C344R1, Q345R1, L346R1, L347R1, V348R1, and C349R1.

The effect of double Cys replacements on transport activity was determined under standard test conditions (70 mM Na⁺, 10 μM proline) by using E. coli WG170 complemented with plasmid-encoded PutP variants as previously described (21,28). Under these conditions, the majority of double Cys mutants exhibited an initial rate of transport of minimum 23% of PutP(ΔCys), which in turn has 50% of the initial rate of transport and 100% of the steady-state level of proline accumulation of the wild-type. Exceptions were mutants 328/332, 328/340, 328/341, 328/345, and 328/346, with initial rates of ∼14%, 9%, 1.8%, 6%, and 9.7% of PutP(ΔCys). The latter inhibitory effects on transport activity were in agreement with the previously reported importance of corresponding single Cys mutants for Na⁺-coupled proline uptake (21,28). The effect of in situ alkylation of single-Cys mutants was tested by Raba et al. (28) using membrane-permeant N-ethylmaleimide (NEM). Among the Cys-mutants used in this work, C344 and L347C exhibited highly reduced activity of less than 8% after NEM labeling, whereas T341C and V348C exhibited moderately reduced activity (40% and 48%, respectively). The transport activity of all other single-Cys mutants was not significantly altered by NEM treatment.

DEER measurements

Four-pulse DEER measurements were performed with a Bruker Elexsys 580 spectrometer (Bruker Biospin GmbH, Karlsruhe, Germany) equipped with a 3 mm split-ring resonator under conditions of strong overcoupling (Q ≈ 100) at a temperature of 50 K. Before insertion into the probe head, the samples were shock-frozen in liquid nitrogen to avoid crystallization of water. The four-pulse DEER sequence (π/2)_ν1 − τ₁ − (π)_ν1 − t′ − (π)_ν2 − τ₁ + τ₂ − t′ − (π)_ν1 − τ₂ − echo was used (14). The π/2 and π pulses at the observer frequency ν₁ had equal pulse lengths of 32 ns to ensure equal excitation bandwidths, whereas the π pulse at the pump frequency ν₂ had a length of 12 ns to maximize modulation depth while still keeping the two excitation bands separate. The long interpulse delay was τ₂ = 2000 ns, except for double mutants W325R1/C344R1 and W325R1/C349R1, where it was 2200 ns. An initial value of t′ = 80 ns and an increment of Δt′ = 8 ns were used to acquire the time trace. To suppress proton modulation, data were added for eight equidistant values of τ₁ between 200 and 256 ns. A phase cycle [+(+x),−(−x)] was applied to the first pulse. The pump frequency ν₂ (typically 9.33 GHz) was set to the center of the resonator mode and to coincide with the global maximum of the nitroxide spectrum. The observer frequency ν₁ was set to the local maximum at the low-field edge of the spectrum (ν₁ − ν₂ = 65 MHz). Accumulation times for the data sets varied between 8 and 14 h. Data were analyzed for dipolar evolution times t = t′ − τ₁ ≥ 0. Analysis of the data in terms of distance distributions and mean distances was performed with the program DeerAnalysis2006 (29). The number of spins per molecules was determined based on the calibration performed previously with a series of biradicals and a triradical (30).

Rotamer library

The lowest-energy MTSSL rotamer R- of the previous library (12) was supplemented with peptide backbone atoms to an NH₂-C^αRH-COH structure, geometry-optimized with ADF 2004.01 using the BLYP density functional and a DZP basis set with effective core potentials for inner electrons (31). From this reference structure a set of 108 initial rotamer structures was generated by systematically varying side-chain dihedrals χ₁, χ₂, and χ₄ in steps of 120°, and χ₃ and χ₅ in steps of 180°, according to the expected shape of the angular potential (32). All initial starting structures were geometry-optimized twice, first in vacuum and then in a dielectric continuum with permittivity 80.1, corresponding to water, using the COSMO solvation model and the same functional and basis set as above. As a result of strong intramolecular clashes, 10 rotamers had to be discarded. The water structures of the remaining 98 rotamers comprise the library.

Structure determination

An ideal α-helix backbone with dihedral angles ϕ_i = −57° and ψ_i = −48° for all residues was generated as a starting structure and the appropriate side chains were added with SCWRL3.0 (33). For a given position p and length l of the loop region, the 2l dihedral angles ϕ_i and ψ_i were determined in the following way: All 98 rotamers of the library were attached and their total Lennard-Jones interaction potentials with the protein were computed based on the optimized potential for liquid simulations force field (34). Rotamer populations were calculated assuming a Boltzmann distribution at a temperature of 175 K corresponding to solidification of a lipid membrane. The distance distribution of a spin label pair was computed by generating a histogram of N-O midpoint distances for all possible combinations of rotamers weighted with the product of their populations. Rotamers with populations below a cutoff value of 0.001 were considered as clashing rotamers and discarded. The distance distribution was convoluted with a Gaussian function with standard deviation of 0.5 Å to account for librational fluctuation of dihedrals within their respective potential minima. DEER form factors were computed from the distance distributions and fitted together with a two-dimensionally homogeneous background function to the primary experimental data using DeerAnalysis2006 (29) subroutines. The global RMSD between simulated and experimental data was computed by summing the individual RMSDs weighted by the inverse noise level corresponding to a maximum likelihood estimate. For the best-fit structure, side chains were repacked with SCWRL3.0, rotamer populations were recomputed, and the whole fit procedure was repeated once, giving the final structure for these values of p an l.

Such best-fit structures were computed for loop lengths l = 4 … 6 and all feasible loop starting positions p within TM domain IX. At least 10 structures with the smallest RMSD within a shallow RMSD minimum basin were provisionally accepted. Up to five additional structures were accepted if their RMSD values were only significantly larger than that of the worst accepted structure. These structures were checked against those lower limit distance constraints from DEER data sets that were not used in model fitting. Structures that violated at least one of the lower limits were rejected. The remaining structures form the final structural ensemble (see also Supplementary Material). A flow chart of the algorithm is given in Fig. 2.

Figure 2.

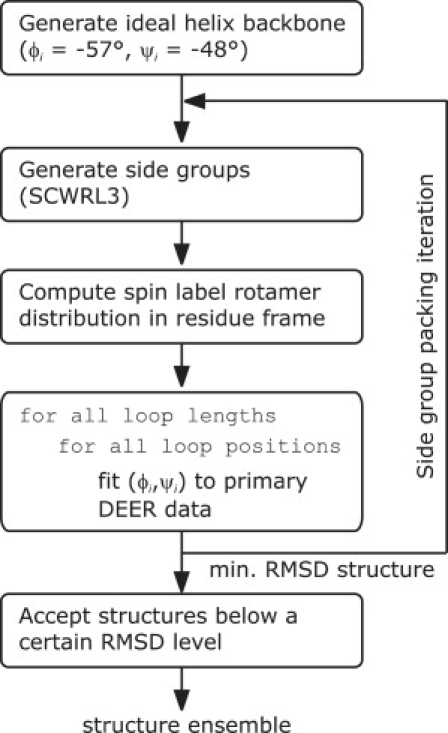
Flow chart for generating an ensemble of helix-loop-helix models that fit DEER data by matching the label-to-label distance distributions inherent in these data.

Results and Discussion

Test of the helix-loop-helix model for TM domains in transporters

Most membrane proteins belong to the structure type of α-helical bundles, and many TM helices are not ideal straight helices—they are often bent or kinked (35). Any technique for elucidating the structural models of such proteins thus must be able to characterize not only the relative arrangement of helices (11) but also their backbone shape. The main limitation of SDSL/EPR techniques in this context is the relatively small number of constraints that can be obtained. Structural models thus need to be coarse-grained, i.e., defined by a minimum of adjustable parameters. To derive such a model, we selected three α-helical transporters with known structures: the Na⁺/H⁺ antiporter NhaA of E. coli (PDB code: 1ZCD) (36), the leucine transporter LeuT_Aa of Aquifex aeolicus (PDB code: 2A65) (20,37,38), and the H⁺/Cl⁻ antiporter ClC of E. coli (PDB code: 1KPK) (39). For all TM domains in these transporters, we analyzed dihedral angles ϕ_i and ψ_i. A plot typical of a strongly kinked helix is shown in Fig. 1. Here, apparently most of the dihedral angles are very close to values for an ideal α-helix, with significant deviations being confined to a continuous loop region that comprises residues 14–19.

Figure 1.

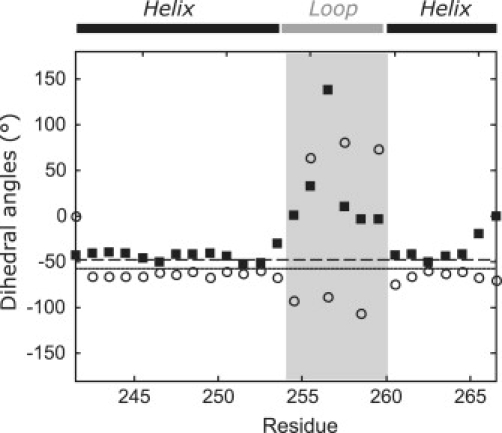
Dihedral angles ϕ (open circles) and ψ (solid squares) for residues for the typical strongly kinked TM domain VI of LeuT_Aa. The solid (−57°) and dashed (−48°) lines correspond to values for an ideal α-helix for ϕ and ψ, respectively. The range assigned to a loop in a helix-loop-helix model is marked as a gray box.

This suggests a model for kinked helical TM domains that consists of two ideal α-helices joined by a loop whose position p in the domain and length l are variable. Ideal α-helix geometry is assumed for the helical parts, whereas the backbone of the loop is completely defined by 2l dihedral angles. We fitted this idealized model with loop lengths varying from l = 1 to 7 for all possible loop positions to all TM domains found in the crystal structures of NhaA, LeuT_Aa, and ClC. The results for the closest relative of PutP, LeuT_Aa, are given in Table 1. Except for TM domain XI, all domains are modeled with backbone RMSDs of less than 0.5 Å, which compares favorably to the experimental uncertainty of the x-ray data. TM domain XI is doubly kinked near its ends and can be fitted with a backbone RMSD of 0.11 Å, assuming two loop regions (lengths of two residues each, positioned at residues 8 and 24 out of 30). Similar results are obtained for the other two transporters NhaA and ClC (see Tables S1 and S2, respectively, in the Supplementary Material).

Table 1.

Performance of a helix-loop-helix model in describing the x-ray structure (20) of TM domains in the leucine transporter LeuT_Aa of Aquifex aeolicus (PDB identifier 2A65)

TM domain	Loop position, p	Loop length, l	Backbone RMSD (Å)
I	14	6	0.15
II	14	2	0.17
III	22	1	0.45
IV	11	2	0.05
V	7	3	0.06
VI	15	5	0.06
VII	16	7	0.09
VIII	21	4	0.12
IX	14	3	0.05
X	9	3	0.09
XI	23	1	1.50
XII	17	2	0.06

Such simplified backbone models have to be supplemented with side-group coordinates to fit them to primary DEER data because the fitting procedure requires predicted conformational distributions of the spin labels (12), which in turn depend on the conformations of neighboring side groups. Because we have no independent information on side-group conformations, these have to be predicted by an ab initio method, such as SCWRL3 (33). Therefore, we tested how well experimental coordinates of side groups are predicted by SCWRL3 for transporters. We found side-group RMSDs of 1.76 Å (NhaA), 1.52 Å (LeuT_Aa), and 1.27 Å (ClC). Although significant, such deviations below 2 Å are not expected to bias the predicted conformational distribution of the spin label to an extent that exceeds other uncertainties of our methodology.

As a final test of the model, we tried to reproduce the shape of the typical moderately kinked TM domain VIII in LeuT_Aa, which may be functionally homologous to TM domain IX in PutP, from synthetic DEER data by the same fit procedure (see flow chart in Fig. 2) that is applied to TM domain IX of PutP (vide infra). For this validation of the fit procedure, rotamer distributions (7,12) for 21 labeling positions were predicted based on experimental backbone and side-group coordinates from the x-ray structure (20). Distance distributions for 20 label pairs were obtained from these rotamer distributions and converted to synthetic DEER form factors with subroutines of the DeerAnalysis2006 package (29). An ideal helix backbone (all ϕ_i = −57° and ψ_i = −48°) was generated and side groups were added with SCWRL3 (33). By starting from an ideal helix model, we were able to ascertain that a kink (loop segment) is introduced only for those TM domains that cannot be modeled with sufficient precision by an ideal helix. A rotamer distribution was computed for this initial model and the NO midpoint coordinates of all rotamers at all labeling positions were stored in a local frame defined by the backbone atoms N, C, and C^α of the labeled residue. For all possible choices of loop position p and loop length 3 ≤ l ≤ 7, the dihedral angles (ϕ_i, ψ_i) in the loop region were fitted by minimizing the global RMSD with regard to all synthetic DEER form factors. A loop length of l = 6 was deemed satisfactory, and of all structures with this length, the one with the lowest RMSD was subjected to SCWRL3 side-group packing to adapt side-group conformations to the backbone deformation. A new rotamer distribution was computed and all fits were repeated. The 11 structure models with the lowest RMSD were accepted.

The backbone coordinates of this ensemble are shown in Fig. 3 A. The backbone RMSD for the whole ensemble is 0.68 Å, whereas the backbone RMSD with respect to the experimental structure (Fig. 3 B) is 1.99 Å. The larger RMSD with regard to the experimental structure indicates a systematic deviation of the structural model. This systematic deviation could be traced back mainly to imperfections in SCWRL3 side group packing and corresponding deviations in the rotamer distribution. The dependence of the RMSD on loop length l and position p and the acceptance level are plotted in Fig. S1, and the agreement of simulated time-domain data and distance distributions between the original structure, an ideal helix model, and the best-fit helix-loop-helix model are shown in Fig. S2. Corresponding data for the discontinuous TM domain VI of LeuT_Aa are given in Figs. S3 and S4.

Figure 3.

Validation of the fit procedure on synthetic DEER data generated from the crystal structure (20) of LeuT_Aa (PDB identifier 2A65) for TM domain VIII. (A) Backbone traces for the structural ensemble (11 structures) color-coded by RMSD per residue with respect to the mean structure. (B) Backbone trace from the crystal structure.

TM domain IX of PutP is kinked

An additional complication arises with experimental DEER data, as these data correspond to a convolution of the form factor due to spin labels in the same protein molecule with a background function due to spin labels in neighboring protein molecules. At short distances separation of the two components is straightforward (29). We find that the background is best fitted by a homogeneous two-dimensional spatial distribution of protein molecules as is expected for membrane proteins in liposomes. However, these background fits are not perfect and distance distributions obtained by Tikhonov regularization contain a minor spurious peak at a distance of ∼4.5–5.5 nm.

For any given helix-loop-helix model in our structure fit and a given double mutant the form factor F(t) is uniquely determined by the set of dihedral angles (ϕ_i, ψ_i). To fit the primary data set of this double mutant we have to vary the modulation depth Δ and background density factor k as defined in (29). At short distances this is again straightforward, but preliminary test runs showed that for the four longest distances, corresponding to double mutants 328/348, 328/349, 325/344, and 325/349, the background fits become unstable and may result in unrealistically small or large modulation depths Δ. We thus decided to exclude these data sets from the fit procedure shown in Fig. 2. Note that background fits performed separately with DeerAnalysis2006 rather than during structure fitting are stable for these mutants and give modulation depths that correspond to numbers of spins per molecule of 1.45, 1.28, 1.27, and 1.42, respectively, similar to the values found for the data sets used (Table 2). Indeed, for the maximum dipolar evolution times of 2.0 μs (328/348 and 328/349) or 2.3 μs (325/344 and 325/349) achieved in the experiments model computations with simulated data sets show that the expected distances of less than 5 nm can still be determined whereas the width of the distributions becomes uncertain above 4 nm and the shape of the distributions above 3 nm.

Table 2.

Comparison of experimental mean label-to-label distances 〈r_exp〉 with mean distances 〈r_ideal〉 in an ideal helix model and 〈r_best〉 in the best-fit model for TM domain IX of PutP

Label positions	〈rexp〉 (Å)	〈rideal〉 (Å)	〈rbes〉 (Å)	Spins/molecule
328–330	17.0	17.2	17.3	1.27
328–332	16.8	16.7	16.6	1.42
328–336	18.2	18.9	18.4	1.34
328–339	22.9	19.4	22.3	1.37
328–340	25.5	22.3	22.6	1.43
328–341	28.1	23.4	26.6	1.49
328–342	22.6	22.3	22.6	1.52
328–343	27.7	23.6	27.2	1.54
328–344	32.0	27.1	32.1	1.37
328–345	30.2	27.4	28.2	1.35
328–346	26.2	27.1	27.2	1.20
328–347	35.7	29.8	33.8	1.50

The number of spins per molecule characterizes the degree of labeling.

Thus these data sets can still provide lower limits for the mean distance between the labels. Structural models that gave a good fit of the remaining 12 data sets, but violated one or more of these lower limit constraints, were rejected. The experimental distance distributions, obtained by Tikhonov regularization using the program DeerAnalysis2006 (29), are shown in Fig. 4 (black lines) together with distributions for the best-fit helix-loop-helix model (red lines) and the best possible fit by assuming an ideal helix and varying only background parameters Δ and k (blue lines). The corresponding fits of the primary data are given in Fig. S5. For double mutants 328/330–336 fits by the ideal helix and the helix-loop-helix models nearly coincide and are both good, except for double mutant 328/336. The larger deviation for the latter mutant might be caused by deficiencies in SCWRL3 side group prediction. More likely, our rotamer library overestimates conformational freedom of the spin labeled side group for site 336 with neighboring leucine and alanine side groups, which is one of the least constrained labeling sites used in this study. For double mutant 328/339 the fit by the helix-loop-helix model is surprisingly worse than the one by the ideal helix, although this position is still in the first α-helical section. We attribute this to perturbations by side groups in the loop section, whose conformations may not be correctly predicted.

Figure 4.

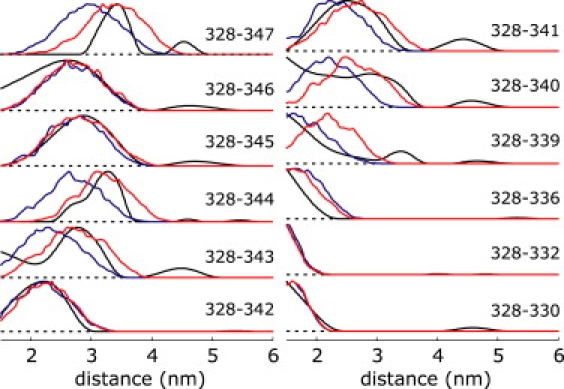
Experimental label-to-label distance distributions for TM domain IX of PutP (black traces), fits for the best helix-loop-helix model (red lines), and fits assuming an ideal helix (blue lines).

Starting with double mutant 328/340, but except for double mutants 328/342, and 328/345, fits by the helix-loop-helix model are significantly better than fits by an ideal helix. In only one further case, for double mutant 328/347 the helix-loop-helix model exhibits a significant deviation from experimental data, corresponding to a slightly longer distance in the experiment than in the structural model. This may again be due to deficiencies in SCWRL3 side group prediction and modeling of the spin label by the rotamer library.

Experimental mean distances are compared to mean distances for an ideal helix model and for the best-fit helix-loop-helix model in Table 2. Again with the exception of double mutant 328/339, agreement is better for the helix-loop-helix model that has a total RMSD for the mean distances of 1.00 Å compared to 3.28 Å for the ideal helix model.

Of the 12 initially accepted structures (Fig. 5) four had to be rejected as they violated lower distance limits derived from the four data sets not used in fitting. The ensemble of the remaining eight structures corresponds to a well defined, moderately kinked backbone of this TM domain RMSD of 1.9 Å (Fig. 6 A). Not surprisingly, variability of the coordinates is larger in the loop region than in the helix regions.

Figure 5.

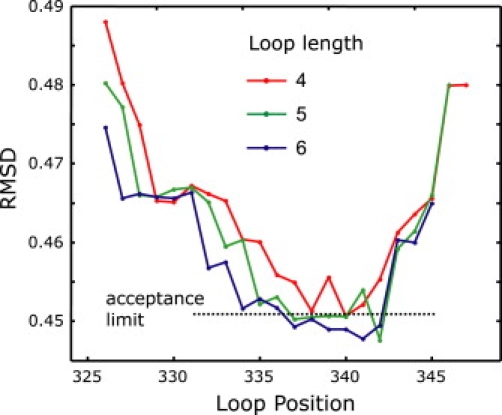
Dependence of the RMSD between simulated and experimental DEER traces for best-fit helix-loop-helix models on loop length and position for TM domain IX of PutP. The acceptance limit for including structures in the final ensemble is shown as a dotted line.

Figure 6.

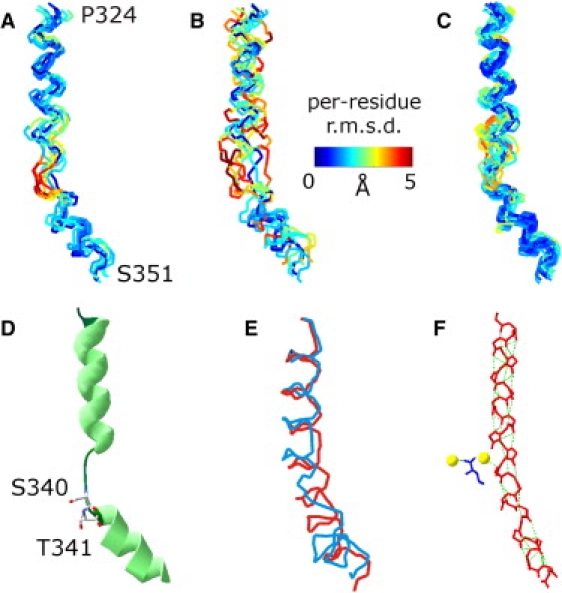
Helix-loop-helix models for the backbone of TM domain IX in PutP. (A) Ensemble obtained by using the 12 DEER data sets with lower limit constraints from four additional data sets (eight structures). (B) Ensemble obtained by using the same data sets as in A with pseudorandom numbers added to double the noise level (eight structures). (C) Ensemble obtained from all combinations of only 11 out of the 12 DEER data sets with lower limit constraints from four additional data sets (26 structures). (D) Cartoon of the representative model of the ensemble with 26 structures with ligand-binding residues S340 and T341 shown as stick. (E) Comparison of TM domain IX in PutP (red) with TM domain VIII in a crystal structure (37) of LeuT_Aa (blue, PDB identifier 2Q72). (F) Backbone model including carbonyl oxygens from the crystal structure (37) of TM domain VIII in LeuT_Aa (red) with bound sodium ions (yellow) and substrate leucine (blue). Hydrogen bonds are visualized as dotted green lines (PDB identifier 2Q72).

We have tested stability of the fit by a similar approach as used in (12). In a first series of test fits, we doubled noise in the input data by adding pseudorandom numbers. The resulting ensemble of eight structures (Fig. 6 B) has a backbone RMSD of 2.7 Å, yet the general shape of the TM domain and the location of the loop region are preserved. This double-noise test demonstrates that the measurement time per sample cannot significantly be shortened without compromising the quality of the structural model.

In a second series of test fits we restricted ourselves to loop length 5 and performed 12 structure determinations, each one excluding one of the originally used 12 primary DEER data sets. To keep the size of the total ensemble manageable, the number of accepted structures for each fit was reduced by a factor of two. This provides altogether 65 acceptable structures, of which 37 are consistent with the lower limit constraints from the remaining four data sets. To condense this ensemble further, we performed a cluster analysis and selected those 26 structures that have the smallest RMSD (Fig. 6 C). This ensemble has a backbone RMSD of 1.6 Å. Again, the general shape and location of the loop region are preserved. However, the significant increase in backbone RMSD for some of the accepted models indicates that at least 10 to 11 constraints are needed to obtain a structural model with sufficient precision.

Because we employed spin labels with a size similar to the one of the bulkiest natural amino acid side groups, the question arises as to whether the spin labels might have introduced the observed kink. For the spin labels at our reference points 325 and 328, this possibility can be safely excluded, since these points are remote from the kink. Because the sites near the kink have been found to be highly accessible to water (28) and labeling efficiencies are high, the labels at these sites are not expected to alter the structure. In most cases studied so far by SDSL techniques, spatial restrictions at a labeling site have led to poor labeling efficiency rather than to alterations in the structure. Furthermore, the kink is strongly sensed at at least three labeling sites: 343, 344, and 347. It appears rather unlikely that the labels at all three sites induce a consistent structural distortion.

Note also that the helix-loop-helix model used in structural modeling amounts to an assumption regarding the secondary structure. Alternative secondary structures may also be consistent with our data. Between residues 328 and 339 the observed incremental changes in distances and their periodicity strongly suggest an α-helical structure, whereas between residues 340 and 345 the data are not consistent with either an α-helix or a β-sheet. The prevalence of an α-helical structure between residues 324 and 327 at the one end and between residues 346 and 351 at the other end cannot be rigorously proved based on the experimental data alone. The assumption is supported by secondary structure prediction with PredictProtein (40), which is displayed in Fig. S6 B.

In principle, such helix scans and structural modeling could be applied to each TM domain in an α-helical protein. This would provide coarse-grained backbone structures for these TM domains. An entire helical bundle with N TM domains could then be constructed by treating the predetermined backbone structures of the domains as rigid bodies and elucidating their relative translation and orientation, as demonstrated previously (11,12). Because for each pair there are six degrees of freedom and there are (N − 1) independent pairs, this would require fits of another 6(N − 1) parameters, which may require the preparation of and distance measurements on ∼10(N − 1) further double mutants. Since some of the prepared mutants may not be suitable for labeling, the total number of required mutants may well exceed 300 for a protein of the size of PutP. Although a considerable effort is required, such an approach to a coarse-grained structural model is feasible with currently available methodology.

Recently, a different approach for deriving structural models from EPR data was suggested (41) that required fewer constraints by making extensive use of structure prediction by the program Rosetta (42). This approach was shown to provide full atom models with 1.0 and 2.6 Å RMSD for the soluble proteins T4-lysozyme (107 residue helical domain) and αA-crystallin (88 residue β sandwich), respectively. For small and medium-sized soluble proteins it may be better suited than the approach suggested here. For membrane proteins, de novo structure predictions are currently less reliable. Furthermore, with current algorithms and computers, they are restricted to proteins with up to 200 residues, well below the size of the transporters. Nevertheless, judicial use of constraints from such predictions or from molecular dynamics simulations may help to decrease the number of required experimental constraints.

Functional implications of the structural model

TM domain IX appears to line the translocation pathway, with residues S340 and T341 taking part in ligand binding and transport (21). Residues involved in ligand binding are frequently found at the apex of a hydrophilic cavity in the transporter, as described for lactose permease, glycerol-3-phosphate transporter (both members of the major facilitator family), and neurotransmitter transporter relatives (43–46). In fact, a Cys accessibility analysis of TM domain IX of PutP suggests that the domain participates in the formation of an inwardly oriented cavity. Proline binding in the presence of Na⁺ blocks this accessibility (28).

In all of our structural models, residue S340 is found in the loop region; in most models this also applies to residue T341. These residues are visualized as stick models in a representative structure from the ensemble of 26 structures (Fig. 6 D). This structure has the lowest RMSD with respect to all the other structures. Note that the orientation of the OH groups relative to the kink differs within the ensemble.

The structure shows that the inwardly oriented, ligand-sensitive cavity suggested by Raba et al. (28) may be due to a kink in the helix that starts approximately at residue S340. However, the loop already starts around residue V338. Between residues 338 and 340 the domain continues in the direction of the first helical part. However, the backbone is twisted so that the side groups of these residues point to different directions than in an ideal helix. These residues may belong to the hinge that alters its conformation when residues S340 and T341 bind substrate. Possibly, a reorganization of this loop facilitates accessibility of the proline-binding site from the outside.

Of interest, a very similar kink is observed in the putatively homologous TM domain VIII of LeuT_Aa (20,37,38), although all x-ray structures correspond to substrate-bound states. If the two domains are aligned at T354/S355 of LeuT_Aa and S340/T341 of PutP, and are restricted to the same length (Fig. 6 E), our model (red) superimposes on the x-ray structure of TM domain VIII of LeuT_Aa (blue) with a backbone RMSD of 1.98 Å. The bend of the cytoplasmic end with respect to the periplasmic end in LeuT_Aa appears to open access to the substrate-binding site. Some of the residues in this bend do not exhibit the hydrogen bond pattern typical of α-helical secondary structure (Fig. 6 F). In contrast, the homologous TM domain IX in vSGLT in the substrate-bound state (19) can be well described by the model of an ideal α-helix (E. M. Wright, University of California, Los Angeles, personal communication, 2008). If TM domain XI in PutP on substrate binding indeed performs a hinge motion that closes an inwardly oriented cavity, it would also be expected to be approximately straight in the substrate-bound state.

Conclusions

Most kinked helices in membrane proteins can be described with a backbone RMSD of less than 0.5 Å by helix-loop-helix models with loop lengths l of seven residues or less. Such models have free 2l+1 parameters, namely, two dihedral angels per loop residue and the loop position. These parameters can be determined by means of pulsed EPR distance distribution measurements on doubly spin-labeled mutants. For TM domain IX of the proline/Na⁺ transporter PutP of E. coli, we obtain structural ensembles whose backbone coordinate variation is characterized by an internal RMSD of less than 2 Å. Taking into account systematic errors of about the same magnitude due to imperfect prediction of conformations for unlabeled side groups, and the conformational distribution of spin-labeled side groups, the backbone RMSD of the representative structure of the ensemble from the mean native structure is expected to be less than 3 Å. At this resolution, kinks in helices can clearly be discerned and their functional relevance can be discussed. The kink in TM domain IX of PutP appears to be a hinge that closes the inwardly oriented cavity on substrate binding and opens it for substrate release to the interior of the cell.

The newly introduced methodology for determining the shape of a single TM domain in a membrane protein could be combined with a previously introduced methodology for establishing the relative position and orientation of two rigid structures (11,12) to provide structural models of the whole TM domain bundle. For a protein of the size of PutP, determining 13 TM domain shapes and 12 relative positions and orientations of TM domain pairs would require measurements on ∼300 double mutants. It has to be taken into account that some of the intended labeling sites may not be accessible due to tight packing, although the flexibility and size of MTSSL spin labels allows for a surprisingly high success rate in labeling. To enhance the feasibility of such an approach for deriving coarse-grained structural models of whole membrane proteins, the number of required mutants should thus be decreased by systematically taking into account internal restraints and accessibility information. Work along these lines is now in progress.

Supplementary Material

Two tables and six figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(08)00039-8.