Skip to main content
PMC home page
Annals of Botany logoLink to Annals of Botany
. 2007 Dec 18;101(4):561–571. doi: 10.1093/aob/mcm320

Inequality of Size and Size Increment in Pinus banksiana in Relation to Stand Dynamics and Annual Growth Rate

Juha M Metsaranta 1,*, Victor J Lieffers 1
PMCID: PMC2710195  PMID: 18089583

Abstract

Background and Aims

Changes in size inequality in tree populations are often attributed to changes in the mode of competition over time. The mode of competition may also fluctuate annually in response to variation in growing conditions. Factors causing growth rate to vary can also influence competition processes, and thus influence how size hierarchies develop.

Methods

Detailed data obtained by tree-ring reconstruction were used to study annual changes in size and size increment inequality in several even-aged, fire-origin jack pine (Pinus banksiana) stands in the boreal shield and boreal plains ecozones in Saskatchewan and Manitoba, Canada, by using the Gini and Lorenz asymmetry coefficients.

Key Results

The inequality of size was related to variables reflecting long-term stand dynamics (e.g. stand density, mean tree size and average competition, as quantified using a distance-weighted absolute size index). The inequality of size increment was greater and more variable than the inequality of size. Inequality of size increment was significantly related to annual growth rate at the stand level, and was higher when growth rate was low. Inequality of size increment was usually due primarily to large numbers of trees with low growth rates, except during years with low growth rate when it was often due to small numbers of trees with high growth rates. The amount of competition to which individual trees were subject was not strongly related to the inequality of size increment.

Conclusions

Differences in growth rate among trees during years of poor growth may form the basis for development of size hierarchies on which asymmetric competition can act. A complete understanding of the dynamics of these forests requires further evaluation of the way in which factors that influence variation in annual growth rate also affect the mode of competition and the development of size hierarchies.

Key words: Annual growth rate, asymmetric competition, competition index, dendroecology, Gini coefficient, jack pine, Lorenz asymmetry coefficient, volume increment

INTRODUCTION

Size variability in plant populations may be due to differences in competitive status, genetics, the differential effects of herbivores and pathogens (Weiner and Thomas, 1986), or to spatial and temporal environmental heterogeneity (Schwinning and Weiner, 1998; Wichmann, 2001). In tree populations, size variability also contributes to the structural diversity of a forest stand, which is important for many ecological functions (Brassard and Chen, 2006). Studies of size variability in tree populations have focused mainly on fitting various probability distribution functions to size (diameter) distributions [as noted in Garcia (2006), there are hundreds of papers concerning diameter distribution models in forestry literature databases]. However, size variability in tree populations can also be described as a size hierarchy, and so can be described by other characteristics such as its degree of size inequality (Weiner and Solbrig, 1984). Changes in size inequality are often attributed to changes in the mode of competition during different stages of stand development (e.g. Gates et al., 1983; Weiner and Thomas, 1986; Newton and Smith, 1988; Kenkel et al., 1997). Previous studies have observed that inequality is greater at higher densities (Brand and Magnussen, 1988; Knox et al., 1989), increases prior to self-thinning and decreases as self-thinning progresses (Mohler et al., 1978; Knox et al., 1989). In addition, although previous studies have examined the relationship between size and size increment [also known as the distribution modifying function (Westoby, 1982; Weiner, 1990; Weiner and Damgaard, 2006)], there has been little attention placed on examining the inequality of size increment itself.

Inter-tree competition is considered to be either a resource pre-emption (size asymmetric) process or a resource depletion (size symmetric) process. Immediately after stand initiation, individual trees are small in comparison with their relative density, so if competition exists at all, its mode is symmetric. Over time, as trees grow larger and a size hierarchy begins to develop, the mode of competition is thought to become asymmetric as larger trees pre-empt light from smaller trees. Tree size at any given point contains a ‘memory’ of the processes that influenced that individual as it grew from a smaller size, and therefore changes in the inequality of tree size should be best explained by long-term changes in stand characteristics, such as density, mean tree size and the average amount of competition. In contrast, the size increment of individual trees varies greatly from year to year in response to transient factors such as annual variation in weather and insect defoliation (e.g. Larsen and MacDonald, 1995; Brooks et al., 1998; Hofgaard et al., 1999; Hogg et al., 2005; Hogg and Wein, 2005). These factors may have different effects on large and small individuals (Orwig and Abrams, 1997; Piutti and Cescatti, 1997; Wichmann, 2001). Therefore, the inequality of size increment may be more strongly related to annual variation in stand-level growth rate, which can be considered a surrogate variable accounting for the transient environmental factors affecting a stand. The influence of these transient factors on the mode of competition between plants is, at present, not well understood (Schwinning and Weiner, 1998).

The present study uses detailed growth data obtained from tree-ring reconstruction to investigate annual changes in the inequality of size and size increment in four even-aged fire origin jack pine (Pinus banksiana) stands. When combined with cross-dating of recent and historical mortality, tree-ring reconstruction can give annual data on the size and growth rate of individual trees (e.g. Henry and Swan, 1974; Oliver and Stephens, 1978; Johnson and Fryer, 1989; Stoll et al., 1994; Carrer and Urbinati, 2001). Although intensive to collect, these data can be advantageous because they follow the growth and mortality of individuals over time (Weiner, 1995) and are at an annual resolution. We hypothesize that at any given time, tree sizes are more equal than tree size increments, and that annual trends in inequality will be more variable for size increment than for size. We also hypothesize that, because sizes change slowly, the inequality of tree sizes will be best predicted by long-term changes in stand population parameters such as stand density, mean tree size and the average amount of competition. In contrast, because the inequality of tree size increment is more variable, we hypothesize that it will be best predicted by short-term population parameters such as stand-level annual growth increment.

MATERIALS AND METHODS

Study area

Plots were established in fire-origin jack pine (Pinus banksiana Lamb.) stands on sandy soils located in the boreal forest of western Canada (Fig. 1). The study sites were located near (1) Candle Lake, Saskatchewan (53·9°N, 104·7°W) and (2) Thompson, Manitoba (55·9°N, 98·6°W) (Fig. 1). The Candle Lake sites were in the Boreal Plains ecozone, the Thompson sites in the Boreal Shield ecozone (Ecological Stratification Working Group, 1996). Based on spatially interpolated climate normals for the period 1970–2000 (McKenney et al., 2006), the mean annual temperature was −0·3 °C at Candle Lake and −2·8 °C at Thompson. The mean annual precipitation was 466 mm at Candle Lake and 516 mm at Thompson.

Fig. 1.

Fig. 1.

Open in a new tab

The location of the study plots in Manitoba and Saskatchewan, Canada. The Candle Lake sites are located in the Boreal Plains ecozone. The Thompson sites are located in the Boreal Shield ecozone.

Field methods

In each region, a plot was sampled in a region on a mesic (relatively nutrient-rich) site and a xeric (relatively nutrient-poor) site, determined on the basis of ecological classification and indicator species. The plots were sampled in the summer of 2005, so the last complete year of growth observed was 2004. The polar coordinates of each living tree, standing dead tree and lying log in a 900-m2 (30 × 30-m) area were mapped using a surveying transit and tape measure. Height was measured for living trees, and breast height diameter for all trees. Two randomly orientated increment cores were extracted at breast height from living trees and a cross-sectional disc was cut from dead trees. Some (n = 25) trees at each site were also cored near ground level to estimate stand ages. The samples were a complete census of all living and dead trees recognizable at the time of sampling. Study plot characteristics are summarized in Table 1.

Table 1.

Summary of selected stand characteristics of the study plots

Site Ecological type* Stump age (year of origin) dbh age (year of origin) Mean dbh (cm) Mean height (m) Live + dead density (ha−1) Live density (ha−1)
Candle Lake – Rich c1·2-jack pine–black spruce/Labrador tea/feather moss 90 (1916) 84 (1922) 17·4 15·9 1767 1267
Candle Lake – Poor a1.1 jack pine/bearberry/ lichen 90 (1916) 84 (1922) 12·7 13·0 2556 1656
Thompson – Rich v16 jack pine mixed-wood/feather moss 73 (1933) 71 (1935) 15·9 13·7 1900 1367
Thompson – Poor v26 jack pine–black spruce/lichen 73 (1933) 69 (1937) 9·4 8·0 3222 2089
Open in a new tab

*At Candle Lake, ecological classification is according to Beckingham et al. (1996), and at Thompson, according to Zoladeski et al. (1995).

Laboratory methods

The samples were air-dried, the cores were mounted on grooved boards and cross-sectional discs were cut into 1–2-cm-thick slices. These were polished with up to 600 grit sandpaper, scanned as 1600-dpi greyscale images and imported into WinDendro (Regent Instruments, Quebec, Canada) for ring width measurement. When suppressed, jack pine can form light rings (Volney and Mallett, 1992) that were not always visible on the scanned images. Simultaneously, suppressed samples were examined with a microscope and rings not visible on the scanned images were added to the WinDendro file. Trees were considered to be functionally dead when radial growth ceased at breast height (Mast and Veblen, 1994), which may have underestimated year of death in some cases of extreme suppression (<5 % of samples). Year of death was determined by cross-dating against a master chronology developed from a sample (n = 25) of the largest trees at each site. Samples were cross-dated visually by reference to narrow marker years (Yamaguchi, 1991) induced by periodic jack pine budworm (Choristoneura pinus Freeman) defoliation (Volney, 1988). Dating accuracy was checked by calculating the correlation between the raw ring widths on a sample and the raw ring widths on the site master chronology, as well as shifting sample dates ±1–5 years. This was done iteratively until most (82 % living, 76 % dead) samples had the highest correlation at the final assigned date (91 % ± 1 year for living trees, 90 % ± 1 year for dead trees). The average correlation between a dead sample and the master chronology at the final assigned date was R2 = 0·88 (s.d. = 0·09, range = 0·76–0·99, n = 429). For living trees, it was R2 = 0·81 (s.d. = 0·19, range = 0·58–0·99, n = 536). The study sites were even-aged, so visual cross-dating was sufficient to date samples confidently, and the correlation tests were used only to identify gross errors. Some samples were too decomposed to measure ring widths. In these cases, the mean year of death of the three largest and three smallest trees nearest in diameter, of the same class (snag or lying log), and at the same plot as an excessively decomposed tree was used as an estimate of its year of death, and the mean ring widths of these same trees were used as an estimate of its growth. In a test, this method was unbiased with a mean absolute difference of ±3·3 years between the true and estimated year of death (Metsaranta et al., 2007). Jack pine snags remain standing long enough and lying logs decompose slowly enough that these techniques can reliably reconstruct growth in these forests for up to 50 years into the past (Metsaranta et al., 2007).

Determining size and growth rate

Stemwood volume and volume increment were used to describe tree size and size increment. The diameter (inside bark Dib) of each tree was determined annually from the ring-width measurements and this was used to estimate cumulative volume and volume increment using three equations. First, diameter inside bark (Dib) was converted to diameter outside-bark (Dob) using Husch et al. (2003).

graphic file with name mcm32006.jpg 1

From data in Halliwell and Apps (1997), k was estimated to be 0·964 (n = 221, r2 = 0·99). Second, heights were predicted using the Chapman–Richards function:

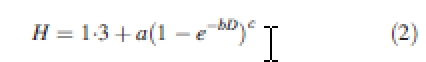graphic file with name mcm32007.jpg 2

where H is tree height (m) and D is outside bark diameter (cm). From data in Halliwell and Apps (1997) and the plots in the present study, the parameters were estimated to be a = 18·87, b = 0·11 and c = 1·48 (r2 = 0·98) for Candle Lake, and a = 19·65, b = 0·08 and c = 1·56 (r2 = 0·98) for Thompson. Third, volume was determined from H and D using the taper equation of Kozak (1988):

graphic file with name mcm32008.jpg 3

where the components of the equation are as defined in Kozak (1988). Parameters for Candle Lake were obtained from Gál and Bella (1994), and for Thompson from Klos (2004). The total volume of each tree was determined using numerical integration, and all individual tree values were summed to obtain total stand volume. Individual tree volume increment was obtained by subtracting volume in year (y − 1) from volume in year y. Whole-stand volume increment was obtained by summing individual tree values and was expressed in units of m3 ha−1 year−1. The accuracy of these scaling methods was tested for a variety of species, height and volume estimation methods and it was found that they usually predict volume increment with a mean error of less than 5 % and always predict volume increment with a mean error of less than 10 %, relative to volume increment obtained by full stem analysis.

Determining competition

The level of competition to which each tree was subject over time was found by annually determining a distance-weighted absolute size index of competition for each tree. The index is similar to Hegyi's (1974) relative size index, but uses the absolute size of competitors rather than weighting them by the size of the subject tree. The absolute size of competitors may be a better measure of competition than relative size (Ramseier and Weiner, 2006). The index was calculated as

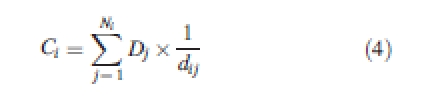graphic file with name mcm32009.jpg 4

where Ci is the index for subject tree i, Dj is the diameter of competitor j, dij is the distance between subject tree i and competitor j, and Ni is the number of competitors for subject tree i. As trees grow, the definition of which trees compete with each other changes, so the competitor search radius for each tree was made to be temporally variable based upon an estimate of its crown width. Crown width was estimated from diameter using

graphic file with name mcm32010.jpg 5

where W is crown width (m) and D diameter (cm). From the data in Halliwell and Apps (1997), the parameters were estimated to be a = 0·353 and b = 0·682 (n = 235, r2 = 0·69). The search radius for competitors was defined as 3·5 times the crown width in a given year (Lorimer, 1983), and the index was calculated only for those trees where the search radius did not fall outside of the plot. At each site, the average amount of competition that trees in each plot were subject to in each year was calculated, and this was used as a predictor of the trends in size and size increment inequality. To help interpret competition effects, trends in the variability of competition to which trees at each site were subject were also determined by calculating the coefficient of variation (CV %) of the competition index.

Quantifying inequality

The Gini coefficient (Weiner and Solbrig, 1984) used to describe annual changes in the inequality of size and size increment. Annual changes in the Lorenz asymmetry coefficient to were also calculated to establish whether the observed trends in inequality were primarily due to large or small trees (Damgaard and Weiner, 2000). The Gini coefficient is the difference between the sample Lorenz curve and the line of perfect equality, where the Lorenz curve is a plot of the cumulative number of individuals (x-axis) against the cumulative proportion of their total size (y-axis). The Gini coefficient ranges from 0 to 1, where 0 indicates perfect equality (the size or growth of all individuals is the same, or the amount of competition each tree is subject to is the same) and 1 indicates perfect inequality (one tree contains all of the size or growth, or faces all the competition). It can be calculated from data ordered by increasing size as (Dixon et al., 1987)

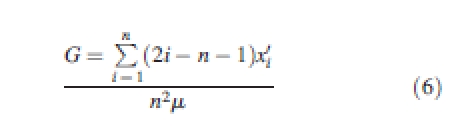graphic file with name mcm32011.jpg 6

The Lorenz asymmetry coefficient (S) summarizes the degree of asymmetry in a Lorenz curve. This is important because populations with different Lorenz curves can have the same Gini coefficient, depending on whether most of the inequality is due to large or small individuals (Weiner and Solbrig, 1984). The Lorenz asymmetry coefficient is defined as the point at which the slope of the Lorenz curve is parallel to the line of equality. It is defined as

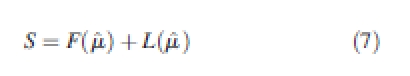graphic file with name mcm32012.jpg 7

and is calculated using the following three equations from Damgaard and Weiner (2000):

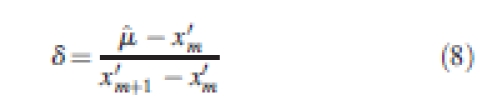graphic file with name mcm32013.jpg 8
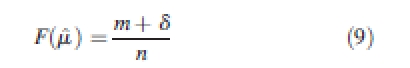graphic file with name mcm32014.jpg 9
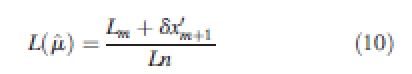graphic file with name mcm32015.jpg 10

When S > 1, the inequality present is due mostly to a small number of very large individuals. When S < 1, the inequality present is due mostly to a large number of very small individuals. Coefficients and 95 % confidence intervals were calculated from 1000 bootstrap samples (Dixon et al., 1987) for each set of annual data on size and size increment at each plot.

Statistical analysis

We examined how changes in the inequality of size and size increment over time are affected by long-term population parameters (age, stand density and competition) and short term population parameters (stand-level annual volume increment). The temporal development of the Gini coefficients for volume and volume increment at each site was modelled using stand density (DENS), mean tree volume (SIZE), the average competition index (COMP), and stand-level annual volume increment in the current year (AVI) and one year previously (AVI1) as predictor variables. Multiple linear regression was used to estimate the parameters and to determine the significance of each of these variables as predictors of annual changes in size and size increment inequality. The LM function in the STATS package for the R Statistical System (R Development Core Team, 2007) was used to perform these calculations. As the data were time series, the potential confounding effects of serial autocorrelation were examined by using generalized least squares to estimate the parameters with the GLS function in the NLME package (Pinheiro et al., 2007) for R, assuming that the residuals followed a first-order autoregressive (AR1) error structure. The parameter estimates obtained by GLS were not substantially different from those obtained by ordinary least squares, so only the results obtained by ordinary least squares are presented. In general, stand density, mean tree size and average competition were expected to be significant predictors of changes in both size and size increment inequality. It was also expected that stand-level annual volume increment would be a significant predictor of inequality of size increment, but would not be a significant predictor of inequality of size.

RESULTS

Size and growth rate inequality

From 1950 to 2004, the Gini coefficient for size was nearly always less than 0·5, meaning that tree sizes could be characterized as equal (Fig. 2). During the same time period, the Gini coefficient for size increment was also generally less than 0·5, but there were periods at all sites when it was greater than 0·5, indicating that size increment could often be considered more unequal than equal (Fig. 2). Size inequality generally declined over time. Based upon the 95 % confidence intervals, the nutrient-poor sites had more unequal tree sizes. Size increment was more unequal than size, and its inequality was also more variable from year to year than inequality in size, showing both increasing and decreasing trends from year to year, depending upon the site. Inequality in size increment was not different at rich and poor sites.

Fig. 2.

Fig. 2.

Open in a new tab

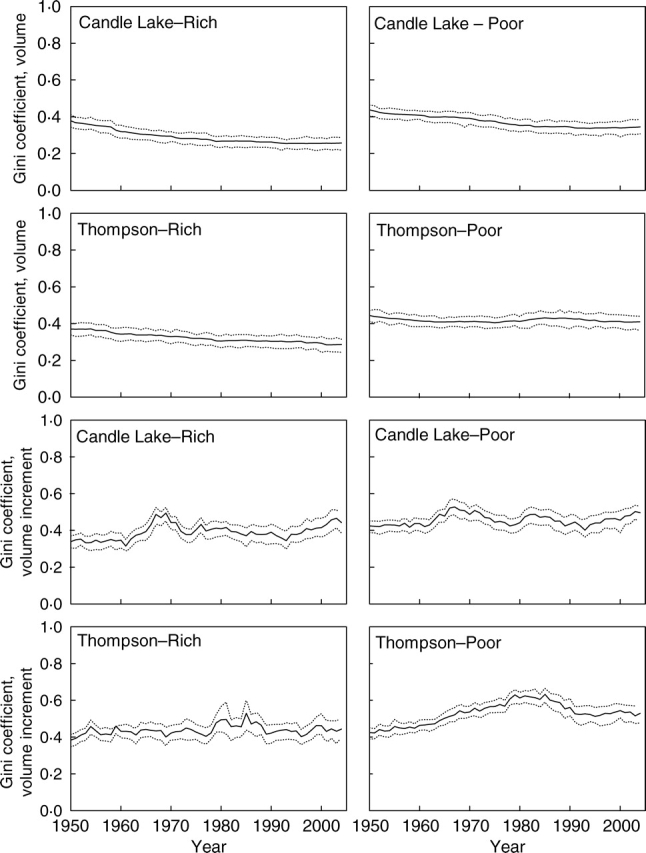
Annual trajectories of the Gini coefficient for size and size increment since 1950 at each study plot. The solid line represents the Gini coefficient, and the dotted lines are 95 % confidence intervals calculated from 1000 bootstrap samples.

The Lorenz asymmetry coefficient for size increment was also more variable from year to year than the Lorenz asymmetry coefficient for size (Fig. 3). For the vast majority of the time, the Lorenz asymmetry coefficient for size was not significantly different from 1, indicating that the observed inequality in tree size was not due to either large or small trees. The Lorenz asymmetry coefficient for size increment, however, had many periods of time when it was significantly less than 1 at all sites, indicating that the observed inequality in size increments was often due to larger numbers of trees with small size increments. There was one clear exception to this trend. At the nutrient-rich site at Candle Lake, the two years (1966 and 1967) with Lorenz asymmetry coefficients greater than 1 correspond to the years with the lowest growth rate at that site, and also to two years during which the historical records of the Canadian Forest Insect and Disease Survey indicate that this area was subject to a jack pine budworm defoliation event. In this specific case, the observed inequality in growth rates at this stand was due to a small number of trees that had high growth rates, most likely because they were not defoliated and continued to grow at a normal rate.

Fig. 3.

Fig. 3.

Open in a new tab

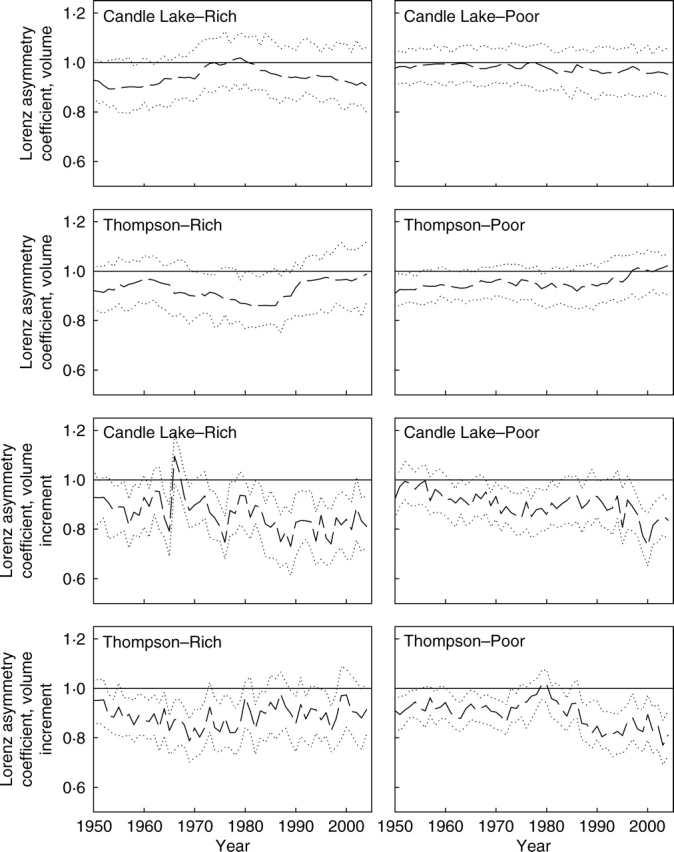
Annual trajectories of the Lorenz asymmetry coefficient for size and size increment since 1950 at each study plot. The solid line indicates the value 1, where the Lorenz curve is symmetric. The dashed line represents the Lorenz asymmetry coefficient, and the dotted lines are 95 % confidence intervals calculated from 1000 bootstrap samples.

Average competition and competition variability

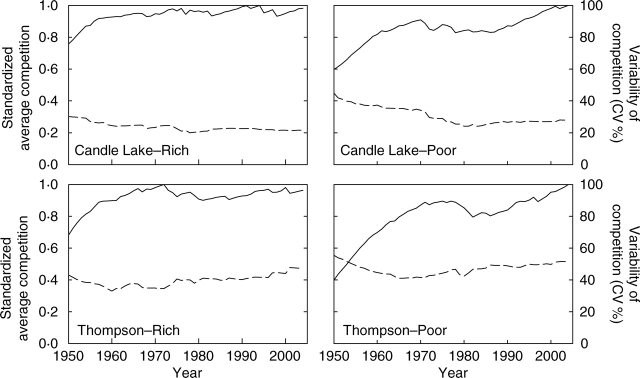
The average amount of competition (standardized by the maximum average annual competition observed at a given site so that each plot could be compared on the same scale) showed both increasing and decreasing trends over time at each plot (Fig. 4). Initially, average competition increased at each site up to about 1970 (Fig. 4). After that point, it stayed relatively constant at the nutrient-rich sites, while the nutrient-poor sites showed a second increase in average competition that started about 15 years later (about 1985, Fig. 4). Overall, the increase in average competition from its minimum value was higher at nutrient-poor sites (where the minimum value was 0·4–0·6 times the maximum) than at nutrient-rich sites (where the minimum value was 0·7–0·8 times the maximum). The CV % for competition ranged from 20 to 50 % at all sites (Fig. 4), indicating that even though the average amount of competition that trees were subject to changed over time, the amount that each tree was subject to in a given year tended be similar. In addition, although there were periods of time at each site where the CV % for competition had small increasing or decreasing trends, the value of the CV % at any given site ranged only in the order of ±10 % over the whole study period, indicating that the variability in the amount of competition to which trees were subject to did not change substantially over time.

Fig. 4.

Fig. 4.

Open in a new tab

Annual trajectories of the average amount of competition to which each tree is subject (solid line) and the coefficient variation (CV %) of competition to which each tree is subject (dashed line) at each study plot. Competition was quantified using a distance-weighted absolute size index (eqn 4), with a variable search radius defined as 3·5 times each tree's crown width.

Regression model results

Size inequality was well described by long-term changes in stand dynamics. With the exception of the nutrient-rich site at Thompson, density, mean tree size and average competition were significant predictors of size inequality at all four sites (Table 2). At three of the four sites, size inequality was positively associated with density and mean tree size, and negatively associated with average competition. At the nutrient-poor site at Thompson, size inequality was negatively associated with all three predictors. Only at the rich site at Candle Lake was stand-level annual volume increment (in this case, lagged by 1 year) a significant predictor of changes in size inequality. Variability in the significance and sign of the coefficients associated with the predictor variables indicates that to some extent the specific relationships between these predictors and changes in inequality were site specific.

Table 2.

Parameter estimates, standard errors and P-values for the regression model for inequality of size and size increment

Candle Lake–Rich
 Candle Lake–Poor
 Thompson–Rich
 Thompson–Poor
Mean s.e. P Mean s.e. P Mean s.e. P Mean s.e. P
Volume
 Intercept 2·3 × 10−1 4·6 × 10−2 <0·01 1·6 × 10−1 1·1 × 10−2 <0·01 2·1 × 10−1 2·8 × 10−2 <0·01 5·5 × 10−1 8·8 × 10−3 <0·01
 DENS 1·5 × 10−4 1·8 × 10−5 <0·01 1·1 × 10−4 4·0 × 10−6 <0·01 9·7 × 10−5 1·6 × 10−5 <0·01 −2·1 × 10−5 2·3 × 10−6 <0·01
 SIZE 3·9 × 10−1 1·2 × 10−1 <0·01 1·1 × 10 0 9·9 × 10−2 <0·01 1·6 × 10−1 1·4 × 10−1 0·26 −1·2 × 10 0 2·6 × 10−1 <0·01
 COMP −3·2 × 10−3 3·7 × 10−4 <0·01 −1·0 × 10−3 1·0 × 10−4 <0·01 −8·1 × 10−4 1·3 × 10−4 <0·01 −1·4 × 10−3 1·0 × 10−4 <0·01
 AVI 7·2 × 10−4 1·4 × 10−3 0·61 3·8 × 10−4 9·9 × 10−4 0·70 9·5 × 10−4 1·1 × 10−3 0·41 −2·4 × 10–3 2·7 × 10–3 0·37
 AVI1 4·4 × 10−3 1·4 × 10−3 <0·01 −1·0 × 10−3 9·9 × 10−4 0·32 −1·3 × 10−3 1·0 × 10−3 0·22 −3·9 × 10–3 2·8 × 10–3 0·17
 Adjusted R2 0·97 <0·01 0·99 <0·01 0·98 <0·01 0·85 <0·01
Volume increment
 Intercept 3·1 × 10−1 2·5 × 10−1 0·23 4·1 × 10−1 8·9 × 10−2 <0·01 6·4 × 10−1 2·0 × 10−1 <0·01 8·2 × 10−2 5·7 × 10−2 <0·01
 DENS 1·3 × 10−4 9·7 × 10−5 0·18 −2·5 × 10−5 3·1 × 10−5 0·42 −1·4 × 10−5 1·1 × 10−4 0·89 −1·2 × 10−4 1·5 × 10−5 <0·01
 SIZE 1·0 × 10 0 6·6 × 10−1 0·12 −1·2 × 10 0 7·7 × 10−1 0·12 −4·7 × 10−1 9·9 × 10−1 0·63 −1·1 × 10 1 1·7 × 10 0 <0·01
 COMP −1·9 × 10−3 1·9 × 10−3 0·32 3·7 × 10−3 8·2 × 10−4 <0·01 −1·0 × 10−3 9·6 × 10−4 0·28 6·1 × 10−3 6·5 × 10−4 <0·01
 AVI −2·8 × 10−3 7·6 × 10−3 0·71 −1·4 × 10−2 7·8 × 10−3 0·07 −2·0 × 10−2 8·2 × 10−3 0·02 −4·9 × 10−2 1·7 × 10−2 <0·01
 AVI1 −2·4 × 10−2 7·5 × 10−3 <0·01 −2·0 × 10−2 7·8 × 10−3 0·01 −8·8 × 10−3 7·2 × 10−3 0·23 −1·9 × 10−2 1·8 × 10−2 0·29
 Adjusted R2 0·41 <0·01 0·54 <0·01 0·42 <0·01 0·85 <0·01
Open in a new tab

The variables in the table are stand density (DENS), mean tree volume (SIZE), average amount of competition to which each tree is subject (COMP), where competition is calculated using a distance-weighted absolute size index, and stand-level annual volume increment in the current year (AVI) and 1 year previously (AVI1).

Parameters in bold type were significant at P <0·05.

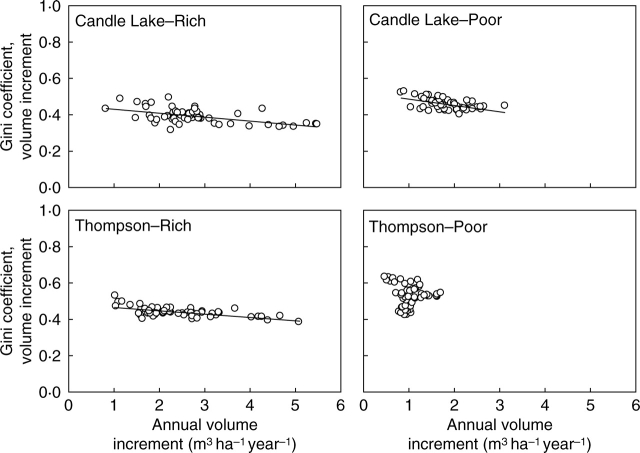
Some combinations of density, mean tree size and average competition were also significantly associated with changes in the inequality of size increment at all but the rich site at Candle Lake, where only stand-level annual volume increment (in this case lagged by 1 year) was a significant predictor (Table 2). Again, the sign and significance of the coefficients for these predictors varied, indicating that the specific relationship between them and changes in the inequality of growth rate were also site specific. Stand-level annual volume increment was a significant predictor of changes in the inequality of size increment at all four sites. At Candle Lake, the significant predictor was lagged by 1 year, while at Thompson it was not. In all cases, the sign of the coefficients for this predictor (significant or not) were negative, indicating increasing inequality in volume increment when stand growth rates were low. Figure 5 plots the relationship between the inequality of size increment and variation in the stand-level annual volume increment to demonstrate this relationship graphically.

Fig. 5.

Fig. 5.

Open in a new tab

Plots of the relationship between the inequality of size increment, as quantified by the Gini coefficient, and stand-level annual volume increment at each study plot. Significant regression lines are shown.

DISCUSSION

Overall, these results showed that factors influencing the annual growth rate of the stand in a given year were also influencing the inequality in growth rates for individual trees in that year. The inequality in size increment was higher in years with poor growth, indicating that it was the years with poor growth that contributed most to the generation of the size hierarchy in these populations. The average amount of competition to which each tree was subject was a predictor of the inequality of size at all four sites, and of the inequality of size increment at two of the four sites. However, changes in competition, or at least in the way that it was quantified here, were not generally sufficient to explain the observed inter-annual variation in the inequality of size increment. This contention is supported by the fact that the annual growth rate was a significant predictor of inequality in size increment at all four sites. Secondly, there was a high degree of variability in inequality in size increment from year to year, even though the CV % of the competition index showed that each tree was subject to a relatively similar amount of competition in a given year, and that the overall variability in the competition index stayed relatively constant from year to year.

In jack pine, poor growth is probably related to drought or defoliation, the dominant agents of selection on the sandy, nutrient-poor sites on which this species is dominant in this region. In most years, inequality in size increment was primarily due to large numbers of trees with low growth rates (Fig. 3), but was also due to small numbers of trees with high growth rates during some years of low growth rate, at some sites. For example, the period with high values for the Lorenz coefficient of asymmetry for the nutrient-rich site at Candle Lake during the 1960s (Fig. 3) was coincident with a period of defoliation (Volney, 1988), suggesting that defoliation caused inequality in size increment to be due to a small number of trees with large growth rates. The trees with large growth rates during these years probably escaped defoliation, and would be in a position of relative competitive advantage. Defoliation in jack pine causes greater mortality in suppressed than dominant trees (Gross, 1992), and escaping defoliation may be one of the factors that allowed the surviving trees to become dominant.

Previous studies have shown that competitive status of trees affects their response to variation in precipitation. For example, Orwig and Abrams (1997) and Wichmann (2001) have noted that increased water availability benefits large trees more than small trees. In a study of European beech, Piutti and Cescatti (1997) showed that growth was negatively correlated with precipitation under water deficit conditions for small trees, but that growth in large trees showed no relationship with water deficit conditions. Similarly, Orwig and Abrams (1997) showed that, in general, small trees were more severely affected by drought than large trees for a wide variety of species and site types. In contrast to the periods of defoliation, the general trend in this study was that inequality in size increment was mostly due to a large number of trees with small growth rates (Fig. 3). The trees that performed poorly may have been poorly adapted to drought, possibly due to inappropriate genetics, a poor micro-site or shallow rooting depth. During low precipitation periods, better-adapted trees could maintain some growth and become relatively larger compared with poorly adapted trees during these drought years. Similar to the situation for trees that escape defoliation, this advantage would improve their relative competitive status and allow them to become dominant in future years.

Size was more equal than size increment, and size inequality was also less variable from year to year. In a given region, size inequality was higher at nutrient-poor than nutrient-rich sites. This conforms to expectation because self-thinning, which acts to reduce inequality by removing the smallest individuals, typically occurs more slowly at nutrient-poor sites. However, this observation may have been confounded by density also being higher at poor sites. The observed greater inequality in size increment also conformed to expectation. In some years, the growth rate for individual trees can be close to zero, which would result in high inequality. By contrast, it is not possible for tree size to be close to zero, so there is less potential for inequality in size. Overall, some combination of stand density, mean tree size and average competition index were significant predictors of size inequality at all sites. These variables all change over time in a highly interactive manner, which was reflected in the variation in the sign and significance of the coefficients for these predictors. The observed relationships were site-specific and not always consistent with the expectation of increasing inequality of size at high stand densities or high levels of competition. Self-thinning mortality generally decreases size inequality by removing the smallest individuals. However, small changes in the relative position of dead trees in the overall size distribution of the stand can result in either increases or decreases in the inequality of the size distribution in the years following a mortality event, and these changes can also be influenced by the growth rate of the surviving trees (Kenkel et al., 1997). Factors causing years of high and low growth rate may also concurrently influence the probability of mortality for trees of slightly different size classes. For example, years of high growth rate may increase the probability of mortality for only the smallest trees, as high growth rates may increase the asymmetry of competition and cause ‘regular’ or autogenic mortality associated with stand dynamics (Oliver and Larsson, 1996). On the other hand, years of low growth rate may increase the probability of mortality for all size classes and cause ‘irregular’ or allogenic mortality (Oliver and Larsson, 1996), which is not necessarily exclusively in the smallest size classes, particularly if the causes of low growth are environmental.

Mean tree size, stand density and average competition were also significant predictors for the inequality of size increment at all but the nutrient-rich site at Candle Lake, where stand-level annual volume increment (lagged by 1 year) was the only significant predictor. This indicates that inequality in size increment was also somewhat related to stand dynamics. Again, however, the sign and significance of the coefficients were not consistent, indicating that observed relationships were also site-specific. These inconsistencies are suggestive of changes in the relative importance of one-sided (where small trees have little effect on large trees) and two-sided (where small trees also have an important effect on large trees) competition over time, both of which are observed to occur in even-aged tree populations (Brand and Magnussen, 1988). The site-specific nature of the relationships between variables associated with stand dynamics and size and size-increment inequality suggests that the relative importance of these two modes of competition over time is also site-specific.

The results of this study suggest that factors influencing the annual growth rate are also influencing the development of size hierarchy in these forests, and that it is primarily the years with low growth rate that influence this development. Studies quantifying competition effects on tree growth usually measure subject trees and their competitors at a single point in time only, resulting in static estimates of competition indices for only single points in time (Burton, 1993). Spatial or aspatial indices of competition (e.g. Lorimer, 1983; Tome and Burkhardt, 1989; Holmes and Reed, 1991; Biging and Dobbertin, 1992, 1995) are the dominant mechanism for generation of size hierarchy in many tree growth models. Using these indices usually results in moderately increased correlations between observed and predicted growth rates over time. However, there is clearly much residual variability in the growth response in these models that is not explained by competition. Schwinning and Weiner (1998) indicated that the effects of transient factors such as weather variation and defoliation on development of size hierarchies are poorly understood, but the data presented in the present study indicate consistent and significant effects of yearly growing conditions. The sensitivity of jack pine to variation in weather (Larsen and MacDonald, 1995; Brooks et al., 1998; Hofgaard et al., 1999) and periodic defoliation by jack pine budworm (Volney, 1988; Gross, 1992) is clearly important to the differentiation of growth rates of trees within populations as their effects are likely to be different from those induced by density-dependent effects (Weiner and Thomas, 1986). Differences in growth rate among trees during years of poor growth may form the basis for development of size hierarchies on which asymmetric competition can act. This suggests that a complete understanding of the process of competition in these forests requires further evaluation of how factors that influence variation in the annual growth rate also affect how size hierarchies are generated in these populations.

ACKNOWLEDGEMENTS

We thank Derek Bakker, Jennifer Hofman, Michael Laczek and Theresa Mundell for assistance in the field. Fieldwork was supported by Circumpolar-Boreal Alberta research grants and the Natural Science and Engineering Council of Canada, and J.M.M. was supported by a Natural Science and Engineering Research Council of Canada scholarship, a Province of Alberta Graduate Fellowship and a Prairie Adaptation Research Collaborative graduate scholarship.

LITERATURE CITED

  1. Beckingham JD, Neilsen DG, Futoransky VA. Field guide to the ecosites of the mid-boreal ecoregions of Saskatchewan. Edmonton, AB: Natural Resources Canada, Canadian Forest Service, Northern Forestry Centre; 1996. Special Report 6. [Google Scholar]
  2. Biging GS, Dobbertin M. A comparison of distance-dependent competition measures for height and basal area growth of individual conifer trees. Forest Science. 1992;38:695–720. [Google Scholar]
  3. Biging GS, Dobbertin M. Evaluation of competition indices in individual tree growth models. Forest Science. 1995;41:360–377. [Google Scholar]
  4. Brand DG, Magnussen S. Asymmetric, two-sided competion in even aged monocultures of red pine. Canadian Journal of Forest Research. 1988;18:901–910. [Google Scholar]
  5. Brassard BW, Chen HYH. Stand structural dynamics of North American boreal forests. Critical Reviews in Plant Science. 2006;25:115–137. [Google Scholar]
  6. Brooks JR, Flanagan LB, Ehrlinger JR. Responses of boreal conifers to climate fluctuations: indications from tree-ring widths and carbon isotope analyses. Canadian Journal of Forest Research. 1998;28:524–533. [Google Scholar]
  7. Burton PJ. Some limitations inherent to static indices of plant competition. Canadian Journal of Forest Research. 1993;23:2141–2152. [Google Scholar]
  8. Carrer M, Urbinati C. Spatial analysis of structural and tree-ring related parameters in a timberline forest in the Italian Alps. Journal of Vegetation Science. 2001;12:643–652. [Google Scholar]
  9. Damgaard C, Weiner J. Describing inequality in plant size or fecundity. Ecology. 2000;81:1139–1142. [Google Scholar]
  10. Dixon PM, Weiner J, Mitchell-Olds T, Woodley R. Bootstrapping the Gini coefficient of inequality. Ecology. 1987;68:1548–1551. [Google Scholar]
  11. Ecological Stratification Working Group. A National Ecological Framework for Canada. Ottawa, ON: Agriculture and Agri-Food Canada, Research Branch, Centre for Land and Biological Resources Research and Environment Canada, State of Environment Directorate; 1996. [Google Scholar]
  12. Gál J, Bella IE. New stem taper functions for 12 Saskatchewan timber species. Edmonton, AB: Natural Resources Canada, Canadian Forest Service, Northern Forestry Centre; 1994. Information Report NOR-X-338. [Google Scholar]
  13. Garcia O. Scale and spatial structure effects on tree size distributions: implications for growth and yield modeling. Canadian Journal of Forest Research. 2006;36:2983–2993. [Google Scholar]
  14. Gates DJ, McMurtrie R, Borough CJ. Skewness reversal of distribution of stem diameter in plantations. Australian Forest Research. 1983;13:267–270. [Google Scholar]
  15. Gross HL. Impact analysis for a jack pine budworm infestation in Ontario. Canadian Journal of Forest Research. 1992;22:818–831. [Google Scholar]
  16. Hegyi F. A simulation model for managing jack pine stands. In: Fries J, editor. Growth models for tree and stand simulation. Stockholm: Royal College of Forestry; 1974. pp. 74–90. [Google Scholar]
  17. Halliwell DH, Apps MJ. Boreal Ecosystem–Atmosphere Study (BOREAS) biometery and auxiliary sites: overstory and understory data. Edmonton, AB: Natural Resources Canada, Canadian Forest Service, Northern Forestry Centre; 1997. [Google Scholar]
  18. Henry JD, Swan JMA. Reconstructing forest history from live and dead plant material: an approach to the study of forest succession in southwest New Hampshire. Ecology. 1974;55:772–783. [Google Scholar]
  19. Hofgaard A, Tardif J, Bergeron Y. Dendroclimatic response of Picea mariana and Pinus banksiana along a latitudinal gradient in the eastern Canadian boreal forest. Canadian Journal of Forest Research. 1999;29:1333–1346. [Google Scholar]
  20. Hogg EH, Wein RW. Impacts of drought on forest growth and regeneration following fire in southwestern Yukon, Canada. Canadian Journal of Forest Research. 2005;35:2141–2150. [Google Scholar]
  21. Hogg EH, Brandt JP, Kochtubajda B. Factors affecting interannual variation in growth of western Canadian aspen forests during 1951–2000. Canadian Journal of Forest Research. 2005;35:610–622. [Google Scholar]
  22. Holmes MJ, Reed DD. Competition indices for mixed species northern hardwoods. Forest Science. 1991;37:1338–1349. [Google Scholar]
  23. Husch B, Beers TW, Kershaw JA. Forest mensuration. 4th edn. Hoboken, NJ: John Wiley and Sons; 2003. [Google Scholar]
  24. Johnson EA, Fryer GI. Population dynamics in lodgepole pine–engelmann spruce forests. Ecology. 1989;70:1335–1345. [Google Scholar]
  25. Kenkel NC, Hendrie ML, Bella IE. A long-term study of Pinus banksiana population dynamics. Journal of Vegetation Science. 1997;8:241–254. [Google Scholar]
  26. Klos R. Ecologically based taper equations for major tree species in Manitoba. Canada: Lakehead University; 2004. MSc thesis. [Google Scholar]
  27. Knox RG, Peet RK, Christensen NL. Population dynamics in Loblolly pine stands: changes in skewness and size inequality. Ecology. 1989;70:1153–1166. [Google Scholar]
  28. Kozak A. A variable-exponent taper equation. Canadian Journal of Forest Research. 1988;18:1362–1368. [Google Scholar]
  29. Larsen CPS, MacDonald GM. Relations between tree-ring widths, climate, and annual area burned in the boreal forest of Alberta. Canadian Journal of Forest Research. 1995;25:1746–1755. [Google Scholar]
  30. Lorimer CG. Tests of age-independent competition indices for individual trees in natural hardwood stands. Forest Ecology and Management. 1983;6:343–360. [Google Scholar]
  31. Mast JN, Veblen TT. A dendrochronological method of studying tree mortality patterns. Physical Geography. 1994;15:529–542. [Google Scholar]
  32. Metsaranta JM, Lieffers VJ, Wein RW. Dendrochronological reconstruction of jack pine snag and downed log dynamics in Saskatchewan and Manitoba, Canada. Forest Ecology and Management. 2007 (in press) [Google Scholar]
  33. Mohler CL, Marks PL, Sprugel DG. Stand structure and allometry of trees during self-thinning of pure stands. Ecology. 1978;66:599–614. [Google Scholar]
  34. Newton PF, Smith VG. Diameter distributional trends within mixed black spruce/balsam fir and pure black spruce stand types. Forest Ecology and Management. 1988;25:123–138. [Google Scholar]
  35. Oliver CD, Larsson BC. Forest stand dynamics. Update Edition. New York: John Wiley and Sons; 1996. [Google Scholar]
  36. Oliver CD, Stephens EP. Reconstruction of a mixed-species forest in Central New England. Ecology. 1978;58:562–572. [Google Scholar]
  37. Orwig DA, Abrams MA. Variation in radial growth responses to drought among species, site, and canopy strata. Trees: Structure and Function. 1997;11:474–484. [Google Scholar]
  38. Pinheiro J, Bates D, Debroy S, Sarkar D. NLME: linear and nonlinear mixed effects models. Vienna: R Foundation for Statistical Computing; 2007. version 3·1–81. R Package. [Google Scholar]
  39. Piutti E, Cescatti A. A quantitative analysis of the interactions between climatic response and intraspecific competition in European beech. Canadian Journal of Forest Research. 1997;27:277–284. [Google Scholar]
  40. R Development Core Team. R: a language and environment for statistical computing. Vienna: R Foundation for Statistical Computing; 2007. [Google Scholar]
  41. Ramseier D, Weiner J. Competitive effect is a linear function of neighbour biomass in experimental populations of Kochia scoparia. Journal of Ecology. 2006;94:305–309. [Google Scholar]
  42. Schwinning S, Weiner J. Mechanisms determining the degree of size symmetry in competition among plants. Oecologia. 1998;113:447–455. doi: 10.1007/s004420050397. [DOI] [PubMed] [Google Scholar]
  43. Stoll P, Weiner J, Schmid B. Growth variation in a naturally established population of Pinus sylvestris. Ecology. 1994;75:660–670. [Google Scholar]
  44. Tome M, Burkhardt H. Distance-dependent competition measures for predicting growth of individual trees. Forest Science. 1989;35:816–831. [Google Scholar]
  45. Volney WJA. Analysis of historic jack pine budworm outbreaks in the Prairie provinces of Canada. Canadian Journal of Forest Research. 1988;18:1152–1158. [Google Scholar]
  46. Volney WJA, Mallett KI. Light rings and the age of jack pine trees. Canadian Journal of Forest Research. 1992;22:2011–2013. [Google Scholar]
  47. Weiner J. Size hierarchies in experimental populations of annual plants. Ecology. 1985;66:743–752. [Google Scholar]
  48. Weiner J. Asymmetric competition in plant populations. Trends in Ecology and Evolution. 1990;5:360–364. doi: 10.1016/0169-5347(90)90095-U. [DOI] [PubMed] [Google Scholar]
  49. Weiner J. Following the growth of individuals in crowded plant populations. Trends in Ecology and Evolution. 1995;10:389–390. doi: 10.1016/s0169-5347(00)89150-8. [DOI] [PubMed] [Google Scholar]
  50. Weiner J, Damgaard C. Size-asymmetric competition and size-asymmetric growth in a spatially explicit zone-of-influences mode of plant competition. Ecological Research. 2006;21:770–712. [Google Scholar]
  51. Weiner J, Solbrig OT. The meaning and measurement of size hierarchies in plant populations. Oecologia. 1984;61:334–336. doi: 10.1007/BF00379630. [DOI] [PubMed] [Google Scholar]
  52. Weiner J, Thomas SC. Size variability and competition in plant monocultures. Oikos. 1986;47:211–222. [Google Scholar]
  53. Westoby M. Frequency distributions of plant size during competitive growth of stands: the operation of distribution modifying functions. Annals of Botany. 1982;50:733–735. [Google Scholar]
  54. Wichmann L. Annual variations in competition symmetry in even-aged sitka spruce. Annals of Botany. 2001;88:145–151. [Google Scholar]
  55. Yamaguchi DK. A simple method for cross-dating increment cores from living trees. Canadian Journal of Forest Research. 1991;21:414–416. [Google Scholar]
  56. Zoladeski CA, Wickware GM, Delorme RJ, Sims R, Corms IGW. Forest ecosystem classification for Manitoba: field guide. Edmonton, AB: Natural Resources Canada, Canadian Forest Service, Northern Forestry Centre; 1995. Special Report 2. [Google Scholar]

Articles from Annals of Botany are provided here courtesy of Oxford University Press

RESOURCES