Abstract
Background
The contribution of vegetation to shallow-slope stability is of major importance in landslide-prone regions. However, existing slope stability models use only limited plant root architectural parameters. This study aims to provide a chain of tools useful for determining the contribution of tree roots to soil reinforcement.
Methods
Three-dimensional digitizing in situ was used to obtain accurate root system architecture data for mature Quercus alba in two forest stands. These data were used as input to tools developed, which analyse the spatial position of roots, topology and geometry. The contribution of roots to soil reinforcement was determined by calculating additional soil cohesion using the limit equilibrium model, and the factor of safety (FOS) using an existing slope stability model, Slip4Ex.
Key Results
Existing models may incorrectly estimate the additional soil cohesion provided by roots, as the spatial position of roots crossing the potential slip surface is usually not taken into account. However, most soil reinforcement by roots occurs close to the tree stem and is negligible at a distance >1·0 m from the tree, and therefore global values of FOS for a slope do not take into account local slippage along the slope.
Conclusions
Within a forest stand on a landslide-prone slope, soil fixation by roots can be minimal between uniform rows of trees, leading to local soil slippage. Therefore, staggered rows of trees would improve overall slope stability, as trees would arrest the downward movement of soil. The chain of tools consisting of both software (free for non-commercial use) and functions available from the first author will enable a more accurate description and use of root architectural parameters in standard slope stability analyses.
Key words: Landslide, root area ratio, slope stability, 3D digitizing, Quercus alba, soil cohesion, soil internal friction angle
INTRODUCTION
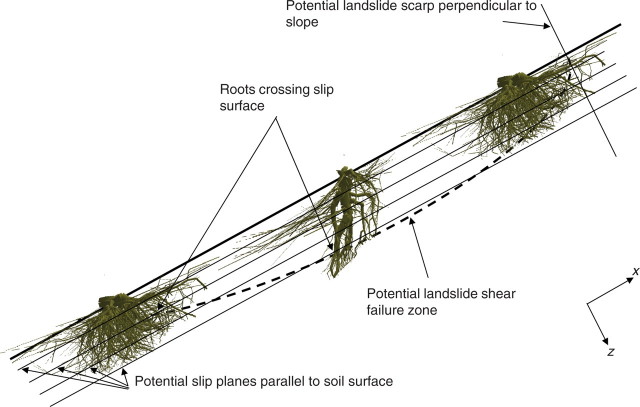
In an era in which climate change is taking place and natural catastrophes, e.g. resulting from storms, flooding and landslides, are becoming more frequent, it is necessary to find effective and economical methods to reduce soil mass movement on a large scale. The reinforcement of soil by vegetation is a highly promising solution with regard to reducing superficial landslide risk and erosion on both natural and man-made slopes (Gray and Leiser, 1982; Barker et al., 2004; Reubens et al., 2007; Stokes et al., 2007). On forested slopes, reinforcement is provided by both thin and coarse roots, the former acting more as tensile elements within the soil matrix, whereas large-diameter roots can also act as tendons or anchors connecting planted surface layers to underlying or adjacent stable soil zones (Fig. 1). Although information has been made available in recent years concerning the mechanical behaviour of soil–root interactions (Dupuy et al., 2005a; Mickovski et al., 2005; Norris, 2005; Hamza et al., 2007), few data exist on how the spatial arrangement of roots within soil contributes to soil fixation.
Fig. 1.
Roots crossing potential slip planes will reinforce the slope against landslides. Trees with many thick vertical roots will fix soil better in the middle of the slope whereas trees with oblique roots will reinforce the top or toe of the slope better.
The reinforcement of a potential landslide plane, or slip surface, by a woody root is mainly a function of (1) its tensile strength, and of the following characteristics at the point of intersection: (2) root cross-sectional area (CSA), (3) root angle towards the crossing plane, (4) mean root length to the previous branch and (5) total root length after the intersection point (Wu et al., 1988; Wu, 1995). Tensile strength increases with decreasing root diameter (e.g. Gray and Leiser, 1982; Bischetti et al., 2005; Genet et al., 2005), and therefore a large number of thin woody roots should improve slope stability. The number of roots crossing the slip surface has also been shown to have a major effect on slope stability as the presence of roots significantly increases the shear resistance of soil (Cammeraat et al., 2005; van Beek et al., 2005).
The maximum possible root contribution to soil strength is traditionally estimated from measuring the fraction of corresponding soil CSA occupied by roots, or the root area ratio (RAR – Gray and Leiser, 1982; Shields and Gray, 1992). Largest fine and coarse root distributions are generally measured by mapping the intersection of roots on successive profile walls of soil parallel to the soil surface (Böhm, 1979; Gray and Leiser, 1982) but in some cases on vertical soil profiles only (Bischetti et al., 2005). RAR is classically estimated as the product of diameter and the number of roots in different diameter classes. Root length and volume distribution with depth have also been measured on uprooted seedlings as an indirect measure of RAR (Nilaweera and Nutalaya, 1999; Mattia et al., 2005). However, these traditional methods do not take into account the three-dimensional (3D) distribution of woody roots within a root system (Reubens et al., 2007). In trees growing on mountain slopes, notwithstanding age effects (Genet et al., 2006), a radial asymmetry is often observed, due to differential gradients of water and nutrients around the tree, as well as the mechanical stresses induced by growth on a slope and the dominant wind direction (Danjon et al., 2005; Di Iorio et al., 2005; Khuder et al., 2006; Nicoll et al., 1995, 2006). Therefore, if traditional profiling methods are used, results may under- or over-estimate RAR, depending on where the profile was positioned around the tree. In addition, within a forest, root distribution is highly heterogeneous depending on the distance between trees and tree size, yet mean values of RAR for a slope are usually included in global slope stability models. Therefore, patches with few roots may lead to local soil slippage, but these patches are rarely taken into account in slope stability analyses.
Using the limit equilibrium model developed by Wu (1976) and elaborated upon by Waldron (1977), the contribution of a root to the shear resistance of soil (ΔS), can be written as:
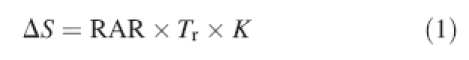 |
1 |
where:
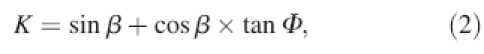 |
2 |
Tr is root tensile strength, RAR is root area ratio, β is angle of shear distortion of root crossing the potential slip plane and Φ is soil internal friction angle.
The model assumes that roots are elastic, orientated perpendicular to the slip plane, fully mobilized in tension and that the effective value for Φ is unaffected by root reinforcement. According to Wu et al. (1979), where Φ is 20–40° and β = 40–70°, K varies between 0·92 and 1·21. As geometric information is often not available, K is usually set to 1·2 regardless of the value of Φ (Bischetti et al., 2005; Mattia et al., 2005; Genet et al., 2006; Reubens et al., 2007).
Once the ΔS provided by roots to the soil has been calculated, it can then be added as a parameter to slope stability models, e.g. Slip4Ex (Greenwood, 2006). Slip4Ex calculates the factor of safety (FOS) for a given slope depending on input data on slope geometry, soil physical characteristics and other environmental parameters, e.g. water table level. FOS for slope stability is the ratio of shear strength to shear stress and so indicates whether a slope is stable or not. By using such models, it is possible to determine under what conditions FOS will evolve. Although Slip4Ex can calculate the FOS of heterogeneous slopes, only one value of FOS is given for the entire slope (Greenwood, 2006); therefore, it is not easy to detect if local patches of instability occur along the slope, due to, for example, differences in vegetation.
To investigate how variations in tree root system architecture influence shallow-slope stability, a chain of tools was developed to measure coarse root geometry and morphology of trees in situ. RAR and ΔS provided by roots can then be calculated in successive planes parallel to the slope (Fig. 1). These tools were then tested on two adult Quercus alba trees of different sizes growing in neighbouring stands. Results are presented with regard to how root geometry influences soil reinforcement by using Wu et al.'s (1979) model and the consequences for shallow-slope stability on a large scale. The utility of the tools developed and how they can be improved are also discussed.
EXPERIMENTAL STUDIES
Plant and site description
To provide data from real trees which could then be used for analysis with the tools developed in this study, it was necessary to measure root system architecture of trees growing on sloping ground. Two white oak (Quercus alba L.) trees of different sizes were selected for the study. One dominant (tree D) and one suppressed tree (tree S) were sampled in two nearby similar stands located in the University of Georgia's Warnell School of Forest Resources Whitehall Research Forest, 5 km from Athens, Georgia, USA (33°56′00″N, 83°22′00″W). These stands are composed of 60- to 100-year-old mixed pine and hardwood consisting primarily of naturally regenerated white oak, Liriodendron tulipifera L., Sassafras albidum (Nutt.) Nees and Cornus florida L. on a former cotton estate. Stand density was approximately 650 trees per hectare. The stocking rate within a 12·5-m-diameter circle around the trees was 21 m2 ha−1 basal area for tree D and 15·3 m2 ha−1 basal area for tree S.
The forest site has never been managed, thus resulting in closely spaced etiolated tree growth of maximum 30 m canopy height. Soils were well-drained, nutrient-depleted regolithic clays derived from granite and mica gneiss bedrock. Tree S had grown over an isolated fissured gneiss boulder at a depth of 0·45 m. Around the boulder, at 0·6 m radial distance, the bedrock was at 1·5 m depth. Around tree D, soil depth was in excess of 2·0 m. Slope angle was 12° for tree D and 18° for tree S. Upslope azimuth was 72° for tree D and 105° for tree S. The slopes had been subject to heavy erosion in the past but which was relatively slight under the present forest cover.
Root architecture measurement
The two root systems were progressively excavated in situ using high-velocity air-lances to loosen and remove soil from around their trunks outwards and downwards with little or no damage to the roots. A 1·35-m-long Air-Spade 2000 (CEG, Verona, PA, USA) and the shorter Soil Pick (MBW, Slinger, WI, USA) were supplied with compressed air from a standard 4·25 m3 min−1 road-works compressor. Even roots of diameter less than 1–2 mm were exposed and undamaged but eventually snapped due to continuous flexing as the work proceeded. The root systems were exposed to depths of over 1·65 m for tree D and 1·4 m for tree S over most of their individual canopy areas. To maintain the root systems exactly in their original position they were stabilized by suspending major roots from wooden planks spanning from the stump to the edges of the excavation. The advantage of using such a technique is that the exact spatial position of each root can be determined, thus collating very precise data.
The topology and position coordinates of both root systems were measured with a 3D digitizer (3SPACE Fastrak, Polhemus, Long Ranger Option, Polhemus, Colchester, VT, USA) using low-frequency electromagnetic field sensing (Sinoquet and Rivet, 1997) and driven by 3A software (Adam et al., 1999; a newer, similar software, PiafDigit, is freely available for non-commercial use at http://www2.clermont.inra.fr/piaf/eng/download/download.php). The device consists of an electronic unit, a magnetic transmitter and a small hand-held receiver positioned at each point to be measured (Danjon et al., 1999a, b). The receiver measures the xyz spatial coordinates within a sphere of 4-m radius around the transmitter sufficient for the root digitizing in this study. The transmitter was positioned at about 1·5 m above the stump in the upslope direction.
The root systems were measured in situ, i.e. still in the soil with roots held in their original positions. For tree D, all roots above an initial diameter of 10 mm were measured, and this threshold was set to 5 mm for tree S. Measurements were taken at each root branching point and at 0·2-m intervals along each root in the absence of any branches of roots larger than the above sizes. On long roots with small taper the measurements were made only at approximately 0·5-m intervals.
Root diameter was measured vertically and horizontally using a micrometer. Root measurements were taken starting from the stump working progressively downwards and outwards, measuring each branch of each root to its tip and then returning to the main root until its end was reached. After measurement, roots were cut as required to enable access to adjacent remaining roots. Each root system required 1 week for excavation and measurement. The coordinates of each point were recorded in a xyz orthonormal reference frame centred on the centre of the tree collar. The positive x-axis was orientated horizontally upslope, and z was orientated vertically in the soil. The stump and taproot were considered to be the first-order root.
Root-specific densities by root diameter class were measured in the laboratory using the water displacement method (the bark was included).
Analysis
To derive root characteristics as a function of distance to the soil surface, and to compute characteristics of roots crossing planes parallel to the slope, the root system data coordinates were rotated 12° or 18° around the y-axis. Therefore, +x was upslope and parallel to the soil surface (Fig. 1). Root axes and segment parameters were computed according to Danjon et al (1999a, b) using the AMAPmod freeware (available for Linux and Windows platforms: https://gforge.inria.fr/frs/?group_id=79; Godin et al., 1997), additional computation and graphics were made with the R open statistical package (Ihaka and Gentleman, 1996; see http://www.r-project.org/).
As the length of segments of long horizontal roots was often more than 0·4 m, the technique used in Danjon et al. (1999a, b) to compute the distribution of root length or volume could not be used. Instead, each segment was virtually divided into 10-mm-long segments; parameters of these segments were used to compute root spatial distribution.
The estimated volume of each root segment was computed using the formulae for a truncated cone. Mean diameter of a segment was computed from the measured volume divided by the length of the segment. The five root size classes (fine, thin, medium, large, very large) were determined from the 2-, 5-, 10- and 20-mm-diameter limits (Böhm, 1979). The mean specific gravity of roots in the five diameter classes were 0·48, 0·48, 0·54, 0·59 and 0·62, respectively. Data were then used to estimate dry weight (Bert and Danjon, 2006).
The stump was defined as the first 0·25 m of the first-order root in both trees. In accordance with Nicoll et al. (1995), it was not included in root volume computations because it makes no active contribution to tree stability and does not contribute directly to soil reinforcement. The branching angle was defined as the angle between the root of the higher order and the parent root segment.
Within the horizontal roots originating above 0·5 m depth, the segments located within twice the collar diameter radial distance were considered to be part of the zone of rapid taper (ZRT) close to the trunk (Danjon et al., 2005). Roots with an angle greater than −30° towards the soil surface were considered as parallel to slope, roots with an angle towards the soil surface less than −50° were considered perpendicular to the slope, and the remaining were considered as oblique roots. Roots above 0·5 m distance from the soil surface were classified as shallow, and roots below 1·1 m distance from the soil surface were classified as deep. Roots between 0·5 and 1·1 m distance to the soil were classified as intermediate depth roots. Relative CSA of large broken ends was computed by summing the breaking CSA of broken ends larger than 10 mm, divided by collar diameter of the tree. These data indicate if the root systems were damaged during the excavation process.
Three sectors were defined for the study of the effect of slope on root architecture: an ‘upslope’ quarter, a ‘downslope’ quarter and a discontinuous ‘perpendicular to slope’ half.
Potential contribution to soil reinforcement
The potential soil reinforcement due to roots was assessed by computing several characteristics of roots crossing planes parallel to the slope surface at given depths. These parameters included position of intersection, CSA, mean angle towards the plane, root length to the preceding branch and cumulative root length downstream of the intersection.
The 3D distribution of RAR was displayed as a multiple 2D graph for four planes parallel to the slope at 0·30-m depth intervals (Fig. 1). The RAR was computed for 40 surfaces of unequal size determined by dividing each plane into eight 45° radial sectors in each of the five 0·5-m radial distance rings spanning the 0–2·5-m radial distance interval at depths of 0·3, 0·6, 0·9 and 1·2 m.
To calculate ΔS using Wu's (1976) model, we made several assumptions: no tensile strength data are available for roots of white oak, and therefore we used a generic equation for several conifer and broadleaved species (Genet et al., 2005):
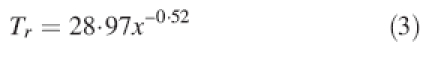 |
3 |
where x is root diameter.
As we did not carry out shear tests of soil and root blocks in situ (Wu and Watson, 1998), no data are available for β (eqn 2). Usually, this angle is assumed to be 45° (Wu, 1976; Abernethy and Rutherfurd, 2001; Greenwood, 2006), but it is highly unlikely that roots deform to such an extent (Abernethy and Rutherfurd, 2001). Therefore, instead of β, we used the actual angle at which the root crossed the potential slip surface. As the position of the slip surface was not known in the soil, ΔS was computed as for RAR, i.e. for 40 surfaces of unequal size determined by dividing each plane into eight 45° radial sectors in each of the five 0·5-m radial distance rings spanning the 0–2·5-m radial distance interval at depths of 0·3, 0·6, 0·9 and 1·2 m.
In eqn (2), K is a factor taking into account that roots are randomly orientated with respect to the potential slip surface plane, which in most cases varies between 1·0 and 1·3 (Waldron, 1977; Wu et al., 1979). To test how K varies depending on root angle across a potential slip plane, we computed the mean K weighted by the root CSA at several depths and for a range of values of Φ, for both trees.
To determine if root architecture influences soil reinforcement locally along a forested slope, isocontour graphs were then created to represent the ΔS provided by roots at a depth of 0·9 m within a forest plantation. The benefit of representing the data in such a way is that it is possible to determine if gaps between trees will result in possible local soil slippage. Data from both trees were used, and the spatial position of trees in both straight and staggered lines perpendicular to the slope was shown to demonstrate the heterogeneous nature of soil reinforcement by roots along a forested slope. To estimate the influence of spacing on ΔS, stem density was set to either 4·50 or 2·25 m between trees.
Inclusion of data in a slope stability model
Once ΔS had been calculated, it was possible to use these data in the model of slope stability, Slip4Ex (Greenwood, 2006). Slip4Ex calculates the overall FOS of a slope using geometrical information and is particularly relevant to the contribution of vegetation to slope stability. FOS <1·0 indicates that a slope is unstable, a value between 1·0 and 1·3 that the slope should be monitored regularly and an FOS of >1·3 indicates a stable slope. No soil mechanical data were available for the study site, but for demonstration purposes, we assumed that soil was clay with Φ = 20°, a cohesion of 5 kN m−2 and a bulk unit weight of soil of 19 kN m−3 (data taken from Greenwood, 2006). Slope angle was 12° for tree D and 18° for tree S and it was assumed that the height of the water table was 0 m, as landslides often occur when soil is saturated. As input to Slip4Ex, we used mean ΔS and mean root angle per 1·0-m slice of soil for roots in the two up- and downslope sectors only. As Slip4Ex is a 2D model, it was not possible to include data from the sectors perpendicular to the slope direction. Slope height (between the slip surface and soil surface) was considered as the depth of the potential slip plane where ΔS had previously been calculated, i.e. 0·3, 0·6, 0·9 and 1·2 m. Slopes were considered as having only one tree, either tree D or tree S positioned in the middle of the slope, and therefore each slope was considered to be 8 m long. Although not representative of field conditions, such an analysis allowed us to determine the contribution of each tree to the FOS and to demonstrate how root architectural data can be included in standard slope stability models.
RESULTS
Root architecture and distribution
Root systems were largely undamaged through excavation as there were few broken root ends (Table 1). The two root systems showed different rooting strategies in that tree D had no taproot, but tree S had a large taproot which forked at 0·67 m depth (Fig. 2). The root system of the suppressed tree had about half the volume and length of that of tree D (Table 1).
Table 1.
Summary data for both root systems computed from 3D digitizing data. Tree D and tree S are the dominant and suppressed tree, respectively
| Variable | Units | Tree D | Tree S |
|---|---|---|---|
| Collar diameter | cm | 32·7 | 22·8 |
| Stump dry weight/below-ground dry weight | % | 13·3 | 20 |
| Taproot dry weight/root without stump dry weight | % | 0 | 34·7 |
| CSA of large broken ends | % | 8·9 | 9·8 |
| Mean segment length | cm | 26·2 | 25·3 |
| Maximum distance to soil surface | cm | 147 | 140 |
| Maximum distance to soil surface for first-order roots | cm | 16·6 | 67·6 |
Fig. 2.

Surface view perpendicular to the soil and side view of the root system for (A) tree D and (B) tree S, reconstructed using AMAPmod. Vertical side view was after 90° rotation.
The dominant tree had a fairly homogeneous distribution of root length, i.e. approximately 25 % root length in both up- and downslope sectors and almost 50 % root length in the sector perpendicular to the slope (Table 2). However, there was a strong upslope increase in root dry weight, at the expense of the downslope sector. Therefore, roots were thicker upslope than downslope (Table 2). Branching rate was assessed using the mean inter-lateral length. Both trees had lower inter-lateral length downslope (Table 2). Order 2 axes encompassed more than half the root volume, comprising 60 and 84 % of root dry weight in tree D and S, respectively.
Table 2.
Root size and branching characteristics
| Tree D | Tree S | Tree D |
Tree S |
||||||
|---|---|---|---|---|---|---|---|---|---|
| Variable | Unit | total | up | pp | do | up | pp | do | |
| Length | m | 432 | 172 | 24% | 56% | 21% | 7·6% | 45% | 48% |
| Dry weight | kg | 79·6 | 32·8 | 39% | 48% | 13% | 4·8% | 28% | 67% |
| Root number | n | 706 | 347 | 26% | 58% | 17% | 6·3% | 42% | 52% |
| Mean inter-lateral length | cm | 10·2 | 10·7 | 11·1 | 10·8 | 6·84 | 13·2 | 11·8 | 9·6 |
| Mean branching angle | degree | 46 | 44·8 | 46·1 | 46·3 | 44·9 | 51·2 | 39·9 | 47·9 |
| Percentage of root dry weight in several root types | |||||||||
| Order 2 roots | % | 51·9 | 70·5 | 60·4 | 46·7 | 45·9 | 84·1 | 75·5 | 67·5 |
| ZRT | % | 13·8 | 10·8 | 13·3 | 16·1 | 7·1 | 5·04 | 29 | 3·7 |
| Parallel* | % | 47·6 | 24·6 | 55·4 | 44·7 | 35 | 18·8 | 61·9 | 9·7 |
| Oblique* | % | 24·7 | 33·9 | 27·4 | 24·3 | 17·8 | 0·4 | 18·6 | 42·6 |
| Perpendicular* | % | 27·8 | 41·5 | 17·2 | 31 | 47·2 | 80·8 | 19·5 | 47·7 |
| Shallow | % | 66 | 33·4 | 72·1 | 62·3 | 61·2 | 60·3 | 67·2 | 17·7 |
| Intermediate | % | 31·4 | 61·4 | 26·8 | 34·3 | 34·6 | 39·7 | 32·3 | 74·8 |
| Deep | % | 2·6 | 5·24 | 1·1 | 3·38 | 4·1 | 0 | 0·5 | 7·5 |
Entire root systems and % or value in each slope orientated sector: upslope/perpendicular to slope/downslope (respectively ‘up’, ‘pp’ and ‘do’). Angle toward soil surface and distance to the soil limits for three root classes: 30 and 50° toward soil surface and 0·5 and 1·1 m distance to soil surface. ZRT, zone of rapid taper of horizontal shallow roots, near the stump.
* Angle toward soil surface is computed on a per root basis, the other variables on a per segment basis.
Both trees had a low percentage of root dry weight in the ZRT downslope (Table 2). The circular distribution as a function of depth was around 2/3 for shallow roots, 1/3 for intermediate deep roots and 1/25 for deep roots, except in the downslope quarter of tree S, where the proportion of shallow roots was less than 1/5.
Potential contribution to soil reinforcement
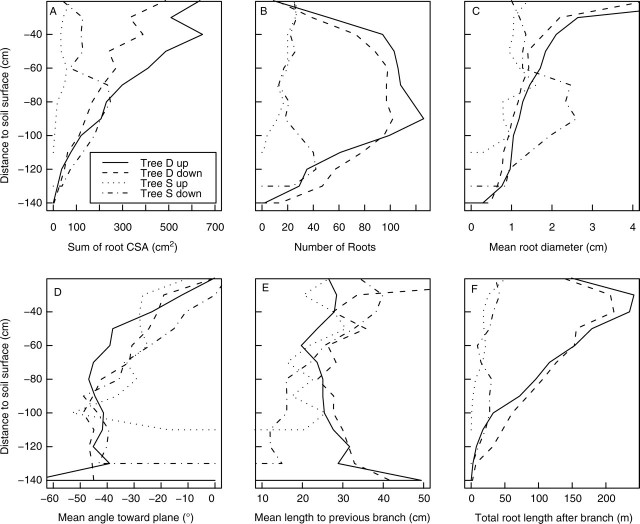
The one-dimensional distribution of up- and downslope characteristics as a function of distance to the soil surface was used to characterize the potential sliding planes (Fig. 3). Tree S had a very low root CSA upslope whereas in tree D, root CSA constantly decreased below 0·4 m depth and was two-fold higher upslope (600 cm2) than downslope in shallow horizons (Fig. 3A). The number of roots was highest in tree D (Fig. 3B), although mean root diameter differed little between trees (Fig. 3C). The mean angle of roots toward the planes parallel to the slope was approximately −30° above 0·7 m depth and −45° below 0·70 m depth in both trees (Fig. 3D). The mean length to the previous branch was generally constant (0·25 m) between depths of 0·3 and 1·1 m (Fig. 3E), whereas total root length after intersecting the slip surface showed a linear decrease between 0·4 and 1·2 m depth in tree D (Fig. 3F).
Fig. 3.
Vertical distributions of different root parameters where roots intersect planes parallel to the slope at 0·1-m intervals. Upslope and downslope profile for each tree: root number, CSA, mean diameter, mean angle toward soil surface, mean length to the previous branch and mean cumulative root length after the intersection.
Multiple 2D maps showing where roots intersect given planes parallel to the slope (Fig. 4) provide an overview of the spatial structure of root reinforcement. In tree D, the 0·3-m depth plane showed intersections of large roots within a radial distance of 0·5 m and few impacts of small roots up to within a radial distance of 1·8 m.
Fig. 4.
Multiple 2D distribution of roots intersecting four planes parallel to the slope at 0·3-m intervals for tree D. Each intersection is represented by a circle proportional to its diameter. The scale is the same for coordinates and for diameters. The (0,0) coordinates correspond to the line passing through the centre of the stump and are perpendicular to the soil surface.
Above a depth of 0·7 m, RAR was around 5 % close to the trunk (0·0–0·5 m radial distance) in tree D, but zero or very low in sectors situated beyond a radial distance of 1·0 m (Fig. 5A). Conversely, at a depth of 0·9 m, a large number of thinner roots were evenly distributed within a 1·0-m radial distance and RAR ranged from 0·14 to 3·30 %. In other words, the area reinforced by roots of the dominant tree at a depth of 0·5 and 1·0 m was approximately 4·0 m2, corresponding to 160 roots and a total CSA of 400 cm2, i.e. 40 roots m−2 or 1 % RAR (Fig. 5A).
Fig. 5.
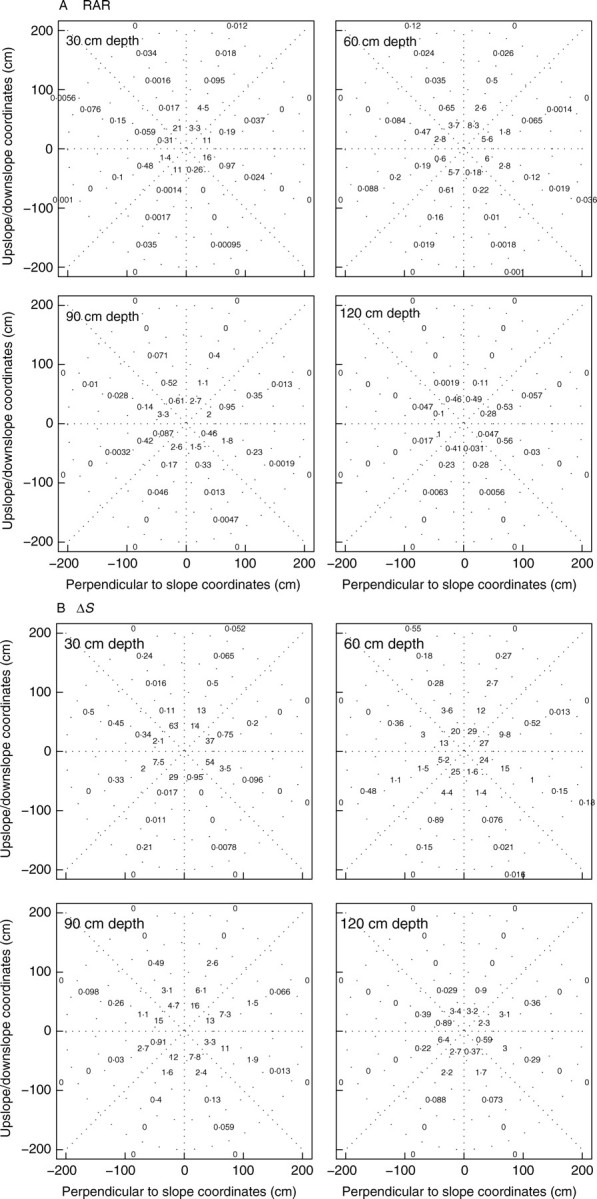
Multiple 2D distribution of (A) root area ratio (RAR), and (B) ΔS in four planes parallel to the slope at 0·3-m depth intervals for tree D. The RAR (%) is given for 40 surfaces of unequal size determined from dividing each plane into eight 45° radial sectors in each of the five 0·5-m radial distance rings spanning the 0–2·5-m radial distance interval. Small dots are the limits between surfaces for which the RAR and ΔS was computed. Φ is set to 20°.
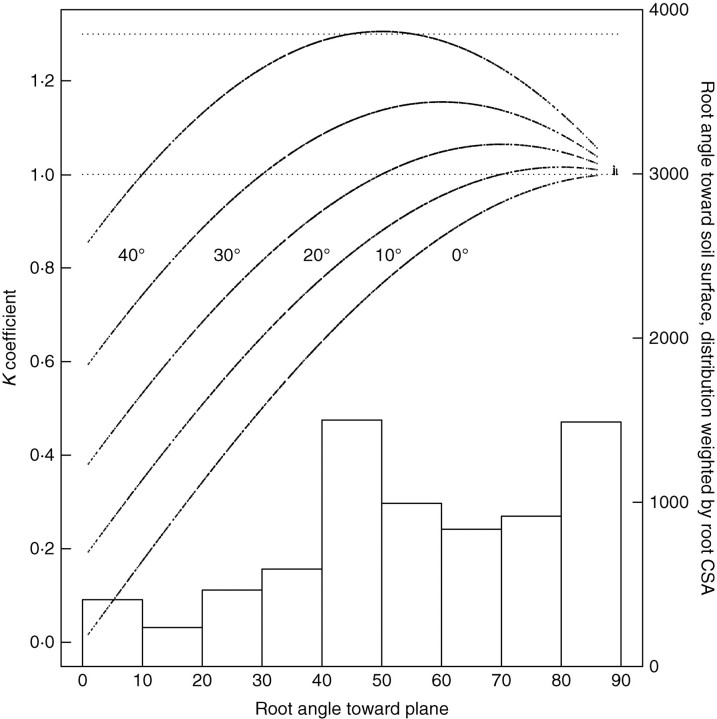
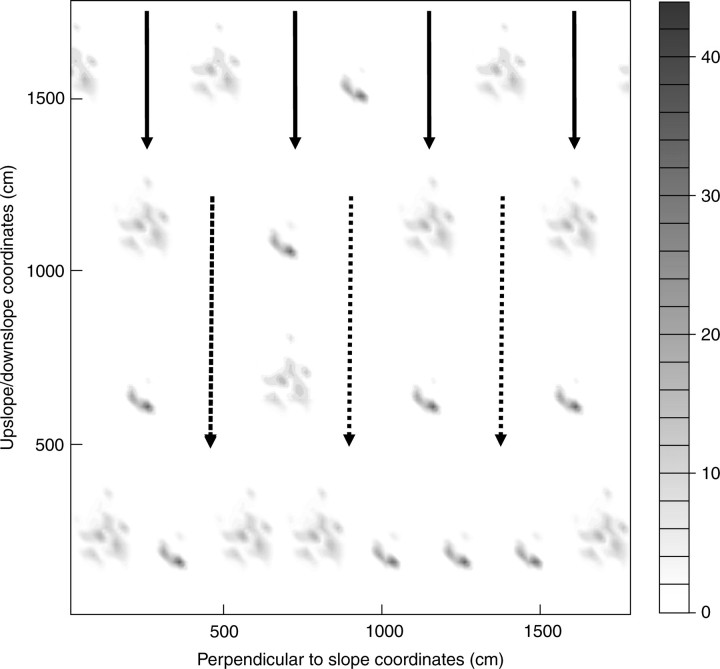
The spatial distribution of ΔS was computed in the same way as above (Fig. 5B), and also along vertical planes which represent the scarp of a landslide, i.e. the origin of failure. The weighted mean of K at several depths for tree D and a range of values for Φ for tree S indicate that the mean K is often lower than 1·2 (Table 3, Fig. 6). The spatial pattern of ΔS on a 0·9-m-deep plane in a virtual forest stand is given in Fig. 7. In this forest, the reinforcement of soil by vertical roots occurs really only beneath the tree, leaving large patches of soil unoccupied by roots where local soil slippage can occur. These patches with low ΔS were much smaller between staggered rows of trees compared with aligned rows, or when stand density was increased.
Table 3.
Weighted mean additional soil cohesion parameter K computed for four planes parallel to the slope (depth −30, −60, −90, −120 cm) for tree D and tree S
| Angle | Tree D |
Tree S |
||||||
|---|---|---|---|---|---|---|---|---|
| Depth (cm) | −30 | −60 | −90 | −120 | −30 | −60 | −90 | −120 |
| Φ = 0° | 0·63 | 0·83 | 0·77 | 0·70 | 0·82 | 0·90 | 0·80 | 0·61 |
| Φ = 10° | 0·75 | 0·92 | 0·86 | 0·81 | 0·91 | 0·96 | 0·90 | 0·74 |
| Φ = 20° | 0·88 | 1·01 | 0·97 | 0·94 | 1·01 | 1·02 | 1·00 | 0·89 |
| Φ = 30° | 1·03 | 1·11 | 1·08 | 1·08 | 1·13 | 1·10 | 1·13 | 1·05 |
| Φ = 40° | 1·22 | 1·24 | 1·23 | 1·26 | 1·27 | 1·18 | 1·28 | 1·25 |
For five values of Φ, K was computed for each root crossing the corresponding plane. Mean K was weighted by the CSA of each root impact.
Fig. 6.
K coefficient (black lines) plotted against absolute root angle towards the potential slip plane, computed for all root intersections on planes parallel to the slope at depths from 0·1 to 1·4 m in classes of 0·1 m, using a Φ ranging from 0° to 40°. The corresponding histogram of root angles weighted by the CSA at the intersection point is also shown. Data shown are for tree D.
Fig. 7.
Two-dimensional spatial distribution of ΔS provided by roots on a 0·9-m-deep plane parallel to the slope in a virtual stand composed of tree D and tree S in aligned and staggered rows of different spacing density. In the upper rows, the mean distance between trees (4·5 m) was the same as that in the field, whereas in the bottom row, spacing between trees is 2·25 m. K was computed using Φ of 20° and the real angle between the root and the plane. The grid size for the reinforcement calculation was 0·25 × 0·25 m. Arrows show how soil slippage could occur between rows in zones of low or zero ΔS. In staggered rows, soil slippage (solid arrows) could be arrested by trees downslope, whereas in aligned rows (dotted arrows), slippage can progress downslope with less hindrance. Shades of grey define evenly spaced isocontours of ΔS in kN m−2 (see the scale on the right of the graph).
Inclusion of data in a slope stability model
Depending on the position of the potential slip surface, the FOS for unrooted soil varied between 2·8–3·7 and 1·8–2·0 for slopes with trees D and S, respectively (Table 4). When the mean value for ΔS of roots was included, the FOS increased, depending on the quantity of roots present (Table 4). Where ΔS was high and the potential slip surface deepest (1·2 m), FOS increased the most (Table 4).
Table 4.
Factor of safety (FOS) for unrooted (−) and rooted (+) soil on slopes with trees D and S
| Factor of safety |
||||
|---|---|---|---|---|
| Depth of potential slip surface (m) | Slope − Tree D | Slope + Tree D | Slope − Tree S | Slope + Tree S |
| 0·3 | 2·85 | 11·36 | 1·87 | 8·20 |
| 0·6 | 2·95 | 7·04 | 1·76 | 3·73 |
| 0·9 | 3·26 | 4·81 | 1·91 | 2·38 |
| 1·2 | 3·66 | 3·96 | 2·03 | 2·13 |
The FOS of unrooted soil increased when the potential slip surface was deeper, but was reduced as ΔS decreased with depth in rooted soil.
DISCUSSION
The chain of tools (Fig. 8) developed and tested on trees in situ provided highly accurate information concerning root spatial distribution along a slope (all functions used in this chain of tools are available upon request from the first author). The threshold for measured roots had to be set to a relatively small value in this study (5 mm) because such thin roots can make a large contribution to soil reinforcement (Waldron and Dakessian, 1982). Although a more rapid assessment may have been performed by extracting the whole root systems manually or with a mechanical shovel, as in Di Iorio et al. (2005) and Nicoll et al. (2006), it would not then have been possible to determine the exact position of the less rigid roots in the soil matrix, and the small roots may have been lost. Nevertheless, measuring root systems in situ is time consuming and cannot be envisaged on large numbers of trees.
Fig. 8.
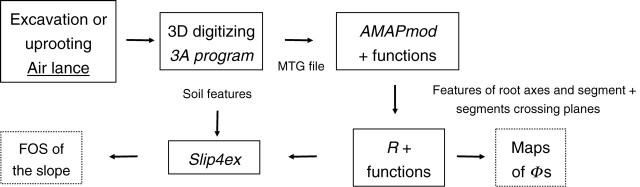
Flow chart showing the order in which the chain of tools was used. Software names are in italics.
Many studies (e.g. Nicoll et al., 1995; Danjon et al., 2005) have shown that root architecture for the same species in a given stand can be highly variable, as for the two studied trees. Therefore, it is very difficult to predict how a tree can reinforce soil in a forest, depending on species only. Information on the soil profile would nevertheless indicate rooting depth to a certain extent. Tree D, having many oblique roots, but without any central taproots, would be more useful for fixing soil at the top or toe of a slope (Fig. 1), where roots crossing the more vertical slip surface would reinforce soil better (van Beek et al., 2005; Cammeraat et al., 2005). Tree S, however, with its long, central taproots would fix soil better at the centre of the slope, where lateral roots are less likely to traverse the slip surface (Fig. 1). The AMAPmod and R functions developed enable us to examine root distribution in any such potential failure plane, and therefore it was possible to calculate root intersection across planes either vertical or parallel to the soil surface. This system would also be suitable for comparing root systems uprooted in a landslide, e.g. recording the points where the roots broke during soil movement, with intact root systems in an undisturbed area. Similarly, after a landslide had occurred, a comparison of root architecture between regenerated young trees and existing nearby older trees could also be envisaged. This kind of information would be useful in determining how, for example, age, species and planting history affect shallow-slope stability.
The values of RAR we found for Q. alba are similar to those found for Larix decidua Mill., Fagus sylvatica L. and Picea abies L. on silt with clayey sand (0·10–0·35 %, Bischetti et al., 2005). In mixed natural forests of the Oregon coast range, USA, the mean RAR ranged between 0·1 and 1 % in 1·2-m-deep pits dug midway between neighbouring trees (Schmidt et al., 2001), whereas Abernethy and Rutherfurd (2001) found values of 0·001–0·756 % in Eucalyptus camaldulensis Labill. and Melaleuca ericifolia Smith. growing along riverbanks in Australia. Therefore, values of RAR are highly variable and particularly susceptible to the effects of larger roots.
The simple limit equilibrium model developed by Wu (1976) was used to determine the contribution of roots to reinforcement (eqn 2). This model is most suitable for thin or intermediate size flexible roots which are not necessarily perpendicular to the failure surface. In field studies on a variety of root systems, the shear resistance contributed by roots is usually under-estimated by 0·2–0·33 times the value given by eqn (2) (Wu, 2007). The reason for this under-estimation is because only a fraction of roots crossing the failure surface can be expected to reach ultimate tension. The orientation of these roots, particularly in heart or plate root systems (Köstler et al., 1968), will also range from 0 to 90° and as our results show, influence hugely the value of K. In Wu et al. (1979), K was simplified to 1·2 where β = 40–70° and Φ is 20–40°; however, our results, where the actual root angle crossing the slip plane was used, show that 1·2 is realistic only when values of Φ nearing 40° and root angles between 40 and 50° are used. In a similar study, Greenway (1987) calculated K using several values of Φ and β, and determined that values of K = 1·2 were reached when an angle of Φ was >35° and β was 50–60°. In the present study, when using the actual angle of roots crossing the slip surface, rather than β, an under-estimation of approximately 10° therefore occurred. Nevertheless, using actual data for root angle may incur less error than assuming β = 45° (Gray and Leiser, 1982; Abernethy and Rutherfurd, 2001; Greenwood, 2006), especially when working with soils where Φ is low.
In taprooted systems, i.e. tree S, where roots were large, stiff and vertically orientated, the limit equilibrium model (Wu, 1976) is less suitable for calculating ΔS. Wu (2007) suggested using the cable model (Oden, 1967) in such cases. The cable model takes into account root bending stiffness, the length and displacement of the root and is useful when the soil shear zone is relatively thick (Nakamura et al., 2007). Where bending stiffness is modulus of elasticity (E) multiplied by the second moment of inertia (I), once E is known for a species (E decreases with distance from the stem, Khuder et al., 2007), it would also be possible to include the calculation of EI in our list of functions. However, if a very large, central taproot is present, it would also be useful to calculate the resistance at initial failure using the analogy that a taproot is similar to a laterally loaded foundation pile (Broms, 1964). No root mechanical or displacement data are available for our root systems as we did not carry out shear tests of the root–soil blocks in situ (Wu and Watson, 1998). However, to test these models and compare values of ΔS, such shear tests should be carried out and detailed measurements of root system architecture and mechanical properties for root segments (Bert and Danjon, 2006) should be taken to determine the accuracy of each model.
As ΔS decreased with distance from the tree stem, any reinforcement provided by the vertical roots was negligible. In the forest studied, where the mean spacing distance between trees was 4·5 m (Fig. 7), and trees were planted in straight rows, the mean FOS for the vegetated slope varied from 4·0 to 11·4 and 2·1 to 8·2 for trees D and S, respectively, depending on the depth of the potential slip surface. However, the overall slope FOS does not provide information regarding gaps between trees, where a lack of root growth should result in an FOS equivalent to that of unrooted soil, as has also been found in hilly grassland (Terwilliger and Waldron, 1991). In our forest, FOS of unrooted soil was >1·3, and therefore slope stability was not compromised; however, at a site with instability problems, localized soil slippage could occur between trees, as the downwards motion of soil would not be hindered. If rows of trees were staggered in a plantation, or stem density increased (Fig. 7), although ΔS is minimal between rows, downwards soil slippage could be arrested by the presence of trees, particularly with less spacing between them. However, in the present study, horizontal roots that did not cross the slip surface were not taken into consideration in the calculations of ΔS, but do provide a certain amount of reinforcement along a slope (Zhou et al., 1997). The spatial distribution of trees in forests prone to landslides has been relatively little studied (but see Schmidt et al., 2001; Sakals and Sidle, 2004; Kokutse et al., 2006) and further work should be carried out on the interaction between trees and slope stability, depending on species, planting density, age and management. Our chain of tools would be particularly useful for such a study.
The type of data obtained here could be used in spatial/temporal models of root cohesion in forest soils (Sakals and Sidle, 2004) and 3D models of the non-homogeneous distribution of trees on slopes with different types of root system architecture (Kokutse et al., 2006). Combined with an architectural analysis (Atger and Edelin, 1994), data could also be used as input in simulation models of 3D dynamics of root architecture (Jourdan and Rey, 1997) and branching density models (Dupuy et al., 2005b). The latter type of model could predict root branching density at potential slip planes deep in the soil using information from the shallow layer only, and therefore complete excavation of the root system would not be necessary. Such tools could then be used to forecast the development of root architecture on a slope as a function of age and forest type and could provide as output all quantitative characteristics needed for the evaluation of slope reinforcement by vegetation.
ACKNOWLEDGEMENTS
We thank Laurent Burnel (INRA, France), Dale Porterfield, Ron Hendrick and Lee Ogden (Whitehall Forest, Warnell School of Forest Resources, University of Georgia, USA), for technical and logistic support, and Thierry Fourcaud (CIRAD, France) for comments on the manuscript. John Greenwood (Nottingham Trent University, UK) provided valuable help with the Slip4Ex calculations. Financial support was provided for D.H.B. by the Royal Academy of Engineers Foresight Scheme, the Warnell School of Forest Resources, UGA and the EC QLK5-2001-00289 Eco-Slopes Project. Thanks are due to CEG, Pittsburgh. for loan of the Air-Spade.
LITERATURE CITED
- Abernethy B, Rutherfurd ID. The distribution and strength of riparian tree roots in relation to riverbank reinforcement. Hydrological Processes. 2001;15:63–79. [Google Scholar]
- Adam BH, Sinoquet H, Godin C, Dones N. 3A – a software for the acquisition of plant architecture. 1999 Version 2.0. Clermont-Ferrand: UMR PIAF INRA-UBP. [Google Scholar]
- Atger C, Edelin C. Premières données sur l'architecture comparée des systèmes racinaires et caulinaires. Canadian Journal of Botany. 1994;72:963–975. [Google Scholar]
- Barker DH, Watson AJ, Sombatpanit B, Northcut B, Magliano AR. Ground and water bioengineering for erosion control and slope stabilization. Science Publishers.; 2004. [Google Scholar]
- van Beek LPH, Wint J, Cammeraat LH, Edwards JP. Observation and simulation of root reinforcement on abandoned Mediterranean slopes. Plant and Soil. 2005;278:55–74. [Google Scholar]
- Bert D, Danjon F. Carbon concentration variations in the roots, stem and crown of mature Pinus pinaster (Ait.) Forest Ecology and Management. 2006;222:279–295. [Google Scholar]
- Bischetti GB, Chiaradia EA, Simonato T, Speziali B, Vitali B, Vullo P, Zocco A. Root strength and root area of forest species in Lombardy. Plant and Soil. 2005;278:11–22. [Google Scholar]
- Böhm W. Method of Studying Root Systems. New York: Springer-Verlag; 1979. Ecological Studies series Vol. 33. [Google Scholar]
- Broms BB. Lateral resistance of piles in cohesive soils. ASCE – Journal of the Soil Mechanics and Foundation Division. 1964;90:27–64. [Google Scholar]
- Cammeraat ER, van Beek R, Kooijman A. Vegetation succession and its consequences for slope stability in SE Spain. Plant and Soil. 2005;278:135–147. [Google Scholar]
- Danjon F, Sinoquet H, Godin C, Colin F, Drexhage M. Characterisation of structural tree root architecture using 3D digitising and AMAPmod software. Plant and Soil. 1999;a 211:241–258. [Google Scholar]
- Danjon F, Bert D, Godin C, Trichet P. Structural root architecture of 5-year-old Pinus pinaster measured by 3D digitising and analysed with AMAPmod. Plant and Soil. 1999;b 217:49–63. [Google Scholar]
- Danjon F, Fourcaud T, Bert D. Root architecture and wind-firmness of mature Pinus pinaster. New Phytologist. 2005;168:387–400. doi: 10.1111/j.1469-8137.2005.01497.x. [DOI] [PubMed] [Google Scholar]
- Di Iorio A, Lasserre B, Scippa GS, Chiatante D. Root system architecture of Quercus pubescens trees growing on different sloping conditions. Annals of Botany. 2005;95:351–361. doi: 10.1093/aob/mci033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dupuy L, Fourcaud T, Stokes A. A numerical investigation into factors affecting the anchorage of roots in tension. European Journal of Soil Science. 2005;a 56:319–327. [Google Scholar]
- Dupuy L, Fourcaud T, Stokes A, Danjon F. A density based approach for the modelling of root architecture: application to Maritime pine (Pinus pinaster Ait.) root systems. Journal of Theoretical Biology. 2005;b 236:323–334. doi: 10.1016/j.jtbi.2005.03.013. [DOI] [PubMed] [Google Scholar]
- Genet M, Stokes A, Salin F, Mickovski SB, Fourcaud T, Dumail J, van Beek LPH. The influence of cellulose content on tensile strength in tree roots. Plant and Soil. 2005;278:1–9. [Google Scholar]
- Genet M, Stokes A, Fourcaud T, Hu X, Lu Y. Soil fixation by tree roots: changes in root reinforcement parameters with age in Cryptomeria japonica D. Don. plantations. In: Marui H, Marutani T, Watanabe N, et al., editors. Interpraevent 2006: Disaster Mitigation of Debris Flows, Slope Failures and Landslides; September 25–27, 2006; Niigata, Japan. Tokyo: Universal Academy Press, Inc; 2006. pp. 535–542. [Google Scholar]
- Godin C, Costes E, Caraglio Y. Exploring plant topological structure with the AMAPmod software: an outline. Silva Fennica. 1997;31:355–366. [Google Scholar]
- Gray DH, Leiser AT. Biotechnical slope protection and erosion control. New York: Van Nostrand Reinhold; 1982. [Google Scholar]
- Greenway DR. Vegetation and slope stability. In: Anderson MG, Richards KS, editors. Slope stability. New York: John Wiley and Sons Ltd; 1987. pp. 187–230. [Google Scholar]
- Greenwood J. SLIP4EX – A program for routine slope stability analysis to include the effects of vegetation, reinforcement and hydrological changes. Geotechnical and Geological Engineering. 2006;24:449–465. [Google Scholar]
- Hamza O, Bengough AG, Bransby MF, Davies MCR, Hallett PD. Mechanics of root pull-out from soil: a novel image and stress analysis procedure. In: Stokes A, Spanos I, Norris JE, Cammeraat LH, editors. Eco- and ground bio-engineering: the use of vegetation to improve slope stability. Developments in plant and soil sciences. Dordrecht: Springer; 2007. pp. 213–221. [Google Scholar]
- Ihaka R, Gentleman R. R: a language for data analysis and graphics. Journal of Computational and Graphical Statistics. 1996;5:299–314. [Google Scholar]
- Jourdan C, Rey H. Modelling and simulation of the architecture and development of the oil-palm (Elaeis guineensis Jacq) root system 1. The model. Plant and Soil. 1997;190:217–233. [Google Scholar]
- Khuder H, Danjon F, Stokes A, Fourcaud T. Growth response and root architecture of Black locust seedlings growing on slopes and subjected to mechanical perturbation. In: Salmén L, editor. Proc. 5th Plant Biomechanics Conference – Stockholm; August 28–September 1 2006; STFI-Packforsk AB, Stockholm. pp. 299–303. [Google Scholar]
- Khuder H, Stokes A, Danjon F, Gouskou K, Lagane F. Is it possible to manipulate root anchorage in young trees? Plant and Soil. 2007;294:87–102. [Google Scholar]
- Kokutse N, Fourcaud T, Kokou K, Neglo K, Lac P. 3D numerical modelling and analysis of forest structure on hill slopes stability. In: Marui H, Marutani T, Watanabe N, et al., editors. Interpraevent 2006: Disaster Mitigation of Debris Flows, Slope Failures and Landslides; September 25–27, 2006; Niigata, Japan. Tokyo: Universal Academy Press, Inc; 2006. pp. 561–567. [Google Scholar]
- Köstler J-N, Brueckner E, Bibelriether H. Die Wurzeln der Waldbäume. Hamburg: Paul Parey; 1968. [Google Scholar]
- Mattia C, Bischetti GB, Gentile F. Biotechnical characteristics of root systems of typical Mediterranean species. Plant and Soil. 2005;278:23–32. [Google Scholar]
- Mickovski SB, Van Beek LPH, Salin F. Uprooting resistance of vetiver grass (Vetiveria zizanioides) Plant and Soil. 2005;278:33–41. [Google Scholar]
- Nakamura H, Nghiem QM, Iwasa N. Reinforcement of tree roots in slope stability: a case study from the Owaza slope in Iwate Prefecture, Japan. In: Stokes A, Spanos I, Norris JE, Cammeraat LH, editors. Eco- and ground bio-engineering: the use of vegetation to improve slope stability. Developments in plant and soil sciences. Dordrecht: Springer; 2007. pp. 81–90. [Google Scholar]
- Nicoll BC, Easton EP, Milner AD, Walker C, Coutts MP. Wind stability factors in tree selection: distribution of biomass within root systems of sitka spruce clones. In: Coutts M, Grace J., editors. Wind and wind related damage to trees. Cambridge: Cambridge University Press; 1995. pp. 276–301. [Google Scholar]
- Nicoll BC, Berthier S, Achim A, Gouskou K, Danjon F, van Beek LPH. The architecture of Picea sitchensis structural root systems on horizontal and sloping terrain. Trees Structure and Function. 2006;20:701–712. [Google Scholar]
- Nilaweera NS, Nutalaya P. Role of tree roots in slope stabilisation. Bulletin of Engineering Geology and the Environment. 1999;57:337–342. [Google Scholar]
- Norris JE. Root reinforcement by hawthorn and oak roots on a highway cut-slope in Southern England. Plant and Soil. 2005;278:43–53. [Google Scholar]
- Oden JT. The mechanics of elastic structures. New York: McGraw-Hill; 1967. [Google Scholar]
- Reubens B, Poesen J, Danjon F, Geudens G, Muys B. The role of fine and coarse roots in shallow slope stability and soil erosion control with a focus on root system architecture: a review. Trees: Structure and Function. 2007;21:385–402. [Google Scholar]
- Sakals ME, Sidle R. A spatial and temporal model of root cohesion in forest soils. Canadian Journal of Forest Research. 2004;34:950–958. [Google Scholar]
- Schmidt KM, Roering JJ, Stock JD, Dietrich WE, Montgomery DR, Schaub T. The variability of root cohesion as an influence on shallow landslide susceptibility in the Oregon Coast Range. Canadian Geotechnical Journal. 2001;38:995–1024. [Google Scholar]
- Shields FD, Gray DH. Effects of woody vegetation on the structural integrity of sandy levees. Water Resources Bulletin. 1992;28:917–931. [Google Scholar]
- Sinoquet H, Rivet Measurement visualization of the architecture of an adult tree based on a three-dimensional digitising device. Trees: Structure and Function. 1997;11:265–270. [Google Scholar]
- Stokes A, Spanos I, Norris JE, Cammeraat LH. Eco- and ground bio-engineering: the use of vegetation to improve slope stability. Developments in plant and soil sciences. Dordrecht: Springer; 2007. [Google Scholar]
- Terwilliger VJ, Waldron LJ. Effects of root reinforcement on soil-slip patterns in the Transverse Ranges of southern California. Geological Society of America Bulletin. 1991;103:775–785. [Google Scholar]
- Waldron LJ. The shear resistance of root-permeated homogeneous and stratified soil. Soil Science Society of America Journal. 1977;41:343–349. [Google Scholar]
- Waldron LJ, Dakessian S. Effect of grass, legume and tree roots on soil shearing resistance. Soil Science Society of America Journal. 1982;46:894–899. [Google Scholar]
- Wu TH. Investigation of landslides on Prince of Wales Island. Geotechnical Engineering report 5. Columbus, OH: Civil Engineering Department, Ohio State University; 1976. [Google Scholar]
- Wu TH. Slope stabilization. In: Morgan RPC, Rickson RJ, editors. Slope stabilization erosion control. A bioengineering approach. London: Spon; 1995. pp. 221–264. [Google Scholar]
- Wu TH. Root reinforcement analyses and experiments. In: Stokes A, Spanos I, Norris JE, Cammeraat LH., editors. Eco- and ground bio-engineering: the use of vegetation to improve slope stability. Developments in plant and soil sciences. Vol. 103. Dordrecht: Springer; 2007. pp. 21–30. [Google Scholar]
- Wu TH, Watson A. In-situ shear tests in soil blocks with roots. Canadian Geotechnical Journal. 1998;35:579–590. [Google Scholar]
- Wu TH, McKinnell WP, Swanston DN. Strength of tree roots and landslides on Prince of Wales Island, Alaska. Canadian Geotechnical Journal. 1979;16:19–33. [Google Scholar]
- Wu TH, McOmber M, Erb RT, Beal BE. A study of soil root interaction. Journal of Geotechnical Engineering, ASCE. 1988;114:1351–1375. [Google Scholar]
- Zhou Y, Watts D, Cheng X, Li Y, Luo H Xiu Q. The traction effect of lateral roots of Pinus yunnanensis on soil reinforcement: a direct in situ test. Plant and Soil. 1997;190:77–86. [Google Scholar]