The Derivation of Sink Functions of Wheat Organs using the GREENLAB Model

Abstract

Background and Aims

In traditional crop growth models assimilate production and partitioning are described with empirical equations. In the GREENLAB functional–structural model, however, allocation of carbon to different kinds of organs depends on the number and relative sink strengths of growing organs present in the crop architecture. The aim of this study is to generate sink functions of wheat (Triticum aestivum) organs by calibrating the GREENLAB model using a dedicated data set, consisting of time series on the mass of individual organs (the ‘target data’).

Methods

An experiment was conducted on spring wheat (Triticum aestivum, ‘Minaret’), in a growth chamber from, 2004 to, 2005. Four harvests were made of six plants each to determine the size and mass of individual organs, including the root system, leaf blades, sheaths, internodes and ears of the main stem and different tillers. Leaf status (appearance, expansion, maturity and death) of these 24 plants was recorded. With the structures and mass of organs of four individual sample plants, the GREENLAB model was calibrated using a non-linear least-square-root fitting method, the aim of which was to minimize the difference in mass of the organs between measured data and model output, and to provide the parameter values of the model (the sink strengths of organs of each type, age and tiller order, and two empirical parameters linked to biomass production).

Key Results and Conclusions

The masses of all measured organs from one plant from each harvest were fitted simultaneously. With estimated parameters for sink and source functions, the model predicted the mass and size of individual organs at each position of the wheat structure in a mechanistic way. In addition, there was close agreement between experimentally observed and simulated values of leaf area index.

INTRODUCTION

Functional–structural crop models aim at simulating plant development and growth. An architectural model for wheat based on L-systems has been developed for winter wheat (Fournier et al., 2003) and spring wheat (Evers et al., 2005, 2007). With accurate description of organ size and geometry, the resulting 3-D architecture is very realistic, and can be used to compute the light regime within the wheat canopy. As yet in these L-system based models, the functions describing organ size (sheath length, blade length, blade area, etc.) in relation to phytomer rank follow a predefined pattern, because they are fitted directly to data using empirical functions, i.e. without consideration of the underlying processes that give rise to the final size of the organs. Current research is addressing the implementation of carbon gain and partitioning from which the distribution of organ mass and size along phytomer rank can be derived. The resulting sink functions may be used in the L-system-based wheat model to explore the response of tillering to light quality and light quantity (Evers et al., 2005, 2007).

In this context, the current paper presents calibration of the GREENLAB model (de Reffye and Hu, 2003; Yan et al., 2004; Kang and de Reffye, 2007) for the spring wheat cultivar ‘Minaret’. Data from four dates throughout the life cycle of the plant, describing the mass of individual leaf blades, sheaths, internodes and ears of main stem and tillers and of the root system as a whole, were fitted simultaneously to the GREENLAB model, yielding one single set of model parameters, including those defining sink functions. The application of sink functions in L-system-based models allows, in principle, the size and the number of organs, especially leaf blades, to become an emergent property of the simulation, rather than being prescribed in advance.

Previous calibration of the GREENLAB model has been done on single-stem wheat (Zhan et al., 2000) and on maize from a field experiment (Guo et al., 2006), using the generalized non-linear least-square method presented in Zhan et al. (2003). Model validation has been made on maize with independent data from other years (Ma et al., 2006). Therefore to date, all model fitting and validation has been performed for monoculm plants. Here we introduce a new feature to the GREENLAB capabilities: calibration on a branching source–sink system, exemplified by tillering wheat.

MATERIAL AND METHODS

Experiment set-up

An experiment was conducted in a growth chamber in Wageningen, the Netherlands, from October, 2004 to February, 2005. Spring wheat plants, Triticum aestivum cultivar ‘Minaret’, were grown in eight containers. These containers held a layer of medium-textured sandy soil of approximately 35 cm depth; seeds were sown at 100 plants m⁻² in a regular grid of 10 × 10 cm, at a depth of approximately 5 cm. The soil was enriched with fertilizer resulting in 15 g N m⁻² to ensure a non-limited development, and appropriate biocides were sprayed to control pests and diseases. Day length of the growth chamber was set at 15 h, with light intensity at around 425 µmol m⁻² s⁻¹ at the level of the top of the canopy. The light was emitted by 400 W SON–T Agro Philips lamps and 400 W HPIT Plus Philips lamps (3·5 lamps m⁻²). Temperature was 17 °C (0900–2100 h), and 11 °C (2100–0900 h); relative humidity was 75 %.

Measurements

Six plants per harvest were sampled destructively, excluding plants that were at the edge of a container. Measured data included the dimensions and fresh and dry mass of leaf blades, sheaths, internodes, ears and roots. There were four harvests in total: at maturity (i.e. ligule appearance) of the fourth main-stem leaf, at maturity of the seventh main-stem leaf, at the flowering stage, and during grain filling. ‘Leaf states’ were monitored two or three times per week for the main stem and all tillers of six plants. The considered ‘leaf states’ included tip appearance, leaf blade expansion, maturity and death. These six monitored plants were the ones that were used for the fourth harvest. Prior to harvests, incoming radiation was measured at the top of the canopy using a Sunfleck ceptometer (Delta-T devices).

Naming system for leaves and tillers

The main stem arises from the embryonal axis and gives birth to the first-order branches, or ‘primary tillers’, from its axillary buds in the leaf axils. ‘Secondary tillers’ are borne from the buds in the leaf axils on the primary tillers, including the buds in the axil of the prophyll at the base. Tillers and leaves are distinguished here using the same naming method as Evers et al. (2005), where a wheat phytomer is defined as a set of an internode with a tiller bud at the bottom, a node above the internode, a sheath inserted on the node, and a leaf blade. This definition is botanically correct, but is different from the one presented by Klepper et al. (1998), where the tiller bud is in the axil of the leaf on the node. Leaves are numbered acropetally, beginning with the first foliar leaf, L1. The coleoptile tiller is named T1, instead of T0 in Klepper et al. (1982). Tiller leaves and secondary tillers are associated with the name of the primary tillers. For example, the first leaf on T1 is L11. Similar to the coleoptile tiller, tillers arising from the axil of the prophyll have a ‘1’ for the second digit. For example, the tiller that appears from the axis of the prophyll of T2 is T21.

Description of a potential and real wheat topology

In the current study, the main stem consisted of eight phytomers below the ear. The first four-to-five phytomers showed internodes that did not elongate (‘short’ internodes), and the rest of the phytomers produced internodes that did elongate (‘long’ internodes). Tillers emerged only from the short internodes located at the bottom of the parent shoot. The potential tillering pattern, which is related to plant type, has been defined in Bos and Neuteboom (1998). Following this definition, a complete potential pattern of tillers up to secondary order is illustrated for the current experiment in Fig. 1A, with the example of five short internodes (concerning summed phytomer number, see below) being present per axis. The number of phytomers of primary tillers decreased acropetally from T1 to T5. In addition, for the secondary tillers the number of phytomers decreased with an increase in tiller position, which was associated with the decrease in the number of short internodes (for example, 4 to 0 from T1 to T5). The number of long internodes was the same for all tillers, resulting in a similar height for all shoots. The potential pattern of plant structure helps in understanding the behaviour of the plant.

Fig. 1.

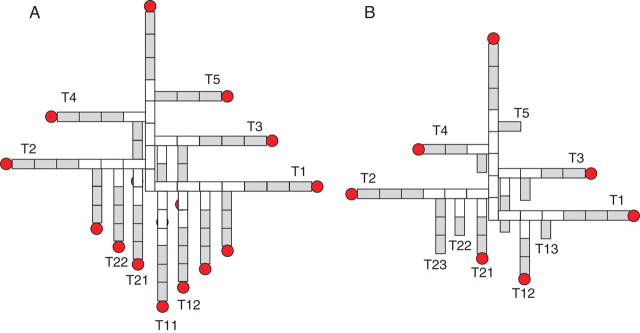
Illustration of wheat topology including primary and secondary tillers: (A) a potential pattern and (B) a real example. The white rectangles represent short internodes, and the shaded ones represent long internodes. A circle represents an ear.

In reality, however, in a plant stand the topology per plant is not so regular: the number of tillers, as well as the number of phytomers in tillers, is often lower than the potential pattern. Figure 1B shows an example of an actual wheat topology observed in this experiment, in which some tiller buds remained dormant. The potential pattern can be regarded as the upper boundary of actual wheat topology.

Summed phytomer number

In the main stem, phytomers are numbered or ranked acropetally without ambiguity, i.e. one to eight for the main stems in Fig. 1. For tillers, two kinds of phytomer number can be distinguished. One is to regard the first phytomer in the tiller as rank one. According to this criterion, in Fig. 1A, the top phytomer on T1 is of rank seven. Another way is to count the ‘summed phytomer number’, from the base of the plant to the phytomer in question (Bos and Neuteboom, 1998). In that case, all tillers in the ideal potential tiller pattern as in Fig. 1A have the same summed number of phytomers (eight) as the main stem.

Modelling wheat development in GREENLAB

In the GREENLAB model, the different types of stem can be represented by integer numbers, using the concept of ‘physiological age’ (PA) (Barthélémy and Caraglio, 2007). PA is estimated a posteriori by analysing the morphological, anatomical and/or functional attributes of a botanical entity (Barthélémy and Caraglio, 2007). In the GREENLAB model for wheat, the PA of phytomers on the main stem is given as ‘1’, primary tillers are of PA ‘2’, and so on. The maximum PA of a plant is P_m. As negligibly few tillers of higher order were observed in this study, P_m is set to 3. Another concept, ‘chronological age’ (CA) of an organ or a tiller, is the number of growth cycles (see below) that it has experienced since it was born.

Simulation of plant development is based on growth cycles (GCs). One GC corresponds to the thermal time it takes to generate a phytomer. In the current application of GREENLAB to an annual plant such as wheat, a growth cycle is equal to a phyllochron, the time between the moments of appearance of two successive main stem leaves (Klepper et al., 1982). The GREENLAB organogenesis model simulates plant topology with the automaton concept (Zhao et al., 2001). The initial state of a stem is a seed (for the main stem) or a bud (for a tiller). New phytomers are produced at the top of the stem at each growth cycle until the development of the stem finishes. The maximum number of phytomers in a stem of a given PA is another parameter of the automaton, being eight for the main stem and tillers in the sense of summed phytomer number. When the tip of the main stem transforms into a flower, the tillers become reproductive as well.

Computing the number of phytomers in the model

The number of growing organs is an important variable for computing plant substrate demand in GREENLAB (see below). For the potential pattern in Fig. 1A, the number of organs produced can be computed with the substructure method as presented in Cournède et al. (2006). A substructure is a component of a plant grown from a bud. Let S^{q, p}_{n, i} be the number of phytomers of PA p and CA i in a tiller of PA q (q ≤ p) and CA n (n ≥ i). S^{q, p}_{n, i} can be computed recurrently from the tillers of higher order born from the short internodes, as in eqn (1):

1

*1 is taken only when n−i+1 is smaller than 8.

The number of phytomers of PA p and CA i at plant age n is N^p(n, i) = S^1,p_{n, i}. The total number of phytomers in a plant at CA n is sum of those of each PA and CA:

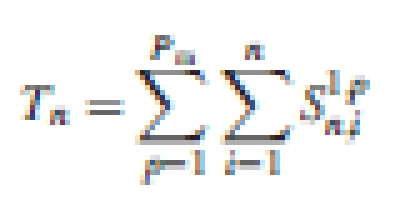Using eqn (1) for the potential pattern in Fig. 1A, from cycle 1 to 8 the total number of phytomers at each cycle is T = [1, 3, 7, 14, 25, 41, 62, 87].

Given the number of organs per phytomer, the number of organs, O, of PA p and CA i at plant age n, N^p_O(n, i), can be computed in a similar manner; O indicating organ type: B = blade, S = sheath, I = internode, F = ear (fruit in general), R = root. This variable is important in giving the total demand and leaf area (see below).

Biomass production and partitioning in GREENLAB

At each growth cycle, the assimilates available for growth, called ‘biomass’ in the GREENLAB environment, are supposed to be located in a virtual common pool (Heuvelink, 1995). From the common pool, biomass is partitioned dynamically among individual organs according to their number, age and relative sink strength. The relative sink strength for organs of given type O and PA p is denoted as P^p_O, which is a dimensionless variable indicating the ability of different kinds of organs in competing for biomass. The relative sink strength of all leaf blades in the main stem is set to 1 as a reference value, i.e. P¹_B = 1.

The growth rate of an individual organ can change from its first appearance through to full expansion. In the model, for an organ O of CA i and PA p, its actual sink strength varies with time in GCs, as expressed in eqn (2):

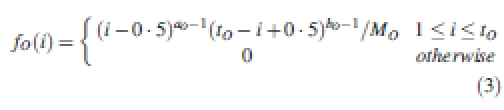2

where f_O is an organ-type-specific function indicating the pattern of change in sink strength in each cycle before the organ stabilizes in mass. It can be any empirical function that is suitable. In GREENLAB, because of its flexible form, a normalized discrete Beta function (Abramowitz and Stegun, 1972) was chosen for f_O, as in eqn (3):

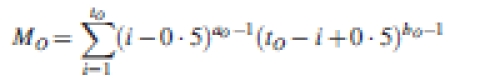3

where

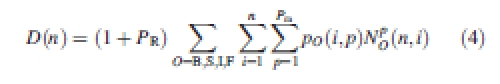is a normalizing factor. t_O is the organ expansion duration in cycles. The form of f_O is controlled by the parameters a_O and b_O. Different combinations of values of a_O and b_O result in bell-shaped, J-shaped, or U-shaped forms. A bell-shaped curve means quick growth in the middle period and small increments at the beginning and end of its growth procedure.

Relative source and sink functions are computed in GREENLAB. The model does not compute (gross) photosynthesis and net growth after subtraction of carbon losses due to growth respiration and maintenance respiration. The omission of respiration is a justifiable simplification as long as the gain in mass per unit substrate utilization does not differ too much between the different organ types; this is the case for wheat. Such differences become large when some of the plant's organs accumulate relatively greater proportions of fat, oil or protein compared with the rest of the organs (Penning de Vries, 1974). Assimilate ‘demand’ of an organ is thus derived from its net gain in mass and is not augmented with the substrates that are used in respiration. Hence, in cycle n, the appearing and growing organs compose the total plant demand for biomass, as expressed in eqn ( 4):

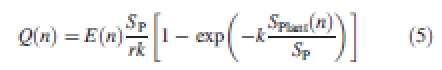4

N^p_O(n, i) is the number of organs of type O, PA p and CA i present in the plant at cycle n. P_R is the relative sink strength of the root system, being the ratio between the sink strength of the root system and the aerial parts.

As outlined in previous papers on GREENLAB (Yan et al., 2004; Guo et al., 2006), growth per time step (referred to as ‘biomass production’) is assumed to be proportional to leaf area per unit ground area and plant transpiration, which in turn depends on weather variables. In GREENLAB the effects of light, water and temperature are accounted for in a function E(i) (Wu et al., 2004). Hence, the biomass production for a plant in cycle n, Q(n) (g plant⁻¹ GC⁻¹), is calculated using the Beer–Lambert Law to account for a diminishing contribution per unit leaf area as the latter increases, as in eqn (5):

5

S_P (cm²) is the ground area available to a plant, computed as the inverse of the population density. r and k are two empirical parameters to be estimated with inverse modelling (i.e. finding the parameter set that reduces the difference between model output and measured data, listed in the target data; see below, ‘Model calibration’): k is analogous to the extinction coefficient in the Beer–Lambert Law. S_Plant/S_P gives the leaf area index (LAI), where S_Plant is the total functioning leaf area of a plant, being the sum of the individual leaf areas, as in eqn (6):

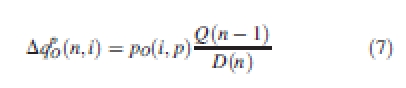6

In eqn (6), t^p_a is the life span of a leaf blade of PA p from appearance to senescence. For some plants this value changes according the position of the leaves in the plant (Vos and Biemond, 1992). S^p_B(n, i) is the surface area of a leaf blade of PA p and CA i at plant age n, computed according to its dry mass, q: S^p_B(n, i) = q_B(n, i)/e^p. e^p is the specific leaf weight (the ratio between dry mass and surface area of individual leaf blade, in g cm⁻²), an input variable of the model, obtained from observation.

A growing organ gains mass at each cycle proportional to its sink strength and the ratio between the biomass supply from the last cycle and current demand, as shown in eqn (7):

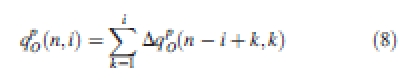7

The organ mass is the accumulation of its increment in previous cycles, as in eqn (8):

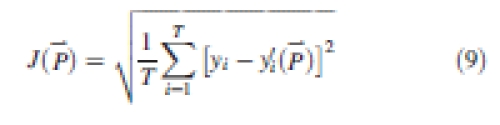8

From the mass, the length and diameter of internodes are obtained using an allometric relationship (Yan et al., 2004), as well as the area of the leaf blade using specific leaf weight. The mass and size of organs are therefore the result of source–sink dynamics. The most important output is the individual leaf area, which is used to compute biomass production for the next cycle.

In summary, the growth of the plant is represented with a set of recurrent mathematical formulae, based on several assumptions regarding botany and ecophysiology (Yan et al., 2004; Guo et al., 2006). The size and mass of organs are calculated in a mechanistic way, based on modelling their competition within the developing plant structure. Nevertheless, parts of the model are still empirical, for example eqn (5) and the expansion law, f, for each organ type.

Model calibration

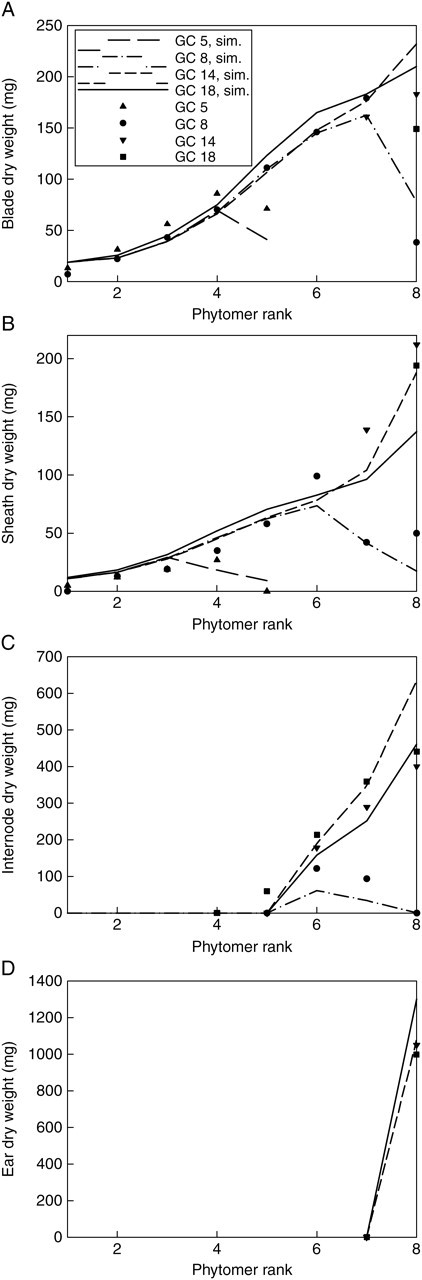
Several parameters controlling sink and source values are difficult to measure directly, including the relative sink strength, P^p_O, in eqn (2), the parameters a_O and b_O of the expansion function eqn (3), and r and k in eqn (5). These parameters are estimated by fitting the measured organ mass (the target) with the model output. The aim of model calibration is to find a set of parameters such as to minimize the difference between the model output and the measured data. The goodness of fit is expressed in the root-mean-squared error (RMSE) between the target data, y, and the corresponding model output y′(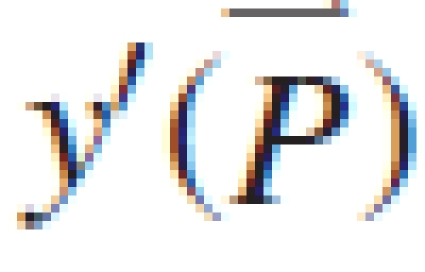), being functions of model parameters (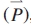), as shown in eqn (9).

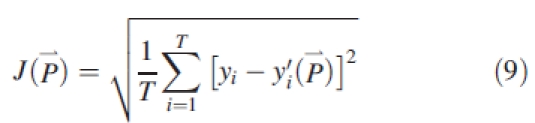9

where J(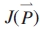) is RMSE. The generalized non-linear least-square method (Press et al., 1992) was used for the fitting process. The Levenberg–Marquardt algorithm was adopted by using the MINPACK library (Argonne National Laboratory, Argonne, USA). The software for model simulation, calibration and visualization was developed by the authors, and is freely available online (www.greenscilab.org).

The target data, y, are the mass of individual organs from one stage (in a single fitting procedure) or several stages (in a multi-fitting procedure: data from several dates in one analysis); the latter giving a better accuracy of parameter estimation (Guo et al., 2006). For single-stem crops without much variation in total phytomer number,such as maize (Guo et al., 2006; Ma et al., 2006), the target data can be the average mass of organs of the same phytomer rank. For the wheat in current study, however, the plant topology varies from one plant to another, especially for the tillers. This prevents the use of the average data of the six samples. Therefore, rather than calculating the average plant, one individual plant with median tillering level from each of the four sampling dates was taken for building the target file.

According to eqn (4), the number of organs in the sample plant needs to be known to be able to allocate biomass to a specific structure. That number is derived from the observed topological structure, which is coded in the target file that can be read by the software for calibration. For each tiller, its position, parent shoot and possible sub-tillers are recorded. The historical development of this plant also needs to be known in order to obtain the number of organs in previous cycles. This was deduced from the recorded structure. For example, there are four phytomers in T3 at plant age eight in Fig. 1A: thus there were three, two, one, zero phytomers in T3 at plant age seven, six, five, four respectively. Each tiller is processed this way.

An important assumption in GREENLAB is that organs appearing in the same cycle compete for assimilates from a common pool. Therefore, those organs of the same CA and PA and of the same type are regarded as being of the same mass – noted as q^p_O(i, j) in eqn (8). To construct the corresponding target, the data for organs of the same PA and CA in a plant were averaged. For example, in Fig. 1B, the top phytomers of all primary tillers are supposed to appear together at cycle 8, thus the average mass of their leaf blades is noted as q²_B(8, 1) in the target. Similarly, all q^p_B(8, i) (1 ≤ p ≤ 3, 1 ≤ i ≤ 8) were computed.

RESULTS

Time duration per growth cycle

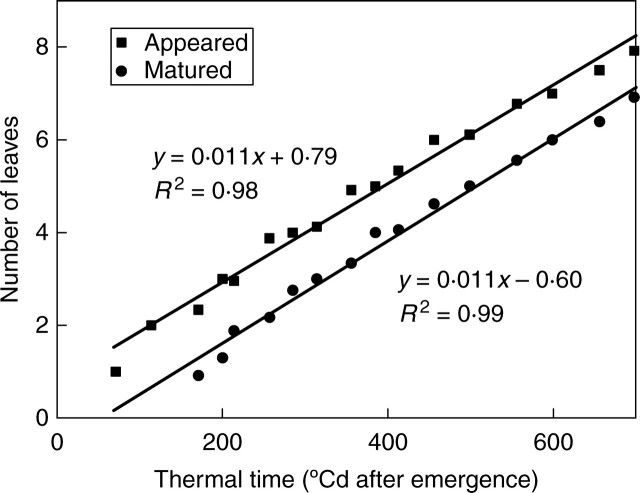
With base temperature T_b = 0 °C (Gallagher, 1979), phytomer production per unit thermal time was 0·011 °Cd⁻¹ for the main stem (Fig. 2, slope of the line for main stem). According to this development speed, the thermal time per GC was 87·7 °Cd. With an average day and night temperature of 14 °C in this experiment, the number of days per GC was 6·15. At the four measurement dates (thermal time 399, 698, 1254 and 1553 °Cd), the corresponding ages of plants were 5, 8, 14 and 18 GCs, respectively.

Fig. 2.

Number of leaves that have appeared and matured on the main stem in wheat as a function of thermal time.

Expansion duration of organs

Expansion duration of an organ (t_O in eqn 3) is an input parameter that can be directly estimated from observations. According to the main stem data (Fig. 2), the thermal time for the full expansion of a leaf blade was 126 °Cd (i.e. from tip appearance to ligule appearance), which corresponds to nearly two GCs for main stem and tillers. The thermal time it takes for full expansion of leaves was constant along the stem (Fig. 2). This differed from the case of maize in Guo et al. (2006), in which leaf expansion duration increased acropetally before becoming stable.

Internode elongation occurs at the end of sheath extension (defined by collar appearance) of the same phytomer (Fournier et al., 2003). It can be seen from the data for internodes at cycle 8 (circles in Figs 3 and 4) that the mass of the third internode from the top continued to increase after cycle 8, which means that its expansion had not finished at CA 3. An expansion duration of four GCs is taken for internodes. The sequence of growth (first leaf blade, followed by the sheath and then the internode) was simulated by calibration of the parameters that control the expansion. For the ear, it was observed that the dry mass did not vary during the last two measurements, so an expansion duration of seven GCs is sufficient. The root system is regarded as a whole here, and it is supposed to have a constant relative sink strength, P_R, compared with the aerial part, as in eqn (4), with unlimited expansion duration.

Fig. 3.

Mass of organs at each phytomer rank from four measurement dates for the main stem (PA 1), from measurement (symbols) and simulation (lines).

Fig. 4.

Mass of organs at each summed phytomer rank from four measurement dates for primary tillers (PA 2), from measurement (symbols) and simulation (lines).

Functioning duration of leaves

The leaf blade stayed green for several cycles before senescing. The leaf functioning duration t^p_a is one of the parameters that influence source activity (eqn 6). According to observations, for main stem (p = 1) t^p_a was set to eight GCs for the leaves associated with short internodes, and was increased to 11 GCs from phytomer rank six to eight (elongated ones). For the primary tillers, t^p_a was set to seven GCs for the leaves from short internodes, and then took values 8, 9, 10 for the top three leaves, respectively. For secondary tillers it was set to three.

Specific leaf weight

In GREENLAB the leaf blade area is computed from leaf mass using the specific leaf weight. Values were 0·0037 g cm⁻² for leaves of the main stem, 0·0035 g cm⁻² for leaves of primary tillers, and 0·0033 g cm⁻² for leaves of secondary tillers.

Climate effects

According to the recorded data over the canopy, the light intensity was stable during the experiment, with an average 416 µmol m⁻² s⁻¹ during the day. As the other climate conditions (temperature, humidity) were set to be constant during the experiment, E in eqn (5) was constant during growth cycles. Without losing generality, it was set to 1, and the effect of the actual value of E is captured in the empirical parameter r in eqn (5).

Results of model calibration

At the first measurement date (growth cycle, GC = 5) the internodes had not yet started to elongate, and only the mass of leaf sheaths and blades were measured for the upper part of the wheat plants. At the second measurement date (GC = 8), the leaves on the main stem had finished their development, and the long internodes had begun to elongate. On the last two measurement dates most leaves had senesced, and only productive tillers were present. As more and more organs had appeared over time, multi-fitting, i.e. one analysis on pooled data from all dates (Guo et al., 2006), was necessary in order to catch the full growth process.

In total, 19 parameters needed to be calibrated: parameters b_O (eqn 3) that control the shape of the sink change function, f, for leaf blade, sheath, internode and ear (values of a_O are set to 1); the relative sink strength P^p_O (eqn 2) of these four types of organs for each PA, except that the sink strength of the leaf blade of the main stem was set to a reference value of 1. The root system was regarded as a whole, thus only one sink value P_R (eqn 4) needed to be estimated. Other parameters are the initial biomass, Q₀, the leaf blade resistance, r, and the light extinction efficient, k. Prior knowledge about the plants can be of great value in the fitting process (for example the general pattern of sink-strength change of organs over time, or the ratio of sink strength between different values of PA). Suitable initial values of the parameters decrease the risk of falling into a local minimum in the fitting process (in which case fitting is not achieved). Table 1 shows the set of parameters that give the fitting results displayed in Figs 3–6. In contrast to the initial biomass, Q₀ (0·013 g), the parameters in Table 1 are dimensionless.

Table 1.

Calibrated parameters of wheat, fitted with the least- square-root method

(A) PB, PS, PI, PF and PR are sink strength of organs (blade, sheath, internode, ear and root system), see eqn (2)
Sink strength	PA 1	PA 2	PA 3
Blade (PB)	1	0·56	0·3
Sheath (PS)	0·47	0·32	0·14
Internode (PI)	0·67	0·40	0·20
Ear (PF)	0·57	0·23	0
Root (PR)	0·1	0·1	0·1
(B) bB, bS, bI and bF are parameters controlling the form of sink function of organs, see eqn (3). r and k are linked to source function, see eqn (5)
bB	bS	bI	bF	r	k
0·53	2	0·45	0·6	11	0·52

Fig. 6.

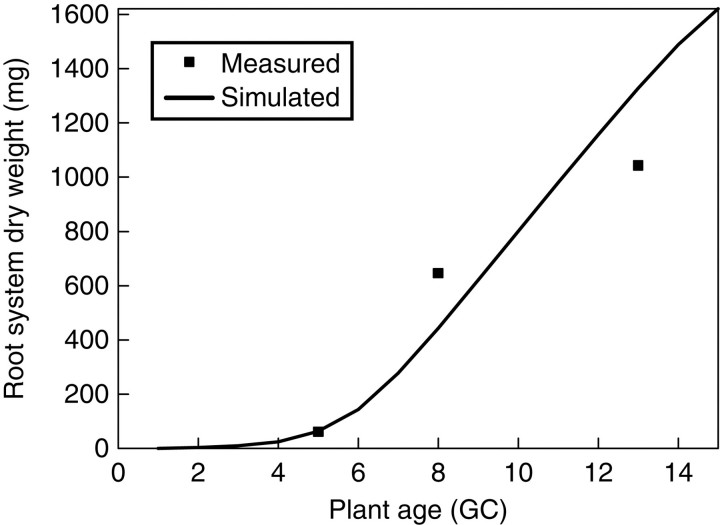
Mass of the root system per plant from measurement (symbols) and simulation (line) plotted against plant age, expressed in growth cycles (GC).

Figures 3–6 show the target data and the model output using the parameter values listed in Table 1. In total, 195 data are fitted simultaneously, being organ type × P_m × number of phytomer in axis (5, 8, 8, 8, respectively, for each stage) and root system, excluding missing data (e.g. fallen leaves). The total J(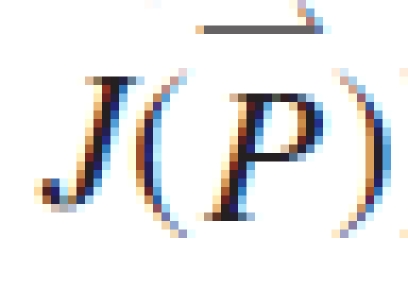)) computed with eqn (9) is 0·15 g. Note that the four target plants have different topologies. Therefore, curves for individual organs displayed in Figs 3 and 4, computed for the four dates with the same parameter set, do not exactly fall on top of each other, although the old organs have finished expansion long before the later dates and thus should keep the same mass as on earlier dates. The main stem data was the most regular, as the observed number of phytomers produced was stable, while those from PA 2 had more experimental variation. No ear was produced on tillers of PA 3 in these plants. The mass of the root system was not measured at the last sampling date. Thus only three data points were available in the target data, as shown in Fig. 6.

The phytomer number in Figs 3–5 is the summed phytomer number. It can be seen from the fitted curve for the blade in Fig. 3 that at GC 18 only the last leaf was present. Moreover, the blade mass at GC 18 was lower than at GC 14. This may have been caused by assimilate remobilization due to grain filling. Here, this phenomenon is not taken into consideration, i.e. the organs do not lose biomass after they have reached maturity; the changing role of organ from sink to source would otherwise have to be made explicit in the model.

Fig. 5.

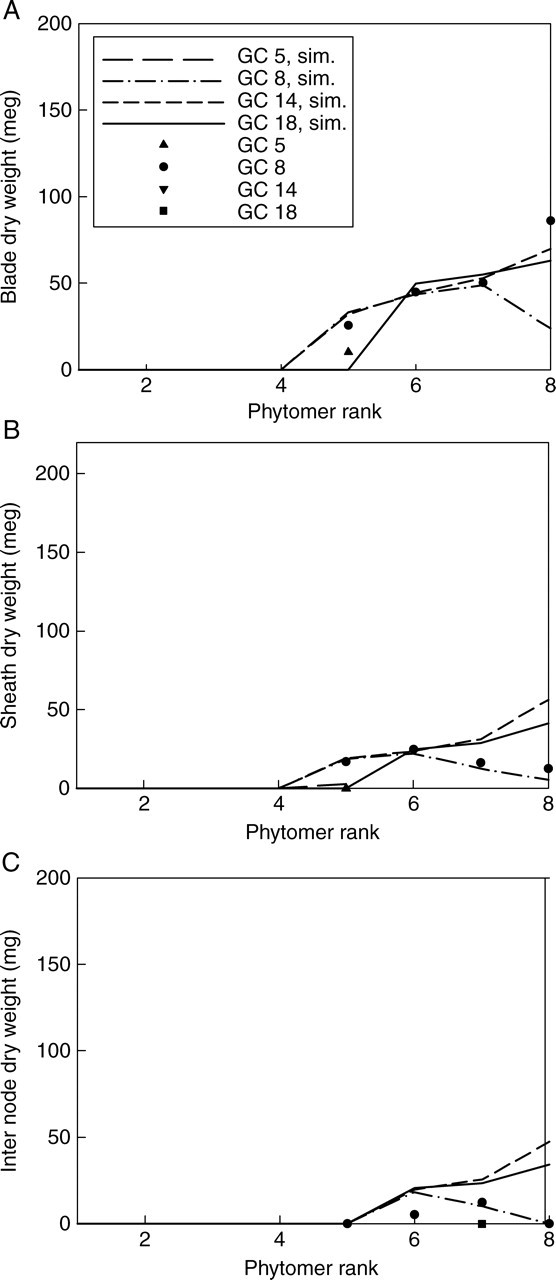
Mass of organs at each summed phytomer rank from four measurement dates for secondary tillers (PA 3), from measurement (symbols) and simulation (lines).

Sink functions

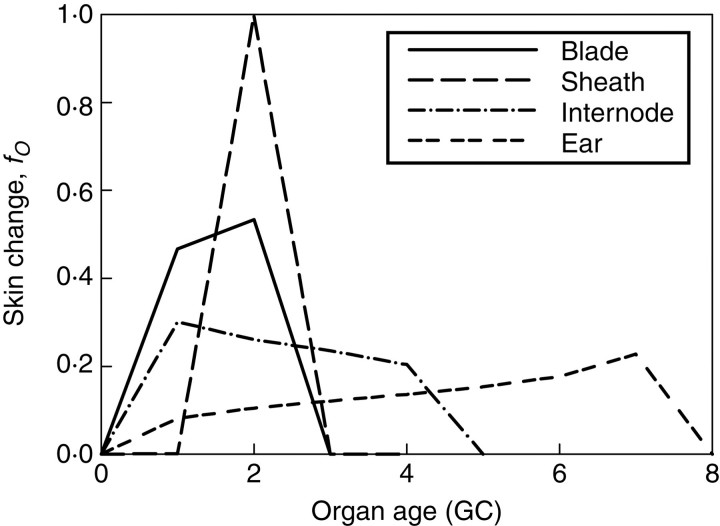
Using the parameters for sink-change function, f, as presented in Table 1, the normalized change over GCs of relative sink strength is shown in Fig. 7. The x-axis is the age of organs in cycles, and the y-axis indicates the pattern of change of the relative sink strength (see eqn 3) of each type of organ; the value of which is zero at an organ age older than the expansion duration, t_O. Each type of organ has its own specific pattern of expansion and related sink strength, P_O. Together with the developmental sequence of organs, the growth process of a shoot can be simulated. For phytomers with short internodes at the base of the plant, where leaves are the only organs, a new leaf the blade (possibly hidden) starts expansion growth a bit earlier than its sheath, as the value of f_B(1) is greater than f_S(1). Both organs finish expansion in two GCs. For phytomers with long internodes, the duration of internode growth extends over more CGs (i.e. 5) than those of leaf blades and leaf sheaths. The top phytomer represents the whole ear, which has a long period of growth. While the development model gives the number and age of sink organs during plant growth, the competition of organs, resulting in specific shares of allocation of resources, is simulated according to sink functions.

Fig. 7.

Sink-change function of organs (blade, sheath, internode and ear), expressed against growth cycles (GC).

Simulation with the calibrated model

Using the simulated leaf area, the simulated leaf area index was compared to the leaf area index at the four sampling dates. They were closely related, with the RMSE being 0·598. The corresponding 3-D wheat plants with potential tiller pattern were drawn (Fig. 8) to visualize the results of this functional–structural model.

Fig. 8.

Simulated wheat architectures at the four sampling dates.

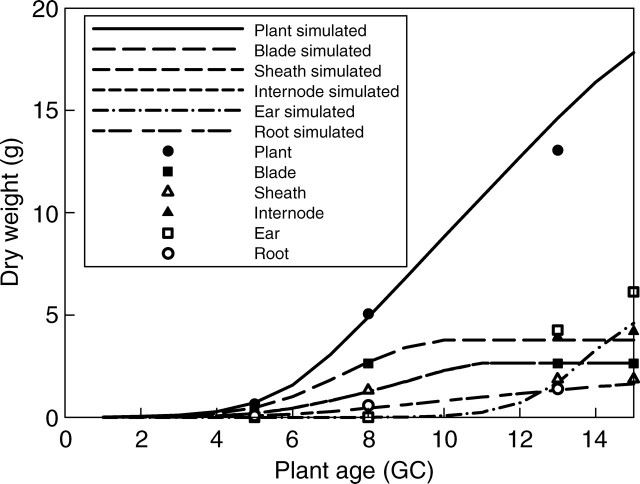
The accumulated biomass increment per plant at each cycle, computed with eqn (5), was compared to the real data (Fig. 9). According to the increment value (data not shown), leaf blade and sheath were the dominant sinks in the vegetative state, followed by the internode and finally the ear. The pattern of biomass increment of the plant is in line with that of PAR interception of existing wheat growth models (Porter et al., 1993).

Fig. 9.

Dry mass of a plant and its partitioning among different types of organs, from observation (symbols) and simulation (lines).

DISCUSSION AND CONCLUSIONS

This paper presents a calibration exercise using the GREENLAB model for a spring wheat crop grown in a climate chamber. Both the aerial part and the underground part were included in the fitting target, and the aerial part consisted of vegetative and reproductive organs, with tillers up to the secondary order. Therefore the work here gives a complete example of applying the GREENLAB model to branching cereal crops including the grain-filling stage. From Figs 3–9, one can conclude that although the model is simple in principle, it captures most of the features of plant development and growth.

GREENLAB assumes all organs of a particular type have the same sink properties for a given PA (equivalent to tillering order in the case of wheat), and consequently change in organ mass along the shoot is the result of competitive interactions among growing organs. In cereals, very pronounced relationships can be seen between properties of phytomers on tillers and on the main stem, expressed by relative phytomer number (RPN) (Evers et al, 2005). GREENLAB can reproduce similar patterns because organs of the same type and RPN expand over the same duration with the same expansion law, f_O. This can be seen if one plots the mass of organs of the same type and different PA (Figs 3–5) in one graph.

In this study, we have fitted to detailed data from a branching structure, where the topology of the plant needed to be recorded. The procedure of transforming from original data to the target data is thus tedious. Moreover, although multiple plants were taken in this study, the data from the rest of the plants were not fully used; as a result, the parameters may be not representative enough for the population. An alternative choice is to fit an average (in the sense both of topology and organ mass) plant instead of individual ones.

The current work was done for wheat plants from a fixed environment. Our next work is modelling and verification of different wheat tillering levels and production under different population densities, using a similar approach to the one in this article with extension to stochastic modelling.