Abstract
Background and Aims
The Finite Element Method (FEM) has been used in recent years to simulate overturning processes in trees. This study aimed at using FEM to determine the role of individual roots in tree anchorage with regard to different rooting patterns, and to estimate stress distribution in the soil and roots during overturning.
Methods
The FEM was used to carry out 2-D simulations of tree uprooting in saturated soft clay and loamy sand-like soil. The anchorage model consisted of a root system embedded in a soil block. Two root patterns were used and individual roots removed to determine their contribution to anchorage.
Key Results
In clay-like soil the size of the root–soil plate formed during overturning was defined by the longest roots. Consequently, all other roots localized within this plate had no influence on anchorage strength. In sand-like soil, removing individual root elements altered anchorage resistance. This result was due to a modification of the shape and size of the root–soil plate, as well as the location of the rotation axis. The tap root and deeper roots had more influence on overturning resistance in sand-like soil compared with clay-like soil. Mechanical stresses were higher in the most superficial roots and also in leeward roots in sand-like soil. The relative difference in stresses between the upper and lower sides of lateral roots was sensitive to root insertion angle. Assuming that root eccentricity is a response to mechanical stresses, these results explain why eccentricity differs depending on root architecture.
Conclusions
A simple 2-D Finite Element model was developed to better understand the mechanisms involved during tree overturning. It has been shown how root system morphology and soil mechanical properties can modify the shape of the root plate slip surface as well as the position of the rotation axis, which are major components of tree anchorage.
Key words: Acclimative growth, anchorage, biomechanics, tree uprooting, rotation axis, root architecture, root eccentricity, secondary growth, von Mises stresses
INTRODUCTION
Tree resistance to overturning during high winds has become a well-researched topic over the last 25 years, with huge amounts of field data available, particularly on temperate conifer species e.g. Sitka spruce (Picea sitchensis; see Nicoll et al., 2006a), maritime pine (Pinus pinaster; Stokes, 1999; Cucchi and Bert, 2003; Danjon et al., 2005) and balsam fir (Abies balsamea; Ruel et al., 2000, 2003; Achim et al., 2005). However, it is not yet known which shape of root system is best for increased tree mechanical stability. If an optimal morphology can be determined, it may then be possible to manipulate root systems or soil properties to achieve increased resistance to overturning.
Tree anchorage strength is governed by several factors, e.g. root architecture (Danjon et al., 2005; Dupuy et al., 2005a, b, 2007), soil physical and mechanical properties (Moore, 2000; Dupuy et al., 2005b; Nicoll et al., 2006a), the depth, shape and weight of the root–soil plate (Coutts, 1986) and the location of the rotation axis with regard to the force vector. The rotation axis is the point about which the root system rotates during overturning and its position can modify the anchorage strength of a tree (Ennos, 1994; Dupuy et al., 2005b, 2007). Nevertheless, few studies have been carried out on the location of this axis, due to the difficulty in observing it in field experiments (Crook and Ennos, 1997). In the few models of root anchorage which exist, the rotation axis has been considered as a fixed point at the base of the tree trunk (Niklas et al., 2002) or on the leeward side of the stem (Blackwell et al., 1990). However, it is likely that the position of the rotation axis depends on root system architecture and soil properties, but no studies have yet been carried out to test this hypothesis.
Field experiments on tree anchorage usually involve winching a tree sideways until failure and measuring the force required to uproot or break the tree (see Peltola, 2006). Variables then measured can include stem size and mass, root–soil plate dimensions (Nicoll et al., 2005, 2006b) and root system architecture (Khuder et al., 2007). However, although winching tests provide useful information, they are time consuming and can be difficult or even dangerous to carry out. Therefore, the use of numerical modelling would allow us to carry out virtual winching experiments and would be an ideal tool for studying how root–soil plate shape, root system morphology and the location of the rotation axis affect anchorage. Models can be controlled to have the same volume but different branching patterns, root number, size or depth, which is never the case in the field, therefore it would also be possible to determine, for example, how the removal of one or several roots would affect anchorage. Sophisticated numerical models which simulate tree overturning exist already (Dupuy et al., 2005a, b, 2007). These models integrate the use of Finite Element Method (FEM; Zienkiewicz and Taylor, 1989) techniques with real or simulated root architectural data. Simulations of uprooting can also be carried out at a very local level within the root system (Dupuy et al., 2005a), or can involve overturning of the whole root system in different types of soil (Dupuy et al., 2005b, 2007). Validation of these numerical techniques with field experiments have shown the methodology to be reliable (Dupuy et al., 2007), therefore such models can be used with accuracy to better understand tree overturning.
The FEM models of root anchorage developed by Dupuy et al., (2005a, b, 2007) were in two (2-D) or three (3-D) dimensions. Although 3-D models are useful for integrating real root system architectural data, 2-D models can be used to determine the influence of each element of the root system and their interaction on tree anchorage. Mechanical stresses within any part of the root–soil matrix can be visualized and how these stresses are affected by root system morphology and root loss can be calculated.
As a tree sways in the wind, mechanical stresses concentrate in the areas most likely to undergo failure, e.g. the stem and lateral root bases (Ancelin et al., 2004; Fournier et al., 2006). Trees respond to these stresses by laying down extra wood in those areas, often leading to cross-sections of stems (Telewski, 1995) or roots (Nicoll and Ray, 1996, Stokes et al., 1998; Di Iorio et al., 2007) which are eccentric in shape. However, different directions of root eccentricity, i.e. above or below the root, have been found and may depend on tree species, or differences in root architecture and soil type. Von Mises' stress criterion, i.e. a value that represents an average of stress components, has been used to describe and demonstrate that this biomechanical adaptation of secondary growth is seen as a local response of the cambium to mechanical stress (Mattheck and Breloer, 1995). Within a root system it is difficult to predict where mechanical stresses will be most concentrated, as both root system architecture and the external loading environment (soil type and wind direction) will determine stress distribution. FEM could be used to explore the relationship between root system architecture, soil medium and the adaptation of growth to mechanical stress (including von Mises stresses). Therefore, the areas most likely to fail in a tree subjected to wind loading could be identified.
The aim of this study was to show that removing important structural elements of the root system can deeply modify the shape of the root–soil plate and the position of the rotation axis, the major components of root overturning. As a consequence of these changes in the root–soil mechanical interaction, it was expected that the location of mechanical stresses within the root system would also be modified, resulting in different growth responses, which could explain differences in root eccentricity.
For this purpose, a 2-D FEM model was developed which allowed overturning of theoretical root systems with different branching patterns to be simulated in two different soil types similar to saturated clay and loamy sand. To determine the contribution of different root elements to anchorage, overturning simulations were carried out on root systems with individual lateral roots or the tap root removed. The length of the tap root was also varied to estimate the role it plays in tree anchorage. Stress distribution within the soil and individual roots was determined, along with the position of the rotation axis during overturning. Results are discussed with regard to consequences for tree stability and how the feedback between biomechanical models and plant growth models can be used in future studies of tree adaptive growth and anchorage.
MATERIALS AND METHODS
Root system types and patterns
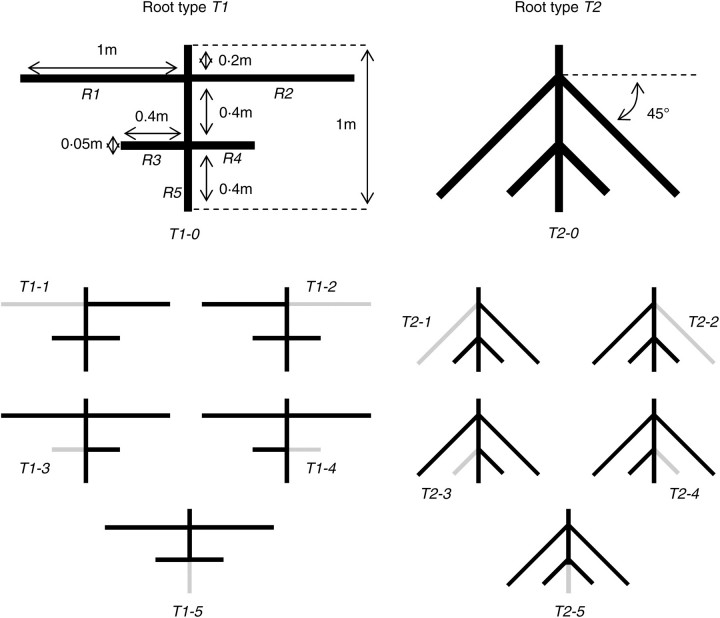
Two types of schematic herringbone-like root systems T1 and T2 were considered, differing only in the insertion angle of lateral roots with regard to the tap root (Fig. 1). Root type T1 consisted of horizontal lateral roots, i.e. the insertion angle with regard to the soil surface was 0°, whereas T2 had oblique lateral roots with an insertion angle of 45°. Each root system consisted of two pairs of opposite roots, i.e. R1–R2 and R3–R4, attached to the vertical tap root at depths of 0·2 m and 0·6 m from the soil surface, respectively. The length of the tap root and each shallow lateral, R1 and R2, was 1·0 m, and the length of each of the deeper laterals R3 and R4, was 0·4 m. The 0·4-m-long part of the tap root located just below the R3 and R4 junction point was named R5. All root elements were 50 mm in diameter.
Fig. 1.
Geometrical description of the 12 root patterns Ti-j, i = 1,2, j = 1,…,5 (black lines) defined from root types T1 and T2 after removal of root element Rj (grey lines). T1-0 and T2-0 are the reference patterns, i.e. without removed root elements.
From each root system type described above, six root patterns were then defined (Fig. 1). To calculate the relative effect of each root element on anchorage efficiency, each root type had the lateral roots Rj, with j = 1,…,4, and the tap root distal extremity R5 removed one by one. The control, or reference pattern, was considered as that without any root elements removed and was named T1-0 for root system type T1 and T2-0 for root system type T2. Each root pattern with a root element Ri removed was then named T1-j or T2-j, with j = 1,…,5.
Effect of the tap root on tree anchorage
To determine the specific effect of the tap root on the anchorage of root types T1 and T2 in both clay and sandy soils, simulations were performed whereby tap root length was increased from 0·6 m to 1·6 m. All lateral roots were retained for these simulations and the initial configuration was similar to root patterns Ti-5, i = 1,2, which were considered as reference patterns. To remove any effects caused by the changes in tap root size, non-dimensional values were used in the calculation of anchorage strength, i.e. the tap root : maximum lateral root length ratio (TM) and the current pattern : reference Ti-5 strength ratio (CRi, i = 1,2).
Root and soil mechanical properties
Two contrasting theoretical soils S1 and S2 were considered in this study (Table 1), which can be considered representative of a saturated soft clay and a loamy sand with low cohesion (total absence of cohesion can induce numerical convergence difficulties), respectively. Both soils were modelled as an elastic perfectly plastic material, i.e. without considering hardening (Dupuy et al., 2005a, b). The yield criterion that defines the limit of soil failure was given by the Mohr–Coulomb model, which assumes that failure is controlled by the maximum shear stress (τ) and that τ depends on the normal stress σ, conventionally negative in compression. This Mohr–Coulomb linear criterion was expressed as τ = c–σtan(ϕ), where c is soil cohesion and ϕ is soil internal angle of friction. The elastic part of the soil constitutive law was assumed to be linear isotropic and governed by the Young's modulus Esoil and Poisson's ratio νsoil. Values of soil mechanical parameters that were used in the simulations are given in Table 1.
Table 1.
Soil properties used in the simulations for the two idealistic soils S1 and S2 corresponding to saturated clay and loamy sand
| Soil properties | Soil type S1 | Soil type S2 |
|---|---|---|
| Young's modulus Esoil (MPa) | 5·0 | 10·0 |
| Poisson's ratio νsoil | 0·45 | 0·25 |
| Cohesion c (kPa) | 5·0 | 2·0 |
| Friction angle ϕ (°) | 2·0 | 40·0 |
| Volumetric weight ρ (kN m−3) | 1·0 | 1·5 |
Root material was considered to be elastic linear and characterized by a Young's Modulus E of 5·0 GPa and a Poisson's coefficient ν = 0·3. The density of root wood was 1000 kg m−3 (Dupuy et al., 2005a) and the apparent soil density, i.e. accounting for seepage forces acting within the soil, of S1 and S2 were 1000 kg m−3 and 1500 kg m−3, respectively (ONUAA, 1977).
Finite element model of root anchorage
Numerical simulations of overturning were carried out with the Finite Element Method (FEM; Zienkiewicz and Taylor, 1989) using the software ABAQUS (http://www.abaqus.com). FEM is based on a spatial discretization of the studied domain, e.g. the root–soil medium, and aims at reducing the continuum field functions, e.g. force, displacement, stress or strain, to their values at particular points, i.e. nodes and integration points.
A 2-D FEM anchorage model similar to those developed by Dupuy et al. (2005a, b) was developed consisting of three parts: (1) the root pattern as defined in the previous section; (2) a rectangular surrounding soil domain (8 m large × 4 m deep); (3) a rigid stem (8 m long). The root surface and soil were bound together, and specific root–soil contact properties not considered. Boundary conditions were applied to the soil domain to ensure symmetrical displacements of the lateral edges with regard to the vertical Y-plan and symmetrical displacements of the soil lower edge with regard to the horizontal X-plan. Soil and root domains were meshed using 6-node modified quadratic plane strain triangles, CPE6M, available in the ABAQUS element library. The thickness of plane strain elements was taken as 0·05 m.
Simulations of tree bending tests were carried out imposing a horizontal displacement to the stem at its top end, i.e. at 8·0 m high. The total horizontal displacement was 1·0 m when a soft clay-like soil was considered, and 3·0 m for a sandy soil. The Finite Element calculation was performed considering two steps. The first step allowed the initial geostatic stress to be computed according to the soil–root weight. The second step corresponded to tree uprooting, i.e. to the horizontal displacement of the top of the stem. This static analysis step also took into consideration forces due to gravity. For simplicity, the model only considered the effective resulting stress field, i.e. soil water pressure was not explicitly computed but was considered in the definition of the soil apparent density (see previous section). An iterative procedure, i.e. splitting the total prescribed displacement into small increments, was used during both calculation steps, allowing geometrical nonlinearity due to the large displacement of the whole system, to be taken into account during the simulation.
Output of the model
Output results were analysed with regard to the following criteria.
Response curve of the root–soil system, stiffness and strength
The response curve is representative of the behaviour of the whole mechanical system and was defined as f-d, i.e. force versus displacement, calculated at the top end of the stem. In this approach, as the simulation was driven by an imposed displacement (simulation input), the resulting force was defined as the ‘reaction force’ RF (simulation output) calculated at this point. At any stage of the movement, the stiffness of the system is defined by the slope of the tangent at the current point of the f-d curve. Anchorage strength corresponds theoretically to the maximum force reached before failure. In the present analyses, strength was defined as the maximum reaction force calculated in the considered displacement range, as it was assumed that severe plasticization of the system had already occurred at this stage. In each soil type, the relative difference in strength between root patterns T1-j and T2-j, j = 1,…,5, was defined as
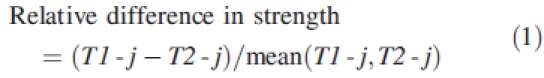 |
1 |
and used to compare the relative effect of removing root j from the two root types. Strength loss of root type Ti, i = 1,2, after removing root element Rj, j = 1,…,5, was defined with regard to the reference root pattern Ti-0 by
| 2 |
Soil deformation, root–soil plate and rotation axis
Field output, e.g. displacement at nodes, stresses and strains in elements, were visualized using the ABAQUS CAE visualization module. This information was suitable for locating shear surfaces and deducing the shape of the root–soil plate that was defined as the rotated part of the soil domain. Mapping of logarithmic total strains, i.e. both elastic + plastic strains which had accumulated during the simulation, also allowed different modes of failure to be predicted in the soil. Logarithmic strain components were normal strains LE11 and LE22, and shear strain LE12, as defined in the ABAQUS list of variables. The location of high positive LE11 and LE22 values indicated zones where opening modes of failure were in progress. LE12 values indicated zones likely to fail in a shear mode. The displacement field was also used to locate the root–soil plate rotation axis or hinge at any stage of the simulation. This axis was defined as the point of the domain, within or near the border of the root–soil plate, where no lateral displacements were observed.
Von Mises stresses at the root surface
Von Mises stress is a scalar function of the stress tensor components and can be expressed in the principal axes as σν = {[(σ1 − σ2)2 + (σ2 − σ3)2 + (σ3 − σ1)2]/2}1/2 where σ1, σ2 and σ3 are the principal stress components. This function provides a measure of the overall magnitude of the stress tensor and is often used as an indicator of the average stress state. Von Mises stress values were determined at given points on the upper and lower surfaces of each lateral root element, i.e. Rj, j =1,…,4. This information was used to investigate the hypothesis that root secondary radial growth is proportional to the local mechanical stress induced by external loads (Mattheck and Breloer, 1995). Relative von Mises stresses were also calculated, i.e. the difference between stresses at the upper σνup and lower σνdown surfaces of each root element divided by their mean.
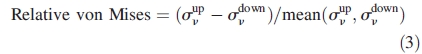 |
3 |
These values can be used to quantify the relative difference between stresses on both surfaces of each root, allowing the extent and direction of pith eccentricity to be determined.
Statistical analysis
Statistical analyses were carried out using Minitab 13. The normality of data was investigated with an Anderson–Darling test; all data were normally distributed (P > 0·05). A Student's t-test was carried out to determine if significant differences occurred in relative overturning force of different rooting patterns in the two soil types. Analysis of variance (one way and General Linear Model) was performed to determine if significant differences occurred in overturning force, von Mises stresses and relative von Mises stresses, between root elements with regard to root system type, rooting pattern and soil type. Fisher's Least Significant Difference tests were performed to identify when von Mises stresses were significantly different between different root elements (where P < 0·05).
RESULTS
Response curves and anchorage strength
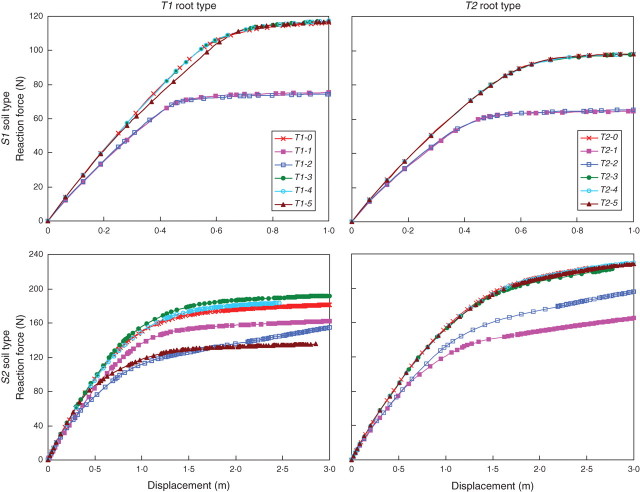
The response curves, i.e. the force-displacement (f-d) curves, of the soil–root systems were derived from the FEM simulations of overturning (Fig. 2). Numerical convergence problems were sometimes encountered in soil type S2, when the reference node, i.e. the point of the stem where a horizontal displacement was imposed and the resulting reaction force computed, was displaced >1·5 m. Such problems are explained by local instabilities that introduce strong non-linearity and make the iterative solver we used in ABAQUS unable to find the solution. In this case, the calculation stopped prematurely before reaching the maximum imposed displacement (see response curves of T1-4, T1-5 and T2-3 in soil S2 in Fig. 2). These convergence problems were due to numerical instabilities specific to soils with low cohesion.
Fig. 2.
Reaction force versus displacement curves resulting from the simulations of T1 and T2 root pattern types in soil types S1 and S2. Reaction forces were computed in the stem at the point where a horizontal displacement was imposed, i.e. at a height of 8·0 m from the soil surface. The maximum displacement considered in the simulations was 1·0 m in S1 and 3·0 m in S2.
The f-d curves allowed the stiffness of the root–soil systems to be calculated at any stage of the simulation. Stiffness at any given displacement is defined as the tangent to the f-d curve at the corresponding point. In soil type S1, f-d curves, which can also be defined as the temporal evolution of the system's stiffness, can be split into two different trajectories. The stiffness of root types T1-1, T1-2, T2-1 and T2-2 decreased more rapidly than that of the other root patterns, thus the reaction force is smaller for a given displacement. Furthermore, the response curve trajectories did not change when opposite lateral roots were removed, i.e. R1 vs. R2 and R3 vs. R4, thus indicating a perfectly symmetrical behaviour.
In soil type S2 the response curves were not grouped into two distinct pathways as was the case in S1. Except in the cases where roots R3 and R4 were removed, the f-d curves followed different trajectories. The symmetrical behaviour that was observed in S1 when two opposite roots were removed did not occur. For example, the stiffness of T1-2 was smaller than that of T1-1 at the beginning of the overturning simulation, but was higher at the end of the test, when the T1-1 response curve had already reached its threshold value.
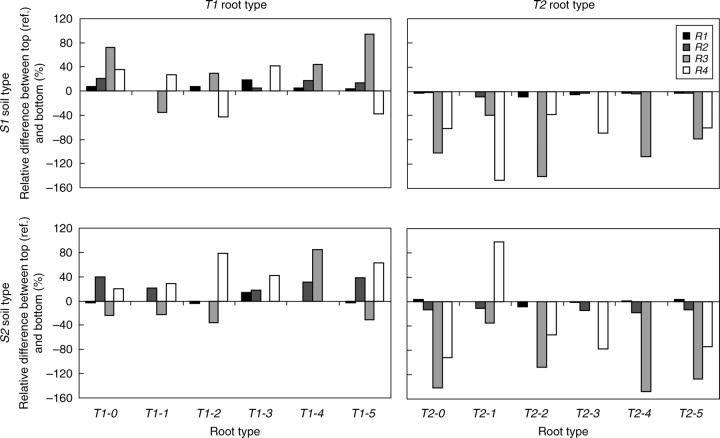
With regard to relative anchorage strength, significant differences were found between T1 and T2 root patterns in soil types S1 and S2 (t = 6·0, P = 0·002). T1 root patterns were 16·5 % stronger on average than T2 root patterns in soil type S1 (Fig. 3). This difference was quite stable for each root pattern with a standard deviation of only 2·0 %. However, in soil type S2, the opposite trend was observed. The oblique roots present in T2 patterns penetrate deeper into the soil and are thus associated with a better anchorage, as the anchorage strength of T1 was 23·5 % weaker on average than that of T2. In soil S2, it was also observed that element R1 had almost the same contribution to anchorage whatever the root type, i.e. <2 % of the relative difference between the two root types T1 and T2. In contrast, tap root R5 contributed more to the anchorage of T2 than that of T1 in S2 with a relative difference >50 %.
Fig. 3.
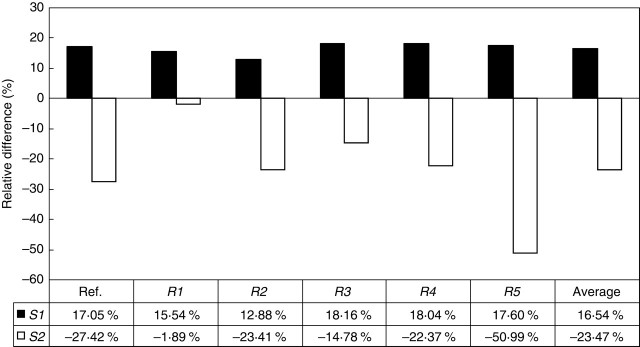
Relative differences in anchorage strengths between root types T1 and T2 in soil types S1 and S2 for the reference patterns (ref. =Ti-0, i = 1,2), i.e. without any root elements removed, and after removing root elements Rj, j = 1,…,5. According to eqn 1, a positive (or negative) percentage value x means that T1 strength anchorage is x % greater (or less) than T2 with regard to the mean strength of T1 and T2. The mean strength differences were calculated from the relative differences in strength of the six patterns.
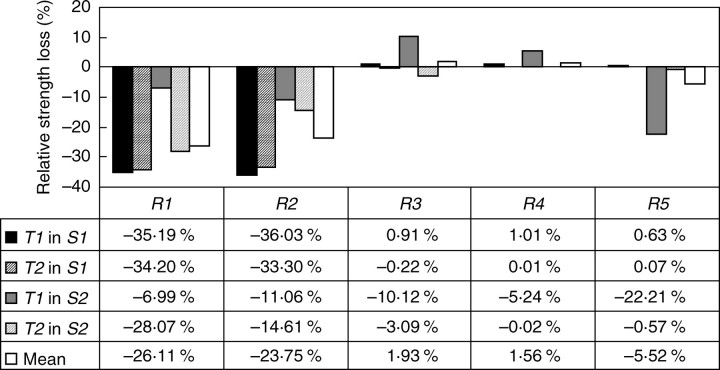
The decrease in anchorage strength, i.e. strength loss (Fig. 4) when root elements were removed clearly indicated that the shallow roots R1 and R2 had a significant effect on root anchorage (mean strength loss was 26·1 % and 23·7 %, respectively), whereas the deeper roots R3 and R4 had almost no influence (mean strength loss was 1·9 % and 1·6 %, respectively). The contribution of R1 and R2 was particularly large in S1 where the strength loss was of the same order of magnitude, i.e. >30 %, after these root elements were removed. Participation of R1 to anchorage was less dominant in root type T1 in S2, i.e. strength loss was only 7·0 %, whereas the tap root played a more significant role (22·2 % strength loss). Except for root type T1 in soil type S2, removal of R3 and R4, as well as part of the tap root R5, had a negligible effect on anchorage, as the decrease in anchorage strength was only <1 %.
Fig. 4.
Strength loss in root types T1 and T2, after removing Rj (j = 1,…,5), calculated in comparison with the reference patterns T1-0 and T2-0 (see eqn 2). For each root element removed, mean strength loss is given considering the whole corresponding root patterns in the two soil types S1 and S2.
In S2, the contribution of roots R1 and R2 to anchorage strength ranged from only 7·0 to 28·1 %, and was lower than that in S1. Root depth and orientation of lateral roots with regard to the direction of pulling thus appear to be important factors in such a soil. In root system type T2, the removal of R5 resulted in a decrease of only 0·6 % in anchorage, whereas in T1, the contribution of the tap root R5 to anchorage was 22·2 %, i.e. more than twice that of roots R1 (7·0 %) and R2 (11·1 %).
Surprisingly, when either roots R3 or R4 were removed from root pattern T1-3 in soil type S2, there was an increase in anchorage strength of up to 10·1 % (Fig. 4). This unexpected increase in overturning resistance was too large to be due to numerical artefacts, but can be explained considering the eccentric or deep location of the hinge (Fig. 8) together with the size and location of the root plate centre of mass (see following sections). The strength loss due to the removal of root element R5 was <0·6 %, but in root type T1, the contribution of the tap root was estimated at about 22 %, which was more than twice (123·9 %) the mean contribution of roots R1 and R2.
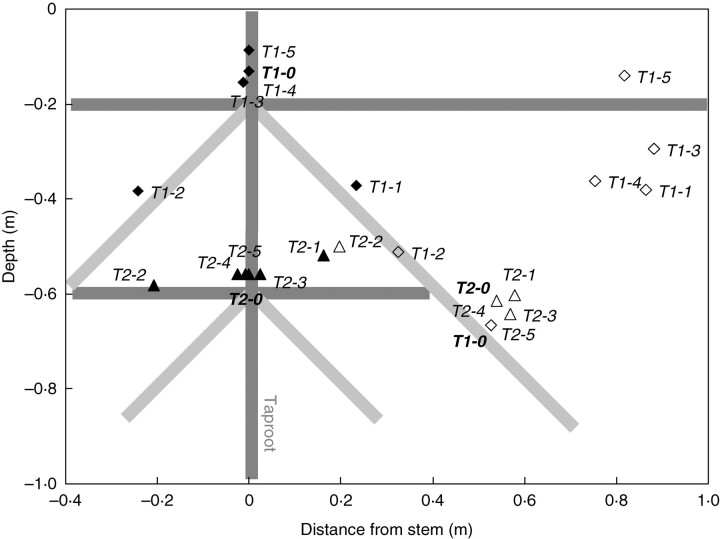
Fig. 8.
Position of rotation axes for T1 (dark grey lines) and T2 (light grey lines) patterns in soil types S1 (T1 = closed diamonds, T2 = closed triangles) and S2 (T1 = open diamonds, T2 = open triangles) estimated at the maximum stem displacement in both soil types. Reference patterns, i.e. without removed root elements, are indicated in bold type.
Analysis of the contribution of the tap root to anchorage strength showed that the tap root effect was greater in soil type S2 (Fig. 5). In soil S2, the CR1 ratio (T1 anchorage strength), increased exponentially with the increase in the TM ratio (tap root length). This increase in the CRi ratio was also observed in other situations, but was less significant and only appeared after the TM ratio reached a particular threshold. T2 anchorage strength in S2 increased only when TM was >1·0. In soil type S1, no effect of the tap root was observed when TM was <1·0 and <1·4 for root types T1 and T2, respectively.
Fig. 5.
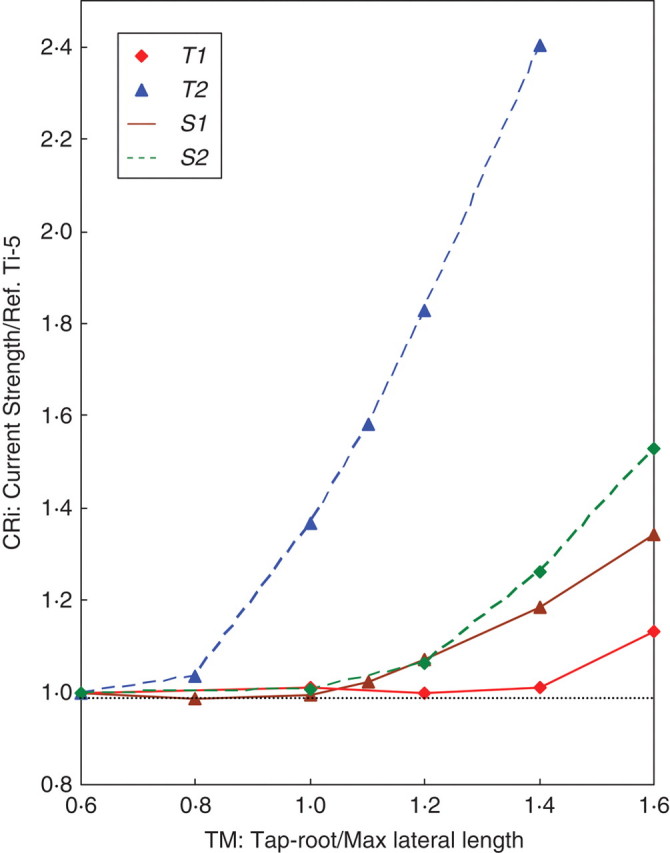
Effect of tap root length on the anchorage strength of root types T1 and T2 in soil types S1 and S2. Non-dimensional values are given by dividing tap root length and current anchorage strength by R1 root length and Ti-5, i= 1,2 reference strength, respectively.
Root–soil plate shape and location of the rotation axes
The modes of failure, i.e. shear or opening mode, were different in soil types S1 and S2, resulting in different shapes of the root–soil plates (Fig. 6). In S1, a circular slip surface appeared which corresponded mainly to a shearing mode of failure that occurred in the zones of highest LE12 components. The induced rotation was characterized by an upward movement of the windward side and a downward movement on the leeward side of the root–soil plate. This circular shape was induced by the most external root tips. Therefore, when one of these longest root elements was removed, the radius of the circular slip surface was modified, thus influencing tree anchorage. The circumference of the slip surface was estimated at 3·2 m for root patterns T1-0, T1-3, T1-4 and T1-5, and 3·0 m for root patterns T1-1 and T1-2.
Fig. 6.
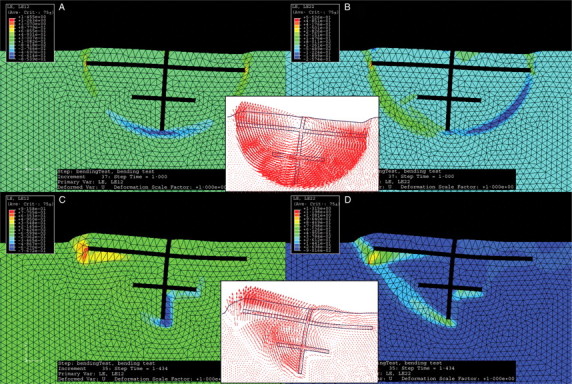
Field of logarithmic strain components: logarithmic shear strain in the same plane as the figure LE12 (A, C) and logarithmic normal strain in the vertical upward direction LE22 (B, D). These strains were calculated for the root pattern T1-0 in soil types S1 (A, B) and S2 (C, D). Associated displacement fields are shown for both soil types (red arrows correspond to the total displacement of mesh nodes).
In soil type S2, local opening modes of failure initiated in zones with high positive LE11 and LE22 values, resulting in a more complex root–soil shape (Fig. 6). Upward swelling of the soil surface all around the stem was observed. This shape also appeared to be more sensitive to a modification in root branching patterns. Thus, these results are consistent with the more variable response curves that were observed in S2 (Fig. 2).
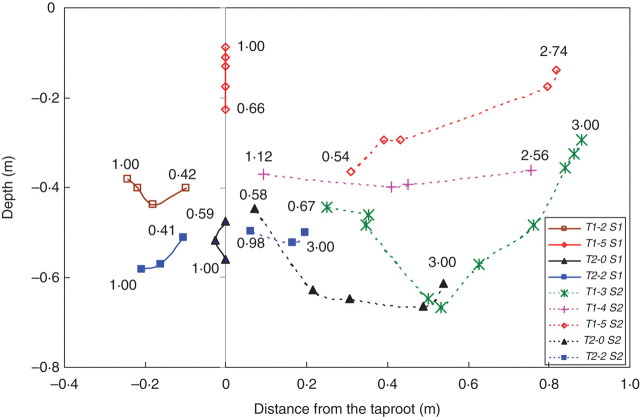
The rotation axis of root–soil plates was more difficult to localize in soil type S2 where the medium deformation was more complex and the position of the hinge more peripheral. The rotation axis was also only detectable when a sufficient rotation of the soil block was initiated. The rotation of the root–soil plate resulted from a local plasticization, i.e. irreversible deformation, which occurred within the soil due to either an opening or shearing mode of failure. During the root–soil plate movement, the rotation axis was displaced depending on the propagation of plastic strains in the soil medium (Fig. 7). This displacement was always centripetal and could be very large, e.g. about 0·9 m for root pattern T1-3 in S2. Depending on the root element that was removed, the rotation axis could move upwards, e.g. T1-5 in S1 and S2, or downwards, e.g. T2-0 in S1, or could have even more complex trajectories, e.g. T1-3 in S2 changed from downwards at the beginning of overturning to upwards at the end. It was also observed that the most significant displacement of the root–soil plate rotation axis occurred in soil type S2. In this soil, the final positions of the rotation axes were clearly located on the windward side of the root system (Fig. 8). The position of the rotation axes could also be classified into two groups, one at a distance of about 0·8 m from the tap root and a depth of about 0·3 m. The second group was at a depth of 0·6 m and a distance of 0·6 m from the tap root. The first group was mainly associated with root type T1, the second group to root type T2. In soil type S1, the rotation axes were aligned vertically with the tap root, except when root elements R1 and R2 were removed in both root types. In this case, the rotation axis still remained at a distance of <0·3 m from the tap root. Rotation axes of T2 root types in S1 were located at a depth of about 0·6 m, whereas they stayed close to the soil surface in root types T1, i.e. <0·2 m deep, except for T1-2 and T1-3 which were both 0·4 m deep.
Fig. 7.
Representative trajectories of some rotation axes in S1 (continuous lines) and S2 (dashed lines) soil types during tree overturning simulations. Data labels indicate the corresponding displacement of the stem (m).
Von Mises stresses at the root surface
The Von Mises stress field was a criterion that represented the average mechanical stress state of roots during overturning. At the scale of the whole root system, the highest stress values were located in the proximal part of the tap root, and close to the point of insertion of roots R1 and R2 in S1 (associated with a point-symmetric deformation of these two opposite roots), or in R2 only in soil type S2 (associated with a bending of the leeward root only, the windward root being mainly in tension).
Local mechanical stresses occurring in roots were analysed when the bending moment calculated at the stem base was 400 N m−1, i.e. RF = 50 N at the stem tip. This value corresponds to a point situated on the initial linear part of the f-d response curves (Fig. 2) and it was assumed that this pre-failure state provided a good indication of the mechanical stresses experienced by trees during their growth. Analysis of the von Mises stress distribution along the upper and lower surfaces of the roots revealed a decrease in stress from the point of attachment to the tip of the root elements. Relative differences in von Mises values between the upper and lower surfaces of the roots (see eqn 3 and Fig. 9) varied in the 0·2 m closest to the stem, with little change further along the root.
Fig. 9.
Relative differences in von Mises stresses between the upper and lower surfaces (see eqn 3), at the mid-point of root segments R1 (black), R2 (dark grey), R3 (light grey) and R4 (white). These values were recorded when the reaction force calculated at the stem tip reached 50 N. Results are given for root types T1 and T2 in soil types S1 and S2.
When mean von Mises stresses were calculated in the four lateral root segments of T1-0 and T2-0, no significant differences were found with regard to root type or soil type, either on the upper or lower sides of the roots. However, when individual roots were taken into account, stresses in the windward roots R1 and the leeward roots R2, regardless of root pattern and soil type, were three to four times significantly greater compared with the deeper root elements R3 and R4 both on the upper and lower sides of the roots (Table 2).
Table 2.
Von Mises stresses were significantly different in root segments R1 and R2 compared with R3 and R4, regardless of root pattern and soil type
| Root surface | Von Mises stresses in individual root segments (MPa) |
|||||
|---|---|---|---|---|---|---|
| R1 | R2 | R3 | R4 | F3,12 | P | |
| Upper | 0·75 ± 0·11a | 0·62 ± 0·07a | 0·13 ± 0·05b | 0·20 ± 0·08b | 15·1 | <0·001 |
| Lower | 0·74 ± 0·12a | 0·57 ± 0·11a | 0·20 ± 0·04b | 0·21 ± 0·05b | 10·1 | <0·001 |
Data are means ± s.e.
No significant differences were found between the upper and lower root surfaces. Where superscript letters differ, data are significantly different (P > 0·05).
When individual root elements were removed, no significant differences in von Mises stresses were found at the mid point of root segments with regard to root system type, soil type or stresses above and below the root. However, significant differences were found in the remaining root elements after individual elements had been removed. The removal of windward root R1 resulted in an increase in stress on the upper side of R2 which was significantly greater than in both R3 and R4 (Table 3). On the lower side of R2, von Mises stresses were significantly greater than in R4, but not in R3 (Table 3). When leeward R2 was removed, von Mises stresses were significantly greater in R1 compared with R3 and R4 along both the upper and lower root surfaces (Table 3). On removal of windward R3, stresses were significantly higher in R1 and R2 compared with R4 both above and below the root (Table 3). The same trend was observed when leeward R4 was removed along both the upper and lower root surfaces (Table 3).
Table 3.
When individual root elements were removed from root patterns, significant differences in von Mises stresses were found in the remaining roots, both on the upper and lower surfaces
| Removal of root elements | Von Mises stresses in remaining root elements (MPa) |
||||||
|---|---|---|---|---|---|---|---|
| Root surface | R1 | R2 | R3 | R4 | F2,9 | P | |
| R1 | Upper | – | 1·10 ± 0·02a | 0·45 ± 0·01b | 0·31 ± 0·02b | 6·8 | 0·016 |
| Lower | – | 1·14 ± 0·06a | 0·67 ± 0·02a,b | 0·24 ± 0·02b | 5·9 | 0·023 | |
| R2 | Upper | 1·35 ± 0·14a | – | 0·17 ± 0·11b | 0·25 ± 0·08b | 34·4 | <0·001 |
| Lower | 1·41 ± 0·18a | – | 0·20 ± 0·06b | 0·34 ± 0·13b | 24·8 | <0·001 | |
| R3 | Upper | 0·69 ± 0·03a | 0·60 ± 0·1a | – | 0·20 ± 0·06b | 13·7 | 0·002 |
| Lower | 0·65 ± 0·06a | 0·60 ± 0·12a | – | 0·20 ± 0·01b | 11·1 | 0·004 | |
| R4 | Upper | 0·66 ± 0·04a | 0·68 ± 0·11a | 0·13 ± 0·07b | – | 16·9 | 0·001 |
| Lower | 0·66 ± 0·04a | 0·66 ± 1·3a | 0·16 ± 0·05b | – | 12·2 | 0·003 | |
Data are means ± s.e.
Where superscript letters differ, data are significantly different (P > 0·05).
When the relative difference in von Mises stresses between the upper and lower surfaces of root elements was examined, several trends were observed (Fig. 9). This relative difference was significantly greater in the deeper roots R3 and R4 compared with shallow roots R1 and R2, regardless of soil type, in both T1 (R1 + R2: 13·8 ± 2·7 %; R3 + R4: 44·6 ± 4·9 %; F1,38 = 30·3, P < 0·001) and T2 (R1 + R2: 6·5 ± 1·2 %; R3 + R4: 90·1 ± 8·3 %; F1,38 = 98·6, P < 0·001). When all roots were considered together, the relative difference in von Mises stresses was positive in type T1 (17 ± 5 %), but negative in type T2 (–43 ± –9 %, F1,78 = 35·4, P < 0·001).
When mean relative von Mises stresses were calculated in the four lateral root segments of T1-0 and T2-0 during overturning simulations, relative stresses in T1-0 (21 ± 10 %) were significantly greater than those in T2-0 (–51 ± 20 %, F1,14 = 10·7, P = 0·006). No significant differences were found with regard to soil type or stresses in individual root elements. When individual root elements were removed, no significant differences were found with regard to soil or system type when R1 was removed. When R2 was removed, the only significant differences were between root system types, where relative stresses in T1 (5 ± 18 %) were significantly greater than in T2 (−60 ± 22 %, F1,10 = 5·1, P = 0·047). When R3 was removed, again, the only significant differences in relative stresses were between root system types, with T1 (23 ± 6 %) significantly greater than T2 (−28 ± 14 %, F1,10 = 10·9, P = 0·008). Finally, when R4 was removed, relative stresses were again higher in T1 (30 ± 13 %) only, compared with T2 (−47 ± 27 %, F1,10 = 7·0, P = 0·025).
DISCUSSION
Tree anchorage strength is the result of several coupled factors, including the material properties of roots and soil, the location of the slip surface in the soil, the shape and weight of the root–soil plate and the location of the rotation axis with regard to the force vector (Coutts, 1986; Ennos, 1994; Dupuy et al., 2005b, 2007). All these factors are dynamically linked together and it has been shown that root architecture, i.e. root topology and geometry, can play a significant role in defining these interactions.
Simulations performed in two different soil types, which represented a saturated soft clay (S1) and a loamy sand with small cohesion (S2), showed that the shape of the root–soil plate was intrinsically defined by root architecture in association with the mode of failure in the soil, i.e. opening or shearing mode. In our 2-D calculations in soil type S1, only the longest root elements, usually two or three roots, were involved in the formation of the plate. The first important consequence of this result is that roots located inside this predefined root plate do not contribute to anchorage strength. This result indicates that total root biomass cannot be correlated to overturning resistance of trees in such soil conditions, except maybe when a large proportion of this total biomass is allocated to the main roots defining the soil-plate formation. (M. Abd Ghani, A. Stokes and T. Fourcaud, unpubl. res.), studying Eugenia grandis in Malaysia, also found an absence of significant relationships between root biomass and tree resistance to lateral winching. However, the present numerical study considered roots with relatively large cross-sectional areas, i.e. quite stiff roots, and did not take into consideration the decrease in root cross-sectional area from the point of insertion to the root tip. To extrapolate this result to more realistic root morphologies, i.e. considering taper, it could be expected that the zone of rapid taper, as defined by Wilson (1975), is a major component defining the shape and size of the root–soil plate. In such a case, the thinner distal parts of the roots should cross the potential slip surface and consequently increase the anchorage resistance of the tree. This component of the resistive moment is proportional to root tensile strength and has been quantified in previous studies as a major factor involved in tree anchorage (Coutts, 1986; Stokes, 2002). Further numerical investigations should clarify the relationship between the zone of rapid taper, root cross-sectional area and material properties at the potential slip surface and their influence on tree anchorage.
Simulations performed in soil type S1 (saturated soft clay), resulted in two different paths of response curves only, even when all root patterns were considered. This stable behaviour is due to the root elements having little effect on the position of the slip surface. The rotation axes were also grouped together in a small area close to the centre of the circular root–soil plates, thus also contributing to the stable behaviour observed. In a field experiment, Mickovski and Ennos (2002) carried out overturning experiments on Scots pine trees (Pinus sylvestris) growing in clay soil during the rainy season. These authors found that the mode of failure of the root–soil plate was qualitatively very similar to the results of the present simulations, i.e. the rotation axis was below the tree base and the leeward laterals were pushed into the soil. In such soil conditions, Mickovski and Ennos (2003) also reported that asymmetry in the lateral root system did not appear to cause asymmetry in anchorage rigidity, which is consistent with the present results in soil type S1.
It was also shown that in soil type S1, the removal of the distal part of the tap root did not change anchorage behaviour of the given root patterns. This result therefore indicates that the tap root, if too short with regard to the length of lateral roots, is not an element that defines the shape and size of the root–soil plate, which is thus determined by the dimensions of lateral roots. Nevertheless, increasing the tap root : lateral root length ratio increases the influence of tap root length on anchorage. This effect of the tap root started to be significant when its tip was outside the slip surface that was initially defined by the reference root pattern Ti-0, i = 1,2, i.e. when the tap root:lateral root length ratio was >1·0 and >1·4 for root types T1 and T2, respectively. Within this range, an increase in tap root length resulted in an increase of the surface area of the slip surface, as well as a deeper rotation axis. Therefore, if able to reach its full potential with regard to rooting depth, the tap root acts as a rigid stake held in place with lateral roots holding it in position like guy ropes (Ennos, 1994). In young trees, where the vertical growth of the tap root is not usually hindered, such a root system is effective in preventing stem movement and toppling (Khuder et al., 2007). However, in older trees where rooting depth is often arrested by seasonal waterlogging or hard pans in the soil, tap roots are short and thick compared with the lateral roots and play only a small role in tree anchorage (Danjon et al., 2005). Therefore, the tap root becomes defunct with regard to anchorage if unable to grow vertically. It would be prudent in such cases to encourage the growth of lateral roots, although in practice this may be difficult to achieve (Khuder et al., 2007).
The relationship between the different components of anchorage was more complex in soil type S2, which was close to sand with low cohesion (loamy sand). The present results indicated that when main lateral roots are attached to the tap root near the soil surface, leeward roots contribute more to anchorage efficiency than windward roots if they grow deeper in the soil. In such a case, the role of the tap root itself is negligible but on the contrary, if shallow lateral roots growing horizontally, i.e. root type T1, are considered, the tap root constitutes the main root element that contributes to anchorage. It was also shown that the position of the rotation axis was very sensitive to modifications in root architecture. Contrary to the behaviour observed in S1, the rotation axis was usually located on the leeward side of the tap root, and behaved like a hinge. This leeward location of the hinge was also observed in the tap-rooted tropical species Mallotus wrayi during lateral winching experiments, although soil type was not given (Crook and Ennos, 1997). In the present experiments, as the root–soil plate was largely situated on the windward side of the hinge, more importance was given to the weight of the detached root–soil area in resisting overturning. The soil weight is a component which contributes to the resistive moment counterbalancing the pulling forces on the tree. The importance of root–soil weight on tree anchorage was quantified by Coutts (1986) as 13–45 % that of the total anchorage system. This root–soil weight component of the resistive moment (Mw) is thus a function of the plate weight Wp and the length of the lever-arm La, i.e. the distance between the plate's centre of mass and the hinge, and is given by Mw = WpLa. The difference in hinge positions with regard to the root pattern can explain the variability of the response curve paths between the different simulations (Fig. 2). The total weight of root–soil plate, as well as the position of the centre of mass, was also involved in this behaviour, but it was not possible to quantify their respective impact. With regard to these factors, the unexpected increase in overturning resistance observed in soil type S2 after removing root elements R3 and R4 in root type T1 (see Fig. 4) could be explained as follows: the hinge of T1-3 moved towards the soil surface, but it was also displaced to the leeward side (see Fig. 7), possibly increasing the distance with the root–soil plate centre of mass, and consequently the resistive moment. Similarly, the T1-4 hinge moved horizontally in a leeward direction, therefore this deeper and eccentric position increased anchorage strength. Even if this increase in distance between the hinge and centre of mass of the root–soil plate seems to make sense intuitively, this hypothesis cannot be proved, as the position of the centre of mass probably also changed due to the modifications in root patterns. As the shape and, consequently, the weight of the root–soil plate also changed, it is difficult to measure the real impact of each component on the increase or decrease in anchorage.
Due to the particular overturning mechanism that occurs in soil type S2, i.e. the whole root–soil plate turning around an eccentrically positioned windward hinge, trees can thus utilize a maximum amount of soil mass to counterbalance the effect of wind loading. Danjon et al. (2005) studying adult maritime pine (Pinus pinaster) showed that particular root morphologies allow non-cohesive soil blocks to be enclosed in small traps formed by secondary roots, thus increasing root anchorage efficiency. This phenomenon could be simulated and its effect quantified in subsequent numerical studies.
With regard to the radial growth of lateral roots, several authors have postulated that anisotropic secondary growth of structural roots corresponds to an adaptive response to mechanical stress (Mattheck and Breloer, 1995; Nicoll and Ray, 1996; Stokes et al., 1998). In studies carried out on 46-year-old Sitka spruce (Picea sitchensis), Nicoll and Ray (1996) showed that lateral root thickness was greater above rather than below the biological centre. The soil conditions corresponded to a peaty gley and the Sitka spruce root system was composed mainly of horizontal lateral roots (Coutts and Nicoll, 1991). However, Stokes et al. (1998) showed that lateral roots near the trunk of tap-rooted maritime pine growing on a sandy podzol had more secondary growth beneath the biological centre of the root and Di Iorio et al. (2007) found that eccentric growth in lateral roots of Turkey oak (Quercus cerris) in brown clay, changed from the root base to its tip. The biological centre of the root was inversed from below to above the geometrical centre of the root at a distance of 0·20–0·25 m from the tap root. The mean angle of lateral roots with regard to the soil surface was about 25° (156° from the vertical) at 0·10 m from the tap root, which is an intermediate angle between the T1 and T2 types in the present study. The differences observed in root eccentricity in these studies therefore may be explained partly by root system shape.
The present results show that in T2 root systems, relative von Mises stresses were significantly greater than in T1 root systems, regardless of soil type. It was also shown here that von Mises stresses in shallow roots were significantly higher than those in deeper roots, even if the relative difference of von Mises stresses between the top and bottom sides were greater in the deeper R3 and R4 roots, no matter what the soil type. Therefore, more assimilates should be invested in roots close to the soil surface if anchorage is to be improved. Such preferential allocation of root biomass at the uppermost soil surface has also been discussed by Mickovski and Ennos (2003) studying Pinus peuce in brown clay soil, and by Danjon et al. (2005) with regard to mature maritime pine growing in sandy soil.
The FEM model developed here allowed changes in root anchorage capacity to be quantified when structural elements of the root system were removed. Variations in root–soil strength were mainly due to different locations of the rotation axis and a modification in the shape of the root–soil plate. Associated variations in the distribution of mechanical stresses in roots could explain the differences observed in root eccentricity as a result of root growth adaptation (Nicoll and Ray, 1996; Di Iorio et al., 2007).
In the future, stepwise mechanical analyses could be implemented in process-based growth models to simulate the biomechanical adaptation of roots to abiotic stresses, as performed by Fourcaud et al. (2003) on aerial tree architecture. Such models would need to be validated with field data, but they would provide a valuable tool to understand temporal and spatial variations in biomechanical strategies throughout tree growth. More information is also needed on the mechanism of tree anchorage in different soil hydrological situations, particularly with regard to variations in moisture content throughout the soil profile. Again FEM is ideally suited to modelling such behaviour, especially when appropriate field experiments would be difficult to carry out and interpret.
ACKNOWLEDGMENTS
This study was partly carried out while J-N. Ji was studying for an MSc at LIAMA and Beijing Forestry University, China. Grant support from China Key Basic Research Program (973 Program) ‘Influence and Control of Forest Vegetation Covers on Agricultural Ecological Environments in Western China’ (2002CB111502) is acknowledged. Thanks are due to Dr S. Mickovski (University of Dundee, UK) for his helpful comments during this work.
LITERATURE CITED
- Achim A, Ruel J-C, Gardiner BA. Evaluating the effect of precommercial thinning on the resistance of balsam fir to windthrow through experimentation, modelling, and development of simple indices. Canadian Journal of Forest Research. 2005;35:1844–1853. [Google Scholar]
- Ancelin P, Courbaud B, Fourcaud T. Developing an individual tree based mechanical model to predict wind damage within forest stands. Forest Ecology and Management. 2004;203:101–121. [Google Scholar]
- Blackwell PG, Rennolls K, Coutts MP. A root anchorage model for shallowly rooted Sitka spruce. Forestry. 1990;63:73–91. [Google Scholar]
- Coutts MP. Components of tree stability in Sitka spruce on peaty gley soil. Forestry. 1986;59:173–197. [Google Scholar]
- Coutts MP, Nicoll BC. Orientation of lateral roots of trees. I. Upward growth of surface roots and deflection near the soil surface. New Phytologist. 1991;119:227–234. doi: 10.1111/j.1469-8137.1991.tb01025.x. [DOI] [PubMed] [Google Scholar]
- Crook MJ, Ennos AR. The increase in anchorage with tree size of the tropical tap rooted tree Mallotus wrayi King (Euphorbiaceae) In: Jeronimidis G, Vincent JFV, editors. Plant biomechanics. Reading: Centre for Biomimetics, University of Reading; 1997. pp. 31–36. [Google Scholar]
- Cucchi V, Bert D. Wind-firmness in Pinus pinaster Ait. stands in southwest France: influence of stand density, fertilisation and breeding in two experimental stands damaged during the 1999 storm. Annals of Forest Science. 2003;60:209–226. [Google Scholar]
- Di Iorio A, Lasserre B, Scippa GS, Chiatante D. Pattern of secondary thickening in a Quercus cerris root system. Tree Physiology. 2007;27:407–412. doi: 10.1093/treephys/27.3.407. [DOI] [PubMed] [Google Scholar]
- Danjon F, Fourcaud T, Bert D. Root architecture and wind-firmness of mature Pinus pinaster. New Phytologist. 2005;168:387–400. doi: 10.1111/j.1469-8137.2005.01497.x. [DOI] [PubMed] [Google Scholar]
- Dupuy L, Fourcaud T, Stokes A. A numerical investigation into factors affecting the anchorage of roots in tension. European Journal of Soil Sciences. 2005;a 56:319–327. [Google Scholar]
- Dupuy L, Fourcaud T, Stokes A. A numerical investigation into the influence of soil type and root architecture on tree anchorage. Plant and Soil. 2005;b 278:119–134. [Google Scholar]
- Dupuy L, Fourcaud T, Lac P, Stokes A. A generic 3D finite element model of tree anchorage integrating soil mechanics and real root system architecture. American Journal of Botany. 2007;94:1506–1514. doi: 10.3732/ajb.94.9.1506. [DOI] [PubMed] [Google Scholar]
- Ennos AR. The biomechanics of root anchorage. Biomimetics. 1994;2:129–137. [Google Scholar]
- Fourcaud T, Blaise F, Lac P, Castera P, de Reffye P. Numerical modelling of shape regulation and growth stresses in trees. II. Implementation in the AMAPpara software and simulation of tree growth. Trees – Structure and Function. 2003;17:31–39. [Google Scholar]
- Fournier M, Stokes A, Coutand C, Fourcaud T, Moulia B. Tree biomechanics and growth strategies in the context of forest functional ecology. In: Herrel A, Speck T, Rowe N, editors. Biomechanics: a mechanical approach to the ecology of animals and plants. Boca Raton, FL: CRC Press; 2006. pp. 1–34. [Google Scholar]
- Khuder H, Stokes A, Danjon F, Gouskou K, Lagane F. Is it possible to manipulate root anchorage in young trees? Plant and Soil. 2007;294 [Google Scholar]
- Mattheck C, Breloer H. The body language of trees. London: HMSO; 1995. [Google Scholar]
- Mickovski SB, Ennos AR. A morphological and mechanical study of the root systems of suppressed crown Scots pine. Pinus sylvestris. Trees – Structure and Function. 2002;16:274–280. [Google Scholar]
- Mickovski SB, Ennos AR. Anchorage and asymmetry in the root system of. Pinus peuce. Silva Fennica. 2003;37:161–173. [Google Scholar]
- Moore J. Effects of soil type of the root anchorage strength of. Pinus radiata. Forest Ecology and Management. 2000;135:63–71. [Google Scholar]
- Nicoll BC, Ray D. Adaptative growth of tree root systems in response to wind action and site conditions. Tree Physiology. 1996;16:891–898. doi: 10.1093/treephys/16.11-12.891. [DOI] [PubMed] [Google Scholar]
- Nicoll BC, Achim A, Mochan S, Gardiner BA. Does sloping terrain influence tree stability? A field investigation. Canadian Journal of Forest Research. 2005;35:2360–2367. [Google Scholar]
- Nicoll BC, Gardiner BA, Rayner B, Pearce AJ. Anchorage of coniferous trees in relation to species, soil type, and rooting depth. Canadian Journal of Forest Research. 2006;a 36:1871–1883. [Google Scholar]
- Nicoll BC, Berthier S, Achim A, Gouskou K, Danjon F, van Beek LPH. The architecture of Picea sitchensis structural root systems on horizontal and sloping terrain. Trees – Structure and Function. 2006;b 20:701–712. [Google Scholar]
- Niklas KJ, Molina-Reaner F, Tinoco-Ojanguren C, Paolillo DJ. The biomechanics of Pachycereus pringlei root systems. American Journal of Botany. 2002;89 doi: 10.3732/ajb.89.1.12. [DOI] [PubMed] [Google Scholar]
- ONUAA. Amenagement des bassins versants. Cahier FAO conservation des sols. 1977;Vol. 1 Organisation des Nations Unis pour l'Alimentaire et l'Agriculture. http://www.fao.org/docrep/006/AD071F/AD071f00.HTM#som . 22 February 2007. [Google Scholar]
- Peltola H. Mechanical stability of trees under static loads. American Journal of Botany. 2006;93:1501–1511. doi: 10.3732/ajb.93.10.1501. [DOI] [PubMed] [Google Scholar]
- Ruel JC, Quine CP, Meunier S, Suarez J. Estimating windthrow risk in balsam fir stands with the ForestGales model. Forestry Chronicle. 2000;76:329–337. [Google Scholar]
- Ruel JC, Larouche C, Achim A. Changes in root morphology after precommercial thinning in balsam fir stands. Canadian Journal of Forest Research. 2003;33:2452–2459. [Google Scholar]
- Stokes A. Strain distribution during anchorage failure of Pinus pinaster Ait. at different ages and tree growth response to wind-induced root movement. Plant and Soil. 1999;217:17–27. [Google Scholar]
- Stokes A. The biomechanics of tree root anchorage. In: Waisel Y, Eshel A, Kafkaki U, editors. Plant roots – the hidden half. New York, NY: Plenum Publishing; 2002. pp. 175–186. [Google Scholar]
- Stokes A, Berthier S, Sacriste S, Martin F. Variations in maturation strains and root shape in root systems of Maritime pine (Pinus pinaster Ait.) Trees – Structure and Function. 1998;12:334–339. [Google Scholar]
- Telewski FW. Wind-induced physiological and developmental responses in trees. In: Coutts MP, Grace J, editors. Wind and trees. Cambridge: Cambridge University Press; 1995. pp. 237–263. [Google Scholar]
- Wilson BF. Distribution of secondary thickening in tree root systems. In: Torrey JG, Clarkson DT, editors. The development and function of roots. New York, NY: Academic Press; 1975. pp. 197–219. [Google Scholar]
- Zienkiewicz OC, Taylor RL. The finite element method. Vol. I. London: McGraw-Hill; 1989. Basic formulations and linear problems. [Google Scholar]