Abstract
The large number of variables involved in many biophysical models can conceal potentially simple dynamical mechanisms governing the properties of its solutions and the transitions between them as parameters are varied. To address this issue, we extend a novel model reduction method, based on “scales of dominance,” to multi-compartment models. We use this method to systematically reduce the dimension of a two-compartment conductance-based model of a crustacean pyloric dilator (PD) neuron that exhibits distinct modes of oscillation—tonic spiking, intermediate bursting and strong bursting. A cursory analysis of the scales of dominance in a trajectory of this sixteen-variable model leads to a globally-reduced, nine-variable model. In a finer analysis we divide the trajectory into intervals dominated by a smaller number of variables, resulting in a locally-reduced hybrid model whose dimension varies between two and six in different temporal regimes. Both reduced models exhibit the same modes of oscillation as the sixteen-dimensional model over a comparable parameter range. The reduced models highlight low-dimensional organizing structure in the dynamics of the PD neuron, and the dependence of its oscillations on parameters such as the maximal conductances of calcium currents. Our technique could be used to build hybrid low-dimensional models from any large multi-compartment conductance-based model in order to analyze the interactions between different modes of activity.
Keywords: model reduction, compartmental modeling, oscillations, stomatogastric, hybrid dynamical system
Introduction
A major challenge in contemporary computational neuroscience is the analysis of high-dimensional, biophysically realistic models. Mathematical approaches in computational neuroscience have progressed from analysis of abstract neural systems at steady state (Wilson and Cowan, 1972 Wilson and Cowan, 1991) to more biologically realistic situations in which systems are in rhythmic or chaotic states (Terman, 1991; Kopell and LeMasson, 1994). A further increase in the biophysical sophistication of neural models has been driven by the availability of increasingly detailed electrophysiological and anatomical data about neuronal dynamics. Bifurcation theory (Guckenheimer and Holmes, 1983; Strogatz, 2001) is particularly helpful in understanding the qualitative change in the behavior of dynamical systems models as parameters are varied. However, the direct application of bifurcation theory becomes prohibitively difficult as the complexity of the model increases beyond a few dynamical variables, and heuristic arguments are commonly used to justify restricting analysis to smaller, approximate models (Fitzhugh, 1961; Meunier, 1992; Chow and Kopell, 2000).
In this study, we have two aims. The first is to show how a novel reduction technique (Clewley et al., 2005) can be extended to apply to multi-compartment biophysical neuron models. The second is to demonstrate that the technique is useful in the analysis of a real neural system that shows different qualitative behaviors in different parameter regimes. We focus on spiking and bursting behavior in a conductance-based model of the pyloric dilator (PD) neuron, a member of the pacemaker ensemble of the pyloric network in the well-characterized crustacean stomatogastric nervous system (Nusbaum and Beenhakker, 2002; Marder and Bucher, 2007). The PD neuron typically spikes tonically when it is synaptically isolated from the network but, in some preparations, is also capable of producing rhythmic bursts of action potentials and can thus be considered a conditional burster (Miller and Selverston, 1982; Marder, 1984).
A recent modeling study by Soto-Treviño et al. (2005) produced a biophysically-realistic multi-compartment model of the PD neuron and its electrically-coupled counterpart, the anterior burster (AB) neuron. We use the mathematical technique of “dominant scales,” developed by Clewley et al. (2005), to analyze this PD neuron model and systematically identify a critical time interval within the inter-spike interval, in which the dynamics of only a subset of ionic currents govern whether the neuron transitions from tonic spiking to bursting activity. Subsequently, we analyze the interactions among this select subset of ionic currents to characterize the differences in tonic and bursting activity. Our analysis elucidates the biological mechanisms underlying the change in qualitative behavior of the PD neuron model by determining local and low-dimensional approximations to a high-dimensional biophysical model. This methodology also serves as a case study in the context of a multitude of similar transitions in neuronal outputs from other models that could be investigated in a similar fashion.
Methods
The model PD neuron involves two compartments to provide a spatial segregation of spike production from other ionic properties. These compartments will be referred to as the axonal and the soma/neurite (S/N) compartments. The system of ordinary differential equations (ODEs) describing the dynamics of the PD neuron are given in the Appendix, and their full description can be found in Soto-Treviño et al. (2005). Unless otherwise stated, all numerical solutions to the ODEs were calculated using the software package PyDSTool (http://pydstool.sourceforge.net).
Full details of the dominant scale method and its implementation in software is given in Clewley et al. (2005). We summarize it briefly here, and highlight its extension to multi-compartment neural models. The method applies to any variable of interest in the system, and measures the influence of “input” variables on it along a given trajectory. In the present work we focus on the membrane potential V of the S/N compartment and define its “inputs” to be those variables on which the differential equation for V directly depends. The current balance ODE for V takes the form
| (1) |
where Cm is the membrane capacitance, Iext is an externally-applied direct current, Ii are the ionic currents, and Iaxial is the axial current. The current due to an ion channel type i is calculated a conductance multiplied by a driving force: , where Ei denotes the reversal potential of the current. For the purposes of this investigation we found it sufficient to base our analysis only on the activity of activation variables. As a result, it is notationally convenient to re-write the conductance gsp as an activation variable s, raised to a power p, and any inactivation variables are absorbed within the maximal conductance to create a non-constant factor g. (Note that the method itself does not preclude explicit analysis of inactivation variables.) There are no associated activation or inactivation variables for terms representing electrical coupling. Instead, the membrane potential of the coupled compartment can be treated as the input variable, and thus provides the basis for extending the dominant scale method to multi-compartment models.
All 16 ODEs describing the model PD neuron can be written in the form
| (2) |
The equations for the compartmental membrane potentials take this form after a simple algebraic rearrangement described in Appendix B, which reflects the conditional linearity of the equations in the Hodgkin-Huxley formalism and of first-order kinetic equations in general. This view of the ODEs permits an intuitive comparison of the instantaneous target value x∞(t) and time scale τx(t) for each variable, which may depend on the state variables.
For the voltage equation, V∞(t) will be referred to as the “instantaneous target voltage” (dotted curve in Fig. 1; defined in Appendix B). V∞(t) provides structural and organizational information about the vector field, playing a similar role to a slowly varying steady state. The channel conductances play the role of non-constant eigenvalue-like quantities that measure the rates of attraction toward V∞(t). This can be appreciated by supposing that all inputs to the differential equation for V are held constant. Then, by definition, V∞(t) ≡ V∞ = const. and τV(t) ≡ τV = const., so that Eq. (2) for the V variable is an autonomous first-order linear equation with a steady state at V∞, with which there is associated a single (negative) eigenvalue −1/τV.
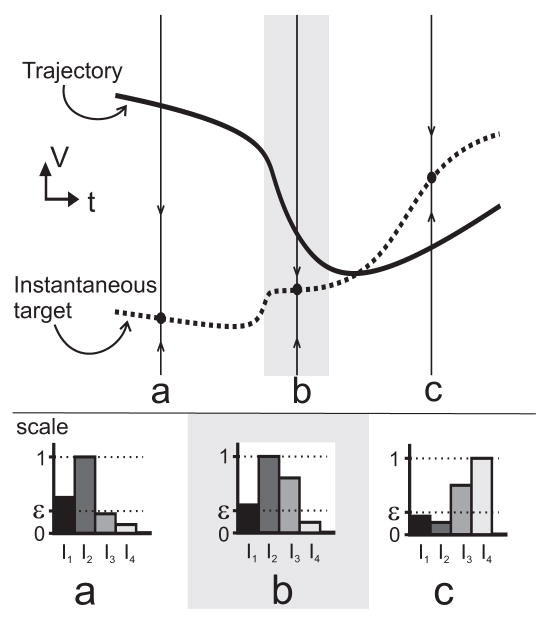
Figure 1.
Schematic diagram exemplifying a hypothetical dominant scale analysis with respect to four time-varying input terms, I1–I4. The top panel shows V(t) (solid) and its associated asymptotic target state V∞(t) (dashed). Three snapshots of the dynamics are taken at representative times a, b, and c. Arrows on the solid vertical lines at these times indicate the instantaneous direction of flow of the variable towards its target. Three time intervals are distinguished, each containing one of the snapshots; a gray box shows the second interval. Each interval corresponds to an “epoch” of the dynamics. The bottom panel indicates hypothetical relative scales of influence of the four inputs. The input with largest influence at a moment in time is considered at a scale of magnitude 1. Compared to the most dominant input, those inputs whose relative scale of influence is above a pre-defined threshold ε are considered active while the remaining inputs are considered inactive. In this example, the second input is most dominant in the two epochs that contain snapshots (a) and (b). In epoch (a) I1 shares the same scale of influence and, so does I3 in epoch (b). In epoch (c), I3 and I4 are most dominant instead. The dynamics show different qualitative trends in each epoch.
Our definition of influence is the sensitivity of V∞ with respect to an input variable s, given by
| (3) |
This measures how strongly the inputs influence the local structure of the vector field, and provides predictive information about the response of a compartment to a perturbation. For conductance-based neuron models, the sensitivity can be defined explicitly (Appendix B). This definition of influence extends to input terms in Eq. (1) arising from electrical coupling between compartments.
The dominant scale method is applied to one or more known trajectories of the model system, which is typically calculated by numerical integration. The influences of input variables on a variable of focus (here, V) are computed over a trajectory. These values are ranked and normalized, and those that are larger than some small positive parameter ε ∈ (0,1) at each moment in time are classified as inputs that are active; the remaining inputs are considered inactive. This is shown schematically in Figure 1 (bottom row). The time interval within which the set of active variables stays the same is defined to be an “epoch” (a, b and c in Fig. 1). Changes in the set of active inputs through time define epoch boundaries (where changes in ranking within a set are ignored). Additionally, active variables are marked “fast” or “slow” relative to V over the duration of an epoch, according to a small time-scale parameter γ ∈ (0,1): variables whose time scales are smaller than γτV are considered fast whereas those that are larger than τV/γ are considered slow. In summary, lower-dimensional reduced models approximate the full dynamics over the duration of an epoch, where the reduced model is a projection of the full system onto the space of the active variables.
The dominant scale method has been implemented in an open-source Matlab code known as DSSRT (Dominant Scale System Reduction Tool), available at http://www.cam.cornell.edu/~rclewley/DSSRT.html. DSSRT requires details of the ODEs, the parameter values and a numerically computed trajectory of the system on which the analysis is performed. DSSRT does not fully automate the analysis, and relies on input from the user in order to obtain optimal results. In particular, it requires appropriate values for ε and γ. The heuristic that we use for choosing the values is that they should lead to a decomposition of the inputs into as few epochs as possible over the course of the trajectory. Additionally, small changes in the values should not make a large qualitative difference to the pattern of epochs. DSSRT provides information about the relative influence strengths and time scales of variables along a trajectory that can aid in the optimal selection of these values. For the current study we chose the values ε =1/5 and γ = 2/7, which robustly distinguished the most dominant scales of influence and time along the trajectories considered. Other values of ε and γ with the same order of magnitude produced similar qualitative results.
The present version of DSSRT (v1.32) is unable to analyze differential equations for the calcium-dependent ion kinetics, although the trajectory used is calculated using the full set of equations. As a result, in our analysis of the model PD neuron two variables have to be approximated by constants. These are (1) the reversal potential ECa and (2) the calcium dependence of the steady-state activation of IKCa. These approximations are not disruptive because the constants can be chosen differently for the analysis of different sub-regimes of the dynamics within which the true values remain approximately constant. By comparison to simulations of the full 16-dimensional model we will demonstrate that these approximations do not affect the validity of the qualitative low-dimensional models.
The number of epochs that are automatically determined by DSSRT may be large and involve distinctions in the dynamics that are too fine-grained for our purposes. However, to elucidate the analysis of the dynamics most intuitively, DSSRT supports a heuristic amalgamation of certain epochs into what we will call “sub-regimes.”
Results
The two-compartment model of the PD neuron described above will be referred to as the full model (F). We use DSSRT to reduce this model to a sequence of low-dimensional sub-regimes that can be thought of as a piecewise-local model (L). Our methodological goal will be demonstrated by the successful reproduction of the distinct tonic spiking and bursting behaviors by model L. Our scientific goal is to identify the significant factors that contribute to these intrinsic output modes. We examine the dynamics in the different states of L to elucidate the details of interactions between the variables of F. We will also compare the performance and complexity of L to make a single, global reduction of the model (G)—this being the traditional form of model reduction.
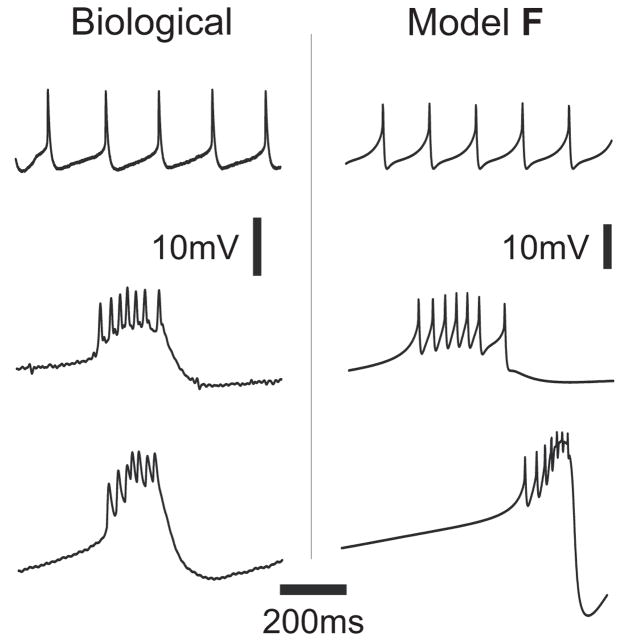
The left column in Figure 2 shows experimental evidence of distinct activity patterns from synaptically-isolated biological PD neurons, indicating that this neuron can produce a variety of outputs including tonic spiking (top), weak (middle) or strong (bottom) bursting. These behaviors are captured by the model PD (Fig. 2, right column) as described in Soto-Treviño et al. (2005). For both the biological and model PD neurons a DC current injection cannot induce a bursting state from a tonically spiking state. However, Figure 2 illustrates that the model PD can produce regular bursting when the maximal conductance of the calcium currents is increased, for example, by exogenous neuromodulators (Johnson et al., 2003). To uncover the differences in the spiking and bursting mechanisms in the model PD we will make use of the dominant scale method (Clewley et al., 2005) and extend it to situations involving two compartments.
Figure 2.
Three types of activity in the isolated PD neuron. Left: experimental measurements of somatic membrane potential from different isolated PD cells with intact descending modulatory inputs, and no current injection. From the top to the bottom trace these behaviors are referred to as (top) tonic spiking, (middle) intermediate bursting, and (bottom) bursting. (Recordings from P. Rabbah and F. Nadim) Right: Full model F in (Soto-Treviño et al., 2005) with different values for the maximal conductances of the calcium currents, gCaT and gCaS. From top to bottom in μS: (gCaT, gCaS) = (60, 22.5), (61.8, 23.18) and (92, 35). All other parameters are as in Table 2.
The proper activity of the PD model neuron, both in isolation and as part of the network, is crucially based on the fact that ionic currents responsible for spike production are spatially segregated from other voltage-gated ionic currents. This conductance-based full model consists of 16 ODEs (see Appendix A) that describe two compartments, one representing the axon, and the other the soma/primary neurite (S/N). We denote by Vaxon and V the membrane potential of the respective compartments. The axonal compartment is responsible for spike generation via the usual fast sodium and potassium currents, INa and IKd, and corresponds to a specific parameter regime of a standard Hodgkin-Huxley compartment. As the interactions between the variables within such a compartment are already well understood (Suckley and Biktashev, 2003; Clewley et al., 2005), we will focus on reducing only the S/N compartment.
In the absence of coupling to the axonal compartment the membrane potential of the S/N compartment produces large-amplitude (approx. 50mV) slow oscillations, which are generated by three outward currents, four inward currents and a leak current IL. The outward currents are a delayed-rectified potassium current IKd, a calcium-dependent potassium current IKCa and a transient potassium current IA. Two of the inward currents are carried by calcium: ICaT and ICaS; the other two are a hyperpolarization-activated IH current and a persistent sodium current INaP. We denote the total calcium current ICaS + ICaT as ICa. The axonal and S/N compartments are intrinsically very different from each other; they interact via an axial current Iaxial with maximal conductance gaxial. Unless otherwise stated, the values of the calcium current maximal conductances gCaT and gCaS that were used for setting the neuron in a tonic spiking regime are 60 and 22.5 μS, respectively. These will be referred to as the “reference values” for these parameters. We increased these by 54% (to 92 and 35 μS) in order to set the neuron in a bursting regime.
Characterizing the changing roles in the critical sub-regime
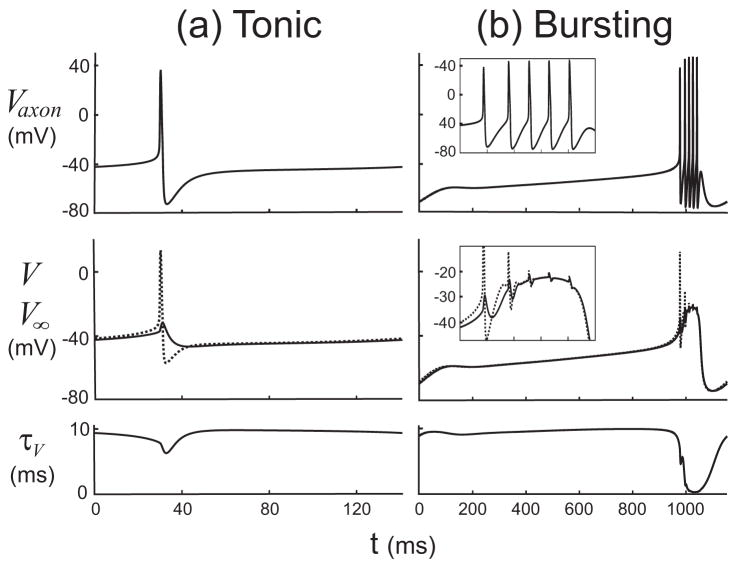
In this section we examine the key quantities that are used by the DSSRT software in its analysis of the S/N compartment: the instantaneous target voltage V∞(t) (Fig. 1) of the membrane voltage V and its characteristic time scale τV(t). Figure 3 shows these quantities, together with Vaxon, over one cycle of the periodic orbits for the tonic spiking (Fig. 3(a)) and bursting (Fig. 3(b)) regimes. In contrast to its behavior during spiking, τV can be seen to drop from approximately 10 ms to almost zero during a burst, corresponding to the neuron entering a “high-conductance regime” (Shelley et al., 2002) in which V is strongly slaved to V∞ (Fig. 3(b), bottom panel).
Figure 3.
Plots over one cycle period of (a) tonic spiking, and (b) bursting activity of the axonal compartment membrane potential Vaxon, the voltage V and its target voltage V∞, and the time scale for V (from top to bottom). Insets show the variables during the burst (both in the same time interval of 960 to 1060 m). The inset in the second panel of (b) shows the increasing control of the large currents on V, as V∞ becomes an increasingly better approximation of V over the time range of 960 to 1060 ms. τV falls to almost zero as the slaving of V to V∞ develops during a burst.
DSSRT computes the influence strengths Ψs, defined in Eq. (3), over a tonic spiking or bursting trajectory, using Eq. (1). We note that, due to the strongly dissipative nature of the equations, we need only analyze a single periodic orbit for each regime, as qualitatively equivalent orbits will exhibit the same pattern of changing influences. Here, the inputs s correspond to the activation variables of the currents in the S/N compartment and the voltage of the axon compartment, Vaxon. Values of Ψs larger than the small positive parameter ε = 1/5 at each moment in time correspond to inputs that are considered “active.”
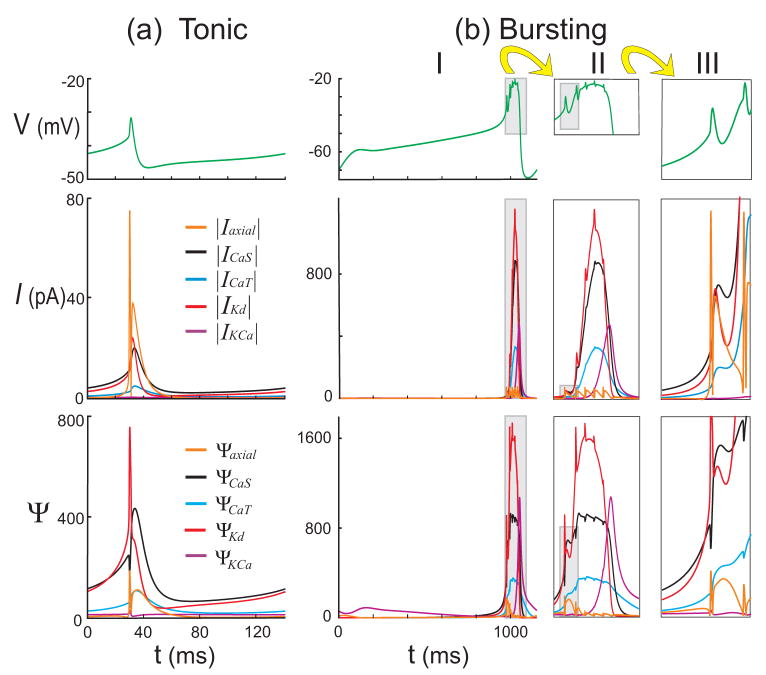
Figure 4 compares the Ψs values, for the currents CaS, CaT, Kd and the axial current flowing between the S/N and Axon compartments, with the corresponding current magnitudes. In both the tonic spiking and bursting regimes the influence strengths for all other inputs were at all times smaller than ε times the largest influence strength. The figure is suggestive of the different roles being played by the inputs to the S/N compartment. For instance, in the tonic regime (Fig. 4(a)), the current magnitudes show that axonal spikes are important for generating large instantaneous rates of change in V. In contrast, the corresponding influence strength Ψaxial is relatively small so that V∞ is insensitive to the axial current during most of the cycle. This indicates that axial spikes have a very localized impact on the net change to V over a cycle, whereas the calcium and the delayed rectifier potassium currents ICa and IKd dominate the position of V∞ for most of the cycle. In the bursting regime (Fig. 4(b)), we observe that ICa and IKd do not fully reset after the first spike (Fig. 4(b)III, middle panel), and quickly build up to large levels (with opposite signs). Ψaxial becomes smaller compared to the calcium and rectifying potassium inputs as the burst progresses (Fig. 4(b)II, middle panel), reflected in the plateau nature of V despite receiving strong spikes from the axon compartment. As Ψaxial becomes smaller during a burst, we see that V exhibits smaller excursions (Fig. 4(b)II, compare top and bottom panels). In the tonic regime, we also note that IKCa remains negligible in size. Only in the later part of a burst does this current become significant to both the rate of change of V and the control of V∞.
Figure 4.
Comparative measures of influence of the most influential variables for (a) the tonic and (b) the bursting regimes. The regions shown in gray boxes in (b)I are expanded in II; they show activity during the active phase of a burst (with a time range 960 to 1100 ms). Similarly, gray boxes in (b)II are expanded in III to show the first two spikes of the active phase in the same scale as (a). Variables were considered non-significant if their current magnitudes and Ψ values were at least a factor of ε =1/5 smaller than the largest. Top panels: S/N voltage traces for reference. Middle panels: current magnitudes over one cycle. Bottom panels: Ψ values over one cycle.
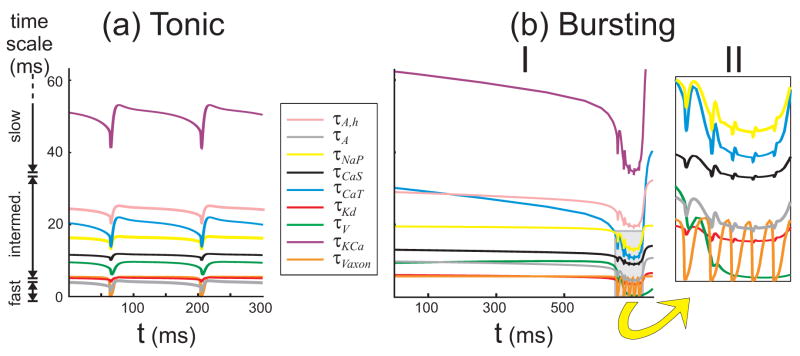
The second aspect to the dominant scale method considers the characteristic time scales τs of the inputs s to the S/N compartment. In Figure 5 we compare the time evolution of these in periodic orbits of the full model. Three time scales, which have much larger values, are not shown in the figure: the activation of IH (τH ~ 1000 ms), the inactivation of INaP (τNaP,h ~ 550 ms), and the inactivation of ICaT (τCaT,h ~ 200 ms). DSSRT defines three time-scale groups using the comparative scaling parameter γ = 2/7 (Fig. 5(a), left of the panels). During tonic spiking, the slow group of variables contains K(Ca) and H, whose time scales are larger than τV/γ ≈ 35 ms. The fast group only exists during a spike event (it consists only of the axon membrane potential) during which τVaxon < γτV ≈ 2.8 ms. The intermediate group includes the remaining currents and the axon membrane potential between spike events (Fig. 5(a)). We classify channels that include inactivation variables according to the faster of the two associated time scales. In the bursting regime (Fig. 5(b)) the groupings are the same except during the active phase of the burst, when the two membrane potentials become comparably fast during spikes and everything else is much slower (Fig. 5(b)II). This shift is due to the influence of the large conductances of CaT and CaS currents that develop during the burst (Fig. 4(b)II, middle panel).
Figure 5.
The time evolution of the characteristic time scales for the most significant variables, during the (a) tonic spiking and (b) bursting regimes. The gray box in (b)I is expanded in II. Three time scale groups are identified: fast, intermediate, and slow. τA, τNaP, τCaS, τCaT, τKd and τKCa refer to the time scales of the associated activations, and τA,h refers to that of the inactivation hA.
A globally reduced approximate model
We begin by determining a global reduction (G) of the PD neuron model F. The passive leak term was not classified as an influential input at the chosen value of ε. We performed comparative simulations (not shown) that demonstrated that the leak current has a subtle modulatory effect on the dynamics during the recovery from a burst. We chose to retain the leak term in G because it helped match the qualitative behavior to F without contributing to model complexity or computational cost.
IH has a negligible influence during spiking and the active phase of bursting, but plays a role in the recovery of the cell between bursts and thus cannot be omitted. However, as noted earlier, the influence of the A and NaP currents remain smaller than ε throughout tonic spiking and bursting. Thus, we removed their associated activation (m) and inactivation (h) variables mA, hA, mNaP, and hNaP. Additionally, the observed slow time scale of hCaT and its minimal fluctuation over the tonic and bursting cycles (not shown) leads us to approximate it to a constant value of 0.65.
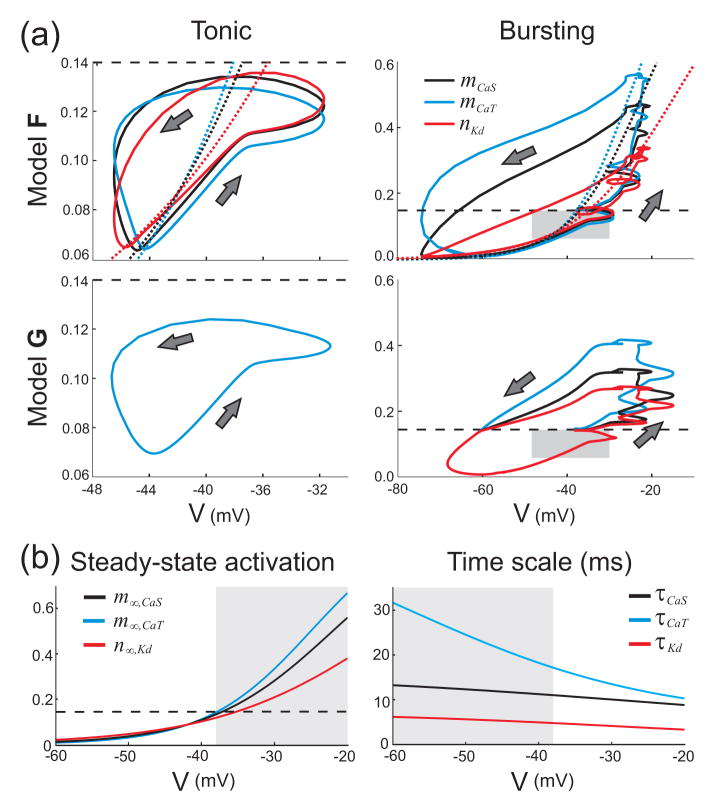
The “lumping” of similar variables into a single dynamic variable is a common reduction technique, and may require appropriate rescalings to be calculated. However, for a single model to reproduce different qualitative behaviors a globally appropriate lumping may not be possible. Figure 6(a) summarizes the most important part of the global reduction by showing the most dominant activation variables (mCaT, mCaS, and nKd) versus V for one cycle of the tonic spiking (left column) and bursting (right column) regimes, comparing F (top row) and G (bottom row). The dashed line in these figures indicates an effective excitability threshold (θ = 0.14, defined below). Below this threshold, the three crucial currents evolve almost identically in F, so that the CaS, CaT and Kd currents remain in balance. This situation applies to the whole of the tonic spiking regime, and for the inter-burst interval in the bursting regime (including the first spike of a burst). As was seen in Figure 4, the K(Ca) current is substantially more dominant than the CaS, CaT or Kd currents at the end of a burst, and so it is the up-sweep of the trajectories of mCaT, mCaS, and nKd that is more important to match to the full model than the down-sweep.
Figure 6.
Lumped variables describing the global reduction. (a) Activation levels of crucial currents plotted versus S/N compartment V simulated for model F (upper panels) and G (lower panels), for one cycle of tonic (left column), and bursting regime (right column). The direction of motion around the limit cycles is shown by the arrows. The steady-state activation curves for the three currents are shown for F as dotted lines (see (b) also). The threshold of nonlinear activation scaling θ = 0.14 is shown as a dashed line (approximate for F and exact for G). The gray boxes in the right column indicate the axis ranges of the plots in the left column. The three activation trajectories for G in (a) are identical. (b) Time scales of activation and steady-state activation curves for the CaS, CaT and Kd conductances as a function of the S/N compartment voltage, showing regions in which they are approximately the same (white) and a region in which they diverge (gray). The regions are determined by the choice of the threshold for nonlinear activation scaling θ = 0.14.
The similarity in the bursting regime is different and requires rescaling of the variables. To explore this, we plotted the steady-state activation curves m∞,CaT, m∞,CaS, and n∞,Kd (Fig. 6(b), left panel) as a function of the S/N compartment’s membrane potential, V. These steady-state activations are comparable in size when V remains in the tonic regime as indicated by the white region. In the bursting regime these targets diverge as V depolarizes (left panel, gray region) as do the time scales (Fig. 6(b), right panel). It is clear that a single lumped variable will not suffice for both regimes, but as part of our hand-tuned reduction using conventional methods we made two state-dependent forms of lumping in the model as described below.
We lump mCaT, mCaS, and nKd together into a single variable x depending on whether x is above or below the threshold of “nonlinear activation scaling,” chosen at θ = 0.14 as the observed excitability threshold: the point where the steady state activations begin to diverge as V is increased (Fig. 6(b), dashed line in the left panel). Note that our analysis is not sensitive to the precise value of this threshold. When x <θ, the rescaling is linear and x is described by the equation for mCaT, the most dominant variable for that regime (although mCaS also works satisfactorily). Above this threshold, mCaT and nKd are nonlinear rescalings of x according to a curve-fitting method (described in Appendix C). In this range, x is described by the equation for mCaS (which is now most dominant). The result of these reductions is a set of equations with nine dynamic variables. Although this model is technically “hybrid,” in that its definition involves a discrete change to the vector field as a function of the state (Van Der Schaft and Schumacher, 2000), this change is minor and does not modify the dimension of the system. We contrast this with the more aggressive reduction we perform in the next section.
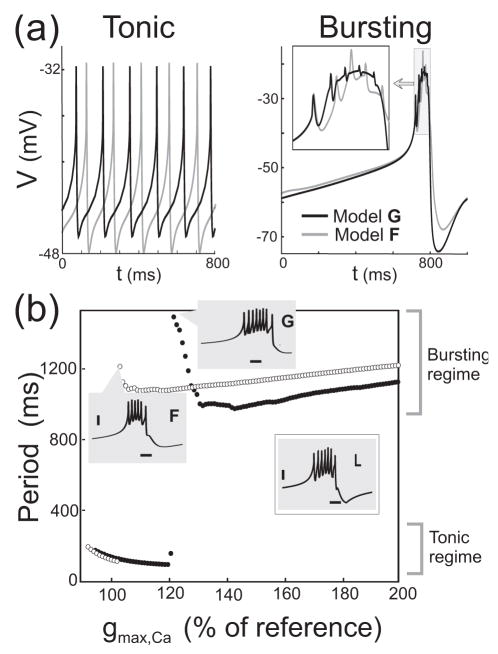
We examined whether the simplified set of currents is adequate to exhibit the transition from tonic spiking to bursting. In particular, in the high activation state, can the three activation variables with similar kinetics be safely approximated by nonlinearly scaled versions of a single, lumped variable? We evaluated this by comparing qualitative properties of simulated trajectories from models F and G. Although our parameter choices do not produce an exact fit to F, they are sufficient for G to exhibit the same types of behaviors (Figure 7(a)). Furthermore, we measured the spiking and bursting periods for G as gCaT and gcas were varied, and found a progression from quiescence to tonic spiking to bursting similar to that for F (Fig. 7(b)). Notably, the intermediate form of bursting (shown in Figure 2) is also found in G, where the spike in [Ca2+] only reaches approximately 8 μM, as compared to approximately 4 or 43 μM, respectively, during tonic spiking or a full burst. In both F and G this intermediate form of bursting is found in a narrow parameter range shortly after the transition from spiking to bursting (Fig. 7(b)).
Figure 7.
The globally reduced model produces the same qualitative outputs as the full model. (a) Voltage traces for models F and G show that the spike timing and qualitative form is similar in both tonic (left panel), and bursting (right panel) parameter regimes. The inset in the right panel is over the time range 700–800 ms. In the tonic regime the threshold θ = 0.14 is never crossed. (b) Period of spiking (lower traces) and bursting (higher traces) as a function of gCaT and gCaS, which were varied together as a percentage of their reference values: model F (open markers) and G (filled markers). Both models show no activity below 90% of the reference maximal conductances. The gray boxes show time courses V for representative “intermediate bursting” behavior (between tonic spiking and full bursting) at the parameter values indicated. A plot of the intermeduate bursting for model L (described later) is shown in the inset for comparison, at 120% of the reference maximal conductances.
A piecewise locally-reduced model
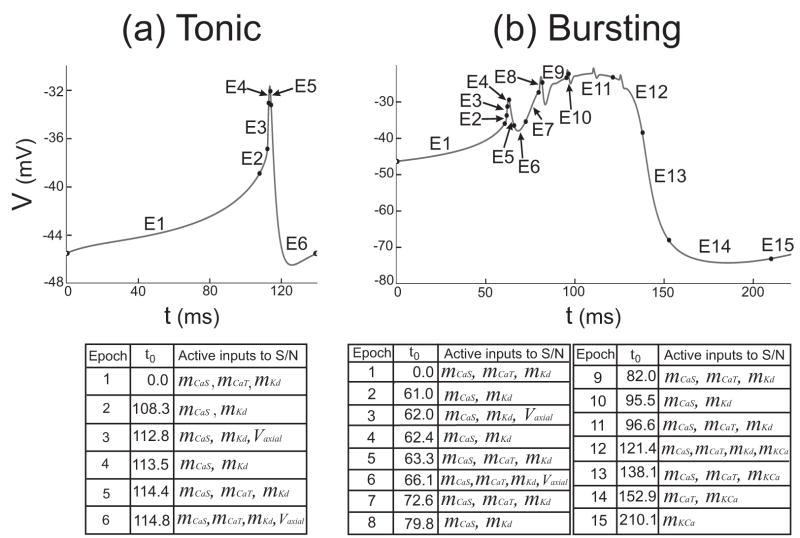
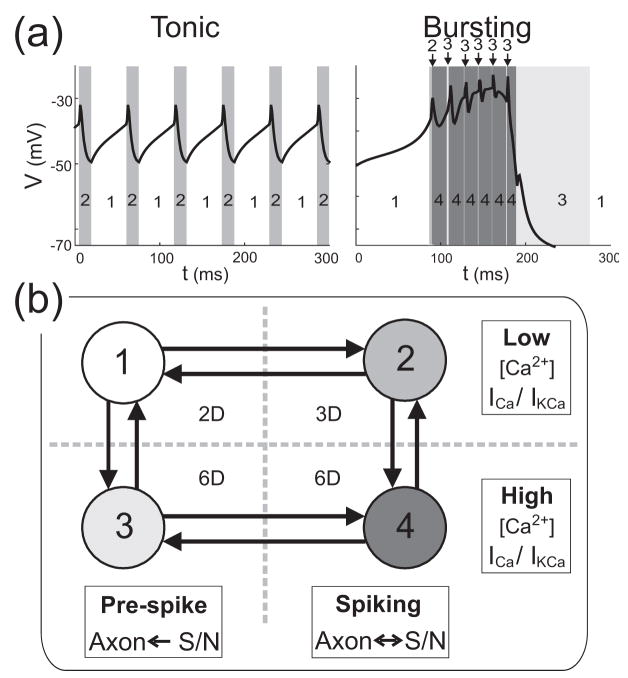
The analysis using DSSRT provides detailed temporal information about the changing influence of variables in the dynamics of the neural model. We used this information to build the locally reduced hybrid model L by considering the epochs involved in the tonic spiking and bursting regimes. In the tonic regime, DSSRT determined six epochs over one spiking period as marked in Figure 8(a). The six epochs were condensed further into two “sub-regimes” based on the methods described in Clewley et al. (2005). The first sub-regime consisted of the first two epochs, for which influence from Vaxon is negligible and the S/N compartment is effectively uncoupled from the axonal compartment. The second sub-regime corresponds to the last four epochs in which the S/N compartment receives significant input from the axonal compartment (except in epochs 4 and 5, which are very short in duration and not mechanistically significant). For sub-regime 2, the input from the calcium current ICaT is the least dominant of the four inputs during epochs 5 and 6, and simulations (not shown) indicated that the threshold ε could be increased in this sub-regime to eliminate mCaT and hCaT with no loss of qualitative accuracy in computed trajectories. The two sub-regimes associated with tonic spiking are shown in Fig. 9(a) (left panel).
Figure 8.
Time epochs as defined by DSSRT. The time epochs marked to indicate each subset of dominant variables on the S/N compartment for tonic spiking (a) and bursting (b). Each table shows the dominant variables present in the epoch starting at time t0.
Figure 9.
Four sub-regimes defined using the epochs determined by DSSRT. (a) The sub-regimes 1–4 marked for tonic spiking and bursting in model L. (b) State transition diagram for L. Each state corresponds to one sub-regime of the vector field. The effective dimension of each state is shown in the center of the diagram. The rows indicate that states 3 and 4 are high –[Ca2+] (and ICa/IKCa activation) versions of states 1 and 2. The columns indicate that states 1 and 3 represent dynamics between axonal spikes (when the axial communication is mainly from S/N to the axon) whereas states 2 and 4 represent dynamics during axonal spikes, when there is feedback from the axon compartment and the input from the transient calcium current is removed. The horizontal dotted line indicates the nonlinear activation threshold θ (when transitioning from states 1 and 2 to 3 and 4) or the threshold θKCa (in the opposite direction). The vertical dotted line indicates the axonal spike threshold (from states 1 and 3 to 2 and 4), or the recovery threshold (in the opposite direction).
For the bursting regime we performed a similar analysis to obtain four sub-regimes, the first two of which were identical to those of tonic spiking because they involved the same active variables. The remaining sub-regimes were drawn from epochs 7–15 in Figure 8(b) according to the following criterion: the exact pattern of active variables need not be reproduced perfectly by the sub-regimes, but a minimal number of sub-regimes were desired. The following observations guided this choice. In epochs 7–15 the intracellular calcium concentration [Ca2+] is in its high state (not shown). IKCa becomes active in epochs 12–15, but its slow time scale of activation means that it builds up slowly only when the high state of [Ca2+] is reached. (Note the dominance of ΨKCa at the end of the burst and during the interburst interval as shown in Fig. 4(b) I & II, bottom panels.) This suggests that mKCa should be included in all the remaining sub-regimes in order that it can become a dominant variable at the right time during a burst, avoiding what can be loosely called a “shadowing error” (Clewley et al., 2005). Despite the fact that epochs 7 and 8, respectively, have the same active inputs as epochs 1 and 2, the high state of [Ca2+] implies that the dynamics for the CaS and CaT activations are not the same as in epochs 1 and 2. This suggests making a sub-regime that is a high- [Ca2+] analog of the first sub-regime. Thus, we chose sub-regime 3 to have the variables present in sub-regime 1 and also mKCa and [Ca2+].
The pattern of active variables in epochs 7–12 roughly follows that of epochs 1–6 except without the axial input. Although the influence of the axial input is not large enough to be considered dominant in epochs 7–12, it plays a modulatory role in creating the small S/N voltage spikes. We chose sub-regime 4 to be a high- [Ca2+] analog of sub-regime 2, in symmetry with the pattern of epochs condensed into sub-regimes 1 and 2. As we are primarily interested in the differences between tonic spiking to bursting, and in the interest of simplicity, we chose not to create a separate sub-regime for the K(Ca)-dominated epochs 13–15, or for the remainder of the bursting trajectory. The sub-regimes associated with bursting are shown in Fig. 9(a) (right panel).
The four sub-regimes that constitute model L are formally defined in Appendix D. Computationally, they are treated as four smooth vector fields connected by discrete events. In each sub-regime, the dynamics of the model PD neuron is dominated by a different subset of the variables. Fig, 9(b) depicts model L as a state transition diagram, in the form of a 2×2 grid where each of the four states represents one sub-regime of the vector field. The arrangement on the grid reflects the suggestion that states 3 and 4 are versions of states 1 and 2 (respectively) except with high levels of ICa/IKCa activation. As such, states 3 and 4 require explicit dynamics for [Ca2+] whereas, for states 1 and 2, DSSRT suggests that [Ca2+] can set to be a constant low value. The value was set at 3.8 μM, the maximum value of [Ca2+] in the tonic regime and the minimum in the burst regime. The columns of the grid provide a division whereby states 1 and 3 represent the dynamics between axonal spikes, and states 2 and 4 represent the dynamics during axonal spiking and the subsequent refractory period.
From the output of DSSRT it can be observed that the transitions to sub-regimes 2 and 4 from sub-regimes 1 and 3 (respectively) occur when Vaxon depolarizes to approximately 5 mV above V. This provides a convenient way to define the transition event in the hybrid system specification. In the opposite direction, the transitions back to sub-regimes 1 or 3 occur after the spike refractory when V and Vaxon return to within 5 mV of each other. This choice of transition events reflects the intuition that the axial coupling is most influential when the difference |V − Vaxon| is sufficiently large. The validity of these transition choices is critical to extending our method to models with two or more compartments. During the rapid changes in Vaxon during spiking, dominant scale analysis of the axonal compartment shows that it is effectively independent of the S/N compartment and therefore can be treated temporarily as an autonomous input (Clewley et al., 2005). This guarantees that after sodium currents become dominant in the axon, the spike will occur and we will transition from sub-regime 1 to 2 or from 3 to 4 and back as described.
Based on observations of model G, the transitions from 1 to 3 and from 2 to 4 are determined by the increasing of mCaT through θ. In states 3 and 4 (high ICa/IKCa activation), ICa increases significantly in a positive feedback loop with V. When the S/N compartment becomes persistently depolarized there is a steady increase in [Ca2+] and consequently the slow IKCa becomes fully activated. This terminates the burst, returning the system to state 1. The return to low ICa/IKCa activation occurs when mKCa decreases below the threshold θKCa = 0.1, which happens later than the fall of mCaT below θ because mKCa decays more slowly. Therefore, mKCa is the more accurate indicator for the return to low ICa/IKCa activation. Note however that the qualitative dynamics of L are insensitive to the precise choices of the event transition thresholds.
Model L successfully reproduces both the tonic and bursting behaviors seen in experiments using different patterns of state (i.e. sub-regime) transitions (Fig. 9(b)) without need for the hand-tuned curve fitting (as in model G). We observe that while tonic spiking, states 3 or 4 are never entered. In contrast, the bursting regime begins in the same way as the tonic regime but at some point enters state 4 (from states 1 and 2) and continues to oscillate between states 3 and 4 until it reverts to state 1 from state 3. As expected, neither the spike nor burst periods were accurately reproduced as these are influenced by NaP, A and H currents that were removed. Model L also produces intermediate bursts when gCaT and gCaS were set to 120% their reference values (inset of Figure 7). The intermediate bursts involved [Ca2+] peaks between 8 and 13 μM that were comparable to those in F and G.
Phase plane analysis of the transition from tonic spiking to bursting
Phase plane diagrams for analysis of high-dimensional systems have limited usefulness because the diagrams only represent projections of trajectories and cross-sections of the null-surfaces at individual time points. In general, this makes it nullclines intersections of the nullcline (cross-sectional) curves in a non-autonomous phase plane do not correspond to actual equilibria. Nevertheless, one can obtain useful information about transient dynamics from such diagrams with careful consideration for the fine structure of the dynamics at different time points along a trajectory. We will demonstrate the use of phase-plane analysis in model L to characterize the transition to bursting in the PD neuron by comparing hybrid states 2 and 4. The precisely defined domains of analysis for the sub-regimes of model L and the lower dimensionality compared to models F or G allow greater confidence in the interpretation of the phase planes. In particular, they enable us to neglect the effect of dynamics in the remainder of the system.
The top panels in Figure 10 show plots of V and Vaxon over the duration of hybrid states 2 and 4 for the tonic (a) and bursting (a) regimes. The instants labeled t0, t1 and t2 respectively correspond to the beginning of the state, the peak of the V spike and the end of the state. The bottom panels of Figure 10 show the dynamics in the (mCaS, V) phase plane for the V trajectories shown in the top panels. The course of the trajectory in this phase plane requires careful interpretation, as the V nullcline changes at each instant (marked 0, 1 and 2 for t0, t1 and t2). The V∞ value for a given instant along a trajectory corresponds to the value of the V nullcline at that time. The quasi-steady fixed points of the system are given by the intersection of the V nullclines and the nullcline m∞,,CaS (V) (closed circles if attracting, open circles if repelling).
Figure 10.
Phase plane analysis for sub-regimes 2 and 4 of model L. Top panels: Voltage traces over the duration of hybrid states 2 and 4 are shown for reference for the tonic and bursting regime. Bottom panels: Non-autonomous phase plane projections in (mCaS, V) showing dynamics through hybrid state 2 in the tonic regime and states 2 and 4 in the bursting regime, where the axial input can be treated as an autonomous external input signal. Three snapshots of the nullclines are highlighted during the motion through each state (the gray mCaS nullcline remains the same): at t0, the onset of the state; t1, at the peak of the spike in V; and t2, when the state ends. Black curves show the projected trajectory and arrow indicates the direction of motion. Colored marks on the trajectory correspond to times ti. During states 2 and 4 the V nullcline (colored and numbered according to ti) is controlled predominantly by the axial input. (a) In state 2 of the tonic regime mCaS does not pass above the threshold of nonlinear activation scaling, θ = 0.14 (dotted line). (t1 − t0 ≈ 2.03 ms, t2−t1≈9.85 ms). (b1) In state 2 of the bursting regime the higher value of gCaS allows mCaS to increase above θ while the axial spike is depolarizing V. This leads to an early exit from state 2 into state 4. (t1−t0 ≈ 2.25 ms, t2−t1≈0.7 ms). (b2) In state 4 of the bursting regime the upper crossing of the nullclines is repelling, and remains above θ. (t1−t0 ≈ 0.9 ms, t2−t1 ≈ 6.5 ms).
In the tonic regime (Figure 10(a)), Iaxial(t) depolarizes V quickly from V(t0) to V(t1) but this depolarization is not enough for mCaS to cross its activation threshold θ = 0.14 (dotted line) before Iaxial(t) hyperpolarizes V to V(t2). In contrast, for state 2 in the bursting case (Fig. 14(b1)), the higher value of gCaS modifies the shape of the V nullclines, and therefore the location of the V∞ values. Together with a decrease in τCaS (V), the axonal compartment spike still acts to depolarize V, allowing mCaS to increase and cross θ. This leads to an early exit from state 2 into state 4. In state 4 of the burst regime (Fig. 14(b2)), the V nullclines now additionally depend on nKd, which distorts their shape compared to state 2. In particular, the V nullclines have two crossings with the mCaS nullcline, and the upper one is repelling. The axonal compartment spike no longer restores V∞ to a hyperpolarized value. Instead, there is a net increase in V∞ during the spike, seen by the V nullcline increasing to the right, and V continues to rise as the state is exited.
The main difference between states 2 and 4 through the transition to bursting is that the effect of Iaxial is diminished as ICa builds up (see Fig. 4(b)II). The fact that mCaS has a slower time scale than the Vaxon spike rise time means that Iaxial (t) has an asymmetric effect: for every Vaxon spike up-sweep, V quickly depolarizes by an amount roughly controlled by the initial value of mCaS (i.e., through ICa), but when the V spike down-sweep starts to hyperpolarize as a response to the Vaxon spike down-sweep, the slower ICa has increased and counters the remainder of the Iaxial(t) peak. This process repeats over each axonal compartment spike, with the V spike getting smaller each time because of the increasing level of ICa (a phenomenon often referred to as spike block).
Discussion
In the past few years there has been an explosion in the number of detailed biophysical models of neurons and networks (Hines et al., 2004). Due to the large number of variables involved in most biophysical models, a mathematical analysis of the dynamics of the solutions or the transitions between different modes of activity is prohibitively difficult. As a result, such models are often analyzed by simulating the model at various parameter values. This provides an understanding of the roles of different components but produces little insight into how these components interact to produce specific dynamical outputs. Our focus on local parameter variation and bifurcation is complementary to the broader search for parameter ranges in which these behavioral regimes can be found (Prinz et al., 2004a).
We have shown that the dominant scales method (Clewley et al., 2005) can be extended to multi-compartment models. We applied the method to the study of tonic spiking and bursting in the two-compartment model PD neuron of Soto-Treviño et al. (2005) (model F), in order to discover the low-dimensional dominant dynamics in each of the two mechanisms. Guided by the output of the software tool DSSRT, we first derived a single, globally reduced, model G that qualitatively captured the tonic and bursting regimes of F. This was intended as a “best effort” to use conventional reduction techniques for comparison with our method. For instance, in attempting to minimize the number of dimensions in G, ad hoc approximations were made that involved hand-fitted rescaling functions. The success of model G affirms the presence of an effective activation threshold separating low and high [Ca2+] states – corresponding to the tonic and bursting regimes, respectively. We then derived a piecewise low-dimensional description of the dynamical system (model L) by more systematically analyzing the changing patterns of influence between the variables in the full dynamics. This derivation did not require the curve fitting of any functional relationships.
Simulation of model L showed that it was capable of reproducing the various behaviors seen in F despite requiring integration of only 6 to 9 variables. The number or variables can be decreased by taking into account the results of a prior dominant scale reduction of the 4-dimensional axonal compartment in Clewley et al. (2005), which have been omitted here.
The analysis suggests that it is functionally equivalent to a 1-dimensional integrate-and-fire compartment. Simulations of such a further reduced model are almost indistinguishable to the trajectories of L (not shown), and involve integrating only between 3 and 6 variables. Furthermore, an increase in gCaT and gCaS in F led to a transition from spiking to bursting via an intermediate form of bursting. Model L could also reproduce this transitional behavior with similar spike levels in [Ca2+] to those observed in F and G, despite the fact that its derivation did not involve analysis of an intermediate bursting trajectory. These results indicate that our characterization of the tonic and bursting regimes was rich enough to support additional qualitative states present in the full system.
For a dynamical system near a bifurcation point, asymptotic analysis or other rigorous methods may be used to derive an optimal normal form representation of the local dynamics. Although we have not established rigorous theory for our method, the correspondence in the results of dominant scale analysis applied to the original Hodgkin-Huxley model with those of asymptotic analysis performed by Suckley and Biktashev (2003) suggests that our method focuses on mathematically-significant features in the dynamics and yields parsimonious and appropriate local models. Our method identifies temporal intervals in the dynamics of the full system within which local reductions are derived. Although much faster than doing traditional asymptotic analysis by hand, the cost of our method lies in the need to compute trajectories for hybrid dynamical systems, which involves accurate determination of zero-crossings of “test functions” that define the state transition events between the individual vector fields. The changes in the pattern of hybrid states strongly suggest the presence of one or more bifurcations in the dynamics of the full system, although a rigorous bifurcation analysis is beyond the scope of this work. We fully expect that studying the hybrid model representation further could characterize other aspects of the original model PD neuron’s dynamics but we did not attempt this in this study.
The role of the axon in the transition to bursting
The changing pattern of dominant inputs to the two compartments over the course of a spike shows that axial coupling has a subtler role than to promote synchronized activity. Between spikes the S/N compartment restores the axonal compartment towards its spike threshold via this coupling. Without axial coupling the axonal compartment remains quiescent and the depolarizing currents of the S/N compartment can build up without the axonal spikes to counter their effect. Thus, the high ICa/IKCa state is inevitably entered, and the membrane potential V in F follows a trajectory that resembles the envelope of a burst without spikes. On the other hand, if the axial coupling is so strong that the two compartments are effectively unified, the cell only exhibits bursting (Soto-Treviño et al., 2005, Fig. 6).
The finding that axial coupling plays changing roles in the PD neuron supports the view that current flowing between neural compartments acts in a more complex manner than merely as a co-promoter of activity or as a drive towards synchrony (Sherman and Rinzel, 1992; Chow and Kopell, 2000; Medvedev and Kopell, 2001). For instance, it has been shown that the switch from spiking to bursting in pancreatic β-cells can be controlled by the strength of coupling between two electrically-coupled cells having similar currents but different parameters (de Vries and Sherman, 2001): stronger coupling led to spiking whereas weaker coupling led to bursting. As shown in Soto-Treviño et al. (2005), the PD neuron activity (model F), despite involving two very different compartments, can also switch from bursting to spiking as the strength of the axial coupling is increased. In light of the results described above, this transition can be interpreted as follows: the increase in axial conductance increases the influence of the axial current into the S/N compartment. The timing of the axonal spikes is such that it prevents the activation of the calcium currents from reaching the excitability threshold θ, which has the resetting effect on the S/N membrane potential, as described as state 2 of model L.
Our results and interpretations are also consistent with the description of the soma-dendritic “ping-pong” mechanism for the Pinksy-Rinzel model of bursting given by Bose and Booth (2005). The ping-pong mechanism relies on a separation of time scales between the two electrotonically-coupled compartments, and a “proper balance in strength or timing of interaction” between them. In their analysis of a piecewise reduced model of a two-compartment neuron, Bose and Booth determined that the activation of ICa during the active phase of the burst ultimately causes spike block and disrupts the ping-pong pattern, leading to a transition to the silent phase of the burst.
Relation to other approaches
Our method of dominant scales extends the principles of quasi-steady state approximation that is popularly used in modeling chemical kinetics (Murray, 1989). While the quasi-state method focuses on separations in time scale only, our method also incorporates information about multiple scales in terms of a measure of influence of variables over each other. This method strives to bring greater objectivity to the process of model reduction through the use of an algorithmic process. However, as it is the case in other reduction methods and in the process of model development and analysis, interpretative steps may still be necessary in determining an efficient representation for a reduced model.
Kepler et al. (1992) describe a complementary method of systematic reduction known as “equivalent potentials,” which they apply globally to reduce the number of differential equations representing a system of ODEs. Golomb et al. (1993) applied a variant of this method to their reduction of an STG model, which took into account calcium dependence and also the significant separation of time scales in the activation variables. Their reduced model showed qualitatively similar dynamics and bifurcation structure. The mathematical nature of lumping using equivalent potentials is rigorously determined in comparison to the hand-tuned curve fitting used for deriving model G. However, here we attempt to objectively measure which variables are dominant in a particular sub-regime before lumping any together, and we retain the original units for all the variables. As observed by Golomb et al., activation variables whose time constants were significantly dissimilar over the critical range of membrane potential values could not be lumped together. It was for this reason we pursued the locally reduced, hybrid model L, which makes the use of lumping more powerful. Model L included lumped variables in sub-regimes 1 and 2 where their time constants were similar, while the other sub-regimes used individual representations for those variables.
Butera et al. (1996) used a similar technique in their study of low-order reductions of an 11-dimensional bursting model neuron based on a multiple time scale analysis. Their reductions were most powerful when a heuristically determined interaction between the fast and slow sub-systems was included, making the model effectively hybrid. We also note that our separation of time scales in the reduced analysis of bursting is equivalent to the “effective leak” method of Guckenheimer et al. (2005).
Experimental tests
The hypothesis that the maximal conductance parameters gCaT and gCaS can control a transition from spiking to bursting (or vice-versa) could be tested by applying neuromodulators that have a specific impact on these conductances, or by using a dynamic clamp protocol (Prinz et al., 2004b) to add or remove calcium conductances. We have explored the variation of other parameters in order to control similar transitions, and have found qualitatively similar dynamics. In this study, we focused on calcium conductances in the S/N compartment, but changes that affect the effective structure of the axon compartment can also modify the behavior of both biological and model PD neurons. This would be consistent with experimental results which show that antidromic spiking activity in the axon can disrupt bursting in the de-afferented PD soma (Bucher et al., 2003), and switch it to tonic activity.
Acknowledgments
NIH Grant MH-60605 (FN), NSF Grant FIBR 0425878 (RC). We would like to thank the reviewers for their helpful comments.
Appendices
A. Differential equations describing the PD neuron model
In each compartment the membrane potential, V, is given by the current balance equation , where . The exponents pi, qi are integers between 0 and 4; the capacitance C, maximal conductances gi and reversal potentials Ei are given in the tables below. Each activation mi, or inactivation variable hi varies according to the equation , with x = mi or hi. The voltage-dependent functions τx(V)and x∞(V) are described in Tables 1 and 2.
Table 1.
Voltage and calcium dependence for the steady-state activation m and inactivation h of the ionic currents.
| mp,hq | x∞ | τx (ms) | |||
|---|---|---|---|---|---|
| INa | m3 |
|
|
||
| h |
|
|
|||
| ICaT | m3 |
|
|
||
| h |
|
|
|||
| ICaS | m3 |
|
|
||
| INap | m3 |
|
|
||
| h |
|
|
|||
| Ih | m |
|
|
||
| IK | m4 |
|
|
||
| IKCa | m4 |
|
|
||
| IA | m3 |
|
|
||
| h |
|
|
Table 2.
Parameter values of the full PD model F.
| gi (μS) | Erev (mV) | ||
|---|---|---|---|
| AXON | INa | 1110 | 50 |
| IK | 150 | −80 | |
| IL | 0.00081 | −55 | |
| C | 6.0 nF | ||
| SOMA | ICaT | 22.5 | Nernst potential with an extracellular [Ca2+] of 13mM |
| ICaS | 60 | ||
| INap | 4.38 | 50 | |
| Ih | 0.219 | −20 | |
| IK | 1576.8 | −80 | |
| IKCa | 251.85 | −80 | |
| IA | 39.42 | −80 | |
| IL | 0.105 | −55 | |
| C | 12.0 nF | ||
| [Ca2+] | , τca = 300 ms, F=0.515 μ M/nA, Co=0.5 μ M | ||
| Iaxial | gaxial =1.05 μS | ||
B. Definitions for the dominant scale method
Using the convenient algebraic form of the Hodgkin-Huxley equations, we re-write the differential equation for the membrane potential as
| (4) |
where
| (5) |
and
| (6) |
The differential equation for the intra-cellular calcium concentration can also be put in this form:
| (7) |
The differential equations for the activation and inactivation variables of all the ionic membrane channels are already in this form.
The definition of the influence strength in Eq. (3) for an input variable s to Eq. (1) can be expanded in the case of the Hodgkin-Huxley formalism to give
| (8) |
where gmax is the input’s maximal conductance, Es its reversal potential (Erev = Vaxon for the coupling term to the axon compartment), and p and q are the powers on the conductance’s activation and inactivation variables s and h, respectively. q is zero if there is no inactivation variable for this input, and we treat the inactivation variable as secondary to the activation variable by formally absorbing it into a non-constant maximal conductance defined by g(t) = gmaxh(t)q. We focus the sensitivity analysis on the variable V, so that the inputs s are the activations for the CaT, CaS, Kd, NaP, H, K(Ca), A, leak, axial coupling conductances and the external bias current.
C. Nonlinear scaling of activations in the globally reduced model
In the globally reduced model neuron (G), rescaled versions of a single activation variable x (based on mCaT) replaced the dynamics of three other activation variables in model F. In a low calcium activation state the activation variables are treated as identical (Fig. 6(a)). However, when a threshold θ is reached the relationship between them becomes nonlinear (Fig. 6(b)). This suggests fitting a simple power law to describe all three variables using just one. The activation re-scalings are given by
| (9) |
where the values for c, p are set, respectively to (1.25, 1) for mCaT, (1.2, 1.2) for mCaS, and (0.85, 1.2) for nKd. The time constant and activation curve of x is switched from that of mCaT to mCaS at the threshold θ =0.14, when an ad hoc factor of 0.7 on τCaS is also introduced that provides a better fit to the duration of the burst envelope observed in model F.
D. Definition of the hybrid system for the S/N compartment
Model L consists of the definition of the vector fields and the discrete events for transitioning between them, according to the following rules:
Each current is determined by the same equations as for the full model. The axonal compartment is the same as in F.
The ICaT inactivation variable hCaT is set to the constant value of 0.7.
The passive leak current is retained only in the axonal compartment.
Currents that are missing in some states are held constant.
[Ca2+] is held constant at 3.8 μM for states 1 and 2.
In addition to V, the following variables were active in different states:
State 1: mCaS = nkd = x ≡ mCaT
State 2: nKd = y ≡ mCaS, axial coupling.
State 3: CaT, CaS, Kd, K(Ca), [Ca2+].
State 4: CaS, Kd, K(Ca), [Ca2+], axial coupling.
Different states have different sets of lumped or un-lumped variables. Therefore, when a state transition was made some of these variables required initialization from the available activation values of the previous state. Transition event from state 1 to 2 and from 3 to 4: Vaxon − V ≥ E (“axonal spike threshold”) assuming initially that Vaxon −V < E. Transition event from state 2 to 1 and from 4 to 3: V − Vaxon ≤ E (“recovery threshold”) assuming initially that V −Vaxon>E. Notice that the left-hand sides of these inequalities are not absolute values, and therefore these two conditions are not inverses of each other. The first condition is met when Vaxon becomes more depolarized than V by at least an amount equal to E. The second condition is met when Vaxon depolarizes to become close to V, by an amount less than E. We used E = 5 mV. Transition event from state 1 to 3 and from 2 to 4: x ≥ θ. Transition event from state 3 to 1 and from 4 to 2: mKCa < θKCa, where θKC = 0.10.
Contributor Information
Robert Clewley, Department of Mathematics and Statistics, Georgia State University, Atlanta, GA 30303. rclewley@gsu.edu.
Cristina Soto-Treviño, Department of Mathematical Sciences, New Jersey Institute of Technology, Newark, NJ 07102. cristina@stg.rutgers.edu.
Farzan Nadim, Department of Mathematical Sciences, New Jersey Institute of Technology and Department of Biological Sciences, Rutgers University, Newark, NJ 07102. farzan@njit.edu.
References
- Amit DJ, Tsodyks MV. Quantitative study of attractor neural networks retrieving at low spike rates I: Substrate - spikes, rates, and neuronal gain. Network. 1991;2:259–274. [Google Scholar]
- Bose A, Booth V. Bursting in two-compartment neurons: A case study of the Pinsky-Rinzel model. In: Coombes S, Bressloff P, editors. Bursting: The genesis of rhythm in the nervous system. World Scientific; 2005. pp. 123–144. [Google Scholar]
- Bucher D, Thirumalai V, Marder E. Axonal Dopamine Receptors Activate Peripheral Spike Initiation in a Stomatogastric Motor Neuron. J Neuroscience. 2003;23:6866–6875. doi: 10.1523/JNEUROSCI.23-17-06866.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butera RJ, Clark JW, Byrne JH, Rinzel J. Dissection and reduction of a modeled bursting neuron. Journal of Computational Neuroscience. 1996;3:199–223. doi: 10.1007/BF00161132. [DOI] [PubMed] [Google Scholar]
- Chow CC, Kopell N. Dynamics of spiking neurons with electrical coupling. Neural Computation. 2000;12:1643–1678. doi: 10.1162/089976600300015295. [DOI] [PubMed] [Google Scholar]
- Clewley R, Rotstein HG, Kopell N. A Computational Tool for the Reduction of Nonlinear ODE Systems Possessing Multiple Scales. Multiscale Modeling and Simulation. 2005;4:732–759. [Google Scholar]
- de Vries G, Sherman A. From spikers to bursters via coupling: help from heterogeneity. Bulletin of Mathematical Biology. 2001;63:371–391. doi: 10.1006/bulm.2001.0228. [DOI] [PubMed] [Google Scholar]
- Fitzhugh R. Impulses and physiological states in theoretical models of nerve membrane. Biophysics Journal. 1961;1:445–466. doi: 10.1016/s0006-3495(61)86902-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golomb D, Guckenheimer J, Gueron S. Reduction of a Channel-Based Model for a Stomatogastric Ganglion LP Neuron. Biological Cybernetics. 1993;69:129–137. [Google Scholar]
- Guckenheimer J, Holmes P. Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields. New-York: Springer-Verlag; 1983. [Google Scholar]
- Guckenheimer J, Tien JH, Willms AR. Bifurcations in the fast dynamics of neurons: implications for bursting. In: Coombes S, Bressloff P, editors. Bursting: The Genesis of Rhythm in the Nervous System. Singapore: World Scientific; 2005. [Google Scholar]
- Hines ML, Morse T, Migliore M, Carnevale NT, Shepherd GM. ModelDB: A Database to Support Computational Neuroscience. Journal of Computational Neuroscience. 2004;17:7–11. doi: 10.1023/B:JCNS.0000023869.22017.2e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson BR, Kloppenburg P, Harris-Warrick RM. Dopamine modulation of calcium currents in pyloric neurons of the lobster stomatogastric ganglion. J Neurophysiol. 2003;90:631–643. doi: 10.1152/jn.00037.2003. [DOI] [PubMed] [Google Scholar]
- Kepler TB, Abbott LF, Marder E. Reduction of Conductance-Based Neuron Models. Biological Cybernetics. 1992:66. doi: 10.1007/BF00197717. [DOI] [PubMed] [Google Scholar]
- Kopell N, LeMasson G. Rhythmogenesis, amplitude modulation, and multiplexing in a cortical architecture. Proc Natl Acad Sci USA. 1994;91:10586–10590. doi: 10.1073/pnas.91.22.10586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E. Mechanisms underlying neurotransmitter modulation of neuronal circuit. TINS. 1984;7:48–53. [Google Scholar]
- Marder E, Bucher D. Understanding Circuit Dynamics Using the Stomatogastric Nervous System of Lobsters and Crabs. Annual Review of Physiology. 2007;69:1–26. doi: 10.1146/annurev.physiol.69.031905.161516. [DOI] [PubMed] [Google Scholar]
- Medvedev GS, Kopell N. Synchronization and transient dynamics in chains of electrically coupled Fitzhugh-Nagumo oscillators. Siam J Appl Math. 2001;61:1762–1801. [Google Scholar]
- Meunier C. Two and three dimensional reductions of the Hodgkin-Huxley system: separation of time scales and bifurcation schemes. Biological Cybernetics. 1992;67:461–468. doi: 10.1007/BF00200990. [DOI] [PubMed] [Google Scholar]
- Miller JP, Selverston AI. Mechanisms underlying pattern generation in lobster stomatogastric ganglion as determined by selective inactivation of identified neurons. II. Oscillatory properties of pyloric neurons. J Neurophysiol. 1982;48:1378–1391. doi: 10.1152/jn.1980.44.6.1102. [DOI] [PubMed] [Google Scholar]
- Murray JD. Mathematical Biology. New York: Springer-Verlag; 1989. [Google Scholar]
- Nusbaum M, Beenhakker M. A small-systems approach to motor pattern generation. Nature. 2002;417:343–350. doi: 10.1038/417343a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prinz AA, Bucher D, Marder E. Similar network activity from disparate circuit parameters. Nature Neuroscience. 2004a;7:1345–1353. doi: 10.1038/nn1352. [DOI] [PubMed] [Google Scholar]
- Prinz AA, Abbott LF, Marder E. The dynamic clamp comes of age. TINS. 2004b;27:218–224. doi: 10.1016/j.tins.2004.02.004. [DOI] [PubMed] [Google Scholar]
- Shelley M, McLaughlin D, Shapley R, Wielaard J. States of High Conductance in a Large-Scale Model of the Visual Cortex. Journal of Computational Neuroscience. 2002;13:93–109. doi: 10.1023/a:1020158106603. [DOI] [PubMed] [Google Scholar]
- Sherman A, Rinzel J. Rhythmogenic effects of weak electrotonic coupling in neuronal models. Proc Natl Acad Sci USA. 1992;89:2471–2474. doi: 10.1073/pnas.89.6.2471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soto-Treviño C, Rabbah P, Marder E, Nadim F. A Computational Model of Electrically Coupled, Intrinsically Distinct Pacemaker Neurons. Journal of Neurophysiology. 2005;94:590–604. doi: 10.1152/jn.00013.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strogatz SH. Nonlinear Dynamics and Chaos. Perseus Books; 2001. [Google Scholar]
- Suckley R, Biktashev V. The Asymptotic Structure of the Hodgkin-Huxley Equations. International Journal of Bifurcation and Chaos. 2003;13:3805–3826. [Google Scholar]
- Terman D. Chaotic spikes arising from a model of bursting in excitable membranes. Siam J Appl Math. 1991;51:1418–1450. [Google Scholar]
- Van Der Schaft A, Schumacher JM. An Introduction to Hybrid Systems. London: Springer-Verlag; 2000. [Google Scholar]
- Wilson HR, Cowan JD. Excitatory and inhibitory interactions in localized populations of model neurons. Biophysics Journal. 1972;12:1–24. doi: 10.1016/S0006-3495(72)86068-5. [DOI] [PMC free article] [PubMed] [Google Scholar]