Abstract
Evolutionary game theory studies frequency dependent selection. The fitness of a strategy is not constant, but depends on the relative frequencies of strategies in the population. This type of evolutionary dynamics occurs in many settings of ecology, infectious disease dynamics, animal behavior and social interactions of humans. Traditionally evolutionary game dynamics are studied in well-mixed populations, where the interaction between any two individuals is equally likely. There have also been several approaches to study evolutionary games in structured populations. In this paper we present a simple result that holds for a large variety of population structures. We consider the game between two strategies, A and B, described by the payoff matrix . We study a mutation and selection process. If the payoffs are linear in a, b, c, d, then for weak selection strategy A is favored over B if and only if σa + b > c + σd. This means the effect of population structure on strategy selection can be described by a single parameter, σ. We present the values of σ for various examples including the well-mixed population, games on graphs and games in phenotype space. We give a proof for the existence of such a σ, which holds for all population structures and update rules that have certain (natural) properties. We assume weak selection, but allow any mutation rate. We discuss the relationship between σ and the critical benefit to cost ratio for the evolution of cooperation. The single parameter, σ, allows us to quantify the ability of a population structure to promote the evolution of cooperation or to choose efficient equilibria in coordination games.
1 Introduction
Game theory was invented by John von Neuman and Oskar Morgenstern (1944) to study strategic and economic decisions of humans (Fudenberg & Tirole 1991, Binmore 1994, Weibull 1995, Samuelson 1997, Binmore 2007). Evolutionary game theory was introduced by John Maynard Smith in order to explore the evolution of animal behavior (Maynard Smith & Price 1973, Maynard Smith 1982, Houston & McNamara 1999, McNamara et al 1999, Bshary et al 2008). In the meanwhile, evolutionary game theory has been used in many areas of biology including ecology (May & Leonard 1975, Doebeli & Knowlton 1998), host-parasite interactions (Turner & Chao 1999, Nowak & May 1994), bacterial population dynamics (Kerr et al 2002), immunological dynamics (Nowak et al 1995), the evolution of human language (Nowak et al 2002) and the evolution of social behavior of humans (Trivers 1971, Axelrod & Hamilton 1981, Boyd & Richerson 2005, Nowak & Sigmund 2005). Evolutionary game theory is the necessary tool of analysis whenever the success of one strategy depends on the frequency of strategies in the population. Therefore, evolutionary game theory is a general approach to evolutionary dynamics with constant selection being a special case (Nowak & Sigmund 2004).
In evolutionary game theory there is always a population of players. The interactions of the game lead to payoffs, which are interpreted as reproductive success. Individuals who receive a higher payoff leave more offspring. Thereby, successful strategies outcompete less successful ones. Reproduction can be genetic or cultural.
The traditional approach to evolutionary game theory is based on the replicator equation (Taylor & Jonker 1978, Hofbauer et al 1979, Zeeman 1980, Hofbauer & Sigmund 1988,1998, 2003, Cressman 2003), which examines deterministic dynamics in infinitely large, well-mixed populations. Many of our intuitions about evolutionary dynamics come from this approach (Hofbauer & Sigmund 1988). For example, a stable equilibrium of the replicator equation is a Nash equilibrium of the underlying game. Another approach to evolutionary game theory is given by adaptive dynamics (Nowak & Sigmund 1990, Hofbauer & Sigmund 1990, Metz et al 1996, Dieckman et al 2000) which also assumes infinitely large population size.
However if we want to understand evolutionary game dynamics in finite-sized populations, we need a stochastic approach (Riley 1979, Schaffer 1988, Fogel et al 1998, Ficici & Pollack 2000, Alos-Ferrer 2003). A crucial quantity is the fixation probability of strategies; this is the probability that a newly introduced mutant, using a different strategy, takes over the population (Nowak et al 2004, Taylor et al 2004, Imhof & Nowak 2006, Nowak 2006a, Traulsen et al 2006, Lessard & Ladret 2007, Bomze & Pawlowitsch 2008). In this new approach, the Nash equilibrium condition no longer implies evolutionary stability.
There has also been much interest in studying evolutionary games in spatial settings (Nowak & May 1992, 1993, Ellison 1993, Herz 1994, Lindgren & Nordahl 1994, Ferriere & Michod 1996, Killingback & Doebeli 1996, Nakamaru et al 1997, 1998, Nakamaru & Iwasa 2005, 2006, van Baalen & Rand 1998, Yamamura et al 2004, Helbing & Wu 2008). Here most interactions occur among nearest neighbors. The typical geometry for spatial games are regular lattices (Nowak et al 1994, Hauert & Doebeli 2004, Szabó & Tőke 1998, Szabó et al. 2000), but evolutionary game dynamics have also been studied in continuous space (Hutson & Vickers 1992, 2002, Hofbauer 1999).
Evolutionary graph theory is an extension of spatial games to more general population structures and social networks (Lieberman et al 2005, Ohtsuki et al 2006a,b, Pacheco et al 2006, Szabó & Fath 2007, Taylor et al 2007a, Santos at al 2008, Fu et al 2008). The members of the population occupy the vertices of a graph. The edges determine who interacts with whom. Different update rules can lead to very different outcomes of the evolutionary process, which emphasizes the general idea that population structure greatly affects evolutionary dynamics. For example, death-birth updating on graphs allows the evolution of cooperation, if the benefit-to-cost ratio exceeds the average degree of the graph b/c > k (Ohtsuki et al 2006). Birth-death updating on graphs does not favor evolution of cooperation. A replicator equation with a transformed payoff matrix can describe deterministic evolutionary dynamics on regular graphs (Ohtsuki & Nowak 2006b). There is also a modified condition for what it means to be a Nash equilibrium for games on graphs (Ohtsuki & Nowak 2008).
Spatial models have also a long history of investigation in the study of ecosystems and ecological interactions (Levin & Paine 1974, Durrett 1988, Hassel et al 1991, Durrett & Levin 1994). There is also a literature on the dispersal behavior of animals (Hamilton & May 1977, Comins et al 1980, Gandon & Rousset 1999). Boerlijst & Hogeweg (1991) studied spatial models in prebiotic evolution. Evolution in structured populations can also be studied with the methods of inclusive fitness theory (Seger 1981, Grafen 1985, 2006, Queller 1985, Taylor 1992b, Taylor & Frank 1996, Frank 1998, Rousset & Billiard 2000, Rousset 2004, Taylor et al 2000, 2007b).
In this paper, we explore the interaction between two strategies, A and B, given by the payoff matrix
| (1) |
We consider a mutation-selection process in a population of fixed size N. Whenever an individual reproduces, the offspring adopts the parent's strategy with probability 1 u and adopts a random strategy with probability u. We say that strategy A is selected over strategy B, if it is more abundant in the stationary distribution of the mutation-selection process. We call this concept `strategy selection'.
In the limit of low mutation (u → 0), the stationary distribution is non-zero only for populations that are either all-A or all-B. The system spends only an infinitesimal small fraction of time in the mixed states. In this case, the question of strategy selection reduces to the comparison of the fixation probabilities, ρA and ρB (Nowak et al 2004). Here, ρA is the probability that a single A mutant introduced in a population of N - 1 many B players generates a lineage of offspring that takes over the entire population. In contrast, the probability that the A lineage becomes extinct is 1 - ρA. Vice versa, ρB denotes the probability that a single B mutant introduced in a population of N - 1 many A players generates a lineage that takes over the entire population. The fixation probabilities measure global selection over the entire range of relative abundances. The condition for A to be favored over B in the limit of low mutation is
| (2) |
For positive mutation rate (0 < u < 1), the stationary distribution includes both homogeneous and mixed states. In this case, strategy selection is determined by the inequality
| (3) |
Here x is the frequency of A individuals in the population. The angular brackets denote the average taken over all states of the system, weighted by the probability of finding the system in each state. In the limit of low mutation, (3) is equivalent to (2).
In this paper we focus on structured populations and the limit of weak selection. We analyze (3) to deduce that the condition for strategy A to be favored over strategy B is equivalent to
| (4) |
The parameter σ depends on the population structure, the update rule and the mutation rate, but it does not depend on the payoff values a, b, c, d. Thus, in the limit of weak selection, strategy selection in structured populations is determined by a linear inequality. The effect of population structure can be summarized by a single parameter, σ. Therefore, we call inequality (5) the `single-parameter condition'.
Note that σ = 1 corresponds to the standard condition for risk-dominance (Harsanyi & Selten 1988). If σ > 1 then the diagonal entries of the payoff matrix, a and d, are more important than the off-diagonal entries, b and c. In this case, the population structure can favor the evolution of cooperation in the Prisoner's Dilemma game, which is defined by c > a > d > b. If σ > 1 then the population structure can favor the Pareto-efficient strategy over the risk-dominant strategy in a coordination game. A coordination game is defined by a > c and b < d. Strategy A is Pareto efficient if a > d. Strategy B is risk-dominant if a + b < c + d. If σ < 1 then the population structure can favor the evolution of spite.
The paper is structured as follows. In Section 2 we present the model, the main result and the necessary assumptions. In Section 3 we give the proof of the single-parameter condition, which holds for weak selection and any mutation rate. In Section 4 we show the relationship between σ and the critical benefit-to-cost ratio for the evolution of cooperation. An interesting consequence is that for the purpose of calculating σ it suffices to study games that have simplified payoff matrices. Several specific consequences are then discussed. In Section 5 we present several examples of evolutionary dynamics in structured populations that lead to a single-parameter condition. These examples include games in the well-mixed population, games on regular and heterogeneous graphs, games on replacement and interaction graphs, games in phenotype space and games on sets. Section 6 is a summary of our findings.
2 Model and results
We consider stochastic evolutionary dynamics (with mutation and selection) in a structured population of finite size, N. Individuals adopt either strategy A or B. Individuals obtain a payoff by interacting with other individuals according to the underlying population structure. For example, the population structure could imply that interactions occur only between neighbors on a graph (Ohtsuki et al 2006), inhabitants of the same island or individuals that share certain phenotypic properties (Antal et al 2008). Based on these interactions, an average (or total) payoff is calculated according to the payoff matrix (1). We assume that the payoff is linear in a, b, c, d, with no constant terms. For instance, the total payoff of an A individual is [a × (number of A-interactants) + b × (number of B-interactants)]. The effective payoff of an individual is given by 1 + w · Payoff. The parameter w denotes the intensity of selection. The limit of weak selection is given by w → 0.
Reproduction is subject to mutation. With probability u the offspring adopts a random strategy (which is either A or B). With probability 1 - u the offspring adopts the parent's strategy. For u = 0 there is no mutation, only selection. For u = 1 there is no selection, only mutation. If 0 < u < 1 then there is mutation and selection.
A state S of the population assigns to each player a strategy (A or B) and a 'location' (in space, phenotype space etc). A state must include all information that can affect the payoffs of players. For our proof, we assume a finite state space. We study a Markov process on this state space. We denote by Pij the transition probability from state Si to state Sj. These transition probabilities depend on the update rule and on the effective payoffs of individuals. Since the effective payoff is of the form 1 + w · Payoff and the payoff is linear in a, b, c, d, it follows that the transition probabilities are functions Pij(wa, wb, wc, wd).
We show that
Theorem
Consider a population structure and an update rule such that
the transition probabilities are infinitely differentiable at w = 0
the update rule is symmetric for the two strategies and
in the game given by the matrix , strategy A is not disfavored.
Then, in the limit of weak selection, the condition that strategy A is favored over strategy B is a one parameter condition:
| (5) |
where σ depends on the model and the dynamics (population structure, update rule, the mutation rates) but not on the entries of the payoff matrix, a, b, c, d.
Let us now discuss the three natural assumptions.
Assumption (i). The transition probabilities are infinitely differentiable at w = 0.
We require the transition probabilities Pij(wa, wb, wc, wd) to have Taylor expansions at w = 0. Examples of update rules that satisfy Assumption (i) include: the death birth (DB) and birth-death (BD) updating on graphs (Ohtsuki et al 2006), the synchronous updating based on the Wright-Fisher process (Antal et al 2008, Tarnita et al 2009) and the pairwise comparison (PC) process (Traulsen et al 2007).
Assumption (ii). The update rule is symmetric for the two strategies.
The update rule differentiates between A and B only based on payoff. Relabeling the two strategies and correspondingly swapping the entries of the payoff matrix must yield symmetric dynamics. This assumption is entirely natural. It means that the difference between A and B is fully captured by the payoff matrix, while the population structure and update rule do not introduce any additional difference between A and B.
Assumption (iii). In the game given by the matrix , strategy A is not disfavored.
We will show in the proof that the first two assumptions are sufficient to obtain a single-parameter condition. We need the third assumption simply to determine the direction of the inequality in this condition. Thus, if (iii) is satisfied, then the condition that A is favored over B has the form (5). Otherwise, it has the form σa + b< c + σd.
3 proof
In the first part of the proof we will show that for update rules that satisfy our assumption (i) in Section 2, the condition for strategy A to be favored over strategy B is linear in a, b, c, d with no constant terms. More precisely, it can be written as
| (6) |
Here k1, k2, k3, k4, are real numbers, which can depend on the population structure, the update rule, the mutation rate and the population size, but not on the payoff values a, b, c, d.
In the second part of the proof we will show that for update rules that also satisfy our symmetry assumption (ii) in Section 2, this linearity leads to the existence of a σ. Furthermore, using assumption (iii) we show that the condition that A is favored over B becomes
| (7) |
3.1 Linearity
As we already mentioned, we study a Markov process on the state space and we are concerned with the stationary probabilities of this process. A more detailed discussion of these stationary probabilities can be found in Appendix B.
In a state S,let xS denote the frequency of A individuals in the population. Then the frequency of B individuals is 1 - xS. We are interested in the average frequency of A individuals, the average being taken over all possible states weighted by the stationary probability that the system is in those states. Let us denote this average frequency by ⟨x⟩. Thus
| (8) |
where πS is the probability that the system is in state S. The condition for strategy A to be favored over strategy B is that the average frequency of A is greater than 1/2
| (9) |
This is equivalent to saying that, on average, A individuals are more than 50%.
We analyze this condition in the limit of weak selection w → 0. The frequency xS of A individuals in state S does not depend on the game; hence, it does not depend on w. However, the probability πS that the system is in state S does depend on w. For update rules satisfying assumption (i), we show in Appendix B that πS is infinitely differentiable as a function of w. Thus, we can write its Taylor expansion at w = 0
| (10) |
The (0) superscript refers to the neutral state w = 0 and evaluated at w = 0. The notation denotes terms of order w2 or higher. They are negligible for w → 0.
Hence, we can write the Taylor expansion of the average frequency of A
| (11) |
Since is the probability that the neutral process (i.e. when w = 0) is in state S, the first sum is simply the average number of A individuals at neutrality. This is 1/2 for update rules that satisfy Assumption (ii) because in the neutral process, A and B individuals are only differentiated by labels.
Thus, in the limit of weak selection, the condition (9) that A is favored over B becomes
| (12) |
As we already mentioned, the frequency xS of A individuals in state S does not depend on the game. However, does depend on the game. We will show in Appendix B that is linear in a, b, c, d with no constant terms. Hence, from (12) we deduce that our condition for strategy A to be favored over strategy B is linear in a, b, c, d and is of the form (6).
3.2 Existence of Sigma
We have thus shown that for structures satisfying assumption (i), the condition for strategy A to be favored over strategy B has the form (6): k1a + k2b > k3c + k4d. For structures which moreover satisfy our symmetry condition (assumption (ii)), we obtain the symmetric relation by simply relabeling the two strategies. Thus, strategy B is favored over strategy A if and only if
| (13) |
Since both strategies can not be favored at the same time, strategy A must be favored if and only if
| (14) |
Since both conditions (6) and (14) are if and only if conditions that A is favored over B, they must be equivalent. Thus, it must be that (14) is a scalar multiple of (6), so there must exist some λ > 0 such that k4 = λk1 = λ2k4 and k3 = λ2k3. Hence, we conclude that λ = 1 and that k1 = k4 = k and k2 = k3 = k′. So the condition that A is favored over B becomes
| (15) |
Note that this condition depends only on the parameter σ = k/k′. Thus, in general, the condition that A is favored over B can be written as a single-parameter condition. However, one must exercise caution in dividing by k′ because its sign can change the direction of the inequality. This is where we need assumption (iii). Assumption (iii) holds if and only if k′ ≥ 0 and then we can rewrite (15) as
| (16) |
If (iii) doesn't hold, then k′ < 0 and hence (15) becomes σa + b < c + σd.
Note that σ could also be infinite (if k′ = 0) and then the condition that A is favored over B reduces to a > d. If σ = 0 then the condition is simply b > c.
4 Evolution of Cooperation
In this section we find a relationship between the critical benefit-to-cost ratio for the evolution of cooperation (Nowak 2006b) and the parameter σ. In a simplified version of the Prisoner's Dilemma game a cooperator, C, pays a cost, , for another individual to receive a benefit, . We have . Defectors, D, distribute no benefits and pay no costs. We obtain the payoff matrix
| (17) |
For structures for which condition (5) holds, we can apply it for payoff matrix (17) to obtain
| (18) |
For σ > 1 this condition means that cooperators are more abundant than defectors whenever the benefit-to-cost ratio is larger than the critical value
| (19) |
Alternatively, σ can be expressed by the critical ratio as
| (20) |
Here we have σ > 1. Note that even without the assumption , the same σ is obtained from (18), only some care is required to find the correct signs.
Thus, for any population structure and update rule for which condition (5) holds, if the critical benefit-to-cost ratio is known, we can immediately obtain σ and vice versa. For example, for DB updating on regular graphs of degree k we know that (Ohtsuki et al 2006). Using equation (20), this implies σ = (k + 1)/(k - 1) which is in agreement with equation (27).
This demonstrates the practical advantage of relationship (20). In order to derive σ for the general game (1), it suffices to study the specific game (17) and to derive the critical benefit-cost ratio, . Then (20) gives us the answer. Thus
Corollary
In the limit of weak selection, for all structures for which strategy dominance is given by a single parameter condition (5), for the purpose of studying strategy dominance, it suffices to analyze one-parameter games (eg. the simplified Prisoner's Dilemma).
The practical advantage comes from the fact that it is sometimes easier to study the specific game (17) than to study the general game (1). Specifically, using (17) often spares the calculation of probabilities that three randomly chosen players share the same strategy (for example, coefficient η in Antal et al, 2008).
Wild and Traulsen (2007) argue that the general payoff matrix (1) allows the study of synergistic effects between players in the weak selection limit, as opposed to the simplified matrix (17) where such effects are not present. Here we demonstrated that these synergistic effects do not matter if we are only interested in the question whether A is more abundant than B in the stationary distribution of the mutation-selection process. Of course, our observation does not suggest that the analysis of general games, given by (1), can be completely replaced by the analysis of simpler games, given by (17). Questions concerning which strategies are Nash equilibria, which are evolutionarily stable or when we have coexistence or bi-stability can only be answered by studying the general matrix. For such analyses see Ohtsuki & Nowak (2006, 2008) or Taylor & Nowak (2007).
Note also that instead of the simplified Prisoner's Dilemma payoff matrix, we can also consider other types of simplified payoff matrices in order to calculate σ. Two examples are
| (21) |
5 Examples
Let us consider a game between two strategies A and B that is given by the payoff matrix (1). We study a variety of different population structures and always observe that for weak selection the condition for A to be favored over B can be written in the form σa + b > c + σd. For each example we give the value of σ. The derivations of these results have been given in papers which we cite. For the star we present a new calculation. These observations have led to the conjecture that for weak selection the effect of population structure on strategy selection can `always' be summarized by a single parameter, σ.
Moreover, for some of the examples, we use the Corollary to find the parameter σ for structures where only the Prisoner's Dilemma has been studied. Such structures include: the regular graph of degree k and the different interaction and replacement graphs when the population size is not much larger than the degree, as well as the phenotype space.
5.1 The well-mixed population
As first example we consider the frequency dependent Moran process in a well mixed population of size N (Nowak et al 2004, Taylor et al 2004, Nowak 2006a) (Fig.1a). In the language of evolutionary graph theory, a well-mixed population corresponds to a complete graph with identical weights. Each individual interacts with all other N - 1 individuals equally likely and obtains an average (or total) payoff. For both DB and BD updating we find for weak selection and any mutation rate
| (22) |
Hence, for any finite well-mixed population we have σ < 1. In the limit N → ∞, we obtain σ = 1, which yields the standard condition of risk-dominance, a + b > c + d.
Figure 1.
Various population structures for which σ values are known. (a) For the well-mixed population we have σ = (N - 2)/N for any mutation rate. (b) For the cycle we have σ = (3N - 8)/N (DB) and σ = (N - 2)/N (BD) for low mutation. (c) For DB on the star we have σ = 1 for any mutation rate and any population size, N ≥ 3. For BD on the star we have σ = (N3 - 4N2 + 8N - 8)/(N3 - 2N2 + 8), for low mutation. (d) For regular graphs of degree k we have σ = (k + 1)/(k - 1) (DB) and σ = 1 (BD) for low mutation and large population size. (e) If there are different interaction and replacement graphs, we have σ = (gh+l)/(gh-l)(DB) and σ = 1 (BD) for low mutation and large population size. The interaction graph, the replacement graph and the overlap graph between these two are all regular and have degrees, g, h and l, respectively. (f) For `games in phenotype space' we find (DB or synchronous) for a one dimensional phenotype space, low mutation rates and large population size. (g) For `games on sets' σ is more complicated and is given by (36). All results hold for weak selection.
For a wide class of update rules - including pairwise comparison (Traulsen et al 2007) - it can be shown that (22) holds for any intensity of selection and for any mutation rate (Antal et al 2009). The σ given by (22) can also be found in Kandori et al (1993), who study a process that is stochastic in the generation of mutants, but deterministic in following the gradient of selection.
5.2 Graph structured populations
In such models, the players occupy the vertices of a graph, which is assumed to be fixed. The edges denote links between individuals in terms of game dynamical interaction and biological reproduction. Individuals play a game only with their neighbors and an average (or total) payoff is calculated. In this section we consider death-birth (DB) updating and birth-death (BD) updating. In DB updating, at any one time step, a random individual is chosen to die, and the neighbors compete for the empty spot, proportional to their effective payoffs. In BD updating, at any one time step, an individual is chosen to reproduce proportional to effective payoff; his offspring replaces randomly one of the neighbors (Ohtsuki et al 2006).
5.2.1 Cycle
Let us imagine N individuals that are aligned in a one dimensional array. Each individual is connected to its two neighbors, and the ends are joined up (Fig. 1b). The cycle is a regular graph of degree k = 2. Games on cycles have been studied by many authors including Ellison (1993), Nakamaru et al (1997), Ohtsuki et al (2006) and Ohtsuki & Nowak (2006a). The following result can be found in Ohtsuki & Nowak (2006a) and holds for weak selection.
For DB updating and low mutation (u → 0) we have
| (23) |
Note that σ is an increasing function of the population size, N, and converges to σ = 3 for large N.
We have also performed simulations for DB on a cycle with non-vanishing mutation (Fig. 2a). We confirm (23) and also find that σ depends on the mutation rate, u.
Figure 2.
Numerical simulations for DB updating confirm the linear inequality σa + b > c + σd. We study the payoff matrix a = 1, b = S, c = T , and d = 0 for -1 ≤ S ≤ 1 and 0 ≤ T ≤ 2. The red line is the equilibrium condition T = S + σ. Below this line A is favored. (a) For a cycle with N = 5 and mutation rate, u = 0.2, we find σ = 1.271. The theoretical result for low mutation is σ = 1.4. Thus, σ depends on the mutation rate. (b) For a star with N = 5 we find σ = 1 for u = 0.1. (c) For a regular graph with k = 3 and N = 6 we find σ = 0.937 for u = 0.1. The prediction of (29) for low mutation is σ = 1. Here again σ depends on the mutation rate. (d) For this random graph with N = 10 and average degree k = 2 we find σ = 1.636 for u = 0.05. For all simulations we calculate total payoffs and use as intensity of selection w = 0.005. Each point is an average over 2 × 106 runs.
For BD updating we have
| (24) |
Hence, for BD updating on a cycle we obtain the same σ-factor as for the well-mixed population, which corresponds to a complete graph. The cycle and the complete graph are on the extreme ends of the spectrum of population structures. Among all regular graphs, the cycle has the smallest degree and the complete graph has the largest degree, for a given population size. We conjecture that the σ-factor given by (24) holds for weak selection on any regular graph.
We have also performed simulations for BD on a cycle with non-vanishing mutation (Fig.3a). They confirm (24).
Figure 3.
Numerical simulations for BD updating confirm the linear inequality σa + b > c + σd. We study the payoff matrix a = 1, b = S, c = T , and d = 0 for -1 ≤ S ≤ 1 and 0 T ≤ 2. The red line is the equilibrium condition T = S + σ. Below this line A is favored. (a) For a cycle with N = 5 and mutation rate, u = 0.2, we find σ = 0.447. The theoretical result for low mutation is σ = 0.6. Thus, σ depends on the mutation rate. (b) For a star with N = 5 we find σ = 0.405 for u = 0.1. The theoretical result for low mutation is σ = 0.686. This shows that σ depends on the mutation rate. (c) For a regular graph with k = 3 and N = 6 we find σ = 0.601 for u = 0.1. The theoretical prediction for low mutation is σ = 0.666. Here again σ depends on the mutation rate. (d) For this random graph with N = 10 and average degree k = 2 we find σ = 0.559 for u = 0.05. For all simulations we calculate total payoffs and use as intensity of selection w = 0.005. Each point is an average over 2 × 106 runs.
5.2.2 Star
The star is another graph structure, which can be calculated exactly. There are N individuals. One individual occupies the center of the star and the remaining N - 1 individuals populate the periphery (Fig.1c). The center is connected to all other individuals and, therefore, has degree k = N - 1. Each individual in the periphery is only connected to the center and, therefore, has degree k = 1. The average degree of the star is given by . For large population size, N, the star and the cycle have the same average degree. Yet the population dynamics are very different. The calculation for the star for both BD and DB updating is shown in Appendix A.
For DB updating on a star we find
| (25) |
This result holds for weak selection and for any population size N ≥ 3 and any mutation rate u. Simulations for the star are in agreement with this result (Fig.2b).
For BD updating on a star we find
| (26) |
This result holds in the limit of low mutation, u → 0. Note also that in the limit of N large we have σ = 1. Simulations confirm our result (Fig.3b).
5.2.3 Regular graphs of degree k
Let us now consider the case where the individuals of a population of size N occupy the vertices of a regular graph of degree k ≥ 2. Each individual is connected to exactly k other individuals (Fig. 1d).
For DB updating on this structure, Ohtsuki et al (2006) obtain (see equation 24 in their online material)
| (27) |
This result holds for weak selection, low mutation and large population size, N ⪢ k. The parameter σ depends on the degree of the graph and is always larger than one. For large values of k, σ converges to one. The limit of large k agrees with the result for the complete graph, which corresponds to a well-mixed population.
For BD updating on a regular graph of degree k ⪡ N, in the limit of weak selection and low mutation, Ohtsuki et al (2006) find
| (28) |
Hence, for any degree k, we have the simple condition of risk-dominance. Population structure does not seem to affect strategy selection under BD updating for weak selection and large population size.
Our proof of the linear inequality is not restricted to homogeneous graphs. Random graphs (Bollobás 1995) also satisfy our assumptions, and therefore we expect the single parameter condition to hold. We have performed computer simulations for a random graph with N = 10 and average degree k = 2. We find a linear condition with σ = 1.636 for DB updating and σ = 0.559 for BD updating (see Fig.2d, 3d).
For a regular graph of degree k, the calculation of Ohtsuki et al (2006) is only applicable if the population size is much larger than the degree of the graph, N ⪢ k. For general population size N however, we can obtain the σ parameter using our corollary and the results of Taylor et al (2007a) and Lehmann et al (2007). They obtained a critical benefit-to-cost ratio of . Using the relationship (20), we obtain
| (29) |
As a consistency check, taking N → ∞ in (29) leads to (27). Moreover, setting k = 2 in (29) leads to (23), and setting k = N - 1 in (29) agrees with (22), as expected.
Computer simulations for a regular graph with k = 3 and N = 6, for mutation rate u = 0.1 suggest that σ = 0.937. The corresponding prediction of (29) for low mutation is σ = 1. Thus we conclude that σ depends on the mutation rate u (Fig.2c).
For the BD updating on a regular graph with general population size N, we can similarly obtain the relevant σ from the result of Taylor et al (2007a). For the Prisoner's Dilemma they find a critical benefit-to-cost ratio of . Hence, using relationship (20) we obtain
| (30) |
Note that the results In Taylor et al (2007a) hold for any homogeneous graph that satisfies certain symmetry conditions (`bi-transitivity'). Hence, for BD updating on a wide class of graphs, the condition for strategy dominance is the same as the risk-dominance condition in a well-mixed population.
Computer simulations for a regular graph with k = 3 and N = 6, for mutation rate u = 0.1 suggest that σ = 0.601. The corresponding prediction of (29) for low mutation is σ = 0.666. Thus we conclude that σ depends on the mutation rate u (Fig.3c).
5.2.4 Different interaction and replacement graphs
Individuals could have different neighborhoods for the game dynamical interaction and for the evolutionary updating. In this case, we place the individuals of the population on the edges of two different graphs (Ohtsuki et al 2007). The interaction graph determines who meets whom for playing the game. The replacement graph determines who learns from whom (or who competes with whom) for updating of strategies. The vertices of the two graphs are identical; the edges can be different (Fig. 1e).
Suppose both graphs are regular. The interaction graph has degree h. The replacement graph has degree g. The two graphs define an overlap graph, which contains all those edges that the interaction and replacement graph have in common. Let us assume that this overlap graph is regular and has degree l. We always have l ≤ min {h, g}. The following results hold for weak selection and large population size (Ohtsuki et al 2007):
For DB updating we find:
| (31) |
For BD updating we find
| (32) |
Again BD updating does not lead to an outcome that differs from well-mixed populations.
For different replacement and interaction graphs with general population size, N, we can obtain σ via the critical benefit-to-cost ratio in the Prisoner's Dilemma game (17). Using the result of Taylor et al. (2007), we obtain . Hence, we have
| (33) |
As a consistency check, g = h = l = k reproduces (29).
5.3 Games in phenotype space
Antal et al (2008) proposed a model for the evolution of cooperation based on phenotypic similarity. In addition to the usual strategies A and B, each player also has a phenotype. The phenotype is given by an integer or, in other words, each player is positioned in a one dimensional discrete phenotype space (Fig.1f). Individuals interact only with those who share the same phenotype. The population size is constant and given by N. Evolutionary dynamics can be calculated for DB updating or synchronous updating (in a Wright-Fisher type process). There is an independent mutation probability for the strategy of players, u, and for the phenotype of players, v. When an individual reproduces, its offspring has the same phenotype with probability 1 - 2v and mutates to either one of the two neighboring phenotypes with equal probability v. During the dynamics, the whole population stays in a finite cluster, and wanders together in the infinite phenotype space (Moran 1975, Kingman 1976).
The resulting expression for σ is derived using the corollary. It is complicated and depends on all parameters, including the two mutation rates, u and v. The expression simplifies for large population sizes, where the main parameters are the scaled mutation rates μ = Nu, ν = Nv for BD updating (or μ = 2Nu, ν = 2Nv for synchronous updating). It turns out that σ is a monotone decreasing function of μ, and a monotone increasing function of ν. Hence cooperation is favored (larger σ) for smaller strategy mutation rate and larger phenotypic mutation rate. In the optimal case for cooperation, μ → 0, sigma becomes only a function of the phenotypic mutation rate
| (34) |
The largest possible value of sigma is obtained for very large phenotypic mutation rate ν → ∞, where
| (35) |
This is the largest possible sigma for games in a one-dimensional phenotype space.
Note that this example has seemingly an infinite state space, which is not something we address in our proof, but a subtle trick turns the state space into a finite one. A detailed description can be found in Antal et al (2008).
5.4 Games on sets
Tarnita et al (2009) propose a model based on set memberships (Fig.1g). They consider a population of N individuals distributed over M sets. To obtain analytical results, we also assume that each individual belongs to exactly K sets, where K ≤ M. If two individuals belong to the same set, they interact; if they have more than one set in common, they interact several times. An interaction is an evolutionary game given by (1).
The system evolves according to synchronous updating (Wright-Fisher process). There are discrete, non-verlapping generations. All individuals update at the same time. The population size is constant. Individuals reproduce proportional to their effective payoffs. An offspring inherits the sets of the parent with probability 1 - v or adopts a random configuration (including that of the parent) with probability v. Any particular configuration of set memberships is chosen with probability . Similarly, the offspring inherits the strategy of the parent with probability 1 - u; with probability u, he picks a random strategy. Thus, we have a strategy mutation rate, u, and a set mutation rate, v.
The resulting expression for σ is complicated and depends on all parameters, including the two mutation rates. The expression simplifies for large population size, where the main parameters are the two effective mutation rates μ = 2Nu and ν = 2Nv as well as M and K. We find
| (36) |
Note that sigma is a one humped function of the set mutation rate ν. There is an optimum value of ν, which maximizes sigma.
For low effective strategy mutation rate (μ → 0) and effective set mutation rate ν ⪢ 1 we obtain the simplified expression of σ
| (37) |
Note that for large values of ν, sigma decreases with ν and increases with M/K.
For low effective strategy mutation rate and low effective set mutation rate ν → 0, we obtained the following simplified expression for σ
| (38) |
Note that, on the other hand, for low values of ν, σ increases with ν. Hence, there will be an optimum set mutation rate.
6 Conclusion
We have studied evolutionary game dynamics in structured populations. We have investigated the interaction between two strategies, A and B, given by the payoff matrix
| (39) |
We have shown that the condition for A to be more abundant than B in the stationary distribution of the mutation-selection process can be written as a simple linear inequality
| (40) |
This condition holds for all population structures that fulfill three natural assumptions, for any mutation rate, but for weak selection. The parameter σ captures the effect of population structure on `strategy selection'. We say that `strategy A is selected over strategy B' if it is more abundant in the stationary distribution of the mutation-selection process. It is important to note that σ does not capture all aspects of evolutionary dynamics in structured populations, but only those that determine strategy selection.
The single parameter, σ, quantifies the degree to which individuals using the same strategy are more likely (σ > 1) or less likely (σ < 1) to interact than individuals using different strategies. Therefore σ describes the degree of positive or negative assortment among players who use the same strategy (for the purpose of analyzing strategy selection). Note that our theory does not imply that σ must be positive; negative values of σ are possible in principle, although for all of the examples presented in this paper we have σ > 0. The value of σ can depend on the population structure, the update rule, the population size, the mutation rate, but it does not depend on the entries of the payoff matrix. For each particular problem the specific value of σ must be calculated. Here we have shown that there always exists a simple linear inequality with a single parameter, σ, given that some very natural assumptions hold.
ACKNOWLEDGMENTS
We are grateful to two anonymous referees for their extremely helpful and brilliant comments which greatly strengthened our paper. CET would like to thank R. Berinde for useful discussions. This work was supported by the John Templeton Foundation, the National Science Foundation/National Institutes of Health joint program in mathematical biology (NIH Grant R01GM078986), the Japan Society for the Promotion of Science, the China Scholarship Council and J. Epstein.
Appendix A : Calculations for the star
A.1. DB updating
We consider a star structured population of size N. A hub is the node lying in the center that is connected to the other N - 1 nodes, each of which is called a leaf. Each leaf is connected only to the hub.
We consider the two strategies, A and B. A state of the population is fully described by the number of A-players in the hub and the number of A-players in the leaves. Thus, for the star with N nodes we have 2N states which we will denote by (0, i) and (1, i), where i = 0,…N - 1 is the number of A players on the leaves. (0, i) means that there is a B in the hub; (1, i) means that there is an A in the hub.
DB updating on a star satisfies our assumptions (i) and (ii). It can be shown (as we do in general in Appendix B) that for the star, is linear in a, b, c, d. Thus, we know that a single parameter condition must be satisfied for the star. However, it is hard to calculate directly what is for all states S. We use the symmetry of the star to deduce the σ for any mutation and weak selection.
Then, for DB updating we can write the following transition probabilities:
| (41) |
and
| (42) |
So all these transition probabilities don't depend on a, b, c, d independently, but in fact on b - d and a - c. Thus, πS, the probabilities of finding the system in each state, also depend only on a - c and b - d, and not on a, b, c, d independently.
Hence, we conclude that our expression (12) which gives the sigma condition depends on a - c and b - d linearly. Thus, it must be of ther form:
| (43) |
where g and h are functions of the parameters N and u.
However, this has to be precisely the sigma relation for the star (since it is derived from (12)), and hence must be identical to σa + b > c + σd (and here we know that σ > 0). This implies that the coefficients of a and -d must be equal (and respectively those of b and -c). Hence we conclude that g(N, u) = h(N, u) and hence σ = 1, for any population size N and any mutation rate u.
A.2. BD updating
Let xi,j be the probability that A fixates in the population given initial state is (i, j). Also, let and be the transition probabilities as in the diagram below.
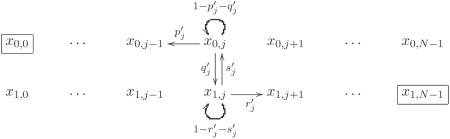 |
We normalize these probabilities as follows:
| (44) |
Now we have the following diagram. We have pj + qj = 1 and rj + sj = 1 there.
 |
Direct calculation shows
| (45) |
For BD updating, we obtain
| (46) |
where
| (47) |
The result suggests that a leaf is (N - 1) times more advantageous than the hub.
As before we obtain the σ-factor as
| (48) |
Appendix B: Continuity and Linearity for πS
In this Appendix we will show that the probability πS that the system is in state S is continuous at w = 0, infinitely differentiable and moreover that is linear in a, b, c, d. We show this for processes satisfying our assumptions. This part of the proof works not only for constant death or constant birth updates, but for any update rules that do not introduce any functions that do not have Taylor expansions at w = 0.
Note that given the effective payoff function 1+w·payoff, we introduce w together with a, b, c and d. Thus, our transition probabilities from state Si to state Sj will be functions Pij(wa, wb, wc, wd). So, unless we differentiate with respect to w or evaluate at w = const, whenever we have a degree k term in w, it must be accompanied by a degree k term in a, b, c or d and vice versa. Moreover, w can not be accompanied by a constant term, i.e. a term that does not contain a, b, c or d.
The probability πS that the system is in state S also depends on w. For our structures and update rules we will now show that πS is continuous and differentiable at w = 0. In order to find πS, we need the transition probabilities Pij to go from state Sj to state Si. Then the vector of probabilities π(S) is an eigenvector corresponding to eigenvalue 1 of the stochastic matrix P. The matrix P is primitive, i.e. there exists some integer k such that Pk > 0. This is because we study a selection-mutation process and hence our system has no absorbing subset of states.
Since the matrix P is stochastic and primitive, the Perron-Frobenius theorem ensures that 1 is its largest eigenvalue, that it is a simple eigenvalue and that to it, there corresponds an eigenvector with positive entries summing up to 1. This is precisely our vector of probabilities.
To find this eigenvector we perform Gaussian elimination (aka row echelon reduction) on the system Pv = v. Since 1 is a simple eigenvalue for P, the system we need to solve has only one degree of freedom; thus we can express the eigenvector in terms of the one free variable, which without loss of generality can be vn:
| (49) |
The eigenvector that we are interested in is the vector with non-zero entries which sum up to 1. For this vector we have
| (50) |
For our structures and update rules, the transition probabilities have Taylor expansions around w = 0 and thus can be written as polynomials in w. As before, since any w is accompanied by a linear term in a, b, c, d, the coefficients of these polynomials have the same degree in a, b, c, d as the accompanying w. Because of the elementary nature of the row operations performed, the elements of the reduced matrix will be fractions of polynomials (i.e. rational functions of w). Thus, hi above are all rational functions of w. Therefore, from (50) we conclude that vn must also be a rational function of w. This implies that in our vector of probabilities, all the entries are rational functions. Thus πS is a fraction of polynomials in w which we write in irreducible form. The only way that this is not continuous at w = 0 is if the denominator is zero at w = 0. But in that case, limw→0 πS = ∞ which is impossible since πS is a probability. Therefore, πS is continuous at w = 0.
Moreover, we can write
| (51) |
We have obtained this form for πS by performing the following operations: Taylor expansions of the transition probabilities and elementary row operations on these Taylor expansions. Hence, any w that was introduced from the beginning was accompanied by linear terms in a, b, c, d and no constants, and due to the elementary nature of the above operations, nothing changed. So b0S and c0S contain no a, b, c, d terms whereas b1S and c1S contain only linear a, b, c, d and no degree zero terms. Differentiating πS once we obtain
| (52) |
We want to show the linearity of which is (0). Thus, we have
| (53) |
Since b0S, c0S contain no a, b, c, d and b1S, c1S are linear in a, b, c, d for all S and have no free constant terms, we conclude that is linear in a, b, c, d and has no free constant term.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alos-Ferrer C. Finite population dynamics and mixed equilibria. Int. Game Theory Review. 2003;5:263–290. [Google Scholar]
- Antal T, Nowak MA, Traulsen A. Strategy abundance in 2×2 games for arbitrary mutation rates. J. Theor. Biol. 2009;257:340–344. doi: 10.1016/j.jtbi.2008.11.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Antal T, Ohtsuki H, Wakeley J, Taylor PD, Nowak MA. Evolutionary game dynamics in phenotype space. 2008 E-print arXiv:0806.2636. [Google Scholar]
- Axelrod R, Hamilton WD. The evolution of cooperation. Science. 1981;211:1390–1396. doi: 10.1126/science.7466396. [DOI] [PubMed] [Google Scholar]
- Binmore K. Game Theory and the Social Contract. MIT Press; Cambridge, MA: 1994. [Google Scholar]
- Binmore K. Playing for Real: A Text on Game Theory. Oxford University Press; 2007. [Google Scholar]
- Boerlijst MC, Hogeweg P. Spiral wave structures in pre-biotic evolution: hypercycles stable against parasites. Physica D. 1991;48:17–28. [Google Scholar]
- Bollobás B. Random Graphs. Academic Press; New York: 1995. [Google Scholar]
- Bomze I, Pawlowitsch C. One-third rules with equality: second-order evolutionary stability conditions in finite populations. J. Theor. Biol. 2008 doi: 10.1016/j.jtbi.2008.06.009. To be published. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyd R, Richerson PJ. Solving the Puzzle of Human Cooperation. In: Levinson S, editor. Evolution and Culture. MIT Press; Cambridge, MA: 2005. p. 105132. [Google Scholar]
- Bshary R, Grutter A, Willener A, Leimar O. Pairs of cooperating cleaner fish provide better service quality than singletons. Nature. 2008;455:964–967. doi: 10.1038/nature07184. [DOI] [PubMed] [Google Scholar]
- Comins HN, Hamilton WD, May RM. Evolutionarily stable dispersal strategies. J. Theor. Biol. 1980;82:205–230. doi: 10.1016/0022-5193(80)90099-5. [DOI] [PubMed] [Google Scholar]
- Cressman R. Evolutionary Dynamics and Extensive Form Games. MIT Press; Cambridge, MA: 2003. [Google Scholar]
- Dieckmann U, Law R, Metz JAJ, editors. The Geometry of Ecological Interactions: Simplifying Spatial Complexity. Cambridge University Press; Cambridge, UK: 2000. [Google Scholar]
- Doebeli M, Knowlton N. The evolution of interspecific mutualisms. P. Natl. Acad. Sci. U.S.A. 1998;95:8676–8680. doi: 10.1073/pnas.95.15.8676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durrett R. Lecture Notes on Particle Systems and Percolation. Wadsworth & Brooks/Cole Advanced Books & Software; Stamford, CT: 1988. [Google Scholar]
- Durrett R, Levin SA. The importance of being discrete (and spatial) Theor. Popul. Biol. 1994;46:363–394. [Google Scholar]
- Ellison G. Learning, local interaction, and coordination. Econometrica. 1993;61:1047–1071. [Google Scholar]
- Ewens WJ. Mathematical population genetics. vol. 1. Theoretical introduction, Springer; New York: 2004. [Google Scholar]
- Ferriere R, Michod RE. The evolution of cooperation in spatially heterogeneous populations. Am. Nat. 1996;147:692–717. [Google Scholar]
- Ficici SG, Pollack JB. Effects of finite populations on evolutionary stable strategies. In: Whitley D, Goldberg D, Cantu-Paz E, Spector L, Parmee I, Beyer HG, editors. Proceedings of the 2000 Genetic and Evolutionary Computation Conference; San Francisco, CA. Morgan-Kaufmann; 2000. pp. 927–934. [Google Scholar]
- Fogel G, Andrews P, Fogel D. On the instability of evolutionary stable strategies in small populations. Ecol. Model. 1998;109:283–294. [Google Scholar]
- Frank SA. Foundations of Social Evolution. Princeton University Press; Princeton, NJ: 1998. [Google Scholar]
- Fu F, Wang L, Nowak MA, Hauert C. Evolutionary Dynamics on Graphs: Efficent Method for Weak Selection. 2008 doi: 10.1103/PhysRevE.79.046707. To be published. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fudenberg D, Tirole J. Game Theory. MIT Press; Cambridge, MA: 1991. [Google Scholar]
- Gandon S, Rousset F. The evolution of stepping stone dispersal rates. Proc. R. Soc. B. 1999;266:2507–2513. doi: 10.1098/rspb.1999.0953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gintis H. Game Theory Evolving. Princeton University Press; Princeton, USA: 2000. [Google Scholar]
- Grafen A. A geometric view of relatedness. Oxford Surv. Evol. Biol. 1985;2:28–89. [Google Scholar]
- Grafen A. Optimization of inclusive fitness. J. Theor. Biol. 2006;238:541–563. doi: 10.1016/j.jtbi.2005.06.009. [DOI] [PubMed] [Google Scholar]
- Hamilton WD. The genetical evolution of social behaviour, I and II. J. Theor. Biol. 1964;7:1–52. doi: 10.1016/0022-5193(64)90038-4. [DOI] [PubMed] [Google Scholar]
- Hamilton WD, May RM. Dispersal in stable habitats. Nature. 1977;269:578–581. [Google Scholar]
- Harsanyi JC, Selten R. A General Theory of Equilibrium Selection in Games. MIT Press; Cambridge MA: 1988. [Google Scholar]
- Hassell MP, Comins HN, May RM. Spatial structure and chaos in insect population dynamics. Nature. 1991;353:255–258. [Google Scholar]
- Hauert C, Doebeli M. Spatial structure often inhibits the evolution of cooperation in the snowdrift game. Nature. 2004;428:643–646. doi: 10.1038/nature02360. [DOI] [PubMed] [Google Scholar]
- Helbing D, Yu W. Migration as a mechanism to promote cooperation. Advances in Complex Systems. 2008;11:641–652. [Google Scholar]
- Herz AVM. Collective phenomena in spatially extended evolutionary games. J. Theor. Biol. 1994;169:65–87. doi: 10.1006/jtbi.1994.1130. [DOI] [PubMed] [Google Scholar]
- Hofbauer J. The spatially dominant equilibrium of a game. Ann. Oper. Res. 1999;89:233–251. [Google Scholar]
- Hofbauer J, Sigmund K. The Theory of Evolution and Dynamical Systems. Cambridge University Press; Cambridge, UK: 1988. [Google Scholar]
- Hofbauer J, Sigmund K. Adaptive dynamics and evolutionary stability. Appl. Math. Lett. 1990;3:75–79. [Google Scholar]
- Hofbauer J, Sigmund K. Evolutionary Games and Population Dynamics. Cambridge University Press; Cambridge, UK: 1998. [Google Scholar]
- Hofbauer J, Sigmund K. Evolutionary game dynamics. B. Am. Math. Soc. 2003;40:479–519. [Google Scholar]
- Hofbauer J, Schuster P, Sigmund K. A note on evolutionary stable strategies and game dynamics. J. Theor. Biol. 1979;81:609–612. doi: 10.1016/0022-5193(79)90058-4. [DOI] [PubMed] [Google Scholar]
- Houston AI, McNamara JM. Models of Adaptive Behaviour: An Approach Based on State. Cambridge University Press; Cambridge, UK: 1999. [Google Scholar]
- Hutson V, Vickers GT. Travelling waves and dominance of ESSs. J. Math. Biol. 1992;30:457–471. [Google Scholar]
- Hutson V, Vickers GT. Backward and forward traveling waves in evolutionary games. Methods Appl. Anal. 2002;9:159–176. [Google Scholar]
- Imhof LA, Nowak MA. Evolutionary game dynamics in a Wright-Fisher process. J. Math. Biol. 2006;52:667–681. doi: 10.1007/s00285-005-0369-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kandori M, Mailath GJ, Rob R. Learning, mutation, and long run equilibria in games. Econometrica. 1993;61:29–56. [Google Scholar]
- Kerr B, Riley MA, Feldman MW, Bohannan BJM. Local dispersal promotes biodiversity in a real-life game of rock-paper-scissors. Nature. 2002;418:171–174. doi: 10.1038/nature00823. [DOI] [PubMed] [Google Scholar]
- Killingback T, Doebeli M. Spatial evolutionary game theory: Hawks and Doves revisited. Proc. R. Soc. B. 1996;263:1135–1144. [Google Scholar]
- Kingman JFC. Coherent random-walks arising in some genetic models. Proc. R. Soc. Lond. Ser. A. 1976;351:19–31. [Google Scholar]
- Lehmann L, Keller L, Sumpter DJT. The evolution of helping and harming on graphs: the return of inclusive fitness effect. J. Evol. Biol. 2007;20:2284–2295. doi: 10.1111/j.1420-9101.2007.01414.x. [DOI] [PubMed] [Google Scholar]
- Lessard S, Ladret V. The probability of a single mutant in an exchangeable selection model. J. Math. Biol. 2007;54:721–744. doi: 10.1007/s00285-007-0069-7. [DOI] [PubMed] [Google Scholar]
- Levin SA, Paine RT. Disturbance, patch formation, and community structure. P. Natl. Acad. Sci. U.S.A. 1974;71:2744–2747. doi: 10.1073/pnas.71.7.2744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lieberman E, Hauert C, Nowak MA. Evolutionary dynamics on graphs. Nature. 2005;433:312–316. doi: 10.1038/nature03204. [DOI] [PubMed] [Google Scholar]
- Lindgren K, Nordahl MG. Evolutionary dynamics of spatial games. Physica D. 1994;75:292–309. [Google Scholar]
- May RM, Leonard W. Nonlinear aspects of competition between three species. SIAM J. Appl. Math. 1975;29:243–252. [Google Scholar]
- Maynard Smith J. Evolution and the Theory of Games. Cambridge University Press; Cambridge, UK: 1982. [Google Scholar]
- Maynard Smith J, Price GR. The logic of animal conflict. Nature. 1973;246:15–18. [Google Scholar]
- McNamara J, Gasson C, Houston A. Incorporating rules for responding into evolutionary games. Nature. 1999;401:368–371. doi: 10.1038/43869. [DOI] [PubMed] [Google Scholar]
- Metz JAJ, Geritz SAH, Meszena G, Jacobs FJA, van Heerwarden JS. Adaptive dynamics, a geometrical study of the consequences of nearly faithful reproduction. In: van Strien SJ, Verduyn Lunel SM, editors. Stochastic and Spatial Structures of Dynamical Systems, K. Ned. Akad. Van Wet. B. Vol. 45. North-Holland Publishing Company; Amsterdam, Holland: 1996. pp. 183–231. [Google Scholar]
- Moran PAP. Wandering distributions and electrophoretic profile. Theor. Popul. Biol. 1975;8:318–330. doi: 10.1016/0040-5809(75)90049-0. [DOI] [PubMed] [Google Scholar]
- Nakamaru M, Matsuda H, Iwasa Y. The evolution of cooperation in a lattice-structured population. J. Theor. Biol. 1997;184:65–81. doi: 10.1006/jtbi.1996.0243. [DOI] [PubMed] [Google Scholar]
- Nakamaru M, Nogami H, Iwasa Y. Score dependent fertility model for the evolution of cooperation in a lattice. J. Theor. Biol. 1998;194:101–124. doi: 10.1006/jtbi.1998.0750. [DOI] [PubMed] [Google Scholar]
- Nakamaru M, Iwasa Y. The evolution of altruism by costly punishment in lattice structured populations: score dependent viability versus score dependent fertility. Evol. Ecol. Res. 2005;7:853–870. [Google Scholar]
- Nakamaru M, Iwasa Y. The coevolution of altruism and punishment: role of the selfish punisher. J. Theor. Biol. 2006;240:475–488. doi: 10.1016/j.jtbi.2005.10.011. [DOI] [PubMed] [Google Scholar]
- Nowak MA. Evolutionary Dynamics. Harvard University Press; 2006a. [Google Scholar]
- Nowak MA. Five rules for the evolution of cooperation. Science. 2006b;314:1560–1563. doi: 10.1126/science.1133755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowak MA, May RM. Evolutionary games and spatial chaos. Nature. 1992;359:826–829. [Google Scholar]
- Nowak MA, May RM. The spatial dilemmas of evolution. Int. J. Bifurcat. Chaos. 1993;3:35–78. [Google Scholar]
- Nowak MA, May RM. Superinfection and the evolution of parasite virulence. Proc. R. Soc. B. 1994;255:81–89. doi: 10.1098/rspb.1994.0012. [DOI] [PubMed] [Google Scholar]
- Nowak M, Sigmund K. The evolution of stochastic strategies in the prisoner's dilemma. Acta Appl. Math. 1990;20:247–265. [Google Scholar]
- Nowak MA, Sigmund K. Evolutionary dynamics of biological games. Science. 2004;303:793–799. doi: 10.1126/science.1093411. [DOI] [PubMed] [Google Scholar]
- Nowak MA, Sigmund K. Evolution of indirect reciprocity. Nature. 2005;427:1291–1298. doi: 10.1038/nature04131. [DOI] [PubMed] [Google Scholar]
- Nowak MA, Bonhoeffer S, May RM. Spatial games and the maintenance of cooperation. P. Natl. Acad. Sci. U.S.A. 1994;91:4877–4881. doi: 10.1073/pnas.91.11.4877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowak MA, May RM, Phillips RE, Rowland-Jones S, Lalloo DG, McAdam S, Klenerman P, Koppe B, Sigmund K, Bangham CRM, McMichael AJ. Antigenic oscillations and shifting immunodominance in HIV-1 infections. Nature. 1995;375:606–611. doi: 10.1038/375606a0. [DOI] [PubMed] [Google Scholar]
- Nowak MA, Komarova NL, Niyogi P. Computational and evolutionary aspects of language. Nature. 2002;417:611–617. doi: 10.1038/nature00771. [DOI] [PubMed] [Google Scholar]
- Nowak MA, Sasaki A, Taylor C, Fudenberg D. Emergence of cooperation and evolutionary stability in finite populations. Nature. 2004;428:646–650. doi: 10.1038/nature02414. [DOI] [PubMed] [Google Scholar]
- Ohtsuki H, Hauert C, Lieberman E, Nowak MA. A simple rule for the evolution of cooperation on graphs and social networks. Nature. 2006a;441:502–505. doi: 10.1038/nature04605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohtsuki H, Nowak MA. Evolutionary games on cycles. Proc. R. Soc. B. 2006b;273:2249–2256. doi: 10.1098/rspb.2006.3576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohtsuki H, Nowak MA. Direct reciprocity on graphs. J. Theor. Biol. 2007;247:462–470. doi: 10.1016/j.jtbi.2007.03.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohtsuki H, Nowak MA. Evolutionary stability on graphs. J. Theor. Biol. 2008;251:698–707. doi: 10.1016/j.jtbi.2008.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohtsuki H, Pacheco J, Nowak MA. Evolutionary graph theory: breaking the symmetry between interaction and replacement. J. Theor. Biol. 2007;246:681–694. doi: 10.1016/j.jtbi.2007.01.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pacheco JM, Traulsen A, Nowak MA. Active linking in evolutionary games. J. Theor. Biol. 2006;243:437–443. doi: 10.1016/j.jtbi.2006.06.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Queller DC. Kinship, reciprocity and synergism in the evolution of social behaviour: a synthetic model. Nature. 1985;318:366–367. [Google Scholar]
- Riley JG. Evolutionary equilibrium strategies. J. Theor. Biol. 1979;76:109–123. doi: 10.1016/0022-5193(79)90365-5. [DOI] [PubMed] [Google Scholar]
- Rousset F. Genetic structure and selection in subdivided populations. Princeton University Press; 2004. [Google Scholar]
- Rousset F, Billiard S. A theoretical basis for measures of kin selection in subdivided populations: finite populations and localized dispersal. J. Evol. Biol. 2000;13:814–825. [Google Scholar]
- Samuelson L. Evolutionary Games and Equilibrium Selection. MIT Press; Cambridge, MA: 1997. [Google Scholar]
- Santos FC, Santos MD, Pacheco JM. Social diversity promotes the emergence of cooperation in public goods games. Nature. 2008;454:213–216. doi: 10.1038/nature06940. [DOI] [PubMed] [Google Scholar]
- Schaffer M. Evolutionarily stable strategies for a finite population and variable contest size. J. Theor. Biol. 1988;132:469–478. doi: 10.1016/s0022-5193(88)80085-7. [DOI] [PubMed] [Google Scholar]
- Seger J. Kinship and covariance. J. Theor. Biol. 1981;91:191–213. doi: 10.1016/0022-5193(81)90380-5. [DOI] [PubMed] [Google Scholar]
- Szabó G, Antal T, Szabó P, Droz M. Spatial evolutionary prisoner's dilemma game with three strategies and external constraints. Phys. Rev. E. 2000;62:1095–1103. doi: 10.1103/physreve.62.1095. [DOI] [PubMed] [Google Scholar]
- Szabó G, Fath G. Evolutionary games on graphs. Phys. Rep. 2007;446:97–216. [Google Scholar]
- Szabó G, Tőke C. Evolutionary prisoner's dilemma game on a square lattice. Phys. Rev. E. 1998;58:69–73. [Google Scholar]
- Tarnita CE, Antal T, Ohtsuki H, Nowak MA. Evolutionary dynamics in set structured populations. 2009 doi: 10.1073/pnas.0903019106. Under submission. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor C, Nowak MA. Transforming the dilemma. Evolution. 2007;61:2281–2292. doi: 10.1111/j.1558-5646.2007.00196.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor C, Fudenberg D, Sasaki A, Nowak MA. Evolutionary game dynamics in finite populations. B. Math. Biol. 2004;66:1621–1644. doi: 10.1016/j.bulm.2004.03.004. [DOI] [PubMed] [Google Scholar]
- Taylor PD. Altruism in viscous populations-an inclusive fitness model. Evol. Ecol. 1992a;6:352–353. [Google Scholar]
- Taylor PD. Inclusive fitness in a homogeneous environment. Proc. R. Soc. B. 1992b;249:299–302. [Google Scholar]
- Taylor PD, Frank S. How to make a kin selection argument. J. Theor. Biol. 1996;180:27–37. doi: 10.1006/jtbi.1996.0075. [DOI] [PubMed] [Google Scholar]
- Taylor PD, Jonker LB. Evolutionary stable strategies and game dynamics. Math. Biosci. 1978;40:145–156. [Google Scholar]
- Taylor PD, Irwin A, Day T. Inclusive fitness in finite deme-structured and stepping-stone populations. Selection. 2000;1:83–93. [Google Scholar]
- Taylor PD, Day T, Wild G. Evolution of cooperation in a finite homogeneous graph. Nature. 2007a;447:469–472. doi: 10.1038/nature05784. [DOI] [PubMed] [Google Scholar]
- Taylor PD, Day T, Wild G. From inclusive fitness to fixation probability in homogeneous structured populations. J. Theor. Biol. 2007b;249:101–110. doi: 10.1016/j.jtbi.2007.07.006. [DOI] [PubMed] [Google Scholar]
- Traulsen A, Pacheco JM, Imhof L. Stochasticity and evolutionary stability. Phys. Rev. E. 2006;74:021905. doi: 10.1103/PhysRevE.74.021905. [DOI] [PubMed] [Google Scholar]
- Traulsen A, Nowak MA. Evolution of cooperation by multi-level selection. P. Natl. Acad. Sci. USA. 2006;103:10952–10955. doi: 10.1073/pnas.0602530103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Traulsen A, Shoresh N, Nowak MA. Analytical results for individual and group selection of any intensity. B. Math. Biol. 2008;70:1410–1424. doi: 10.1007/s11538-008-9305-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trivers RL. The evolution of reciprocal altruism. Q. Rev. Biol. 1971;46:35–57. [Google Scholar]
- Turner PE, Chao L. Prisoner's dilemma in an RNA virus. Nature. 1999;398:441–443. doi: 10.1038/18913. [DOI] [PubMed] [Google Scholar]
- van Baalen M, Rand DA. The unit of selection in viscous populations and the evolution of altruism. J. Theor. Biol. 1998;193:631–648. doi: 10.1006/jtbi.1998.0730. [DOI] [PubMed] [Google Scholar]
- von Neumann J, Morgenstern O. Theory of Games and Economic Behavior. Princeton University Press; Princeton, NJ: 1944. [Google Scholar]
- Wild G, Traulsen A. The different limits of weak selection and the evolutionary dynamics of finite populations. J. Theor. Biol. 2007;247:382–390. doi: 10.1016/j.jtbi.2007.03.015. [DOI] [PubMed] [Google Scholar]
- Weibull JW. Evolutionary Game Theory. MIT Press; Cambridge, MA: 1995. [Google Scholar]
- Yamamura N, Higashi M, Behera N, Wakano J. Evolution of mutualism through spatial effects. J. Theor. Biol. 2004;226:421–428. doi: 10.1016/j.jtbi.2003.09.016. [DOI] [PubMed] [Google Scholar]
- Zeeman EC. Population dynamics from game theory. In: Nitecki ZH, Robinson RC, editors. Proceedings of an International Conference on Global Theory of Dynamical Systems; Lecture Notes in Mathematics; Springer, Berlin. 1980. [Google Scholar]





