How can we learn efficiently to act optimally and flexibly?

When we walk to a shop in a town, we want to get there in the shortest time. However, finding the shortest route in a big city is quite tricky, because there are countless possible routes and the time taken for each segment of a route is uncertain. This is a typical problem of discrete optimal control, which aims to find the optimal sequence of actions to minimize the total cost from any given state to the goal state. The problems of optimal control are ubiquitous, from animal foraging to national economic policy, and there have been lots of theoretical studies on the topic. However, solving an optimal control problem requires a huge amount of computations except for limited cases. In this issue of PNAS, Emanuel Todorov (1) presents a refreshingly new approach in optimal control based on a novel insight as to the duality of optimal control and statistical inference.

Thestandard strategy in optimal control is to identify the “cost-to-go” function for each state, such as how much time you need from a street corner to your office. If such a cost-to-go function is available for all of the states, we can find the best route by simply following the nearest state with the lowest cost-to-go. More specifically, we use the formulation

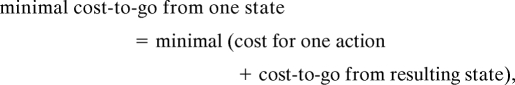which is known as the “Bellman equation” (2). When there are n possible states, like n corners in your town, we have a system of n Bellman equations to solve. One headache in solving Bellman equations is the “minimal” operation. When there are many possible resulting states, because of randomness in state transition or choices of many possible actions, finding the minimal cost-to-go is not a trivial job. An easy solution has been known only for the case when the state transition is linear and the cost is a quadratic (second-order) function of the action and the state (3).

What is remarkable in Todorov's proposal (1) is a wild reformulation of “action” and its cost. He recognizes the action as tweaking of the probability of the subsequent state and defines the action cost by the deviation of the tweaked state probability distribution from that with no action at all, called “passive dynamics.” Specifically, he takes so-called Kullback–Leibler divergence, which is the expected logarithmic ratio between the state distributions with an action and with passive dynamics. And in this particular setting, the minimization in the Bellman equation is achieved by reweighting the state distribution under the passive dynamics by the exponential of the sign-flipped cost-to-go function. This analytical form of minimization dramatically reduces the labor of solving the Bellman equation. Indeed, when we define the exponential of the sign-flipped cost-to-go function as the “desirability function,” the Bellman equation becomes

which is a linear equation. With the knowledge of the cost at each state and the transition probability between the states under passive dynamics, the desirability function is given as an eigenvector of a matrix, which can be readily computed by common numerical software. Once the desirability function is derived, the optimal action is given by reweighting the state transition probability under passive dynamics in proportion to their desirability. Fig. 1 shows examples for desirability function and optimal actions in a simple shortest-time problem on a street grid.

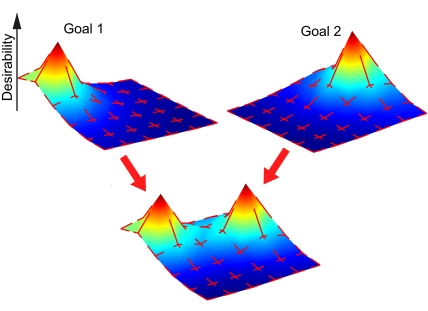
Fig. 1.

Examples of desirability function in a task of city block navigation. An agent gains a reward (negative cost) of 1 by reaching to a particular corner (goal state), but pays a state cost of 0.1 for being in a nongoal corner and an action cost for deviating from random walk to one of adjacent corners. (Upper) Two examples of desirability functions with 2 different goal states. The desirability function has a peak at the goal state and serves as a guiding signal for navigation. The red segments on each corner show the optimal action, with the length proportional to the optimal probability of moving to that direction. (Lower) Shown is the desirability function when the reward is given at either goal position. In this case, the desirability function is simply the sum of the 2 desirability functions and the optimal action probability is the average of the 2 optimal actions probabilities weighted by the levels of 2 desirability functions at a given state. This compositionality allows flexible combination and selection of preacquired optimal actions depending on the given goal and the present state.

One question is how widely this new formulation of action and action costs applies to real-world problems. In the article in this issue of PNAS (1) and related papers (4–6), Todorov has demonstrated that this principle can be extended to continuous-state, continuous-time optimal control problems and can be applied to a wide variety of tasks, including finding the shortest path in complex graphs, optimizing internet packet routing, and driving up a steep hill by an underpowered car.

Another issue is how to learn to act. In the standard formulation of optimal control, the cost or reward for being in a state, the cost for performing an action, and the probability of state transition depending on the action are explicitly given. However, in many realistic problems, such costs and transitions are not known a priori. Thus, we have to identify them before applying optimal control theory or take a short cut to learn to act based on actual experiences of costs and transitions. The latter way is known as reinforcement learning (7, 8). In Todorov's formulation (1), it is also possible to directly learn the desirability function without explicit knowledge of the costs and transitions, which he calls “Z-learning.” The simulation result suggests that convergence Z-learning is considerably faster than the popular reinforcement learning algorithm called Q-learning (9). However, one problem with Z-learning is to find out the actual method of tweaking the state distribution as directed by the desirability function. It may be trivial in tasks like walking on grid-like streets, but may require another level of learning, for example, for shifting the body posture by stimulating hundreds of muscles.

Having a linear form of Bellman equation brings us another merit of compositionality of optimal actions (5). When there are two fairly good goals to achieve, what will be your optimal action? When the two goals are compatible, it may be a good idea to mix the actions for the two, but when they are far apart, you should make a crisp choice of which goal to aim at. For the linear form of Bellman equation, the boundary condition of the desirability function is specified by the cost at the goal states. Thus, once we calculate the desirability functions from boundary conditions for a number of standard goals, we can derive the desirability function for a new goal if its cost or reward is expressed as a weighted combination of those for standard goals. The optimal action for the new composite goal takes an intuitive form: the optimal actions for component goals are weighted in proportion to the weights for the goals and the desirability at the present state as shown in Fig. 1 Lower. This desirability-weighted combination gives an elegant theoretical account of when actions can be mixed or should be crisply selected; it depends on the overlap of the desirability functions.

It is noteworthy that this new proposal (1) came from a researcher who has been working on the theory and experiments of human movement control (10, 11), where acting swiftly in the face of the delay and noise in sensory feedback poses a major challenge. This new formulation of optimal control is backed by a new insight of the duality between action and perception (6). In the world with noisy or delayed sensory inputs, finding the real present state of the world is not a trivial task. In the continuous domains, the Kalman filter (12) has been known as an optimal state estimator under linear dynamics, quadratic cost, and Gaussian noise, called the LQG setting. In the discrete domain, under the framework of hidden Markov models, many algorithms for state estimation have been developed in the field of machine learning research (13). It was almost a half-century ago when Kalman (12) pointed out the similarity between the equation for optimal state estimation by Kalman filter and the Bellman equation for optimal action in the LQG setting. Although this duality has been recognized as sheer coincidence or just theoretical beauty, studies in the brain mechanisms for perception and control led Todorov (6) to find the general duality between the computations for optimal action and optimal perception. The unusual definition of action cost by Kullback–Leibler divergence in the new control scheme turns out to be quite natural when we recognize its duality with optimal state estimation in hidden Markov models.

With the favorable features of efficient solution and flexible combination, it is tempting to imagine if something similar could be happening in our brain. It has been proposed that human perception can be recognized as the process of Bayesian inference (14) and that they could be carried out in the neural circuit in the cerebral cortex (15, 16). By noting the duality between the computations for perception and action, it might be possible that, while the optimal sensory estimation is carried out in the sensory cortex, optimal control is implemented in the motor cortex or the frontal cortex. Neural activities for expected rewards, related to the cost-to-go function, have been found in the cerebral cortex and the subcortical areas including the striatum and the amygdala (8, 17–19). It will be interesting to test whether any neural representation of desirability function can be found anywhere in the brain. It is also interesting to think about whether off-line solution, like iterative computation of eigenvectors, and on-line solution, like Z-learning, can be implemented in the cortical or subcortical networks in the brain. There indeed is evidence that motor learning has both on-line and off-line components, the latter of which develops during resting or sleeping periods (20). It should also be possible to test whether human subjects or animals use desirability-weighted mixture and selection of actions in reaching for composite targets.

The series of works by Todorov (1, 4–6) is a prime example of a novel insight gained in the crossing frontlines of multidisciplinary research. It will have a wide impact on both theoretical and biological studies of action and perception.